Spectral Absorption from Two-view Hyperspectral Images
Kenta Kageyama, Ryo Kawahara
a
and Takahiro Okabe
b
Department of Artificial Intelligence, Kyushu Institute of Technology,
680-4 Kawazu, Iizuka, Fukuoka 820-8502, Japan
Keywords:
Spectral Imaging, Passive Measurement, Spectral Absorption Coefficient, Matrix Factorization.
Abstract:
When light passes through a liquid, its energy is attenuated due to absorption. The attenuation depends both
on the spectral absorption coefficient of a liquid and on the optical path length of light, and is described by the
Lambert-Beer law. The spectral absorption coefficients of liquids are often unknown in real-world applications
and to be measured/estimated in advance, because they depend not only on liquid media themselves but also
on dissolved materials. In this paper, we propose a method for estimating the spectral absorption coefficient
of a liquid only from two-view hyperspectral images of an under-liquid scene taken from the outside of the
liquid in a passive and non-contact manner. Specifically, we show that the estimation results in Non-negative
Matrix Factorization (NMF) because both the objective variables and the explanatory variables are all non-
negative, and then study the ambiguity in matrix factorization. We conducted a number of experiments using
real hyperspectral images, and confirmed that our method works well and is useful for reconstructing shape of
an under-liquid scene.
1 INTRODUCTION
When light passes through a liquid, a part of the light
is often absorbed and scattered by the liquid, and then
its energy is attenuated in general. For transparent
liquids with negligible scattering, it is known that the
attenuation of light energy due to absorption depends
both on the spectral absorption coefficient of a liquid
and on the optical path length of light in the liquid,
and is described by the Lambert-Beer law (Reinhard
et al., 2008).
The absorption due to liquid is an important clue
to solving computer vision problems; shape recov-
ery of underwater objects (Asano et al., 2016; Murai
et al., 2019; Takatani et al., 2021; Kuo et al., 2021)
and liquid detection on unknown surfaces (Wang
et al., 2021; Wang and Okabe, 2021) are achieved un-
der the assumption that the spectral absorption coeffi-
cients of liquids are known. Unfortunately, however,
the spectral absorption coefficientsof liquids are often
unknown in real-world applications and to be mea-
sured/estimated in advance, because they depend not
only on liquid media themselves but also on dissolved
materials.
Conventionally, the spectral absorption coeffi-
a
https://orcid.org/0000-0002-9819-3634
b
https://orcid.org/0000-0002-2183-7112
cients of liquids are measured via absorption spec-
troscopy (Jones and Kao, 1969; Kao and Davies,
1968) in an active and contact manner. Specifically,
when the Spectral Power Distributions (SPDs) of the
light both before and after transmitting a liquid of in-
terest are known, its spectral absorption coefficient is
derived from the logarithm of the ratio of those SPDs
on the basis of the Lambert-Beer law. In the above
computer vision problems with hyperspectral images
of a scene, however, the SPD of the light before trans-
mitting a liquid, i.e. the spectral radiance on an object
surface under the liquid is unknown.
Accordingly, we propose a method for estimating
the spectral absorption coefficients of liquids in a pas-
sive and non-contact manner. Our proposed method
estimates the spectral absorption coefficient of a liq-
uid only from two-view hyperspectral images of an
under-liquid scene taken from the outside of the liq-
uid. We make use of the fact that the absorption co-
efficient depends on the wavelengths but the optical
path length depends on the scene points. Specifically,
our method estimates the spectral absorption coeffi-
cient on the basis of Non-negative Matrix Factoriza-
tion (NMF) (Berry et al., 2007), because both the
objective variables described by the observed spec-
tral radiance values and the explanatory variables de-
scribed by the spectral absorption coefficients, optical
path lengths, and Fresnel terms are all non-negative.
Kageyama, K., Kawahara, R. and Okabe, T.
Spectral Absorption from Two-view Hyperspectral Images.
DOI: 10.5220/0010917600003124
In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 4: VISAPP, pages
715-721
ISBN: 978-989-758-555-5; ISSN: 2184-4321
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
715

Moreover, we study the ambiguity of our proposed
method based on matrix factorization. We show that
our method using only two-view hyperspectral im-
ages can estimate the spectral absorption coefficient
up to a scale and an offset. We also show that the
estimated spectral absorption coefficient is useful for
shape recovery even though it has the ambiguity; we
show that the shape of an object surface under liquid
is recovered up to a scale.
The main contributions of this paper are threefold.
First, we propose a novel method for estimating the
spectral absorption coefficient of a liquid in a pas-
sive and non-contact manner. The proposed method
achievesthe estimation of a spectral absorption coeffi-
cient only from two-view hyperspectral images with-
out requiring the SPD of the light before transmitting
a liquid. Second, we show that our method can esti-
mate the spectral absorption coefficient up to a scale
and an offset. In addition, we show that the spectral
absorption coefficient with the ambiguity is useful for
under-liquid shape recovery. Third, we conducted a
number of experiments using real hyperspectral im-
ages, and confirmed that our method works well and
is useful for reconstructing shape of an under-liquid
scene.
2 RELATED WORK
2.1 Absorption Measurement
Absorption spectroscopy (Jones and Kao, 1969; Kao
and Davies, 1968) is a classical method for mea-
suring the spectral absorption coefficient of a liquid
of interest in an active and contact manner. When
the SPDs of the light both before and after trans-
mitting the liquid are known, its spectral absorption
coefficient is derived from the logarithm of the ra-
tio of those SPDs on the basis of the Lambert-Beer
law (Reinhard et al., 2008). In the computer vision
problems with hyperspectral images of a scene such
as shape recovery (Asano et al., 2016; Murai et al.,
2019; Takatani et al., 2021; Kuo et al., 2021) and liq-
uid detection (Wang et al., 2021; Wang and Okabe,
2021), however, the SPD of the light before transmit-
ting a liquid, i.e. the spectral radiance on an object
surface under the liquid is unknown. Therefore, we
achieve the estimation of the spectral absorption co-
efficient of a liquid only from two-view hyperspectral
images without requiring the SPD of the light before
transmitting the liquid.
In the community of computer vision, the three-
band (RGB) attenuation coefficient, i.e. the sum-
mation of the absorption and scattering coefficients
of a liquid is often measured or estimated. It is
known that the attenuation coefficient can be esti-
mated from an image of a known calibration target at
known distances (Tsiotsios et al., 2014; Murez et al.,
2015; Akkaynak and Treibitz, 2019), but such estima-
tion requires external hardware and distance measure-
ment. The attenuation/absorption coefficient can be
estimated from multiple images of the same object lo-
cated at different distances; the distances are assumed
to be known (Yamashita et al., 2007), or measured by
a sonar (Kaeli et al., 2011), or recovered via struc-
ture from motion (Jordt-Sedlazeck and Koch, 2013;
Bryson et al., 2016). In contrast, our proposed method
estimates the spectral absorption coefficientonly from
two-view hyperspectral images with neither a known
calibration target nor know distances nor geometric
calibration.
2.2 Computer Vision Applications
The absorption due to liquid is an important clue to
shape recovery. Asano et al. (Asano et al., 2016)
make use of the fact that water absorbs Near InfraRed
(NIR) light (Curcio and Petty, 1951), and show that
the shape (depth) of an under-water scene can be
recovered from two single-view images at different
wavelengths in NIR range. Takatani et al. (Takatani
et al., 2021) extends the above method by using an
event-based camera with temporally modulated illu-
mination, and then achieve robust shape reconstruc-
tion in water. Murai et al. (Murai et al., 2019) re-
construct both the surface normals and depth of a dy-
namic object in water by using multi-directional NIR
lighting. Furthermore, Kuo et al. (Kuo et al., 2021)
achieve shape reconstruction of a dynamic and non-
rigid object in water.
The absorption due to liquid is useful also for liq-
uid detection. Wang et al. (Wang et al., 2021) make
use of the fact that the absorption due to water de-
creases the apparent spectral reflectance on an object
surface. They achieve per-pixel water detection on
surfaces with unknown reflectance by using the low-
dimensional linear model of spectral reflectance from
visible to NIR wavelengths. Further, Wang and Ok-
abe (Wang and Okabe, 2021) extends their method to
water and oil detection on unknown surfaces by si-
multaneously estimating the types of liquids and op-
tical path lengths.
The above applications assume that the spectral
absorption coefficients of liquids of interest (water
and oils) are known. Unfortunately, however, the
spectral absorption coefficients of liquids are often
unknown in real-world applications and to be mea-
sured/estimated in advance. The spectral absorption
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
716

Figure 1: The illustration of our setup for spectral absorp-
tion recovery; our proposed method uses two-view hyper-
spectral images of an under-liquid scene taken from the out-
side of the liquid.
coefficients estimated by using our proposed method
in a passive and non-contact manner are effective for
those computer vision applications.
3 PROPOSED METHOD
We propose a method for estimating the spectral ab-
sorption coefficient of a liquid of interest in a passive
and non-contact manner. As shown in Figure 1, our
proposed method uses two-view hyperspectral images
of an under-liquid scene taken from the outside of the
liquid. We assume that the liquid is spatially uniform
and transparent with negligible scattering and that the
attenuation of light energydue to absorptionobeys the
Lambert-Beer law.
When we observe a point x
x
x on an under-liquid ob-
ject surface from the v-th (v = 1, 2) viewpoint, the
spectral radiance i
v
(x
x
x,λ) of the point x
x
x at the wave-
length λ seen through the liquid is given by
i
v
(x
x
x,λ) = f
v
(x
x
x)r
v
(x
x
x,λ)e
−α(λ)l
v
(x
x
x)
(1)
according to the Lambert-Beer law (Reinhard et al.,
2008). Here, f
v
(x
x
x), r
v
(x
x
x,λ), α(λ), and l
v
(x
x
x) are the
Fresnel term
1
, the spectral radiance of the point be-
fore transmitting the liquid, the spectral absorption
1
We assume that the Fresnel term is independent of the
wavelength of light. Actually, the Fresnel term depends on
the wavelength via the refractive index, but the refractive in-
dexes of liquids such as water are almost constant for visible
wavelengths.
coefficient of the liquid, and the optical path length
in the liquid.
Taking the logarithm of the ratio between i
1
(x
x
x,λ)
and i
2
(x
x
x,λ), we obtain
ln
i
1
(x
x
x,λ)
i
2
(x
x
x,λ)
= ln
f
1
(x
x
x)r
1
(x
x
x,λ)e
−α(λ)l
1
(x
x
x)
f
2
(x
x
x)r
2
(x
x
x,λ)e
−α(λ)l
2
(x
x
x)
= α(λ){l
2
(x
x
x) − l
1
(x
x
x)} + ln
f
1
(x
x
x)
f
2
(x
x
x)
. (2)
Here, we assume that the under-liquid object surface
obeys the Lambert model, and therefore the spec-
tral radiance is independent of viewpoints: r
1
(x
x
x,λ) =
r
2
(x
x
x,λ).
The above equation holds for the corresponding
point x
x
x
p
(p = 1, 2,3,...,P) between the two-view
hyperspectral images with the wavelength λ
w
(w =
1,2,3,...,W). Then, we can rewrite eq.(2) by using
matrices as
S
S
S = A
A
AB
B
B. (3)
Here, the W × P observation matrix S
S
S, the W × 2 ma-
trix A
A
A depending on the wavelengths, and the 2 × P
matrix B
B
B depending on the scene points are given by
S
S
S =




s
11
s
12
··· s
1P
s
21
s
22
··· s
2P
.
.
.
.
.
.
.
.
.
.
.
.
s
W1
s
W2
··· s
WP




, (4)
A
A
A =




α
1
1
α
2
1
.
.
.
.
.
.
α
W
1




, (5)
B
B
B =

l
′
1
l
′
2
··· l
′
P
f
′
1
f
′
2
··· f
′
P

, (6)
where s
wp
= ln{i
1
(x
x
x
p
,λ
w
)/i
2
(x
x
x
p
,λ
w
)}, α
w
= α(λ
w
),
l
′
p
= l
2
(x
x
x
p
) − l
1
(x
x
x
p
), and f
′
p
= ln{ f
1
(x
x
x
p
)/ f
2
(x
x
x
p
)}.
When we take the first/second images from
deep/shallow angles as shown in Figure 1, we can as-
sume that i
1
(x
x
x
p
,λ
w
) ≥ i
2
(x
x
x
p
,λ
w
), l
2
(x
x
x
p
) ≥ l
1
(x
x
x
p
), and
f
1
(x
x
x
p
) ≥ f
2
(x
x
x
2
). Then, all the elements in the matri-
ces S
S
S, A
A
A, and B
B
B in eq.(3) are non-negative. Therefore,
the estimation of the spectral absorption coefficient
results in NMF: factorizing the non-negative obser-
vation matrix S
S
S into the product of the non-negative
matrices A
A
A and B
B
B. Hence, our method can estimate
not only the spectral absorption coefficient α(λ
w
) but
also the difference of the optical path lengths l
2
(x
x
x
p
)−
l
1
(x
x
x
p
) and the ratio of the Fresnel term f
1
(x
x
x
p
)/ f
2
(x
x
x
p
)
as byproducts.
In our current implementation, we factorize the
observation matrix via alternative least squares (Berry
Spectral Absorption from Two-view Hyperspectral Images
717

et al., 2007). Specifically, we minimize the sum of
squares
∑
w,p
(s
wp
− α
w
l
′
p
− f
′
p
)
2
(7)
with respect to the non-negative unknown variable
α
w
, l
′
p
, and f
′
p
. We give random initial values for
{l
′
p
, f
′
p
}, and then iteratively fix one set of variables
({l
′
p
, f
′
p
} or α
w
) and update the other set of variables
via least squares and vice versa.
4 AMBIGUITY ANALYSIS
4.1 Ambiguity in Matrix Factorization
In general, matrix factorization has ambiguity. Since
our proposed method results in the factorization of the
W × P observation matrix S
S
S into the W × 2 matrix A
A
A
and the 2 × P matrix B
B
B, the ambiguity is represented
by using a 2× 2 arbitrary invertible matrix C
C
C as
S
S
S = A
A
AB
B
B = A
A
AC
C
CC
C
C
−1
B
B
B = (A
A
AC
C
C)(C
C
C
−1
B
B
B). (8)
In other words, the matrices {A
A
A,B
B
B} and the matrices
{(A
A
AC
C
C), (C
C
C
−1
B
B
B)} yield the same matrix S
S
S.
Then, from eq.(5), the relationship between the
spectral absorption coefficient estimated by our pro-
posed method
ˆ
α
w
=
ˆ
α(λ
w
) and its ground truth α
w
=
α(λ
w
) is given by




ˆ
α
1
1
ˆ
α
2
1
.
.
.
.
.
.
ˆ
α
W
1




=




α
1
1
α
2
1
.
.
.
.
.
.
α
W
1





c
11
c
12
c
21
c
22

=




c
11
α
1
+ c
21
c
12
α
1
+ c
22
c
11
α
2
+ c
21
c
12
α
2
+ c
22
.
.
.
.
.
.
c
11
α
W
+ c
21
c
12
α
W
+ c
22




.(9)
Here, c
ij
is the element of the matrix C
C
C at the i-th row
and j-th column.
We can derive that c
12
= 0 and c
22
= 1 from the
above equation, because the spectral absorption coef-
ficients are not constant with respect to wavelengths
in general. Therefore, the ambiguity of our proposed
method is represented by the 2×2 invertible matrixC
C
C
defined by
C
C
C =

c
11
0
c
21
1

. (10)
Thus, our method can estimate the spectral absorp-
tion coefficient up to an unknown scale c
11
and an
unknown offset c
21
:
ˆ
α(λ) = c
11
α(λ) + c
21
. (11)
4.2 Ambiguity in Shape Recovery
Asano et al. (Asano et al., 2016) show that the shape
(depth) of an under-water scene can be recovered
from two single-view images at different wavelengths
λ
1
and λ
2
. Specifically, the depth l(x
x
x) of a surface
point x
x
x is described as
l(x
x
x) =
1
2{α(λ
2
) − α(λ
1
)}
ln
i(x
x
x,λ
1
)
i(x
x
x,λ
2
)
, (12)
where i(x
x
x,λ
1
) and i(x
x
x,λ
2
) are the spectral radiance
values seen through water with the two wavelengths.
Therefore, the depth of an under-liquid (under-water
in this case) scene can be recovered if the spectral ab-
sorption coefficient of the liquid is known.
We show that the spectral absorption coefficient
estimated by our proposed method can be used for re-
constructing the shape of an under-liquid scene. Re-
placing the ground truth spectral absorption coeffi-
cient in eq.(12) with the estimated one in eq.(11), the
estimated depth
ˆ
l(x
x
x) is given by
ˆ
l(x
x
x) =
1
2{
ˆ
α(λ
2
) −
ˆ
α(λ
1
)}
ln
i(x
x
x,λ
1
)
i(x
x
x,λ
2
)
=
1
c
11
l(x
x
x). (13)
This is because the offset c
21
in the denominator is
canceled out due to subtraction. Hence, the shape of
an under-liquid scene can be recovered up to an un-
known scale.
5 EXPERIMENTS
5.1 Setup
To confirm the effectiveness of our proposed method,
we conducted a number of experiments using real
hyperspectral images. We tested three scenes in an
acrylic tank: (A) a textured board in dilute methy-
lene blue, (B) gravel in dilute methylene blue, and (C)
gravel in dilute soy sauce. We captured those scenes
from the outside of the tank as shown in Figure 2. We
used a halogen lamp and a hyperspectral camera from
EBA Japan that can capture the range of near UV (380
nm) to near IR (1,000 nm) with the interval of 5 nm,
i.e. 125 spectral channels in total.
5.2 Spectral Absorption Coefficient
First, we studied the performance of our proposed
method by comparing the estimated spectral absorp-
tion coefficients with their ground truths. We mea-
sured the ground truth of the spectral absorption coef-
ficient of a liquid from the hyperspectral images of a
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
718

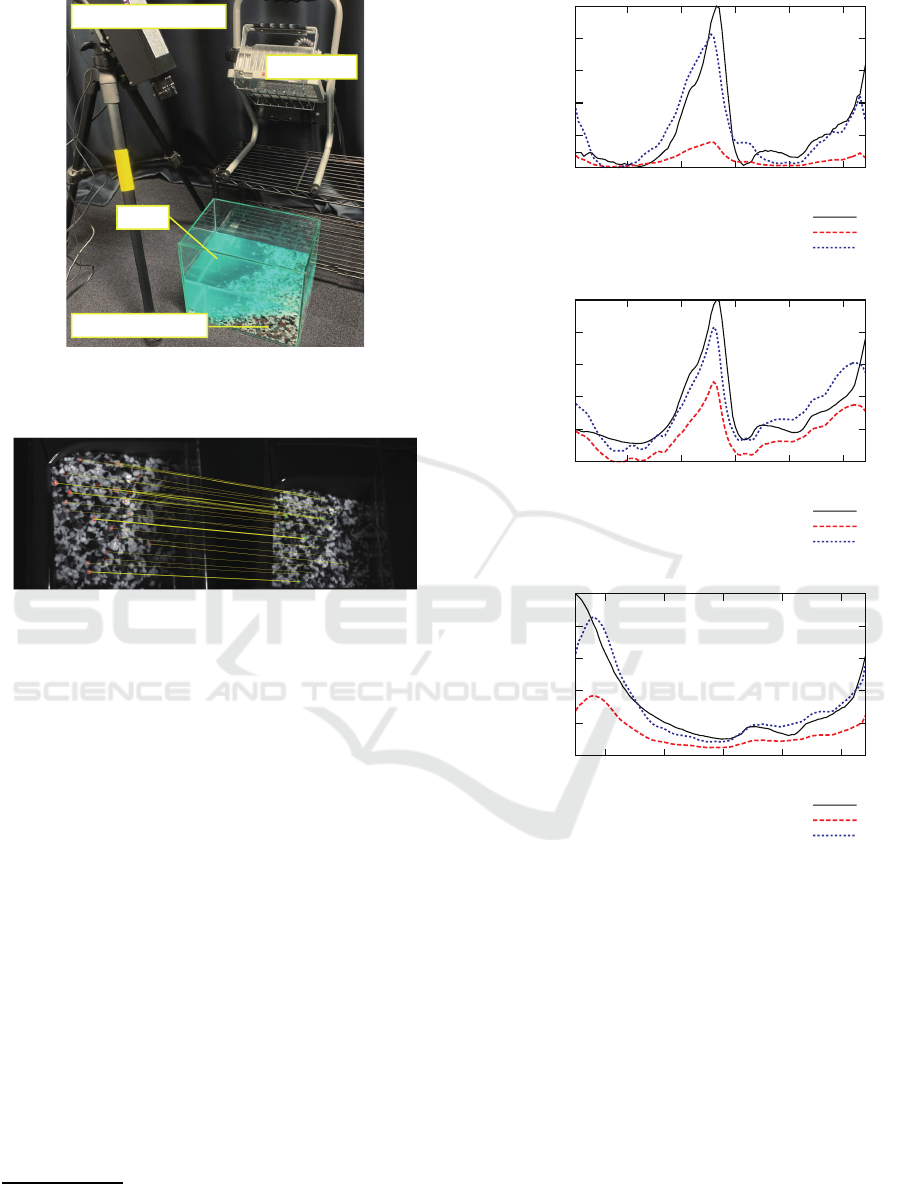
Hyperspectral camera
Light source
Liquid
Under-liquid scene
Figure 2: Our setup for spectral absorption recovery; we
captured an under-liquid scene in an acrylic tank from the
outside by using a hyperspectral camera.
Figure 3: The two-view images of (B) the gravel in dilute
methylene blue at 530 nm and the corresponding points be-
tween them.
target object seen through the liquid with known and
variable depths.
As described in Section 3, our proposed method
requires the correspondence between two hyperspec-
tral images taken from different viewpoints. In our
current implementation, we used MSER (Maximally
Stable Extremal Regions) features (Matas et al., 2004)
in MATLAB in order to achieve the correspondence
between those images. Figure 3 shows the two-view
images of (B) the gravel in dilute methylene blue at
530 nm and the corresponding points between them.
In general, the minimization of the sum of squares in
eq.(7) depends on the random initial values. In our
current implementation, we tested 100 sets of random
initial values, and found out the best solution with the
minimum sum of squares.
Figure 4 shows the spectral absorption coeffi-
cients; (a), (b), and (c) show the results of the three
scenes (A), (B), and (C). The black solid line, the
red dashed line, and the blue dotted line stand for the
ground truth
2
, the estimated one with the ambiguity,
2
We normalize the ground truth of a spectral absorption
coefficient so that its maximum value with respect to wave-
length is equal to 1.
0
0.2
0.4
0.6
0.8
1
500 600 700 800 900
Absorption Coefficient
Wavelength
ground truth
our method with ambiguity
our method w/o ambiguity
(a)
0
0.2
0.4
0.6
0.8
1
500 600 700 800 900
Absorption Coefficient
Wavelength
ground truth
our method with ambiguity
our method w/o ambiguity
(b)
0
0.2
0.4
0.6
0.8
1
500 600 700 800 900
Absorption Coefficient
Wavelength
ground truth
our method with ambiguity
our method w/o ambiguity
(c)
Figure 4: The spectral absorption coefficients; (a), (b), and
(c) show the results of the three scenes (A), (B), and (C).
The black solid line, the red dashed line, and the blue dotted
line stand for the ground truth, the estimated one with and
without the ambiguity.
and the estimated one without the ambiguity, i.e. with
the optimal scale and offset respectively. Since our
proposed method can estimate the spectral absorption
coefficient up to a scale and an offset, we supposed
that the ground truth is known and computed the opti-
mal ones via least squares for comparison. The range
of the wavelength within which the spectral absorp-
tion coefficient is estimated is different; from 405 nm
to 940 nm for the dilute methylene blue and from 450
nm to 940 nm for the dilute soy sauce. This is because
Spectral Absorption from Two-view Hyperspectral Images
719

(a)
(b)
Figure 5: The pseudo color images (left) and the recon-
structed depth maps (right) within the yellow boxes; (a) and
(b) show the results of the two scenes (A) and (B).
we could not estimate the spectral absorption coeffi-
cient at some wavelengths where the observed spec-
tral radiance values are too small due to weak light
source and/or strong absorption.
Comparing the ground truths and the estimated
absorption coefficientswith the ambiguity in Figure 4,
we can see that the estimated ones capture the proper-
ties of the liquids; the dilute methylene blue absorbs
red and green wavelengths and looks bluish
3
, and the
dilute soy sauce absorbs blue and green wavelengths
and looks reddish. Since both the liquids are diluted
by water, we can see the absorption due to water in
NIR wavelengths. Then, we can see that the esti-
mated absorption coefficients with the optimal scale
and offset are almost the same as the ground truths.
The RMS (Root-Mean-Square) errors of the spectral
absorption coefficients are 0.108, 0.108, and 0.070
for (a) the first dilute methylene blue, (b) the second
dilute methylene blue, and (c) the dilute soy sauce
respectively. Those results show that our method
can accurately estimate the spectral absorption coeffi-
cients up to a scale and an offset.
3
The spectral absorption coefficients of the methylene
blue in (a) and (b) are different because their concentrations
are different.
5.3 Application to Shape Recovery
Second, we studied the effectiveness of the estimated
spectral absorption coefficient with the ambiguity for
under-liquid shape recovery. According to Asano et
al. (Asano et al., 2016), we placed the hyperspec-
tral camera and the light source at almost the same
location. In addition, their method assumes that, at
two wavelengths λ
1
and λ
2
in eq.(13), the spectral re-
flectances are almost the same, but the spectral ab-
sorption coefficients are significantly different. It is
known that the spectral reflectances of most materi-
als are almost constant for NIR wavelengths (Choe
et al., 2016). Therefore, we chose the two wave-
lengths λ
1
= 825 nm and λ
2
= 900 nm where the
spectral absorption coefficients are significantly dif-
ferent as shown in Figure 4.
Figure 5 shows the pseudo color images (left) and
the reconstructed depth maps (right) within the yel-
low boxes; (a) and (b) show the results of the two
scenes (A) and (B). Here, the color bar shows the rela-
tionship between the relative depth and the color from
shallow (yellow) to deep (blue). The white pixels in
those depth maps stand for the pixels where the re-
flectance is low and then the radiance values are too
small to estimate the depth. We can see that the recon-
structed depth maps qualitatively show the effective-
ness of the estimated spectral absorption coefficient
with the ambiguity; the depth of the textured board
increases linearly from the top to the bottom, and the
depth of gravel gradually increases from the top left
to the bottom right in the images.
6 CONCLUSION AND FUTURE
WORK
In this paper, we proposed a novel method for es-
timating the spectral absorption coefficient of a liq-
uid only from two-view hyperspectral images of an
under-liquid scene taken from the outside of the liq-
uid in a passive and non-contact manner. Specifically,
we showed that the estimation results in NMF, and
then studied the ambiguity in matrix factorization. We
conducted a number of experiments using real hy-
perspectral images, and confirmed that our method
works well and is useful for reconstructing shape of
an under-liquid scene.
Our future work includes the extension to scatter-
ing medium: the estimation of absorption and scat-
tering coefficients. The integration of spectral imag-
ing with polarimetric imaging (Schechner and Karpel,
2004) and the use of the prior knowledge with re-
spect to attenuation/absorption coefficients (Akkay-
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
720

nak et al., 2017) are other directions of our fu-
ture study. In addition, the integration of camera-
based spectral imaging with illumination-based spec-
tral imaging (Kitahara et al., 2015; Kobayashi and
Okabe, 2016; Wang and Okabe, 2017; Torii et al.,
2019; Koyamatsu et al., 2019) is an interesting direc-
tion to be addressed.
ACKNOWLEDGEMENTS
This work was supported by JSPS KAKENHI Grant
Number JP20H00612.
REFERENCES
Akkaynak, D. and Treibitz, T. (2019). Sea-thru: A method
for removing water from underwater images. In Proc.
IEEE/CVF CVPR2019, pages 1682–1691.
Akkaynak, D., Treibitz, T., Shlesinger, T., Loya, Y., Tamir,
R., and Iluz, D. (2017). What is the space of attenu-
ation coefficients in underwater computer vision? In
Proc. IEEE CVPR2017, pages 568–577.
Asano, Y., Zheng, Y., Nishino, K., and Sato, I. (2016).
Shape from water: Bispectral light absorption for
depth recovery. In Proc. ECCV2016, pages 635–649.
Berry, M., Browne, M., Langville, A., Pauca, V., and Plem-
mons, R. (2007). Algorithms and applications for ap-
proximate nonnegative matrix factorization. Compu-
tational Statistics & Data Analysis, 52(1):155–173.
Bryson, M., Johnson-Roberson, M., Pizarro, O., and
Williams, S. B. (2016). True color correction of au-
tonomous underwater vehicle imagery. Journal of
Field Robotics, 33(6):853–874.
Choe, G., Narasimhan, S. G., and Kweon, I. S. (2016).
Simultaneous estimation of near IR BRDF and fine-
scale surface geometry. In Proc. IEEE CVPR2016,
pages 2452–2460.
Curcio, J. A. and Petty, C. C. (1951). The near infrared ab-
sorption spectrum of liquid water. JOSA A, 41(5):302–
304.
Jones, M. W. and Kao, K. C. (1969). Spectrophotomet-
ric studies of ultra low loss optical glasses II: double
beam method. Journal of Physics E: Scientific Instru-
ments, 2(4):331–335.
Jordt-Sedlazeck, A. and Koch, R. (2013). Refractive
structure-from-motion on underwater images. InProc.
IEEE ICCV2013, pages 57–64.
Kaeli, J. W., Singh, H., Murphy, C., and Kunz, C. (2011).
Improving color correction for underwater image sur-
veys. In Proc. MTS/IEEE OCEANS2011, pages 1–6.
Kao, K. C. and Davies, T. W. (1968). Spectrophotometric
studies of ultra low loss optical glasses I: single beam
method. Journal of Physics E: Scientific Instruments,
1(11):1063–1068.
Kitahara, M., Okabe, T., Fuchs, C., and Lensch, H.
P. A. (2015). Simultaneous estimation of spectral re-
flectance and normal from a small number of images.
In Proc. VISAPP2015, pages 303–313.
Kobayashi, N. and Okabe, T. (2016). Separating reflection
components in images under multispectral and multi-
directional light sources. In Proc. IAPR ICPR2016,
pages 3199–3204.
Koyamatsu, K., Hidaka, D., Okabe, T., and Lensch, H.
P. A. (2019). Reflective and fluorescent separation
under narrow-band illumination. In Proc. IEEE/CVF
CVPR2019, pages 7577–7585.
Kuo, M.-Y. J., Kawahara, R., Nobuhara, S., and Nishino, K.
(2021). Non-rigid shape from water. IEEE TPAMI,
43(7):2220 – 2232.
Matas, J., Chum, O., Urban, M., and Pajdla, T. (2004).
Robust wide-baseline stereo from maximally stable
extremal regions. Image and Vision Computing,
22(10):761–767.
Murai, S., Kuo, M., Kawahara, R., Nobuhara, S., and
Nishino, K. (2019). Surface normals and shape from
water. In Proc. IEEE/CVF ICCV2019, pages 7829–
7837.
Murez, Z., Treibitz, T., Ramamoorthi, R., and Kriegman, D.
(2015). Photometric stereo in a scattering medium. In
Proc. IEEE ICCV2015, pages 3415–3423.
Reinhard, E., Khan, E. A., Akyuz, A. O., and Johnson, G.
(2008). Color Imaging: Fundamentals and Applica-
tions. A K Peters/CRC Press.
Schechner, Y. Y. and Karpel, N. (2004). Clear underwater
vision. In Proc. IEEE CVPR2004, pages 536–543.
Takatani, T., Ito, Y., Ebisu, A., Zheng, Y., and Aoto, T.
(2021). Event-based bispectral photometry using tem-
porally modulated illumination. In Proc. IEEE/CVF
CVPR2021, pages 15638–15647.
Torii, M., Okabe, T., and Amano, T. (2019). Multispectral
direct-global separation of dynamic scenes. In Proc.
IEEE WACV2019, pages 1923–1931.
Tsiotsios, C., Angelopoulou, M. E., Kim, T.-K., and Davi-
son, A. J. (2014). Backscatter compensated photomet-
ric stereo with 3 sources. In Proc. IEEE ICCV2014,
pages 2259–2266.
Wang, C. and Okabe, T. (2017). Joint optimization of
coded illumination and grayscale conversion for one-
shot raw material classification. In Proc. BMVC2017.
Wang, C. and Okabe, T. (2021). Per-pixel water and oil
detection on surfaces with unknown reflectance. In
Proc. EUSIPCO2021, pages 601–605.
Wang, C., Okuyama, M., Matsuoka, R., and Okabe, T.
(2021). Per-pixel water detection on surfaces with
unknown reflectance. IEICE Trans. Information and
Systems, E104-D(10):1555–1562.
Yamashita, A., Fujii, M., and Kaneko, T. (2007). Color reg-
istration of underwater images for underwater sensing
with consideration of light attenuation. In Proc. IEEE
ICRA2007, pages 4570–4575.
Spectral Absorption from Two-view Hyperspectral Images
721