Spectral Classiﬁcation of Microplastics using Neural Networks: Pilot

Feasibility Study

Petr Dolezel

1 a

, Jiri Rolecek

1 b

, Daniel Honc

1 c

, Dominik Stursa

1 d

and Bruno Baruque Zanon

2 e

Faculty of Electrical Engineering and Informatics, University of Pardubice, Studentska 95, Pardubice, Czech Republic

Universidad de Burgos Escuela Polit

ecnica Superior, Burgos, Castilla y Leon, Spain

Keywords:

Microplastics, FTIR Spectra, Spectroscopy, Neural Network, Deep Learning, Spectra Matching.

Abstract:

Microplastics, i.e. synthetic polymers that have particle size smaller than 5 mm, are emerging pollutants that

are widespread in the environment. In order to monitor environmental pollution by microplastics, it is nec-

essary to have available rapid screening techniques, which provide the accurate information about the quality

(type of polymer) and quantity (amount). Spectroscopy is an indispensable method, if precise classiﬁcation

of individual polymers in microplastics is required. In order to contribute to the topic of autonomous spectra

matching when using spectroscopy, we decided to demonstrate the quality and efﬁciency of neural networks.

We adopted three neural network architectures, and we tested them for application to spectra matching. In

order to keep our study transparent, we use publicly available dataset of FTIR spectra. Furthermore, we per-

formed a deep statistical analysis of all the architectures performance and efﬁciency to show the suitability

of neural networks for spectra matching. The results presented at the end of this article indicated the overall

suitability of the selected neural network architectures for spectra matching in microplastics classiﬁcation.

1 INTRODUCTION

Plastic pollution has recently become a huge global

problem. Worldwide plastics production reached

about 367 million tons in 2020 (Kaul, 2021). Approx-

imately 80 percent of produced plastic is disposed of

as various kinds of waste (Chen et al., 2021). Plas-

tic waste, that is improperly deposited, can be disin-

tegrated into small pieces by sunlight, heat, physical

abrasion, eventually directing to the particle size of

microplastic (<5mm) (Xu et al., 2022).

These microplastics are receiving big interest

from the scientiﬁc community as well as from inter-

national institutions, since the effect of microplastics

on organisms and the environment is not yet clearly

known (Rochman et al., 2013; Katare et al., 2022).

One of the open problems is the issue of mon-

itoring of mikroplastics in environment. Only sev-

eral long-term studies, which examine the evolution

of microplastics pollution over the years, have been

https://orcid.org/0000-0002-7359-0764

https://orcid.org/0000-0001-5250-7194

https://orcid.org/0000-0001-8440-5272

https://orcid.org/0000-0002-2324-162X

https://orcid.org/0000-0002-4993-204X

performed. This is caused especially due to the time

and resource consuming process of repeated sam-

ple acquisition, laboratory preparation and evaluation.

In some recent studies, the identiﬁcation and detec-

tion of microplastics is performed by manual visual

counting and sorting under a microscope, based on

color, size, morphology etc. (Hanvey et al., 2017;

Mukhanov et al., 2019). Furthermore, some authors

propose advanced image analysis-based approaches,

which are powerful in case of measuring and count-

ing particles (Lorenzo-Navarro et al., 2020).

However, spectroscopy is an indispensable

method, if precise classiﬁcation of individual poly-

mers in microplastics is required. Raman and Fourier

transform infrared (FTIR) spectroscopy are the most

common techniques for classifying the polymers in

plastic particles (Cowger et al., 2020). Although both

mentioned techniques provide exceptional accuracy,

the application of them requires a complex sequence

of steps, many of which are performed manually

by default (Cabernard et al., 2018). A crucial step,

which is evaluated manually in most cases, is spectra

matching. Speciﬁcally, the Raman or SWIR spectrum

of an examined sample needs to be preprocessed

(ﬁltering, baseline signals removal) and compared

to a reference library of spectra, in order to classify

Dolezel, P., Rolecek, J., Honc, D., Stursa, D. and Zanon, B.

Spectral Classiﬁcation of Microplastics using Neural Networks: Pilot Feasibility Study.

DOI: 10.5220/0010986900003123

In Proceedings of the 15th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2022) - Volume 4: BIOSIGNALS, pages 283-289

ISBN: 978-989-758-552-4; ISSN: 2184-4305

283

the polymer in the sample. Although this process is

simple in theory, it is not easy to automatize it due

to the large variability of the measured spectra. See

Fig. 1 for four examples of high-density polyethylene

FTIR spectrum measured by the same device. Note

the differences in peak numbers, peak positions and

peak heights.

Figure 1: Four examples of high-density polyethylene FTIR

spectrum measured by the same device. Note the differ-

ences in peak numbers, peak positions and peak heights.

Despite the obvious differences, these spectra should be

evaluated as one class.

Despite the obvious uncertainty of machine eval-

uation, several methods, that aim to replace the man-

ual spectra matching, have been proposed. Lorenzo-

Navarro et al. introduced a multi-step method com-

posed from a segmentation step, feature extrac-

tion and classiﬁcation. They considered and tested

different feature extractors and classiﬁers, includ-

ing machine learning and deep learning algorithms

(Lorenzo-Navarro et al., 2020). Alternately, a hybrid

fusion algorithm, that simultaneously combines high-

level fusion with low- and mid-level fusion based on

an ensemble of various classical classiﬁers, is pro-

posed in (Chabuka and Kalivas, 2020). Finally, the

authors (Cowger et al., 2021) offer a comprehen-

sive software tool, which encapsulates a large num-

ber of tools to process and classify microplastic spec-

tra. Moreover, this tool is ”open source” and can be

rapidly adapted to include new techniques.

In order to contribute to the topic of autonomous

spectra matching, we decided to demonstrate the

quality and efﬁciency of convolutional neural net-

works (LeCun et al., 1999) and attention mechanism-

based neural networks (Vaswani et al., 2017) for sig-

nal classiﬁcation. Speciﬁcally, we intuitively under-

stand the problem of spectra matching to be very sim-

ilar to time series classiﬁcation (see Fig. 2). It is

well known that neural networks are a very effective

tool for time series classiﬁcation (Ismail Fawaz et al.,

2019; Franklin and Muthukumar, 2022; Sikdar et al.,

2022). Although some pilot studies have already con-

sidered convolutional neural networks as a tool for

spectra matching (Ng et al., 2020), it is still open

problem and more analyses have to be performed.

Time series length

Dimensions

Input multivariate time series

Nonlinear

transformation

Probability distribution over k classes

Figure 2: A general framefork for time series classiﬁcation.

A nonlinear transformation module processes the input time

series and provides the probability of the input time series

belonging to each class.

In this article, we adopt three neural network ar-

chitectures, that have already proven successful for

time series classiﬁcation, and we test them for ap-

plication to spectra matching. In order to keep our

study transparent, we use publicly available dataset of

FTIR spectra (Chabuka and Kalivas, 2020). Further-

more, we perform a deep statistical analysis of all the

architectures performance and efﬁciency to show the

suitability of neural networks for spectra matching.

2 MATERIALS AND METHODS

2.1 Neural Network Architectures

Many different architectures, from multilayer percep-

tron to long short-term memory recurrent neural net-

work, have been already more or less successfully

implemented for signal classiﬁcation. We aimed at

architectures with exceptional performance and ac-

ceptable response time for real-time implementation.

Based on an extensive literature review, we selected

(1) a variant of a fully-convolutional neural network

classiﬁer adapted from (Wang et al., 2017), (2) an

implementation of a multi-scale convolutional neural

network based on (Cui et al., 2016), and (3) an atten-

tion mechanism-based Transformer architecture pre-

sented in (Vaswani et al., 2017).

BIOSIGNALS 2022 - 15th International Conference on Bio-inspired Systems and Signal Processing

284

2.1.1 Fully-convolutional Neural Network

Classiﬁer

Fully convolutional neural networks provide

efﬁciency and quality especially for semantic

segmentation-related issues (Shelhamer et al., 2017).

In this setting, a fully convolutional neural network

is performed as a feature extractor, followed by a

softmax layer. A number of neurons in the softmax

layer is equal to the number of classes. The explicit

graph of this architecture, as used in this contribution,

is depicted in Fig. 3.

Conv1D

64 filters, kernel size 3

ReLU activation

Batch normalization

Conv1D

64 filters, kernel size 3

ReLU activation

Batch normalization

Conv1D

64 filters, kernel size 3

ReLU activation

Batch normalization

Global average pooling

Soft max

FTIR spectrum

Figure 3: Architecture of a selected fully-convolutional

neural network classiﬁer.

2.1.2 Multi-scale Convolutional Neural Network

The multi-scalability of this network consists in its ar-

chitecture. The ﬁrst part of the architecture works in

three parallel independent branches. Each branch im-

plements a base module to extract features of differ-

ent nature from the input, operating at different fre-

quency scales. The outputs of all branches are con-

catenated and the resulting signal is processed by a

softmax layer. The overall architecture, as we imple-

mented it in our experiments, is depicted Fig. 4. The

architecture of the base module is shown in Fig. 5.

The kernel size of the convolutional layer varies from

8 (the upper module) to 24 (the lower module). The

lower module input is the original FTIR spectrum, the

middle module input is the spectrum downsized to

one half, and the upper module input is the spectrum

downsized to one third of the original.

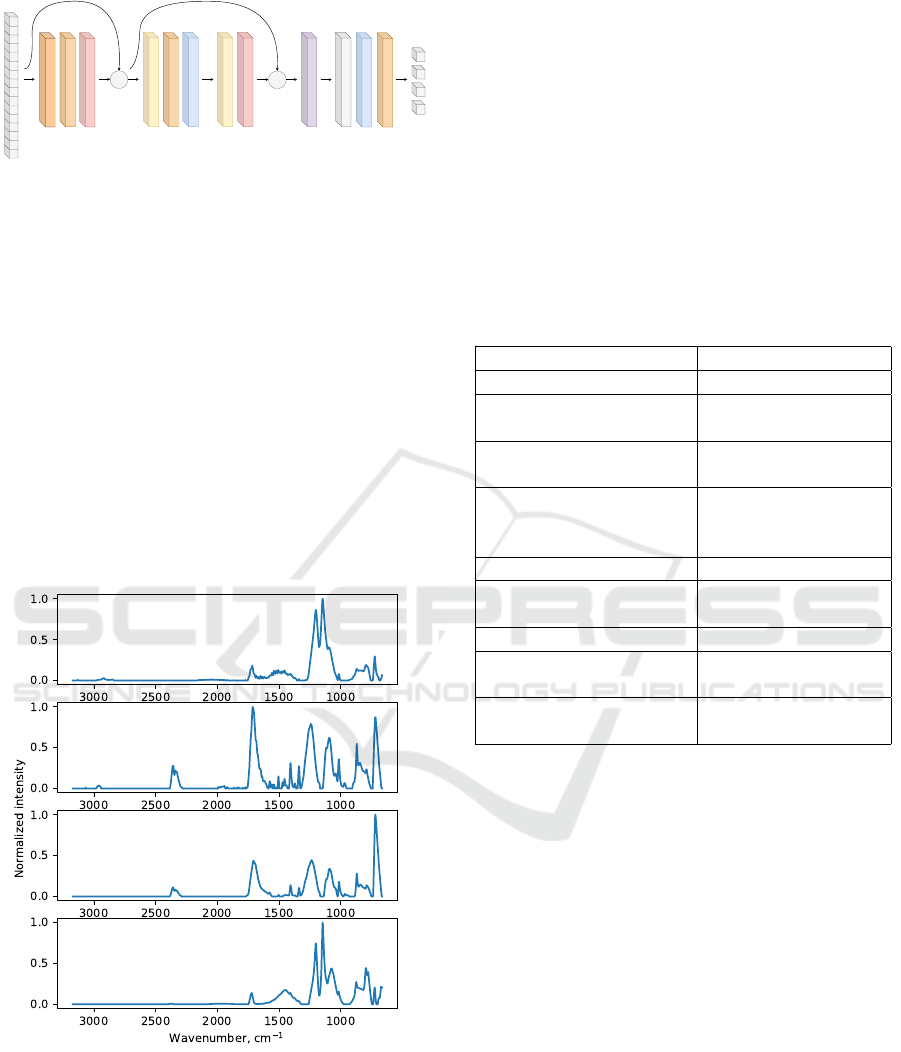
2.1.3 Transformer Architecture

The idea of the Transformer architecture is to propose

a topology based solely on attention mechanisms,

dispensing with recurrence and convolutions entirely

(Vaswani et al., 2017). The architecture was origi-

nally proposed to natural language processing, but it

can be seamlessly adapted to spectra matching. The

FTIR spectrum

Downsampling

Concatenate

Soft max

Base module

Figure 4: Overall architecture of our implementation of a

multi-scale convolutional neural network.

Downsampled FTIR spectrum

Conv1D

10 filters, kernel size [8, 16, 24]

Tanh activation

Global max pooling

Dense, 50 neurons

Tanh activation

Dropout 0.3

Figure 5: Base module for a multi-scale convolutional neu-

ral network.

key part of this architecture is a multi-head attention

layer. Intuitively, this layer allows for attending to

parts of the input sequence in various different ways,

e.g. from the long-term dependency point of view and

the short-term dependency point of view. We imple-

mented a tiny version of this architecture, in order to

keep a comparable size to the other selected architec-

tures - see Fig. 6.

Spectral Classiﬁcation of Microplastics using Neural Networks: Pilot Feasibility Study

285

FTIR spectrum

Multi head attention

Head size 256, 4 heads

Dropout 0.25

Layer normalization

Conv1D

4 filters, kernel size 1

ReLU activation

Dropout 0.25

Conv1D

1 filter, kernel size 1

Layer normalization

Global average pooling

Dense, 50 neurons

ReLU activation

Dropout 0.3

Soft max

Figure 6: Our implementation based on the Transformer ar-

chitecture.

2.2 Dataset

We adopted 272 FTIR spectra from (Chabuka and

Kalivas, 2020). These spectra were acquired using

Thermo Nicolet NEXUS 670 FTIR spectrophotome-

ter with spectral resolution 4 cm

−1

. The dataset

includes 137 spectra of high-density polyethylene

(HDPE) and 135 spectra of polyethylene terephtha-

late (PET), i.e. two balanced classes for classiﬁcation.

Each spectrum consists of 1300 points. Some exam-

ples are shown in Fig. 1 for high-density polyethylene

and in Fig. 7 for polyethylene terephthalate.

Figure 7: Four examples of polyethylene terephthalate

FTIR spectrum.

The dateset was shufﬂed and divided into train-

ing set (160 samples), validation set (41 samples) and

testing set (71 samples).

2.3 Training Details

The Adam algorithm was selected as an optimizer,

since it is generally considered to provide acceptable

performance in most of the cases (Kingma and Ba,

2014). Sparse categorical crossentropy loss function

was used to evaluate training process. Initial weights

were set randomly with Gaussian distribution. The

training experiments were performed 100 times due

to a stochastic character of training. For each training

session, the instance, which performed best over vali-

dation set, was selected for further evaluation. All the

parameters of the training are summarized in Table 1.

Table 1: Parameters of the training.

Input shape 1300 x 1

Training algorithm Adam algorithm

Loss function Sparse categorical

crossentropy

Number of experiments

for each architecture

100

Initialization Normal distribution

(mean = 0, std =

0.05)

Maximum epochs 500

Stopping criterion Maximum epochs

reached

Initial learning rate α 0.001

Exponential decay rate 1

0.9

Exponential decay rate 2

0.999

2.4 Evaluation Metrics

After training of all the considered architectures, ev-

ery network was evaluated. From the training perfor-

mance point of view, the courses of loss function over

the training set and over the validation set during the

training sessions were evaluated. Since 100 distinct

training sessions were performed, the courses were

depicted as sequences of box plots in relation to the

epoch number.

From the classiﬁcation quality point of view, the

confusion matrix for each architecture was prepared.

Again, the confusion matrix shows the average values

including the standard deviation, since 100 training

sessions for each architecture were performed.

Evaluation of the memory size and response time

is also important, especially if the edge computing

implementation is intended. Therefore, the size of

the neural network architectures and their response

times were also considered. The response times

BIOSIGNALS 2022 - 15th International Conference on Bio-inspired Systems and Signal Processing

286

of of the selected architectures were evaluated on

a personal computer with Intel Core i5-8600K (3.6

GHz) CPU, internal memory 16 GB DDR4 330 (2666

MHz), video card NVIDIA PNY Quadro P5000 16

GB GDDR5 PCIe 3.0. The architectures were im-

plemented using TensorFlow 2.7 using Windows 10

operating system.

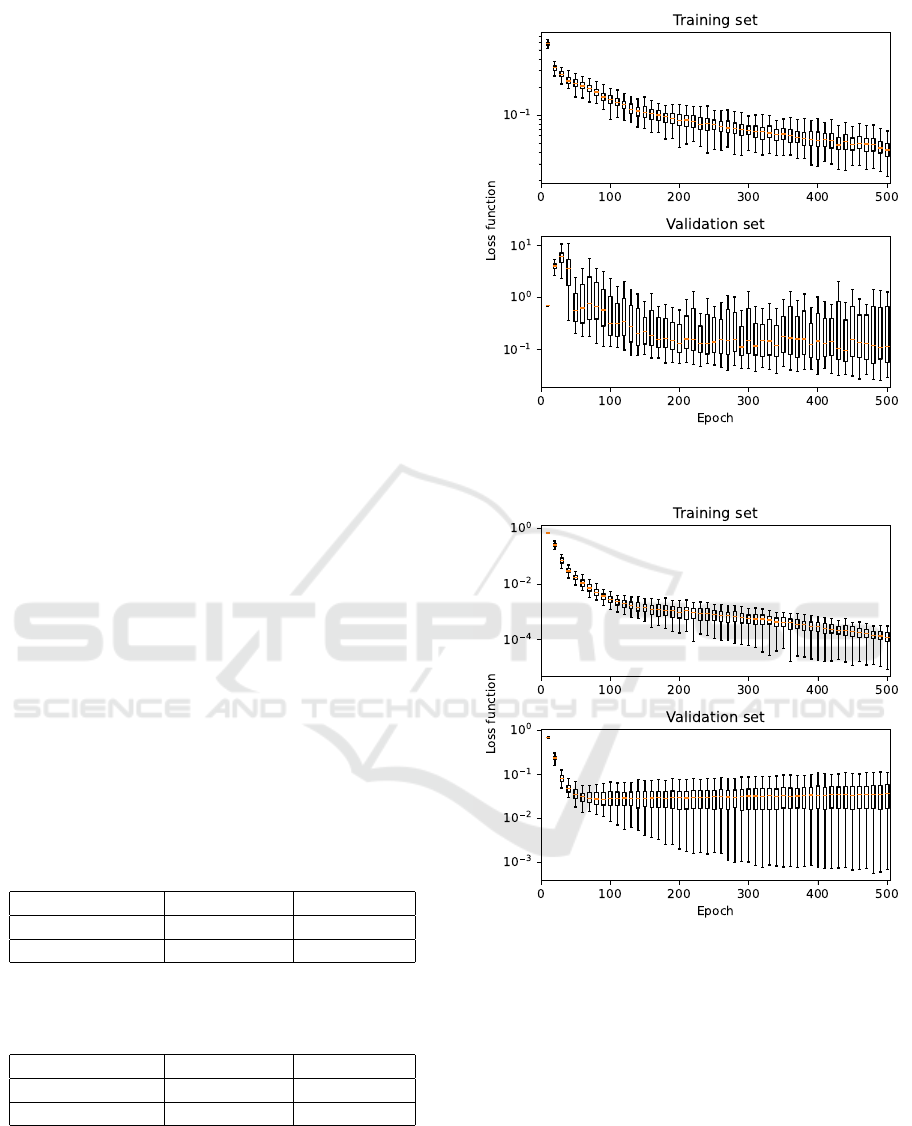
3 RESULTS AND DISCUSSION

The selected architectures were trained and vali-

dated 100 times according to the procedure addressed

above. In order to demonstrate training results, the

courses of the sparse categorical cross entropy loss

function over the training set and over the validation

set are depicted in Fig. 8 for the fully-convolutional

neural network classiﬁer, in Fig. 9 for the multi-scale

convolutional neural network, and in Fig. 10 for the

Transformer architecture. The central lines in the box

graphs, shown in the ﬁgures, are medians of loss func-

tion current values in relation to the epoch number;

the edges of the boxes are 25

and 75

percentiles;

and the whiskers extend to the most extreme data

points (except outliers).

Consequently, the confusion matrices for each ar-

chitecture over the testing set are presented in Table 2,

in Table 3, and in Table 4. Each column of the matri-

ces represents the instances in an actual class (HDPE

or PET) while each row represents the instances in a

predicted class. The values in brackets mean the stan-

dard deviation for each value.

Lastly, the sizes and the relative response times

are shown in Table 5.

Table 2: Confusion matrix for the fully-convolutional neu-

ral network classiﬁer. The values in brackets mean the stan-

dard deviation.

HDPE actual PET actual

HDPE predicted 32.95 (0.22) 1.41 (0.71)

PET predicted 0.05 (0.22) 36.59 (0.71)

Table 3: Confusion matrix for the multi-scale convolutional

neural network. The values in brackets mean the standard

deviation.

HDPE actual PET actual

HDPE predicted 33.00 (0.00) 1.35 (0.48)

PET predicted 0.00 (0.00) 36.65 (0.48)

All the presented results indicate the overall suit-

ability of the selected neural network architectures for

spectra matching. Looking at training performances,

the fully-convolutional neural network classiﬁer pro-

vided the slowest learning curve and additionally, the

Figure 8: Training course for the fully-convolutional neural

network classiﬁer.

Figure 9: Training course for the multi-scale convolutional

neural network.

generalization capability of this model was low - the

evaluation over the validation set provided relatively

high values with a large variance. The learning curve

for the other two architectures was steep and stable,

with the Transformer architecture in particular pro-

viding exceptionally good values of loss function over

the validation set, with low variance.

The confusion matrices, which represent perfor-

mance of each architecture over the testing set, pro-

vided results, that correspond with the training per-

formance. The best performance was provided by

the Transformer architecture, where, statistically, the

Spectral Classiﬁcation of Microplastics using Neural Networks: Pilot Feasibility Study

287

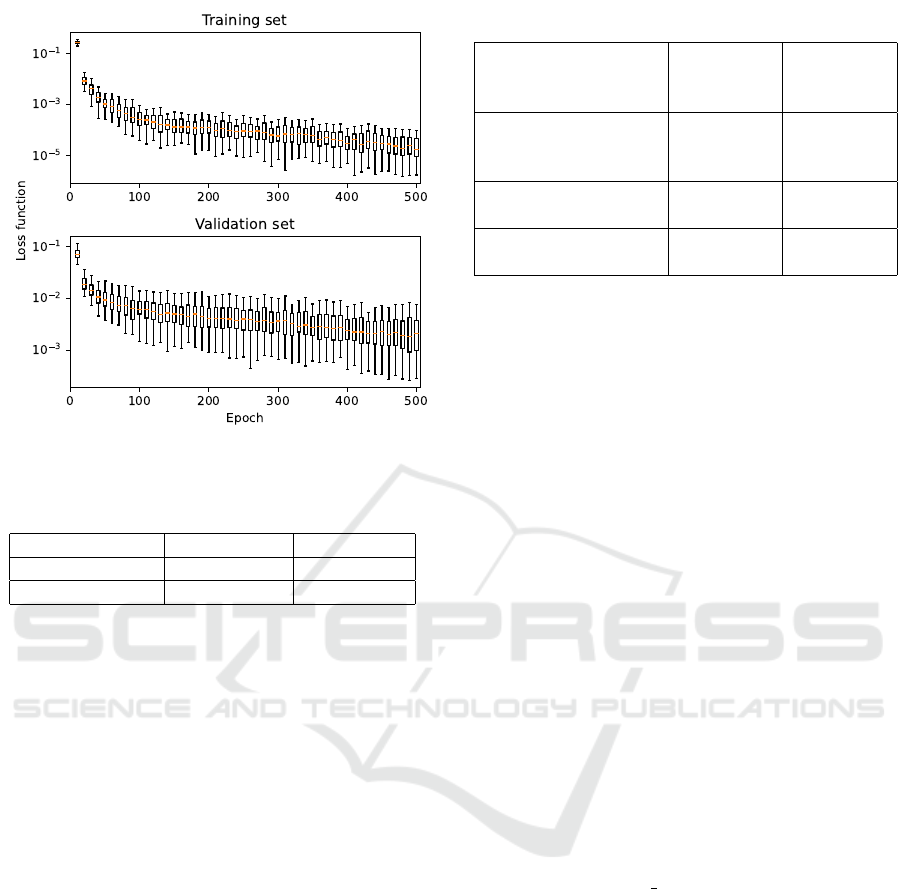
Figure 10: Training course for the Transformer architecture.

Table 4: Confusion matrix for the Transformer architecture.

The values in brackets mean the standard deviation.

HDPE actual PET actual

HDPE predicted 33.00 (0.00) 0.82 (0.38)

PET predicted 0.00 (0.00) 37.18 (0.38)

classiﬁer misclassiﬁed less than one spectrum from

the testing set. The other two architectures performed

a little worse. For the Transformer architecture, 18

training sessions (from 100) provided model, that did

classify all the samples in the testing set correctly. For

the other two architectures, each model provided at

least one misclassiﬁed sample.

Looking at Table 5, the response times of each

classiﬁer are similar; the multi-scale convolutional

neural network was about 20 percent slower than

the other two architectures. Considering the mem-

ory sizes, all the architectures are smaller than 1 MB.

Hence, they are very lightweight and can be consid-

ered for use in edge computing applications.

4 CONCLUSIONS

In this study, three selected neural network architec-

tures are used to classify microplastics FTIR spec-

tra. Although only a limited dataset with two types of

polymer is used, the results look promising to imple-

ment neural network architecture for spectra match-

ing.

The Transformer architecture was particularly

successful with almost 20 percent of training sessions

providing model, that classiﬁes all the samples in the

testing set correctly.

Table 5: Size and response times.

Architecture Relative

response

time

Size (kB)

Fully-convolutional

neural network

classiﬁer

1.00 372

Multi-scale convolu-

tional neural network

1.18 94

Transformer archi-

tecture

1.05 940

The usage of neural networks for spectra match-

ing generally brings major advantages in compari-

son to classical matching techniques. It greatly re-

duces the number of operations required for prepro-

cessing, is not sensitive to noise and has good general-

ization capability. Moreover, lightweight neural net-

works are characterized by low computational power

requirements, which makes them suitable for use in

edge computing applications, such as portable spec-

troscopes.

In a future study, datasets with more classes are

deﬁnitely suggested to be tested in order to justify the

proposed work. With a dataset that covers all the most

common plastics, it will be possible to determine the

optimal neural network architecture with high accu-

racy and efﬁcient response time.

ACKNOWLEDGEMENTS

The work was supported from ERDF/ESF ”Co-

operation in Applied Research between the Uni-

versity of Pardubice and companies, in the Field

of Positioning, Detection and Simulation Tech-

nology for Transport Systems (PosiTrans)” (No.

CZ.02.1.01/0.0/0.0/17 049/0008394).

REFERENCES

Cabernard, L., Roscher, L., Lorenz, C., Gerdts, G., and

Primpke, S. (2018). Comparison of raman and fourier

transform infrared spectroscopy for the quantiﬁcation

of microplastics in the aquatic environment. En-

vironmental Science and Technology, 52(22):13279–

13288.

Chabuka, B. K. and Kalivas, J. H. (2020). Application of

a Hybrid Fusion Classiﬁcation Process for Identiﬁ-

cation of Microplastics Based on Fourier Transform

Infrared Spectroscopy. APPLIED SPECTROSCOPY,

74(9):1167–1183.

Chen, Y., Awasthi, A., Wei, F., Tan, Q., and Li, J. (2021).

Single-use plastics: Production, usage, disposal, and

BIOSIGNALS 2022 - 15th International Conference on Bio-inspired Systems and Signal Processing

288

adverse impacts. Science of the Total Environment,

752.

Cowger, W., Gray, A., Christiansen, S., DeFrond, H.,

Deshpande, A., Hemabessiere, L., Lee, E., Mill, L.,

Munno, K., Ossmann, B., Pittroff, M., Rochman, C.,

Sarau, G., Tarby, S., and Primpke, S. (2020). Critical

review of processing and classiﬁcation techniques for

images and spectra in microplastic research. Applied

Spectroscopy, 74(9):989–1010.

Cowger, W., Steinmetz, Z., Gray, A., Munno, K., Lynch,

J., Hapich, H., Primpke, S., De Frond, H., Rochman,

C., and Herodotou, O. (2021). Microplastic spec-

tral classiﬁcation needs an open source community:

Open specy to the rescue! Analytical Chemistry,

93(21):7543–7548.

Cui, Z., Chen, W., and Chen, Y. (2016). Multi-scale convo-

lutional neural networks for time series classiﬁcation.

Franklin, R. and Muthukumar, B. (2022). Arrhythmia and

disease classiﬁcation based on deep learning tech-

niques. Intelligent Automation and Soft Computing,

31(2):835–851.

Hanvey, J., Lewis, P., Lavers, J., Crosbie, N., Pozo, K., and

Clarke, B. (2017). A review of analytical techniques

for quantifying microplastics in sediments. Analytical

Methods, 9(9):1369–1383.

Ismail Fawaz, H., Forestier, G., Weber, J., Idoumghar, L.,

and Muller, P.-A. (2019). Deep learning for time series

classiﬁcation: a review. Data Mining and Knowledge

Discovery, 33(4):917–963.

Katare, Y., Singh, P., Sankhla, M., Singhal, M., Jadhav,

E., Parihar, K., Nikalje, B., Trpathi, A., and Bhard-

waj, L. (2022). Microplastics in aquatic environ-

ments: Sources, ecotoxicity, detection and remedi-

ation. Biointerface Research in Applied Chemistry,

12(3):3407–3428.

Kaul, A. (2021). Worldwide plastics produc-

tion falls in 2020 due to covid-19: Report.

https://www.republicworld.com/world-news/global-

event-news/worldwide-plastics-production-falls-

in-2020-due-to-covid-19-report.html. Accessed:

2021-11-23.

Kingma, D. P. and Ba, J. (2014). Adam: A method for

stochastic optimization. CoRR, abs/1412.6980.

LeCun, Y., Haffner, P., Bottou, L., and Bengio, Y. (1999).

Object recognition with gradient-based learning. Lec-

ture Notes in Computer Science (including subseries

Lecture Notes in Artiﬁcial Intelligence and Lecture

Notes in Bioinformatics), 1681:319–345.

Lorenzo-Navarro, J., Castrillon-Santana, M., Santesarti, E.,

De Marsico, M., Martinez, I., Raymond, E., Gomez,

M., and Herrera, A. (2020). Smacc: A system for

microplastics automatic counting and classiﬁcation.

IEEE Access, 8:25249–25261.

Mukhanov, V., Litvinyuk, D., Sakhon, E., Bagaev, A.,

Veerasingam, S., and Venkatachalapathy, R. (2019).

A new method for analyzing microplastic particle size

distribution in marine environmental samples. Eco-

logica Montenegrina, 23:77–86.

Ng, W., Minasny, B., and McBratney, A. (2020). Convolu-

tional neural network for soil microplastic contamina-

tion screening using infrared spectroscopy. Science of

the Total Environment, 702.

Rochman, C., Hoh, E., Kurobe, T., and Teh, S. (2013).

Ingested plastic transfers hazardous chemicals to ﬁsh

and induces hepatic stress. Scientiﬁc Reports, 3.

Shelhamer, E., Long, J., and Darrell, T. (2017). Fully con-

volutional networks for semantic segmentation. IEEE

Transactions on Pattern Analysis and Machine Intel-

ligence, 39(4):640–651.

Sikdar, S., Liu, D., and Kundu, A. (2022). Acoustic emis-

sion data based deep learning approach for classiﬁca-

tion and detection of damage-sources in a composite

panel. Composites Part B: Engineering, 228.

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones,

L., Gomez, A., Kaiser, L., and Polosukhin, I. (2017).

Attention is all you need. volume 2017-December,

pages 5999–6009.

Wang, Z., Yan, W., and Oates, T. (2017). Time series clas-

siﬁcation from scratch with deep neural networks: A

strong baseline. volume 2017-May, pages 1578–1585.

Xu, L., Han, L., Li, J., Zhang, H., Jones, K., and Xu, E.

(2022). Missing relationship between meso- and mi-

croplastics in adjacent soils and sediments. Journal of

Hazardous Materials, 424.

Spectral Classiﬁcation of Microplastics using Neural Networks: Pilot Feasibility Study

289