Event Data Downscaling for Embedded Computer Vision

elie Gruel

1 a

, Jean Martinet

1 b

, Teresa Serrano-Gotarredona

2 c

and Bernab

e Linares-Barranco

2 d

Universit

e C

ote d’Azur, CNRS, I3S, France

Instituto de Microelectr

onica de Sevilla IMSE-CNM, Sevilla, Spain

Keywords:

Event Cameras, Computer Vision, Data Reduction, Preprocessing, Visualisation.

Abstract:

Event cameras (or silicon retinas) represent a new kind of sensor that measure pixel-wise changes in brightness

and output asynchronous events accordingly. This novel technology allows for a sparse and energy-efﬁcient

recording and storage of visual information. While this type of data is sparse by deﬁnition, the event ﬂow

can be very high, up to 25M events per second, which requires signiﬁcant processing resources to handle and

therefore impedes embedded applications. Neuromorphic computer vision and event sensor based applications

are receiving an increasing interest from the computer vision community (classiﬁcation, detection, tracking,

segmentation, etc.), especially for robotics or autonomous driving scenarios. Downscaling event data is an

important feature in a system, especially if embedded, so as to be able to adjust the complexity of data to

the available resources such as processing capability and power consumption. To the best of our knowledge,

this works is the ﬁrst attempt to formalize event data downscaling. In order to study the impact of spatial

resolution downscaling, we compare several features of the resulting data, such as the total number of events,

event density, information entropy, computation time and optical consistency as assessment criteria. Our code

is available online at https://github.com/amygruel/EvVisu.

1 INTRODUCTION

Event-based camera are slowly but surely integrating

many embedded systems, such as autonomous vehi-

cles and other robotic applications. However, this

novel type of asynchronous data comes with a heavy

ﬂow of information which can be too much to han-

dle and not always relevant for the task at hand. In

order to optimize the information carried by events,

we believe that it is necessary to formalize the dif-

ferent methods for event data spatial downscaling, as

deﬁned in Fig 1.

1.1 Event Cameras

The idea of a novel bio-inspired event-based sen-

sor, akin to a ”silicon retina” (Mahowald and Mead,

1991), has been developed since the 1990s. In bio-

inspired retinas, the transmitted information is coded

as spikes. Pixels emit spikes whenever relevant infor-

https://orcid.org/0000-0003-3916-0514

https://orcid.org/0000-0001-8821-5556

https://orcid.org/0000-0001-5714-2526

https://orcid.org/0000-0002-1813-4889

mation is captured in the visual ﬁeld. Retinas con-

verting luminance to spike frequency, spatial con-

trast retinas as well as retinas implementing some

spatio-temporal ﬁltering have been proposed. In

2008, Lichtsteiner, Posch and Delbruck presented the

ﬁrst complete design of a Dynamic Vision Sensor

(DVS) (Lichtsteiner et al., 2008) responding only to

temporal brightness change in a scene with no con-

sideration for colours, similar to the organic retina.

Figure 1: A set of fullscale events captured by a sensor of

size width × height is downscaled according to a downscal-

ing factor f actor, set to 2 in this example. Here, all the

events of the original sample occurring in the blue area’s

pixels will correspond to the events occurring in the red

pixel after reduction.

Gruel, A., Martinet, J., Serrano-Gotarredona, T. and Linares-Barranco, B.

Event Data Downscaling for Embedded Computer Vision.

DOI: 10.5220/0010991900003124

In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 4: VISAPP, pages

245-253

ISBN: 978-989-758-555-5; ISSN: 2184-4321

245

The main advantages of such an artiﬁcial retina

are (Gallego et al., 2020):

• the high temporal resolution, thanks to which an

event can be emitted on the timescale of microsec-

onds and avoiding motion blur,

• the high dynamic range, which makes it possible

to use them for extremely dim as well as under

bright sun illumination,

• the high contrast range which allows for highly

contrasted images avoiding dazzling effect caused

by sudden illumination changes, thus scenes with

illumination expanding over 120dB can be sensed

without suffering saturation,

• the low latency and asynchronicity enabled by the

independence between each pixel,

• the absence of redundancy in the information

transmitted, as compared to frame-based sensors,

• the low power consumption, following the model

of biological retinas and substituting the biologi-

cal photoreceptors by photodiodes in the electrical

circuits.

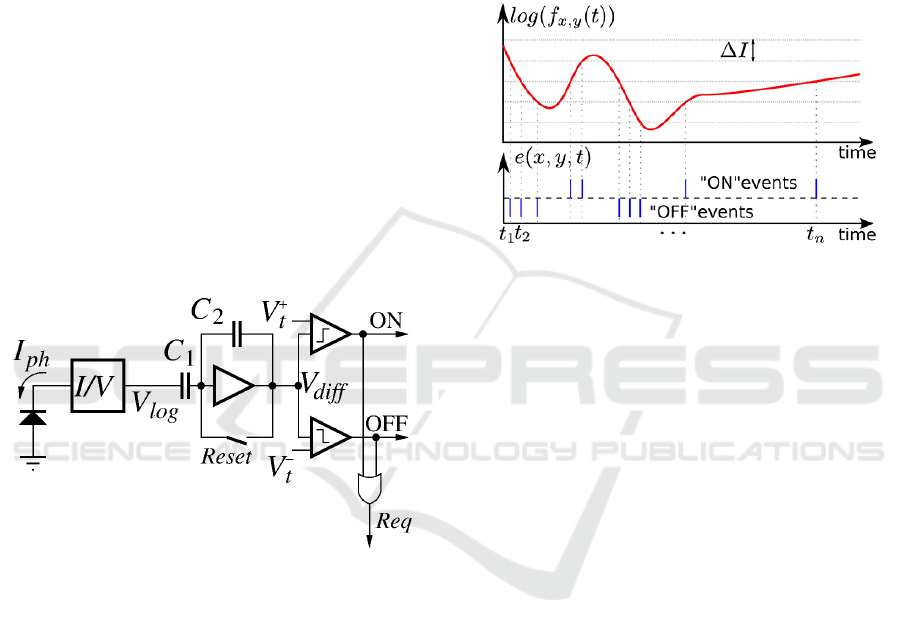
Figure 2: Block diagram of an event camera pixel.

Fig. 2 shows the conceptual schematic of an event

camera pixel. A photosensor produces a current I

proportional to the illumination. A transimpedance

logarithmic circuitry converts the detected current

into a voltage V

log

= A

log(I

) which depends log-

arithmically on the photocurrent. This voltage is the

input to a differencing capacitive ampliﬁer, so that the

voltage difference

∆V

di f f

= −C

∆V

log

= −C

∆I

(1)

That way voltage V

di f f

is proportional to the relative

temporal variation of the photocurrent. Voltage V

di f f

is compared with an upper and a lower voltage thresh-

olds. Each time it goes over the upper (or below the

lower) threshold, the pixel will generate an output ON

(or OFF) event and voltage V

di f f

is reset to a resting

value V

Fig. 3 illustrates the resulting behavior of the event

camera pixel. The upper subﬁgure plots the variation

of a pixel photocurrent along time, while the lower

subﬁgure illustrates the generated ON and OFF out-

put events. As can be observed, each time the pho-

tocurrent increases (or decreases) by a certain relative

variation given by,

∆I

= C

−V

)/(C

) (2)

the pixel generates an ON (OFF) output event.

Figure 3: Illustration of event-based encoding of visual

signals with respect to the predeﬁned threshold ∆I, from

(Lagorce et al., 2015). The luminance captured by the sen-

sor varies over time, and an event is only produced when

its log intersects with lines of equation y = ∆I. The corre-

sponding event is positive when the log-luminance’s slop is

positive at the intersection, and negative otherwise. The in-

terval between each t

and t

i+1

is not monotonous, which is

consistent with the event data asynchronicity.

The event cameras’ particularities described

above grant them advantages in many application

cases compared to more traditional visual sensors

(Gallego et al., 2020). A signiﬁcant ﬁeld of appli-

cations is robotics: autonomous vehicles, drones and

other embedded systems requiring low latency and

low power data handling. Furthermore, they evolve in

uncontrolled lightning conditions thus require a high

dynamic range and high contrast range.

Because of their operating mode, event based

cameras are useful in tasks featuring movements, such

as object tracking (Glover and Bartolozzi, 2016), ges-

ture recognition (Amir et al., 2017), optical ﬂow

estimation (Orchard et al., 2013; Paredes-Valles

et al., 2020), Simultaneous Localization and Mapping

(SLAM) (Kim et al., 2016; Vidal et al., 2018), etc.

Their high resolution and contrast range also valuable

for astronomical studies (Cohen et al., 2017; Chin

et al., 2019). Research on their combined use with

traditional RGB camera becomes more common, with

applications on high-resolution image reconstruction

(Zhang et al., 2021b; Rebecq et al., 2021) and video

deblurring (Zhang et al., 2021a).

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

246

1.2 Motivations

While desktop event vision solutions can afford large

amount of computing resources, embedded applica-

tion typically face limitations in CPU, memory, and

energy usage. Event data is sparse, and yet in some

highly dynamic and textured scenes, the event ﬂow

can be very high, up to 25M event per second, which

requires signiﬁcant processing resources to handle.

Most existing event vision approaches preprocess

event data by simply downscaling the pixel coordi-

nates, which is actually a max-pooling operation in

the event domain. One obvious issue of this sim-

ple event funnelling is that the resulting event density

drastically increases in the reduced spatial dimension,

causing an important information loss.

In embedded systems, only relevant information

should be stored and processed under the form of

downscaled event data. For example, event-based

odometry applied to robotics requires only movement

information in order to process the information in real

time: this need is typically answered by pooling the

events in frames (Rebecq et al., 2017), resulting in the

loss of the data’s asynchronicity.

In neuromorphic machine learning, spiking neu-

ral networks usually can’t handle the ﬂow of informa-

tion the event data represents and downscale this input

by a ﬁrst preprocessing layer, before actually learning

anything.

We can also mention the residual graph convolu-

tionnal techniques which handles each input event as

a node in the graph (Bi et al., 2019): this leads to a

low computational efﬁciency and a substantial simu-

lation run, which can be improved solely by spatially

reducing the input neuromorphic data.

The aforementioned examples are just a few rea-

sons why event downscaling is a real challenge in

neuromorphic computer vision and needs to be for-

malized.

The contributions of this paper are twofold: we

design and implement a number of methods to reduce

the size of event data and we assess the proposed re-

duction methods by analysing reduced data and also

based on the classiﬁcation results.

The remainder of the paper is organized as fol-

lows: ﬁrstly an introduction to event-based cameras

and the motivations behind this work, then a review

of previous use of event data, followed by a com-

plete description of the 6 spatial downscaling meth-

ods implemented in this work, and ﬁnally a a compar-

ison summarising the advantages and disadvantages

of each method.

2 RELATED WORK

Reducing the size of visual data is straightforward for

grayscale and RGB images with interpolation. When

it comes to event data, size reduction is much less triv-

ial. And yet, many papers discussing neuromorphic

computer vision are faced with a substantial event

ﬂow, sometimes too great to perform the task at hand.

In those case, the authors address this issue with vari-

ous techniques presented bellow.

A ﬁrst solution simply consists in creating event

frames, then processing this data as standard visual

images, as seen in (Fang et al., 2021) and (Huang,

2021). This enables the same model to be applied to

any king of visual data, neuromorphic or not. How-

ever its main drawback is that all the data’s asyn-

chronicity, which is a real advantage of event data,

is disregarded; all events are gathered and their times-

tamps discretised.

Spiking neural networks handling event data can

consider each pixel as an input neuron, and each event

produced as an input spike to the neural model. How-

ever this ﬁrst layer is often too important for efﬁ-

cient computation, thus most authors applying this

type of neuromorphic computing on event data re-

solve to convolve the input. For example, (Cordone

et al., 2021) apply multiple convolution layers to the

dataset DVS128 Gesture before processing it.

The non uniform sampling employed by (Bi

et al., 2019) can also be mentioned, although it only

produces satisfying results on a sparse dataset with

well-deﬁned empty areas like the one they use. This

simply amounts to implement a non-uniform grid

sampling inspired from traditional data processing to

event data.

To the best of our knowledge, the only existing

tool for event data downscaling is Tonic’s ”Downsam-

ple” method (Lenz et al., 2021). Tonic is a Python

library for neuromorphic data handling, which has

been created on an original idea dating back from

the 2019 Telluride neuromorphic workshop. It facili-

tates dataset downloads and its conversion to different

event representations (frames, time surfaces, voxel

grids, etc). It also proposes event transformation, such

as denoising, event dropping, polarities merging, spa-

tial and temporal jittering and downsampling.

The ”Downsample” method simply multiplies the

event coordinates by a spatial factor without dropping

any event. It can also be applied to temporal down-

sampling following the same mechanism. Although

it is extremely fast, it has the major ﬂaw of keeping

all the original events thus leading to an increasingly

high density in the produced visual data.

Event Data Downscaling for Embedded Computer Vision

247

3 PROPOSED METHODS

The following subsections present the 7 methods con-

sidered in this work to downscale spatially the data

produced by an event camera. Each method takes

as input a sample of events at maximum resolution

as well as the factor by which to reduce this sam-

ple, and returns the downscaled events as illustrated in

Fig. 1. Depending on the downscaling method used,

the number and frequency of the downscaled events

will not necessarily equal those of the events occur-

ring in the corresponding fullscale regions.

3.1 Simple Event Funnelling

A ﬁrst solution to reduce event data simply is to divide

each event’s coordinates in x and y by the downscal-

ing factor, then remove all the reduced events dupli-

cates (i.e., keep only one occurrence of each event for

a speciﬁc set of coordinates (x,y,t, p) – see Fig. 4).

This method follows the same logic as Tonic’s down-

scaling approach and can also be extended to temporal

reduction.

Thanks to its quickness and simplicity, this solu-

tion could answer the need for downscaling events in

real time on embedded systems. However, the main

drawback is that this process does not drop any event.

The reduced area undergoes a high density of events,

yielding an information loss due to the accumulation

of pixel activation (see Fig. 4). Event funnelling tends

to drastically increase pixel activity (see Fig. 4), espe-

cially when the downscale factor is large. In the ex-

treme yet unlikely case where the data is downscaled

to a 1 × 1 size, the resulting pixel is likely to be con-

stantly active.

Finally, the behavior does not correlate with the

physical mechanism of an actual event camera: the

optical consistency is very low for this method.

3.2 Log-luminance Reconstruction

From an optical point of view, downscaling the spatial

size of an event recording boils down to averaging the

luminance captured by a subset of pixels in the orig-

inal sensor. In a physical implementation of an event

camera formed by a 2D array of pixels as the one

shown in Fig. 2, this method could be implemented by

averaging the photocurrents I

generated by neigh-

bor pixels and performing the transimpedance loga-

rithmic conversion and posterior voltage ampliﬁca-

tion and differentiations as explained in Section. In-

troduction. In order to implement this behavior, the

log-luminance is reconstructed for each pixel in the

fullscale dataset: each event occurring on the same

pixel increases (if positive) or decreases (if negative)

the log-luminance level by one unit. The mean log-

luminance is then computed for each region of size

f actor

in the sensor. Lastly, the downscaled events

are generated: an event occurs at every timestep

where the average log-luminance crosses a threshold

line; the event is positive if the gradient is positive,

and vice-versa.

To achieve a pixel’s log-luminance reconstruction,

all events from this pixel is translated into points of

coordinates (x show the timestamps, y is the level

reached) where the initial level is arbitrarily set to 0

and contrast threshold set to 1 (see Fig. 3).

3.2.1 Event Count

A ﬁrst approach to log-luminance reconstruction con-

sists in estimating the mean log-luminance reached by

Figure 4: Schematic illustration for event funnelling and event counts methods. A sensor of size 2 × 2 outputs negative

and positive at each pixel across time, which are downscaled using Simple Event Funnelling (red frame on top) and Log-

Luminance Event count (green frame at the bottom). In this example, the downscaling factor is set to 2.

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

248

(a)

(b)

Figure 5: Schematic illustration for log-luminance reconstruction. A sensor of size 2× 2 outputs negative and positive at each

pixel across time, which are downscaled using log-luminance reconstruction with linear (a) and cubic (b) interpolation. In

this example, the downscaling factor is set to 2.

a downscaled pixel every time an event occurs in the

corresponding fullscale region - in other words, re-

alise a normalised event count in the fullscale region

as presented in Fig. 4. If its value crosses a contrast

threshold, an event is produced; an additional value

keeps track of the slope, in order to set this event’s

polarity depending on the slope. It is also necessary

to handle the constraint posed by the fact that an event

is only produced if the entire threshold has been cov-

ered since the last event. The slope value allows to

answer this by identifying the extrema, thus prevent-

ing events to occur when the log-luminance crosses a

threshold directly following an extremum.

This approach’s main disadvantage is the loss of

neuromorphic asynchronicity. A reduced event can

only occur at the timesteps where a fullscale event

took place, which wouldn’t be the case with actual

log-luminance reconstruction, as depicted in the fol-

lowing paragraphs. This drawback is also an asset:

this reduction method can easily downscale events as

they are being recorded, and its algorithm simplicity

is a plus for an embedded system.

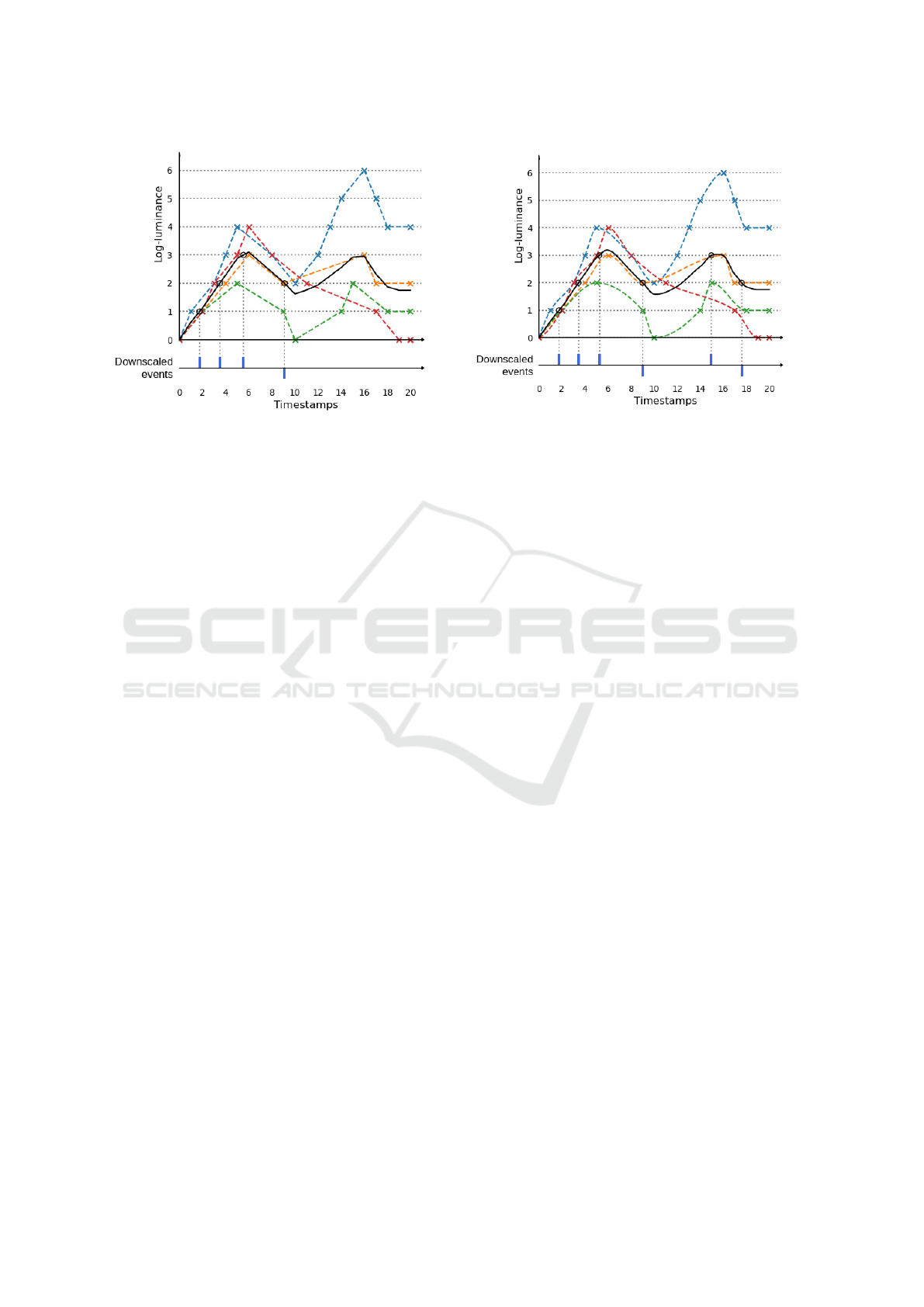
3.2.2 Linear Estimation

The second approach is to actually reconstruct the

log-luminance curve as a polyline, where each event

in the log-luminance graph is linked to its neighbors

in time by a line as presented in Fig. 5a. This allows

for a quick computation and interpolation of the inter-

sections between the thresholds and the curve. How-

ever, it is not as faithful to the physical reality as we

would like it to be.

3.2.3 Cubic Estimation

In this ﬁnal approach, the log-luminance of each neu-

ron is interpolated as a cubic curve strictly running

through the events on the log-luminance graph as seen

in Fig. 5b. The cubic interpolation was implemented

using Scipy’s method PChipInterpolator, an imple-

mentation of the Piecewise Cubic Hermite Interpo-

lating Polynomial. This algorithm is a third-degree

piecewise polynomial function which seeks to match

the derivatives of each point with its neighbors. Thus

its extrema coincide with the data’s extrema, which is

not the case of all cubic interpolation algorithm who

tend to greatly overshoot (Rabbath and Corriveau,

2019). As similar tools, this cubic interpolator I takes

as input a set of values (x, y,x

) and returns the y

data

interpolated for all x

values with respect to the rela-

tion between y and x:

I(x,y,x

) = y

with x

max

//threshold

∑

x=x

min

//threshold+threshold

(x)

(3)

In our case, the coordinates are those of the events

in the corresponding log-luminance graph: the x-axis

correspond to the events’ log-luminance and the

ordinates to the timestamps. From a set of known

log-luminance levels x

, the cubic interpolation

outputs the timestamps y

where the events’ log-

luminance crosses those levels.

This approach reconstructs a curve close to an ac-

tual log-luminance curve recorded by an event cam-

era, granting a high score of optical consistency to

Event Data Downscaling for Embedded Computer Vision

249

this approach. However, the existing tools allow-

ing the cubic interpolation of y values according to

a set of x parameters requires the x set to be strictly

monotonous, without any duplicates. The ﬁrst hin-

der can be removed by splitting the (x,y) dataset pre-

sented in Eq. 3 at the different log-luminance’s ex-

trema:

(x,y) =

ext

∑

i=0

ext

i+1

∑

t=t

ext

) (4)

with S

the i

subset of the events comprised between

two extrema, n

ext

the total number of extrema in the

dataset i.e. the number of segments S

, and t

ext

and

ext

i+1

respectively the timestamps of the i

and (i +

extrema.

The second hinder mentioned above is more com-

plex to avoid: although it is a rare occurrence, mul-

tiple events still happen at the same coordinates and

in the same timestamps with a frequency of X. This

requires us to only keep one specimen of duplicates,

thus lightly skewing the data processing.

Furthermore, it shares one disadvantage with the

linear estimation approach: both those approach can-

not be computed strictly in real time since they need

to know the future behavior of the curve, that is to say

the next events that will occur on the monitored pixel.

We can work around this problem by inserting a slight

delay between the data recording and processing.

3.3 Events to Video to Events

Since it is possible to reconstruct a grayscale video

from an event stream, a last simple technique

would be to use existing downscaling methods on a

grayscale reconstruction of the event data, then trans-

late this reduced image back into events. This is

equivalent to reconstructing a downscaled luminance

and computing downscaled events from it, but it has

some important drawbacks. The main one lies in

the total loss of event data’s asynchronicity since the

grayscale video produced from the neuromorphic data

is built from the pooling of information into frames.

Moreover, its implementation in practice is com-

putationally heavy, which is not suited for embed-

ded applications. Lastly, this method needs two sets

of grayscale data to be created during the process

(fullscale from events, then downscale) leading to

high memory consumption, while embedded systems

are limited in data storage.

A pipeline implementing such a downscaling pro-

cess is the following:

1. translate the event data into grayscale frames

thanks to Events-to-Video library introduced in

(Rebecq et al., 2019). This module actually

consists in a machine learning model trained on

a set of datasets comprising neuromorphic and

grayscale recordings of the same scenes.

2. rescale the grayscale frames thus obtained with

one of the many existing image processing tools.

3. ﬁnally translate the downscaled grayscale frames

into events by using the library Video-to-Events

from (Gehrig et al., 2020). This library recon-

structs the log-luminance variations between each

grayscale frame, then outputs the corresponding

events according to user-deﬁned negative and pos-

itive contrast thresholds.

This pipeline requires the event dataset to be

downscaled either to be one of the datasets the Events-

to-Video model has been trained on, or to contain a

set of grayscale frames recorded simultaneously as

the neuromorphic data. Since this method is very ar-

guable considering the motivations for event down-

scaling, it was not implemented to be compared in

this paper. Note that the dataset used in our experi-

ments (see Section Datasets) does not meet either of

these two criteria.

4 EXPERIMENTS

4.1 Datasets

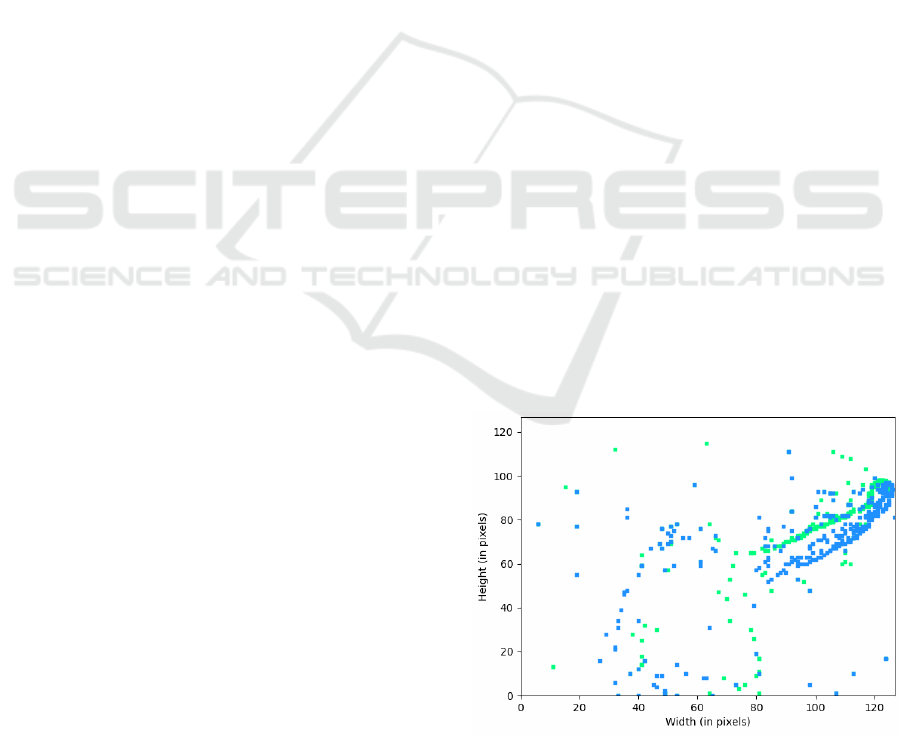
The different methods of reduction where applied

to the neuromorphic dataset DVS128 Gesture widely

used as a benchmark in event data processing, and we

assessed the results according to the criteria described

in the following sections.

Figure 6: Events grouped in a frame from a sample of the

gesture ”left hand clockwise” (class 7) of the DVS128 Ges-

ture dataset. Positive events are depicted in green, negative

in blue.

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

250

Table 1: Features of the original DVS128 Gesture dataset, and of the 5 downscaling methods described in Section 3.

Methods Number of Temporal Information Computation Optical

events density entropy time consistency

Original fullscale data 194,398 1.95e

−7

2.94e

−6

- -

Simple Event Funnelling 186,414 2.95e

−6

3.65e

−5

103.20 ms *

Tonic Downscale 194,312 5.40e

−5

4.31e

−4

3.20 ms *

Log-luminance

Event Count 7,778 1.25e

−7

1.88e

−6

0.83 s **

Linear Estimation 624 8.58e

−9

1.56e

−7

2.63 s ***

Cubic Estimation 435 8.92e

−9

1.66e

−7

2.94 s ****

Hand gesture recognition is a skill used daily in

the human society and is tightly integrated with ver-

bal communication, hence the need of computational

learning of such data. Since it relies heavily low la-

tency, this task is well suited for event-based compu-

tation. Building on this notion, Amir et al. presented

at CVPR 2017 a complete hand gesture neuromorphic

dataset called DVS128 Gesture (Amir et al., 2017).

To this end, 29 subjects were recorded performing 11

different hand gestures under 3 kinds of illumination

conditions, by a DVS128 camera (see Fig 6). A total

of about 133 samples are available for each gesture,

each composed roughly of 400,000 events and of di-

mension 128×128 pixels, for a duration of 6 seconds

approximately. The dataset is split in two sub-datasets

to facilitate machine learning training: the train sub-

category received 80% of the recorded samples and

the test 20%, with an even distribution of the 11 ges-

tures between them.

This dataset was chosen according to its relevance

to our motivations: DVS128 Gesture represents dy-

namic information to be processed temporally, which

would be the case in most embedded systems.

4.2 Comparison

Table 1 compares between the 6 methods presented

above and with the Tonic’s ”Downsample” tool ac-

cording to 5 criteria described in the following sec-

tion.

Number of Events. The mean number of events per

sample was calculated over the whole DVS28 Gesture

dataset at fullscale and downscaled by the 7 methods

mentioned in Table 1.

Temporal density Events temporal density D cor-

responds to the activation probability of pixels aver-

aged over the whole sensor:

D =

∑

x=0

∑

y=0

x,y

w · h

(5)

with w and h respectively the width and height of the

sensor. The activation probability P

x,y

is calculated as

the number of events (positive or negative) occurring

at a given pixel divided by the time length of the sam-

ple:

x,y

∑

max

t=t

min

δ(x

,x) · δ(y

,y)

max

−t

min

(6)

with P

x,y

the activation probability of one pixel of co-

ordinates (x, y), t

min

and t

max

respectively the mini-

mum and maximum timestamp of the sample, and δ

the Kronecker delta function, which returns 1 if the

variables are equal, and 0 otherwise.

Information Entropy. If we consider the informa-

tion brought by positive (or negative) events accord-

ing to Shannon’s information theory, we can estimate

the entropy H of the dataset as the average over all

pixels and polarities p of the entropy H

x,y,p

H =

∑

p∈{−,+}

∑

x=0

∑

y=0

x,y,p

2 · w · h

with H

x,y,p

∑

∈{P

x,y,p

}

−P

· log

)

(7)

where P

x,y,p

is the probability of event (probability

for the pixel of being active), and P

x,y,p

= 1 − P

x,y,p

the dual probability of no event, for the polarity p at

location (x,y). H

x,y,p

becomes lower when the pixel

is either never active or always active. Entropy values

in Table 4.2 are averaged from both polarities.

Computation Time. The computation time of each

method presented in this paper was calculated on a

Event Data Downscaling for Embedded Computer Vision

251

panel of over 500,000,000 events. The values pre-

sented in the Table 1 correspond to the average calcu-

lation period for the downscaling of 100,000 events,

expressed in seconds.

It should be noted that the values produced for

the SNN Pooling method are not obtained from the

similar panel of event data as the other. As a matter

of fact, since the computation time for one sample

using either technique exceeds 10 min, we chose to

assess our criteria on a small set of downsampled

events using SNN Pooling.

The values of these criteria conﬁrm the hypotheses

we outlined above. Tonic’s ”Downscale” method has

the highest number of events, thus the highest event

density; this spatial reduction does not lead to a sig-

niﬁcant drop of event ﬂow, thus does not answer our

need for reduced data to handle. The same goes for

the Simple Event Funneling, which does ignore all

event duplicates. Even though the computation time

of those two methods is low, the output data is too

important to be processed more efﬁciently than the

original one. We should also point out that their in-

formation entropy is quite low, due to the constant ac-

tivation of the sensor’s pixels.

The log-luminance techniques are the most con-

sistent with the optical reality behind event data

recording. It drops a large amount of data, thus signif-

icantly improving any embedded computation, while

maintaining a relatively high level of information en-

tropy. SNN Pooling is also promising by its behav-

ior closely related to one of an event-camera, but it

is extremely sensible to the weight of its connection:

here the weight is probably too high hence its poor

results. We intend to take advantage of the high com-

putational efﬁciency offered by SpiNNaker (Furber

et al., 2013) or Loihi (Davies et al., 2018) in order

to assess the optimal hyperparameters.

5 CONCLUSION

Event cameras take an increasing part in current trend

in computer vision, with a number of possible appli-

cations in robotics and autonomous driving. While

standard frame-based data (grayscale and RGB) are

easily downscaled – which is a very common pre-

processing step, there currently exists no straightfor-

ward equivalent for event data.

In this paper, we introduce and compare 7 meth-

ods for event data downscaling for embedded com-

puter vision applications. Our results show that the

choice of the reduction methods greatly inﬂuences

the event features of the reduced dataset, namely the

number of events, the density, and information en-

tropy. The proposed methods offer a panel of so-

lutions to choose from depending on the target task

(classiﬁcation, detection, tracking, etc.)

Our future work include the assessment of the pro-

posed methods on a classical computer vision tasks

such as classiﬁcation, in order to evaluate the accu-

racy loss brought by the proposed methods. Along

this line of research, we intend to develop event reduc-

tion using spiking neural networks, a relevant spatial

downscaling method for the neuromorphic processing

of event based data. This new type of asynchronous

artiﬁcial neural network is closer to biology than tra-

ditional artiﬁcial networks, mainly because they seek

to mimic the dynamics of neural membrane and ac-

tion potentials over time. The Leaky Integrate-and-

Fire neuron model more speciﬁcally simulates the

increase of the membrane potential lead by the fre-

quency of input spikes coupled with a constant slow

decrease. We believe that this mechanism is well

suited to implement an event downscaling method

which temporally pools input events. Preliminary re-

sults lead us to understand that hyperparametrisation

may have a signiﬁcant inﬂuence on this preprocess,

which we would like to discuss in the foreseeable fu-

ture. Besides, one important aspect for real time ap-

plications is the ability of the proposed methods to

operate in real time, so as to directly reduce the in-

put event ﬂow and save compute, memory and energy

in embedded systems. Therefore we will evaluate the

real time capability of the methods. A relevant ap-

plication of the proposed methods is to implement a

foveation mechanism, such as in (Gruel et al., 2021).

Finally, it will be useful to extend the spatial down-

scaling to temporal downscaling to further adjust the

density of event ﬂow.

ACKNOWLEDGEMENTS

This work was supported by the European Union’s

ERA-NET CHIST-ERA 2018 research and innova-

tion programme under grant agreement ANR-19-

CHR3-0008.

The authors are grateful to the OPAL infrastruc-

ture from Universit

e C

ote d’Azur for providing re-

sources and support.

REFERENCES

Amir, A., Taba, B., Berg, D., Melano, T., McKinstry, J.,

Di Nolfo, C., Nayak, T., Andreopoulos, A., Garreau,

G., Mendoza, M., Kusnitz, J., Debole, M., Esser, S.,

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

252

Delbruck, T., Flickner, M., and Modha, D. (2017). A

Low Power, Fully Event-Based Gesture Recognition

System. In Computer Vision and Pattern Recognition

(CVPR), pages 7388–7397, Honolulu, HI. IEEE.

Bi, Y., Chadha, A., Abbas, A., Bourtsoulatze, E., and An-

dreopoulos, Y. (2019). Graph-based object classiﬁca-

tion for neuromorphic vision sensing.

Chin, T.-J., Bagchi, S., Eriksson, A., and Schaik, A. V.

(2019). Star tracking using an event camera. 2019

IEEE/CVF Conference on Computer Vision and Pat-

tern Recognition Workshops (CVPRW).

Cohen, G., Afshar, S., van Schaik, A., Wabnitz, A., Bessell,

T., Rutten, M., and Morreale, B. (2017). Event-based

sensing for space situational awareness.

Cordone, L., Miramond, B., and Ferrante, S. (2021). Learn-

ing from Event Cameras with Sparse Spiking Con-

volutional Neural Networks. In IEEE, editor, Inter-

national Joint Conference On Neural Networks 2021

(IJCNN 2021), page 8, Conf

erence virtuelle, China.

Davies, M., Srinivasa, N., Lin, T.-H., Chinya, G., Cao, Y.,

Choday, S. H., Dimou, G., Joshi, P., Imam, N., Jain,

S., Liao, Y., Lin, C.-K., Lines, A., Liu, R., Math-

aikutty, D., McCoy, S., Paul, A., Tse, J., Venkatara-

manan, G., Weng, Y.-H., Wild, A., Yang, Y., and

Wang, H. (2018). Loihi: A neuromorphic many-

core processor with on-chip learning. IEEE Micro,

38(1):82–99.

Fang, W., Yu, Z., Chen, Y., Masquelier, T., Huang, T., and

Tian, Y. (2021). Incorporating learnable membrane

time constant to enhance learning of spiking neural

networks. In International Conference on Computer

Vision (ICCV), pages 2661–2671.

Furber, S. B., Lester, D. R., Plana, L. A., Garside, J. D.,

Painkras, E., Temple, S., and Brown, A. D. (2013).

Overview of the spinnaker system architecture. IEEE

Transactions on Computers, 62(12):2454–2467.

Gallego, G., Delbruck, T., Orchard, G., and al. (2020).

Event-based vision: A survey. IEEE Transactions on

Pattern Analysis and Machine Intelligence.

Gehrig, D., Gehrig, M., Hidalgo-Carri

o, J., and Scara-

muzza, D. (2020). Video to events: Recycling video

datasets for event cameras. In IEEE Conf. Comput.

Vis. Pattern Recog. (CVPR).

Glover, A. and Bartolozzi, C. (2016). Event-driven ball de-

tection and gaze ﬁxation in clutter. 2016 IEEE/RSJ In-

ternational Conference on Intelligent Robots and Sys-

tems (IROS).

Gruel, A., Martinet, J., Linares-Barranco, B., and Serrano-

Gotarredona, T. (2021). Stakes of foveation on event

cameras. In ORASIS 2021, Saint Ferr

eol, France. Cen-

tre National de la Recherche Scientiﬁque [CNRS].

Huang, C. (2021). Event-based timestamp image encod-

ing network for human action recognition and antic-

ipation. In 2021 International Joint Conference on

Neural Networks (IJCNN), pages 1–9.

Kim, H., Leutenegger, S., and Davison, A. J. (2016). Real-

time 3d reconstruction and 6-dof tracking with an

event camera. Computer Vision – ECCV 2016 Lecture

Notes in Computer Science, page 349–364.

Lagorce, X., Ieng, S.-H., Clady, X., Pfeiffer, M., and Benos-

man, R. (2015). Spatiotemporal features for asyn-

chronous event-based data. Front. Neurosci. - Neu-

romorphic Engineering.

Lenz, G., Chaney, K., Shrestha, S. B., Oubari, O., Pi-

caud, S., and Zarrella, G. (2021). Tonic: event-based

datasets and transformations. Documentation avail-

able under https://tonic.readthedocs.io.

Lichtsteiner, P., Posch, C., and Delbruck, T. (2008). A

128x128 120 db 15 us latency asynchronous tempo-

ral contrast vision sensor. IEEE Journal of Solid-State

Circuits.

Mahowald, M. and Mead, C. (1991). The Silicon Retina.

Sci. American.

Orchard, G., Benosman, R., Etienne-Cummings, R., and

Thakor, N. V. (2013). A spiking neural network ar-

chitecture for visual motion estimation. 2013 IEEE

Biomedical Circuits and Systems Conference (Bio-

CAS).

Paredes-Valles, F., Scheper, K. Y. W., and Croon, G. C. H.

E. D. (2020). Unsupervised learning of a hierarchi-

cal spiking neural network for optical ﬂow estimation:

From events to global motion perception. IEEE Trans-

actions on Pattern Analysis and Machine Intelligence,

42(8):2051–2064.

Rabbath, C. and Corriveau, D. (2019). A comparison

of piecewise cubic hermite interpolating polynomials,

cubic splines and piecewise linear functions for the

approximation of projectile aerodynamics. 31st Inter-

national Symposium on Ballistics.

Rebecq, H., Horstschaefer, T., and Scaramuzza, D. (2017).

Real-time visual-inertial odometry for event cameras

using keyframe-based nonlinear optimization.

Rebecq, H., Ranftl, R., Koltun, V., and Scaramuzza, D.

(2019). Events-to-video: Bringing modern computer

vision to event cameras. IEEE Conf. Comput. Vis. Pat-

tern Recog. (CVPR).

Rebecq, H., Ranftl, R., Koltun, V., and Scaramuzza, D.

(2021). High speed and high dynamic range video

with an event camera. IEEE Transactions on Pattern

Analysis and Machine Intelligence, 43(6):1964–1980.

Vidal, A. R., Rebecq, H., Horstschaefer, T., and Scara-

muzza, D. (2018). Ultimate slam? combining events,

images, and imu for robust visual slam in hdr and

high-speed scenarios. IEEE Robotics and Automation

Letters, 3(2):994–1001.

Zhang, L., Zhang, H., Zhu, C., Guo, S., Chen, J., and Wang,

L. (2021a). Fine-grained video deblurring with event

camera. In Loko

c, J., Skopal, T., Schoeffmann, K.,

Mezaris, V., Li, X., Vrochidis, S., and Patras, I., ed-

itors, MultiMedia Modeling, pages 352–364, Cham.

Springer International Publishing.

Zhang, Z., Yezzi, A., and Gallego, G. (2021b). Im-

age reconstruction from events. why learn it?

arXiv:2112.06242.

Event Data Downscaling for Embedded Computer Vision

253