Estimating Body Shapes from Measurements

Margarida Lima

, Joaquim Jorge

and Jo

ao Pereira

INESC-ID Lisboa, Instituto Superior T

ecnico da Universidade de Lisboa, Av. Rovisco Pais, Lisbon, Portugal

Keywords:

Virtual Garment Fitting, Body Shape, PCA, Linear Transformation, Body Measurements.

Abstract:

e-Commerce now represents more than a third of apparel sales in the USA and accounts for most sales growth

year on year. However, it is still hard for people to buy clothes online because they have no idea how they

will look. Thus, we present an approach to model an approximation of a human body shape with a given

set of body measurements to ﬁt virtual clothes. To estimate a new body shape from body measurements, we

developed two different models by using respectively linear transformations and PCA weights. Additionally,

we selected the minimum number of body measurements required to estimate a similar shape as the ground

truth. Finally, we evaluated our approach by comparing our results with estimations and visual evaluation

via pictures and measurements taken from real people. Results show that we can approximate human shape

through measurements with sufﬁcient ﬁdelity to simulate garment ﬁtting.

1 INTRODUCTION

The percentage of online shopping increases year af-

ter year, and e-commerce captured an even greater

share of apparel sales throughout 2020 due to the

coronavirus pandemic with a leaps and bound growth

of 33.6%, to a total of $800 billion. The growth

pattern is expected to maintain reaching $908 bil-

lion in 2021 (Goldman, 2021). However, many still

prefer to buy clothes in physical stores instead of e-

commerce sites

One of the reasons relates to the

difﬁculty of modeling garments realistically and thus

hardly to know how a piece of clothing would look

when dressed (Pezzini, 2021). Most devices do not

have the resources to realistically simulate the fab-

ric’s physics, material, and texture. We approached

this problem by comparing two models, one only us-

ing linear transformations and the other using fea-

ture extraction, to see which is the best approach to

model a new body shape from only body measure-

ments. We also wanted to see whether using PCA

was helpful in mapping body shape with body mea-

surements. Therefore, we contributed by modeling

realistic 3D triangular meshes of human bodies, con-

sidering a set of body measurements that accurately

https://orcid.org/0000-0003-1762-8091

https://orcid.org/0000-0001-5441-4637

https://orcid.org/0000-0002-8120-7649

https://www.lsretail.com/resources/why-physical-

stores-are-still-vital-for-retail

output a polygon mesh with approximately the exact

measurements as the ones inserted by the user with

a similar body shape. We also deﬁned the minimum

body measurements required to produce a mesh with

a similar body shape as the original one. Since our

target was virtual garment ﬁtting, the produced body

shape needed to resemble the original one the clos-

est possible. Thus, the mesh quality evaluation was

performed by considering two criteria. The ﬁrst one

consisted of comparing the ﬁnal mesh directly with

the estimated one by measuring the distance between

the correspondent vertices of both meshes. Since we

did not scan people to validate our approach, we com-

pared the ﬁnal mesh with silhouettes extracted from

pictures during the tests with real people. Thus, at

the testing phase, the users needed to manually insert

their body measurements and an RGB image of them-

selves wearing minimal or tight clothes. The second

criterion consisted of analyzing the ﬁnal mesh mea-

surements and seeing how closely these matched the

original.

2 RELATED WORK

Until recently, body representation has been used al-

most entirely in the gaming industry to create realistic

characters. Amaury and Thalmann describe in (Aubel

and Thalmann, 2000) two major models to represent

the human body: surface models where a mesh only

318

Lima, M., Jorge, J. and Pereira, J.

Estimating Body Shapes from Measurements.

DOI: 10.5220/0011002900003124

In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 1: GRAPP, pages

318-325

ISBN: 978-989-758-555-5; ISSN: 2184-4321

has skeleton and skin and multilayered techniques in-

cluding fat and muscle layers.

Surface Models. Most recent work done in creating

parametric avatars has been accomplished using ma-

chine learning techniques on a mesh database derived

from 3D scanned bodies of real people. After scan-

ning the necessary meshes, a system that estimates

body parameters can be trained. The usage of neu-

ral networks proved to be efﬁcient in this topic. Re-

cent works PIFuHD (Saito et al., 2020) used neural

implicit functions for shape representation. In HS-

Nets (Dibra et al., 2016), the parameters themselves

are computed based on images as input, and are used

to reconstruct the 3D human shapes by using a statis-

tical human shape model based on SCAPE (Anguelov

et al., 2005). In HS-Nets, to learn the global mapping

from the data to the parameters, a convolutional neu-

ral network (CNN) is trained. This CNN is trained

by feeding the images from different views into the

network. However, providing a 3D mesh with this

system might lead to a wrong human body shape

representation by misleading its body measurements.

The same argument is applied to Detailed Human

Depth Network (DHDNet) (Zhang et al., 2020), where

Zhang uses CNNs in order to estimate a detailed and

completed depth map from a single RGB image that

contains occlusions of human body. Since informa-

tion is retrieved from an RGB image, there is no cer-

tain that the displayed body representation of the indi-

vidual in the image respects its body measurements.

After obtaining the desired parameters, we can esti-

mate a 3D model. The usage of blend shapes allows

an approach without requiring any machine learning

technique. Morphing requires a target shape to be

able to morph from the base shape until the desired

one. However, this kind of process requires a lot of

modeling work. One example is HMR (Kanazawa

et al., 2018), Zhang builds a standard model to be de-

formed and to recover occluded surface details using

the depth information. Both HMD (Zhu et al., 2019)

and Seo in (Seo and Magnenat-Thalmann, 2003) use

blend shapes to update the shape of a model in real

time by using an iterative interface. IntExMa (Volz

et al., 2007) uses a morphing algorithm to comply

with the desired body measurements as input. An-

other example is (Loper et al., 2015) where blend

shapes are used not only for body poses but also for

animations. SMPL (Loper et al., 2015) is a skinned

vertex based model that accurately represents a wide

variety of body shapes in natural human poses. This

project deforms a mesh according to its body pose us-

ing blend shapes, that were calculated through princi-

pal component analysis (PCA). Learning the human

body shape through PCA is a strategy used by a lot

of projects (Baek and Lee, 2012) (Anguelov et al.,

2005) (Loper et al., 2015) (Chen et al., 2019) and it

is an effective strategy to learn the variation between

different human body shapes, that is why this strategy

will be used in this proposal as well to learn the blend

shapes that most realistic modify a human 3D mesh.

Seo in (Seo and Magnenat-Thalmann, 2003), uses a

template mesh as using a database of 3D scanned

meshes from real people, and it is used as examples

to correspond a template mesh deformations with the

body measurements.

2.1 Multi-layered Models

Multi-layered Models. A multilayered model also

composed by some intermediary layers such as mus-

cle and fat layer which improves animation results.

This way, when the skeleton moves, that motion will

be reproduced by all layers with the skin reproducing

them all. Multi-layer Lattice (Iwamoto et al., 2015)

achieve that using voxels. With a mesh and muscle-

to-fat ratio as an input, this mechanism is able to ﬁll

the interior and to get separated layers without any ex-

tra modeling work. Each voxel was classiﬁed accord-

ing to the muscle-to-fat ratio parameter that the user

inserted. The differentiation between layers is useful

for animation purposes, in which each layer behaves

differently. For instance, the fat should be much more

elastic than muscles. Another approach is to use pre-

vious modeled parts and adjust them to the inside of

the input mesh, like in Outside-In (Pratscher et al.,

2005). Similarly to Multi-layer Lattice, Outside-In

takes a mesh as ﬁlls the insides with artiﬁcial mus-

cles. Users can change muscle size in order to shape

avatars to taste.

3 OVERVIEW

Our development work was divided into three stages:

preprocessing, model generation, and evaluation. We

ﬁrst repaired and segmented the samples in the pre-

processing phase before extracting the body measure-

ments. That was accomplished by using three dif-

ferent distances between points on the mesh: length,

height, and girth. The usage of geodesics was impor-

tant because it takes into account the mesh surface to

compute the distance. It simulates what a tailor would

do while measuring people. We then used that infor-

mation to build two models that estimate a new shape

based on a set of body measurements in the model

generation stage. The ﬁrst one used feature extraction

to learn the principal components that vary in a human

body, and the second directly mapped body measure-

Estimating Body Shapes from Measurements

319

ments with coordinates using linear transformations.

Finally, we validated the results obtained according to

the shape and body measurements using both samples

from the dataset and tested with real people.

3.1 Preprocessing

The input meshes were delivered by the Semantic

Parametric Reshaping of Human Body Models (Yang

et al., 2014), a dataset with 3000 meshes, where 1500

are male and 1500 are female. Each mesh contains

12500 vertices and all meshes are positioned in a

neutral pose. All samples have been placed in point

to point correspondence, means that for two meshes

and m

all vertices v

∀i in V are in the same

semantic region. We use this dataset to extract the

coordinates of each samples as well as their body

measurements. We used manual segmentation in a

single mesh using Blender interface

, and replicate

it to the other meshes using a Python and Blender

integration module - blenderpy

. This is possible

due the point-to-point correspondence on the dataset.

Mesh Repair. The results of (Yang et al., 2014)

assume all meshes do not contain any non-manifold

vertices. However, a preliminary analysis using

Blender led us to conclude that most meshed con-

tained non-manifold vertices which could interfere

with extracting body measurements. We ﬁxed these

problems using Wrap 3, a professional tool developed

by Russian 3D Scanner

Body Measurements. Users manually inserted body

measurements as the system’s input. The measure-

ments required were split into three different cate-

gories: girth that measures the distance around the

middle of something, length and height that measure

the distance between two points. While lengths are

measured on the mesh surface heights are not. The

point correspondence property of the dataset is use-

ful once more to extract the body measurements, we

manually selected the initial and target points used

to measure in one sample of the dataset and repli-

cated it to the remaining meshes. Height measures

the distance between two points using the Euclidean

Distance on the z axis (the vertical one). The length

measures the distance between two points considering

the mesh’s surface that contains the initial and target

points. For this measurements we used the geodesic

distance. We calculate a geodesic using a modiﬁed

Dijkstra search algorithm (Dijkstra, 1959) to ﬁnd the

https://www.blender.org/

https://pypi.org/project/bpy/

https://www.russian3dscanner.com/

shortest paths between vertices. Differently from Di-

jkstra, geodesics can intersect edges to form straight-

line paths. Last, we compute girth measurements by

intersecting a plane with the mesh.

3.2 Model Generation

We compared two distinct methodologies against

each other. The ﬁrst uses linear transformations to

output a new body shape, while the second applies

feature extraction to explain the maximum variance

in the human body. But ﬁrst, we performed unsu-

pervised feature selection on the original dataset

to obtain the minimum measurement subset that

accounted for as much information as possible.

Since there was no a priori classiﬁcation of shapes,

supervised methodologies for body measurement

selection were ineffective. Feature selection reduced

characteristics to approximately 17%, down to seven

features from the initial 41. Both of our models used

the subset returned from the feature selection process

to output new body shapes.

Feature Selection. Unsupervised Feature Selection

consisted on analyzing the dataset to ﬁlter 34 mea-

surements out of 41. We proceeded to the distribution

analysis of each variable. We replaced all outliers

that were outside of the µ ± 3σ Gaussian boundary

by missing values, to prevent entropy in our system.

The missing values count after replacing the outliers

indicated that girth measurements were more affected

by missing values than the other measurements,

specially the underbust girth, bicep girth, armhole

girth and knee girth. Since those measurements were

prone to high amounts of error, we decided to exclude

them from the ﬁnal subset. Next, we normalized all

variables, sorted them by variance and selected the

ten variables that vary the most, resulting in the mea-

Table 1: Top 10 body measurements subset per gender

sorted by higher (1) to lower (7) variance. Both subsets

have 6 elements in common, but with a different variance

level. BM stands for body measurement.

Gender

Male Female

1 Bust Girth Bust Girth

2 Hip Girth Hip Girth

3 Thigh Girth Abdomen Girth

4 Rise Length Thigh Girth

5 Waist Girth Height

6 Abdomen Girth Waist Girth

7 Height Mid-Thigh Girth

8 Underbust-to-Belly-

Button Length

Waist Height

9 Neck Girth Inseam Height

10 Waist Height Hip-to-Ankle Height

GRAPP 2022 - 17th International Conference on Computer Graphics Theory and Applications

320

surements represented in Table 1. Next we calculated

the correlation between the top 10 measurements and

concluded that all height measurements are highly

correlated. Thus, besides height, any other height

measurement in the top ten could be removed without

losing information loss. By only maintaining the

height measurement from the top ten measurements,

the female subset resulted with seven measurements

and the male one with nine. In the male dataset, the

neck girth is correlated with the rise and underbust to

belly button lengths and we only maintained the neck

girth measurement. We ended up with two subsets

of seven body measurements, as shown in Table 2

with a highly uncorrelated variation. Both subsets

shared six measurements, leaving only one unique

measurement for each gender: neck girth for males

and mid-thigh girth for females. We thus reduced the

initial dataset by almost 83%.

Estimating Body Shapes with PCA The feature se-

lection was applied on the dataset containing the body

measurements, while the feature extraction was per-

formed on the coordinates dataset. The feature extrac-

tion was performed on the coordinates dataset using

Principal Component Analysis (PCA). We ﬁrst calcu-

lated the template meshes for each gender, that are

the mean of all samples. We then followed a sim-

ilar approach to Wuhrer proposal for estimating hu-

man shapes based of body measurements (Wuhrer and

Shu, 2012). As input to the method, it was given a

database of n triangular manifold shapes S

,..., S

n−1

human bodies with similar posture and a set of mea-

surements M. Let M

denote the measurements corre-

sponding to S

. Our aim is to estimate a shape S

new

that interpolates the distances M

new

. This approach

proceeded by learning the correlation between the

shapes and the measurements. The template meshes

S were used to calculate how much the samples dif-

fer from the average shape. Therefore, there is a new

dataset D that is composed by the differences between

all shapes of S and

S. Let D be a (3v × n) matrix. We

performed PCA in D, and it yielded a matrix W that

Table 2: Final body measurements subset per gender sorted

by higher (1) to lower (7) variance. Both subsets have the

ﬁrst 6 elements in common (even with a different sequence)

and only the last element of both subsets is unique.

Gender

Male Female

1 Bust Girth Bust Girth

2 Hips Girth Hips Girth

3 Thigh Girth Abdomen Girth

4 Waist Girth Thigh Girth

5 Abdomen Girth Height

6 Height Waist Girth

7 Neck Girth Mid-Thigh Girth

corresponded to the transformed dataset D. The ma-

trix W and matrix D are the representation of the same

information but in different spaces. By applying PCA

to D we extracted the information in the dataset by

creating a new coordinates system that ﬁtted the data

where it varies the most. We lost information regard-

ing the variables of D because new ones were created.

However, if D and W are the same matrix in different

coordinates systems, there was some matrix A that de-

ﬁnes the transformation between them. Thus, a new

shape S

new

can be estimated via Equation 1 where the

sum of the template mesh

S and the weights of a new

set of measurements W

new

transformed by A yields

new

= AW

new

+ µ (1)

However we still needed to calculate matrices A

and W

new

. We knew that W is D transformed into the

PCA coordinate system, thus A is responsible for the

coordinate system swapping. So we can infer A from

D and W, according to Equation 2 with D

being the

pseudo-inverse of D.

W = AD ⇔ A = W D

(2)

To calculate the weights matrix W

new

, we took into

consideration the body measurements and the PCA

weights W

of each shape S

. For that, we learned a

linear mapping from M

to W

with i = 0, ..., n − 1,

by transforming each M

to a new coordinate system

. To perform this, we calculated another transfor-

mation matrix B that maps body measurements to its

corresponding PCA weights, as shown in Equation 3,

where M

is the pseudo-inverse of B.

W = BM ⇔ B = W M

(3)

With this, we were able to relate the body mea-

surements to the information extracted from the hu-

man body variation through PCA and give it a weight.

To reproduce the results obtained in (Wuhrer and Shu,

2012) we normalized each entry of W by its corre-

spondent PCA eigenvalue. Finally, to estimate a new

shape X

new

based on a new set of body measurements

new

, we transformed M

new

to the PCA coordinates,

that resulted in a weight vector W

new

and then trans-

formed W

new

to the coordinate system that dictates the

shapes. Therefore, we rewrote the Equation 1 into

Equation 4.

new

= ABM

new

+ µ (4)

The mapping between the measurements and the

PCA weights of the 3D shapes allowed us to ﬁnd

an new shape S

new

given a new set of measurements

new

. With this process we understood how much the

human shape vary from the average human shape

We related that variation with the body measurements

M and estimate new shapes S

new

with a new set of

Estimating Body Shapes from Measurements

321

body measurements M

new

. By adding the weights cor-

responding to a new set of body measurements W

new

to the template mesh

S we obtained a new shape that

respects the variation dictated by M

new

3.2.1 Body Shape from Linear Transforms

Body Shape from Linear Transforms. In this

model, a shape can be directly obtained from the body

measurements. We accomplished this by creating a

transformation matrix between the coordinates and

body measurements datasets. Let us use the same ma-

trices and variables as in the previous model and as-

sume that there is a function T that maps a measure-

ments vector M into a vector of vertices coordinates S.

In this case, A represents a linear transformation map-

ping the space of body measurements to the space of

3D coordinates, as represented as in Equation 5.

new

= AM

new

(5)

Notice that S

new

returns a column vector with 3v ele-

ments, therefore A was a (3v × m) matrix. Also note

that A had 3v rows and m columns, whereas the trans-

formation was from ℜ

to ℜ

. To calculate the trans-

formation matrix A we needed to start from Equation

5 and isolate A, just as demonstrated in Equation 6.

S = AM ⇔ A = SM

(6)

4 EXPERIMENTAL EVALUATION

We divided the evaluation into validation and evalua-

tion processes. The validation was intended to verify

if models were performing as expected. We observed

which model performed the best and used the winner

to the ﬁnal evaluation process that involved real

users. Both processes were evaluated regarding the

shape and measurements of the estimated results.

4.1 Validation

To validate both models, we selected four different

samples from the database. These included two male

and two female scans, one smaller and the other

larger. Using samples that cover many variations

of human shape is essential to see whether the

techniques can deal with comprehensive cases.

Body Shape. We calculated the distance between

the correspondent vertices of the ground truth

samples and the estimated ones. With all distances

calculated, we visualized the error using a color

Figure 1: PCA Error color map using different measure-

ment sets. Each column corresponds to a subset of the top

ten body measurements or from the selected seven from Ta-

ble 2, from left to right: (a) top two (b) top four (c) top six

(d) top eight (e) top ten (f) selected six (g) selected seven (h)

original shape. The yellow parts denote higher error, while

the areas in dark blue are closer to the original shape.

map, like represented in Figures 2 and 1. Each

column represents a different subset, from right to

left: top 2, top 4, top 6 , top 8, top 10, selected 6,

selected 7 and ground truth. We estimated the same

shape using the seven different body measurement

subsets. To address to a speciﬁc estimation we use

the nomenclature (xy) where x is the row number and

y the column. We saw that the results were often

better when using more measurements. This was

supported by the MSE values, since they were higher

as the number of measurements used to estimate a

new shape decreases. However, in Figure 2 we saw

that the difference between (1d) and (1e) is almost

0 and their MSE difference was about 0.0002. This

GRAPP 2022 - 17th International Conference on Computer Graphics Theory and Applications

322

Figure 2: Linear Model Error color map with different mea-

surements set. Each column corresponds to a subset of the

top ten body measurements or from the selected seven from

Table 2, from left to right: (a) top two (b) top four (c) top

six (d) top eight (e) top ten (f) selected six (g) selected seven

(h) original shape. The yellow parts have a higher distance

error, while the dark blue parts are closer to the original

shape.

indicates that the insertion of the body measurements

nine and ten is irrelevant, and that we can obtain the

same results using only the ﬁrst eight measurements.

In (1c) of Figure 2 we noticed a big difference in the

height comparing the original sample. This happened

specially to male meshes because the height is not

part of the top six measurements, however it is

more noticeable in (1c) than in (2c). This happened

because of the high values of the remaining measure-

ments, like waist bust, abdomen, etc. Like sample

SPRING306’s body measurements were way higher

than average on the dataset and there were not many

samples with bigger sizes, the model estimated a new

shape using the information that it had. This resulted

in a shape that was very similar to the average male

body, but in a bigger scale. This explained why

in (1b) and (1c) of Figure 1 had a higher distance

difference of sample SPRING0306 in their feet and

head, since the center of all meshes is on their groin.

To produce a shape with such big measurements,

the model scaled the shape in order to respect them

and the model ends up being huge because in top six

measurements we do not have height as a constraint.

This effect is also visible in (1b) regarding the top

four measurements, however in (1a) it is not visible.

It is visible that in (1a), (1b) and (1c) the main

differences regarding the original mesh are in the

belly. Sample (1g) was characterized by having larger

dimensions and our linear model had difﬁculties rep-

resenting those dimensions to perfection. However

it returned a shape with larger dimensions but not

as big as the ones inserted. This happened because

groups of male with larger dimensions were poorly

represented in the Semantic Parametric Reshaping

of Human Body Models dataset (Yang et al., 2014).

The estimation presented in (1a) was very similar to

those in columns (1d) and (1e). While its maximum

error was similar(15cm), it failed to represent the

belly more similarly. We expected the columns (1g)

and (1g) to perform better since the subsets were

composed by body measurements that were obtained

through feature selection, represented in Table 2.

However, missing measures such as height and

underbust-to-belly button hurt the returned shape,

especially on the belly of the estimations where they

had a higher distance error. Analyzing the estimation

of sample SPRING0306 and its MSE values, we

concluded that the best subset of body measurements

is the top eight.

Body Measurements. We validated the body mea-

surements extracted from the estimated shapes with

the original ones. The body measurement extraction

of the estimated shapes was made just like the extrac-

tion of the measurements of the original shape was

made. We observed that our linear model was more

able to estimate shapes that belong to a group that is

well represented in the dataset than samples that are

poorly represented. Which means that the estimated

measurements of average shapes were more similar to

the original ones. In one of the female estimations we

observed that all subsets, except for top four and top

two, performed relatively well with a bigger error rate

on the girth measurements. Thus, since the subsets

obtained from Table 2 did not produce better results,

we discarded them for the evaluation, focusing on the

top eight with the linear model, instead.

4.2 Evaluation

We approached six different people, among friends

and family, including ﬁve females and one male.

Their ages ranged between 21 and 46 years, with 23

years on average. To perform the tests, we asked each

individual to extract ten body measurements accord-

ing to our selection and take two full-body pictures

of themselves: a frontal and a proﬁle one. We then

used the photos to compare the estimated mesh with

the user’s body shape. Finally, we extracted the body

measurements of the estimated mesh and compared

those to the measures taken by subjects.

Estimating Body Shapes from Measurements

323

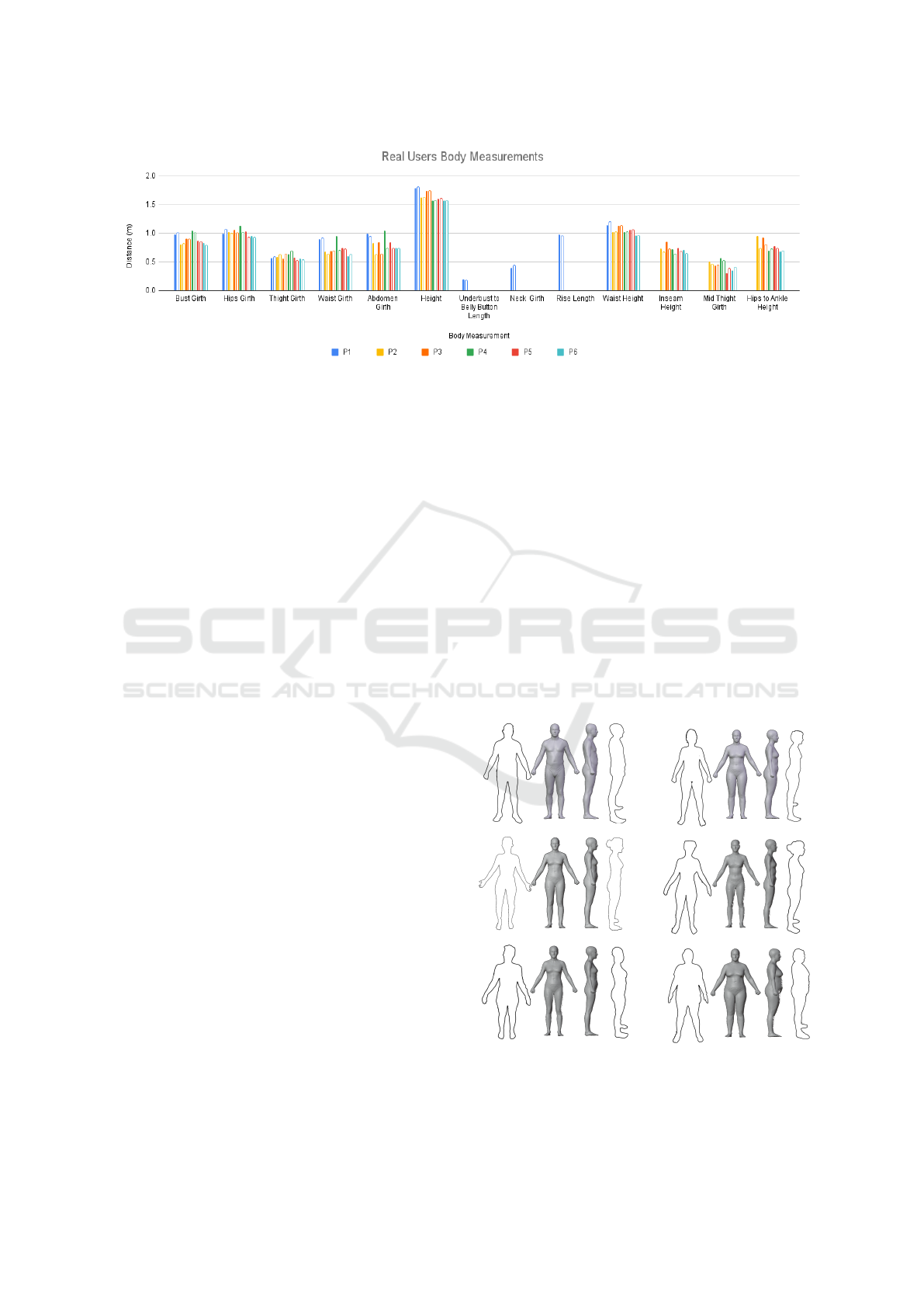
Figure 3: Real users’ ﬁnal measurements. Each subject corresponds to a different color. The solid bar denotes the actual

measurement value (ground truth of a speciﬁc person) and the hollow one its estimated value. To simplify the comparison, we

show each user’s original measurement value and the estimated one. We evaluated the top ten measurements of each gender,

represented in Table 1. There are six common measurements, while the last four are gender-speciﬁc.

Body Shape. To evaluate the body shape, we took

two pictures of the users: a frontal and a proﬁle one

and extracted their silhouette. Finally, these images

were placed side by side with their estimated. In

Figure 4 we can see the ﬁnal results. We noticed

that our model had difﬁculty modeling the waist of

estimated shapes. In cases where the original shape

had hips relatively larger than the waist, as P3 does,

our model returned a shape with a larger waist than

it should. However, our model estimated shapes

with a waist relatively similar to the hips as having

smaller waists. The data set contains the most typical

shape variations: A more slim appearance for both

represented genders and a waist thinner than the hip

for females. This made possible for our model to

return better estimations regarding P1, P2, P3, P4

and P5. Since P6 belongs to a group that is poorly

represented in the dataset, the model struggled to

estimate its shape. Our model also had difﬁculties

estimating fuller thighs. P2 is a good example.

We see that the frontal silhouette had fuller thighs,

something that the estimation does not. However, the

interior of the thighs is not very similar. However,

the estimations returned new shapes that were pretty

similar to the original ones. We asked subjects

whether the estimation was similar to their bodies.

They pointed the issues that we related in this paper

but said that overall the estimated shapes looked like

them. We concluded that our model could correctly

estimate body shapes from a few body measurements.

Body Measurements. We evaluated the body mea-

surements of the estimations and compared them with

the original ones and the results obtained from mea-

suring estimations are represented in Figure 3. We

noticed that the estimated height and waist height

measurements in female estimations were the same

as the original ones. However, the other height mea-

surements had some errors associated because people

found it difﬁcult to understand how to measure them-

selves. Other slight errors may be associated with the

ﬂuctuation of the waist point in the dataset meshes.

The measurement that had more error associated was

abdomen girth, with a distance difference reaching

up to 31cm. We believe this is also because the ver-

tex ﬂuctuations on the meshes and the girth extracted

might sometimes be more similar to the waist than the

abdomen itself. The estimations of the bust girth were

usually smaller than the original, reaching a distance

difference of 5cm in the worst case. However, some

measurements did not behave like this: thigh girth and

mid-thigh girth estimations had a higher measurement

value than the original value.

Figure 4: Visual comparison of real users silhouette with

their correspondent shape estimation using the top 8 mea-

surements subset. From left to right and top to bottom we

called these estimations P1, P2, P3, P4, P5 and P6.

GRAPP 2022 - 17th International Conference on Computer Graphics Theory and Applications

324

5 CONCLUSIONS

We compared two models, one using PCA weights

and the other using linear transformations to esti-

mate new shapes and concluded that PCA weights

are less adequate to estimate body shapes from mea-

surements. While evaluating with real users, we es-

timated our linear model using our top eight subsets.

Then, similarly to the validation step, we evaluated

the resulting body shape and measurement estima-

tions. We conclude that our model is not appropri-

ate for estimating new shapes with similar body mea-

surements as the original form. Moreover, since we

aim to develop a virtual dressing room, there are con-

cerns about how similar the estimated shape is to the

actual user body. If the measurements differ, instead

of helping people, our technique may mislead them

into buying the wrong size clothes. On the other side,

our model provided new body shapes that were very

similar to the original ones. The users also supported

this because the majority said that the estimation had

a similar shape to theirs. Our models can then sim-

ulate garment ﬁtting and rendering in virtual dress-

ing rooms. Future work includes estimating measure-

ments from a single photograph for a more expedited

user experience.

ACKNOWLEDGEMENTS

The work reported in this article was partly supported

by national funds through Fundac¸

ao para a Ci

encia e

a Tecnologia (FCT) under project UIDB/50021/2020.

REFERENCES

Anguelov, D., Srinivasan, P., Koller, D., Thrun, S., Rodgers,

J., and Davis, J. (2005). Scape: Shape completion

and animation of people. In ACM SIGGRAPH 2005

Papers, SIGGRAPH ’05, page 408–416, New York,

NY, USA. Association for Computing Machinery.

Aubel, A. and Thalmann, D. (2000). Realistic deformation

of human body shapes. In Magnenat-Thalmann, N.,

Thalmann, D., and Arnaldi, B., editors, Computer An-

imation and Simulation 2000, pages 125–135, Vienna.

Springer Vienna.

Baek, S.-Y. and Lee, K. (2012). Parametric human body

shape modeling framework for human-centered prod-

uct design. Computer-Aided Design, 44(1):56 – 67.

Digital Human Modeling in Product Design.

Chen, Y., Song, Z., Xu, W., Martin, R. R., and Cheng, Z.-

Q. (2019). Parametric 3d modeling of a symmetric

human body. Computers & Graphics, 81:52 – 60.

Dibra, E., Jain, H.,

Oztireli, C., Ziegler, R., and Gross,

M. (2016). Hs-nets: Estimating human body shape

from silhouettes with convolutional neural networks.

In 2016 Fourth International Conference on 3D Vision

(3DV), pages 108–117.

Dijkstra, E. W. (1959). A note on two problems in connex-

ion with graphs. Numerische mathematik, 1(1):269–

271.

Goldman, S. (2021). Post-pandemic e-commerce: The un-

stoppable growth of online shopping.

Iwamoto, N., Shum, H. P. H., Yang, L., and Morishima,

S. (2015). Multi-layer lattice model for real-time dy-

namic character deformation. Computer Graphics Fo-

rum, 34(7):99–109.

Kanazawa, A., Black, M. J., Jacobs, D. W., and Malik,

J. (2018). End-to-end recovery of human shape and

pose. In Proceedings of the IEEE Conference on Com-

puter Vision and Pattern Recognition (CVPR).

Loper, M., Mahmood, N., Romero, J., Pons-Moll, G., and

Black, M. J. (2015). Smpl: A skinned multi-person

linear model. ACM Trans. Graph., 34(6).

Pezzini, G. (2021). Why physical stores are still vital for

retail.

Pratscher, M., Coleman, P., Laszlo, J., and Singh, K.

(2005). ¡i¿outside-in¡/i¿ anatomy based character

rigging. In Proceedings of the 2005 ACM SIG-

GRAPH/Eurographics Symposium on Computer An-

imation, SCA ’05, page 329–338, New York, NY,

USA. Association for Computing Machinery.

Saito, S., Simon, T., Saragih, J., and Joo, H. (2020). Pi-

fuhd: Multi-level pixel-aligned implicit function for

high-resolution 3d human digitization. In Proceed-

ings of the IEEE Conference on Computer Vision and

Pattern Recognition.

Seo, H. and Magnenat-Thalmann, N. (2003). An automatic

modeling of human bodies from sizing parameters. In

Proceedings of the 2003 Symposium on Interactive 3D

Graphics, I3D ’03, page 19–26, New York, NY, USA.

Association for Computing Machinery.

Volz, A., Blum, R., H

aberling, S., and Khakzar, K. (2007).

Automatic, body measurements based generation of

individual avatars using highly adjustable linear trans-

formation. In Duffy, V. G., editor, Digital Hu-

man Modeling, pages 453–459, Berlin, Heidelberg.

Springer Berlin Heidelberg.

Wuhrer, S. and Shu, C. (2012). Estimating 3d human shapes

from measurements. Machine Vision and Applica-

tions, 24(6):1133–1147.

Yang, Y., Yu, Y., Zhou, Y., Du, S., Davis, J., and Yang,

R. (2014). Semantic parametric reshaping of human

body models. In 2014 2nd International Conference

on 3D Vision, volume 2, pages 41–48.

Zhang, T., Wang, J., Zhu, Q., and Yin, B. (2020). See

through occlusions: Detailed human shape estimation

from a single image with occlusions. In 2020 IEEE In-

ternational Conference on Image Processing (ICIP),

pages 2646–2650.

Zhu, H., Zuo, X., Wang, S., Cao, X., and Yang, R. (2019).

Detailed human shape estimation from a single image

by hierarchical mesh deformation. In Proceedings of

the IEEE/CVF Conference on Computer Vision and

Pattern Recognition (CVPR).

Estimating Body Shapes from Measurements

325