Teaching and Learning 3D Transformations in Introductory Computer

Graphics: A User Study

Thomas Suselo, Burkhard C. W

unsche and Andrew Luxton-Reilly

School of Computer Science, University of Auckland, Auckland, New Zealand

Keywords:

Computing Education, 3D Transformations, Computer Graphics, Spatial Skills.

Abstract:

Three-dimensional (3D) transformations are fundamental in computer graphics and hence an important com-

ponent of introductory courses in this ﬁeld. So far there has been no research investigating the learning

challenges and whether they are predominantly related to the underlying mathematics, problem solving skills,

programming issues, or a lack of visuospatial abilities. In this paper we present a user study investigating

which 3D transformation concepts students struggle with and why. Our results suggest that most students

understand primitive transformations, but often make errors with sequences of transformations, e.g., due to

not understanding how transformations affect each other or what the correct order of operations is in English

language, OpenGL code, or as a matrix product. Other frequent errors are misunderstanding the rotation direc-

tion (i.e., clockwise vs. anti-clockwise) and misinterpreting scaling factors. In addition, many students seem

to lack spatial reasoning skills to interpret images of 3D transformations and to make mental models of their

effect. Our results illustrate common misconceptions and problems, and we discuss strategies for educators to

improve the teaching of 3D transformations in computer graphics.

1 INTRODUCTION

Three-dimensional (3D) transformations are an es-

sential component of many introductory computer

graphics courses (Balreira et al., 2018), and are used

for modelling, view transformations, texturing, and

rendering. Evidence from the ﬁeld of mathemat-

ics (Kakoma, 2015; Ada and Kurtulus, 2010; Mbusi,

2016), previous research (Oberd

orfer et al., 2019;

Suselo et al., 2022), and our own experience, suggest

that many students ﬁnd this topic difﬁcult. A possi-

ble reason might be that computer graphics in general

requires a diverse range of skills, such as mathemat-

ics, programming, problem-solving and visuospatial

skills (Naiman, 1996; Schweitzer et al., 2010; Suselo

et al., 2017).

While the topic of 3D transformations in computer

graphics has not been thoroughly investigated, several

authors investigated teaching and learning of geome-

try. It has been suggested that spatial skills, including

mental rotation skills (Anderson et al., 2008; Kalo-

girou and Gagatsis, 2011), are an essential compo-

nent of geometry education (Jones and Tzekaki, 2016;

Leikin and Lev, 2007; Kinach, 2012; Lohman, 1996;

Sutton and Williams, 2012).

Teaching 3D transformations in the context of

computer graphics is more complex, since there is

a plain-language description, a mathematical repre-

sentation, and also a representation in program code,

which in itself can be based on different representa-

tions such as scene graphs or matrix stacks.

Many tools have been proposed to support teach-

ing of computer graphics concepts such as 3D trans-

formations (Suselo et al., 2019; W

unsche et al.,

2021). However, we could ﬁnd only one study in-

vestigating 3D transformations in the context of com-

puter graphics. Suselo et al. analysed data from

eleven years of exam results and propose that the dif-

ﬁculty of a question is predominantly determined by

the way students need to apply concepts to ﬁnd a so-

lution, rather than the concepts tested (Suselo et al.,

2021). The authors suggest that lack of spatial rea-

soning skills impedes learning but they do not inves-

tigate at what steps of the solutions process students

struggle most.

In this research we aim to identify which aspects

of the transformation topic pose particular challenges

for students by evaluating how students approach 3D

transformation questions, and at what point misunder-

standings occur.

Our research informs educators of common prob-

126

Suselo, T., Wünsche, B. and Luxton-Reilly, A.

Teaching and Learning 3D Transformations in Introductory Computer Graphics: A User Study.

DOI: 10.5220/0011003100003124

In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 1: GRAPP, pages

126-135

ISBN: 978-989-758-555-5; ISSN: 2184-4321

lems in teaching and learning 3D transformations, and

discusses how these could be overcome.

2 RESEARCH QUESTION

In this research we aim to answer the following re-

search questions:

RQ 1: What concepts related to 3D transforma-

tions do students struggle with most and why?

RQ 2: When solving 3D transformation ques-

tions, at what point during the solution process do

students have difﬁculties?

3 RELATED WORK

Researchers have developed and experimented with

a variety of tools to support teaching of computer

graphics ranging from using graphics APIs (Cun-

ningham, 2000; Cunningham and Shiﬂet, 2003;

Angel et al., 2006), to modelling and animation

tools (Elyan, 2012; Kadam et al., 2013), game en-

gines (Dickson, 2015; Smith and Sung, 2019), visu-

alisation tools (Dias et al., 2006), and custom made

tools (Suselo et al., 2019; Reina et al., 2014). More

recent frameworks also integrate automatic assess-

ment capabilities (Andujar et al., 2018; W

unsche

et al., 2018; W

unsche et al., 2019; W

unsche et al.,

2021).

While most tools support teaching of 3D transfor-

mations, they typically have limited functionality that

only allows students to perform such transformations

and receive visual feedback. Tools using a construc-

tivist approach have the advantage that students can

obtain an intuitive understanding of transformations,

without having to know and understand the underly-

ing mathematical representations.

Several researchers have proposed specialised

tools for teaching transformations in order to empha-

sise the relationship between mathematical represen-

tations, programming constructs implementing them,

and the visual effect (Felkel et al., 2018). A recently

explored medium is AR/VR since the presentation of

spatial knowledge in an immersive way might im-

prove understanding (Suselo et al., 2018; Suselo et al.,

2021; Oberd

orfer et al., 2019).

We were unable to ﬁnd research about student

problems with 3D transformations in computer graph-

ics apart from our analysis of exam results mentioned

above (Suselo et al., 2022). However, several au-

thors investigated misconceptions in geometry within

a mathematics curriculum.

Ozerem conducted a study with 28 high school

pupils and found that common errors were using

wrong formulas, lack of recognition and perception

of properties, errors in calculations, and omitting de-

tails (

Ozerem, 2012). Kakoma analysed 1000 scripts

from ﬁnal year high school students and found that

the majority of students did not understand basic con-

cepts in Euclidean transformations (rotation, trans-

lation, scaling) and that most errors where concep-

tual (Kakoma, 2015) . Ada and Kurtulus investigated

geometric misconceptions of 126 university students

in their third year of study of mathematics educa-

tion. The authors report that the most common mis-

take was that students seemed to understand the al-

gebraic meaning of translation and rotation, but not

their geometric meaning (Ada and Kurtulus, 2010).

Mbusi found that students lacked both procedural and

conceptual knowledge about transformations, and of-

ten struggled to visualise their effect (Mbusi, 2016).

Turgut et al. report that prospective elementary math-

ematics teachers could rotate ﬁgures in 2D if a ro-

tation axis was provided, but generally failed to ﬁnd

the centre of rotation of rotated ﬁgures (Turgut et al.,

2014).

4 METHODOLOGY

4.1 Context of Study

We performed a study investigating students’ prob-

lems with 3D transformation at the University of

Auckland, a leading research-focused urban univer-

sity in New Zealand.

Participants of the user study were third and fourth

year students, who were majoring in Computer Sci-

ence (≈ 90%) or Software Engineering (≈ 10%)

and had completed a 3rd year introductory computer

graphics module.

The module was delivered over 6 weeks and con-

sisted of the following components:

Week 1: OpenGL introduction and geometric

primitives

Week 2: Illumination, shading and shadows

Week 3: 3D transformations and modelling

Week 4: Texture mapping

Week 5: Ray tracing

Week 6: Parametric curves and surfaces

The topics are consistent with those identiﬁed in a sur-

vey of introductory computer graphics courses (Bal-

reira et al., 2018), except that we do not teach anima-

tions due to lack of time. The OpenGL component is

Teaching and Learning 3D Transformations in Introductory Computer Graphics: A User Study

127

taught using a bottom-up methodology, ﬁrst teaching

students the fundamentals and then more advanced

graphics concepts. This teaching methodology has

been reported to be the most common approach for

introductory computer graphics (Suselo et al., 2017).

The module uses C/C++ for programming tasks,

but most students only have a minimal exposure to

this language (about 2 weeks in a year 2 “computer

systems” paper) and will have predominantly used

Python and Java before entering the course. Students

are given web links for self-learning the basics of

C/C++.

4.2 Demographics

Our user study had 20 participants (14 male, 6 female)

all of whom were current students and had completed

the introductory computer graphics module described

above. Fifteen of the students had completed the mod-

ule three months before the study, and ﬁve students

more than one year before the study. Eighteen stu-

dents were between 20 and 30 years old and two stu-

dents were older than 30 years.

During the user study participants were individu-

ally interviewed and asked to solve 2D and 3D trans-

formation problems (explained below) and verbalise

their thoughts during the solution process. The inter-

viewer made notes of these thoughts and observed all

steps of the solution process. The total time for this

study was 30 minutes.

Participants received a $30 supermarket voucher

as a token of our appreciation.

4.3 User Study Activities

We selected three problems about 3D transforma-

tions, and one about a 2D transformation. In order

to gain more insight into the solution process, the

problems were divided into multiple tasks covering

conceptual understanding, ability to write OpenGL

code, and ability to write mathematical representa-

tions (transformation matrices). This resulted in 12

questions:

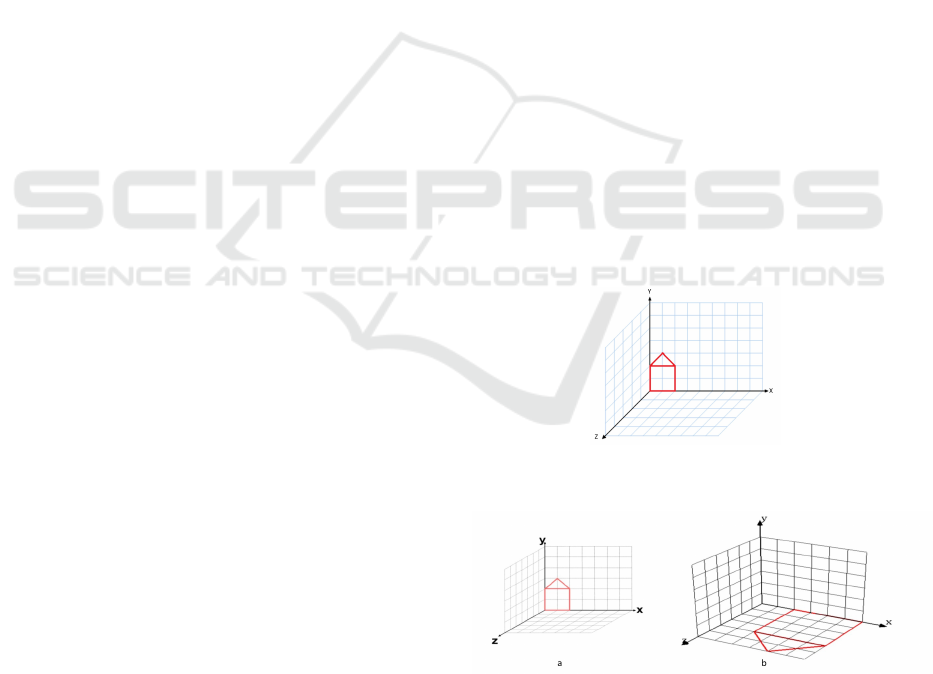
• Problem #1: Rotate the 2D shape in ﬁgure 1 by

◦

around the x-axis.

– Q1: How do you determine the rotation direc-

tion?

– Q2: How do you determine the position of the

shape after rotation?

– Q3: Please draw the rotated shape.

• Problem #2: Transform the 2D shape in ﬁgure 2

(a) into the shape in ﬁgure 2 (b) by using a se-

quence of primitive 3D transformations.

– Q4: Please describe the required transforma-

tions in plain English.

– Q5: Please write down a sequence of OpenGL

commands performing the required transforma-

tion.

– Q6: Please write down a sequence of homo-

geneous 3D matrices performing the required

transformation.

• Problem #3: Transform the 2D shape in ﬁgure 3

(a) into the shape in ﬁgure 3 (b) by using a se-

quence of primitive 2D transformations.

– Q7: Please describe the required transforma-

tions in plain English.

– Q8: Please write down a sequence of OpenGL

commands performing the required transforma-

tion.

– Q9: Please write down a sequence of homo-

geneous 2D matrices performing the required

transformation.

• Problem #4: Transform the 3D shape in ﬁgure 4

(a) into the shape in ﬁgure 4 (b) by using a 3D

transformation.

– Q10: Please describe the required transforma-

tion in plain English.

– Q11: Please write down the OpenGL command

for performing the required transformation.

– Q12: Please write down a homogeneous 3D

matrix performing the required transformation.

Figure 1: User study problem #1: Rotating a 2D shape

around the x-axis.

Figure 2: User study problem #2: Transform a given 2D

shape (a) into another shape (b) using a sequence of primi-

tive 3D transformations.

GRAPP 2022 - 17th International Conference on Computer Graphics Theory and Applications

128

5 RESULTS

5.1 Conceptual Understanding

The ﬁrst problem, and the ﬁrst task of the remaining

three problems, tested conceptual understanding by

asking students to describe the solution in plain En-

glish and/or by drawing it.

For question Q1 eight participants mentioned the

right-hand rule and described it correctly. Two

students described it incorrectly: one used the in-

dex ﬁnger to point along the axis, and another

one used the thumb to point along the rotation

axis, but then thought the ﬁngers would specify

the clockwise-direction. Seven participants used a

“clock” metaphor, e.g., facing the x-axis and imagin-

ing there is a clock, using a pen aligned with the x-axis

and imagining it was a clock, or looking at their mo-

bile phone (which had an analogue-clock representa-

tion). Three participants said “I visualise it”, but were

unable to be more speciﬁc.

Figure 3: User study problem #3: Transform a given 2D

shape (a) into another shape (b) using a sequence of primi-

tive 2D transformations.

Figure 4: User study problem #4: Transform a given 3D

shape (a) into another shape (b) using a 3D transformation.

For question Q2 eight students indicated on paper

how the object would move, two students described

how speciﬁc points would move, and ten students ex-

plained what they assumed would be the ﬁnal position

of the house shape.

For question Q3 ﬁfteen students drew the rotated

shape correctly and ﬁve incorrectly. From the incor-

rect solutions two students used the wrong right-hand

rule (see above) and three students described the rota-

tion correctly, but were apparently unable to mentally

perform the rotation and hence drew it incorrectly.

For question Q4 (problem #2) we asked partici-

pants to explain in plain English how the object in

ﬁgure 2 is transformed. Only eight students gave a

completely correct explanation. For the incorrect an-

swers the following errors were observed (multiple er-

rors were possible):

• Six participants made errors in the order. In all

cases students said they would ﬁrst translate by 2

in the x-direction, and then scale by 2 in both the

x- and y-directions. While this order is possible, it

is only correct when translating by one, since the

scaling will double the distance to the origin.

• Seven participants described a wrong rotation (six

rotated 90

◦

clockwise and one by 180

◦

• Two participants described an incorrect scaling,

i.e., only scaled in the x-direction or did not spec-

ify the coordinate directions.

For question Q7 (problem #3) we asked partici-

pants to explain in plain English how the object in

ﬁgure 3 is transformed. Only four students gave a

completely correct explanation. Three of them ﬁrst

scaled in the x-direction, then translated by y=-1 and

x=3, and then rotated by 30

◦

anti-clockwise. One stu-

dent came up with a different solution, i.e., translating

by 1.5 in y-direction, scaling by 2 in the y-direction,

and then rotating by 60

◦

clockwise. For the incorrect

answers the following errors were observed (multiple

errors were possible):

• Nine participants made errors in the order. In most

cases students translated by 3 in the x-direction

after rotating 30

◦

anti-clockwise. A few students

did the scaling after the rotation and/or transla-

tion.

• Two students speciﬁed an incorrect translation

amount, i.e., rotated ﬁrst and then tried to com-

pute the translation amount using the Pythagorean

theorem, but computed it incorrectly.

• Two students rotated clockwise rather than anti-

clockwise.

• Two students had a correct solutions except that

they forgot to translate by -1 in the y-direction be-

fore the rotation.

• Two solutions were completely incorrect and it

was unclear what the students tried to do and

hence we were unable to classify the errors.

For question Q10 (problem #4) we asked partici-

pants to explain in plain English how the object in ﬁg-

ure 4 is transformed. Fourteen students answered cor-

rectly that the object needs to be translated by 2 units

in the y-direction. Five students answered -2 units in

Teaching and Learning 3D Transformations in Introductory Computer Graphics: A User Study

129

the y-direction. We are unsure whether they misinter-

preted the question (i.e., transformed the object from

part (b) of the ﬁgure into that in part (a)), or whether

students believed that it must be a negative translation

because the object is on the negative y-axis. One stu-

dent said that a rotation around the x-axis is necessary

to get the image in (b).

5.2 OpenGL Code

As mentioned previously only 8 out of 20 partici-

pants managed to describe the solution for question

Q4 correctly in plain English. From those eight par-

ticipants only three managed to write completely cor-

rect OpenGL code for question Q5. For the remaining

17 students the following errors were observed (mul-

tiple errors are possible):

• Six participants wrote the OpenGL commands in

the same order as in English language, whereas it

should have been the opposite order.

• Seven participants reversed the order from their

English language description correctly, but ended

up with incorrect results since that description was

wrong.

• One participant used neither the same nor the re-

verse order as in English language.

• Three participants used a scale factor of zero pro-

ducing an incorrect result (ﬁve more students used

a scale factor of zero for a coordinate which didn’t

effect the result).

• Three participants scaled or translated in an incor-

rect coordinate direction.

• One participant didn’t answer that question.

As mentioned previously only 4 out of 20 partic-

ipants managed to describe the solution for question

Q7 correctly in plain English. None of the 20 partic-

ipants managed to write completely correct OpenGL

code for the solution. From the four participants who

described the solution correctly in English, two wrote

the solution using the same order as in English lan-

guage, and two performed a rotation by −30

◦

even

though they speciﬁed for Q6 correctly that the rota-

tion needs to be anti-clockwise. For the remaining 16

participants the following errors were observed (mul-

tiple errors are possible):

• Three participants wrote the OpenGL commands

in the same order as in English language, whereas

it should have been the opposite order.

• Nine participants generated an incorrect English

language description, but correctly translated it

into OpenGL code by reversing the order of com-

mands.

• Two participant used neither the same nor the re-

verse order as in English language.

• Six participants used a scale factor of zero produc-

ing an incorrect result (two more students used a

scale factor of zero where it didn’t effect the re-

sult).

• Two participants scaled or translated in an incor-

rect coordinate direction.

• One participant didn’t answer the question.

For question Q11 twelve students provided the

correct answer (all of them had answered question

Q10 correctly). Two of the students who answered

question 10 correctly used in the OpenGL code the

3D translation vector (1,2,1) instead of (0,2,0).

5.3 Mathematical Description

For question Q6 only one participant gave the correct

answer. For the remaining 19 participants the follow-

ing errors were observed:

• Ten participants did not provide an answer.

• Four participants wrote down at least one matrix

for the scaling, translation and rotation compo-

nent, but none of these components was correct.

• Two participants got one matrix correct (transla-

tion or scaling).

• Three participants provided the correct translation

and scaling matrix, but made errors in the rotation

matrix.

For question Q9 no participant gave the correct an-

swer and the following errors were observed:

• Twelve participants did not provide an answer.

• Six participants wrote down at least one matrix for

the scaling, translation and rotation component,

but none of these components was correct.

• Two participants provided the correct translation

and scaling matrix, but made errors in the rotation

matrix.

For question Q12 only two participants gave the

correct answer, both of them also answered questions

Q10 and Q11 correctly. For the remaining 18 partici-

pants the following errors were observed:

• Nine participants did not provide an answer.

• Four participants made the same mistake as in the

English language description, i.e., translated by -2

in y-direction.

• Six participants didn’t know the correct format of

a translation matrix, i.e., either had translation pa-

rameters in incorrect positions or wrote the trans-

lation matrix as a 3× 3 matrix without a homoge-

neous component.

GRAPP 2022 - 17th International Conference on Computer Graphics Theory and Applications

130

6 DISCUSSION

6.1 Common Problems

Our results from analysing conceptual understanding

(explaining a solution in plain English) suggests that

for a proportion of students (in our case at least 25%)

problems existed even for fundamental concepts such

as simple rotations or translations of 3D objects or

correct scale factors (using a scale factor of 0 instead

of 1 if the coordinate should stay unchanged). De-

spite being taught and emphasised in lectures, more

than half of the students couldn’t recall the right-hand

rule. However, about a third of students made their

own mental model of rotations and were able to use it

correctly.

Problems were particularly evident for sequences

of transformations. While all students seemed to have

a general idea of what to do (i.e., for problem #2 and

#3 to use a translation, scaling and rotation), more

than half of the students didn’t seem to have a mental

model of how a transformation would effect a subse-

quent transformation (e.g., scaling before or after a

translation, or how the position of an object effects

the result of a rotation).

One surprising result was that many students who

were able to describe the solution correctly in plain

English, made mistakes when writing the solution as

OpenGL code. The most common problems were us-

ing the wrong order of commands or selecting wrong

values for parameters not required in the conceptual

explanation (e.g. students translated “scale by 2 in

x-direction” into OpenGL code scaling by 2 in x-

direction and by 0 in the other dimensions, rather

than scaling by 1 in the dimensions where the object

should not change).

Students struggled with writing down correct

transformation matrices. For the simplest problem

only 2 out of 20 students were able produce a correct

matrix, and for the most complex problem nobody

gave the correct answer. We observed many basic

errors, e.g., incorrect parameters or incorrect format

(writing a translation as non-homogeneous matrix).

6.2 Causes of Problems

Student problems with remembering basic facts such

as scaling by one rather than zero, or clockwise vs.

anti-clockwise rotation direction could have two rea-

sons: (1) The user study participants completed the

computer graphics module at least 3 months (for ﬁve

of them even more than a year) before the study, and

they might have simply forgotten certain details. Note

that none of the participants was a current postgrad-

uate student in computer graphics. (2) We used a

web-based teaching and assessment tool (W

unsche

et al., 2018; W

unsche et al., 2019), which was used

for weekly programming labs. The tool might have

encouraged students to solve problems by trial-and-

error, rather than thinking deeply about the meaning

and effect of different commands and parameters.

Participants in our user study seemed to ﬁnd ques-

tions using sequences of transformations and differ-

ent representations more difﬁcult. This could be due

to these questions having a relatively high cognitive

load, since students have to create a mental model of

the problem, associating it with different representa-

tions (e.g., OpenGL code and visuals), and ﬁnding a

solution. This ﬁnding is in line with research that cog-

nitive systems can quickly be overburdened causing

errors in performing relatively complex tasks (Huang

et al., 2009). While some previous research has

shown that graphical representations can improve un-

derstanding (Ziemkiewicz and Kosara, 2008; Jones

and Tzekaki, 2016), research in cognitive science in-

dicates that the effectiveness of graphical represen-

tations depends on users’ working memory capac-

ity (Lohse, 1997) and memory updating ability (Xing

et al., 2019). Hence for many students with existing

deﬁcits (mathematics, visuospatial skills), our teach-

ing tools and assessment tasks might have been too

complex. This observation correspond with the “vi-

sual chunking theory” that students with high spatial

abilities are able to solve problems with a lower cog-

nitive load by using “visual chunking” (Stieff et al.,

2020).

Related to this is that many of our questions used

visual representations and participants with low visu-

ospatial skills might have struggled to translate the vi-

sual representation into appropriate actions (Gilhooly

and Murphy, 2005). Furthermore, research in mathe-

matics education suggests that the beneﬁts of imagery

depend on users’ abilities, i.e., high achievers pre-

fer and beneﬁt from schematic imagery, whereas low

achievers prefer more simplistic pictorial images (van

Garderen, 2006).

We attribute participants’ problems with writing

down mathematical equations to a combination of is-

sues:

• We observed that many students struggle with

mathematics and often don’t know simple con-

cepts such as vector arithmetic or matrix multi-

plications.

• Because of students’ reducing mathematics abili-

ties our teaching has become progressively more

programming-based (emphasising conceptual un-

derstanding and giving students visual feedback).

Teaching and Learning 3D Transformations in Introductory Computer Graphics: A User Study

131

Hence it is possible to get good grades without

understanding the underlying mathematics, which

might have encouraged students to study mathe-

matical representations less.

• As mentioned previously students completed the

computer graphics module at least three months

before the user study and hence might have for-

gotten many details.

6.3 Implications on Teaching

We consider mathematics to be very important and

provide students with self-learning material and

teach all material exceeding high-school mathematics

knowledge. However, we suggest that for an introduc-

tory course reliance on mathematics abilities should

be reduced where possible, in order to make it acces-

sible to students with a wider range of backgrounds

(e.g. creative industries).

We believe that students can learn and apply com-

puter graphics concepts such as 3D transformations

without memorising the exact mathematical details

(formulas). We removed a mathematics prerequisite

around 2013 and did not observe any change in per-

formance in subsequent years. A subsequent study (to

be published), showed that correlation between suc-

cess in computer graphics and mathematics abilities

was similar to correlation with general academic per-

formance.

Our research indicates that understanding of 3D

scenes and 3D transformations requires visuospatial

(spatial reasoning) skills. This corresponds to obser-

vations that spatial skills are correlated with success

in 3D geometric thinking (Pittalis and Christou, 2010;

Fujita et al., 2020), other mathematical ﬁelds (Cheng

and Mix, 2014; Lowrie and Logan, 2018; Lowrie

et al., 2018), and introductory programming (Cooper

et al., 2015; Parkinson and Cutts, 2018; Parkinson,

2020; Bockmon et al., 2020).

While spatial reasoning skills can be

trained (Lowrie et al., 2019; Sorby et al., 2013;

Uttal et al., 2012) this is rarely part of school and

university curricula and many researchers call for

a more spatially enriched education (Maranto and

Wai, 2020; Gold et al., 2018; Stieff and Uttal, 2015;

Uttal et al., 2012). We believe spatial skills should be

trained as part of a computer graphics and computing

curriculum in general.

We recommend instructors to take into account

that students with low socio-economic status have sta-

tistically lower spatial skills (M

ohring et al., 2021).

Hence the way course content is presented and as-

sessed may disadvantage students from these groups.

We believe AR/VR tools might be particular suit-

able both for training spatial skills (Pathak et al.,

2020), as well as for improving teaching and learn-

ing of computer graphics. Reasons are their immer-

sive nature and the potential to reduce cognitve load in

users by providing a better understanding of 3D con-

cepts (Oberd

orfer and Latoschik, 2018; Oberd

orfer

et al., 2019; Suselo et al., 2018; Demitriadou et al.,

2019; Mart

ın-Guti

errez et al., 2015; Suselo et al.,

2021).

7 LIMITATIONS

Our user study had only 20 participants and it is un-

clear whether they provided an appropriate represen-

tation of the student cohort. We analysed grades from

participants and they varied from failed to A grades,

and had a similar distribution to the entire cohort, but

overall were slightly higher.

Participants from the user study completed the

computer graphics module between 3 months and

more than a year ago, and might have forgotten many

concepts by the time of the user study. This might

have contributed to the fact that many students didn’t

know details, such as the deﬁnition of anti-clockwise

or mathematical representations, but had a satisfac-

tory conceptual understanding of transformations.

8 CONCLUSION AND FUTURE

WORK

Our user study showed that most students conceptu-

ally understood primitive transformations, but often

missed important details, e.g., confusing clockwise

and anti-clockwise direction, and in particular found

it hard to apply these concepts to solve more complex

problems.

Many students did not understand how transfor-

mations affect each other, or misunderstood how the

order of the execution of transformations is related to

the order they are written in English language, the or-

der of function calls in OpenGL code, or as a ma-

trix product. We recommend that these differences

are emphasised in teaching and assessment.

Many difﬁculties seemed to be related to the rep-

resentation of transformations and users’ inability to

construct a solution mentally. We suggest that this

might be caused by differences in visuospatial skills

and we believe such skills should be trained, and

AR/VR tools should be used to improve students’ spa-

tial understanding

GRAPP 2022 - 17th International Conference on Computer Graphics Theory and Applications

132

In future work we would like to investigate the ef-

fect of visuospatial skills in more detail, i.e., test stu-

dents’ spatial reasoning skills and correlate them with

performance for different assessment types in order

to investigate which spatial skills are most important,

i.e. spatial perception, spatial visualisation, mental

rotation or visuospatial memory. We would like to

provide a more spatially enriched curriculum and test

whether it improves students’ performance.

Furthermore, we want to investigate ways to in-

tegrate formative feedback into our teaching tools to

make students more aware of misconceptions (Sanna

et al., 2012; Lamberti et al., 2014; Hodgkinson et al.,

2016). Ideally we would like to add concepts from

intelligent tutoring systems (ITS), such as automatic

difﬁculty adjustment and customised lesson content,

in order to ensure that students can built up knowl-

edge incrementally and repeat basic concepts where

required (Crow et al., 2018).

ACKNOWLEDGEMENTS

The authors of the paper would like to acknowledge

and thank our students and the user study participants

for their interest, effort and contribution. The user

study was approved by University of Auckland Hu-

man Participants Ethics Committee Reference num-

ber 019021.

REFERENCES

Ada, T. and Kurtulus, A. (2010). Students’ misconceptions

and errors in transformation geometry. International

Journal of Mathematical Education in Science and

Technology, 41:901–909.

Anderson, K. L., Casey, M. B., Thompson, W. L., Burrage,

M. S., Pezaris, E. E., and Kosslyn, S. M. (2008). Per-

formance on middle school geometry problems with

geometry clues matched to three different cognitive

styles. Mind, Brain, and Education, 2:188–197.

Andujar, C., Chica, A., Fair

en, M., and Vinacua, A.

(2018). GL-Socket: A CG Plugin-based Framework

for Teaching and Assessment. In Proc. of Eurograph-

ics 2018 - Education Papers, pages 25–32, Goslar,

Germany. The Eurographics Association.

Angel, E., Cunningham, S., Shirley, P., and Sung, K.

(2006). Teaching computer graphics without raster-

level algorithms. SIGCSE Bull., 38(1):266–267.

Balreira, D. G., Walter, M., and Fellner, D. W. (2018). A

survey of the contents in introductory computer graph-

ics courses. Computers & Graphics, 77:88–96.

Bockmon, R., Cooper, S., Gratch, J., Zhang, J., and Dorod-

chi, M. (2020). Can students’ spatial skills predict

their programming abilities? In Proceedings of the

2020 ACM Conference on Innovation and Technology

in Computer Science Education (ITiCSE ’20), pages

446–451, New York, NY, USA. Association for Com-

puting Machinery.

Cheng, Y.-L. and Mix, K. S. (2014). Spatial training im-

proves children’s mathematics ability. Journal of Cog-

nition and Development, 15(1):2–11.

Cooper, S., Wang, K., Israni, M., and Sorby, S. (2015). Spa-

tial skills training in introductory computing. In Pro-

ceedings of the Eleventh Annual International Confer-

ence on International Computing Education Research

(ICER ’15), pages 13–20, New York, NY, USA. Asso-

ciation for Computing Machinery.

Crow, T., Luxton-Reilly, A., and W

unsche, B. C. (2018).

Intelligent tutoring systems for programming educa-

tion: A systematic review. In Proceedings of the 20th

Australasian Computing Education Conference (ACE

2018), pages 53–62, New York, NY, USA. Associa-

tion for Computing Machinery.

Cunningham, S. (2000). Re-inventing the introductory

computer graphics course: Providing tools for a wider

audience. Computers & Graphics, 24(2):293–296.

Cunningham, S. and Shiﬂet, A. B. (2003). Computer graph-

ics in undergraduate computational science education.

In Proceedings of the 34th Technical Symposium on

Computer Science Education (SIGCSE 2003), pages

372–375, New York, NY, USA. Association for Com-

puting Machinery.

Demitriadou, E., Stavroulia, K.-E., and Lanitis, A. (2019).

Comparative evaluation of virtual and augmented re-

ality for teaching mathematics in primary education.

Education and Information Technologies, 25:381–

401.

Dias, P., Madeira, J., and Santos, B. S. (2006). Using vtk

as a tool for teaching and applying computer graph-

ics. In Brown, J. and Hansmann, W., editors, Proc. of

Eurographics 2006 - Education Papers, pages 61–67,

Goslar, Germany. The Eurographics Association.

Dickson, P. E. (2015). Using unity to teach game develop-

ment: When you’ve never written a game. In Proceed-

ings of the 2015 ACM Conference on Innovation and

Technology in Computer Science Education (ITiCSE

2015), pages 75–80, New York, NY, USA. Associa-

tion for Computing Machinery.

Elyan, E. (2012). Enhanced interactivity and engagement:

Learning by doing to simplify mathematical concepts

in computer graphics and animation. In Proceedings

of the 2012 IEEE Global Engineering Education Con-

ference (EDUCON), pages 1–8, Marrakech, Morocco.

IEEE.

Felkel, P., Magana, A. J., Folta, M., Sears, A. G., and Benes,

B. (2018). I3t: Using interactive computer graphics to

teach geometric transformations. In Post, F. and

ara,

J., editors, Proc. of Eurographics 2018 - Education

Papers, page 1, Goslar, DEU. The Eurographics As-

sociation.

Fujita, T., Kondo, Y., Kumakura, H., Kunimune, S., and

Jones, K. (2020). Spatial reasoning skills about 2d

representations of 3d geometrical shapes in grades

4 to 9. Mathematics Education Research Journal,

32(1):235–255.

Teaching and Learning 3D Transformations in Introductory Computer Graphics: A User Study

133

Gilhooly, K. and Murphy, P. (2005). Differentiating insight

from non-insight problems. Thinking & Reasoning,

11(3):279–302.

Gold, A. U., Pendergast, P. M., Ormand, C. J., Budd,

D. A., Stempien, J. A., Mueller, K. J., and Kravitz,

K. A. (2018). Spatial Skills in Undergraduate Stu-

dents—Inﬂuence of Gender, Motivation, Academic

Training, and Childhood Play. Geosphere, 14(2):668–

683.

Hodgkinson, B., Lutteroth, C., and W

unsche, B. C. (2016).

glGetFeedback - Towards Automatic Feedback and

Assessment for OpenGL 3D Modelling Assignments.

In Proceedings of Image and Vision Computing New

Zealand (IVCNZ 2016), pages 1–6, Palmerston North,

New Zealand. IEEE.

Huang, W., Eades, P., and Hong, S.-H. (2009). Measuring

effectiveness of graph visualizations: A cognitive load

perspective. Information Visualization, 8(3):139–152.

Jones, K. and Tzekaki, M. (2016). Research on the Teaching

and Learning of Geometry, chapter 1, pages 109–149.

SensePublishers, Rotterdam.

Kadam, K., Sahasrabudhe, S., Iyer, S., and Kamat, V.

(2013). Integration of blender 3d in basic computer

graphics course. In 21st International Conference on

Computers in Education (ICCE 2013), pages 477–

479, Bali, Indonesia. Asia-Paciﬁc Society for Com-

puters in Education.

Kakoma, L. (2015). Understanding students’ misconcep-

tions: An analysis of ﬁnal grade 12 examination ques-

tions in geometry. Pythagoras, 36(1):1–11.

Kalogirou, P. and Gagatsis, A. (2011). A ﬁrst insight of

the relationship between students’ spatial ability and

geometrical ﬁgure apprehension. Acta Didactica Uni-

versitatis Comenianae Mathematics, 11:27–39.

Kinach, B. M. (2012). Fostering spatial vs. metric un-

derstanding in geometry. Mathematics Teacher,

105(7):534–540.

Lamberti, F., Sanna, A., Paravati, G., and Carlevaris, G.

(2014). Automatic grading of 3D computer anima-

tion laboratory assignments. IEEE Transactions on

Learning Technologies, 7(3):280–290.

Leikin, R. and Lev, M. (2007). Multiple solution tasks as a

magnifying glass for observation of mathematical cre-

ativity. In Proceedings of the 31st International Con-

ference for the Psychology of Mathematics Education,

volume 3, pages 161–168, Seoul, Korea. The Korea

Society of Educational Studies in Mathematics Seoul.

Lohman, D. F. (1996). Spatial Ability and G, chapter 1,

pages 97–116. Lawrence Erlbaum Associates, Inc.,

Hillsdale, NJ, US.

Lohse, G. L. (1997). The role of working memory on graph-

ical information processing. Behaviour & Information

Technology, 16(6):297–308.

Lowrie, T. and Logan, T. (2018). The Interaction Between

Spatial Reasoning Constructs and Mathematics Un-

derstandings in Elementary Classrooms, chapter 1,

pages 253–276. Springer International Publishing,

Cham, Switzerland.

Lowrie, T., Logan, T., Harris, D., and Hegarty, M.

(2018). The impact of an intervention program on stu-

dents’ spatial reasoning: student engagement through

mathematics-enhanced learning activities. Cognitive

Research: Principles and Implications, 3(50):1–10.

Lowrie, T., Logan, T., and Hegarty, M. (2019). The inﬂu-

ence of spatial visualization training on students’ spa-

tial reasoning and mathematics performance. Journal

of Cognition and Development, 20(5):729–751.

Maranto, R. and Wai, J. (2020). Why intelligence is miss-

ing from american education policy and practice, and

what can be done about it. Journal of Intelligence,

8(1):1–12.

Mart

ın-Guti

errez, J., Contero, M., and Alca

niz, M. (2015).

Augmented reality to training spatial skills. Procedia

Computer Science, 77:33 – 39.

Mbusi, N. (2016). Misconceptions and related errors

displayed by pre-service foundation phase teachers

in transformation geometry. In Proceesings of the

ISTE International Conference on Mathematics, Sci-

ence and Technology, page 1, Limpopo, South Africa.

UNISA.

ohring, W., Ribner, A. D., Segerer, R., Libertus,

M. E., Kahl, T., Troesch, L. M., and Grob, A.

(2021). Developmental trajectories of children’s spa-

tial skills: Inﬂuencing variables and associations with

later mathematical thinking. Learning and Instruc-

tion, 75:101515.

Naiman, A. C. (1996). Interactive teaching modules for

computer graphics. SIGGRAPH Comput. Graph.,

30(3):33–35.

Oberd

orfer, S., Heidrich, D., and Latoschik, M. E. (2019).

Usability of gamiﬁed knowledge learning in vr and

desktop-3d. In Proc, of the Conference on Hu-

man Factors in Computing Systems (CHI ’19), pages

175:1–175:13, Glasgow, Scotland UK. ACM.

Oberd

orfer, S. and Latoschik, M. E. (2018). Effectivity of

afﬁne transformation knowledge training using game

mechanics. In Proceedings of the 10th International

Conference on Virtual Worlds and Games for Serious

Applications (VS Games ’18), pages 1–8, New York,

NY, USA. IEEE.

Ozerem, A. (2012). Misconceptions in geometry and sug-

gested solutions for seventh grade students. Procedia

- Social and Behavioral Sciences (Proc. of the 3rd In-

ternational Conference on New Horizons in Education

(INTE 2012)), 55:720–729.

Parkinson, J. (2020). Investigating spatial skills in comput-

ing education. In Proceedings of the 2020 ACM Con-

ference on International Computing Education Re-

search (ICER ’20), pages 340–341, New York, NY,

USA. Association for Computing Machinery.

Parkinson, J. and Cutts, Q. (2018). Investigating the rela-

tionship between spatial skills and computer science.

In Proceedings of the 2018 ACM Conference on Inter-

national Computing Education Research (ICER ’18),

pages 106–114, New York, NY, USA. Association for

Computing Machinery.

Pathak, A., Chang, J. S. K., Resch, G., Doucette, A.,

Yeboah, G., Welsh, T. N., Nitsche, M., and Mazalek,

A. (2020). Thinking through the box: Evaluating a

3d game to engage penetrative thinking. Frontiers in

Virtual Reality, 1:33.

GRAPP 2022 - 17th International Conference on Computer Graphics Theory and Applications

134

Pittalis, M. and Christou, C. (2010). Types of reason-

ing in 3d geometry thinking and their relation with

spatial ability. Educational Studies in Mathematics,

75(2):191–212.

Reina, G., M

uller, T., and Ertl, T. (2014). Incorporat-

ing modern opengl into computer graphics educa-

tion. IEEE Computer Graphics and Applications,

34(4):16–21.

Sanna, A., Lamberti, F., Paravati, G., and Demartini, C.

(2012). Automatic assessment of 3D modeling ex-

ams. IEEE Transactions on Learning Technologies,

5(1):2–10.

Schweitzer, D., Boleng, J., and Graham, P. (2010). Teach-

ing introductory computer graphics with the process-

ing language. Journal of Computing Sciences in Col-

leges, 26(2):73–79.

Smith, G. and Sung, K. (2019). Teaching computer graph-

ics based on a commercial product. In Tarini, M. and

Galin, E., editors, Proc. of Eurographics 2019 - Ed-

ucation Papers, pages 63–70, Goslar, Germany. The

Eurographics Association.

Sorby, S., Casey, B., Veurink, N., and Dulaney, A. (2013).

The role of spatial training in improving spatial and

calculus performance in engineering students. Learn-

ing and Individual Differences, 26:20 – 29.

Stieff, M. and Uttal, D. (2015). How much can spatial train-

ing improve stem achievement? Educational Psychol-

ogy Review, 27(4):607–615.

Stieff, M., Werner, S., DeSutter, D., Franconeri, S., and

Hegarty, M. (2020). Visual chunking as a strategy for

spatial thinking in stem. Cognitive Research: Princi-

ples and Implications, 5(15):1–15.

Suselo, T., W

unsche, B. C., and Luxton-Reilly, A. (2017).

The journey to improve teaching computer graph-

ics: A systematic review. In Proceedings of the

25th International Conference on Computers in Ed-

ucation (ICCE 2017), pages 361–366, Christchurch,

New Zealand. APSCE.

Suselo, T., W

unsche, B. C., and Luxton-Reilly, A. (2018).

Mobile augmented reality as a teaching medium in an

introductory computer graphics course. In Proceed-

ings of the 6th International Conference on Learning

and Teaching in Computing and Engineering (LaTiCE

2018), pages 1–5, Auckland, New Zealand. IEEE.

Suselo, T., W

unsche, B. C., and Luxton-Reilly, A. (2019).

Technologies and tools to support teaching and learn-

ing computer graphics: A literature review. In Pro-

ceedings of the Twenty-First Australasian Comput-

ing Education Conference (ACE 2019), pages 96–105,

Sydney, NSW, Australia. ACM.

Suselo, T., W

unsche, B. C., and Luxton-Reilly, A. (2021).

Using mobile augmented reality for teaching 3d trans-

formations. In Proceedings of the 52nd ACM Tech-

nical Symposium on Computer Science Education

(SIGCSE 2021), pages 872––878, New York, NY,

USA. Association for Computing Machinery.

Suselo, T., W

unsche, B. C., and Luxton-Reilly, A. (2022).

Why are 3d transformations in computer graphics dif-

ﬁcult? an analysis of a decade of exam questions. In

Proceedings of the Twenty-Fourth Australasian Com-

puting Education Conference (ACE 2022), pages 1–

10, New York, NY, USA. ACM.

Sutton, K. and Williams, A. (2012). Developing a

discipline-based measure of visualisation. In Pro-

ceedings of The Australian Conference on Science

and Mathematics Education, pages 115–120, Sydney,

Australia. Open Journal Systems.

Turgut, M., Yenilmez, K., and Anapa, P. (2014). Symmetry

and rotation skills of prospective elementary mathe-

matics teachers. Bolema, 28(48):383–402.

Uttal, D., Meadow, N., Tipton, E., Hand, L. L., Alden, A.,

Warren, C., and Newcombe, N. (2012). The malleabil-

ity of spatial skills: A meta-analysis of training stud-

ies. Psychological bulletin, 139(2):352–402.

van Garderen, D. (2006). Spatial visualization, visual im-

agery, and mathematical problem solving of students

with varying abilities. Journal of Learning Disabili-

ties, 39(6):496–506. PMID: 17165617.

unsche, B. C., Chen, Z., Shaw, L., Suselo, T., Leung,

K.-C., Dimalen, D., Mark, W. v. d., Luxton-Reilly,

A., and Lobb, R. (2018). Automatic assessment of

OpenGL computer graphics assignments. In Proc. of

the 23rd Annual ACM Conference on Innovation and

Technology in Computer Science Education (ITiCSE

2018), pages 81–86, New York, NY, USA. ACM.

unsche, B. C., Huang, E., Shaw, L., Suselo, T., Leung,

K.-C., Dimalen, D., Mark, W. v. d., Luxton-Reilly,

A., and Lobb, R. (2019). CodeRunnerGL - an inter-

active web-based tool for computer graphics teaching

and assessment. In Proc. of the International Confer-

ence on Electronics, Information, and Communication

(ICEIC 2019), pages 1–7, New York, NY, USA. IEEE.

unsche, B. C., Leung, K.-C., Dimalen, D., Mark, W.

v. d., Suselo, T., Alex, Marylyn Shaw, A., Luxton-

Reilly, A., and Lobb, R. (2021). Using an assess-

ment tool to create sandboxes for computer graphics

teaching in an online environment. In Proceedings of

the 10th Computer Science Education Research Con-

ference (CSERC 2021), pages 1–10, New York, NY,

USA. ACM.

Xing, Q., Lu, Z., and Hu, J. (2019). The effect of working

memory updating ability on spatial insight problem

solving: Evidence from behavior and eye movement

studies. Frontiers in Psychology, 10:927.

Ziemkiewicz, C. and Kosara, R. (2008). The shaping of in-

formation by visual metaphors. IEEE Transactions on

Visualization and Computer Graphics, 14(6):1269–

1276.

Teaching and Learning 3D Transformations in Introductory Computer Graphics: A User Study

135