Analysis on the Applicability of RNN, LSTM, and GRU Deep

Learning Algorithms for Stock Price Prediction

Tianya Xu

Business school, Central University of Finance and Economic, Beijing, 100000, China

Keywords: Stock Price Prediction, Deep Learning, Applicability, RNN, LSTM, GRU, Algorithms.

Abstract: There are many studies based on deep learning algorithms to predict stock prices. Although the prediction

results are good in the experimental environment, the accuracy drops dramatically in the actual stock market.

Most scholars want to solve the problem by enhancing the algorithmic model. But the author assesses the

applicability between algorithm and stock data as another reason for that problem, and hopes to find out

whether there is a matching problem between the algorithm and data by analyzing the prediction result of

different types of stock data based on the different algorithms. This paper performs stock price prediction

based on RNN, LSTM, and GRU algorithms on four stocks with different fluctuation types and determines

the applicability of the three algorithms by analyzing the regression evaluation index of prediction results.

The result shows that the fluctuation of stock price has a significant impact on the accuracy of the three

algorithms. The LSTM algorithm fits best for the fluctuation type that stock price showing large cyclical

fluctuations, whose correlation coefficient reaches at 0.8067, while the GRU algorithm fits best for the

fluctuation type that shows slump in stock price, whose correlation coefficient reaches at 0.8072.

1 INTRODUCTION

Due to the high return of the stock market, the stock

market has been attracting a lot of attention, involving

the deep learning field. Researchers hope to gain

more profits by studying the pattern of stocks and

making predictions about price movements. Stock

price prediction is a classical prediction problem

based on time-series data and very suitable to deep

learning algorithms. But it is difficult to extract

accurate features of the stock price for prediction,

because the behavior of the stock market is complex

and non-linear, and stock data has noise, numerous

dimensions, and significant uncertainties. Jiang

Weiwei collected and organized the existing stock

price prediction -related literature based on the deep

learning algorithm. It can be seen that the accuracy

dramatically decreases when it comes to the actual

market, although the prediction results are good in the

experimental environment (Jiang, 2021).

In response to this problem, most scholars worked

on optimizing algorithmic models, hoping to improve

the prediction results by exploring new algorithmic

https://orcid.org/0000-0001-9145-4929

models, such as the transformer model, which is

considered to have significant advantages in mining

extremely long-term dependencies from financial

time series. It is difficult for RNN-based methods to

learn dependencies in many steps (Ding, Wu, Sun,

Guo, Guo, 2020). The transformer model generally

outperforms traditional deep tilt models in predicting

stock prices, with accuracy 4.68% higher than short-

term memory (LSTM) (Zhang and Zhang 2020).

Some scholars improved the existing algorithm

model to improve the defective points, such as a

stacked LSTM model, which adds early-stopping,

rectified linear units (Relu) activation function,

overcome gradient explosion, gradient disappearance

(Zhang, LI, Chen, Chrysostomou, Yang, 2021). Other

scholars introduced special algorithms for pre-

processing to improve the accuracy of existing

models before importing them, such as EMD, which

can theoretically be applied to the decomposition of

any type of time-series signal, and decompose a

complex signal into a finite sum of eigenmode

functions (IMFs) and residual waves. The IMF

component contains the local eigen-signals of the

original signal at different time scales. The LSTM

model after introducing EMD preprocessing not only

Xu, T.

Analysis on the Applicability of RNN, LSTM, and GRU Deep Learning Algorithms for Stock Price Prediction.

DOI: 10.5220/0011175000003440

In Proceedings of the International Conference on Big Data Economy and Digital Management (BDEDM 2022), pages 301-305

ISBN: 978-989-758-593-7

301

improves the prediction accuracy, but also reduces

the time delay (Jin, Yang, Liu 2020).

In this paper, the author considers the main factor

that affects the prediction accuracy of the actual stock

market is not the algorithm. However, due to the poor

adaptability of the algorithm to the fluctuation of

stock price, the prediction accuracy decreases.

According to the two-year stock data, four stocks

with different price fluctuations in the two-year

period are selected to explore the prediction accuracy

under RNN, LSTM and GRU (Shahi, Shrestha,

Neupane, Guo, 2020). These three main time series

deep learning algorithm models are widely used and

discussed at present. The author aims to find the

optimal algorithm corresponding to the stocks with

different fluctuation types by comparing the

regression evaluation indexes of the result, to analyze

the applicability of RNN, LSTM, and GRU deep

learning algorithms for stock price prediction. This

paper shows an adaptation problem between the

fluctuation situation of the stock price and the

algorithm. Besides, a new research direction is

proposed, which enables scholars in the field of stock

price prediction to focus on algorithmic research

breakthroughs and explore more into the issue of

matching data to algorithms. The author also suggests

that follow-up studies could categorize historical data

of the stock market and select the corresponding

existing optimal algorithm for stock price prediction,

contributing to higher accuracy in the actual stock

market in the future.

2 METHODOLOGY

2.1 Data Source and Pre-processing

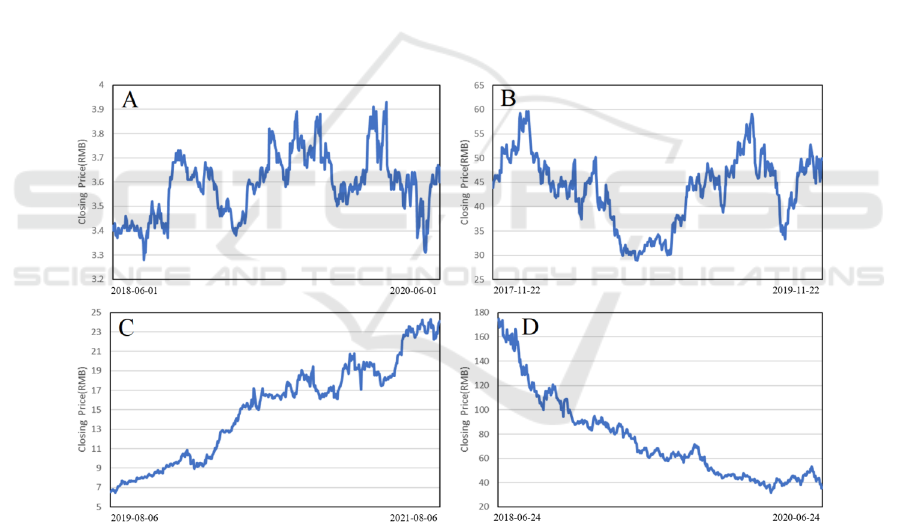
This paper takes 2 years as the time interval, and

selects 4 stocks with different price fluctuation

situations: 601288.SH (almost stable), 002049.SZ

(large fluctuation cycle), 002468.SZ (soar),

603605.SH (slump) (as shown in figure 1).

Figure 1: The price fluctuation situation of four stocks in two years (A-601288.SH, B-002049.SZ, C-002468.SZ, D-

603605.SH).

The stock trading data is retrieved through the

Tushare API (Pan, Li, Li 2020), containing the daily

opening price (Open), high price (High), low price

(Low), closing price (Close), and trading volume

(Volume). These five feature values are used as input

to predict the closing price of the 61st day with the

historical data of every 60 trading days to extract the

feature of the stock price fully.

Since both stock price data and trading volume

data are used as the input feature parameters, and the

values of both are vastly different, this paper

normalizes the data to eliminate the influence of the

magnitude between them to improve the model

accuracy and convergence speed. The processed data

are divided into training set and test set in order. Due

to the different number of trading days in different

time periods, the last 100 trading days data are used

BDEDM 2022 - The International Conference on Big Data Economy and Digital Management

302

as the test set to evaluate the short-term prediction

accuracy of the model.

2.2 Model Construction

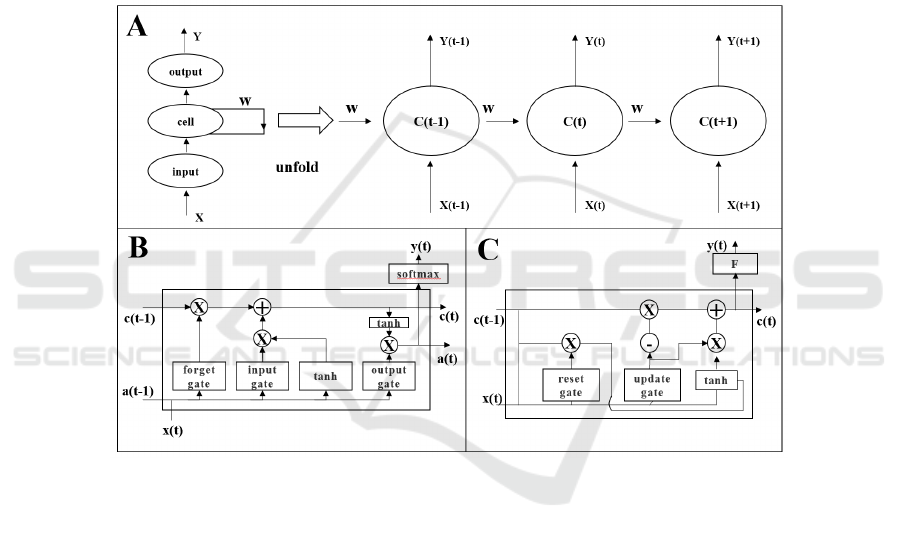
The author will use RNN, LSTM and GRU models

for experiments, and the structure of those models is

shown in figure 2 (Shahi, Shrestha, Neupane, Guo,

2020).

2.2.1 RNN Model

In the traditional RNN (recurrent neural network), all

W is the same W. When passing

through the same cell,

the input memory will be retained, plus another input

to be predicted, so the prediction includes all the

previous Memory plus this input. All RNNs have a

chain form of repeating neural network modules. In a

standard RNN, this repeated module has only a

simple structure, such as one tanh layer. When the

weight is greater than 1, the backpropagation of the

error will always enlarge the error and eventually

cause the gradient to explode, when the weight is less

than 1, the error will continue to shrink, leading to the

disappearance of the gradient, which in turn leads to

the slow update of the weight of the network. The

effect of long-term memory makes RNN too

forgetful.

Figure 2: The structure of the RNN, LSTM and GRU model (A-RNN, B-LSTM, C-GRU).

2.2.2 LSTM Model

LSTM is a special RNN model to solve the problem

of gradient disappearance and gradient explosion in

the back propagation process. By introducing a gate

mechanism, it solves the long memory problem in the

RNN model. LSTM has three gates to protect and

control the cell state: forget gate, update gate and

output gate. The cell state is similar to a conveyor

belt. Run directly on the entire chain, with only a few

linear interactions. It will be easy for the information

to circulate on it and stay the same.

2.2.3 GRU Model

GRU was proposed by Cho, et al. (Chung, Gulcehre,

Cho, Bengio, 2014), and its feature is to combine the

forget gate and the input gate into a single update

gate, introducing another reset gate. The final model

is simpler than the standard LSTM model, the

parameters are 1/3 less, it is not easy to overfit, and

the effect is similar to LSTM, and even surpasses

LSTM in some applications.

2.2.4 Parameter Setting

TensorFlow is currently the leading framework for

deep learning and neural network computing. It is

based on a low-level C++ backend, but is typically

controlled via Python. This paper will be based on

Google's TensorFlow2.3 framework for stock price

prediction in Keras API (Raschka, Mirjalili, 2017),

Python version 3.8, Keras version 1.0.8. In terms of

model parameter settings, the number of neurons in

Analysis on the Applicability of RNN, LSTM, and GRU Deep Learning Algorithms for Stock Price Prediction

303

the three models is uniformly set to 100, the batch

size to 64, the number of iterations (epoch) to 300, the

loss function (loss) set by mean square error (MSE),

the optimizer (optimizer) set by Adam at

0.0001(Kingma, Ba, 2014), and the time step t to 60.

2.3 Performance Index

In order to evaluate the prediction performance of the

algorithmic model on stock prices, four regression

evaluation metrics, mean square error (MSE), root

mean square error (RMSE), mean absolute error

(MAE), and R-squared (R2), are used in this paper to

quantify the model performance. The four metrics are

calculated as shown in equation (1)-(4).

𝑀𝑆𝐸 =





∑

(𝑦



−𝑦



)





(1)

𝑅𝑀𝑆𝐸 =







∑ (

𝑦



−𝑦





)







(2)

𝑀𝐴𝐸 =





∑ |

(𝑦



−𝑦



)





(3)

𝑅



=1−

∑

(𝑦



−𝑦



)







∑

(𝑦



−𝑦)







⁄

(4)

Where y



is the true value, y



 is the predicted

value, y is the mean of the true value, and m is the

sample size. MSE, RMSE, and MAE are used to

measure the deviation between the true value and the

predicted value, with smaller values indicating that

the predicted value is closer to the true value, and R



is used to measure the degree of model fit, with closer

to 1 indicating that the model fits better.

3 RESULT

The prediction experiments were conducted based on

RNN, LSTM and GRU models for the four selected

stocks respectively, forming 12 experimental groups,

and the prediction experiments of each group would

be repeated 10 times due to the randomness of deep

learning algorithm (Scardapane, Wang, 2017).

Finally, a total of 120 experiments were conducted in

this paper, and the experimental results with smaller

MSE were selected in each group, 12 experimental

groups’ result as shown in table 1.

Table 1: Regression evaluation index of the result.

STOCK ALGORITHM MSE RMSE MAE R2

601288.SH Stable

RNN 0.0006 0.0247 0.0207 -0.5900

LSTM 0.0010 0.0313 0.0273 -4.8909

GRU 0.0005 0.0216 0.0183 -1.7951

002049.SZ

Large Fluctuation

RNN 2.9393 1.7144 1.2641 0.7503

LSTM 2.0368 1.4272 1.0878 0.8067

GRU 2.4346 1.5603 1.1402 0.7478

002468.SZ

Soar

RNN 0.0525 0.2292 0.1998 0.7150

LSTM 0.0344 0.1855 0.1424 0.7117

GRU 0.0268 0.1638 0.1319 0.8072

603605.SH

Slump

RNN 46.0314 6.7846 5.7093 0.6195

LSTM 56.1527 7.4935 6.2176 0.6137

GRU 46.8088 6.8417 5.5568 0.6699

4 DISCUSSION

For the fluctuation type that stock price’s fluctuation

is not significant, almost stable (601288.SH), R



negative, none of the three algorithms can fit

correctly. The main reason for this problem is that the

stock price fluctuates steadily around the mean,

resulting in a scattered distribution of features, with

numerous local optima, and the algorithms cannot

accurately capture the right features for fitting.

However, the minor fluctuation results in lower

values of MSE, making the prediction results of either

algorithm more accurate and with less error.

For the fluctuation type that stock price showing

large cyclical fluctuations (002049.SZ), and the trend

of soar (002468.SZ), the R



under all three

algorithms is large than 0.7, and the MSE, RMSE,

and MAE are all at low values. However, the best

prediction result is under the LSTM algorithm when

the stock price is in large cyclical fluctuations, while

the results of the GRU algorithm are better under the

trend of soaring. It can be speculated that the main

reason for the difference is that the GRU algorithm

BDEDM 2022 - The International Conference on Big Data Economy and Digital Management

304

logic has a selectivity for past information when

calculating the current state information, i.e., whether

the current information is generated by past

information while the LSTM algorithm selects the

same proportion of past and present information for

output. Under the soaring trend of stock price, the

GRU algorithm is more likely to strengthen the

weights of the features involved in the rising trend to

get better prediction results. While the weights of the

features just under a single-period wave are

strengthened in the cyclical fluctuations, this high

weight memory by GRU cause a decrease in the

accuracy in the multi-period fluctuations.

For the fluctuation type that show slump in stock

price (603605.SH), the R



of three algorithms are

all larger than 0.6, showing a good correlation.

However, the MSE value is as high as 45 and the

RMSE and Mae values are also large, which can

hardly be used as a short-term stock price forecast.

The main reason is that the stock price related data is

more complicated in the plunge market than in the

rise market. As in psychology, people are more risk

averse compared to profit taking, and the panic of the

plunge leads to too large initialized values of weights

and more outliers. Moreover, the amount of learning

data is not enough to adjust them, resulting in the

large final MSE value, although the correlation

coefficient is good.

5 CONCLUSIONS

For the four different fluctuation types of the stock

price in 2 years, this paper uses three different

algorithms, RNN, LSTM, and GRU, to perform stock

price prediction, and the prediction accuracy of each

algorithm differs significantly.

1) For the fluctuation type in which stock price is

almost stable, there is not much difference in

prediction accuracy between various algorithms.

2) LSTM algorithm is most suitable for the

fluctuation type with large periodic fluctuation of

stock price, while GRU algorithm is most suitable for

extracting eigenvalues and making the most accurate

prediction under the soaring trend.

3) The performance of the three algorithms is not

satisfactory for the fluctuation type that shows a

slump in stock price. The author plans to follow up

with some new optimization algorithms for

experimentation. In addition, due to the randomness

of the algorithm, 10 trials in each experimental group

may not be enough to find the best-fit point, which

can easily cause errors in the algorithm comparison.

The four types of fluctuation situations selected in

this paper do not represent all fluctuation situations in

the actual stock market. This paper only points out

that the fluctuation type of stock price significantly

impacts the accuracy of the prediction under a deep

learning algorithm. To improve the prediction

accuracy and optimize the algorithm model, choosing

the suitable algorithm fit for the particular fluctuation

situation in stock price is also the main point. Future

research will perform applicability analysis for

prediction under advanced algorithms based on more

complex fluctuation types of stock price.

REFERENCES

Chung, J., Gulcehre, C., Cho, K., & Bengio, Y. (2014).

Empirical evaluation of gated recurrent neural

networks on sequence modeling.

Ding, Q., Wu, S., Sun, H., Guo, J., & Guo, J. (2020).

Hierarchical Multi-Scale Gaussian Transformer for

Stock Movement Prediction. In IJCAI (pp. 4640-4646).

Jiang Weiwei. (2021). Applications of deep learning in

stock market prediction: Recent progress. Expert

Systems with Applications, 184

Jin, Z., Yang, Y. & Liu, Y. Stock closing price prediction

based on sentiment analysis and LSTM. Neural

Comput & Applic 32, 9713–9729 (2020).

https://doi.org/10.1007/s00521-019-04504-2

Kingma, D. P., & Ba, J. (2014). Adam: A method for

stochastic optimization. Computer Science.

Pan Wei and Li Jide and Li Xiaoqiang. (2020). Portfolio

Learning Based on Deep Learning. Future Internet,

12(11), pp. 202-202.

Raschka, S., & Mirjalili, V. (2017). Python Machine

Learning: Machine Learning and Deep Learning with

Python. Scikit-Learn, and TensorFlow. Second edition

ed.

S. Zhang and H. Zhang, "Prediction of Stock Closing Prices

Based on Attention Mechanism," 2020 16th Dahe

Fortune China Forum and Chinese High-educational

Management Annual Academic Conference

(DFHMC), 2020, pp. 244-248, doi:

10.1109/DFHMC52214.2020.00053.

Scardapane, S., & Wang, D. (2017). Randomness in neural

networks: an overview. Wiley Interdisciplinary

Reviews: Data Mining and Knowledge

Discovery, 7(2), e1200.

Shahi TB, Shrestha A, Neupane A, Guo W. Stock Price

Forecasting with Deep Learning: A Comparative

Study. Mathematics. 2020, 8(9):1441.

https://doi.org/10.3390/math8091441

Zhang, X., LI, C., Chen, K-L., Chrysostomou, D., & Yang,

H. (2021) Stock Prediction with Stacked-LSTM Neural

Networks. The 21st IEEE International Conference on

Software Quality, Reliability, and Security.

Analysis on the Applicability of RNN, LSTM, and GRU Deep Learning Algorithms for Stock Price Prediction

305