Random Walk Simulation on Crude Oil Price for the First 20 Years in

the 21

Century

Shaomin Yan

and Guang Wu

National Engineering Research Center for Non-Food Biorefinery, State Key Laboratory of Non-Food Biomass and Enzyme

Technology, Guangxi Academy of Sciences, 98 Daling Road, Nanning, 530007, Guangxi, China

Keywords: Big Data Mining, Crude Oil Close Price, Random Walk, Simulation.

Abstract: The crude oil perhaps is the most important commodity in the world. Therefore, not only the crude oil price

but also its derivates such as futures and warrants are closely following by hedge funds, investment banks and

institutions, individual investors, venture capitals, etc. In reality, the crude oil price is subject to many factors,

which lead it less manipulated and more random. We therefore apply the random walk simulation to study

the crude oil prices for the first 20 years in the 21st century in this report. The results show that the random

walk simulation can follow the general trend closely for a relatively short period, but fails to catch up with

historically unprecedented event.

1 INTRODUCTION

The crude oil perhaps is the most important

commodity in the world. Although the crude oil is a

natural resource, historically there were several oil

crises, which significantly impacted global economy.

In an ideal world, the crude oil price should be

relatively predictable because it should follow the

supply-demand principle while the increase of the

world economy is predictable. In reality, the oil price

influences not only the world economy but also the

world politics. Indeed, many conflicts in Middle East

and Africa have deep roots related to oil explorations

and productions.

Under the circumstance of climate change, as a

fossil energy, the oil is subject to environmental

activists, NGO and governmental policies, and is

relevant to the carbon footprint.

Therefore, not only the crude oil price but also its

derivates such as futures and warrants are closely

following by hedge funds, investment banks and

institutions, individual investors, venture capitals,

etc.

Needless to say, the oil price is also an objective

of enormous studies, which are even too many to cite

here. Of studies, every approach is applied to the oil

https://orcid.org/0000-0001-7642-3972

https://orcid.org/0000-0003-0775-5759

price including fundamental and technological

analyses, mathematical and statistical investigations,

empirical and theoretical examinations, etc. Of

numerous approaches, the random walk is attractive

(Zhu, et al., 2017; Chen, et al., 2017) because the

crude oil as influenced by too many factors to count

should have some property of randomness not as a

local market is subject to manipulation.

Because of particular randomness, we apply the

random walk simulation to study the crude oil prices

for the first 20 years in the 21st century in this report.

2 MATERIALS AND METHODS

2.1 Crude Oil Price Data

The NY Mercantile - NY Mercantile Delayed Price

for the first 20 years in the 21st century was

downloaded from Yahoo Finance (

Yahoo Finance,

2021)

. As always, the crude oil price includes daily

open, high, low, close, adjusted close prices, and

volume. We consequentially use the close price for

the simulations

The data consist of 4991 trading days. We

arbitrarily stratify the data into five fractions: (i) 4991

Yan, S. and Wu, G.

Random Walk Simulation on Crude Oil Price for the First 20 Years in the 21st Century.

DOI: 10.5220/0011191900003440

In Proceedings of the International Conference on Big Data Economy and Digital Management (BDEDM 2022), pages 569-573

ISBN: 978-989-758-593-7

569

close prices from 2001 to 2020, (ii) 3744 close prices

from 2006 to 2020, (iii) 2895 close prices from 2011

to 2020, (iv) 1247 close prices from 2016 to 2020,

and (v) 251 close prices for 2020.

2.2 Random Walk

The random walk (Feller, 1968) is practically

straightforward and easily understandable because it

simply records a movement in x, y coordinates. This

movement starting from the origin is dictated to move

just one unit along both axes. Because the x-axis

represents the time course, so the movement along the

x-axis is always towards the positive direction. In

contrast, the movement along y-axis can go two

ways, i.e. each movement can either be positive, 1, or

negative, –1. Historically, 1/–1 came from tossing a

fair coin, but it now can achieve through a random

number generator in any computer program because

the outcome of tossing a coin is a pseudo-random

event with the Monte Carlo algorithm such as

SigmaPlot (SPSS Inc, 2002).

2.3 Crude Oil Close Price in

Conformation of a Random Walk

To be simulated by random walk, it is better to

convert the crude oil close price into the

conformation of a random walk. This is relatively

easily done by comparing a crude oil close price with

that in its preceding trading day, and by then

assigning 1 or –1 if the comparison results in larger

or smaller.

In the x, y coordinates, both random walk

simulation and crude oil close price in conformation

of a random walk are spotted as the trading date goes

along the x-axis and 1 or –1 moves along the y-axis.

The, we can compare the difference between these

two profiles to determine the good-of-fitness.

Because each seed in the command to generate the

random numbers generates different series of random

numbers, which results in different random walk

simulations, so we find the seed for good-of-fitness

from 100 000 seeds.

2.4 Random Walk in Decimal

Conformation

The conversion of crude oil close price into the 1/–1

conformation would be accused of oversimplifying

the real-life complicated situation although it answers

the simplest question of whether the crude oil goes up

or down overnight. To overcome this shortage, we

should push the classical random walk to the decimal

conformation from the 1/–1 conformation. This is not

difficult to do because we can simply omit the step of

comparison of sequential random numbers and

assignment of the 1 or 1, but directly use these

generated random numbers to form a random walk

simulation. In such a case, we need to set the

command with relevant upper and lower ranges.

2.5 Worked Example

Table I shows a worked example on the procedure to

create random walk simulations. Columns 1 and 2 are

the data documented in NY Mercantile. Column 3 is

the comparison between two sequential crude oil

close prices, for example, the crude oil close price is

$ 61.18 on January 2, 2020 (Columns 1 and 2) while

the price on January 3, is $ 63.05 (Columns 1 and 2),

which is higher than its preceding day, so we assign

1 to the second cell in Column 3, and continue this

comparison until the end of Table I. Column 4 is the

created random walk for the crude oil close price in

the 1/–1 conformation, which is the accumulation of

data in Column 3. Column 5 is the random numbers,

which were generated by SigmaPlot using a seed of

4.33068. Column 6 is the comparison between two

sequential random numbers in Column 5. Column 7

is a random walk, which is in fact a simulation on this

particular seed of 4.33068. Column 8 is the random

numbers, which were generated by SigmaPlot using

a seed of 6.16373 with upper and lower ranges of

standard deviations of crude oil close price for 2020.

Column 9, although it is similar to the operation for

Column 7, is the addition of cells in Column 1 with

the next cells in Column 8, which is a random walk

simulation in the decimal conformation.

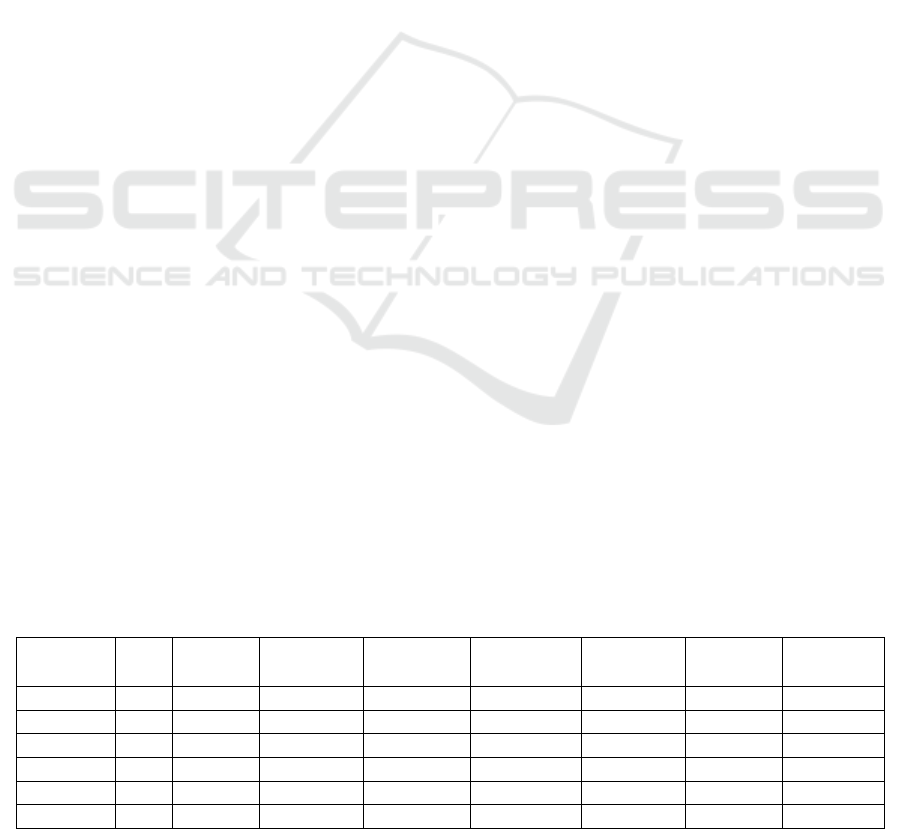
Table 1: Procedure to create random walk simulations.

Date Crude

Oil Close

Price

Compare

Preceding

Close Price

Random Walk in

1 or–1

Conformation

Generated

Random Number

Compare

Preceding

Random Number

Random Walk in

1 or–1

Conformation

Generated

Random

Number

Random Walk

in Decimal

Conformation

January 2, 2020 61.18 0 0.892394 0 –1.293315

January 3, 2020 63.05 1 1 –0.40909 –1 –1 1.915306 63.1

January 6, 2020 63.27 1 2 –0.641479 –1 –2 4.652787 67.75

January 7, 2020 62.7 –1 1 0.860897 1 –1 –2.84741 64.9

January 8, 2020 59.61 –1 0 0.645762 –1 –2 0.478926 65.38

January 9, 2020 59.56 –1 –1 –0.339257 –1 –3 –4.264635 61.11

BDEDM 2022 - The International Conference on Big Data Economy and Digital Management

570

January 10, 2020 5904 –1 –2 –0.412953 –1 –4 –1.34917 59.77

January 13, 2020 58.08 –1 –3 0.878346 1 –3 –0.531944 59.23

January 14, 2020 58.23 1 –2 0.069734 –1 –4 3.44592 62.68

January 15, 2020 57.81 –1 –3 0.191641 1 –3 –1.6466 61.03

3 RESULTS AND DISCUSSION

Figure 1 shows the comparison between the crude oil

close price and its random walk simulation in the 1/–

1 conformation for 2020. Because this conformation

answers the simple question of whether the crude oil

close price is higher or lower in comparison with that

in its preceding day, we can see that there are more

trading days, in which the close price is lower than

that in its preceding day before May 2020. Then there

are more trading days, in which the close price is

higher than that in its preceding day after May 2020,

and the trading days, in which the price may be one

higher or lower than that in the preceding day without

reasoning.

The unique difference between the crude oil price

and other stock indices such as S&P 500 (Yan, Wu,

2020), S&P/TSX (Yan, Wu, 2021), CAC40 (Yan,

Wu, 2021), DAX (Yan, Wu, 2021), KOSPI (Yan,

Wu, 2021), Nasdaq (Yan, Wu, 2021), Hang Seng

(Yan, Wu, 2021), Dow Jones (Yan

, Wu, 2021), and

NIKKEI 225 (Yan, Wu, 2021) is that the crude oil

price experienced a unheard and unprecedented fall

down to the negative territory, $ -37.63 on April 20,

2020. It is still hard and difficult to define or explain

or argue whether this is a random event, but it is

definitely different from all the shocks around the

world, and can be considered as highly irrational.

Figure 2 illustrates this awkward crude oil close

price with its random walk simulation in the decimal

conformation. Likely the random walk simulation can

follow the crude oil close price except for April 20,

2020.

The similar situation can also be observed in

Figure 3, where the unique negative territory fall

down cannot be simulated by the random walk. Based

upon our experience (Yan, Wu, 2020, Yan, Wu,

2021), the difficulty in simulation of this

unprecedented fall down came the command of

random number generator, which has four

parameters, number, seed and upper and lower

ranges. The upper and lower ranges always are hard

to define. Perhaps, we should change these two

parameters into random numbers, i.e. the random

number generator embraces the random number

generators in our future studies.

Figure 1: The crude oil close price in 2020 in 1/–1

conformation (black line) and its random walk simulation

(red line) using the seed of 4.33068.

Figure 2: The crude oil close price in 2020 (black line) and

its random walk simulation (red line) in the decimal

conformation using the seed of 6.16373.

Figure 4 tells the similar story as Figure 3, that is,

the random walk simulation satisfactorily fits the

pathway of crude oil close price. Even it is better than

the simulation in Figure 3, because the simulation

went down the negative valley to some degree.

Figures 5 and 6 reveal another interesting

phenomenon that is the surge of crude oil price in

2008, which researched to $ 145.18 on July 14, 2008.

To some extent, the curve of crude oil close price in

Figure 5 is symmetric with one peak up and one peak

Random Walk Simulation on Crude Oil Price for the First 20 Years in the 21st Century

571

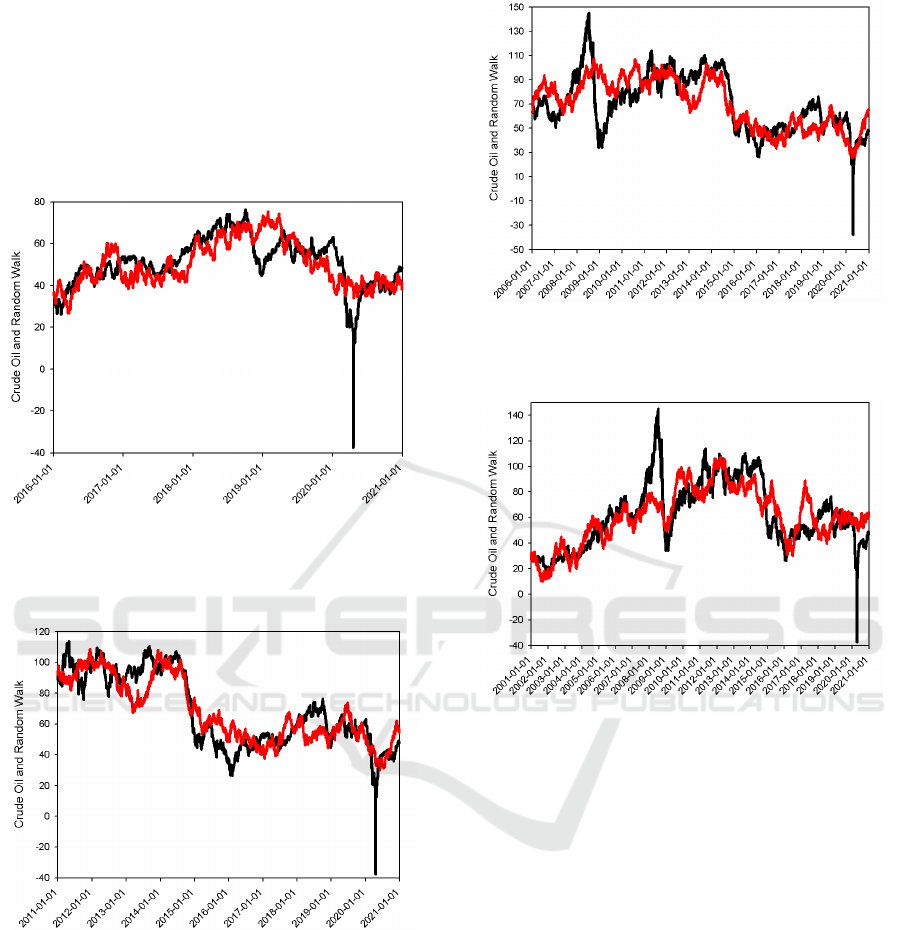
down. In such a case, the symmetry would render a

better simulation for the sake of upper and lower

ranges in random number generator command.

However, this is not the case. Therefore, the deeper

source for this incapable simulation requires further

investigations. In fact, it seems that only the random

walk simulation has the potential to mimic something

in negative territory.

Figure 3: The crude oil close price from 2016 to 2020 (black

line) and its random walk simulation (red line) in the

decimal conformation using any of fifteen seeds from

9.25671 to 9.25485 with increment of 1.

Figure 4: The crude oil close price from 2011 to 2020 (black

line) and its random walk simulation (red line) in the

decimal conformation using the seed of 2.03358.

Perhaps, what happened in Figure 5 becomes

more visible in Figure 6, where we could say that the

simulation ran through the general trend relatively

good, but was unable to rise or fall to any degree. This

indeed is a failure. However, this failure can be

balanced by the facts that other models fail to predict

these two outliers too.

Figure 5: The crude oil close price from 2006 to 2020 (black

line) and its random walk simulation (red line) in the

decimal conformation using the seed of 2.28541.

Figure 6: The crude oil close price from 2001 to 2020 (black

line) and its random walk simulation (red line) in the

decimal conformation using any of two seeds of 0.7239 and

1.42371.

In some sense, our approach is very more empiric

because there is no theoretical proof on whether the

random walk can be applicable to either stock market

or commodity although numerous studies have been

done using various statistical tests such as variance

ratio, unit root, and autocorrelation tests (Lo,

MacKinlay, 1988, Liu, He, 1991, Deo, Richardson,

2003). We lack progress and advance in theoretical

proof.

In our series of reports on random walk simulation

(Yan, Wu, 2020, Yan, Wu, 2021), .we have great

difficulty to unity the term used to describe 1/–1 and

decimal random walk, because the currently popular

software detecting plagiarism would give warning of

the same scientific term used in different reports.

Thus, we had to adopt different terminologies before

exhausting our vocabulary. We had used format,

pattern, form, configuration, conformation, etc., but

they are the same in essence. Nevertheless, we expect

BDEDM 2022 - The International Conference on Big Data Economy and Digital Management

572

to use other terms in our future reports although they

mean the same concept and definition.

4 CONCLUSIONS

In this report, we apply the random walk simulation

to the crude oil close price for the first 20 years in the

21st century, not only because of importance of crude

oil price, but also because of appearance of oil price

in the negative territory due to Covid-19 pandemic,

which was never seen in any stock indices. The

results being clearer than our previous reports (Yan,

Wu, 2020, Yan, Wu, 2021) demonstrate the

incapability to let the simulation to deal with sudden

fall and rise. However, he results do reveal that the

random walk has the potential to lead to the

simulation to follow any unprecedented event. The

results also suggest the possibility to use the random

number generator to embrace other random number

generators in software commands.

ACKNOWLEDGEMENTS

The authors express their thanks for the Scientific

Development Fund of Guangxi Academy of Sciences

(2021YFJ1203).

REFERENCES

Chen, Y., He, K. & G. K. F. Tso. (2017). Forecasting crude

oil prices: a deep learning based model. Precedia

Comput. Sci., 122, 300–307.

Deo, R. S. & M. Richardson. (2003) On the asymptotic

power of the variance ratio test. Econometric Theory

19, 231–239.

Feller, W. 1968. An introduction to probability theory and

its applications. John Wiley, New York, 3rd edition.

Liu, C.Y. & J. He. (1991) A variance ratio tests of random

walks in foreign exchange rates. J. Finan. 46, 773–785.

Lo, A. W. & A. C. MacKinlay. (1988) Stock market prices

do not follow random walks: Evidence from a simple

specification test. Rev. Finan. Studies 1, 41–66.

SPSS Inc., SigmaPlot 2002 for Windows Version 8.02.

(1986–2001).

Yahoo Finance (2021) https://de.finance.yahoo.com/.

Yan, S. & G. Wu. (2020) Fitting of impact of COVID-19

pandemic on S&P 500 Index using random walk.

Conference Publishing Services: ICEMME 4, 1007–

1011.

Yan, S. & G. Wu. (2021a). Simulation of Canadian

S&P/TSX composite index for the first 20 years in the

century with random walk model. Proceedings in

2021 International Conference on Data Mining and

Statistical Applications (DMSA 2021). Conference

Publishing Services: DMSA, 45–48.

Yan, S. & G. Wu. (2021b). Simulation of French CAC40

index for the first 20 years in the 21

century with

random walk model. Proceedings in 2021 International

Conference on Data Mining and Statistical

Applications (DMSA). Conference Publishing

Services: DMSA, 1092–1095.

Yan, S. & G. Wu. (2021c). Simulation of German DAX

index for the first 20 years in 21

century with random

walk model. Proceedings in the 2021 International

Conference on Cloud Computing, Big Data and Digital

Economy. Conference Publishing Services: ICCBD,

913–916.

Yan, S. & G. Wu. (2021d). Simulation of KOSPI index for

the first 20 years in the 21

century using random walk.

Proceedings in the 2nd International Conference on Big

Data and Social Sciences (ICBDSS 2021). Conference

Proceedings Services: ICBDSS, 866–870.

Yan, S. & G. Wu. (2021e) Simulation of NASDAQ

Composite Index for the first 20 years of the 21

century by means of random walk model. Proceedings

in the 2021 International Conference on Education,

Information Management and Service Science.

Conference Publishing Services: EIMSS, 454–457.

Yan, S. & G. Wu. (2021f) Fit Hang Seng index for 21

century with random walk model. Conference

Publication Series: CBFD 66–69.

Yan, S. & G. Wu. (2021g) Simulation of impact of COVID-

19 pandemic on Dow Jones index using random walk.

Proceedings in the 2nd International Conference on

Computing and Data Science (CONFCDS) 2021; 59–

64.

Yan, S. & G. Wu. (2021h) Simulation of NIKKEI 225

index for 21st century using random walk. 2021 2nd

International Conference on Big Data and

Informatization Education (ICBDIE) 330–333.

Zhu, D. M., Ching, W. K., Elliott, R. J., Siu, T. K. & L. M.

Zhang. (2017). Hidden markov models with threshold

effects and their applications to oil price forecasting. J

Indust. Manag. Optim., 13, 757–773.

Random Walk Simulation on Crude Oil Price for the First 20 Years in the 21st Century

573