
Sales Prediction Model based on Multifactorial Linear Regression
Jiyan Liu
a
Department of Mathematics and Department of Economics, University of California San Diego, La Jolla, U.S.A.
Keywords: Sales Prediction, Linear Regression, Multifactorial Regression.
Abstract: Motivated by the sales prediction of ABCtronics, this paper aims to provide integrated process for creating a
proper multiple linear regression model and detailed analysis of according parameters. With multiple
independent variables, the linear regression model exams the relationship between a collection of data-overall
market demand, price per chip and economic condition to the single dependent variable sales volume of
ABCtronics. The target is set to be future prediction of sales volume with three observable variables. All
outputs are statistical results from Minitab which contain regression equation, model summary with R
2
value
and analysis of variance stating the significance level of each variable. With detailed output, a refined multiple
regression model is then developed to get rid of the overall market demand term. Pure regression equation
brings only numerical understanding, i.e., visualization is the next focus. Based on comparison and contrast,
it is verified the accurateness of the refined model. These results shed light on the proper use of multiple linear
regression on sale prediction model.
1 INTRODUCTION
Sales prediction plays a key role in almost every
successful operation of business. As one of the
greatest inventions, it provides forecasting on future
trend of target markets and an insight into proper
allocation of resources e.g., labors and capitals. The
way to maximize firm’ sale target with limited
resources is always considered the priority.
Forecasting sales accurately for a new product is
difficult and complex due to non-availability of past
data. However, such forecast information is crucial for
successful introduction of new products which, in
turn, determines the survival of companies, in many
cases (Meeran, et al, 2013). Hence, proper usage of
sales prediction model can assist the firms with
informed data on each input which may help refine
future supply chain. Moreover, as the number of
databases collected increases, corporations are able to
gain less biased data which not only gives sales
prediction but consumer preferences. Specifically, if
linear regression model is formed, parameter of each
variable would be given and that number tells the unit
change of the regressors. By comparing the
parameters, firms may attribute any boost of sales
volume to some specific determinant factor, which can
a
https://orcid.org/0000-0001-7666-3749
be use to select suitable market target group and
increase efficiency further.
Sales prediction models are now widely used in all
fields. From prior literature, there are already intensive
research on sales prediction in three major fields. First
is the Microsoft Time Series algorithm. It provides us
with optimized regression algorithm for forecasting
continuous real-time values (Kohli, Shreya, et al,
2020). Time Series forecasting, which forecasts based
on time-controlled variable, is an important tool under
this scenario, where the research aim is to predict the
behavior of complex systems solely by analyzing the
past data (A Survey of Time Series Data Prediction on
Shopping Mall, et al, 2013). For example, three
researchers from Indian conduct a survey of time
series data prediction on shopping mall to predict the
next phase of the product price trends and sales
volume. They propose a tree based data mining
algorithm that treats market’s behavior and interest as
input & filter the desired output efficiently & a mining
model of stream data time-series pattern in a dynamic
shopping mall (A Survey of Time Series Data
Prediction on Shopping Mall, et al, 2013). This is a
comparatively complicated model because what
involves are subjective investors who may cause
significant error on the analyzing system, which leads
to its complexity.
598
Liu, J.
Sales Prediction Model based on Multifactorial Linear Regression.
DOI: 10.5220/0011195100003440
In Proceedings of the International Conference on Big Data Economy and Digital Management (BDEDM 2022), pages 598-604
ISBN: 978-989-758-593-7
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
Second is spatial data mining for retail sales
forecasting. The study conducted by Maike Krause-
Traudes, Simon Scheider1 and two other scientists
aim to design a regression model to predict probable
turnovers for potential outlet-sites of a big European
food retailing company (Aina, Abidemi Ayodeji, et al,
2012). The forecast of potential sites is based on sales
data on shop level for existing stores and a broad
variety of spatially aggregated geographical, socio-
demographical and economical features describing the
trading area and competitor characteristics (Aina,
Abidemi Ayodeji, et al, 2012). As a result, Support
Vector Regression (SVR) is applied to provide the
prediction of sales of existing outlets with attributes
(e.g., floor space, number of parking lots, distance to
the next competitor etc.) as well as the relationship
between sales volume and these attributes. Finally, a
novel trigger model for sales prediction with data
mining techniques that focuses on how to forecast
sales with more accuracy and precision is proposed
(Kohli, Shreya, et al, 2020). Then, researchers lay
emphasis on online sales prediction instead of actual
daily sales volume.
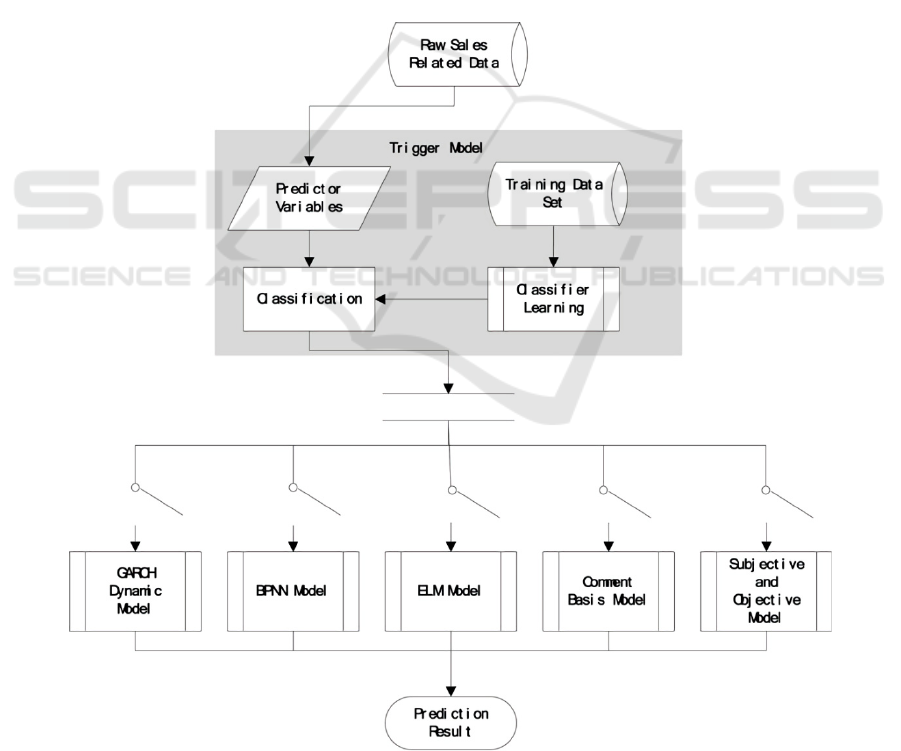
The approximate model they used is shown in Fig.
1. Raw data is first manipulated into available forms,
and then a trigger model is proposed to do the
classification. Next, the classification result shows the
potentially best prediction model for each SKU.
Finally, by use of the most appropriate model, the
prediction is accomplished.
With the model, data is classified and grouped to
facilitate analysis. The trigger model is a combination
of several basic models with Mean Absolute
Percentage Error (MAPE) to evaluate the performance
of proposed method. Compared with the baseline
model ARMA, the trigger model possesses more
accuracy (Huang 2015).
Figure 1: A sketch of the framework of Trigger Model System (Huang 2015).
Sales Prediction Model based on Multifactorial Linear Regression
599

The model considered to use to predict sales
volume in this passage is multiple linear regression
models. Regression analysis is a statistical technique
for estimating the relationship among variables which
have reason and result relation (Uyanık, Gülden Kaya,
Neşe Güler, 2013). As a linear model, multiple
regression provides most direct insight on how change
in single unit of any independent variables affect the
sales volume. Recent research shows extensive use of
multiple linear regression in different fields. For
example, the relationships between Chlorophyll-a and
16 chemical, physical and biological water quality
variables in Camilleri reservoir (Ankara, Turkey)
were studied by using principal component scores
(PCS) in multiple linear regression analysis (MLR) to
predict Chlorophyll-a levels (Çamdevýren, Handan, et
al, 2005). In addition, the simulation of water table
responses is discussed and the use of multiple linear
regression as a modelling technique is considered. The
model permits the consideration of changes in
properties of recharge, discharge and aquifer
parameters simultaneously (Hodgson, Frank D, 1978).
The rest part of the paper is organized as follows:
In the first following part, case used for multiple
regression model in this passage will be introduced
with data and model presented. For visualization,
output from Minitab and graphs would be presented,
along with assumptions for proper utilization of the
model, and how the model is evaluated. Moreover,
results output of software, not only the output
function, given R
2
value and VIF but also the Four in
one graph for the observational data versus the
predicted data with residuals would be explained and
presented one by one with clarification. One can
understand what the data represents and what the
graph indicates without any background knowledge.
Based on analysis provided and output given by graph,
final conclusion would be given with discussions on
limitation of the model. Finally, conclude upon all the
paragraph including future expectations on prediction
of the sales model.
2 DATA AND METHOD
The whole analysis of sales volume and model
prediction is based on the ABCtronics case. In this
case, reader serves as an intern of the ABCtronics firm
which specializes in producing IC chips. Recent
consumer feedback and data shows a dramatic
increase in the rejection rate from XYZfirm, which
causes doubt from the Audit committee (Adhikari,
Arnab, et al, 2016). As the main focus of this passage
the use of multiple linear regression model, analysis
on consumer feedback and rejection rate are ignored,
the main focus would be prediction of future sales
volume by multiple linear regression. Table I provided
historical sales.
Table 1: Historical Sales Figure of Abctronics (Adhikari,
Arnab, Et Al 2016).
ABCtronics’ sales
Year volume (in
millions)
Overall market
demand
(in millions)
Price per
chip (in
$)
Economic
condition
*
2004 2.39 297 0.832 0
2005 3.82 332 0.844 1
2006 3.33 195 0.854 0
2007 2.49 182 1.155 1
2008 1.56 93 1.303 0
2009 0.97 98 1.265 0
2010 1.32 198 1.368 1
2011 1.42 188 1.208 0
2012 1.48 285 1.234 1
2013 1.85 264 1.282 1
Note.∗Economic condition : 1 signfies favorable market condition and 0 signfies
otherwise.
For multiple linear regression model to be
applicable, at least two independent variables are
needed. For multiple linear regression, the proposed
model is shown below:
𝑌=𝛽
+𝛽
𝑋
+𝛽
𝑋
+𝛽
𝑋
+𝜀
1
where ε~ Normal (0, σ²). Here, an error term of
normal distribution with mean 0 and standard
deviation σ² is included accounting for instability of
this model.
From the table, statistics show three different
independent variables and one dependent variable-
ABCtronics’ sales volume. Since statistically
significance of any independent variable cannot be
determined only by looking at the raw data. The first
try includes all three independent variables in the
model and the corresponding results are shown in Eq.
(1) Table Ⅱ Table Ⅲ and Table Ⅳ.
Table 2: Coefficients for all independent variables inclusing
the constant term.
Term Coef SE Coef T-Value P-Value VIF
Constan
t
8.86 1.35 6.57 0.001
Overall
market
demand
-0.00524 0.00258 -2.03 0.089 3.27
Price Per
Chip
-5.505 0.881 -6.25 0.001 2.54
Economic
Condition
1.130 0.342 3.30 0.016 2.44
BDEDM 2022 - The International Conference on Big Data Economy and Digital Management
600

Table 3: Overall Model summary for three independent
variables.
S R-sq R-sq(adj) R-sq(pred)
0.346274 90.75% 86.13% 72.75%
Table 4: Additional Information Including The F-Value.
Source
D
F
Adj SS Adj MS
F-
Value
P-
Value
Regression 3 7.0606 2.3535 19.63 0.002
Overall market
demand
1 0.4930 0.4930 4.11 0.089
Price Per Chip 1 4.6786 4.6786 39.02 0.001
Economic
Condition
1 1.3089 1.3089 10.92 0.016
Erro
r
6 0.7194 0.1199
Total 9 7.7800
sale = 8.86 − 0.00524 market demand
−5.505 Price Per Chip
+ 1.130 Economic Condition
2
Adjusted R
2
from model summary shows that only
86.13% of the variation in the sales volume is
explained by this regression model. Adjusted R
2
is
preferred here since it takes into account the real
variation by adding more variables, which h still
shows high percentage of prediction coverage. To
justify the accurateness of this model, p-values for
each different variable are required, which is shown as
the last column of Analysis of Variance part. Taking a
95% confidence level, p-value of Overall market term
equals 0.089 which is greater than 5%, the passing line
for statistically significance. For any p-value greater
than 5%, independent variable with that specific p-
value is considered statistically insignificant. Getting
rid of that term would provide more accurate result
since insignificant variable attributes little to predict
future sales volume. A refined model is provided
taking only Price per chip and economic condition as
independent variables. With the same regression
model, data output from Minitab is shown in Table Ⅴ,
Table Ⅵ and Eq. (2).
sales = 6.452 − 4.136 Price Per Chip
+0.606 Economic Condition
3
Table 5: Overall Model summary or two variables.
S R-sq R-sq(adj) R-sq(pred)
0.416172 84.42% 79.96% 64.42%
Table 6: Coefficients summary for two variables and the
constant term.
Term Coef
SE
Coef
T-
Value
P-
Value
VIF
Constan
t
6.452 0.766 8.42 0.000
Price Per
Chip
-4.136 0.680 -6.08 0.001 1.05
Economic
Condition
0.606 0.269 2.25 0.059 1.05
The p-value here are comparatively small, which
proves the two independent variables to be statistically
significant. Furthermore, for it not be a biased model,
multicollinearity still needs to be tested.
Multicollinearity defines the correlation between two
independent variables so if too high, the prediction
will not be accurate as variation in one variable affects
the other as well. Variance inflation factor (VIF)is
then chosen to exam the correlation. Here, coefficient
component of above graph gives result of VIF to be
1.05, which is much smaller than the standard value 5.
To sum up, there is no multicollinearity between these
two variables and the refined model seems to be
suitable for predicting the sales figure of ABCtronics.
Table 7: Coefficient for single variable ‘overall market’
term.
Term Coef SE Coef T-Value
P-
Value
VIF
Constan
t
0.753 0.779 0.97 0.362
Overall
market
demand
0.00614 0.00344 1.79 0.112 1.00
3 RESULTS AND DISCUSSION
For the modified model:
Sales Volume = 6.452 − 4.136 price per chip2
+0 .6063 economic condition
4
Adjusted R
2
in this model shows that around
79.96% of the variation in the sales volume is
explained by this regression model, which is
comparatively high for a sales prediction model.
Further clarification for choosing confidence level at
95% is needed. According to the analysis, a simple
linear regression model with overall market demand
was ran before any multiple linear regression.
Sales Prediction Model based on Multifactorial Linear Regression
601
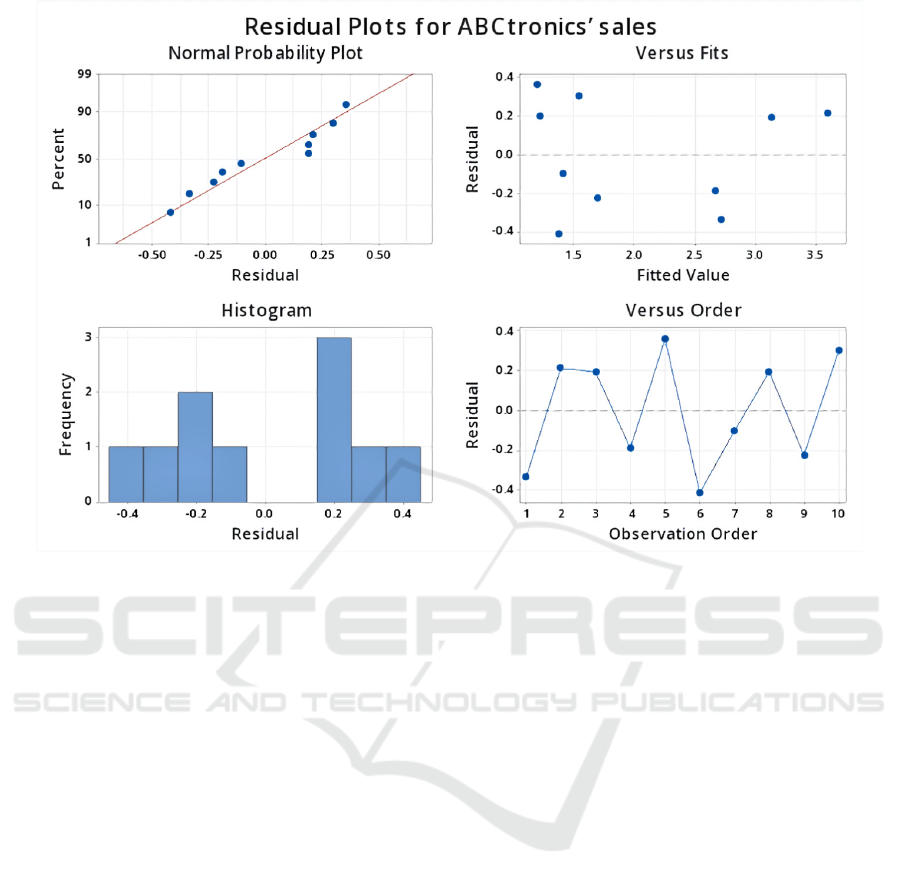
Figure 2: Residual plots for ABCtronics’ sale for all three independent variables.
P-value of this single independent variable is
0.112, which is higher than 10%, corresponding value
of 90% confidence level. Here, eve with a 10% level
of significance, overall market demand is still defined
as statistically insignificant, not to mention the 5%
level. It might work for lower levels of significance
but overall precision would decrease choosing too
low a significant level for any model. Therefore,
getting rid of the demand term may help people to
better estimate sales volume using a multiple
regression model.
From the model, unit increases in price per chip
would lead to approximately 4.136 units decrease in
the sales volume. For the binary economic condition
value, signifies favorable market condition would
lead to 0.6 unit increase in sales volume. For instance,
ABCtronics should operate in favor of market
condition and control their chip price comparatively
low to maximizes sales volume.
To visualize and better compare two different
regression modes with and without overall market
demand variable, Four-in -one graphs with normal
probability plot, histogram, versus fit and versus
order are shown in Fig. 2. With all three independent
variables, top left plot shows how fit the real data to
the fitted line; top right is the verification that
residuals are randomly distributed; bottom left is the
histogram with frequency and bottom right is data of
residual in order.
The top left normal probability curve is a
visualization of R
2
value: predicted value forms the
best fitted line shown as the red straight line. For each
point, it represents the real sales volume from 2004 to
2013.The more variation that is explained by the
model, the closer the data point fall to the fitted
regression line. The distance between reel value point
and the predict line is defined as residuals. The lower
the residuals, better fit is the model of prediction.
From above top left plot, real points are all shown to
be close to the predicted line, which signals high R
2
corresponding to our result-90,75%.
The top right residual fits graph plots residual on
y axis and fitted value on x-axis. The residuals versus
fits plot is used to verify the assumption that the
residuals are randomly distributed and have constant
variance. Therefore, ideally, the points should fall
randomly on both sides of 0. To sum up, the versus fit
plot is at ideal status.
The bottom left histogram graph is easy to
understand -it shows the frequency of each residual.
Larger frequency with small residuals is favorable
since it represents more accurate prediction. But here,
data with 0 residual does not exist due to flaws on
design of the model.
BDEDM 2022 - The International Conference on Big Data Economy and Digital Management
602

The versus order graph is similar to the versus fits
graph but plotted in order that of the date collected.
Independent residuals show no trends or patterns
when displayed in time order. From the graph,
residuals near year 2005 and 2006 may be correlated
since the difference is comparatively low, but the
overall trend of residuals fall randomly around the
center line.
Figure 3: Residual plots for ABCtronics’ sales for two variables.
Getting rid of the overall market term,with two
independent variables ,the top left plot shows better
fit of the real data to the fitted line ;top right is still
the verification that residuals are randomly
distributed; bottom left is the histogram with residual
frequency more in the middle and bottom right is data
of residual in order.
Now, one is able to reproduce the four-in-one
graph with only two independent variables. The
residual plot seems to be closer to the fitted line which
shows increase in R
2
value. Versus fit and order graph
still show random distribution of the residual points
around the center line. The histogram is with more
differences-frequency of predicted data with small
residuals increase a lot comparatively, which shows a
pattern closer approximates to the normal
distribution. Hence, visualization for model of
prediction shows the same result as pure linear
equation that getting rid of the overall market variable
helps refine the multiple regression model.
Multiple linear regression model seems to provide
a proper prediction for future sales volume. However,
nothing can be guaranteed that table provided to
people from ABCtronics is flawless and contains all
factors influential to sales figures. First of all, whether
there is omitted variable that are not mentioned in the
model is unclear. If there is omitted variables which
also determines changes in the sales volume, the
model is then incomplete and biased since not all
factors are included. Moreover, without telling
whether each independent variable correlates with
existing error terms, people are not sure that this is a
good model for prediction. If correlation exists, IV
regression needs to be done to find other better
independent variables. Additionally, real world
economy is more complicated with nonlinear
relationship, only using multiple linear relationship
may not provide desirable results. There are many
clinical problems which do not allow the option of
corroboration by more invasive and disruptive
approaches. For such problems, a more penetrating
approach to data analysis may be the only way to do
justice to the data set (BLACK, A.M.S., P. FOÉx,
1982).
Sales Prediction Model based on Multifactorial Linear Regression
603

4 CONCLUSION
In summary, sales prediction models based on
multiple linear regression is investigated based on
multiple independent variables related to sales
volume. The article starts with examples from
historical successful sale model prediction to the use
of multiple linear regression models among different
fields. Next comes the description of ABCtronics case
which would be used for building own sales prediction
model. Though as a linear regression, multiple
regression models vary a lot depends on how many
independent variables to include. Keep adding
meaningless variables affects nothing about the model
but create more bias. As a result, final model created
in the passage excludes one independent variable from
data provided to promote accuracy. Though the best
fitted model is found using multiple linear regression
here, in real world, linear model is comparatively
incapable of producing accurate sale figure prediction.
Furthermore, if people keeping conducting more
investigations, researchers may find other correlated
independent variables which become determinant
factors to predict sales volume. Including those factors
can further refine the multiple regression model and
give accurate prediction. These results offer a
guideline for more complicated models developed in
sale volume prediction model and give a chance for
people to create their own prediction model even if
one does not specialize in it.
REFERENCES
Mohammed Ali, S.Narasimha Rao, Abdul Rahim “A
Survey of Time Series Data Prediction on Shopping
Mall.” ISSN: 0976-5166 Vol. 4 No.2 Apr-May 2013
http://www.ijcse.com/docs/INDJCSE13-04-02-
100.pdf.
Adhikari, Arnab, et al. “Case—Abctronics: Manufacturing,
Quality Control, and Client Interfaces.” INFORMS
Transactions on Education, vol. 17, no. 1, 2016, pp. 26–
33., https://doi.org/10.1287/ited.2016.0158cs.
Aina, Abidemi Ayodeji, et al. “Spatial Data Mining for
Retail Sales Forecasting.” SSRN Electronic Journal,
2012, https://doi.org/10.2139/ssrn.2060272.
BLACK, A.M.S., and P. FOÉx. “Some Capabilities and
Limitations of Multiple Regression Analysis:
Application to Canine Coronary Blood Flow.” British
Journal of Anaesthesia, vol. 54, no. 12, 1982, pp. 1319–
1329., https://doi.org/10.1093/bja/54.12.1319.
Çamdevýren, Handan, et al. “Use of Principal Component
Scores in Multiple Linear Regression Models for
Prediction of Chlorophyll-a in Reservoirs.” Ecological
Modelling, vol. 181, no. 4, 2005, pp. 581–589.,
https://doi.org/10.1016/j.ecolmodel.2004.06.043.
G. Kohli, Shreya, et al. “Sales Prediction Using Linear and
KNN Regression.” Algorithms for Intelligent Systems,
2020, pp. 321–329., https://doi.org/10.1007/978-981-
15-5243-4_29.
Hodgson, Frank D. “The Use of Multiple Linear Regression
in Simulating Ground-Water Level Responses.”
Ground Water, vol. 16, no. 4, 1978, pp. 249–253.,
https://doi.org/10.1111/j.1745-6584.1978.tb03232.x.
Huang, Wenjie, et al. “A Novel Trigger Model for Sales
Prediction with Data Mining Techniques.” Data
Science Journal, vol. 14, 2015, p. 15.,
https://doi.org/10.5334/dsj-2015-015.
Meeran, S., et al. “Sales Forecasting Using Combination of
Diffusion Model and Forecast Market – an Adaption of
Prediction/Preference Markets.” IFAC Proceedings
Volumes, vol. 46, no. 9, 2013, pp. 87–92.,
https://doi.org/10.3182/20130619-3-ru-3018.00619.
Uyanık, Gülden Kaya, and Neşe Güler. A Study on
Multiple Linear Regression Analysis, vol. 106, 10 Dec.
2013, pp. 234–240.,
https://doi.org/https://doi.org/10.1016/j.sbspro.2013.12
.027.
BDEDM 2022 - The International Conference on Big Data Economy and Digital Management
604
