
Sales Forecasting for Firms based on Multiple Regression Model
Guanyi Wang
a
Ansai Senior High School, Yan’an, China
guanghua.ren@gecacademy.cn
Keywords: Sales Prediction, Linear Model, Multiple Linear Regression.
Abstract: This paper focuses on the building and usage of a multiple linear regression model (MLR) for predicting a
firm’s sales. According to the data provided by a semiconductor manufacturing company, ABCtronics on its
historical sales from 2004 to 2013 and the data with three factors that may affect the sales (i.e., overall market
demand, price per chip, and economic condition), a multiple linear regression model can be built based on
these data. Hence, the future sales figure can be also estimated by using the model. The model is constructed
via the Excel in order to find the values of coefficients for each independent variable. The resulting model
offers a guideline for a way of more accurately and validly forecasting a firm’s sales or predicting other trends
and relationships in a situation of having multiple variables by using a multiple linear regression model.
1 INTRODUCTION
Understanding the sales area and making forecasts of
sales will help corporations set a realistic goal and
understand the scope of their business. Obtaining
accurate sales forecasts is almost as important as
achieving revenue targets themselves. However, with
so many different sales forecasting methods, it is
unknown which technology could provide the most
accurate view. According to CSO insights, 60% of the
forecast transactions are not actually completed. As
expected, the data also showed that 25% of sales
managers were not satisfied with the accuracy of their
forecasts. Prediction is based on the application of data
demand and data in predicting future sales. Sales
forecasts can only be as good as the data they based
on. Prediction experts use three types of sales
forecasting techniques in their sales forecasting.
Prediction techniques are based on the input data types
used to predict the requirements. Choosing the right
forecasting technology can greatly improve the ability
to accurately predict future revenue (Michael, 2021,
Box, Jenkins, 1970, McKenzie, 1984, Hyndman, Rob,
2015, Bao, Yue, Rao, 2017).
As for the prediction model, there are plenty of
factors affecting the prediction model, it is difficult to
predict the time series data, e.g., stock price. In
addition, the impact of different factors on stock price
may be linear or nonlinear. Contemporarily, the
a
https://orcid.org/ 0000-0003-0085-1270
emergence of a good model of stock price has posed a
challenge to researchers. Long and short term memory
is a variant of recurrent neural network, which can
capture time series and has achieved great success in
time series prediction. In addition, convolutional
neural network is we compare our proposed model
with different methods in two real stock data sets. The
results confirm the efficiency and scalability of our
proposed method (Tomas, Martin, Lukas, Jan,
Sanjeev, 2010, Ronald Williams, Geoffrey Hinton,
Rumelhart, David, 1986, Yoshua, Patrice, Paolo,
1994, Hochreiter, Schmidhuber, 1997, Cho,
Merrienboer, Bahdanau, Yoshua 2014, Chen, Zhou,
Dai, 2015, Nelson, Pereira, De Oliveira, 2017, Zhang,
Li, Morimoto, 2019, Chen, Chen, Huang, Huang,
Chen, 2016, Bahdanau, Cho, Bengio, 2014).
The rest part of the paper is organized as follows.
The Sec. 2 will introduce the data origination and
analysis method. The Sec. 3 will display the analysis
results as well as offer a corresponding explanation.
Eventually, a brief summary is given in Sec. 4.
2 DATA AND METHOD
Table I provides ABCtronics’ total sales (in millions)
from 2004 to 2013, as well as data on three factors
that may affect its sales, namely, overall market
demand,
chip unit price, and economic conditions.
628
Wang, G.
Sales Forecasting for Firms based on Multiple Regression Model.
DOI: 10.5220/0011198600003440
In Proceedings of the International Conference on Big Data Economy and Digital Management (BDEDM 2022), pages 628-633
ISBN: 978-989-758-593-7
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Table 1: Historical Sales Figure of ABCtronics.
Year
ABCtronics’ sales volume
(in millions)
Overall market
demand (in millions)
Price per chip
(in $)
Economic
condition*
2004 2.39 297 0.832 0
2005 3.82 332 0.844 1
2006 3.33 195 0.854 0
2007 2.49 182 1.155 1
2008 1.56 93 1.303 0
2009 0.97 98 1.265 0
2010 1.32 198 1.368 1
2011 1.42 188 1.208 0
2012 1.48 285 1.234 1
2013 1.85 264 1.282 1
Note. *Economic condition: 1 signifies favourable market condition and 0 signifies otherwise.
Besides, it contains a dummy variable which is the
economic condition.
In this analysis, the method used for predicting
sales figure for a firm is by utilizing multiple linear
regression model (MLR). Multiple linear regression
model provides an explanation for the relationship
between multiple independent variables and an
outcome variable (dependent variable) through a
mathematical function. The general formula of MLR
can be notated as following:
𝑌=𝛽
+𝛽
𝑋
+𝛽
𝑋
+⋯+𝛽
𝑋
+∈
1
where Y is the dependent variable, 𝛽
is the y-
intercept of the linear model, 𝛽
… 𝛽
are the
coefficients for each independent variables, 𝑋
,
𝑋
…𝑋
are the numbers of independent variables,
and ∈ is the error term which is the difference of the
actual value and predicted value ( ∈=𝑌 −𝐸𝑥).
Referring to the case of ABCtronics, there are three
independent variables which are overall market
demand, chip unit price, and economic conditions,
hence each of them can be 𝑋
, 𝑋
, and 𝑋
respectively. Therefore, the model used for predicting
sales figure for this case is:
𝑌=𝛽
+𝛽
𝑋
+𝛽
𝑋
+𝛽
𝑋
+∈
2
Before the constructing the model, the first thing
to do is to analyze the relationship and correlation
between all the variables. This can be done through
viewing a matrix plot or running a correlation table.
Figure 1: Matrix Plot of overall market demand, chip unit price, economic conditions, and sales volume.
Sales Forecasting for Firms based on Multiple Regression Model
629

Table 2: Correlations between each variable.
Sales volume
Overall market
deman
d
Price per chip Economic condition
Sales Volume 1
Overall Market deman
d
0.533 1
Price
p
er chi
p
-0.855 -0.536 1
Economic Condition 0.146 0.508 0.212 1
From the Fig. 1 and Table II, there is weak
positive relation between sales volume and economic
condition. As well as a weak positive relation
between economic condition and Price per chip.
However, other correlations are either strong or
moderate as the absolute values of these correlations
are around 0.5 to 0.8. The model seeks a smaller
correlation between independent variables, but the
correlation coefficient of overall market demand with
other independent variables are dominantly moderate
with an absolute value around 0.5. This might in turn
affect the model, which possibly lead to the difficulty
for estimating the relationship between each
independent variable and dependent variable
individually. This idea is also used in future testing of
multicollinearity.
Nevertheless, the model is not always perfect as
each predicted value usually have a slightly
difference to the actual value. Thus, evaluating the
multiple linear regression model plays a crucial part
in predicting the sales figure accurately and validly.
The model can be evaluated by residual analysis and
coefficient of determination, which is R-squared:
𝑅
=1−
𝑅𝑆𝑆
𝑇𝑆𝑆
3
where RSS is residual sum of squares which is
explained variation and TSS is the total sum of
squares which is the total variation.
The value of R-squared is always between 0 to 1,
which indicate the percentage of how well this model
could explain the variations in variables. Larger the
R-square value represent a greater and more accurate
model for the future predicting vice versa.
In fact, R-squared value is not always consistent
and accurate as adding more variables for the model
does not appear to lower or decrease R-squared value.
However, adjusted R-squared can be introduced to
deal with this problem in order to increase the validity
and reliability of the MLR. The equation of the
adjusted R-squared is:
𝐴𝑑𝑗𝑢𝑠𝑡𝑒𝑑 𝑅
=1−
1−𝑅
𝑛−1
𝑛−𝑘−1
4
where n is the number of data, and k is the number of
independent variables.
After running the model in Excel, the null
hypothesis that the coefficient is equal to zero is
tested by the p-value for each variable. A low p-value
in this case, 0.05 suggests that the null hypothesis
may be rejected. In other words, because changes in
the predictor’s value are connected to changes in the
dependent variable, an independent variable with a
low p-value is likely to be a useful addition to your
model. A greater or insignificant p-value, on the other
hand, indicates that changes in the independent
variable are unrelated to changes in the responder. If
a p-value is higher than the typical threshold alpha,
0.05, this would indicate that it is not statistically
significant. Thus, this corresponding variable should
be ignored and removed.
Next step is to test the overall significance in the
regression relationship. The overall significance uses
F test statistic to show if there is a linear relationship
between all independent variables and the dependent
variable. We set up the null hypothesis and alternative
hypothesis as H
0
: 𝛽
=𝛽
=...=𝛽
=0 and H
a
: at
least one 𝛽
≠0. The formula of F test is:
𝐹=
𝑀𝑆𝑅
𝑀𝑆𝐸
5
Here,
𝑀𝑆𝑅=
𝑆𝑆𝑅
𝑘
,𝑀𝑆𝐸=
𝑆𝑆𝐸
𝑛−𝑘−1
6
and the critical F value is 𝛼=0.05. There is a need
to test multicollinearity in order to reduce the
standard errors. The variance inflation factor (VIF)
between the independent variables can be used to see
if any correlation exists. The equation of the VIF is:
𝑉𝐼𝐹 =
1
1−𝑅
7
where 𝑅
is the R-squared of independent variables.
If VIF is greater than 5, multicollinearity exists.
The final step of evaluating the model is to do
residual analysis. The regression model is regarded
valid if the residual is closer to 0, which tells how
good the model line fits in the data points. The
residual is defined as:
𝑒=𝑌−𝑌
8
where Y is the actual data value and 𝑌
is the
predicted value. The residual plot can be constructed
BDEDM 2022 - The International Conference on Big Data Economy and Digital Management
630

with residuals on the vertical axis against the
independent variable. The shape and trend of the plot
can be used to identify how well the model fits for
predicting values.
3 RESULTS AND DISCUSSIONS
Based on the data provided from Table I, a regression
result table can be performed using Excel. The result
tables of the model are shown in Tables III-V.
Table 3: Regression Statistics.
Multiple R 0.952
R Square 0.907
Adjusted R Square 0.861
Standard Erro
r
0.346
Observations 10
Table 4: ANOVA Analysis.
ANOVA df SS MS F
Significance
F
Regression 3 7.060 2.353 19.628 0.001
Residual 6 0.719 0.119
Total 9 7.780
Table 5: Regression of Coefficients & statistic Report.
Coefficients
Standard
Erro
r
t Stat P-value
Lower
95%
Upper
95%
Lower
95.0%
Upper
95.0%
Intercept 8.860 1.348 6.571 0.0005 5.561 12.159 5.561 12.159
Overall Market
demand
-0.005 0.002 -2.027 0.088 -0.011 0.001 -0.011 0.001
Price per chip -5.505 0.881 -6.246 0.0007 -7.662 -3.348 -7.662 -3.348
Economic
condition
1.130 0.342 3.303 0.016 0.293 1.967 0.293 1.967
According to the results, the values of 𝛽
,𝛽
,𝛽
and 𝛽
can be found in the column of coefficients
where it highlighted as yellow. Hence, the equation
of this model can be written as:
𝑌
=8.8607 − 0.0052𝑋
− 5.5054𝑋
− 1.1302𝑋
9
However, by interpreting the p-values for each
independent variable in regression model, the
independent variable’s relation can be examined. At
5% level of significance, the p-value for the overall
market demand (X
1
) is more than 0.05 showing a
value around 0.088 which is insignificant. Hence, the
independent variable of overall market demand
should be ignored and perform a new multiple linear
regression model for the independent variables of
price per chip and economic condition (X
2
and X
3
).
Table 6: Regression Statistics.
Multiple R 0.918
R Square 0.844
Adjusted R Square 0.799
Standard Error 0.416
Observations 10
Table 7: ANOVA Analysis.
ANOVA df SS MS F
Significance
F
Regression 2 6.567 3.283 18.959 0.001
Residual 7 1.212 0.173
Total 9 7.780
Table 8: Regression of Coefficients & statistic Report
Coefficients Standard Erro
r
t Stat P-value Lower 95% Upper 95% Lower 95.0% Upper 95.0%
Intercept 6.451 0.766 8.421 6.556 4.640 8.263 4.640 8.263
Price per chip -4.135 0.680 -6.079 0.0005 -5.744 -2.526 -5.744 -2.526
Condition 0.606 0.269 2.250 0.059 -0.030 1.243 -0.030 1.243
Therefore, from the Tables VI-VIII, the new
equation of this model is:
𝑌
=6.4517 − 4.1356𝑋
+ 0.6062𝑋
10
After constructing the equation of the model, the
model should be evaluated through the coefficient of
determination or R-squared. Seen from the tables, the
R-squared value is around 0.84, which means that the
model explains 84% of the total variations. However,
due to the multiple independent variables that the
model has, the evaluation should consider looking at
the adjusted R-squared value which is around 0.80.
Sales Forecasting for Firms based on Multiple Regression Model
631
Hence, around 80% of the variations could be
explained by this model, which is still considerably
good and fit. The regression result table also provides
data for F value and significance F values as shown
in Table X. As the null hypothesis and alternative
hypothesis in this case are H
0
: 𝛽
=𝛽
=0, and H
a
:
at least one 𝛽
≠0. By looking at the value of F in
Table X, which is around 18.96. this value far exceeds
the value of significance F, 0.0015. Thus, rejecting
the null hypothesis by F test statistic, which means
that at least one independent variable is significant.
The model needs to test the multicollinearity in order
to reduce the standard errors. It can be done through
the use of variance inflation factor (VIF) between the
independent variables of price per chip and economic
condition (X1 and X2) to see any correlation exists.
The equation of the VIF is:
𝑉𝐼𝐹 =
1
1−𝑅
𝑅
=0.04521448
11
Based on the Excel, the calculated value of VIF of
these two variables is 1.002048 which means that this
model is not affected by the multicollinearity as the
value is less than 5.
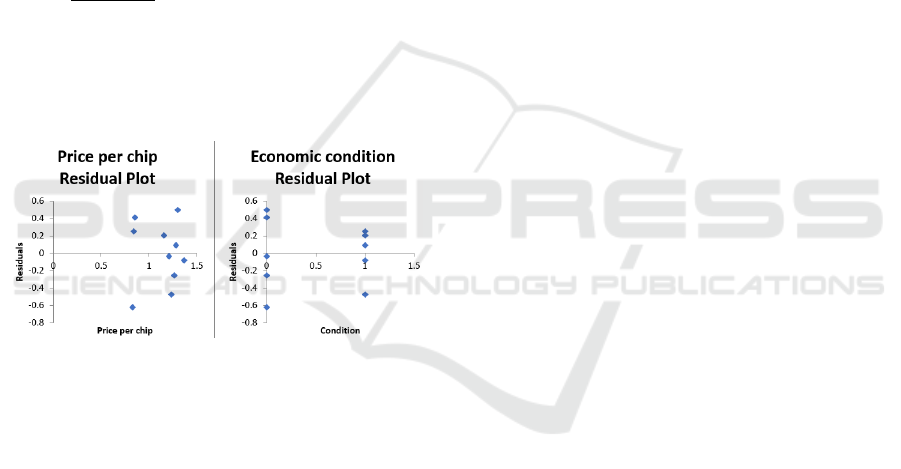
Figure 2: Price per chip and economic condition residual
plot.
The residual plot of two independent variable can
be generated by Excel as shown in Fig. 2. Based on
the results, the residuals values of price per chip and
economic conditions are all less than the absolute
value of 1. There are no U-shaped or inverted U-
shaped appeared in the plot. The residuals are
basically all scattered randomly in both price per chip
and economic condition, which indicates that this
regression model provides a decent fit to the data
given. Finally, this multiple linear regression model
is ready to predict ABCtronics’s future sales figure as
the model is well fitted in the given data.
Throughout the process of developing the
multiple linear regression model for the predicting
sales figures, there are still some limitations of this
model. One of the limitations is there are only ten
given data for each independent variable, which
resulted reducing the reliability of the model. There is
a still high p-value of the economic condition (0.059)
in the new model, even though the overall market
demand variable is removed, whereas, this could be
another limitation.
4 CONCLUSIONS
In summary, we investigate sales prediction model
based on multiple linear regression model. In terms of
the analysis, multiple linear regression model is
increasingly advancing in its evolution and play an
important role in the sales prediction. According to
the models, overall market demand, strongly affect its
sales while chip unit price, and economic condition
has a weak positive correlation between economic
conditions and the price per chip. However, the model
is not always perfect because each predicted value
usually varies slightly from the actual value. This can
be achieved by using the variance expansion factor
between the chip price and economic conditions (X1
and X2). Therefore, there is still a certain space for
development to explore and discover. Overall, these
results still offer a guideline for sales predication
based on multifactorial linear models.
REFERENCES
B. Yoshua, S. Patrice and F. Paolo, "Learning long-term
dependencies with gradient descent is difficult", IEEE
transactions on neural networks, vol. 5, no. 2, pp. 157-
166, 1994.
D. Bahdanau, K. Cho and Y. Bengio, Neural machine
translation by jointly learning to align and translate,
2014.
D. M. Q. Nelson, A. C. M. Pereira and R. A. De Oliveira,
"Stock market's price movement prediction with LSTM
neural networks", Proceedings of the International Joint
Conference on Neural Networks, pp. 1419-26, 2017.
E. D. McKenzie, "General exponential smoothing and the
equivalent ARMA process", J. Forecasting, pp. 333-
344, 1984.
G. E. P. Box and G. Jenkins, Time series analysis
forecasting and control, San Francisco, CA:Holden-
Day, 1970.
Hyndman and J. Rob, "Athanasopoulos George. 8.9
seasonal ARIMA models", Forecasting: principles and
practice oTexts, 2015.
J. F. Chen, W. L. Chen, C. P. Huang, S. H. Huang and A.
P. Chen, "Financial time-series data analysis using deep
convolutional neural networks", 7th International
Conference on Cloud Computing and Big Data
(CCBD), pp. 87-92, 2016.
BDEDM 2022 - The International Conference on Big Data Economy and Digital Management
632

J. Ronald Williams, E. Geoffrey Hinton, Rumelhart and E.
David, "Learning representations by back-propagating
errors", Nature, vol. 323, no. 6088, pp. 533-536, 1986.
K. Chen, Y. Zhou and F. Dai, "A LSTM-based method for
stock returns prediction: A case study of China stock
market", Proceedings: 2015 IEEE International
Conference on Big Data, pp. 2823-4, 2015.
K. Cho, B. V. Merrienboer, D. Bahdanau and B. Yoshua,
On the properties of neural machine translation:
encoder-decoder approaches, 2014.
M. Tomas, K. Martin, B. Lukas, C. Jan and K. Sanjeev,
"Recurrent neural network based language model",
Interspeech, vol. 2, pp. 3, 2010.
Proven Sales Forecasting Methods for Greater Accuracy by
Michael Pici / Jul 02, 2021. Continue reading at
https://www.saleshacker.com/sales-forecasting-
methods/ | Sales Hacker
S. Hochreiter and J. Schmidhuber, "Long Short-Term
Memory", Neural Computation, vol. 9, no. 8, pp. 1735-
1780, 1997.
W. Bao, J. Yue and Y. Rao, "A deep learning framework
for financial time series using stacked autoencoders and
long-short-term memory", PLoS One, vol. 12, no. 7,
2017.
X. Zhang, C. Li and Y. Morimoto, "A multi-factor approach
for stock price prediction by using recurrent neural
networks", Bulletin of Networking Computing Systems
and Software, vol. 8, no. 1, pp. 9-13, 2019.
Sales Forecasting for Firms based on Multiple Regression Model
633
