
Interpolated Experience Replay for Continuous Environments
Wenzel Pilar von Pilchau
1 a
, Anthony Stein
2 b
and J
¨
org H
¨
ahner
1
1
Organic Computing Group, University of Augsburg, Am Technologiezentrum 8, Augsburg, Germany
2
Artificial Intelligence in Agricultural Engineering, University of Hohenheim, Garbenstraße 9, Hohenheim, Germany
Keywords:
Experience Replay, Deep Q-Network, Deep Reinforcement Learning, Interpolation, Machine Learning.
Abstract:
The concept of Experience Replay is a crucial element in Deep Reinforcement Learning algorithms of the
DQN family. The basic approach reuses stored experiences to, amongst other reasons, overcome the problem
of catastrophic forgetting and as a result stabilize learning. However, only experiences that the learner observed
in the past are used for updates. We anticipate that these experiences posses additional valuable information
about the underlying problem that just needs to be extracted in the right way. To achieve this, we present
the Interpolated Experience Replay technique that leverages stored experiences to create new, synthetic ones
by means of interpolation. A previous proposed concept for discrete-state environments is extended to work
in continuous problem spaces. We evaluate our approach on the MountainCar benchmark environment and
demonstrate its promising potential.
1 INTRODUCTION
The combination of neural networks with Reinforce-
ment Learning (RL), also known as Deep RL, has
recently achieved several breakthroughs in the do-
main of Machine Learning. Some prominent exam-
ples range from playing Atari games (Mnih et al.,
2015) over mastering the board game Go on a super-
human level (Silver et al., 2017) to even more com-
plex environments with huge state- and action-spaces
like the video games StarCraft II (Vinyals et al., 2019)
and Dota 2 (Berner et al., 2019).
One well known algorithm in this context is the
so-called Deep Q-Network (DQN) (Mnih et al., 2015)
that replaces the Q-table from the classic Q-Learning
with a neural network. To counteract several prob-
lems that arise here (i.e. correlations of Q-updates
and catastrophic forgetting), the Experience Replay
(ER) was brought back to live, a concept that has
been developed before the wide success of neural net-
works. The ER works as a memory of experienced
situations, similar to the short-term memory of living
individuals, and stores them in a buffer. In the train-
ing phase the learner makes use of them and is able
to increase sample efficiency and stabilize the learn-
ing process this way. However, the stored transitions
are only used in the form they have been gathered and
a
https://orcid.org/0000-0001-9307-855X
b
https://orcid.org/0000-0002-1808-9758
the possibly existing potential in this collection of ob-
servations of the environment is not further exploited.
As after enough time steps has gone by, the stored
experiences are well distributed over the state space,
and the transitions in the buffer represent knowledge
about the environment that just needs to be extracted
and used in the right way. This is our hypothesis at
least.
The Interpolated Experience Replay (IER) does
exactly that. A first study from Pilar von Pilchau et
al. (Pilar von Pilchau et al., 2021) in discrete envi-
ronments with a simplistic and restricted version of
IER showed promising results and justified a deeper
investigation. Our contribution involves the creation
of synthetic experiences by means of interpolation.
These interpolated experiences are stored in an in-
dividual buffer and mixed in for training. A nearest
neighbour search collects valuable samples from the
real buffer and utilizing the technique of Inverse Dis-
tance Weighting Interpolation (Shepard, 1968) new
synthetic experiences are created. In the early explo-
ration phases, when the learner knows little about the
environment and is building up its knowledge slowly,
the IER shows its potential and results in a reduced
learning time. For evaluation purposes we used the
MountainCar problem and tested several configura-
tions of IER. Our second contribution is the extension
to deal with continuous state spaces.
von Pilchau, W., Stein, A. and Hähner, J.
Interpolated Experience Replay for Continuous Environments.
DOI: 10.5220/0011326900003332
In Proceedings of the 14th International Joint Conference on Computational Intelligence (IJCCI 2022), pages 237-248
ISBN: 978-989-758-611-8; ISSN: 2184-3236
Copyright © 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
237

The remainder of the paper is structured as fol-
lows. We give a short introduction of some basic
knowledge like the ER and DQN in Section 2. An
overview of relevant work that has been done in this
area is given in Section 3. A reminder of the basic
functionality of the IER is presented in Section 4 and
followed by our main contribution in Section 5, where
we describe how the IER can be applied for continu-
ous environments. An evaluation on the MountainCar
environment is performed in Section 6. Finally we
conclude the paper with a summary and some ideas
for future work in Section 7.
2 BACKGROUND
In this section we present some background knowl-
edge such as what is an Experience Replay and a short
introduction of the Deep Q-Network.
2.1 Experience Replay
ER is a biological inspired mechanism (McClelland
et al., 1995; O’Neill et al., 2010; Lin, 1992; Lin,
1993) to store experiences and reuse them for train-
ing later on.
An experience is defined as: e
t
=
(s
t
,a
t
,r
t
,s
t+1
,d
t
) where s
t
denotes the state at
time t, a
t
the performed action, r
t
the corresponding
received reward, s
t+1
the follow-up state and d
t
if
the reached state was terminal. Each time step t
the agent stores its recent experience in a dataset
D
t
= {e
1
,...,e
t
}. In a non-episodic/infinite envi-
ronment (and also in an episodic one after a certain
amount of steps) we would run into the problem of
limited storage. To counteract this issue the vanilla
ER is realized as a FiFo buffer. Thus, old experiences
are discarded after reaching the maximum length.
This procedure is repeated over many episodes,
where the end of an episode is defined by a terminal
state. The stored transitions can then be utilized for
training either online or in a specific training phase.
It is very easy to implement ER in its basic form and
the cost of using it is mainly determined by the stor-
age space needed.
2.2 Deep Q-Learning
The Deep Q-Network was first introduced in (Mnih
et al., 2015; Mnih et al., 2013) and is the combina-
tion of classic Q-Learning (Sutton and Barto, 2018;
Watkins and Dayan, 1992) and neural networks. It
approximates the optimal action-value function:
Q
∗
(s,a) = max
π
bbE
r
t
+γr
t+1
+γ
2
r
t+2
+.. .|s
t
= s, a
t
= a, π
.
(1)
To enable large continuous state- and action-
spaces and also make use of generalization, the Q-
function is parametrized by a neural network. Equa-
tion (1) displays the maximum sum of rewards r
t
dis-
counted by γ at each time-step t, that is achievable by
a behaviour policy π = P(a|s), after making an obser-
vation s and taking an action a.
The temporal-difference error δ
t
is used to per-
form Q-Learning updates at every time step:
δ
t
= r
t
+ γmax
a
0
Q(s
t+1
,a
0
) − Q(s
t
,a
t
). (2)
Tsitsiklis et al. (Tsitsiklis and Roy, 1997) showed
that a nonlinear function approximator used in combi-
nation with temporal-difference learning, such as Q-
Learning, can lead to unstable learning or even diver-
gence of the Q-function.
As a neural network is a nonlinear function ap-
proximator, there arise several problems:
1. the correlations present in the sequence of obser-
vations,
2. the fact that small updates to Q may significantly
change the policy and therefore impact the data
distribution, and
3. the correlations between the action-
values Q(s
t
,a
t
) and the target values
r + γ max
a
0
Q(s
t+1
,a
0
) present in the TD-error
shown in (2).
The last point is crucial, because an update to Q
will change the values of both, the action-values as
well as the target values. That could lead to oscilla-
tions or even divergence of the policy. To counter-
act these issues, two concrete actions have been pro-
posed:
1. The use of ER solves, as stated above, the two first
points. Training is performed each step on mini-
batches of experiences (s, a, r, s
0
) ∼ U(D), that are
drawn uniformly at random from the ER.
2. To remove the correlations between the action-
values and the target values, a second neural net-
work is introduced that is basically a copy of the
network used to predict the action-values. This
network is responsible for the computation of the
target values. The target-network is either freezed
for a certain interval C before it is updated again
or “soft” updated by slowly tracking the learned
networks weights utilizing a factor τ. (Mnih et al.,
2015; Lillicrap et al., 2016)
We freeze the target network as presented above
and extend the classic ER with a component to create
synthetic experiences.
NCTA 2022 - 14th International Conference on Neural Computation Theory and Applications
238

3 RELATED WORK
The classical ER, introduced in Section 2.1, has been
improved in many further publications. One promi-
nent improvement is the so called Prioritized Experi-
ence Replay (Schaul et al., 2015) which replaces the
uniform sampling with a weighted sampling in favour
of experience samples that might influence the learn-
ing process most. This modification of the distribu-
tion in the replay induces bias, and to account for
this, importance-sampling has to be used. The au-
thors show that a prioritized sampling leads to great
success. This extension of the ER also changes the de-
fault distribution, but uses real transitions and there-
fore has a different focus.
Another extension of the classic ER is the
so-called Hindsight Experience Replay (HER)
(Andrychowicz and others, 2017). The authors
investigated multi-objective RL problems and used
state-action-trajectories alongside a given goal as
experiences to store in their HER. In complex envi-
ronments the agent was not able to understand what
goal it is intended to reach and therefore was not suc-
cessful. To assist the learner, synthetic experiences
were introduced and saved together with the real
ones. Such an experience replaced the goal with the
last state in the trajectory. This technique helped the
learner to understand what a goal is and subsequently
to reach the environment-given goals. In contrast to
our approach HER uses trajectories as experiences
and solves multi-objective environments, also no
interpolation is used to create synthetic experiences.
The authors of (Rolnick et al., 2018) presented
CLEAR, a replay-based method that greatly reduced
catastrophic forgetting in multi-task RL problems.
Off-policy learning and behavioural cloning from re-
play is used to enhance stability. On-policy learning
guarantees a preserved plasticity. In contrast to our
approach CLEAR does not use any form of synthetic
experiences and is designed for actor-critic algorithms
instead of DQN.
In (Hamid, 2014) the author investigates the ef-
fect of reappearing context informations. Two differ-
ent learners are used to learn the relation of states and
actions and reoccurring sequences into a data stream.
The data comes in three subsequences called context
and the first and the last context are the same while
the middle context differ. The author could show that
the information that was learned in context 1 can be
reused in context 3 even after confronted with a com-
pletely new context in between. The approaches ex-
tracts temporal information from previously observed
experiences to avoid catastrophic forgetting. IER uses
collected experiences to create completely new expe-
riences and therefore differ from this approach.
Sander uses interpolation to create synthetic ex-
periences for a replay buffer (Sander, 2021). In con-
trast to our approach, the used buffer is completely
filled with interpolated experiences and the synthetic
samples are generated from the corresponding neigh-
bourhood with mixup. The interpolation is performed
in every step and until the algorithm stops, while we
start with a high number of interpolations and end up
with very little or even no interpolations as we reach
convergence. The approach from Sander is located,
evaluated and motivated in the control task domain.
This work draws on the methods proposed in e.g.
(Stein et al., 2017; Stein et al., 2018). The authors
used interpolation in combination with an XCS clas-
sifier system to speed up learning in single-step prob-
lems by means of using previous experiences as sam-
pling points for interpolation. Our approach focuses
on a DQN as learning component and more impor-
tantly sequential decision problems.
4 INTERPOLATED EXPERIENCE
REPLAY BASICS
This work builds upon the findings of (Pilar von
Pilchau et al., 2020; Pilar von Pilchau, 2019; Pilar von
Pilchau et al., 2021). We give a short recap of the ba-
sics of the Interpolated Experience Replay (IER) in
the following chapter.
The IER makes use of the architectural concept
of the Interpolation Component (IC) from Stein et al.
(Stein et al., 2017). The actual IER consists of two
separated parts that share a maximum size: (1) The
real experience buffer and (2) the buffer for interpo-
lated experiences (cf. Fig. 1). The original synthetic
experience buffers size is restricted by the amount
of stored real samples and therefore decreasing over
time. If the buffer runs full with real experiences then
there is no space left for synthetic ones. This decision
comes from the expectation that an experience cre-
ated directly from the environment is exact, where in
contrast an interpolated one suffers from uncertainty.
Anyhow, to have the possibility to reserve a small
space for synthetic experiences even if the buffer is
full with real samples, there is a minimum size of the
synthetic buffer introduced s
syn min
. Following this,
the maximum size of the IER is the real buffers max-
imum size plus the synthetic buffers minimum size.
We denote the size of the IER as s
ier
, the size of the
real valued buffer as s
er
and the size of the synthetic
buffer as s
syn
.
To create synthetic experiences the stored real ex-
perience samples are used as sampling points for in-
Interpolated Experience Replay for Continuous Environments
239

Interpolated Experience Replay
real experiences synthetic experiences
s
ier
s
er
s
syn
s
syn min
Figure 1: Intuition of Interpolated Experience Replay mem-
ory.
terpolation. After every step a query point is drawn
from the state space using a query function. Different
query functions were evaluated in (Pilar von Pilchau
et al., 2021), such as drawing at random and different
variations of drawing from the distribution created by
the policy. This query point is then used to gather
all relevant sampling points via a nearest-neighbour
search. A simple averaging of the reward together
with a set of all observed follow-up states is then used
to create a bunch of synthetic experiences for the dis-
crete environment.
For training, the agent samples at random from
the combined buffer of both experiences. The IER is
flooded with synthetic experiences in early steps and
assists the learner when it knows little about the en-
vironment. Following this approach it was possible
to reduce the exploration phase in combination with
increased efficiency and as a result the agent was able
to converge faster.
5 INTERPOLATED EXPERIENCE
REPLAY FOR CONTINUOUS
ENVIRONMENTS
Our approach extends the IER for discrete and non-
deterministic environments (Pilar von Pilchau et al.,
2021) with the ability to interpolate follow-up states
instead of a simple average calculation of just the re-
wards. This makes it possible to use the IER in con-
tinuous environments. In this section we present the
novel functionalities.
Most importantly, it was necessary to allow it for
continuous environments. To achieve this, we needed
to solve the problem of the unknown follow-up state
of a synthetic experience, which is an important com-
ponent. Uncertainty here is expected to harm the
learning process in a way that would make the whole
approach unusable, because the Q-update relies on
predictions of these. In this section, we present a so-
lution for this issue.
5.1 Interpolation of the Follow-up
States
A straightforward solution, following the reward av-
eraging approach of (Pilar von Pilchau et al., 2021),
would be an interpolation of the follow-up state based
on the detected nearest-neighbours. In a very simple
environment where the agent can only move left or
right the state is represented by a position on a line.
Imagine the situation when the query point equals the
biggest yet discovered position to the right. Conse-
quently all sampling points have to be on the left of
this point. An interpolation of the follow-up state for
the action “move right” would result in a position that
is also located to the left of the query point but in fact
should be to the right. This effect (illustrated in Fig. 2)
would create a synthetic experience that is mislead-
ing as it assigns a movement in the wrong direction
to the move to the right action. In fact, the expected
behaviour that we want would be considered as ex-
trapolation which is known to be inaccurate or at least
suffers from uncertainty.
query point
true follow-up state
interpolated follow-up state
sampling points
Figure 2: Illustration of how interpolation of follow-up
states can create misleading results.
As a consequence, we developed a new approach
of interpolating the follow-up state. As the state-
transition of all observed experiences directly corre-
lates with the corresponding start state we decided to
interpolate the state-transition instead. In the above
mentioned example, all state-transitions (calculated
as δ
s
t
= s
t+1
−s
t
) of the discovered nearest-neighbours
are used as sampling points and an interpolated state-
transition is created and added to the sampling point.
As can be seen in Fig. 3 the interpolated follow-up
state equals the real follow-up state in the simple ex-
ample. This effect also holds for more complex states,
like a combination of position and velocity, as long
as s
t+1
is directly dependant from the corresponding
state s
t
. In more complex environments the interpola-
tion might not be exactly the same as the real value but
indeed suffers from reduced uncertainty compared to
the interpolation of the follow-up state directly. Fol-
lowing this approach we are still able to use interpo-
lation techniques for a (potential) extrapolation task.
NCTA 2022 - 14th International Conference on Neural Computation Theory and Applications
240

query point
true/interpolated
follow-up state
sampling points
true/interpolated
state-tranistion
Figure 3: Illustration of the interpolation of state-transitions
to calculate a stable approximation of the follow-up state.
5.2 Interpolation Technique
The equally weighted average interpolation used in
(Pilar von Pilchau et al., 2021) was introduced for a
first analysis of the idea and more complex environ-
ments require more complex interpolation techniques.
Thus, we decided to use Inverse Distance Weight-
ing Interpolation (IDW) (Shepard, 1968) for our ap-
proach.
IDW strives to create an interpolation using a
weighted average, where sampling points that are lo-
cated in closer distance to the query point have big-
ger impact than sampling points located farther away.
IDW is defined as follows:
u(~x) =
∑
N
i=1
w
i
(
~
x)u
i
∑
N
i=1
w
i
(~x)
, ifd(~x,~x
i
) 6= 0 for all i,
u
i
ifd(~x,~x
i
) = 0 for some i,
(3)
with
w
i
(~x) =
1
d(~x,~x
i
)
p
. (4)
The interpolation function tries to find an inter-
polated value u at a given point ~x based on sampling
points u
i
= u(~x
i
)fori = 1, 2, . ..,N. To increase the im-
pact of closer values a weight w
i
is used that includes
a distance metric d together with a variable p called
the power parameter controlling the impact of u
i
.
In our approach, we use experiences e
i
=
(s
i
,a
i
,r
i
,s
i+1
,d
i
) as samples u
i
. A query point ~x =
~x
q
= (s
q
,a
q
) is received via a query function and the
euclidean distance of the states s
i
and s
q
is used as
distance metric d. Furthermore the amount of sam-
pling points is restricted by the action a
q
and a nearest
neighbour search so that only experiences that meet
the following condition are included:
d(~x
q
,~x
i
) ≤ nn
thresh
∧ a
q
== a
i
, (5)
where nn
thresh
defines the maximum search radius.
The interpolation only occurs for the values of r
i
, s
i+1
and d
i
, resulting in the corresponding interpolations
r(~x), s
t+1
(~x) and d(~x). We can then create an interpo-
lated experience:
e
~x
=
s
q
,a
q
,r(~x), s
t+1
(~x),d(~x)
(6)
5.3 Synthetic Buffer Size
To original concept of a shared maximum size as pre-
sented in Section 4 is a quite simple approach and
lacks the ability of fine-tuning. As a consequence, we
introduce two new functionalities: (1) an exploration
mode and (2) the parameter β. The former defines a
minimum size of the synthetic buffer msexpl in rela-
tion of the actual decaying exploration rate ε and the
allowed maximum size s
syn max
:
msexpl
i
= ε
i
∗ s
syn max
. (7)
The parameter β allows a finer tuning of the mini-
mal size of the synthetic buffer in later stages. Thus, β
influences the minimum size of the buffer s
syn min
(cf.
Section 4). Another minimum size msbeta is then de-
fined as follows:
msbeta
i
= bs
syn min
∗ β
i
c, (8)
with
β
i
= max
β
init
−
β
init
M
∗ i
,0
. (9)
β
init
is the initial value that is assigned to β and
1 was found as a good value here. Furthermore, β
decreases after every time step i (an episode in our
approach) until it reaches 0 in time step M.
Following (7) and (8) we can update the minimal
size of the synthetic buffer s
i
syn min
for every episode
as follows:
s
i
syn min
= max
msexpl
i
,msbeta
i
] (10)
Fig. 4 gives a graphical intuition of how the mini-
mum size of the synthetic buffer is determined.
t
size
s
syn max
s
syn min
s
i
syn min
msbeta
i
msexpl
i
Figure 4: Intuition of the synthetic buffers minimal size.
Interpolated Experience Replay for Continuous Environments
241

5.4 Distribution Sampling
An evaluation of different query functions in (Pi-
lar von Pilchau et al., 2021) revealed that the IER
benefits from a sampling method that follows the dis-
tribution that is created by the policy. We can find
an off policy equivalent of this distribution in the real
experience buffer as it was created by the policy. In
discrete environments, it was enough to draw an ex-
perience out of the real valued buffer and use the re-
ceived state-action pair as query point. This is no
longer reasonable for continuous environments, be-
cause we are faced with a much bigger state space and
want to explore it instead of just interpolate points for
which we already know the exact corresponding re-
ward and follow-up state. We needed to adapt this
method to work again and to achieve this, we decided
to draw the query point in a radius r
sq
around the state
received from the drawn real example. To simplify
this parameter for multidimensional state spaces, we
defined it as follows: 0 ≤ r
sq
≤ 1. As we know the
maximum value of each dimension, we are now able
to determine a corresponding radius for each dimen-
sion:
r
d
sq
= r
sq
∗ S
d
max
∀ d ∈ S
dim
, (11)
with S
dim
being the dimensionality of the state
space. If the state space is defined as infinite for one or
more dimensions we can track the maximum discov-
ered value for the appropriate dimension(s) and use
this value(s) instead. To follow an on policy variation
of the distribution we always use the state-action pair
that was recently created by the policy instead of sam-
pling from the buffer. We call the former method Pol-
icy Distribution (PD) and the latter Last State (LS).
To follow the policy distribution even closer we can
choose the action of x
q
according to the actual pol-
icy, otherwise we perform an interpolation for every
action from the action space.
The associated pseudocode that summarizes the
procedure is depicted in Algorithm 1.
5.5 Performant Nearest Neighbour
Search
A straightforward approach of finding all relevant
neighbours that satisfy the first part of (5) would be
an exhaustive search in the real buffer. As this would
result in a computation time of O(N) we were in the
need of finding a more efficient solution. We decided
to go with the ball-tree structure (Omohundro, 1989)
that reduces the computation time to O(logN).
As this technique is designed for a static dataset
we are forced to rebuild the tree in a fixed interval
Algorithm 1: IER for continuous environments.
Initialize D
real
and D
inter
Initialize β, t
βmax
, ε and nn
thresh
Initialize s
syn max
, s
syn min
, IER
size
and t
max
β
dec
=
β
t
βmax
while t not t
max
do
while s is not TERMINAL do
Store experience e in D
if |D
real
| ≥ c
start inter
∧ s
syn min
> 0 then
Get x
q
= (s
q
,a
q
)
from Query Function
Get
e
t
|d(~x
q
,~x
t
) ≤ nn
thresh
∧ a
t
= a
q
from D
real
Store results in D
match
Compute ~x from IDW (x
q
,D
match
)
Create e
~x
= (s
q
,a
q
,r(~x), s
t+1
(~x),t(~x))
Store e
~x
in D
inter
sp = max[s
syn min
,IER
size
− |D
real
|]
while |D
inter
| > min[sp,s
syn
max
] do
Remove e from D
inter
sp = max[s
syn min
,IER
size
− |D
real
|]
end while
end if
end while
β ← β − β
dec
Update ε
s
syn min
← max[mseplx
t
,msbeta
t
]
end while
nn
rebalance
, resulting in a fixed set of searchable expe-
riences until the next rebuild appears. We found this
trade-off to be acceptable as the amount of reduced
time needed for searching outweighs the effect of per-
forming nn search on outdated data, especially as all
data will still be inserted into the set of searchable ex-
periences with a maximum delay of nn
rebalance
.
6 EVALUATION
In this section, we introduce the experimental setup
and afterwards report on the obtained results followed
by a discussion.
6.1 Experimental Setup
6.1.1 Environment
We evaluated our IER approach on the prominent
benchmark MountainCar-v0 environment from Ope-
nAI Gym (Brockman and others, 2016). In this prob-
lem an agent, the mountain car, starts in between two
hills and has to reach the top of the right hill. The
NCTA 2022 - 14th International Conference on Neural Computation Theory and Applications
242

action space covers three actions: (1) move to the
left, (2) move to the right and (3) do nothing. As the
power of the car on its own is not enough to climb the
hill, it has to go as high as possible on one side and
use the gathered speed to reach height on the other
side. By exploiting this effect the agent is able to fi-
nally reach the goal on the right hill. A state is con-
sequently formed out of two parts, (1) the position
and (2) the velocity. An episode is over if the agent
reaches the goal or a maximum time limit of 200 steps
is exceeded. Fig. 5 illustrates the environment.
Car
Goal
v
x
state: [x, v]
Figure 5: A graphical illustration of the MountainCar-v0
environment.
In the version from OpenAI Gym the agent re-
ceives a reward of -1 in every step until it reaches the
goal and receives a reward of 0 instead. To make the
reward function interpolatable, we changed it to the
following continuous version found by
1
:
r(s
t
,s
t+1
) =
200 − t ifs
t+1
is terminal,
100 ∗
E(s
t+1
) − E(s
t
)
else,
(12)
where
E(s) =
sin(3 ∗ x(s))
400
+
v(s)
2
2
, (13)
with x(s) being the position and v(s) the velocity
of the state s. This reward function takes the mechan-
ical energy (kinetic + potential energy) into account,
gives bigger rewards if the agent builds up speed and
height and encourages faster solutions.
6.1.2 Hyperparameter
Preliminary experiments revealed a stable hyperpa-
rameter configuration as given in Table 1.
6.1.3 Experiments
As baseline we used a DQN with vanilla ER and com-
pared it with several configurations of the IER. All ex-
periments were repeated 20 times with random seeds
and the average return over 100 episodes was mea-
sured alongside the standard deviation. The Moun-
tainCar problem is considered to be solved if theagent
receives a minimum return of -110 over 100 episodes
1
https://github.com/msachin93/RL/blob/master/
MountainCar/mountain car.py
Table 1: Overview of hyperparameters applied for the
MountainCar-v0 experiment.
Parameter Value
learning rate α 0.00015
discount factor γ 0.95
epsilon start 1
epsilon min 0
target update frequency C 5
real buffer size s
er
50,000
start learning at size 2,000
minibatch size 32
start interpolation c
start inter
100
double True
duelling True
hidden layer [50, 200, 400]
nn search space nn
thresh
0,005
rebuild interval nn
rebuild
2,000
query radius r
sq
0,05
beta start β
init
1
reduce beta until M 1,500
max size of syn buffer s
syn max
50,000
min size of syn buffer s
syn min
20,000
measured by the original reward function. For the
sake of comparability and to make the result inter-
pretable in relation to this criteria, we print the orig-
inal reward functions results, even if we internally
used the reward function presented above. A suc-
cessful completion of the environment indicates faster
learning. The investigated configurations differ in
the Query Method (Policy Distribution (PD) and Last
State (LS) cf. Section 5.4), and the usage of Explo-
ration Mode (EM) for the calculation of s
syn min
(cf.
Section 5.3) and on policy action selection (cf. Sec-
tion 5.4). A list of all conducted experiments can be
found in Table 2.
Table 2: An overview of all 8 conducted experiments and
the corresponding configurations.
ID PD/LS EM on policy
PD PD
PD op PD X
PD EM PD X
PD EM op PD X X
LS LS
LS op LS X
LS EM LS X
LS EM op LS X X
Each configuration was tested against the baseline
and the differences have been assessed for statistical
significance. A visual inspection of QQ-plots in con-
junction with the Shapiro-Wilk (SW) test revealed that
no normal distribution can be assumed. Since this cri-
terion could not be confirmed for any of the exper-
Interpolated Experience Replay for Continuous Environments
243

Table 3: All conducted experiments and the corresponding
statistical results of the hypothesis tests. In the second col-
umn t
solved
represents the time step when the configuration
solved the problem on average. The next column shows
the standard deviation in episodes over all repetitions for
the time of solving the problem. A lower value of t
solved
indicates faster learning and significantly better results are
displayed as underlined entries.
ID t
solved
±1SD SW MWU
baseline 1751 ±551 0.0
PD 1640 ±773 0.0 0.0924
PD op 1403 ±661 0.0 1.8467e-80
PD EM 1727 ±814 0.0 0.0106
PD EM op
1834 ±864 0.0 2.9039e-07
LS 1479 ±697 0.0 0.0002
LS op 1618 ±762 0.0 0.4809
LS EM 1665 ±784 0.0 0.0003
LS EM op 1619 ±763 0.0 2.1847e-11
iments, we chose the Mann-Whitney-U (MWU) test.
All corresponding p-values for the hypothesis test can
be found in Table 3, together with the average episode
of solving the problem alongside the corresponding
standard deviation (±1SD).
6.2 Experimental Results
The results of all experiments are depicted in Fig. 6.
The dotted brown line at -110 indicates the moment
when the problem is considered as solved in the liter-
ature (Sutton and Barto, 2018). The baseline is repre-
sented by the red dashed and the best configuration by
the blue dash-dotted line. We can see that the baseline
steeply increases until about episode 400, then flattens
and drops at around episode 500 to recover slowly.
Most IER configurations, although also flattening, do
not drop and additionally do not flatten the same level
as the baseline does, except LS op. All configurations
(except PD EM op) solve the problem faster than the
baseline and stay above the baselines curve beginning
at around episode 400.
Figure 6: All conducted experiments.
As the differences between the IER configurations
are not that big, it is difficult to distinguish them and
therefore we provide a reduced view of just the base-
line and the best configuration in Fig. 7. Here we can
observe the same behaviour as described above. The
PD op configuration crosses the dotted line at episode
1403 whereas the baseline needs another 348 more
episodes. In this reduced visualization we can clearly
observe that both curves equal each other in the be-
ginning and then, starting at around episode 300, the
IER configuration remains above the baseline.
Fig. 8, Fig. 9 and Fig. 10 show the errors of the re-
ward, the next step and the terminal tag interpolation
averaged over all repetitions. The blue points repre-
sent the maximum error that occurred in an episode
and the red points depict the average error in an
episode. The first occurring errors can be spotted at
episode 100 which is because interpolation starts not
before this point in time (cf. Section 6.1.2). The max-
imum error of the interpolated error starts to grow,
beginning at around episode 200, this is caused by the
first time that the problem is solved, here a reward
up to 200 is earned. As an interpolated experience
lacks the value for elapsed time steps, that is used in
our custom reward function, we determine a reward of
200 for every experience that solves the environment.
In fact, the reward, and therefore also the interpolated
reward ranges from 0 to 200, dependant of the time
step and, following that the speed and height of the
query point. We can see that the calculated max er-
rors range in between 40 and 100 for the whole run.
The average error on the other side stays below 5 the
whole time. If we take a look at the error of the in-
terpolated follow-up states, we can see that the maxi-
mum error decreases over time and never grows over
a value of 0.012. The average error, also decreasing,
never exceeds a value of 0.002. The terminal tag is
encoded as a boolean and can therefore be either one
or zero. We can observe that in the beginning the max
Figure 7: LS op configuration in comparison with the base-
line.
NCTA 2022 - 14th International Conference on Neural Computation Theory and Applications
244
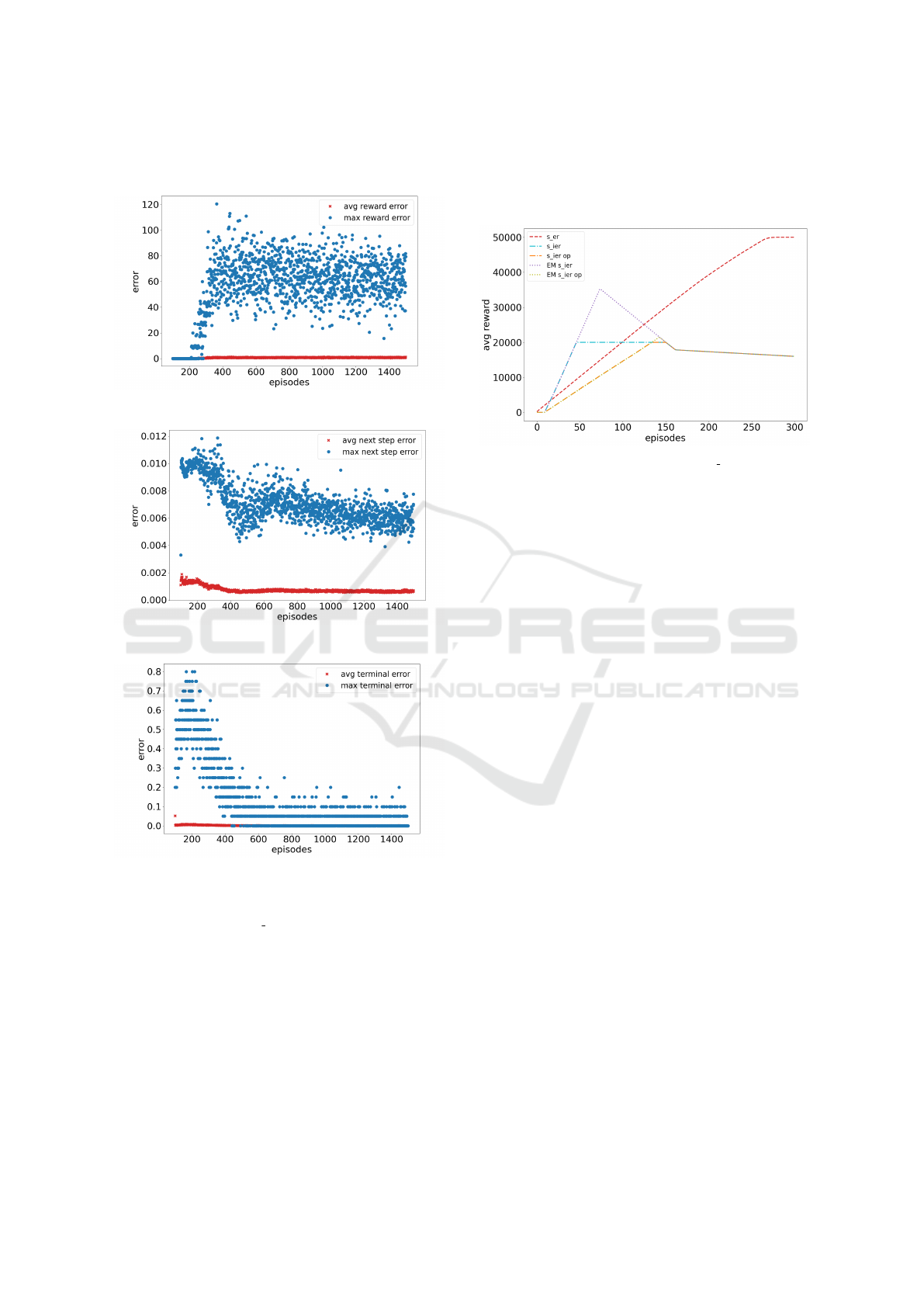
error over all repetitions is close to the maximum but
decreases to around 0.1 in the end.
Figure 8: The interpolation error of the rewards.
Figure 9: The interpolation error of the next steps.
Figure 10: The interpolation error of the terminal tag.
A visualization of the different investigated meth-
ods for calculating s
syn min
is given in Fig. 11. All
modes used beta with the values given in Table 1, the
dotted lines additionally made use of the exploration
mode. The red dashed line represents the size of the
real valued buffer. It can be observed that the usage
of the exploration mode allows a larger size of the
synthetic buffer in the beginning, when exploration is
active, and then meets the decreasing min size set by
beta. The curves for the on policy mode is slightly
shifted to the right caused by lesser interpolations
(one interpolation at maximum per step). We chose to
show not the whole length of the experiments to focus
on the important part that is located in the beginning.
All s
ier
curves decrease to 0 at episode 1500 as deter-
mined by the hyperparameter set in Section 6.1.2.
Figure 11: An intuition of s
syn min
.
6.3 Interpretation
The results from Fig. 6 and Table 3 show that the ma-
jority of the tested configurations perform better than
the baseline and can reach the defined goal in less
episodes. This shows that our approach works and
can assist learners in early learning phases.
The exploration mode functionality did not turn
out to be helpful. It performed less effective than
the configuration with just the β determined min size.
Even if this functionality did not prove to be helpful
here, it remains an important adjusting mechanism for
other environments. Fig. 11 shows that the effect was
not too large in our experiments which also is due to
a short exploration time.
A clear statement about the effect of the on policy
action selection mode turns out to be not that obvious.
The best configuration makes use of it and performs
better than just the PD querying, but that does not
hold for the LS method and in combination with EM
it seems to perform better than just the usage of EM
for both. The difference between PD and LS might
result from the fact that we already try to follow the
policy close enough in the case of LS and pushing the
interpolations even more into that direction harms the
approach rather than helping. On the other hand the
PD method follows the policy to a certain extend, but
remains with some degrees of freedom which is then
limited by the on policy action selection in a way that
appears beneficial. The positive effect in combination
with EM is expected to be due to the decreased num-
ber of interpolations that occur resulting in a maxi-
mum size of the synthetic buffer that almost equals
the configurations without EM (see Fig. 11).
A closer look at Fig. 7 reveals that the PD op con-
figuration performs very well compared to the base-
Interpolated Experience Replay for Continuous Environments
245

line. Not only is the problem solved considerably
faster, but the agent performs also significantly bet-
ter after episode 300.
Considering the interpolation errors from Fig. 8,
Fig. 9 and Fig. 10, we can conclude the following:
The error of the interpolated follow-up states is quite
small and even decreases over time. This indicates
a sufficient accuracy here and also that the interpo-
lation benefits from the exploration of the problem
space. The reward error on the other hand seems quite
high, even if it stays below 50%. One cause (as noted
above) lies in the comparison of the different reward
functions. As a query point does not include a time
step and the internal reward function does require one,
we set the t for the interpolation to zero. This has the
effect that the calculated expected reward that we use
then for the determination of the accuracy is always
200. As it is impossible to reach the goal at time step
0 any interpolation will be assigned an error greater
0. This results in an overestimation of the reward er-
rors for reaching the goal but on the other hand still
gives us a good indication of the quality of our inter-
polations. The other point comes from the fact that
we average the reward of neighbouring experiences,
causing interpolations of transitions slightly to the left
of the goal to be overestimated. However, this effect
turns out to be beneficial, because it increases the area
in which experiences are rewarded and therefore helps
the learner to understand that being near the goal is es-
sential for solving the environment. Another insight is
that the average error is way smaller, which indicates
that most of the interpolations are quite accurate. The
error of the terminal tag seems quite high in the begin-
ning of the training, but this can be explained by the
fact that the agent (in early phases) terminates because
of the time limit which is dependant of the time step.
As t is set to zero for the interpolation (see above) an
interpolated experience that copies such a behaviour
is always punished by the error calculation. Over time
the error decreases and in the end we can achieve a
maximum error at around 0.1 which equals errors of
the terminal tag in 2 of the 20 repetitions. Overall the
mean error is around zero the whole time indicating a
good interpolation of the terminal tag in general.
7 SUMMARY AND FUTURE
WORK
We presented an extension of the IER method, so far
proposed for discrete environments only. Our con-
tribution encompasses the interpolation of follow-up
states which makes the IER ready for continuous state
spaces. We presented a solution to interpolate state-
transitions instead of follow-up states directly. This
procedure solves the occurrence of inaccurate results
when an interpolation technique is used for an ex-
trapolation task. A small example shows when this
happens and why this is reasonable. We introduced
several methods to offer the ability of fine-tuning the
synthetic buffers size.
An evaluation on the MountainCar environment
revealed that the approach works. We conducted nu-
merous experiments which the majority of performed
better than the baseline consisting of a DQN with
vanilla ER applied. Our best configuration was able
to solve the problem about 15% faster (episodes).
The introduced exploration mode mechanic did not
turn out to be useful, but nevertheless remain a useful
mechanism for future investigations.
The presented approach can be used for other en-
vironments as well, if the interpolation of reward,
follow-up state and terminal tag is sufficiently accu-
rate then it is expected that the results resemble those
presented in this paper. The interpolation techniques
used here are still relatively simple and there are more
complex ones (i.e. radial basis function interpola-
tion (Wright, 2003)) that should be able to interpolate
more difficult tasks with bigger state spaces.
We will test the IER for continuous environments
on other problems to ratify the obtained results. Such
will range from CartPole to even more complex prob-
lems like robotic tasks. Even image inputs can be in-
vestigated with the presented approach, an interpola-
tion of the feature outputs of the convolutional part of
the neural network seems like an idea that should be
investigated further. Also other algorithms that uti-
lize an ER will be evaluated with IER. An interesting
example is soft actor-critic (Haarnoja et al., 2018).
Another interesting field, that furthermore bears
some similarities with the examined area, is the re-
search topic of model-based RL. These kind of algo-
rithms create a model to build up knowledge of the
underlying problem which can then be utilized to train
a policy. We locate our approach in between model-
based and model-free RL methods, as we do not build
a complete model but do something similar in com-
bination with model-free RL learners. However, an
investigation of the IER approach from the view of
model-based RL methods could be beneficial.
REFERENCES
Andrychowicz and others (2017). Hindsight Experience
Replay. In Advances in Neural Information Process-
ing Systems 30, pages 5048–5058. Curran Associates,
Inc.
NCTA 2022 - 14th International Conference on Neural Computation Theory and Applications
246

Berner, C., Brockman, G., Chan, B., Cheung, V., Debiak,
P., Dennison, C., Farhi, D., Fischer, Q., Hashme, S.,
Hesse, C., J
´
ozefowicz, R., Gray, S., Olsson, C., Pa-
chocki, J., Petrov, M., Pinto, H. P. d. O., Raiman,
J., Salimans, T., Schlatter, J., Schneider, J., Sidor,
S., Sutskever, I., Tang, J., Wolski, F., and Zhang,
S. (2019). Dota 2 with Large Scale Deep Rein-
forcement Learning. CoRR, abs/1912.06680. arXiv:
1912.06680.
Brockman, G. and others (2016). OpenAI Gym. eprint:
arXiv:1606.01540.
Haarnoja, T., Zhou, A., Hartikainen, K., Tucker, G., Ha, S.,
Tan, J., Kumar, V., Zhu, H., Gupta, A., Abbeel, P.,
and Levine, S. (2018). Soft Actor-Critic Algorithms
and Applications. CoRR, abs/1812.05905. arXiv:
1812.05905.
Hamid, O. H. (2014). The role of temporal statistics in the
transfer of experience in context-dependent reinforce-
ment learning. In 2014 14th International Conference
on Hybrid Intelligent Systems, pages 123–128.
Lillicrap, T. P., Hunt, J. J., Pritzel, A., Heess, N., Erez, T.,
Tassa, Y., Silver, D., and Wierstra, D. (2016). Con-
tinuous control with deep reinforcement learning. In
Bengio, Y. and LeCun, Y., editors, 4th International
Conference on Learning Representations, ICLR 2016,
San Juan, Puerto Rico, May 2-4, 2016, Conference
Track Proceedings.
Lin, L.-J. (1992). Self-improving reactive agents based on
reinforcement learning, planning and teaching. Ma-
chine Learning, 8(3):293–321.
Lin, L.-J. (1993). Reinforcement learning for robots us-
ing neural networks. Technical report, CARNEGIE-
MELLON UNIV PITTSBURGH PA SCHOOL OF
COMPUTER SCIENCE.
McClelland, J. L., McNaughton, B. L., and O’Reilly, R. C.
(1995). Why there are complementary learning sys-
tems in the hippocampus and neocortex: insights
from the successes and failures of connectionist mod-
els of learning and memory. Psychological review,
102(3):419. Publisher: American Psychological As-
sociation.
Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A.,
Antonoglou, I., Wierstra, D., and Riedmiller, M. A.
(2013). Playing Atari with Deep Reinforcement
Learning. CoRR, abs/1312.5602.
Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A.,
Veness, J., Bellemare, M. G., Graves, A., Ried-
miller, M., Fidjeland, A. K., Ostrovski, G., and others
(2015). Human-level control through deep reinforce-
ment learning. nature, 518(7540):529–533. Publisher:
Nature Publishing Group.
Omohundro, S. M. (1989). Five balltree construction al-
gorithms. International Computer Science Institute
Berkeley.
O’Neill, J., Pleydell-Bouverie, B., Dupret, D., and
Csicsvari, J. (2010). Play it again: reactivation of wak-
ing experience and memory. Trends in Neurosciences,
33(5):220 – 229.
Pilar von Pilchau, W. (2019). Averaging rewards as a
first approach towards Interpolated Experience Re-
play. In Draude, C., Lange, M., and Sick, B., edi-
tors, INFORMATIK 2019: 50 Jahre Gesellschaft f
¨
ur
Informatik – Informatik f
¨
ur Gesellschaft (Workshop-
Beitr
¨
age), pages 493–506, Bonn. Gesellschaft f
¨
ur In-
formatik e.V.
Pilar von Pilchau, W., Stein, A., and H
¨
ahner, J. (2020).
Bootstrapping a DQN replay memory with synthetic
experiences. In Merelo, J. J., Garibaldi, J., Wagner, C.,
B
¨
ack, T., Madani, K., and Warwick, K., editors, Pro-
ceedings of the 12th International Joint Conference on
Computational Intelligence (IJCCI 2020), November
2-4, 2020.
Pilar von Pilchau, W., Stein, A., and H
¨
ahner, J. (2021).
Synthetic Experiences for Accelerating DQN Perfor-
mance in Discrete Non-Deterministic Environments.
Algorithms, 14(8).
Rolnick, D., Ahuja, A., Schwarz, J., Lillicrap, T. P., and
Wayne, G. (2018). Experience Replay for Con-
tinual Learning. CoRR, abs/1811.11682.
eprint:
1811.11682.
Sander, R. M. (2021). Interpolated Experience Replay for
Improved Sample Efficiency of Model-Free Deep Re-
inforcement Learning Algorithms. PhD Thesis, Mas-
sachusetts Institute of Technology.
Schaul, T., Quan, J., Antonoglou, I., and Silver, D. (2015).
Prioritized Experience Replay. arXiv e-prints, page
arXiv:1511.05952. eprint: 1511.05952.
Shepard, D. (1968). A Two-Dimensional Interpolation
Function for Irregularly-Spaced Data. In Proceedings
of the 1968 23rd ACM National Conference, ACM
’68, pages 517–524, New York, NY, USA. Associa-
tion for Computing Machinery.
Silver, D., Schrittwieser, J., Simonyan, K., Antonoglou, I.,
Huang, A., Guez, A., Hubert, T., Baker, L., Lai, M.,
Bolton, A., Chen, Y., Lillicrap, T., Hui, F., Sifre, L.,
van den Driessche, G., Graepel, T., and Hassabis, D.
(2017). Mastering the game of Go without human
knowledge. Nature, 550(7676):354–359.
Stein, A., Menssen, S., and H
¨
ahner, J. (2018). What about
Interpolation? A Radial Basis Function Approach to
Classifier Prediction Modeling in XCSF. In Proc.
of the GECCO, GECCO ’18, pages 537–544, New
York, NY, USA. Association for Computing Machin-
ery. event-place: Kyoto, Japan.
Stein, A., Rauh, D., Tomforde, S., and H
¨
ahner, J. (2017).
Interpolation in the eXtended Classifier System: An
architectural perspective. Journal of Systems Archi-
tecture, 75:79–94. Publisher: Elsevier.
Sutton, R. S. and Barto, A. G. (2018). Reinforcement learn-
ing: An introduction. MIT press.
Tsitsiklis, J. N. and Roy, B. V. (1997). An analysis of
temporal-difference learning with function approxi-
mation. IEEE Transactions on Automatic Control,
42(5):674–690.
Vinyals, O., Babuschkin, I., Chung, J., Mathieu, M., Jader-
berg, M., Czarnecki, W. M., Dudzik, A., Huang, A.,
Georgiev, P., Powell, R., Ewalds, T., Horgan, D.,
Kroiss, M., Danihelka, I., Agapiou, J., Oh, J., Dal-
ibard, V., Choi, D., Sifre, L., Sulsky, Y., Vezhnevets,
S., Molloy, J., Cai, T., Budden, D., Paine, T., Gul-
cehre, C., Wang, Z., Pfaff, T., Pohlen, T., Wu, Y.,
Interpolated Experience Replay for Continuous Environments
247

Yogatama, D., Cohen, J., McKinney, K., Smith, O.,
Schaul, T., Lillicrap, T., Apps, C., Kavukcuoglu, K.,
Hassabis, D., and Silver, D. (2019). AlphaStar: Mas-
tering the Real-Time Strategy Game StarCraft II.
Watkins, C. J. C. H. and Dayan, P. (1992). Q-learning. Ma-
chine Learning, 8(3):279–292.
Wright, G. B. (2003). Radial basis function interpolation:
numerical and analytical developments. University of
Colorado at Boulder.
NCTA 2022 - 14th International Conference on Neural Computation Theory and Applications
248
