
Two-dimensional Motif Extraction from Images: A Study using an
Electrocardiogram
Hanadi Aldosari
1,4
, Frans Coenen
1
, Gregory Y. H. Lip
2
and Yalin Zheng
2,3
1
Department of Computer Science, University of Liverpool, Liverpool, U.K.
2
Liverpool Centre for Cardiovascular Science, University of Liverpool and Liverpool Heart & Chest Hospital,
Liverpool, U.K.
3
Department of Eye and Vision Science, University of Liverpool, Liverpool, U.K.
4
College of Computer Science and Engineering, Taibah University, Madinah, Saudi Arabia
Keywords:
2D Motifs, ECG Classification.
Abstract:
A mechanism using the concept of 2D motifs to classify Electrocardiogram (ECG) data is presented. The
motivation is that existing techniques typically first transform ECG data into a 1D signal (waveform) format
and then extract a small number of features from this format for classification purposes. The transformation
into the waveform format introduces an approximation of the data, and the consequent feature selection means
that only a small part of the coarsened signal is utilised. The proposed approach works directly with the image
format, no transformation takes place, features (motifs) are selected by considering the entire ECG image. It
is argued that this produces a better classification than that which can be achieve using the waveform format.
The proposed 2D Motif extraction approach is fully described and evaluated. Good results are returned, a best
accuracy 85% in comparison with a best accuracy of 70% using a comparable 1D waveform approach. An
analysis is also presented with respect to the augmentation of 2D motifs with 2D discords.
1 INTRODUCTION
Cardiovascular Disease (CVD) has become one of the
most common fatal disease of the 21st century. Over
the last thirty years deaths and disability from CVD
have steadily increased. It has been estimated that
in 2019 CVD attributed to one third of deaths world
wide (Roth et al., 2020). CVD is most commonly
caused by irregularities of the rhythm of the heart.
The Electrocardiogram (ECG) is a standard informa-
tion source for diagnosing CVDs. An ECG is an in-
dicator of cardiac electrical activity and this provides
important information about heart conditions. Given
the increasing prevalence of CVD, coupled with the
resource and skills required to analyze ECG records,
there has been a corresponding need for computer
aided support for ECG analysis. Consequently, there
has been significant work directed at using the tools
and techniques of machine learning to classify ECG
data (Ebrahimi et al., 2020; Houssein et al., 2017; Liu
et al., 2021).
The challenge of applying machine learning to
ECG data, as in the case of machine learning in gen-
eral, is the acquisition of suitable training data. Tradi-
tionally, ECG machines produced hard copy printouts
which were then interpreted by a Cardiologist (focus-
ing on what are called the P wave, the QRS complex,
and the T wave). More modern machines can, in ad-
dition, produce digital formats. However, most of the
available data still tends to be in paper print-out for-
mat. The practice is to scan the paper print-out into a
digitised form and then transform it into a 1D signal
(waveform) format. However, the transformation pro-
cess involves information loss as the data is approx-
imated so as to obtain the desired waveform format.
The information loss is compounded if the original
scan is not of good quality; frequently the case. Once
the transformation has taken place the next stage, typ-
ically, is to extract certain features from within the
signal data (features associated with the P wave, the
QRS complex, and the T wave) (Gupta et al., 2021;
Kar and Das, 2011; Mir and Singh, 2021; Seena and
Yomas, 2014). The consequence, it is argued in this
paper, is that the resulting classification is not as good
as it might be because it is based on approximations
and a small number of features.
To address the above, the solution presented in this
paper moves away both from the idea of applying ma-
Aldosari, H., Coenen, F., Lip, G. and Zheng, Y.
Two-dimensional Motif Extraction from Images: A Study using an Electrocardiogram.
DOI: 10.5220/0011380500003335
In Proceedings of the 14th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2022) - Volume 1: KDIR, pages 19-28
ISBN: 978-989-758-614-9; ISSN: 2184-3228
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
19

chine learning to a small number of features extracted
from ECG data that has first been transformed into a
1D waveform format, by considering the ECG data
in its entirety as an image. Influenced by the work
presented in (Aldosari et al., 2021a), where time se-
ries motifs were extracted as features from ID wave-
form ECG signals, the idea presented in this paper
is to extract 2D motifs directly from the ECG image
data. A motif is a frequently repeated pattern. In 1D
this is a sub-sequence of points in a point (time) se-
ries. In 2D this is rectangular sub-matrix, a pixel sub-
matrix in the case of image data. It is argued in (Apos-
tolico et al., 2008; Furfaro et al., 2017), although not
in the context of ECG data, that 2D motifs can pro-
duced high quality image classifications. The work
presented in this paper is thus directed at using 2D
motifs as features, extracted from scanned paper ECG
records.
The application focus for the paper is Atrial Fib-
rillation (AF); a common form of CVD that is in-
dicated by an irregular, and often an unusually fast,
heart rate. We extracted 2D motifs from ECG scanned
images that featured a AF and that featured the normal
rhythm of the heart; thus both positive and negative
examples. A support vector machine (SVM) model, a
widely used machine learning technique for 1D wave-
form ECG data classification (Sm
´
ı
ˇ
sek, 2016), was
them applied to the identified 2D ECG motifs.
The remainder of this paper is structured as fol-
lows. A review of existing work relevant to this paper
is presented in Section 2. A formalism is the pre-
sented in Section 3, and the proposed approach in
Section 4. The evaluation of the proposed approach
is presented and discussed in Section 5. The paper is
concluded in Section 6 with a summary of the main
findings and some suggestions for future work.
2 PREVIOUS WORK
As noted in the introduction to this paper ECG data
typically comes in a paper format, although increas-
ingly ECG machines that can also produce digitised
ECG data are available. However, up until the end of
the 20th century ECG machines could only produce
“print-outs”; it is only more modern machines that
can produce digital formats. Thus, for longitudinal
studies the reliance is on paper format ECG data. The
first step in applying machine learning to such ECG
data thus entails scanning (digitising) the paper for-
mat data into a 2D image format of some kind. In the
context of CVD classification, the practice is then to
transform the 2D digitised ECG data into a 1D wave-
form format. There are a range ECG tools available
to convert 2D digitised ECG to the 1D waveform for-
mat, some directly from a paper scan others from a
digitised image (Badilini et al., 2005; Baydoun et al.,
2019; Chung et al., 2018; Fortune et al., 2021; Khleaf
et al., 2013; Loresco and Africa, 2018; Ravichandran
et al., 2013). The majority of digitisation algorithms
commence with: (i) “skew correction”, to account for
rotated scans, and (ii) “grid removal” to separate the
ECG signal from the paper grid by using techniques
such as histogram filtering. In some cases, further ad-
ditional processing is applied before the extraction of
ECG signals and their storage in a digitised storage
format (Waits and Soliman, 2017). The digitisation
tool used with respect to the work presented in this
paper was that presented in (Fortune et al., 2021).
Digitised ECG signals, allow for the application of
range of techniques. Some specific examples can be
found in (Thanapatay et al., 2010), (Jayaraman et al.,
2012) and (Mishra et al., 2021). All three used digi-
tisation tools to first convert 2D scanned ECG images
into a 1D waveform format; and all three used some
form of feature extraction as a precursor to classi-
fication. In (Thanapatay et al., 2010) a SVM clas-
sification model was applied. In (Jayaraman et al.,
2012) morphological features were extracted from the
digitised signals to which two classification models
were applied, kNN coupled with Dynamic time warp-
ing (DTW) and Adaboost, to detect three different
types of cardiovascular abnormality. In (Mishra et al.,
2021) ECG data was used as the input into a three
layer deep learning model to classify different types
of abnormalities. Further examples of feature extrac-
tion from 1D waveform as a precursor to classifica-
tion can be found in (Gupta et al., 2021; Kar and
Das, 2011; Mir and Singh, 2021; Seena and Yomas,
2014). Although good results have been reported with
respect to waveform CVD classification, the approxi-
mations that the transformation into a waveform for-
mat entails, and the reliance on a small number of fea-
tures, remains problematic.
An alternative to the waveform format, and that
explored in this paper, is to extract salient features
directly from 2D ECG scanned images. Once such
a set of features has been identified established ma-
chine learning techniques, similar to those used in the
context of waveform ECG data, can be applied. The
challenge is then the nature of the features to be ex-
tracted from the ECG image data. Low level image
features such as colour or texture are not applicable
for the effective application of CVD disease classifi-
cation (Bosch et al., 2007). More sophisticated fea-
ture extraction mechanisms are required. This paper
proposes the use of 2D motifs, motifs are repeating
patterns found in data that can be used in tasks like
KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval
20

clustering, classification and anomaly detection. The
motivation is that the use of 1D motifs has provided
promising results in the context of 1D time series
analysis (Torkamani and Lohweg, 2017; Truong and
Anh, 2019; Wankhedkar and Jain, 2019). The signif-
icance is that time series data is analogous to wave-
form data. The idea of 2D motifs, to the best knowl-
edge of the authors, was first proposed in (Apostolico
et al., 2008) and used in (Furfaro et al., 2017) for the
purpose of classify digital images of buildings and im-
ages extracted from video news clippings, using a K-
Nearest Neighbors (kNN) classification model.
3 FORMALISM
The following definitions are used with respect to the
remainder of this paper.
Digital ECG Image: An ECG image I is a n × m
pixel matrix such that p
i j
is the pixel at row i and
column j. Each image will be associated with a
class label c drawn from a set of classes C. A dig-
ital image set D is a set of images with associated
class labels D = {hI
1
, c
1
i, hI
2
, c
2
i, .. . }. The set
D = {D
1
, D
2
, . . . } is the set D segmented accord-
ing to class, such that the sub-set of documents D
i
is associated with the class c
i
.
2D Motifs: A 2D motif M = p × q is a sub-matrix
of an image I, of width p and height q, that oc-
curs with maximal frequency. A motif set, M =
{M
1
, M
2
, . . . }, is a set of 2D motifs extracted from
an image set D, segmented according to class. Not
all the motifs in M will be good discriminators of
class, so we prune M to give M
0
and then M
00
.
2D Discords: A 2D discord S = p ×q is a sub-matrix
of an image I, of width p and height q, that oc-
curs with minimal frequency (thus the opposite of
a motif). A discord set, S = {S
1
, S
2
, . . . }, is set of
2D discords extracted from an image data set D,
segmented according to class. Again, not all the
discords in S will be good discriminators of class,
so we prune S to give S
0
, and then S
00
.
Further discussion concerning the pruning of the sets
M and S is presented in Sections 4.2.4 and 4.2.5.
4 PROPOSED APPROACH
This section presents the proposed approach. The ap-
proach comprises three stages:
1. ECG image data cleaning.
2. 2D motif extraction.
3. Feature vector generation.
Detail concerning each of these three stages is pre-
sented in the following three sub-sections, Sub-
sections 4.1, 4.2 and 4.3.
4.1 ECG Image Data Cleaning
For the application of the proposed approach a four-
step data cleaning process was adopted: (i) cropping,
(ii) conversion to gray scale, (iii) grid removal and (iv)
noise removal. The input was a set of ECG scanned
images. The output was a set of “clean” ECG images
of the form D = {hI
1
, c
1
i, hI
2
, c
2
i, . . . }, where I
i
is a
cleaned ECG image and c
i
is a class label taken from
a set of class labels C. Each of the four steps is con-
sidered in further detail below.
Cropping: Scanned ECG images often include spu-
rious information round the edges of the scan. The
first step was therefore to crop the image so that
only the ECG signals were retained.
Conversion to Gray Scale: The cropped RGB im-
age was then converted to a gray-scale intensity
image. For the evaluation presented later in this
paper routines within the Python OpenCV library
were used for this purposes.
Grid Removal: The third step was directed at re-
moving all spurious data in the gray-scale ECG
data, particularly the background graphical grid
which is a frequent feature of ECG digital im-
ages. This was achieved using the application of
a “binarization” operation designed so that pix-
els related to the ECG traces were allocated the
value 255 (white) and the rest of the image pix-
els the value 0 (black). The desired effect was
that the graphical grid, and the majority spurious
data points, would all be encoded as black pixels.
The challenge was deciding the value of the bina-
rization threshold to be applied to the gray-scale
image. To decide the nature of this threshold,
histograms for a selection ECG image files were
generated. From these histograms it was found
out that the high intensity (background) gray scale
values were in the range 150 − 255, the threshold
value was therefore set at 150. Thus, the proposed
binarization process assigned a value of 0 to each
gray scale pixel whose value was greater than the
150 threshold, and a value of 255 otherwise, as
shown below.
binary(x, y) =
0 if grayscale(x, y) > thresh
255 otherwise
(1)
Two-dimensional Motif Extraction from Images: A Study using an Electrocardiogram
21

Noise Removal: The anticipation was that that some
spurious small patches of white pixels (white
noise) would be retained after the application of
the binarization. To remove this white noise
a morphological erosion operation was applied
whereby the pixels on the boundary of white ob-
jects were removed. This would also have the ef-
fect of reducing the thickness of the ECG traces.
Thus, on completion of the erosion operation a
morphological dilation operation was applied to
add pixels back to the boundaries of the retained
white objects.
4.2 2D Motif Extraction
This section presents the proposed 2D Motif extrac-
tion (dicovery) process. The top-level algorithm is
given in Algorithm 1. The input is: (i) the ECG image
set D = {hI
1
, c
1
i, hI
2
, c
2
i, . . . } from the pre-processing
stage (c
i
is a class label taken from the set of classes
C), (ii) the set C, (iii) the required 2D motif (discord)
width p and height q, (iv) a pre-specified similarity
threshold σ used to determine whether two pixel sub-
matrices are the same or not, and (v) k the number of
motifs (dicords) to be selected. The output is a set of
motifs and a set of discords, M
00
and S
00
, which are
deemed to be good discriminators of class, to be used
in the desired feature vector representation (Stage 3).
The set D = {D
1
, D
2
, . . . } is populated in lines 3 to 5
so that D is segmented according to class. Note that
for the evaluation presented in Section 5, |C| = 2 was
used, hence D = {D
1
, D
2
}.
The set D is then processed to identify the mo-
tifs and discords held in the images associated with
each class (lines 6 to 14). This involves calls to a
number of sub-processes which will be discussed in
further detail later in this sub-section. The output is
the set M = {M
1
, M
2
, . . . } and the S = {S
1
, S
2
, . . . };
where M
i
is the set of motifs associated with class
c
i
∈ C, and S
i
is the set of discords associated with
class c
i
∈ C. For the evaluation presented in Sec-
tion 5, |C| = 2 was used, hence M = {M
1
, M
2
}, and
S = {S
1
, S
2
}. Note the proposed approach may result
in the same motif being identified in several images,
thus M and S are likely to contain repeat occurrences
of motifs and discords. The intuition here for the be-
ing retained was that they would be given more signif-
icance with respect to the generation of the intended
prediction model; conceptually they would be given
a higher weighting. This is one of the novel aspects
of the proposed motif (discord) generation approach
presented here.
The sets M = {M
1
, M
2
, . . . } and S = {S
1
, S
2
, . . . }
are likely to hold some motifs and discords that are
unique to only one image. It was anticipated, that
these would not be good discriminators of class,
hence, for each set of motifs M
i
∈ M associated with
a class c
i
∈ C, and each set set of discords S
i
∈ S
associated with a class c
i
∈ C, unique motifs and
discords were removed, and the reaming motifs and
discords stored in the sets M
0
= {M
0
1
, M
0
2
, . . . } and
S
0
= {S
0
1
, S
0
2
, . . . } respectively (line 15 in Algorithm
1).
The last step in Algorithm 1 was to remove mo-
tifs and discords from M
0
and S
0
that were associated
with more than one class and hence not useful for dis-
tinguishing between classes (line 16 in Algorithm 1).
The result was a set of motifs M
00
= {m
1
, m
2
, . . . }, and
a set of discords S
00
= {s
1
, s
2
, . . . }, that were consid-
ered to be good discriminators of class.
Algorithm 1: 2D Motif Extraction.
1: Input D,C, p, q, σ, k
2: Output M
00
, S
00
3: for ∀hI
i
, c
i
i ∈ D do
4: D
j
∈ D ← D
j
∈ D ∪I
i
, j = i
5: end for
6: for ∀D
i
∈ D do
7: for ∀I
j
∈ D
i
do
8: χ ← genSubMatrices(I
j
, p, q)
Algorithm 2
9: M
j
← getCandidate2Dmotifs(χ, σ)
Algorithm 3
10: M
j
, S
j
←
get2DmotifsAndDiscords(M
j
, k) Algorithm4
11: M ← M ∪ M
j
12: S ← S ∪ S
j
13: end for
14: end for
15: M
0
, S
0
← intraClassPruning(M, S, σ)
Algorithm 5
16: M
00
, S
00
← interClassPruning(M
0
, S
0
, σ)
Algorithm 6
17: return M
00
, S
00
From Algorithm 1, it can be seen that the pro-
posed 2D motif extraction process comprises five sub-
processes: (i) Generate sub-matrices, (ii) Generate
candidate 2D motifs, (iii) Get Top k 2D motifs and
discords, (iv) Intra-class pruning and (v) Inter-class
pruning. Each of these is discussed in further detail in
the following sub-sections.
4.2.1 Sub-matrix Generation
The sub-matrix generation sub-process is given in Al-
gorithm 2. The inputs are a pre-processed image I
associated with a particular class, and the desired sub-
KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval
22

matrix window width d and height q. The sub-matrix
window is slide over the image I pixel by pixel. The
output is a set of sub-matrices χ = {M
1
, M
2
, . . . }. The
algorithm commences, line 2, by defining the empty
set χ in which to hold the extracted sub-matrices.
Then, lines 3 to 7, the p ×q sub-matrices in I are pro-
cessed. We are only interested in sub-matrices that
contain the ECG trace. It was also found that the sub-
matrices located at the edge of the image tended to be
poor discriminators of class. Thus, sub-matrices that
feature only black pixels and those located at the edge
of the input I were not selected for inclusion in χ. We
test for this on line 4. At the end of the process χ is
returned (line 8). Note that if there are only “black”
images in I, the set χ will be empty.
Algorithm 2: Generate Sub-Matrices.
1: Input I, p, q
2: χ =
/
0
3: for ∀sub
i
of size p × q ∈ I do
4: if sub
i
6= black and sub
i
6= located on the edge
of I then
5: χ = χ ∪ sub
i
6: end if
7: end for
8: Return χ
4.2.2 Candidate 2D Motifs
The sub-process for generating candidate 2D motifs
is given in Algorithm 3. The inputs are the set χ
of p × q sub-matrices, generated in the previous step
(Algorithm 2), and the similarity threshold σ. The al-
gorithm returns a set of candidate motifs of the form
M = {hm
1
, count
1
i, hm
1
, count
1
i, . . . } where m
i
is a
candidate motif and count is the corresponding oc-
currence count. The algorithm commences, lines 3,
by defining the set M. The algorithm then processes
each sub-matrix m
i
in χ (lines 4 to 13). First a counter,
count
i
, is defined and set to 0 (line 5), and hm
i
, count
i
i
added to the set M (line 6). Sub-matrix m
i
is then
compared to every other sub-matrix m
j
in χ and if
found to be similar the count updated and m
j
removed
from χ (so that the same sub-matrix is not counted
again later in the process). The similarity between the
sub-matrices, m
i
and m
j
, is determined by calculat-
ing the Euclidean distance between the two matrices
using Equation 2. Euclidean distance measurement
is frequently used for 1D motif similarity checking
(Torkamani and Lohweg, 2017). The calculated Eu-
clidean distance is then compared using the threshold
σ, if the result is less than or equal to σ, m
i
and m
j
are
deemed to be similar.
dist (m
i
, m
j
) =
v
u
u
t
h=(p×q)
∑
h=1
m
i
h
− m
j
h
2
(2)
Algorithm 3: Candidate 2D motifs.
1: Input χ, σ
2: Output M
3: M ←
/
0
4: for ∀m
i
∈ χ do
5: count
i
← 0
6: M ← M ∪ hm
i
, count
i
i
7: for ∀m
j
∈ χ, j 6= i do
8: if dist (m
i
, m
j
) ≤ σ then
9: count
i
= count
i
+ 1
10: χ ← χ with m
j
removed
11: end if
12: end for
13: end for
14: Return M
4.2.3 Top K 2D Motifs and Discords
Once a set of candidate frequent 2D motifs M has
been identified, even after “black sub-matrix” and
“edge matrix” removal, the number of remaining mo-
tifs in M is likely still to be large. It is therefore
proposed that the number of candidate frequent 2D
motifs be limited to the top k most frequent candi-
dates. We were also interested in discords, candi-
dates that only occur once. The third sub-process
in Algorithm 1 is thus the identification of the top
k motifs and the discords. The was conducted us-
ing Algorithm 4. The inputs are the set of motifs
M = {hm
1
, count
1
i, hm
2
, count
2
i, . . . } associated with
a given image, generated by the previous sub-process,
and the threshold k. The algorithm proceeds by first
ordering the candidate motifs in M according to their
occurrence count (line 3). The top k are then selected
as the chosen motifs (line 4). Any candidate mo-
tifs with a count of 1 are deemed to be discords and
placed in S (line 5). The sets M = {m
1
, m
2
, . . . } and
S = {s
1
, s
2
, . . . } are then returned (line 6).
Algorithm 4: Get Top K 2D motifs.
1: input M, k
2: output M, S
3: M ← M sorted in descending order
4: M ← top k motifs
5: S ← motifs with a count of 1
6: Return M, S
4.2.4 Intra-class Pruning
We are interested in motifs and discords that are good
discriminators of class. We are therefore not inter-
Two-dimensional Motif Extraction from Images: A Study using an Electrocardiogram
23

ested in motifs and discords that only appear in one
image. Thus, we wish to remove motifs and discords,
from the sets M = {M
1
, M
2
, . . . } and S = {S
1
, S
2
, . . . }
respectively, that appear in only one image (intra-
class pruning). The sub-process for achieving this is
shown in Algorithm 5. The inputs are the sets M and
S, and the similarity threshold σ. The algorithm com-
mences by declaring the sets M
0
and S
0
to hold the re-
vised sets of motifs and discords (lines 3 and 4). The
set M is processed first, lines 5 to 11. For each motif
m
j
in the set M
i
∈ M (the set of motifs associated with
class c
i
∈ C), if m
j
does nor appear anywhere else in
M
1
the motif is discarded, otherwise it is added to M
0
i
.
A similar process is followed for the set S, lines 12
to 18. At the end of the process the sets M
0
and S
0
will be returned. Note that it might be the case that
the sets M
0
and S
0
are empty. Note also that to de-
termine whether a motif appears only in a single im-
age requires similarity comparison with the motifs for
all the other images associated with the current class.
This requires our similarity threshold σ.
Algorithm 5: Intra-class pruning.
1: input M, S, σ
2: output M
0
, S
0
3: M
0
← {M
0
1
, M
0
2
, . . . M
0
|C|
}
4: S
0
← {S
0
1
, S
0
2
, . . . S
0
|C|
}
5: for ∀M
i
∈ M do
6: for ∀m
j
∈ M
i
do
7: if m
j
appears in more than one image in
M
i
then
8: M
0
i
← M
0
j
∪ m
j
9: end if
10: end for
11: end for
12: for ∀S
i
∈ S do
13: for ∀s
j
∈ S
i
do
14: if s
j
appears in more than one image in S
i
then
15: S
0
i
← S
0
i
∪ m
j
16: end if
17: end for
18: end for
19: Return M
0
, S
0
4.2.5 Inter-class Pruning
The last step is to remove motifs and discords from
M
0
1
and S
0
1
that are not good discriminators of class.
In other words, motifs and discords associated with
more than one class. The sub-process is as shown
in Algorithm 6. The inputs are the sets M
0
=
{M
0
1
, M
0
2
, . . . } and S
0
= {S
0
1
, S
0
2
, . . . } from the previ-
ous sub-process, and the similarity threshold σ. The
outputs are the sets M
00
= {m
1
, m
2
, . . . }, and S
00
=
{s
1
, s
2
, . . . }, where m
i
is a motif and s
i
is a discord.
The algorithm commences by declaring the sets M
00
and S
00
to hold the “double” pruned sets of motifs and
discords. The set M
0
is process first (lines 5 to 11),
and the set S
0
second (lines 12 to 18). Line 7 states
that if the the motif m
0
j
does not appear in the set
of motifs associated with some other class, then m
0
j
should be added to M
00
. Line 14 should be interpreted
in a similar manner but with respect to discords. On
completion, line 19, M
00
, and S
00
are returned. To de-
termine whether a motif or discord appears in the con-
text of another class again requires similarity check-
ing, which again entails the threshold σ to determine
whether two motifs (discords) are the same or not.
Algorithm 6: Inter-class pruning.
1: input M
0
, S
0
, σ
2: output M
00
, S
00
3: M
00
←
/
0
4: S
00
←
/
0
5: for ∀M
0
i
∈ M
0
do
6: for ∀m
0
j
∈ M
0
i
do
7: if ∀M
0
k
∈ M, k 6= i, m
j
6∈ M
0
k
then
8: M
00
← M
00
∪ m
j
9: end if
10: end for
11: end for
12: for ∀S
0
i
∈ S
0
do
13: for ∀s
0
j
∈ S
0
i
do
14: if ∀S
0
k
∈ S, k 6= i, S
j
6∈ S
0
k
then
15: S
00
← S
00
∪ s
j
16: end if
17: end for
18: end for
19: return M
00
, S
00
4.3 Feature Vector Generation
The last process in the proposed approach is the gen-
eration of a set of feature vectors H = {V
1
,V
2
, . . . }.
Each V
i
∈ H is of the form {v
1
, v
2
, . . . , c} where v
i
is
a numerical occurrence count of a motif in M
00
or a
discord in S
00
, in an ECG scanned image I
i
. The final
element c is a class label taken from a set of classes C.
A previously unseen record will have a null value for
the variable c as this is the value we wish to predict.
5 EVALUATION
The evaluation of the proposed 2D motif feature se-
lection mechanism is presented in this section. For
KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval
24

the evaluation the Guangzhou Heart Study data set
was used (Deng et al., 2018). Some detail concerning
this data set is provided in Sub-section 5.1. A SVM
classification model, with Grid Search, was used for
the evaluation. The metrics used were accuracy, pre-
cision, recall and F1 score; Ten-fold cross-validation
was used throughout. The objectives of the evaluation
were:
1. To identify the appropriate values for the parame-
ters σ, k, p, and q.
2. To justify the hypothesis that the retention of du-
plicate motifs and/or discords will have a positive
affect.
3. To compare the operation of the proposed ap-
proach when the motif set is augmented in various
ways.
4. To compare the operation of the proposed ap-
proach with “traditional” a 1D waveform ap-
proach.
Each of these objectives is discussed in further detail
in Sub-sections 5.2, 5.3, 5.4 and 5.5.
5.1 Data Set
The Guangzhou Heart Study data set, used for the
evaluation presented here, comprised 1172 patients;
each patient record was associated with a 12-leads
ECG scanned image and included a diagnosis cover-
ing sinus rhythm and eleven arrhythmia types, such as
atrial fibrillation, atrial flutter, sinus bradycardia, pac-
ing rhythm. Sinus rhythm is the medical term used
to describe the normal rhythm of the heart. For the
evaluation presented here a subset of this database
was used, focused only on two labels, sinus rhythm
and atrial fibrillation. The image resolution was 300
dpi (dots per inch) and each image was stored using
JPEG compression, figure 1, is an example of an ECG
scanned image. All the used images were associated
with only one class.
Figure 1: Example of the ECG scanned image.
5.2 Parameter Setting for 2D Motifs
Discovery
The proposed 2D motif (discord) discovery process
required four parameters:
• σ: The similarity threshold used to compare two
motifs, the maximum distance between two mo-
tifs.
• k: The number of the final frequent motifs to be
selected from each image.
• p: the row size of the 2D motif matrix
• q: the column size of the 2D motif matrix
The values for these parameters dictate the number of
selected motifs (discords) that will be identified and
selected, and consequently the quality of any further
utilisation of the motifs. The lower the σ threshold
value the more strict the similarity requirement. It
was anticipated that as p and q increased, the num-
ber of selected motifs (discords) would decrease as
there would be fewer sub-matrices to choose candi-
date motifs (discords) from. The values for k would
also affect the number of identified candidate frequent
motifs.
To identify the appropriate values for p and q, a
range of values were considered. According to (Dau
and Keogh, 2017), to choose a good candidate 1D
motif the sub-sequence length must be less than 1/20
of the total length. The image lengths and widths
were n = 2420 and m = 815 respectively. Accord-
ingly, using this heuristic, seven parings for p and q
were considered, p = 5, 10, 15, 20, 25, 30, 35, 40 and
q = 15, 30, 45, 60, 75, 90, 105, 120. For the evaluation
σ = 0.2 and k = 5 were used because preliminary ex-
periments (not recorded here) had demonstrated that
these produced good results. The results obtained are
presented in Table 1; best results in bold font. From,
the table, it can be seen that a best accuracy was ob-
tained using p = 30 and q = 90. These were thus the
values used for the further experiments reported on in
the following sub-sections.
To determine the appropriate value for σ, the sim-
ilarity threshold used when matching motifs, a se-
quence of experiments was conducted using a range
of values for σ from 0.05 to 0.50 incrementing in
steps of 0.05. The values p = 30 and q = 90 were
used because they had been shown to produce best re-
sults (see above). The parameter k was again set to
5. The results are presented in Table 2; again best
results shown in bold font. Inspection of the results
indicates that best values were obtained using σ = 0.2
(a recorded F1 score of 84.01%).
The last parameter to consider was k, the number
of top motifs to be selected. Experiments were con-
Two-dimensional Motif Extraction from Images: A Study using an Electrocardiogram
25
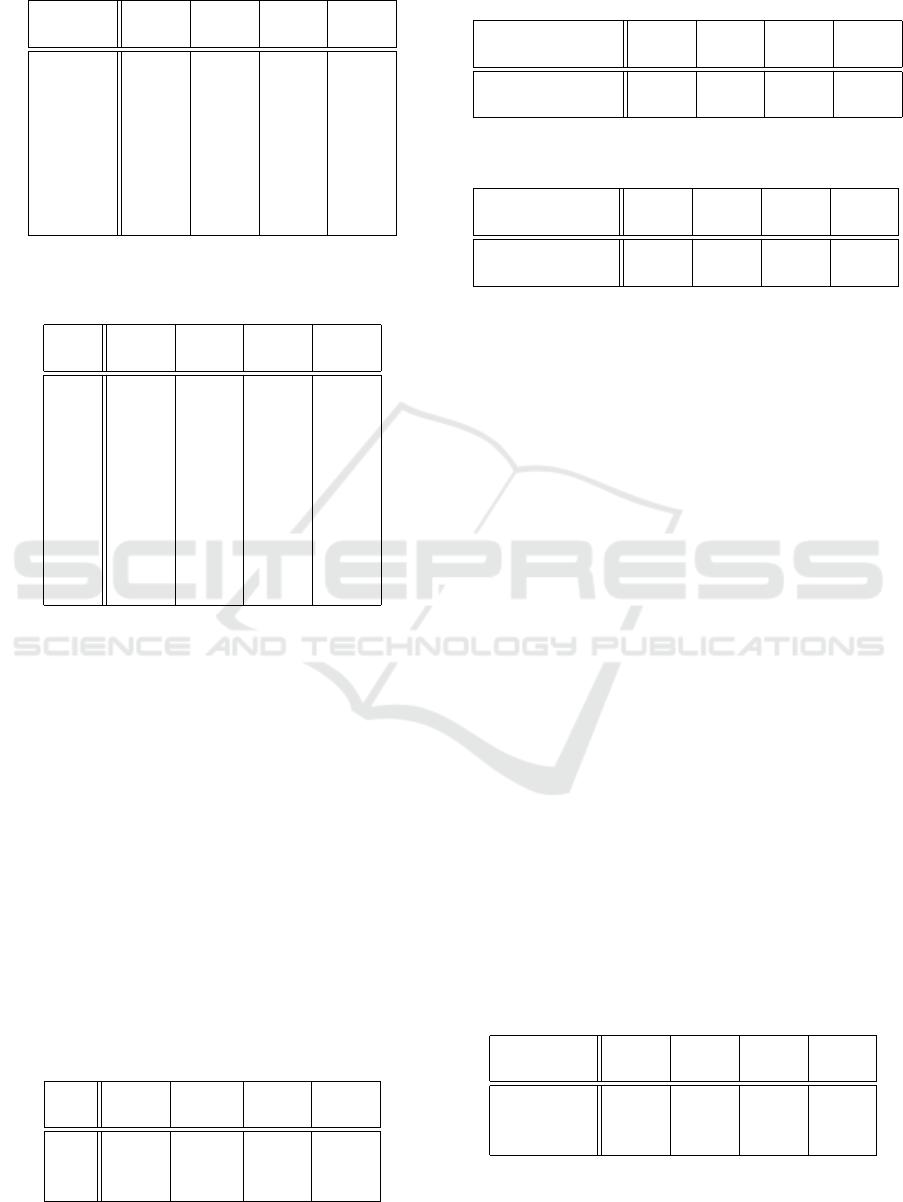
Table 1: Ten fold cross validation classification perfor-
mance using a range of p and q value pairings.
p × q Acc. Prec. Rec. F1
% % % %
5×15 60.25 70.95 60.25 65.16
10×30 61.25 76.11 61.25 67.87
15×45 67.50 70.71 67.50 69.06
20×60 75.00 81.71 75.00 78.21
25×75 81.25 87.88 81.25 84.44
30×90 85.00 89.19 85.00 87.04
35×105 73.75 81.08 73.75 77.72
40×120 73.25 79.27 73.25 76.14
Table 2: Ten fold cross validation classification perfor-
mance for 2D Motif Discovery process using range of σ
values.
σ Acc. Prec. Rec. F1
% % % %
0.05 56.2 60.37 70.00 64.83
0.1 71.25 76.21 71.25 73.64
0.15 78.75 83.58 78.75 81.09
0.2 85.00 89.19 85.00 87.04
0.25 80.00 84.70 80.00 82.28
0.3 75.00 81.58 75.00 78.15
0.35 72.50 78.98 72.50 75.6
0.4 72.50 76.82 72.50 74.59
0.45 62.50 67.67 62.50 64.98
0.5 61.25 72.95 61.25 66.58
ducted using k = {3, 5, 8}; and using p = 30, q = 90
and σ = 0.2 because earlier experiments (see above)
had indicated that these values tended to produce a
best performance. The results are presented in Table
3 (best results presented in bold font). From the table
it can be seen that k = 5 produced the best results.
5.3 Duplicate Removal
As noted earlier in Sub-section 4.2, the proposed mo-
tif generation mechanism, may result in the same mo-
tif (discord) appearing in the final set of motifs (dis-
cords) more than once. The hypothesis here was that
these duplicates should be retained so that a greater
weighting would be attributed to them during model
generation. The second evaluation objective was thus
to demonstrate that this hypothesis was correct. Ex-
Table 3: Ten fold cross validation classification perfor-
mance for 2D Motif Discovery process using k = {3, 5, 8}.
k Acc. Preci. Rec. F1
% % % %
3 68.75 76.30 68.75 72.33
5 85.00 89.19 85.00 87.04
8 83.75 89.00 83.75 86.30
Table 4: Ten fold cross validation classification perfor-
mance for 2D Motif Discovery process when increasing the
motif weight.
Proposed Acc. Prec. Rec. F1
Approach % % % %
No duplicate 71.25 76.50 71.25 73.78
With duplicate 85.00 89.19 85.00 87.04
Table 5: Evaluation Results when motif features are aug-
mented with motifs extracted from the edge of ECG images.
Proposed Acc. Prec. Rec. F1
Approach % % % %
2D motifs (M) 85.00 89.19 85.00 87.04
2D motifs plus 76.25 83.90 76.25 79.89
periments were conducted comparing the proposed
approach to one where duplicates were removed. The
results are given in Table 4. From the table it can be
seen that the result indicated that the potential inclu-
sion of multiple instances of motifs and discords had
a significant positive impact on the effectiveness of
the classification, an accuracy of 85.00% compared
to 71.25%. Thus it was concluded that the hypothesis
was correct, duplicates should be retained.
5.4 Analysis of Proposed Approach
The proposed approach generated motifs by exclud-
ing motifs from matrices located at the edge of an
ECG image. The hypothesis was that these would
not contribute to a good classification. To test this
hypothesis experiments were conducted using motifs
that could have been extracted from the edge of an
image (2D Motifs Plus). The results are presented in
Table 5. From the table it can be seen that this hy-
pothesis was also correct, better results were obtained
when motifs were not extracted from the edge of an
ECG image.
Experiments were also conducted using only dis-
cords, and where the motif features were augmented
with discord features (M+S). The results are pre-
sented in Table 6. Comparing these results, it can be
seen that using motifs on their own (M), produces a
best classification.
Table 6: Evaluation Results when motif features are aug-
mented with discords.
Proposed Acc. Prec. Rec. F1
Approach % % % %
M 85.00 89.19 85.00 87.04
S 45.00 45.00 43.00 43.98
M+S 77.50 82.92 77.50 80.11
KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval
26

5.5 Comparison of 1D and 2D Motifs
Discovery Approaches
In the introduction to this paper the disadvantages of
using 1D waveform representations of ECG data was
noted. Indeed, this was the motivation underpinning
the work presented in this paper. It was hypothesised
that using 2D motifs extracted from untransformed
ECG images would produce a better classification
than that obtained using features selected from 1D
transformed waveform representations of ECG data.
To test this hypothesis the operation of the proposed
approach was tested against a transformed waveform
format approach. The scanned images were trans-
formed into a time series format using a recent algo-
rithm for achieving this (Fortune et al., 2021). Once
the image set had been transformed the 1D motif ap-
proach proposed in (Aldosari et al., 2021b) was used.
Experiments were also conducted using 1D discords
(S), and 1D motifs augmented with discords (M+S).
The results are given in Table 7. For convenience of
comparison the results from Tables 5 have been incor-
porated into the table. The 1D waveform approach,
using motifs as features, was found to work well in
comparison to other 1D waveform approaches that
used “traditional” P wave, QRS complex and the T
wave features (Aldosari et al., 2021a; Aldosari et al.,
2021b). However, from Table 7, it can be seem that a
best performance when using the proposed 2D motif
approach.
Table 7: Comparisons of 1D and 2D approaches.
1D Approach 2D Approach
Rep. Acc. Prec. Rec. F1 Acc. Prec. Rec. F1
% % % % % % % %
M 68.48 70.00 68.48 69.88 85.00 89.19 85.00 87.04
S 67.59 76.60 66.59 71.24 45.00 45.00 43.00 43.98
M+S 72.35 78.74 72.50 75.49 77.50 82.92 77.50 80.11
6 CONCLUSION
In this paper an approach to ECG classification using
2D motifs was proposed and investigated. The hy-
pothesis was that the “traditional” approach to ECG
classification, using transformation to a waveform
format and usage of a limited set of features, re-
sulted in loss of information because of the associ-
ated approximations used, and that a better classifi-
cation could be obtained if the classification model
was built using the original image data without any
transformation. To investigate this idea an approach
founded on 2D motifs was proposed. An idea mo-
tivated by work on 1D motifs as applied to time se-
ries data. The approach utilised four parameters: (i)
a similarity threshold σ used to compare motifs, (ii)
a parameter k that specified the number motifs to be
selected and (iii) the pixel width p and height q of
the 2D motifs to be extracted. The reported evalu-
ation indicated best parameter settings of: σ = 0.2,
k = 5, p = 30 and q = 90. Novel aspects of the pro-
posed approach were that duplicate motifs should be
retained and that motifs should not be extracted from
image edges, the reported evaluation indicated that
this was indeed beneficial. The potential of includ-
ing discords as features was also investigated, but this
was found not to provide any benefit. Most impor-
tantly, the reported evaluation demonstrated that the
hypothesis that more effective classification could be
undertaken when 2D motifs extracted from an entire
image were used as features, then when the image was
transformed into a 1D waveform format and 1D mo-
tifs used as features, was correct. A best accuracy of
85% was obtained using the proposed approach, in
comparison with a best accuracy of 70% using a 1D
waveform format. For future work the authors intend
to investigate improving the performance of 2D motif
extraction from scanned images, and to apply the idea
to alternative application domains.
REFERENCES
Aldosari, H., Coenen, F., Lip, G. Y., and Zheng, Y. (2021a).
Addressing the challenge of data heterogeneity using
a homogeneous feature vector representation: A study
using time series and cardiovascular disease classi-
fication. In International Conference on Innovative
Techniques and Applications of Artificial Intelligence,
pages 254–266. Springer.
Aldosari, H., Coenen, F., Lip, G. Y., and Zheng, Y. (2021b).
Motif based feature vectors: towards a homogeneous
data representation for cardiovascular diseases clas-
sification. In International Conference on Big Data
Analytics and Knowledge Discovery, pages 235–241.
Springer.
Apostolico, A., Parida, L., and Rombo, S. E. (2008). Mo-
tif patterns in 2d. Theoretical Computer Science,
390(1):40–55.
Badilini, F., Erdem, T., Zareba, W., and Moss, A. J. (2005).
Ecgscan: a method for conversion of paper electro-
cardiographic printouts to digital electrocardiographic
files. Journal of electrocardiology, 38(4):310–318.
Baydoun, M., Safatly, L., Abou Hassan, O. K., Ghaziri, H.,
El Hajj, A., and Isma’eel, H. (2019). High precision
digitization of paper-based ecg records: a step toward
machine learning. IEEE journal of translational engi-
neering in health and medicine, 7:1–8.
Bosch, A., Munoz, X., and Marti, R. (2007). Which is the
best way to organize/classify images by content? Im-
age and vision computing, 25(6):778–791.
Two-dimensional Motif Extraction from Images: A Study using an Electrocardiogram
27

Chung, D., Choi, J., Jang, J.-H., Kim, T. Y., Byun, J., Park,
H., Lim, H.-S., Park, R. W., and Yoon, D. (2018).
Construction of an electrocardiogram database includ-
ing 12 lead waveforms. Healthcare informatics re-
search, 24(3):242–246.
Dau, H. A. and Keogh, E. (2017). Matrix profile V: A
generic technique to incorporate domain knowledge
into motif discovery. In Proceedings of the 23rd
ACM SIGKDD International Conference on Knowl-
edge Discovery and Data Mining, pages 125–134.
Deng, H., Guo, P., Zheng, M., Huang, J., Xue, Y., Zhan,
X., Wang, F., Liu, Y., Fang, X., Liao, H., et al.
(2018). Epidemiological characteristics of atrial fibril-
lation in southern china: results from the guangzhou
heart study. Scientific reports, 8(1):1–10.
Ebrahimi, Z., Loni, M., Daneshtalab, M., and Gharehbaghi,
A. (2020). A review on deep learning methods for ecg
arrhythmia classification. Expert Systems with Appli-
cations: X, 7:100033.
Fortune, J., Coppa, N., Haq, K. T., Patel, H., and
Tereshchenko, L. G. (2021). Digitizing ecg image:
new fully automated method and open-source soft-
ware code. medRxiv.
Furfaro, A., Groccia, M. C., and Rombo, S. E. (2017). 2d
motif basis applied to the classification of digital im-
ages. The Computer Journal, 60(7):1096–1109.
Gupta, V., Mittal, M., Mittal, V., and Saxena, N. K. (2021).
A critical review of feature extraction techniques for
ecg signal analysis. Journal of The Institution of En-
gineers (India): Series B, pages 1–12.
Houssein, E. H., Kilany, M., and Hassanien, A. E.
(2017). Ecg signals classification: a review. Interna-
tional Journal of Intelligent Engineering Informatics,
5(4):376–396.
Jayaraman, S., Swamy, P., Damodaran, V., and Venkatesh,
N. (2012). A novel technique for ecg morphology in-
terpretation and arrhythmia detection based on time
series signal extracted from scanned ecg record. Ad-
vances in Electrocardiograms-Methods and Analysis,
pages 127–140.
Kar, A. and Das, L. (2011). A technical review on statisti-
cal feature extraction of ecg signal. In IJCA Special
Issue on 2nd National Conference-Computing, Com-
munication and Sensor Network, CCSN, pages 35–40.
Khleaf, H. K., Ghazali, K. H., and Abdalla, A. N. (2013).
Features extraction technique for ecg recording paper.
In Proceeding of the International Conference on Ar-
tificial Intelligence in Computer Science and ICT.
Liu, X., Wang, H., Li, Z., and Qin, L. (2021). Deep learning
in ecg diagnosis: A review. Knowledge-Based Sys-
tems, 227:107187.
Loresco, P. J. M. and Africa, A. D. (2018). Ecg print-out
features extraction using spatial-oriented image pro-
cessing techniques. Journal of Telecommunication,
Electronic and Computer Engineering (JTEC), 10(1-
5):15–20.
Mir, H. Y. and Singh, O. (2021). Ecg denoising and feature
extraction techniques–a review. Journal of medical
engineering & technology, 45(8):672–684.
Mishra, S., Khatwani, G., Patil, R., Sapariya, D., Shah, V.,
Parmar, D., Dinesh, S., Daphal, P., and Mehendale, N.
(2021). Ecg paper record digitization and diagnosis
using deep learning. Journal of Medical and Biologi-
cal Engineering, pages 1–11.
Ravichandran, L., Harless, C., Shah, A. J., Wick, C. A.,
Mcclellan, J. H., and Tridandapani, S. (2013). Novel
tool for complete digitization of paper electrocardiog-
raphy data. IEEE journal of translational engineering
in health and medicine, 1:1800107–1800107.
Roth, G. A., Mensah, G. A., and et al., C. O. J. (2020).
Global burden of cardiovascular diseases and risk
factors, 1990–2019: Update from the gbd 2019
study. Journal of The American College of Cariology,
(25):2982–3201.
Seena, V. and Yomas, J. (2014). A review on feature extrac-
tion and denoising of ecg signal using wavelet trans-
form. In 2014 2nd international conference on de-
vices, circuits and systems (ICDCS), pages 1–6. IEEE.
Sm
´
ı
ˇ
sek, R. (2016). Ecg signal classification based on svm.
Biomedical Engineering, (1):365–369.
Thanapatay, D., Suwansaroj, C., and Thanawattano, C.
(2010). Ecg beat classification method for ecg printout
with principle components analysis and support vector
machines. In 2010 International Conference on Elec-
tronics and Information Engineering, volume 1, pages
V1–72. IEEE.
Torkamani, S. and Lohweg, V. (2017). Survey on time se-
ries motif discovery. Wiley Interdisciplinary Reviews:
Data Mining and Knowledge Discovery, 7(2):e1199.
Truong, C. D. and Anh, D. T. (2019). A survey on time
series motif discovery. International Journal of Busi-
ness Intelligence and Data Mining, 15(2):204–227.
Waits, G. S. and Soliman, E. Z. (2017). Digitizing paper
electrocardiograms: Status and challenges. Journal of
electrocardiology, 50(1):123–130.
Wankhedkar, R. and Jain, S. K. (2019). A brief survey on
techniques used in discovering time series motifs. In
Proceedings of the International Conference on Ad-
vances in Electronics, Electrical & Computational In-
telligence (ICAEEC).
KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval
28
