Cluster-based Diversity Over-sampling: A Density and Diversity

Oriented Synthetic Over-sampling for Imbalanced Data

Yuxuan Yang

, Hadi Akbarzadeh Khorshidi

and Uwe Aickelin

School of Computing and Information Systems, The University of Melbourne, Grattan Street, Parkville, Victoria, Australia

Keywords: Over-sampling, Diversity Optimisation, Genetic Algorithm, Imbalanced Data, Clustering.

Abstract: In many real-life classification tasks, the issue of imbalanced data is commonly observed. The workings of

mainstream machine learning algorithms typically assume the classes amongst underlying datasets are

relatively well-balanced. The failure of this assumption can lead to a biased representation of the models’

performance. This has encouraged the incorporation of re-sampling techniques to generate more balanced

datasets. However, mainstream re-sampling methods fail to account for the distribution of minority data and

the diversity within generated instances. Therefore, in this paper, we propose a data-generation algorithm,

Cluster-based Diversity Over-sampling (CDO), to consider minority instance distribution during the process

of data generation. Diversity optimisation is utilised to promote diversity within the generated data. We have

conducted extensive experiments on synthetic and real-world datasets to evaluate the performance of CDO

in comparison with SMOTE-based and diversity-based methods (DADO, DIWO, BL-SMOTE, DB-SMOTE,

and MAHAKIL). The experiments show the superiority of CDO.

1 INTRODUCTION

Imbalanced data refers to a scenario whereby there is

a large proportion of instances which are labelled as

“Negative” (majority class) to the number of

instances labelled as “Positive” (minority class).

Performance of subsequent learning classifiers may

be negatively impacted without further treatment of

imbalanced labels. Specifically, the processing of

minority instances would most likely be regarded as

an outlier or anomaly within the dataset (Ali et al.,

2013). The objective for most of the mainstream

classification algorithms is either to minimise

misclassification error or to maximise predictive

accuracy. However, it is often overlooked that these

classification algorithms are constructed on the basis

that the distribution of instances within each class is

relatively balanced. As such, when classifiers are

built on imbalanced datasets, the accuracy of these

algorithms is often biased or have an overwhelming

tendency to predict the majority class, resulting in

high False Negative Rates (FNR) (Sasaki, 2007;

Thabtah et al., 2020).

https://orcid.org/0000-0001-5983-6038

https://orcid.org/0000-0002-2653-4102

https://orcid.org/0000-0002-2679-2275

In the current literature, there are 3 main concepts

used to treat and address imbalanced data, which are

cost-sensitive learning, ensemble-based method, and

re-sampling techniques. The purpose of “re-sampling

techniques” is to create, either randomly or

synthetically, a more balanced representation of the

underlying dataset used for learning. One form of re-

sampling techniques is Over-sampling, where in its

most basic form, involves random sampling. There

are also synthetic ways used to over-sample data

based on many years of research. Synthetic instances

generated are not exact replicas of the original

instances. They broaden the decision region

compared to random over-sampling. As a result,

synthetic methods minimise the likelihood of

overfitting, and reduce False Negative Rate and

stabilise the performance of classifiers (Japkowicz &

Stephen, 2002). However, for most of the synthetic

methods, the generated instances lies along a linear

path between minority data points, and the creation of

synthetic minority data points takes place in the

“feature level” and not on the “data level” (Chawla et

al., 2002). It implies the decision region of minority

Yang, Y., Khorshidi, H. and Aickelin, U.

Cluster-based Diversity Over-sampling: A Density and Diversity Oriented Synthetic Over-sampling for Imbalanced Data.

DOI: 10.5220/0011381000003332

In Proceedings of the 14th International Joint Conference on Computational Intelligence (IJCCI 2022), pages 17-28

ISBN: 978-989-758-611-8; ISSN: 2184-3236

class does not consider a holistic view of the entire

minority data space (Bennin et al., 2017).

In this paper, we designed an algorithm to address

the above issue. The proposed algorithm generates

diversified synthetic instances within the minority

class while considering the distribution of the

minority data space. It is done via optimising both

similarity to minority instances and diversity in

synthetic instances. The optimisation process is

conducted based on genetic algorithm. Our proposed

method guarantees proximity of the generated

synthetic instances to the actual instances in the

minority class. In addition to preserving the

advantage of over-sampling, the proposed algorithm

enables the optimal spread of generated instances in

the data space and help to broaden the decision region

as a result of diversity optimisation.

2 RELATED WORK

SMOTE is a well-known synthetic over-sampling

technique in the literature (Chawla et al., 2002). The

process of generating synthetic minority class

instances is via a random selection of specified k-

nearest neighbours of a minority sample, and

applying a multiplier derived from a uniform random

distribution (0,1). This creates an “synthetic” instance

which will be located between the 2 minority points.

SMOTE has improved the performance of classifiers

trained on imbalance dataset through the process of

expanding decision regions housing nearby minority

instances as compared to basic random over-sampling

which enhanced and narrowed decision regions with

contrasting effects (Chawla et al., 2002)

Recent studies have flagged a limitation of

traditional over-sampling methods (i.e. SMOTE) to

its casual tendency to generate synthetic instances

which extends into the input region of the majority

class instances, thereby negatively impacting the

performance of the subsequent learning classifier

built (Bennin et al., 2017; Sharma et al., 2018). These

studies have identified the dual importance of

maintaining the integrity of the minority sample

region, in addition to enhancing the diversity of

minority class data. Subsequent studies has aimed to

address the above challenge.

ECO-ensemble is an Cluster-based synthetic

oversampling ensemble method (Lim et al., 2016). Its

idea originates on identifying suitable oversampling

cluster regions with Evolutionary Algorithm (EA) to

derive at the optimised ensemble. The SMOTE-

Simple Genetic Algorithm (SMOTE-SGA) method is

proposed to enhance the diversity within the

generated dataset (Tallo & Musdholifah, 2018). The

algorithm determines instances to be generated and

the number of synthetic instances created from the

selected instance (sampling rate) to overcome the

overgeneralization problem in SMOTE.

MAHAKIL is created with the purpose of

generating more diverse synthetic instances (Bennin

et al., 2017). It works by pairing minority instances

with previously generated synthetic instances to

generate instances inspired by the Chromosomal

Theory of Inheritance. It utilised the core concept of

Mahalanobis Distance as the measure for diversity, in

conjunction with inheritance and genetic algorithm.

The fundamental idea is to create synthetic minority

instances which are unique using 2 relatively distant

parent instances which are different to their parents

(i.e. existing minority class). In 2018, SWIM

(Sampling WIth the Majority) was proposed (Sharma

et al., 2018). Synthetic minority instances are

generated based on the distribution of majority class

instances which are effective against extremely

imbalanced data. In 2021, a diversity-based sampling

method with a drop-in functionality was proposed to

evaluate diversity. It is achieved via a greedy

algorithm that is used to identify and discard subsets

that share the most similarity (Yang et al., 2021).

Most recently, Diversity-based Average Distance

Over-sampling (DADO) and Diversity-based

Instance-Wise Over-sampling (DIWO) are proposed

to promote diversity (Khorshidi & Aickelin, 2021).

The objective of the 2 techniques is to generate well-

diverse synthetic instances close to minority class

instances. DADO aims to ensure diversity in the

region among minority class instances. Whereas in

the case of DIWO, the contrasting approach is taken

to ensure synthetic instances are clustered as closely

to the actual minority class instances. DADO

performs better when minority instances are compact,

and immediate surrounding area is located within

minority space. DIWO performs better when minority

instances are widely distributed, and the surrounding

area does not sit within the minority space.

In this paper, we propose a new synthetic

sampling method, namely Cluster-based diversity

oversampling (CDO). Our proposed method

combines the advantage of both DADO and DIWO

by analysing the density distribution of the minority

instances via diversity optimisation.

ECTA 2022 - 14th International Conference on Evolutionary Computation Theory and Applications

3 METHODOLOGY

3.1 Cluster based Diversified

Over-sampling (CDO)

In this section, we aim to describe our new proposed,

Cluster-based Diversity Over-sampling (CDO). The

new proposed method aims to provide a more robust

algorithm compared to DADO and DIWO by

combining the strengths of both approaches. A

clustering algorithm is used to analyse and learn the

density distribution of minority instances. For

instances that are compact and similar to each other

using density clustering method, DADO is applied.

For instances that are widely distributed, DIWO is

applied.

Our preferred choice of clustering method is

DBSCAN as it is more efficient in comparison to

partition-based or hierarchical-based clustering

methods when the problem requires us to determine

the arbitrary shaped clusters (Ester et al., 1996).

DBSCAN was first introduced in 1996 (Ester et al.,

1996). It is a non-parametric density-based clustering

algorithm and it works by enhancing the grouping of

instances which are closely located to each other and

simultaneously identifying points which are placed in

low-density areas (points whose nearest neighbours

are relatively far away). Additionally, we choose

DBSCAN over all other clustering methods due to the

reason that unlike our typical clustering problem, our

objective is to identify instances which are close

together and not clustering all the data points. We also

note the advantage of DBSCAN which allows the

user to select the desired level of similarity required.

The algorithm of CDO is shown in Algorithm 1.

It requires the following Epsilon (

𝑒𝑝𝑠), and Border

Point (𝑝) parameters for clustering. As 𝑝 is a binary

pair of parameter values, if it is true, border points are

assigned to clusters.

3.2 Diversity Optimisation

The choice of the proposed CDO algorithm for

diversity optimisation is the extended form of

NOAH’s algorithm (Ulrich & Thiele, 2011), as

shown in Algorithm 2.

Algorithm 2 contains 3 stages and requires the

following input parameters: population size (n),

number of generations to optimise objective function

(g), number of instances remaining in the population

after bound adaptation (r), percentage improvement

of bound (v) and finally, the stopping criterion

diversity maximisation (c). The above implies that if

the population diversity does not improve for c

generations, convergence of the diversity

maximisation is achieved. The whole algorithm

terminates if the bound does not improve for c

generation, To further optimise the objective

function, Algorithm 2 has also incorporated the usage

of Genetic Algorithm (GA), as it is the most popular

evolutionary algorithm. Mutation and crossover

concepts are utilised to create new instances.

Instances which objective functions are better than

bound value (b) are kept (Algorithm 2, lines 5 and

14). For DADO, the objective function (f) is the

average of distance from all instances in the minority

class. For DIWO, the objective function (f) is the

distance to each instance.

3.3 Diversity-based Selection

The preferred measure of diversity is Solow-Polasky

measure. There are 3 main properties which are

required of a diversity measure, which are namely 1)

monotonicity in variety, 2) monotonicity in distance

and 3) twinning. The first property implies that the

diversity measure will increase or at least be non-

decreasing when an individual element currently not

present in the dataset is added. The second property

requires that the diversity between a particular set S

(i.e. instances) should not be smaller to another set S’,

if all pairings within S are of the distance of all the

pairings within S’. The third property ensures the

diversity measure remains the same when additional

element, already in the set, is added. Solow-Polasky

measure can be expressed in the following equation

(1), where M represents the distance matrix. The

Euclidean distance between elements of set S are

denoted as 𝑑(𝑠



, 𝑠



) . Thereafter, our diversity

measure is derived and computed by the summation

of all inverse matrix of (

𝑀



= 𝑚







𝐷

(

𝑆

)

= 𝑀



= 𝑒

(



,



)



)

To obtain the best diversity amongst all the

instances, the ideal scenario would be to generate all

possible permutation of subsets. However, this cannot

be achieved as it would be computationally infeasible

and expensive. As an alternative methodology, we

propose the use of a greedy approach which would

filter out instances which have the least contribution

to the diversity of our dataset. Our definition of

contribution is defined as the difference in diversity

for our dataset with and without the instance. As

proven in this study (Ulrich & Thiele, 2011), the

difference can be expressed in the following formula:

𝑀



−

𝐴



𝑐

(𝑏



+ 𝑐

)

Cluster-based Diversity Over-sampling: A Density and Diversity Oriented Synthetic Over-sampling for Imbalanced Data

Algorithm 1: Cluster-based diversity over-sampling algorithm (CDO).

/* Step 1: Clustering minority instances */

𝐶 =0

for each point 𝑀 in minority class do:

if 𝑀 is labelled then next

if 𝑀 is not labelled then

NeighborPts ← return all points within 𝑒𝑝𝑠 neighbourhood of 𝑀 (incl. 𝑀)

if size of NeighborPts = 1 then label(𝑀)= NOISE next

𝐶 = 𝐶 +1

label(𝑀)= 𝐶

for each 𝑀’ in NeighborPts do:

if label(𝑀′)= NOISE and 𝑝 = 𝑇𝑟𝑢𝑒 then label(𝑀’) = 𝐶 next

if 𝑀’ is labelled: next

label(𝑀’) = 𝐶

NeighborPts’ ← return all points within eps neighbourhood of 𝑀’ (incl. 𝑀’)

if size(NeighborPts’) > 1 then NeighborPts ← NeighborPts U NeighborPts’

end for

/* Step 2: Perform diversity algorithm for each cluster and NOISE points */

for each 𝐶 do:

𝑃







← NOAH(n, g, r, c, v, f)

end for

for each minority instances 𝑀 marked as NOISE do:

𝑃





← NOAH(n, g, r, c, v, f)

end for

/* Step 3: Combine generated datasets */

𝑃 = 𝑃







𝑈 𝑃







Algorithm 2: Diversity optimisation algorithm (NOAH).

Input: 𝑛, 𝑔, 𝑟, 𝑐, 𝑣

Output: a diverse set of instances 𝑆

1 S = Null; b = ∞; i = 0

2 while 𝑖 < 𝑐 do

/* Step 1: Optimising the objective function */

3 𝑃 ← Generate a population with n instances

4 for g generations do

5 𝑃



← Generate new n instances via mutation and crossover from P with objective values better than b

6 𝑃 ← Select n best instances from 𝑃 ∪ 𝑃



7 end for

/* Step 2: Bound adaptation */

8 𝑃← Select r best instances from 𝑃 ∪ 𝑆

9 𝑏



← Put the objective value of rth best instance in 𝑃 ∪ 𝑆

10 if DIWO and 𝑏−𝑏



< 𝑣× 𝑏 then 𝑖 ←𝑖+1 else 𝑖 ← 0

11 𝑏 ←𝑏



/* Step 3: Diversity maximisation */

12 j = 0

13 while 𝑗 < 𝑐 do

14 𝑃

← Generate new r instances via mutation and crossover from P with objective values better than b

15 𝑃

∴

← Select r best diverse instances from 𝑃

∪ 𝑆

16 end while

17 if diversity of 𝑃

∴

is more than S then 𝑆 ←𝑃

∴

else 𝑗 ←𝑗+1

18 end while

ECTA 2022 - 14th International Conference on Evolutionary Computation Theory and Applications

where A is the distance matrix of the set without that

particular instance,

𝑀 = 

𝐴𝑏

𝑏



𝑐

,

𝑀



= 

𝐴

𝑏



𝑏





𝑐̅

, c

and 𝑐̅ are single elements, b and 𝑏



are vectors and 𝑏



and 𝑏





are their transpose.

4 VALIDATION OF SYNTHETIC

DATASET

4.1 Evaluation Method

The learning classifiers used to evaluate the generated

data are Naïve Bays (NB), Decision Tree (DT), k-

Nearest Neighbour (KNN), and Support Vector

Machine (SVM), and Random Forest (RF). We

choose KNN and RF as they are sensitive to

imbalanced data based on their model assumptions

(Muñoz et al., 2018). DT works based on developing

decision regions which are influenced by re-sampling

methods (Chawla, 2010). SVM with radial kernel is

effective to classify classes which are not separable

linearly.

We measure the performance of the classifiers on

test data using F1-score, G-means, and PR-AUC as

classification accuracy is not an appropriate measure

for imbalanced data.

To calculate F1-score (5), we need to measure

recall and precision shown as (3) and (4). Recall is the

proportion of correctly predicted positive instances to

all instances in the positive class. Precision is the

proportion of correctly predicted positive instances to

all predicted positive instances

R𝑒𝑐𝑎𝑙𝑙 =





)

P𝑟𝑒𝑐𝑖𝑠𝑖𝑜𝑛 =





)

F1=

××



)

PR-AUC denotes the area under the Precision

Recall curve, is a suitable measure for classifiers’

performance especially in the situation of imbalanced

data and is independent of the decision boundary.

The G-means (7) is the geometric mean of true

positive rate (TPR), as (6) and true negative rate

(TNR), which is 1 −𝐹𝑃𝑅.

𝑇𝑃𝑅 =

𝑇𝑃

𝐹𝑁+ 𝑇𝑃

(6)

𝐺−𝑚𝑒𝑎𝑛𝑠=

√

𝑇𝑃𝑅 × 𝑇𝑁𝑅

(7)

4.2 Synthetic Dataset

To examine our proposed methods under different

scenario, 4 2-dimensional datasets are created. There

is an equal split (2) of datasets with an imbalanced

ratio (IR) of 10% and IR of 5%. These datasets are

used in our initial experiments to assist in hyper-

parameter selections. Table 1 provides a summary of

these datasets (DS1-4). There is a varying amount of

cluster within each DS, ranging from 0 (randomly

distributed data points) in DS3 to 5 in DS1. For each

of the 4 synthetic datasets, instances are randomly

divided into training and test datasets with a 75:25

split. DADO, DIWO and our proposed method CDO

are utilised to balance our training datasets. Learning

classifiers are applied onto the balanced training

datasets. Performance of these constructed learning

classifiers is then assessed using the test datasets.

Performance measures (F1, G-Means, and PR-AUC)

are computed for the best performing classifier. The

above process is repeated 30 times.

Table 1: Synthetic datasets characteristics.

Dataset Number of

Clusters

Data

Points

Imbalance

Ratio

DS1 5 200 10%

DS2 2 300 10%

DS3 0 300 5%

DS4 1 300 5%

4.3 Parameter Selection

The distance measures chosen for both objective

function and diversity measure are the optimal

distance measure based on experimental results

(Khorshidi & Aickelin, 2021). Euclidean distance

measure (𝐷



) is chosen for DADO, and Canberra

(𝐷



) is chosen for DIWO.

𝐷



(

𝑥, 𝑦

)



∑ (

𝑥



−𝑦



)





)

𝐷



(

𝑥, 𝑦

)

∑













|





)

Next, we aim to determine the optimal values for 2

hyper-parameters for DBSCAN, Epsilon (eps) and

Border Point (p). We examine the eps using 10

different parameter values, ranging from 0.05 to 50.

A binary pair (“T”, “F”) of p is also examined. Based

on parameter testing result on datasets (DS1, DS2,

DS3, DS4), eps = 0.05 and p = “T” are selected.

4.4 Synthetic Experiment Results

CDO is compared alongside DADO and DIWO on

synthetic datasets. In total, there are 4 synthetic

datasets available and the performance of each of the

3 algorithms are evaluated. 12 different results are

summarised in Table 2. CDO performs better than

Cluster-based Diversity Over-sampling: A Density and Diversity Oriented Synthetic Over-sampling for Imbalanced Data

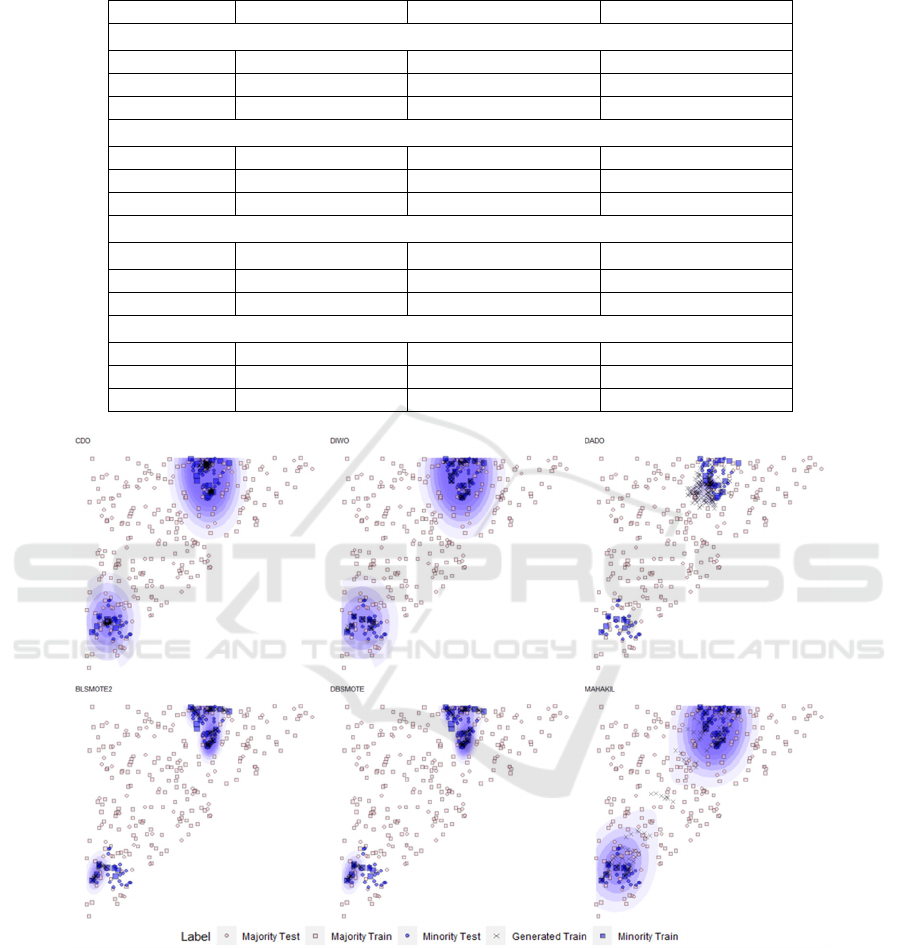
Table 2: Performance results of mean and standard error for each measure across synthetic datasets. Bold numbers indicate

the mean of method performance is the best among all comparable methods.

DADO DIWO CDO

DS 1

F1 0.3516 (± 0.131) 0.4586 (± 0.176) 0.4601 (± 0.179)

G-means 0.6341 (± 0.194) 0.8498 (± 0.080) 0.8456 (± 0.084)

PR-AUC 0.9439 (± 0.030) 0.9594 (± 0.026) 0.9603 (± 0.026)

DS 2

F1 0.1805 (± 0.067) 0.4219 (± 0.116) 0.4244 (± 0.105)

G-means 0.4012 (± 0.182) 0.8342 (± 0.048) 0.8158 (± 0.042)

PR-AUC 0.9516 (± 0.019) 0.9786 (± 0.024) 0.9792 (± 0.023)

DS 3

F1 0.1333 (± 0.047) 0.1092 (± 0.063) 0.1092 (± 0.063)

G-means 0.0693 (± 0.176) 0.4733 (± 0.216) 0.4638 (± 0.250)

PR-AUC 0.9706 (± 0.020) 0.9684 (± 0.022) 0.9687 (± 0.021)

DS 4

F1 0.8623 (± 0.107) 0.8632 (± 0.113) 0.8679 (± 0.099)

G-means 0.9861 (± 0.014) 0.9926 (± 0.007) 0.9907 (± 0.009)

PR-AUC 0.9973 (± 0.011) 0.9974 (± 0.011) 0.9974 (± 0.011)

Figure 1: Plots for synthetic datasets, blue area indicates minority generation density.

DADO in all evaluation metrics over 3 of 4 datasets.

CDO performs better in 2 of 3 evaluation metrics to

DIWO, when 2 or more clusters are detected (DS1

and DS2). CDO outperforms in 1 of 3 evaluation

metrics for DS 3, and 2 of 3 evaluation metrics for

DS4, where datasets have less than 2 clusters

4.5 Graphical Representation

To provide a graphical representation of the synthetic

datasets generated by CDO and its 5 comparable

methods (BL-SMOTE, DB-SMOTE, DIWO, DADO

and MAHAKIL), we created a seperate synthetic

dataset with two clusters, 5% imbalanced ratio in

testing data with a balanced ratio in training data. The

ECTA 2022 - 14th International Conference on Evolutionary Computation Theory and Applications

generated minority data for each algorithm is

displayed in Figure 1. We observe that the region of

synthetic generated instances for CDO, DIWO and

MAHAKIL is relatively similar. However, CDO

stands out for its ability to cover all the data points of

the minority test data with the narrowest region.

MAHAKIL created synthetic data points between the

2 clusters, which occupies a larger region and could

result in over-generalisation and higher false positive

rate. For DADO, BL-SMOTE and DB-Smote, the

region of generated data does not cover all of minority

test data points, which could result in higher false

negative rate.

5 VALIDATION

We validate the proposed CDO algorithm against an

assortment of 10 imbalanced datasets, with varying

dimensions. The datasets and their characteristics are

described in Table 3, and “Ratio” is used to indicate

the original proportion of majority to minority

instances. To replicate the scenarios with low and

extremely low imbalanced ratio, we reduce the

imbalanced ratio to 5% and 10 absolute count of

minority instances.

The data within each of the real-world datasets are

randomly divided into train and test datasets using a

75:25 split respectively. This process is repeated for

30 iterations, resulting in 30 unique variations of

training datasets and accompanying test datasets for

each of the 10 real-world datasets. After the

initialisation step, we apply our proposed method,

CDO, alongside with existing methods in the

literature, namely BL-SMOTE, DB-SMOTE and

MAHAKIL to evaluate algorithm performance. Six

learning classifiers (GLM, NB. DT, KNN, SVM, NN)

are then constructed on each of the training datasets

(n=30). Subsequently, the trained classifiers are

applied onto test datasets.

For each real-world datasets, the best performing

classifier is selected, and we compute the mean and

standard error of the performance measures as F1,

AUC and G-mean. Additionally, we examine the

statistical significance of differences for the

performance measures obtained from CDO, BL-

SMOTE, DB-SMOTE and MAHAKIL using a non-

parametric test, Mann-Whitney test.

5.1 Experimental Results

The mean and standard error (stated in parenthesis) of

our proposed method (CDO) and its comparable

methods (BL-SMOTE, DB-SMOTE and

MAHAKIL) are presented in Table 4 and 5, with 5%

imbalanced ratio and 10 minority instances.

By looking at the performance metrics for 5%

imbalanced ratio (Table 4), it can be concluded that

CDO shows encouraging result as it outperformed its

comparable algorithms in terms of F1 score and G-

Means in 5 out of the 10 datasets. Additionally, CDO

outperformed other comparable methods in 6 out of

the 10 datasets based on PR-AUC.

By looking at the performance metrics for 10

minority instances (Table 5), CDO shows promising

result as it outperformed its comparable algorithms in

terms of F1 score in 4 out of the 10 datasets. It

outperformed other comparable methods in 5 out of

the 10 datasets based on PR-AUC. CDO performed

equivalently well to MAHAKIL in G-Means.

Table 3: Real-word Data Description.

Dataset Name Dim Size Ratio Dataset Name Dim Size Ratio

D1 Wisconsin 9 683 65-35 D6 Glass (0,1,2,3 vs 4,5,6) 9 214 76-24

D2 Diabetes 8 768 65-35 D7 Haberman 3 306 74-26

D3 Ecoli (0,1 vs 5) 6 240 90-10 D8 New Thyroid 5 215 84-16

D4 Ecoli 2 7 336 85-15 D9 Pima 8 768 65-35

D5 Ecoli 3 7 336 90-10 D10 Wine Red Low vs High 11 280 75-25

Cluster-based Diversity Over-sampling: A Density and Diversity Oriented Synthetic Over-sampling for Imbalanced Data

Table 4: Performance results of mean and standard error across datasets with 5% imbalance levels. Bold numbers indicate

the mean of method performance is the best among all comparable methods.

Dataset CDO BL-SMOTE DB-SMOTE MAHAKIL

D1 0.9528 (± 0.022) 0.9443 (± 0.023) 0.9487 (± 0.022) 0.9494 (± 0.023)

D2 0.4834 (± 0.067) 0.4639 (± 0.125) 0.4987 (± 0.096) 0.5964 (± 0.054)

D3 0.9091 (± 0.089) 0.8860 (± 0.095) 0.9113 (± 0.101) 0.9158 (± 0.086)

D4 0.8529 (± 0.091) 0.8467 (± 0.070) 0.8635 (± 0.074) 0.8221 (± 0.111)

D5 0.6441 (± 0.103) 0.6788 (± 0.083) 0.6600 (± 0.081) 0.6365 (± 0.109)

D6 0.8515 (± 0.065) 0.8004 (± 0.084) 0.8181 (± 0.081) 0.8378 (± 0.070)

D7 0.4327 (± 0.127) 0.2555 (± 0.151) 0.3747 (± 0.133) 0.4084 (± 0.139)

D8 0.9628 (± 0.046) 0.9458 (± 0.056) 0.9551 (± 0.043) 0.9571 (± 0.041)

D9 0.4845 (± 0.065) 0.4582 (± 0.120) 0.4888 (± 0.097) 0.5964 (± 0.054)

D10 0.6600 (± 0.105) 0.4915 (± 0.165) 0.5763 (± 0.127) 0.6317 (± 0.117)

G-Means

Dataset CDO BL-SMOTE DB-SMOTE MAHAKIL

D1 0.9681 (± 0.014) 0.9616 (± 0.017) 0.9646 (± 0.016) 0.9668 (± 0.015)

D2 0.5890 (± 0.050) 0.5690 (± 0.102) 0.6025 (± 0.073) 0.6861 (± 0.034)

D3 0.9521 (± 0.066) 0.9109 (± 0.087) 0.9415 (± 0.086) 0.9552 (± 0.065)

D4 0.9260 (± 0.041) 0.9130 (± 0.049) 0.9285 (± 0.043) 0.9108 (± 0.048)

D5 0.8890 (± 0.045) 0.9068 (± 0.053) 0.8841 (± 0.064) 0.8907 (± 0.042)

D6 0.8916 (± 0.059) 0.8378 (± 0.077) 0.8578 (± 0.075) 0.8854 (± 0.060)

D7 0.5883 (± 0.085) 0.3963 (± 0.132) 0.5541 (± 0.090) 0.5767 (± 0.082)

D8 0.9847 (± 0.023) 0.9581 (± 0.047) 0.9762 (± 0.028) 0.9789 (± 0.026)

D9 0.5885 (± 0.050) 0.5671 (± 0.098) 0.5966 (± 0.073) 0.6861 (± 0.034)

D10 0.7450 (± 0.089) 0.5874 (± 0.144) 0.6760 (± 0.115) 0.7442 (± 0.099)

PR AUC

Dataset CDO BL-SMOTE DB-SMOTE MAHAKIL

D1 0.9821 (± 0.062) 0.9778 (± 0.067) 0.9801 (± 0.065) 0.9815 (± 0.061)

D2 0.8279 (± 0.062) 0.8437 (± 0.062) 0.8268 (± 0.067) 0.8175 (± 0.065)

D3 0.9981 (± 0.003) 0.9978 (± 0.003) 0.9985 (± 0.002) 0.9981 (± 0.003)

D4 0.9803 (± 0.039) 0.9769 (± 0.039) 0.9796 (± 0.036) 0.9798 (± 0.038)

D5 0.9934 (± 0.004) 0.9927 (± 0.005) 0.9924 (± 0.005) 0.9925 (± 0.006)

D6 0.9559 (± 0.094) 0.9662 (± 0.068) 0.9614 (± 0.082) 0.9560 (± 0.094)

D7 0.8391 (± 0.056) 0.8222 (± 0.060) 0.8182 (± 0.060) 0.8238 (± 0.064)

D8 0.9990 (± 0.001) 0.9988 (± 0.002) 0.9989 (± 0.001) 0.9989 (± 0.001)

D9 0.8291 (± 0.062) 0.8433 (± 0.062) 0.8259 (± 0.067) 0.8175 (± 0.065)

D10 0.9578 (± 0.057) 0.9488 (± 0.066) 0.9517 (± 0.059) 0.9571 (± 0.056)

ECTA 2022 - 14th International Conference on Evolutionary Computation Theory and Applications

Table 5: performance results of mean and standard error across datasets with 10 minority instances. Bold numbers indicate

the mean of method performance is the best among all comparable methods.

Dataset CDO BL-SMOTE DB-SMOTE MAHAKIL

D1 0.9465 (± 0.021) 0.9358 (± 0.029) 0.9453 (± 0.024) 0.9417 (± 0.025)

D2 0.3799 (± 0.085) 0.2176 (± 0.111) 0.3818 (± 0.081) 0.4434 (± 0.148)

D3 0.8490 (± 0.115) 0.8571 (± 0.105) 0.8725 (± 0.119) 0.8548 (± 0.130)

D4 0.8586 (± 0.082) 0.8438 (± 0.075) 0.8617 (± 0.077) 0.8330 (± 0.089)

D5 0.6509 (± 0.086) 0.6828 (± 0.093) 0.6763 (± 0.076) 0.6456 (± 0.101)

D6 0.8549 (± 0.070) 0.8187 (± 0.089) 0.8240 (± 0.081) 0.8672 (± 0.062)

D7 0.4398 (± 0.108) 0.2822 (± 0.121) 0.3788 (± 0.116) 0.4114 (± 0.118)

D8 0.9753 (± 0.029) 0.9510 (± 0.063) 0.9672 (± 0.037) 0.9716 (± 0.035)

D9 0.3980 (± 0.078) 0.2125 (± 0.114) 0.3846 (± 0.078) 0.4389 (± 0.141)

D10 0.6769 (± 0.074) 0.5128 (± 0.137) 0.6413 (± 0.091) 0.6525 (± 0.099)

G-Means

Dataset CDO BL-SMOTE DB-SMOTE MAHAKIL

D1 0.9625 (± 0.014) 0.9514 (± 0.027) 0.9588 (± 0.019) 0.9580 (± 0.020)

D2 0.5267 (± 0.062) 0.3454 (± 0.159) 0.5372 (± 0.055) 0.6261 (± 0.062)

D3 0.9128 (± 0.101) 0.8908 (± 0.094) 0.9073 (± 0.106) 0.9194 (± 0.096)

D4 0.9301 (± 0.044) 0.9122 (± 0.057) 0.9332 (± 0.042) 0.9188 (± 0.045)

D5 0.8918 (± 0.044) 0.8955 (± 0.060) 0.8975 (± 0.053) 0.8905 (± 0.051)

D6 0.8882 (± 0.066) 0.8516 (± 0.080) 0.8597 (± 0.074) 0.9029 (± 0.049)

D7 0.5905 (± 0.079) 0.4327 (± 0.107) 0.5432 (± 0.078) 0.5765 (± 0.080)

D8 0.9927 (± 0.011) 0.9675 (± 0.055) 0.9787 (± 0.030) 0.9889 (± 0.018)

D9 0.5310 (± 0.064) 0.3476 (± 0.156) 0.5364 (± 0.054) 0.6258 (± 0.061)

D10 0.7691 (± 0.068) 0.6105 (± 0.119) 0.7135 (± 0.071) 0.7467 (± 0.088)

PR AUC

Dataset CDO BL-SMOTE DB-SMOTE MAHAKIL

D1 0.9937 (± 0.004) 0.9855 (± 0.015) 0.9911 (± 0.008) 0.9919 (± 0.007)

D2 0.8099 (± 0.063) 0.7950 (± 0.071) 0.8131 (± 0.055) 0.8064 (± 0.059)

D3 0.9903 (± 0.023) 0.9888 (± 0.024) 0.9894 (± 0.023) 0.9882 (± 0.027)

D4 0.9838 (± 0.029) 0.9817 (± 0.028) 0.9825 (± 0.027) 0.9826 (± 0.028)

D5 0.9902 (± 0.020) 0.9901 (± 0.017) 0.9908 (± 0.016) 0.9893 (± 0.021)

D6 0.9609 (± 0.092) 0.9655 (± 0.075) 0.9625 (± 0.084) 0.9625 (± 0.086)

D7 0.8233 (± 0.065) 0.8139 (± 0.063) 0.8094 (± 0.069) 0.8127 (± 0.067)

D8 0.9923 (± 0.032) 0.9925 (± 0.030) 0.9923 (± 0.031) 0.9923 (± 0.032)

D9 0.8134 (± 0.062) 0.7963 (± 0.070) 0.8139 (± 0.054) 0.8085 (± 0.059)

D10 0.9586 (± 0.054) 0.9449 (± 0.064) 0.9535 (± 0.057) 0.9563 (± 0.053)

Cluster-based Diversity Over-sampling: A Density and Diversity Oriented Synthetic Over-sampling for Imbalanced Data

Table 6: performance results of Mann-Whitney test across datasets with 5% imbalance levels. Each figure reports the

frequency that the selected method is significantly better than its comparable methods within the same dataset (p < 0.05).

Dataset CDO BL-SMOTE DB-SMOTE MAHAKIL Dataset CDO

L-SMOTE

B-SMOTE MAHAKIL

D1 3 0 0 1 D6 2 0 0 2

D2 0 0 1 3 D7 3 0 1 1

D3 0 0 0 0 D8 0 0 0 0

D4 1 1 1 0 D9 0 0 0 3

D5 0 3 0 0 D10 2 0 1 1

G-Means

CDO BL-SMOTE DB-SMOTE MAHAKIL Dataset CDO

L-SMOTE

B-SMOTE MAHAKIL

D1 2 0 0 1 D6 2 0 1 2

D2 0 0 1 3 D7 2 0 1 1

D3 0 0 1 1 D8 3 0 1 1

D4 1 0 1 0 D9 0 0 1 3

D5 0 3 0 0 D10 2 0 1 1

PR-AUC

Dataset CDO BL-SMOTE DB-SMOTE MAHAKIL Dataset CDO

L-SMOTE

B-SMOTE MAHAKIL

D1 1 0 1 1 D6 0 0 0 0

D2 1 3 1 0 D7 3 0 0 0

D3 0 0 0 0 D8 0 0 0 0

D4 0 0 0 0 D9 1 3 1 0

D5 0 0 0 0 D10 0 0 0 1

Table 7: performance results of Mann-Whitney test across datasets with 10 minority instances. Each figure reports the

frequency that the selected method is significantly better than its comparable methods within the same dataset (p < 0.05).

Dataset CDO BL-SMOTE DB-SMOTE MAHAKIL Dataset CDO BL-SMOTE

B-SMOTE MAHAKIL

D1 1 0 1 0 D6 2 0 0 2

D2 1 0 1 3 D7 3 0 1 2

D3 0 0 2 0 D8 2 0 1 1

D4 2 0 2 0 D9 1 0 1 3

D5 0 2 2 0 D10 1 0 1 1

G-Means

CDO BL-SMOTE DB-SMOTE MAHAKIL Dataset CDO BL-SMOTE

B-SMOTE MAHAKIL

D1 2 0 1 0 D6 2 0 0 2

D2 1 0 1 3 D7 2 0 1 2

D3 0 0 1 1 D8 2 0 0 2

D4 2 0 2 0 D9 1 0 1 3

D5 0 0 0 0 D10 2 0 1 1

PR-AUC

Dataset CDO BL-SMOTE DB-SMOTE MAHAKIL Dataset CDO BL-SMOTE

B-SMOTE MAHAKIL

D1 1 0 1 1 D6 0 0 0 0

D2 1 0 0 0 D7 3 0 0 0

D3 0 0 0 0 D8 0 0 0 1

D4 1 0 0 0 D9 1 0 0 0

D5 0 1 1 0 D10 0 0 0 0

The Mann-Whitney test is performed for each

pairing of all 4 comparable methods. This implies that

there are 6 total combinations of pairings available.

Table 6 and 7 displays the results from the test, where

each figure represents the frequency that the specified

method is statistically better than its comparable

method.

From Table 6, CDO performs the best across 10

datasets where there is a 5% imbalanced ratio. It

statistically outperforms its comparable algorithms

on 11 occasions based on F1, 12 occasions based on

ECTA 2022 - 14th International Conference on Evolutionary Computation Theory and Applications

G-Means and 6 occasions based on PR-AUC.

MAHAKIL comes next in line in terms of

performance, where it statistically outperforms its

comparable methods on 11 occasions based on F1, 13

occasions based on G-Means and only 2 occasions

based on PR-AUC. Both BL-SMOTE and DB-

SMOTE only statistically outperform their

comparable methods on 4 occasions using F1. DB-

SMOTE performs significantly better when evaluated

using G-Means, where it outperformed its

comparable methods on 8 occasions. BL-SMOTE

comes last as it only statistically outperformed its

comparable methods on 3 occasions based on G-

Means and on 6 occasions based on PR-AUC.

From Table 7, CDO is the best performing

algorithm for 10 minority instances. It statistically

outperformed its comparable algorithms on 13

occasions based on F1, 14 occasions based on G-

Means and 7 occasions based on PR-AUC. For the

remaining algorithms, MAKAHIL is the 2nd best

performing algorithm as it statistically outperformed

its comparable methods on 12 occasions using F1, 14

occasions using G-Means and 2 occasions using PR-

AUC. DB-SMOTE comes 3rd, as it statistically

outperformed its comparable methods on 12

occasions using F1, 8 occasions using G-Means and

2 occasions using PR-AUC. BL-SMOTE comes last

as it barely outperformed other methods (2 occasions

using F1, 0 occasion on G-Means and 1 occasion on

PR-AUC).

6 DISCUSSIONS

As shown in the statistical test results, although CDO

outperforms MAHAKIL in most cases, CDO and

MAHAKIL have superior performance results when

compared to BL-SMOTE and DB-SMOTE. This can

be explained by their better ability to capture more

information when constructing minority generation

region. Both CDO and MAHAKIL consider the entire

minority class distribution and generating instances

within the boundaries of the identified data generation

region diversely. In contrast, SMOTE-based methods

typically create synthetic instances using linear

interpolation.

If we evaluate the statistical significance of

CDO’s performance, it has better performance

compared to MAHAKIL when minority instances

become more sparse. This is due to the nature of

MAHAKIL algorithm that it only performs well when

minority data distribution is convex and when there

are sufficient number of minority instances

(Khorshidi & Aickelin, 2021). In addition,

MAHAKIL algorithm does not consider clusters

within datasets, which results in a broader generation

region for minority instances and leads to a higher

false positive rate. The main reason for superiority of

CDO in comparison with MAHAKIL in terms of PR-

AUC is that MAHAKIL generates synthetic

instances, even though few, in the majority space (see

Figure 1). This leads to lower precision that can be

picked up by PR-AUC.

7 CONCLUSIONS

In this study, our key objective is to design an

algorithm which generates diversified synthetic

instances within the minority class while considering

the distribution of the minority data space. We

incorporate diversity optimization which optimises

both similarity to minority instances and diversity of

synthetic instances. The proposed algorithm first

utilises clustering technique to identify the

boundaries for the generation of minority instances

and preserve similarity between minority instances.

Subsequently, diversity optimization is incorporated

to promote diversity within clusters. The proposed

method CDO is evaluated on 10 real-world datasets,

and it has statistically superior performance to its

comparable methods. Its superior performance can be

attributed to its ability to identify the minority space

for synthetic data generation and its ability to obtain

optimal spread of generated instances due to genetic

algorithm. The proposed algorithm is evaluated on 2

class imbalance datasets. For future research, we

extend CDO to address multi-class imbalance

problems.

REFERENCES

Ali, A., Shamsuddin, S. M., & Ralescu, A. L. (2013).

Classification with class imbalance problem. Int. J.

Advance Soft Compu. Appl, 5(3).

Bennin, K. E., Keung, J., Phannachitta, P., Monden, A., &

Mensah, S. (2017). Mahakil: Diversity based

oversampling approach to alleviate the class imbalance

issue in software defect prediction. IEEE Transactions

on Software Engineering, 44(6), 534-550.

Chawla, N. V. (2009). Data mining for imbalanced datasets:

An overview. Data mining and knowledge discovery

handbook, 875-886.

Chawla, Bowyer, K. W., Hall, L. O., & Kegelmeyer, W. P.

(2002). SMOTE: synthetic minority over-sampling

technique. Journal of artificial intelligence research,

16, 321-357.

Cluster-based Diversity Over-sampling: A Density and Diversity Oriented Synthetic Over-sampling for Imbalanced Data

Ester, M., Kriegel, H. P., Sander, J., & Xu, X. (1996,

August). A density-based algorithm for discovering

clusters in large spatial databases with noise. In kdd

(Vol. 96, No. 34, pp. 226-231).

Japkowicz, N., & Stephen, S. (2002). The class imbalance

problem: A systematic study. Intelligent data analysis,

6(5), 429-449.

Khorshidi, H. A., & Aickelin, U. (2021). Constructing

classifiers for imbalanced data using diversity

optimisation. Information Sciences, 565, 1-16.

Lim, P., Goh, C. K., & Tan, K. C. (2016). Evolutionary

cluster-based synthetic oversampling ensemble (eco-

ensemble) for imbalance learning. IEEE transactions

on cybernetics, 47(9), 2850-2861.

Muñoz, M. A., Villanova, L., Baatar, D., & Smith-Miles,

K. (2018). Instance spaces for machine learning

classification. Machine Learning, 107(1), 109-147.

Protopapa, K. L., Simpson, J. C., Smith, N. C. E., &

Moonesinghe, S. R. (2014). Development and

validation of the surgical outcome risk tool (SORT).

Journal of British Surgery, 101(13), 1774-1783.

Sasaki, Y. (2007). The truth of the F-measure. Teach tutor

mater, 1(5), 1-5.

Sharma, S., Bellinger, C., Krawczyk, B., Zaiane, O., &

Japkowicz, N. (2018, November). Synthetic

oversampling with the majority class: A new

perspective on handling extreme imbalance. In 2018

IEEE international conference on data mining (ICDM)

(pp. 447-456). IEEE.

Tallo, T. E., & Musdholifah, A. (2018, August). The

implementation of genetic algorithm in smote

(synthetic minority oversampling technique) for

handling imbalanced dataset problem. In 2018 4th

international conference on science and technology

(ICST) (pp. 1-4). IEEE.

Thabtah, F., Hammoud, S., Kamalov, F., & Gonsalves, A.

(2020). Data imbalance in classification: Experimental

evaluation. Information Sciences, 513, 429-441.

Ulrich, T., & Thiele, L. (2011, July). Maximizing

population diversity in single-objective optimization. In

Proceedings of the 13th annual conference on Genetic

and evolutionary computation (pp. 641-648).

Yang, Y. Y., Akbarzadeh HA Khorshidi, H., Aickelin, U.

U., Nevgi, A. A., & Ekinci, E. E. (2021, February). On

the Importance of Diversity in Re-Sampling for

Imbalanced Data and Rare Events in Mortality Risk

Models. In 2021 Australasian Computer Science Week

Multiconference (pp. 1-8).

ECTA 2022 - 14th International Conference on Evolutionary Computation Theory and Applications