
Synthesis of an Evolutionary Fuzzy Multi-objective Energy Management
System for an Electric Boat
Antonino Capillo
a
, Enrico De Santis
b
, Fabio Massimo Frattale Mascioli
c
and Antonello Rizzi
d
Department of Information Engineering, Electronics and Telecommunications,
University of Rome “La Sapienza”, Rome, Italy
Keywords:
Energy Management System, Fuzzy System, Evolutionary Computation, Genetic Algorithm, Electric Vehicle,
e-Boat.
Abstract:
Even though it is known that Renewable Energy Sources (RESs) are necessary to face Climate Change and
pollution, technology is still in a developement phase, aiming at improving energy exploitation from RESs, as
these type of sources suffer from low energy density and variability over time. Thus, proper ICT infrastructures
equipped with a robust software, i.e., Energy Management System (EMS), are needed to ensure that Renewable
Energy (RE) does not go to waste. Relatively small local electrical grids called Microgrids (MGs) represent
the EMS ecosystem, since their main features are the proximity between generation and loads and the presence
of Energy Storage Systems (ESSs) adopted to recover surplus energy. The Vehicle-to-Grid (V2G) paradigm
helps to realize the Smart City, which in substance is an interconnection of MGs hosting electrical vehicles for
an efficient energy management at a larger scale. In this context, e-boats have only recently been considered.
Hence, in this work a Multi-Objective (MO) EMS is synthesized for an e-boat docked in a small Microgrid
(PV generator and ESS) with the aim of maximizing the charging time of the e-boat ESS and spending as little
as possible both for energy purchase and also in terms of ESS wear. A Fuzzy Inference System - Hierarchical
Genetic Algorithm (FIS-HGA) is used to achieve the Pareto Front, with the HGA that is in charge of optimizing
the FIS parameters. Results laid to a balanced trade-off between the two objectives, since the e-boat ESS is
almost fully charged in a reasonable time and with a low cost, compatible with people transportation. Last but
not least, the inference process of a FIS is easily interpretable, in the perspective of an Explainable AI.
1 INTRODUCTION
Renewable Energy Sources (RESs) become a refer-
ence for Humankind day by day, being the RESs en-
ergy production increased since 2010, with a rise es-
timation of about 2.7 times by 2025 (Ellabban et al.,
2014). Nevertheless, some critical aspects of RESs
must be taken into account, aiming at a sustainable
clean energy exploitation. First of all, RESs en-
ergy density is very small, if compared to fossil fu-
els (Layton, 2008). Secondly, RESs are very variable
over time, such that it is difficult to predict clean en-
ergy generation. Since a sustainable energy genera-
tion comes with efficiency and stability, the aforemen-
tioned issues deserve a lot of attention. Operators do
not have control over the RESs generation because it
a
https://orcid.org/0000-0002-6360-7737
b
https://orcid.org/0000-0003-4915-0723
c
https://orcid.org/0000-0002-3748-5019
d
https://orcid.org/0000-0001-8244-0015
depends on geographic location (e.g. it is very diffi-
cult to produce enough solar energy in the shade of an
hill); moreover, assuming to be in a energy-profitable
location, even though PV generators are modular, the
area occupied by panels could not be enough extended
either for geographical, economical or space issues.
If, in addition, the unpredictable nature of RESs is
taken into account, it can be stated that RESs energy
is precious and not even a kWh must be wasted. As a
consequence, it is logical to install RESs generators as
mush close as possible to the loads (es. PV panels on
the roof of a residential building), with the purpose
of avoiding energy transportation losses, in contrast
with centralized energy generation (e.g. thermoelec-
tric power plants), which consists in high energy den-
sity and power plants remote locations. According
to the above logic, also saving excess clean energy
is mandatory, so Energy Storage Systems (ESSs), are
needed. That leads to relatively small electrical grids
or Microgrids (MGs) that fundamentally consist of
RESs generators and load, which are close together,
Capillo, A., De Santis, E., Mascioli, F. and Rizzi, A.
Synthesis of an Evolutionary Fuzzy Multi-objective Energy Management System for an Electric Boat.
DOI: 10.5220/0011527800003332
In Proceedings of the 14th International Joint Conference on Computational Intelligence (IJCCI 2022), pages 199-208
ISBN: 978-989-758-611-8; ISSN: 2184-3236
Copyright © 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
199

ESSs and a link to the Main Grid for service stability
(Badal et al., 2019). That said, even if energy losses
can be avoided, efficiency must further be improved.
In fact, if it was possible to predict RESs energy gen-
eration with enough accuracy, energy flows between
the MG nodes could be optimized. For example, as-
suming that the ESS is completely discharged, if PV
generation in the current hour was much larger than
load demand and, according to the future hour pre-
diction, PV generation was close to zero, it could be
better to store the current-hour excess energy in the
ESS than to sell it to the Main Grid for profit, since
in the next hour it would be necessary to buy energy
from the Main Grid, generally at a much higher price
than in the current hour. In other words, thanks to
an accurate prediction, it was chosen to store energy
for future consumption, being that the best one among
the available alternatives: an optimization task is per-
formed. Thus, when the problem at hand counts much
more variables and bounds, a proper prediction and
optimization software, the Energy Management Sys-
tem (EMS) software, is needed for MG optimal en-
ergy flows (Duman et al., 2021). In the MGs con-
text, Zero Emission Vehicles (ZEVs) ed hybrid vehi-
cles can be seen as nodes, since they can store en-
ergy in their inner ESS and also provide energy to
a MG (for example, a residential building) (Slama,
2021). Consequently, with the ZEVs and hybrid ve-
hicles market expansion, it is interesting to synthesize
EMS algorithms that also consider this kind of nodes.
Even if many works in literature treat ZEVs or hybrid
vehicles energy management in MGs (Alsharif et al.,
2021), research about electric or hybrid boats is rel-
atively young (Balestra and Schjølberg, 2021). With
reference to works focused on e-boats or hybrid boats
themselves, (Rafiei et al., 2021) considers fuel con-
sumption and battery State of Charge (SoC), aiming at
maximizing energy efficiency. In the context of MGs,
(
¨
Ozdemir et al., 2021) is very interesting, as it takes
into account a set of docked hybrid boats. More in de-
tail, the dock consists of RESs generators, Main Grid
link and an Hydrogen storage unit while each boat is
equipped with a fuel cell and an ESS. The overall cost
for charging the hybrid boats (e.g. the purchased en-
ergy cost from the Main Grid) is minimized.
Both for building and docked e-boats EMSs (Xiang
and Yang, 2021),(Hafiz Abdul Muqeet et al., 2021),
Computational Intelligence (CI) and Machine Learn-
ing (ML) techniques are often preferred to exact al-
gorithms for a reasonably faster problem solving, spe-
cially when the problem at hand is very complex. Par-
ticle Swarm Optimization (PSO) (Pozna et al., 2022),
Evolutionary Computation (EC) algorithms (Capillo
et al., 2018), Artificial Neural Networks (ANNs)
(Zamfirache et al., 2022) and Market-Based algo-
rithms (Palm, 2004) are among the most relevant
paradigms. Particularly relevant is the Explainable AI
topic (Li et al., 2022), according to which AI should
provide explanations about the way it solves a prob-
lem, just like a human would do. This way, AI could
be more reliable. Some works like (De Santis et al.,
2013), (De Santis et al., 2017) rely on Fuzzy Logic
for achieving grey-box AI models, since Term Sets
and Fuzzy Rules try to replicate human consciousness
during problem solving.
In this work, a Multi-Objective (MO) optimization
problem for a docked full electric boat equipped with
a PV roof and an ESS is faced, where Pareto Front
(PF) trade-off solutions are found aiming at recharg-
ing the e-boat ESS as soon as possible and at mini-
mizing costs. The PV-roof e-boat model and the dock
design come from the “LIFE for Silver Coast” Eu-
ropean Project (LIFE16 ENV/IT/000337), hereinafter
referred to as “LIFE Project”, whose aim is to realize
a sustaitnable mobility system in Tuscany (IT) only
with electrical vehicles. An AI “explainable” grey-
box EMS, the Fuzzy Inference System - Hierarchical
Genetic Algorithm (FIS-HGA) is synthesized, based
on a FIS whose parameters are optimized by a Ge-
netic Algorithm (GA). The purpose is to synthesize a
grey-box AI model for this specific application. The
EMS design is presented in Sec. 2; the dataset and
the problem formulation are shown in detail in Sec. 3
and Sec. 4, respectively; the optimization procedure
is explained in Sec. 5; the algorithm tests and results
are presented in Sec. 6.
2 EMS DESIGN
2.1 The MG Architecture
In this section, the MG architecture is defined, to-
gether with a simplified version, considering some as-
sumptions described below.
2.1.1 The Basic MG Architecture
The basic MG architecture, as shown in Fig. 1, rep-
resents the docked e-boat with the engine off, in the
generic timeslot k. On the left side, all the dock ele-
ments are enclosed in an orange rectangle, while the
elements related to the e-boat are enclosed in a green
rectangle.
Node N represents the Main Grid, G is the PV gener-
ator, S is the dock ESS, S
0
is the e-boat ESS and G
0
is
the e-boat PV roof. The elements named as BMS and
EMS stand for “Battery Management System” and
FCTA 2022 - 14th International Conference on Fuzzy Computation Theory and Applications
200

G
S
EMS
BMS
E
k
NS'
E
k
GS'
E
k
SS'
Dock
E-boat
G'
E
k
G'S'
p
k
E
k
G*
E
k
G'*
E
k
G'N
E
k
GS'
E
k
GN
N
S'
BMS
Figure 1: The basic MG architecture.
“Energy Management System”, respectively. Square
nodes are bidirectional, since energy can both flow
from and to them. Circle nodes can only provide or
receive energy from other nodes. Regardless a node
is bidirectional or not, it can not both absorb/store
energy from or generate/provide energy to the other
nodes, in the same timeslot k. The BMS, which mea-
sures the State of Energy (SoE) of the ESS, is simu-
lated in a workstation, running also the FIS optimiza-
tion procedure. Energy flows are drawn as solid black
lines in Fig. 1. The amount of energy which flows
from the generic node i to the generic node j is indi-
cated as E
i j
k
. Thus, for example, E
NS
0
k
is the amount
of energy which flows from N to S
0
, during timeslot.
The nodes G and G
0
primarily meet the energy needs
of S
0
. In fact, conveying energy from S, assuming that
the dock ESS had been charged by G or G
0
, would
involve an additional operational cost due to the dock
ESS wear. Furthermore, it would be useless to route
the energy produced by G or G
0
to the Main Grid,
since that energy is primarily necessary to the e-boat
ESS. As a consequence, S and N should not receive
energy from S
0
but only from G and G
0
. The MG in-
formation flows, drawn as dotted black lines in Fig. 1,
are the following: the whole energy produced by G in
the generic timeslot E
G
∗
k
, the whole energy produced
by G
0
in the generic timeslot E
G
0
∗
k
, the Main Grid en-
ergy purchase price p
k
and the EMS decision variable
α, which controls whether S
0
receives the difference
between its energy demand and the whole PV pro-
duction (G and G
0
) from N or from S. It is assumed
that suitable smart meters collect the above mentioned
information.
2.1.2 Simplified MG Architecture
According to the aforementioned considerations, S
0
,
G and G
0
can be grouped in a single node S
0
G
0
G, as
in 2. Thus, the overall PV energy production in the
S
EMS
BMS
E
k
N
E
k
S
p
k
E
k
G+G'
N
S'G'G
BMS
Figure 2: The simplified MG architecture.
generic timeslot E
G+G
0
k
and p
k
are the two inputs of
the EMS and the decision variable α is the system
output.
2.2 System Objectives
The EMS is in charge of optimizing the MG energy
flows for achieving both the minimum overall charg-
ing cost and the minimum charging time of the e-
boat ESS. The quicker the charging process is, the
more stressed the ESS will be and, as a consequence,
the more expensive the charging process will be be-
cause of the ESS wear cost. Moreover, the quicker
the charging process is, the higher the probability of
buying energy from the Main Grid in k is, since S, G
and G
0
could not provide enough energy to meet the
e-boat demand. For the above reasons, the presented
objectives are in contrast to each other, hence the one
at hand is a Multi-Objective Pareto Front problem to
face.
2.3 MG Sizing
According to the LIFE Project, the area dedicated to
the PV panels is about 15 [mq]. Thanks to the Euro-
pean Commission PVGIS tool (EC, 2020), an estima-
tion of the PV generator peak power can be done by
the (1):
P = 1
kW p
m
2
Aη (1)
where P is the PV generator peak power, in [kWp];
A is the area dedicated to the PV panels, in [mq] and
η is the PV panels efficiency. The (1) is generally
used to assess the PV panels peak power when it has
been not provided by the manufacturer yet. Thus, the
peak power is calculated assuming that the PV pan-
els generate a fraction (given by the efficiency) of the
power it would generate under the Standard Condi-
tions (i.e. 1000 W/m2 solar irradiance, a module tem-
perature of 25° C and a solar spectrum corresponding
to an air mass of 1.5). As specified in (Departement of
Energy, 2016), the crystalline Silicon PV panels effi-
Synthesis of an Evolutionary Fuzzy Multi-objective Energy Management System for an Electric Boat
201

ciency is about 0.25 for single-crystal cells while is
roughly 0.20 for multi-crystalline cells. With the aim
of exploiting solar irradiation well throughout the day,
multi-crystalline cells are to be preferred so that η is
set to 0.20. Therefore, the PV generator peak power
is 3 [kWp]. By a similar reasoning, the e-boat PV roof
peak power is about 1, 5 [kWp], since the area of the
PV panels is 8 [mq]. The dock ESS capacity is set
to be equal to the e-boat ESS capacity, which is de-
signed to be 50 [kWh]. This choice guarantees that
the e-boat ESS could be always fully charged when
docked, being the initial dock ESS SoE the 80% of its
capacity while the initial e-boat ESS SoE the 20% of
the same quantity. The ESS (both for dock and e-boat)
charging/discharging energy bound is set to 5 [kWh],
according to the Tesla Powerwall technical features
(Tesla, 2019).
3 DATASET
The dataset consist in hourly PV generation and Main
Grid energy purchase prices figures for 2020. More
detailed information about data and sources are re-
ported below.
3.1 PV Generation
Through the PVGIS tool (EC, 2020), it is possible to
achieve an estimation of the hourly PV production
data for a given geographic position, which for the
LIFE Project is 44.442
◦
N,11.215
◦
W (Orbetello, Tu-
cany, IT). PVGIS tool input values for the dock PV
generator include the peak power of about 3 kWp,
system loss (e.g. from cables) of about 14% and
slope/azimuth figures.
In particular, system loss (for example, losses in ca-
bles, power inverters and dirt on the PV modules) to-
gether with the Slope (angle of the PV modules from
the horizontal plane) are set by default, while the Az-
imuth (the angle of the PV modules relative to South)
is set for a perfect orientation to South. PVGIS tool
input values for the dock PV generator include the
peak power of about 1.5 kWp, system loss (e.g. from
cables) of about 14% and slope/azimuth figures,
whereslope is set to 0 degrees because the e-boat PV
roof is in a fixed position, parallel to the deck.
3.2 Energy Purchase Prices
The Main Grid energy purchase prices come from
the Open Power System Data (Z
¨
urich, 2020). More
precisely, data pertain the Center of Italy (where the
LIFE Project area is located), for 2020.
3.3 Dataset Analysis
Figures about energy purchase prices for 2020 are
available only until 1
st
October 2020, therefore, the
dataset consists of nine months of data, until the end
of September 2020. Since the e-boat is designed to
operate mainly during peak season, the dataset times-
pan is acceptable. No other lack of data is observed.
4 PROBLEM FORMULATION
The problem formulation consists of the following
equations:
min
k,α ε R
T
∑
k=1
(1 − SoE
0
k
)
T
,
(2)
min
k,α ε R
T
∑
k=1
(w
S
0
k
+ w
S
k
+ c
buy
k
)
T
(3)
where:
T ≥ k ≥ 0 (4)
1 ≥ α ≥ 0 (5)
1 ≥ SoE
0
k
≥ 0 (6)
1 ≥ SoE
k
≥ 0 (7)
w
S
0
k
=
SoE
0
k
− 0.5
0.5
12
(8)
w
S
k
=
SoE
k
− 0.5
0.5
12
(9)
c
buy
k
=
(
0 i f E
N
k
≤ 0
p
k
E
N
k
i f E
N
k
> 0
(10)
E
N
k
+ E
S
k
+ E
S
0
GG
0
k
= 0 (11)
E
S
0
k
=
α
E
S
0
max
k
0.49
− E
S
0
max
k
i f α ≤ 0.49
(α − 0.50)
E
S
0
max
k
0.50
i f α ≥ 0.50
(12)
E
N
k
=
−E
S
0
GG
0
k
i f α ≤ 0.49
and |E
S
0
GG
0
k
| < E
Smax
E
Smax
− |E
S
| i f α ≥ 0.50
and |E
S
0
GG
0
k
| ≥ E
Smax
0 i f α ≥ 0.50
and |E
S
0
GG
0
k
| < E
Smax
(13)
FCTA 2022 - 14th International Conference on Fuzzy Computation Theory and Applications
202

E
S
k
=
0 i f α ≤ 0.49
−E
S
0
GG
0
k
i f α ≥ 0.50
and |E
S
0
GG
0
k
| < E
Smax
−E
Smax
i f α1 ≥ 0.50
and |E
S
0
GG
0
k
| ≥ E
Smax
(14)
E
S
0
max
k
= E
Smax
k
= 5 (15)
C
0
= C = 50 (16)
SoE
0
k
= SoE
0
k−1
−
E
S
0
k
C
0
(17)
SoE
k
= SoE
k−1
−
E
S
k
C
(18)
The EMS minimizes two Objective Functions (OFs).
The fist OF, given in (2), is the sum of the e-boat
ESS capacity fractions that are full of energy, over
the whole dataset (T is the total number of times-
lots k and SoE
0
k
is the e-boat ESS State of Energy,
bounded as in (6). Minimizing the OF (2) means
maximizing the number of timeslots the e-boat ESS
is full, i.e. minimizing the ESS charging time. The
second OF is the sum of the overall MG costs over
the whole dataset, i.e. the e-boat ESS wear cost w
S
0
k
given by (8), the dock ESS wear cost w
S
k
given by
(9) and the Main Grid energy purchase c
buy
k
given by
(10). The ESS wear cost formulation comes from
(Ferrandino et al., 2020) such that the more the SoE
deviates from the 50% of the capacity the more the
battery is stressed. The energy purchase cost is con-
sidered everytime there is an energy flow from the
Main Grid, that fore every k where E
N
k
is positive.
In fact, conventionally, a positive amount of energy
for a given node of the MG means that it is provid-
ing energy, while a negative amount means that it is
receiving energy. Thus, when E
N
k
is positive, c
buy
k
is
the product of E
N
k
for the energy purchase price at k.
The MG energy balance is guaranteed by (11). The
EMS output (or decision variable) α is a real-valued
number that is rounded to the second decimal place.
It is in charge of deciding both the amount of energy
to store in the e-boat ESS in k, as shown in (12), and
the node the e-boat ESS can mainly receive energy
from, by ( 13) and (14). More precisely, if α is less
than or equal to 0.49, the e-boat ESS stores energy
never over its technical limit (E
S
0
max
k
) by (12) and it
charges itself primarily from G and G
0
before relying
on N by (13) (i.e. E
S
0
GG
0
k
is negative). With the afore-
mentioned condition on α in k, S does not exchange
any energy. On the other hand, if α is greater than or
equal to 0.50, the e-boat ESS stores energy never over
its technical limit (E
Smax
k
) by (12) and it charges itself
primarily from G and G
0
before relying on S by (14)
(i.e. E
S
0
GG
0
k
is negative). That said, if the amount of
energy E
S
0
GG
0
k
exceeds E
Smax
k
, the difference between
the former and the latter is provided by N, by (13).
With similar reasoning, again by (13) and (14), S and
N receive energy from S
0
G
0
G, if the energy balance of
the former is positive. The values of E
S
0
max
k
and E
Smax
k
are set by (15), according to Section 2.3, as it is for
the ESSs capacity, by (16). Furthermore, timeslot by
timeslot, the SoE of the ESSs is updated by (17) and
(18).
5 THE FIS-GA OPTIMIZATION
In a FIS-GA optimization (De Santis et al., 2013), (De
Santis et al., 2017), the FIS parameters are properly
set by a GA to achieve the problem objectives. In
the following, more details are given about the opti-
mization procedure performed in this work. Accord-
ing to the FIS-HGA paradigm (De Santis et al., 2017),
the GA can control which Rules to delete in the Rule
Base. This feature is useful fore achieving the core of
the most relevant Rules for the problem at hand. Each
one of these new Genes represents the presence or ab-
sence of a MF such that, if the MF is absent, the Rules
with that MF are deleted. The aforementioned Genes
are called Hierarchical Genes. The generic HGA In-
dividual can be represented as follows:
I
h
= [~g
h
, ~g
a
, ~g
MF
, ~g
c
, ~g
w
] (19)
where ~g
h
is the vector of the binary Hierarchical
Genes, ~g
a
is the vector of Antecedents,
~
g
M
F encodes
the MF abscissas, ~g
c
is the vector of Consequents and
~g
h
encodes Rule Weights.
5.1 Design of the MO-FIS-HGA
Algorithm
5.1.1 Optimization Workflow
A MO-FIS-HGA optimization algorithm returns the
optimal FIS models that belong to the Pareto Front.
In fact, as specified in Subsection 2.2, two OFs, in
contrast to each other, are considered. The optimiza-
tion workflow is presented in Fig. 3.
5.1.2 FIS Design
A Mamdami-type FIS consists of 25 Rules in the Rule
Base and a five MFs Term set, for both the two Inputs
Synthesis of an Evolutionary Fuzzy Multi-objective Energy Management System for an Electric Boat
203

START
GA encoding
&
initialization
GA decoding
OF evaluation
process
OF evaluation
process
...
OF evaluation
process
...
GA Selection
END
GA Crossover
& Mutation
OF evaluation
process
far all Individuals
N
k Simulation timeslot
Population bounds
Base FIS structure
Initial Population
Individual 1
FIS structure
Individual N
FIS structure
k = 1
sum = 0
k <= T?
True
k++
Output ( )
False
FIS evaluation
Energy
balance
sum = sum +
E
OF = sumOF = sum OF = sumOF = sum OF = sum
New Population
Initial Population-FO
matrix
Old Population
Individual ...
FIS structure
Population size
ΔT
Time horizon (dataset length)
k+1
Input (E
GG'
; p
k+1
)
α
k+1
check and
SoE update
Max number of
genera
ons
reached ?
True
False
GA Elitism
Pareto Front
(Optimized FIS
structures)
Figure 3: Optimization flowchart.
and the Output. The number of Rules comes from
(20):
n
R
= n
n
In
MFs
(20)
where n
R
is the number of Rules, n
In
is the number of
Inputs (2, in this case) and n
MFs
is the number of MFs
in the Term Set (5 in this case).
5.1.3 HGA Design
The MO-HGA encodes Consequents and Weights as
Genes of its Individuals and the generic current Popu-
lation evolves, generation by generation, with the aim
of finding a PF trade-off between the two OFs. In-
spired by (Dietz et al., 2008), at first, the GA finds
the Individuals with the minimum values of the two
OFs. This Elitism procedure aims at covering the PF
edges. Then, two Selection processes are performed:
the first one, considering the first OF and the second
one considering the second OF. That leads to achieve
two groups of Individuals: the first one, containing
Individuals from the first Selection (i.e. with good
values for the first OF); the second one, as large as
the first one, containing Individuals from the second
Selection (i.e. with good values for the second OF), fi-
nally performing a crossover between the Individuals
of the aforementioned groups. This practice ‘breeds’
Individuals in a way that, Generation by Generation,
the probability that they will reach the inner part of the
Pareto Front increases. Then, Mutation is applied to
remaining Individuals of the current Population, lead-
ing to the updated Population completion and, thus,
to a new Generation. The HGA operators and meta-
parameters, which are set by the operator based on
previous experience on this kind of applications, are
shown in Tab. 1.
Table 1: HGA operators and meta-parameters.
Figure Value
Pop. size 300
Elite Indiv. 1 (per OF)
Selection Op. Tournament
Sel. Tour. size 2
Mutation Op. Uniform
Mut. Fraction 0.2
Crossover Op. One-point
Cros. Fraction 0.8
Stopping cond. Max. Gen.
Max Gen. 50
FIS MFs abscissas are encoded as Genes but further
transformations are done with the aim of reducing the
number of Genes and, therefore, the computational
cost. First of all, the UoD is discretized with 0.01
steps. Then, MFs abscissas are encoded following the
(21 - 35) . With reference to Fig. 4, even if each
triangular MF counts three abscissas, only two real
values are needed, according to the aforementioned
equations and inequalities.
γ = g
0
very low
γ
0
(21)
β = g
00
very low
γ (22)
θ = g
0
very high
(1 − θ
0
) (23)
λ = θ + g
00
very high
(1 − θ) (24)
φ =
φ
0
− (
g
0
l ow
2
L
low
−
L
t
r
2
) i f g
0
low
≥ 1
φ
0
+ (−
g
0
l ow
2
L
low
+
L
t
r
2
) i f 0.01 ≥ g
0
low
< 1
(25)
ξ =
ξ
0
+ (
g
00
l ow
2
L
low
−
L
t
r
2
) i f g
0
low
≥ 1
ξ
0
− (−
g
00
l ow
2
L
low
+
L
t
r
2
) i f 0.01 ≥ g
0
low
< 1
(26)
ω = φ + g
00
low
(ξ − φ)
2
(27)
FCTA 2022 - 14th International Conference on Fuzzy Computation Theory and Applications
204

with
γ
0
= 0.25 (28)
θ
0
= 0.75 (29)
0.04 ≥ g
0
very low
≤ 4.00 (30)
0.01 ≥ g
00
very low
≤ 0.99 (31)
0.04 ≥ g
0
very high
≤ 4.00 (32)
0.01 ≥ g
00
very high
≤ 0.99 (33)
0.01 ≥ g
0
low
≤
1
L
tr
(34)
0.01 ≥ g
00
low
≤ 1.99 (35)
where γ, β, θ, λ, φ, ξ and ω are the MFs abscissas
(Fig. 4), being γ
0
, β
0
, θ
0
, λ
0
, φ
0
, ξ
0
and ω
0
their de-
fault values; g
0
very low
and g
00
very low
are the first and the
second Genes for the “very low” trapezoidal MF, re-
spectively; g
0
very high
and g
0
very high
are the first and the
second Genes for the “very high” trapezoidal MF, re-
spectively; g
0
low
and g
00
low
are the first and the second
Genes for the “low” triangular MF, respectively. The
“low” triangular MF is to be considered representa-
tive of the others triangular MFs; thus, for the sake of
the synthesis, the values of φ
0
, ξ
0
and ω
0
are omitted
in the equations above. The equations and inequal-
ities above guarantee MFs abscissas variations over
the whole UoV also preventing overlaps. This way,
the number of MFs abscissas Genes is 30 (3 overall
Terms Sets - for 2 Inputs and 1 Output - for 5 MFs
per Term Set for 2 Genes per MF) instead of 39 (3
overall Terms Sets - for 2 Inputs and 1 Output - for
5 MFs per Term Set for 2 Genes per trapezoidal MF
and 3 Genes per triangular MF.).
As discussed above, the generic Individual counts 90
Genes: 10 Hierarchical Genes (1 per Input MF for 5
MFs per per Input Term Set for 2 Input Term Sert); 30
MFs Genes; 25 Consequents Genes (1 per Rule for 25
Rules); 25 Weight Genes(1 per Rule for 25 Rules).
5.2 Benchmark and Performance
Metrics
A Dynamic Programming (DP) algorithm is used
as benchmark in this work. According to Litera-
ture (Kim and de Weck, 2005), (Koski, 1985), a
benchmark PF can be achieved by implementing a
mono-objective algorithm with a single weighted-
sum OF, by finding problem solutions for many differ-
ent weights values. In this work, 100 different bench-
mark PF points are achieved by the above procedure.
1
1
x
Figure 4: MF encoding scheme.
With regard to the performance metrics, the following
criteria must be taken into account for a MO optimiza-
tion (Chen et al., 2007), (Unveren and Acan, 2007):
• Proximity of the GA PF points the to the bench-
mark PF points;
• Coverage of the benchmark PF by the GA PF
points;
• Distribution of the GA PF points.
Proximity can be estimated through the Genera-
tional Distance (GD) (Unveren and Acan, 2007), as
follows:
GD =
s
∑
M
i
z
i
M
(36)
where z
i
is the distance between the i-th GA PF point
and its nearest benchmark PF point and M is the total
number of GA PF points. If GD is 0, GA PF points
overlap with the benchmark PF points.
Both coverage and distribution can be evaluated
through the Diversity Metric (DM) (Chen et al.,
2007), (Unveren and Acan, 2007), with reference to
Fig. 5, as follows:
DM =
d
b
+ d
e
+
∑
M−1
i
(d
i
−
¯
d)
d
b
+ d
e
+ (M − 1)
¯
d
(37)
where d
b
and b
e
are the distance between the extreme
GA PF points and the corresponding points in the
benchmark PF, while d
i
and
¯
d are the distance be-
tween two consecutive GA PF points and their mean
value, respectively. It can be seen that the more the
mutual distance between GA PF points is closer to
¯
d
and the distances d
b
and d
e
are small, the more DM
tends to 0, which means a perfect GA PF points cov-
ering and distribution.
Synthesis of an Evolutionary Fuzzy Multi-objective Energy Management System for an Electric Boat
205
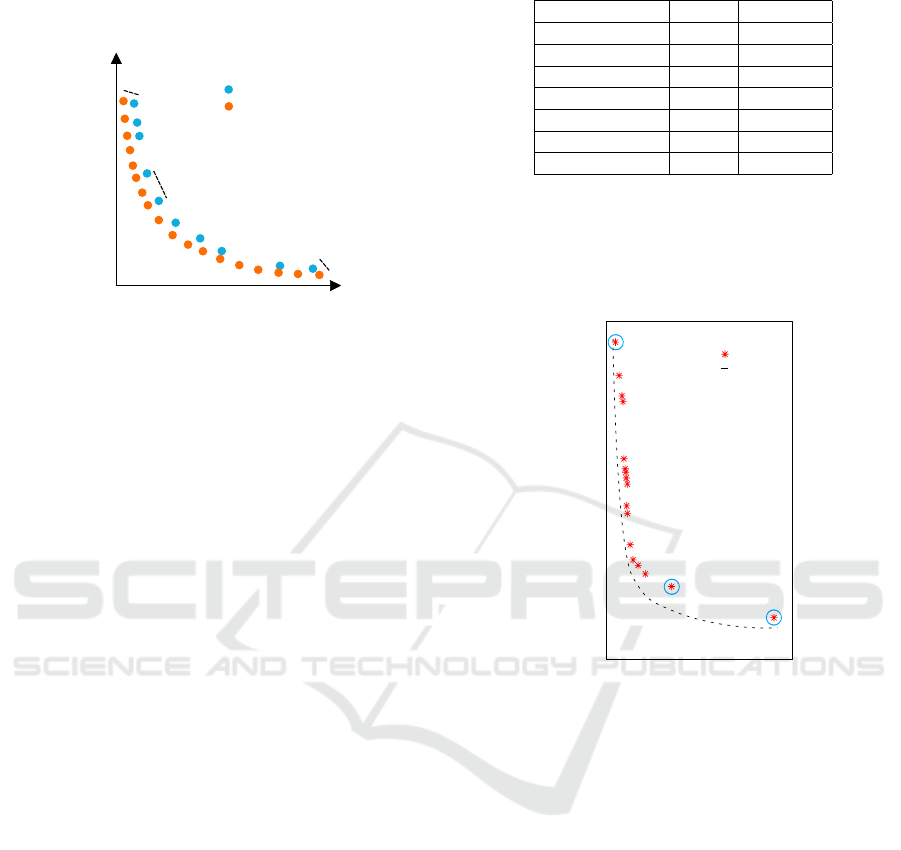
According to (Chen et al., 2007) and (Unveren and
Acan, 2007), values of GD up to about 0.45 and val-
ues of DM up to about 0.40 are acceptable.
OF1
0
OF2
db
di
de
GA PF point
DP PF point
Figure 5: Density Metric (DM) calculation quantities.
6 TESTS AND RESULTS
In order to achieve the optimal FIS models with the
best generalization skills, a k-fold cross-validation is
performed by choosing 5 couples of days (5-fold) in
the dataset trying to cover as much as possible the
whole year. Therefore, each couple consists of one
training day subset and one validation day subset and
the PF solutions (i.e. the optimal FIS models) with
the minimum validation error are selected before be-
ing tested on one day, randomly chosen in the dataset.
More precisely, the error ε is calculated as the sum
of GD and DM performance metrics (38), aiming at
guaranteeing both accuracy and a good PF points dis-
tribution. In fact, the aforementioned sum of perfor-
mance metrics acts as weighted-sum objective func-
tion with equal given both to GD and DM, aspiring at
a good compromise result.
ε = GD + DM (38)
The result of the learning process is the optimal GA
PF, which consists of the best FIS models for the
problem at hand. The optimal GA PF is plotted
against the benchmark PF in Fig. 6 and figures about
the algorithm performance are reported in Tab. 2.
Since the GA is a stochastic algorithm, the values in
Tab. 2 are calculated as averages over 10 runs.
At the best of our knowledge, the proposed algorithm
achieves acceptable results in GD figures but also
promising values of DM, if compared to other GA-
based algorithms (Unveren and Acan, 2007), (Chen
et al., 2007). That could be encouraging for further
improvements of the model.
For three GA PF points, (i.e. FIS models), the result-
ing optimal energy flows are extracted and shown in
Fig. 7, together with an estimation of the energy pur-
chase cost from the Main Grid. The points are chosen
Table 2: MO-FIS-HGA performance metrics.
Figure Mean Variance
Train. GD 0.062 0.002
Train. DM 0.162 0.0013
Val. GD 0.076 0.009
Val. DM 0.162 0.004
Test. GD 0.063 0.009
Test. DM 0.164 0.009
Comp. cost [h] 6.320 0.005
to be the two extreme points of the PF and the one in
the middle (Fig. 6) because in a MO optimization it
is interesting to study both the sharp and the compro-
mise solutions, in order to choose the most suitable
one.
II
III
0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45
0.4
0.6
0.8
1
1.2
1.4
1.6
OF1
FIS-HGA
DP
Figure 6: FIS-HGA Pareto Front selected points.
In the Point I case, for a faster e-boat ESS charge
(about 2 hours), the dock ESS immediately transfers
as much energy as possible to the e-boat ESS, accord-
ing to its technical limits. The larger energy contribu-
tion comes from the Main Grid, with an energy pur-
chase cost that is the higher among the overall cases.
In the opposite case of Point III, a very smaller quan-
tity of energy is absorbed by the e-boat from the Main
Grid, with about a purchase costs less than about the
85%. Moreover, solar energy is exploited to charge
both the e-boat ESS and the dock ESS. That makes it
possible to buy less energy from the Main Grid than
in the other cases and also to charge less rapidly, with
a lower stress for the ESSs (it is better if an ESS SoE
is around 50%). As a consequence, the e-boat ESS is
not fully charged (about 90%) and it takes the whole
day to finish charging. In a compromise solution, in
the Point II case, the energy purchase costs are less
than the 50% if compared to Point I case and at 12
o’clock it is almost fully charged (about 80%). The
last case can be considered the best in terms of lo-
FCTA 2022 - 14th International Conference on Fuzzy Computation Theory and Applications
206
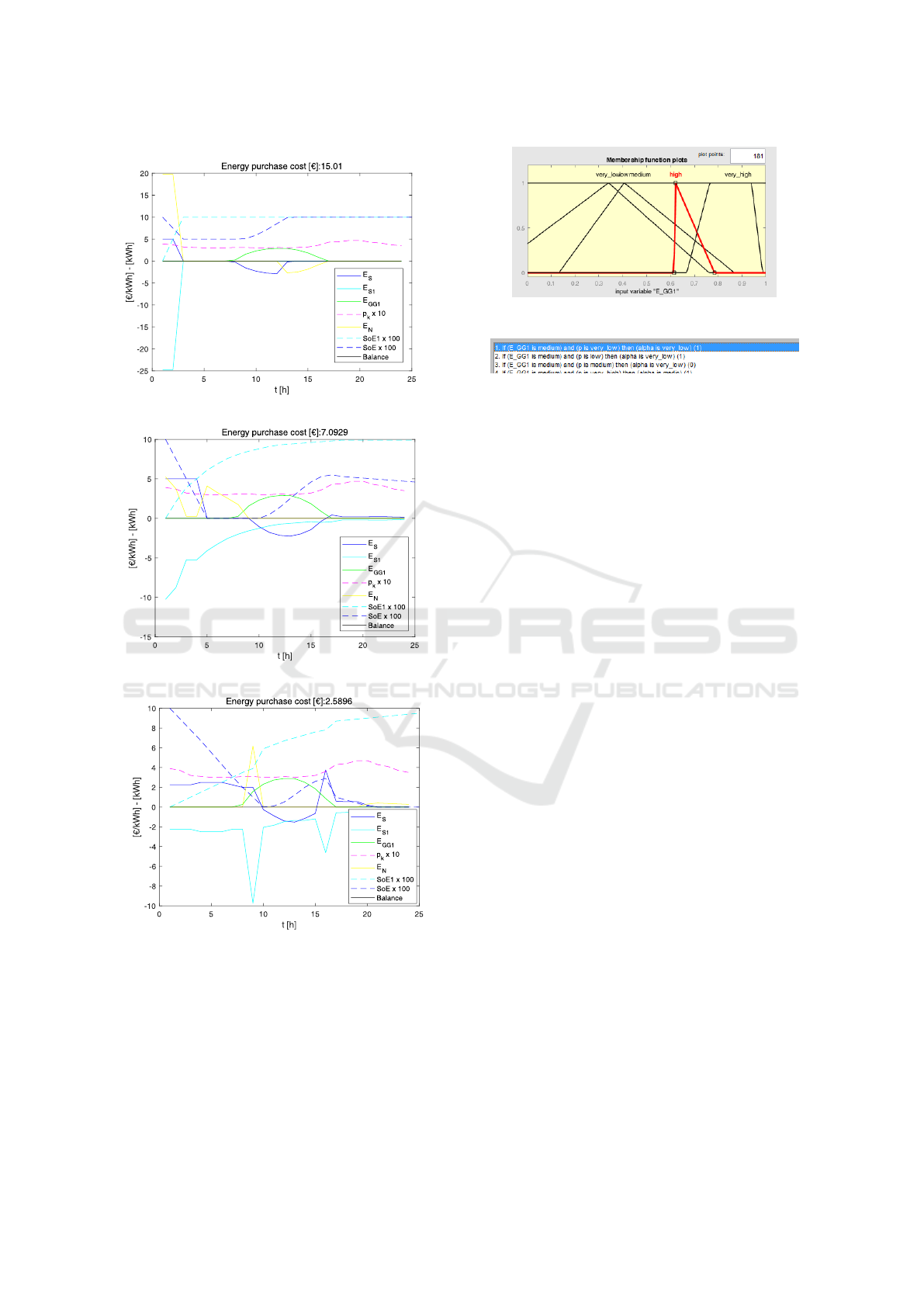
Point I
Point II
Point III
Figure 7: Optimal energy flows from delected FIS-HGA
Pareto Front points.
gistic and economic points of view, so the first Input
Term Set (as an example) of the corresponding FIS
model (Fig. 8) are discussed below for the sake of the
AI Explainability.
Together with the Rule Set (Fig. 9) the Term Sets
make the FIS reasoning comprehensible to humans,
in contrast with AI black-box models.
Figure 8: Point II FIS Term Set for the first Input.
Figure 9: Point II FIS Rule Base excerpt.
7 CONCLUSIONS
An MO EMS is synthesized for a docked e-boat with
the aim of optimizing two conflicting objective func-
tions, i.e. charging the e-boat ESS as soon as possi-
ble within 24h and spending as little as possible both
for energy purchase from the Main Grid and also in
terms of ESS wear. A FIS-HGA algorithm is used to
achieve the Pareto Front for evaluating compromise
solutions. The HGA is in charge of optimizing the
FIS parameters in order to return a FIS model that
meets the needs. Five k-fold, each with one train-
ing and one validation day dataset, are considered for
cross-validation. Results laid to a balanced trade-off
between the two objectives, since the selected solu-
tion make it possible to charge the e-boat ESS in a
reasonable time for people transportation services (it
is almost fully charged at 12 o’ clock) with an over-
all expenditure that is less than 50%, if compared to
the most expensive solution. Having a FIS model as
a function approximation model makes it possible to
know its reasoning process by observing Term Set
and Rule Base, since they are written in a Natural-like
Language. The proposed algorithm achieves good re-
sults in DM figures while only acceptable figures in
GD, if compared to literature. That could be encour-
aging for further improvements of the model. One of
the model flaws is the high computational cost that
requires efforts in writing more efficient code and in
exploiting better parallel computation.
REFERENCES
Alsharif, A., Tan, C. W., Ayop, R., A.Dobi, and Lau, K. Y.
(2021). A comprehensive review of energy manage-
ment strategy in vehicle-to-grid technology integrated
with renewable energy sources. Sustainable Energy
Technologies and Assessments, 47:101439.
Synthesis of an Evolutionary Fuzzy Multi-objective Energy Management System for an Electric Boat
207

Badal, F., Das, P., and et al., S. S. (2019). A survey on
control issues in renewable energy integration and mi-
crogrid. Protection and Control of Modern Power Sys-
tems, 4.
Balestra, L. and Schjølberg, I. (2021). Energy manage-
ment strategies for a zero-emission hybrid domes-
tic ferry. International Journal of Hydrogen Energy,
46(77):38490–38503.
Capillo, A., Luzi, M., Pasc, M., Rizzi, A., and Mascioli, F.
M. F. (2018). Energy transduction optimization of a
wave energy converter by evolutionary algorithms. In
2018 International Joint Conference on Neural Net-
works (IJCNN), pages 1–8.
Chen, L., McPhee, J., and Yeh, W. W.-G. (2007). A diver-
sified multiobjective ga for optimizing reservoir rule
curves. Advances in Water Resources, 30(5):1082–
1093.
De Santis, E., Rizzi, A., and Sadeghian, A. (2017). Hier-
archical genetic optimization of a fuzzy logic system
for energy flows management in microgrids. Applied
Soft Computing, 60:135–149.
De Santis, E., Rizzi, A., Sadeghiany, A., and Frattale
Mascioli, F. M. (2013). Genetic optimization of a
fuzzy control system for energy flow management in
micro-grids. In 2013 Joint IFSA World Congress and
NAFIPS Annual Meeting (IFSA/NAFIPS), pages 418–
423.
Departement of Energy, U. (2016). Crystalline silicon pho-
tovoltaic research. http://www.energy.gov/eere/solar/
crystalline-silicon-photovoltaics-research.
Dietz, A., Azzaro-Pantel, C., Pibouleau, L., and Domenech,
S. (2008). Strategies for multiobjective genetic al-
gorithm development: Application to optimal batch
plant design in process systems engineering. Comput-
ers & Industrial Engineering, 54(3):539–569.
Duman, A. C., Erden, H. S.,
¨
Omer G
¨
on
¨
ul, and
¨
Onder
G
¨
uler (2021). A home energy management system
with an integrated smart thermostat for demand re-
sponse in smart grids. Sustainable Cities and Society,
65:102639.
EC (2020). Photovoltaic geographical information system.
http://re.jrc.ec.europa.eu/pvg tools/en/.
Ellabban, O., H.Abu-Rub, and Blaabjerg, F. (2014). Renew-
able energy resources: Current status, future prospects
and their enabling technology. Renewable and Sus-
tainable Energy Reviews, 39:748–764.
Ferrandino, E., Capillo, A., Frattale Mascioli, F. M., and
Rizzi, A. (2020). Nanogrids: A smart way to inte-
grate public transportation electric vehicles into smart
grids. In 12th International Joint Conference on Com-
putational Intelligence, volume 16.
Hafiz Abdul Muqeet, a. H. M. M., Javed, H., Shahzad, M.,
Jamil, M., and Guerrero, J. M. (2021). An energy
management system of campus microgrids: State-of-
the-art and future challenges. Energies, 14(20).
Kim, I. and de Weck, O. (2005). Adaptive weighted-sum
method for bi-objective optimization: Pareto front
generation. Structural and Multidisciplinary Opti-
mization, 29(2):149–158.
Koski, J. (1985). Defectiveness of weighting method in
multicriterion optimization of structures. Communi-
cations in Applied Numerical Methods, 1(6):333–337.
Layton, B. E. (2008). A comparison of energy densities of
prevalent energy sources in units of joules per cubic
meter. International Journal of Green Energy, 5:438–
455.
Li, X.-H., Cao, C. C., Shi, Y., Bai, W., Gao, H., Qiu, L.,
Wang, C., Gao, Y., Zhang, S., Xue, X., and Chen, L.
(2022). A survey of data-driven and knowledge-aware
explainable ai. IEEE Transactions on Knowledge and
Data Engineering, 34(1):29–49.
Palm, R. (2004). Synchronization of decentralized multiple-
model systems by market-based optimization. IEEE
Transactions on Systems, Man, and Cybernetics, Part
B (Cybernetics), 34(1):665–671.
Pozna, C., Precup, R.-E., Horvath, E., and Petriu, E. M.
(2022). Hybrid particle filter-particle swarm opti-
mization algorithm and application to fuzzy controlled
servo systems. IEEE Transactions on Fuzzy Systems,
pages 1–1.
Rafiei, M., Boudjadar, J., and Khooban, M.-H. (2021). En-
ergy management of a zero-emission ferry boat with a
fuel-cell-based hybrid energy system: Feasibility as-
sessment. IEEE Transactions on Industrial Electron-
ics, 68(2):1739–1748.
Slama, S. B. (2021). Design and implementation of home
energy management system using vehicle to home
(h2v) approach. Journal of Cleaner Production,
312:127792.
Tesla (2019). Pawerwall 2 datasheet. http://www.tesla.com/
powerwall.
Unveren, A. and Acan, A. (2007). Multi-objective optimiza-
tion with cross entropy method: Stochastic learning
with clustered pareto fronts. In 2007 IEEE Congress
on Evolutionary Computation, pages 3065–3071.
Xiang, Y. and Yang, X. (2021). An ecms for multi-objective
energy management strategy of parallel diesel electric
hybrid ship based on ant colony optimization algo-
rithm. Energies, 14(4).
Zamfirache, I. A., Precup, R.-E., Roman, R.-C., and Petriu,
E. M. (2022). Reinforcement learning-based control
using q-learning and gravitational search algorithm
with experimental validation on a nonlinear servo sys-
tem. Information Sciences, 583:99–120.
¨
Ozdemir, H., G
¨
uldorum, H. C., Erdinc¸, O., and
˙
Ibrahim
S¸eng
¨
or (2021). Energy management of a port serv-
ing fuel cell and battery based hybrid green ferries. In
2021 International Conference on Smart Energy Sys-
tems and Technologies (SEST), pages 1–6.
Z
¨
urich, E. (2020). Open power system data. http://data.
open-power-system-data.org/time series/.
FCTA 2022 - 14th International Conference on Fuzzy Computation Theory and Applications
208
