An Extremal Optimization Algorithm for Improving Gaussian Mixture

Rodica Ioana Lung

Center for the Study of Complexity, Babes¸ -Bolyai University, Cluj Napoca, Romania

Keywords:

Clustering, Gaussian Mixture, Extremal Optimization.

Abstract:

Many standard clustering methods rely on optimizing a maximum likelihood function to reveal internal con-

nections within data. While relying on the same model, alternative approaches may provide better insight into

the division of data. This paper presents a new Gaussian mixture clustering approach that uses an extremal

optimization algorithm to maximize the silhouette coefﬁcient. The mean and covariance matrix of each com-

ponent are evolved to maximize each cluster’s priors. Numerical experiments compare the performance of the

expectation-maximization algorithm with the new approach on a set of synthetic and real-world data.

1 INTRODUCTION

Classical approaches for clustering and classiﬁcation

(Zaki and Meira, 2020; Poggio and Smale, 2003)

can be further exploited by considering different

paradigms in the estimation of their parameters. The

Gaussian mixture model (GM) is one of the many

machine learning methods that estimate parameters

to maximize the corresponding log-likelihood func-

tion. However, it is not necessarily true that param-

eters that maximize the log-likelihood function also

offer the best clustering of data. Moreover, the max-

imization problem may have multiple solutions with

varying qualities from the clustering point of view.

The Gaussian mixture model is very popular in ap-

plications due to its robustness. Examples are mul-

tiple: in image analysis (Guo et al., 2022), sensor

fault diagnosis (Zhang et al., 2022a), driving fatigue

detection (Ansari et al., 2022; Zhang et al., 2022b),

environment (Kwon et al., 2022; Malinowski and

Povinelli, 2022), health (He and Guo, 2022), etc.

The silhouette score (SC) is an internal quality

measure for clusters that is often used to evaluate the

performance of algorithms’ output. It is based on the

mean intra-cluster distance and the mean nearest clus-

ter distance. A higher value indicates a better clus-

tering separation. Applications on speciﬁc datasets

report silhouette scores of GMM results better than

those provided by other methods. For example, vari-

ous clustering methods are explored to identify abnor-

https://orcid.org/0000-0002-5572-8141

mal behavior detection in smart homes (Bala Suresh

and Nalinadevi, 2022). GMM results outperform K-

means’ for an aircraft trajectory recognition applica-

tion (Kamsing et al., 2020). HPC computing (Bang

et al., 2020), customer churn (Vakeel et al., 2022),

analysis of background noise in ofﬁces (De Salvio

et al., 2021), and for a image recommender system

for e-commerce (Addagarla and Amalanathan, 2020),

are examples of applications in which GMM has been

used and evaluated based on the SC.

GMM has also been used on COVID-19 data

(Greenwood et al., 2022; Wisesty and Mengko, 2021)

with silhouette score as performance indicator. GMM

models have reported best silhouette scores for med-

ical document clustering (Davagdorj et al., 2022) on

processed data extracted from PubMed. Other med-

ical applications in which GMM results are evalu-

ated based on the SC include: manual muscle testing

grades (Saranya et al., 2020), insula functional par-

cellation (Zhao et al., 2017), where it is used with

an immune clonal selection algorithm, clustering of

hand grasps in spinal cord injury (Dousty and Zariffa,

2020), etc.

In this paper, an attempt to estimate parame-

ters for the Gaussian mixture model by maximizing

the silhouette coefﬁcient is proposed. The under-

lying clustering model is Gaussian mixture, which

consists in providing means and covariance matrices

for multivariate normal distributions corresponding to

each cluster in the data. The expectation maximiza-

tion (EM) algorithm is known to maximize the log-

likelihood function. Instead of using EM, an extremal

Lung, R.

An Extremal Optimization Algorithm for Improving Gaussian Mixture Search.

DOI: 10.5220/0011528000003332

In Proceedings of the 14th International Joint Conference on Computational Intelligence (IJCCI 2022), pages 91-96

ISBN: 978-989-758-611-8; ISSN: 2184-3236

optimization (EO) algorithm searches for parameters

that maximize the SC by randomly modifying the

clusters with the lowest prior probabilities.

2 GAUSSIAN MIXTURE MODEL

Consider the following clustering problem: let D be

a data set containing instances from R

nxd

. Each at-

tribute can be considered as an instance of a random

variable X

, a = 1, . . . , d and X = (X

, . . . , X

) denotes

the vector of random variables, with x

∈ X an in-

stance or data sample from X.

The Gaussian mixture model assumes that each

cluster C

in the data can be described by using a mul-

tivariate normal distribution with probability density

function f (x|µ

, Σ

), where the mean µ

and Σ

are un-

known parameters (Zaki and Meira, 2020). Then the

probability density function for the entire data X is:

f (x) =

∑

i=1

f (x|µ

, Σ

)P(C

) (1)

where k is the number of clusters, and P(C

) are the

prior probabilities or mixture parameters.

The Gaussian mixture model estimates the mean,

covariance matrix, and prior probabilities for the k

clusters by maximizing the log-likelihood function

P(D|θ) where

θ = {µ

, Σ

, P(C

), . . . ,µ

, Σ

, P(C

)} (2)

with

∑

i=1

P(C

) = 1 and

P(D|θ) =

∏

j=1

f (x

). (3)

The log-likelihood function

lnP(D|θ) =

∑

j=1

∑

i=1

f (x

|µ

, Σ

)P(C

)

(4)

Parameter θ

∗

= argmax

lnP(D|θ) it is supposed

to best describe clusters in the data, assuming that

maximizing the sum of ln f (x

) yields the best trade-

off among individual f

function values. As the log-

likelihood function in eq. (4) is difﬁcult to maximize,

approximating θ

∗

is usually performed by using the

expectation maximization (EM) approach. EM com-

putes the posterior probabilities P(C

) of C

given

as:

P(C

) =

)P(C

)

∑

a=1

)P(C

)

. (5)

P(C

) is denoted by w

i j

and is considered the

weight, or contribution of point x

to cluster C

The EM algorithm has three steps: initialization,

expectation, and maximization steps.

In the initialization step, the means µ

for each

cluster C

are randomly initialized by using a uni-

form distribution over each dimension X

. Covariance

matrices are initialized with the identity matrix, and

P(C

) =

In the expectation step posterior probabilities

/weights w

i j

= P(C

) are computed using eq. (5).

In the maximization step, model parameters µ

, Σ

P(C

) are re-estimated by using posterior probabilities

i j

) as weights.

Thus, the mean µ

for cluster C

is estimated as:

∑

j=1

i j

∑

j=1

i j

. (6)

The covariance matrix Σ

for cluster C

is updated

using:

∑

j=1

i j

∑

j=1

i j

, (7)

where x

= x

− µ

The prior probability for each cluster P(C

) is

computed as:

P(C

) =

∑

j=1

i j

(8)

The expectation and maximization steps are re-

peated until convergence, i.e. no more changes occur

in the values of cluster means. It is known that pa-

rameters computed by using EM are indeed maxima

of the log-likelihood function.

Predictions are made based on posterior probabil-

ities w

i j

3 EXTREMAL OPTIMIZATION

GAUSSIAN MIXTURE MODEL

Extremal optimization - EO (Boettcher and Percus,

2001) is a stochastic search method that evolves an in-

dividual by randomly replacing the ﬁtness of its worst

component. EO has proven to be a powerful optimiza-

tion tool for many applications (Lu et al., 2018). It

is suitable for problems in which solutions are repre-

sented by components with different and comparable

ﬁtness values. A global ﬁtness is also used to evalu-

ate the overall quality of the individual. The general

outline of EO is presented in Algorithm 1.

ECTA 2022 - 14th International Conference on Evolutionary Computation Theory and Applications

Algorithm 1: Outline of general EO.

1: Input: Search domain D, objective function f ,

component ﬁtness functions f

, i = 1, . . . , k;

2: Randomly generate potential solution s;

3: Set s

best

= s;

4: for a number of iterations do

5: evaluate f

(s), i = 1, . . . , k;

6: ﬁnd component s

with the worst ﬁtness;

7: replace s

with a random value;

8: if f (s) > f (s

best

) then

9: Set s

best

= s;

10: end if

11: end for

12: Output: s

best

In order to use EO, one needs to deﬁne the search

domain, the objective function f , and the compo-

nent’s ﬁtness functions f

. Within the EO-GM - the

Extremal Optimization Gaussian mixture approach

presented in this paper, the EO is used to search for

the position of the clusters’ means and covariance ma-

trices. An individual is thus deﬁned as

s = {µ

, Σ

, . . . , µ

, Σ

with µ

∈ R

and Σ

∈ R

d×d

. Matrices Σ

have to be

covariance matrices, so they need to be symmetric and

positive semi-deﬁnite. Each mean and covariance ma-

trix µ

and Σ

characterize a component C

, i = 1 . . . , k,

so we can also write

s = (C

, . . . ,C

The ﬁtness of each component

) = P(C

)

is the prior probability of cluster C

, computed using

Eq. (8). Thus, in each EO iteration, the cluster having

the smallest prior probability is randomly altered in

search for a new mean and covariance matrix.

The objective function to be maximized consid-

ered in this approach is the silhouette coefﬁcient SC

(Zaki and Meira, 2020). SC is based on the differ-

ence between the average distance to the points in the

closest cluster and to the points in the same cluster.

For each point x

the silhouette coefﬁcient sc

based on conﬁguration s = (C

, . . . ,C

) is computed

as:

min

out

) − ν

)

max{ν

min

out

), ν

)}

, (9)

where ν

min

out

is the mean distance from x

to all points

in the closest cluster:

min

out

= min

j̸= ˆy

∑

x∈C

||x

− x||

(10)

and n

is the size of cluster C

. Also, ν

) is the

mean distance from x

to points in its own cluster ˆy

) =

∑

x∈C

ˆy

,x̸=x

||x

− x||

ˆy

− 1

. (11)

The value of sc

ranges between -1 and 1, a value

closer to 1 indicates that x

is much closer to points in

its own cluster than to points in the next closest one. A

value close to 0 indicates that x

may lay somewhere

at the boundaries of two clusters. A value closer to -1

indicates that x

is closer to another cluster, so it may

be miss-clustered.

The silhouette coefﬁcient SC is computed as the

average of sc

across all points:

SC(s) =

∑

i=1

(12)

Within the EO-GM algorithm, the SC is used to

evaluate the overall quality of a solution when com-

paring the current individual s with s

best

. If the current

solution is better than the best-known one, it will re-

place it. Otherwise, the search will continue to the

next iteration. Thus, in line 8 of Algorithm 1 the sil-

houette coefﬁcient is used to compare the two indi-

viduals.

One of the motivations behind this approach is to

show that results provided by classical clustering al-

gorithms, such as Gaussian mixture, may be improved

while maintaining the underlying method. In the case

of Gaussian mixture, by using EO, we may ﬁnd mean

values and covariance matrices that better describe

clusters - with respect to an internal ﬁtness measure

such as the silhouette coefﬁcient.

Thus, instead of the random initialization of EO

(line 2, Algorithm 1), the means and covariance matri-

ces determined by expectation maximization are used

to initialize solution s.

EO-GM (Algorithm 2 maximizes the silhouette

coefﬁcient by attempting to increase the prior prob-

abilities of each cluster. The EO algorithm requires

a termination condition. In this approach, the maxi-

mum number of iterations of EO-GM is set to 100×d.

GM-EO does not need any other parameter settings.

4 NUMERICAL EXPERIMENTS

Numerical experiments are performed on a set of syn-

thetic benchmarks and real-world data to illustrate the

potential of the approach.

Data. The synthetic data-sets are generated by us-

ing the make classification function from the

An Extremal Optimization Algorithm for Improving Gaussian Mixture Search

Algorithm 2: Outline of EO-GM.

1: Input: Data set X ⊂ R

n×d

; number of clusters k;

2: Compute initial solution s = {µ

, Σ

, . . . , µ

, Σ

}

using expectation maximization;

3: Set s

best

= s;

4: for a number of iterations do

5: evaluate P(C

), i = 1, . . . , k;

6: ﬁnd component s

with smallest P(C

) ;

7: replace s

with a random value:

8: alter the mean µ

by adding a random multi-

variate normal value (with mean 0 and standard

deviation 0.1);

9: alter Σ

by adding a randomly generated pos-

itive semi-deﬁnite matrix with the same dimen-

sions;

10: if SC(s) > SC(s

best

) then

11: Set s

best

= s;

12: end if

13: end for

14: Output: s

best

Figure 1: Example of two synthetic data sets generated with

class separator values of 2 (left) and 0.5 (right).

sklearn package in Python (Pedregosa et al., 2011).

The make classification function allows the gen-

eration of clustering and classiﬁcation data-sets with

different number of instances, attributes, classes and

different levels of difﬁculty (controlled by a class sep-

arator parameter). The parameters used to generate

the synthetic data sets are:

• Number of instances: 100, 200, 300, 400, and

500;

• Number of classes and attributes: 3, 5,7,9;

• Class separator: 0.5 and 2; clusters generated us-

ing the value 2 are clearly separated, while clus-

ters generated with the value 0.5 are highly over-

lapping. Figure 1 illustrates the differences be-

tween clusters for a data-set with 500 instances

and 2 attributes.

The real data sets used are taken from the UCI

Machine Learning repository (Dua and Graff, 2017).

Table 1 presents their main characteristics.

Table 1: Real data-sets used for numerical experiments and

their main attributes.

No No No

Data-set instances attributes clusters

Cryoptherapy 90 6 2

Dresses 500 12 2

cezariene 80 5 2

Cervical 72 19 2

Immunotherapy 90 7 2

Banknote 1372 4 2

Plrx 182 12 2

Transfusions 748 4 2

Diabetes 768 8 2

Forest 243 12 2

Iris 150 4 3

Wine 178 13 3

Performance Evaluation. For each data-set, 10 in-

dependent runs are performed, and the silhouette co-

efﬁcient for the initial solution - the one provided by

the gaussian mixture expectation maximization algo-

rithm - is compared with the silhouette coefﬁcient of

the solution provided by EO-GM. For each data set,

the ten values are compared by using a paired t-test,

testing the null hypothesis that EO-GM average re-

sults are less than or equal to that of the GM model.

The null hypothesis is rejected if the p-value is less

than 0.05. As an external indicator, the normalized

mutual information (NMI) is computed, and statisti-

cal signiﬁcance tests are performed in a similar man-

ner. The NMI indicator compares the reported clus-

ters with the real partitions; a greater value indicates

a better clustering.

Results. Table 2 presents results of the t-test com-

paring the SC scores reported by GM and EO-GM.

We ﬁnd that in all tested instances the results reported

by EO-GM are signiﬁcantly better as far as the SC

score is concerned. Regarding the NMI score, only in

one instance the NMI values reported by EO-GM are

signiﬁcantly better than those reported by GM.

Figure 2 presents box-plots of NMI values for

each real-world data-set and Table 3 corresponding

p-values. For three of the data sets, increasing the

SC indicator also led to better NMI values. Only for

one data-set (forest), EO-GM did not ﬁnd a better SC

value.

5 CONCLUSIONS

Gaussian mixture models describe clusters in data by

using multivariate normal distributions. In this paper

these parameters are estimated by using an extremal

ECTA 2022 - 14th International Conference on Evolutionary Computation Theory and Applications

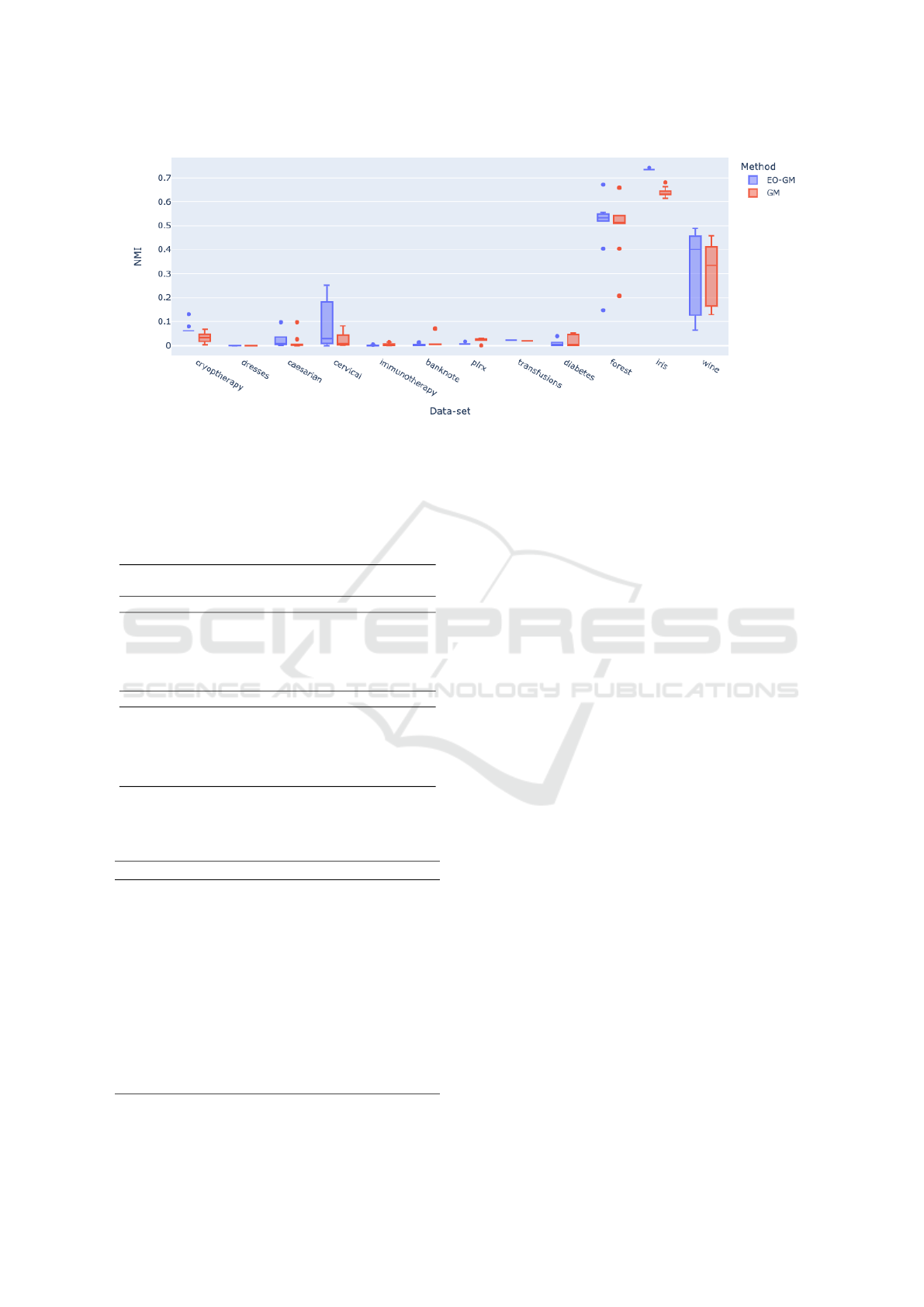
Figure 2: NMI values reported by the two methods on the real data-sets.

Table 2: Synthetic data-sets. p-values of the t-test compar-

ing the SC score between GM and EO-GM. A value lower

than 0.05 indicates that EO-GM scores are higher. A *

indicates that there is signiﬁcant difference between corre-

sponding NMI values. A

−

sign indicates that NMI values

reported by GM are signiﬁcantly better.

No Number of attributes

Inst. 3 5 7 9

class separator 2

100 0.01521 0.00153 0.00408* 0.00066

200 0.05781 0.00077 0.00863 0.01105

300 0.00190 0.01035 0.00155 0.00608

400 0.00055 0.07050 0.01238 0.00176

500 0.00857 0.00145 0.00172

−

0.0000

class separator 0.5

100 0.00579 0.01269 0.00700 0.00343

200 0.00066 0.00002 0.00038 0.00121

300 0.00020

−

0.00060 0.00144

−

0.00456

400 0.00706

−

0.00000 0.00033 0.00002

500 0.00216 0.00020 0.00000

−

0.00035

Table 3: T-Test results for real-world data-sets comparing

NMI and SC values.

Data-set p-value (NMI) p-value (SC)

cryoptherapy 2.5133e-04 1.7874e-07

dresses 7.3222e-02 1.3253e-07

cezariene 7.3215e-02 3.9972e-02

cervical 2.3410e-02 1.1954e-04

immunotherapy 9.7516e-01 4.8135e-03

banknote 8.4498e-01 4.0949e-02

plrx 9.9905e-01 1.6340e-04

transfusions 0.000e+00 0.000e+00

diabetes 9.6145e-01 3.7300e-02

forest 3.6748e-01 6.2947e-02

iris 3.0751e-08 1.2630e-06

wine 2.5037e-01 8.2896e-04

optimization algorithm maximizing the silhouette co-

efﬁcient measure. Parameters that describe better the

clusters are computed by evolving an individual en-

coding them directly. The component with the low-

est prior probability is randomly replaced each iter-

ation. Numerical experiments indicate that such an

approach has the potential to better reveal intercon-

nections within data, while using the same model to

describe the clusters.

ACKNOWLEDGEMENTS

This work was supported by a grant of the Romanian

Ministry of Education and Research, CNCS - UEFIS-

CDI, project number PN-III-P4-ID-PCE-2020-2360,

within PNCDI III.

REFERENCES

Addagarla, S. and Amalanathan, A. (2020). Probabilistic

unsupervised machine learning approach for a similar

image recommender system for E-commerce. Symme-

try, 12(11):1–17.

Ansari, S., Du, H., Naghdy, F., and Stirling, D. (2022). Au-

tomatic driver cognitive fatigue detection based on up-

per body posture variations. Expert Systems with Ap-

plications, 203. cited By 0.

Bala Suresh, P. and Nalinadevi, K. (2022). Abnormal Be-

haviour Detection in Smart Home Environments, vol-

ume 96 of Lecture Notes on Data Engineering and

Communications Technologies. Pages: 300.

Bang, J., Kim, C., Wu, K., Sim, A., Byna, S., Kim, S.,

and Eom, H. (2020). HPC Workload Characterization

Using Feature Selection and Clustering. pages 33–40.

Boettcher, S. and Percus, A. G. (2001). Optimization with

extremal dynamics. Phys. Rev. Lett., 86:5211–5214.

An Extremal Optimization Algorithm for Improving Gaussian Mixture Search

Davagdorj, K., Wang, L., Li, M., Pham, V.-H., Ryu, K.,

and Theera-Umpon, N. (2022). Discovering Themati-

cally Coherent Biomedical Documents Using Contex-

tualized Bidirectional Encoder Representations from

Transformers-Based Clustering. International Jour-

nal of Environmental Research and Public Health,

19(10).

De Salvio, D., D’Orazio, D., and Garai, M. (2021). Unsu-

pervised analysis of background noise sources in ac-

tive ofﬁces. Journal of the Acoustical Society of Amer-

ica, 149(6):4049–4060.

Dousty, M. and Zariffa, J. (2020). Towards Clustering Hand

Grasps of Individuals with Spinal Cord Injury in Ego-

centric Video. volume 2020-July, pages 2151–2154.

Dua, D. and Graff, C. (2017). UCI machine learning repos-

itory.

Greenwood, D., Taverner, T., Adderley, N., Price, M.,

Gokhale, K., Sainsbury, C., Gallier, S., Welch, C.,

Sapey, E., Murray, D., Fanning, H., Ball, S., Ni-

rantharakumar, K., Croft, W., and Moss, P. (2022).

Machine learning of COVID-19 clinical data identi-

ﬁes population structures with therapeutic potential.

iScience, 25(7).

Guo, J., Chen, H., Shen, Z., and Wang, Z. (2022). Im-

age denoising based on global image similar patches

searching and hosvd to patches tensor. Eurasip Jour-

nal on Advances in Signal Processing, 2022(1). cited

By 0.

He, M. and Guo, W. (2022). An integrated approach

for bearing health indicator and stage division us-

ing improved gaussian mixture model and conﬁdence

value. IEEE Transactions on Industrial Informatics,

18(8):5219–5230. cited By 0.

Kamsing, P., Torteeka, P., Yooyen, S., Yenpiem, S., Dela-

haye, D., Notry, P., Phisannupawong, T., and Chan-

numsin, S. (2020). Aircraft trajectory recognition via

statistical analysis clustering for Suvarnabhumi Inter-

national Airport. volume 2020, pages 290–297.

Kwon, S., Seo, I., Noh, H., and Kim, B. (2022). Hyperspec-

tral retrievals of suspended sediment using cluster-

based machine learning regression in shallow waters.

Science of the Total Environment, 833. cited By 0.

Lu, Y., Chen, Y., Chen, M., Chen, P., and Zeng, G. (2018).

Extremal Optimization: Fundamentals, Algorithms,

and Applications. CRC Press.

Malinowski, M. and Povinelli, R. (2022). Using smart me-

ters to learn water customer behavior. IEEE Trans-

actions on Engineering Management, 69(3):729–741.

cited By 0.

Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V.,

Thirion, B., Grisel, O., Blondel, M., Prettenhofer,

P., Weiss, R., Dubourg, V., Vanderplas, J., Passos,

A., Cournapeau, D., Brucher, M., Perrot, M., and

Duchesnay, E. (2011). Scikit-learn: Machine learning

in Python. Journal of Machine Learning Research,

12:2825–2830.

Poggio, T. and Smale, S. (2003). The mathematics of learn-

ing: Dealing with data. Notices of the American Math-

ematical Society, 50:2003.

Saranya, S., Poonguzhali, S., and Karunakaran, S. (2020).

Gaussian mixture model based clustering of Man-

ual muscle testing grades using surface Electromyo-

gram signals. Physical and Engineering Sciences in

Medicine, 43(3):837–847.

Vakeel, A., Vantari, N., Reddy, S., Muthyapu, R., and Cha-

van, A. (2022). Machine Learning Models for Predict-

ing and Clustering Customer Churn Based on Boost-

ing Algorithms and Gaussian Mixture Model.

Wisesty, U. and Mengko, T. (2021). Comparison of dimen-

sionality reduction and clustering methods for sars-

cov-2 genome. Bulletin of Electrical Engineering and

Informatics, 10(4):2170–2180.

Zaki, M. J. and Meira, Jr, W. (2020). Data Mining and

Machine Learning: Fundamental Concepts and Algo-

rithms. Cambridge University Press, 2 edition.

Zhang, B., Yan, X., Liu, G., and Fan, K. (2022a). Multi-

source fault diagnosis of chiller plant sensors based on

an improved ensemble empirical mode decomposition

gaussian mixture model. Energy Reports, 8:2831–

2842. cited By 0.

Zhang, J., Lu, H., and Sun, J. (2022b). Improved driver

clustering framework by considering the variability of

driving behaviors across trafﬁc operation conditions.

Journal of Transportation Engineering Part A: Sys-

tems, 148(7). cited By 0.

Zhao, X.-W., Ji, J.-Z., and Yao, Y. (2017). Insula

functional parcellation by searching Gaussian mix-

ture model (GMM) using immune clonal selection

(ICS) algorithm. Zhejiang Daxue Xuebao (Gongxue

Ban)/Journal of Zhejiang University (Engineering

Science), 51(12):2320–2331.

ECTA 2022 - 14th International Conference on Evolutionary Computation Theory and Applications