Parameterising the SA-UNet using a Genetic Algorithm

Mahsa Mahdinejad

1 a

, Aidan Murphy

2 b

, Patrick Healy

1 c

and Conor Ryan

1 d

Univercity of Limerick, Limerick, Ireland

University Colledge Dublin, Dublin, Ireland

Keywords:

Deep Learning, Evolutionary Algorithm, Image Segmentation.

Abstract:

Deep learning is an excellent way for effectively addressing image processing, and several Neural Networks

designs have been explored in this area. The Spatial Attention U-Net architecture, a version of the famous

U-Net but which uses DropBlock and an attention block as well as the common U-Net convolutional blocks,

is one notable example. Finding the best combination of hyper-parameters is expensive, time consuming and

needs expert input. We show the genetic algorithm can be utilized to automatically determine the optimal

combination of Spatial Attention U-Net hyper-parameters to train a model to solve a Retinal Blood Vessel

Segmentation problem. Our new approach is able to ﬁnd a model with an accuracy measure of 0.9855, an

improvement from our previous experimentation which found a model with accuracy measure of 0.9751. Our

new methods exhibit competitive performance with other state-of-the-art Retinal Blood Vessel Segmentation

techniques.

1 INTRODUCTION

Diabetes is a severe and common disease that, if left

untreated, may result in death (Ogurtsova et al., 2017)

or vision loss (Ciulla et al., 2003). Diabetic Retinopa-

thy (DR), a type of blindness caused by diabetes, is

caused by damage and accumulation of blood vessels

in the eye. Speciﬁcally, the production of hard exu-

dates around the fovea is one of the major causes of

blindness. However, early detection and laser photo-

coagulation may help to limit the progression of DR

in the retina.

As DR is not evident until after a diabetes di-

agnosis, early identiﬁcation of DR involves profes-

sional, manual evaluation of retinal images. Spe-

cialists are increasingly using image processing and

machine learning approaches to help them investi-

gate retinal problems and diagnose DR (Winder et al.,

2009). The process of extracting blood vessels from

retinal images using these methodologies is known as

the Retinal Blood Vessel Segmentation task.

To solve the challenge of identifying blood vessels

in images of eyes, state-of-the-art Neural Networks

(NNs) techniques are used. The Convolutional NN

https://orcid.org/0000-0003-4288-3991

https://orcid.org/0000-0002-6209-4642

https://orcid.org/0000-0002-3824-7442

https://orcid.org/0000-0002-7002-5815

(CNN) (LeCun et al., 1995), is an improved version

of the traditional NN that has become the “go to” ap-

proach when dealing with image segmentation prob-

lems. The availability of powerful supercomputers to

train larger and more complex CNNs has led to their

success in an increasingly wider range of image pro-

cessing tasks. This success has come at the expense of

complexity, however, with many popular CNN archi-

tectures taking hundreds (possibly thousands) of GPU

hours to successfully train. As a consequence, de-

signing and experimenting with a CNN architecture

and selecting the appropriate hyper-parameters for a

given task is becoming more and more difﬁcult.

In this paper, we use an evolutionary approach to

automatically search for both suitable CNN architec-

ture and parameters. Speciﬁcally, we use a genetic

algorithm (GA) (Holland, 1975), to create a CNN

which can accurately solve a retinal blood vessel seg-

mentation problem.

We use a state-of-the-art CNN, the SA-UNet (Spa-

cial Attention U-Net), as a baseline for the search

space. Similar to our previous work (Popat et al.,

2020; Houreh et al., 2021), we allow the GA to select

the SA-UNet hyper-parameters during the evolution-

ary process. The SA-UNet has been shown to out-

perform the U-Net, which was used in previous ex-

perimentation. Including an attention block increases

the SA-UNet representation capabilities, allowing it

Mahdinejad, M., Murphy, A., Healy, P. and Ryan, C.

Parameterising the SA-UNet using a Genetic Algorithm.

DOI: 10.5220/0011528100003332

In Proceedings of the 14th International Joint Conference on Computational Intelligence (IJCCI 2022), pages 97-104

ISBN: 978-989-758-611-8; ISSN: 2184-3236

to focus on relevant elements in the image while sup-

pressing unneeded ones. That is to say, the SA-UNet

removes noise and irrelevant background units of the

images.

We explain the background of our methods in sec-

tion 2. The experimental setup is described and dis-

cussed in detail in section 3 and the results are then

presented in section 4. Finally, our conclusions and

future work are presented in section 5.

2 BACKGROUND

2.1 Image Segmentation

Image segmentation is an important area of research

in computer vision and machine learning. Au-

tonomous driving, urban navigation and medical im-

age processing all require precise, reliable and effec-

tive segmentation algorithms.

Medical image segmentation is a key aspect in

many current clinical procedures. It is used for a

variety of purposes, including diagnostics, treatment

planning and treatment administration. Professional

therapists usually undertake these visual analyses. As

a result, developing robust and dependable image seg-

mentation algorithms is an essential requirement in

medical image analysis. Image segmentation is the

process of breaking down a digital image into sev-

eral subgroups, reducing the complexity of the image

and making further processing or analysis of the im-

age easier. Other important picture tasks include im-

age level classiﬁcation and detection. Classiﬁcation

involves treating each image as though it belonged to

the same category. The process of identifying and rec-

ognizing items is known as detection.

2.2 Convolutional Neural Networks

Deep learning (DL) is a subset of machine learning

that deals with artiﬁcial neural networks (ANNs) in

general, especially those with numerous complex lay-

ers. Over the last decade, CNNs have achieved break-

throughs in a range of pattern recognition domains,

extending from image processing to speech recogni-

tion. The most advantageous feature of CNNs is that

they reduce the number of parameters in ANN. This

accomplishment has motivated both researchers and

developers to consider larger and larger models in or-

der to perform challenging tasks that were previously

impossible to solve with traditional ANNs. The most

signiﬁcant assumption about issues solved by CNN is

that they should not contain spatially dependent prop-

erties. It is only required that objects are detected, re-

gardless of where they appear in the images. Another

essential property of CNN is the ability to extract ab-

stract features as input propagates deeper levels.

2.3 The U-Net & SA-UNet

The current state-of-the-art techniques used to ad-

dress the blood vessel segmentation challenge are all

NN-based approaches. One of the many NN designs

proposed by researchers is the U-net (Ronneberger

et al., 2015), a variation of a fully CNN that, accord-

ing to the authors, can give reasonable prediction with

a small training dataset.

The U-net architecture is a U shape encoder-

decoder with skip connections between them. The en-

coder takes the input characteristics and reduces their

dimension, while the decoder takes the encoder’s fea-

tures and provides the best match to the actual input

or planned output.

The U-net is divided into two sections, the con-

tracting path and the expanding path, which are po-

sitioned on the left and right sides, respectively. The

contracting path is used for down sampling, whereas

the expanding path is used for up sampling.

The main advantage of this design is its capacity

to take a broader context into account while producing

a prediction from the real image pixel by pixel, which

is especially useful for retinal blood vessel segmenta-

tion.

Previously we aimed to optimise the U-Net, ob-

taining a smaller model than the base U-Net (Houreh

et al., 2021; Popat et al., 2020). This reduces the cost

and time to train the model and makes it more suit-

able to run on small or embedded devices. There was,

however, a trade-off in accuracy with this more com-

pact model. As newer state-of-the-art models have

increased the performance on benchmarks higher and

higher, this trade-off can no longer be justiﬁed as the

gap in precision between the models grows larger and

larger.

Several U-Net modiﬁcations have been proposed

to increase the network’s performance. Some work

has modiﬁed the architecture of the U-Net, such as the

Dual Encoding U-Net (DEU-Net) (Wang et al., 2019).

This is a modiﬁcation of the U-Net with a novel ar-

chitecture, using two encoders and attention blocks.

Another example is the U-Net++ (Zhou et al., 2018),

which aims to reduce the feature maps gap between

the encoder and decoder.

One of the more notable models is the spatial at-

tention U-Net (SA-UNet) (Guo et al., 2021). The SA-

UNet has two major differences compared to the U-

Net. Firstly, it uses spatial attention (Woo et al., 2018)

at the bottom of the U-Net, shown in Fig. 2 and, sec-

ECTA 2022 - 14th International Conference on Evolutionary Computation Theory and Applications

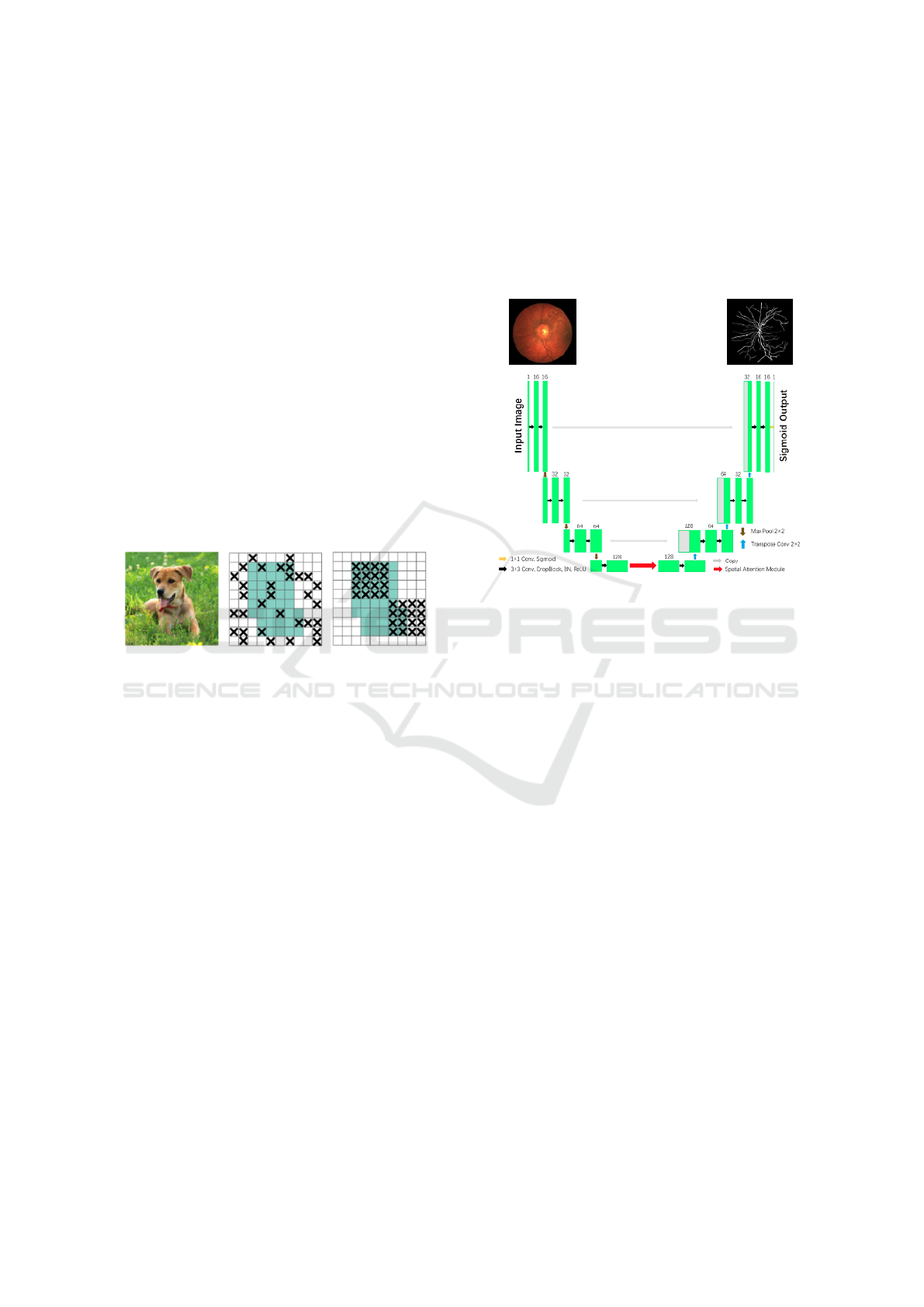
ondly, to mitigate overﬁtting, it uses DropBlock (Ghi-

asi et al., 2018) instead of Dropout (see below for a

description of both DropBlock and Dropout). The

SA-UNet has shown improved performance over the

base U-Net, improving the AUC (see Section 3.5) on

the DRIVE dataset from 0.9755 to 0.9864.

The SA-UNet is adopted as the base model in our

study.

Supervised machine learning projects often must

deal with training sets of small size. This can be due

to the lack of available data, the expense associated

with collecting it or many other reasons. Most CNN

models require vast amounts of data to learn correctly

and are prone to overﬁt (Dietterich, 1995) and per-

form poorly when trained on restricted datasets.

Dropout (Baldi and Sadowski, 2013) is a regular-

ization algorithm in which certain layer’s outputs are

ignored or ”dropped out” stochastically during train-

ing. This approach shows that Dropout may break

apart situations in which network layers co-adapt to

correct mistakes made by previous layers, and mak-

ing the model more reliable.

Figure 1: An illustration comparing the approaches of

Dropout and DropBlock for ignoring units in an input im-

age (Ghiasi et al., 2018).

DropBlock is a robust CNN regularization

method, similar to Dropout, by setting the input’s

units to 0, and guaranteeing that no units are reliant

on each other during training time. It differs from

Dropout in that it eliminates continuous regions rather

than individual random units from a layer’s feature

map, shown in Fig. 1.

DropBlock has been shown to effectively avoid

network overﬁtting, allowing for the use of very small

sample datasets to effectively train CNNs. DropBlock

requires the user to specify the value of two parame-

ters, namely, block size, which determines the num-

ber of pixels in each block, and keep probability, the

chance of the block being shut down.

A major challenge in retinal segmentation is the

lack of contrast between the blood vessel area and the

background in the retinal fundus images. Much work

has been done to overcome this absence of distinction,

with attention shown to be among the most power-

ful techniques (Vaswani et al., 2017). The SA-UNet

utilises attention to help the network learn better by

converting a query and a collection of critical values

into output. Spatial attention helps the model to learn

structural information, which is essential for achiev-

ing state-of-the-art results, by emphasising important

units and reducing noises and inﬂuence of the back-

ground. In this process ﬁrst max-pooling and average

pooling operations are applied along the channel axis,

then concatenates them to build an efﬁcient feature

detector.

Figure 2: SA-UNet architecture (Guo et al., 2021).

2.4 Evolutionary Algorithm

Evolutionary Algorithms (EAs) are population-based

optimization techniques, inspired by natural selec-

tion. The works of some of the early computer vi-

sionaries show signs of evolutionary discovery. Con-

cepts in Biological Computing, Biological Mathemat-

ics and Machine Learning, for example, were created

by Alan Turing (Turing, 1990) and John von Neu-

mann (Burks, 1986).

An EA experiment begins by creating a population

of different solutions and specifying a ﬁtness func-

tion and then evolves them over many generations.

The stronger individuals will survive and be passed

down to future generations, while the weaker individ-

uals will die out. In our experiments, an individual is

a NN architecture and its associated parameters.

2.4.1 Genetic Algorithm

A Genetic Algorithm (GA) (Holland, 1975), a sub

ﬁeld of EAs, takes its inspiration from genetics by

representing solutions as ‘genes’ and using biolog-

ically inspired operators to modify individuals to

drive the evolution. GAs are frequently used to

produce high-quality solutions to optimization and

search challenges.

Our experiments use a GA to tune the set of pa-

rameters of a segmentation method.

Parameterising the SA-UNet using a Genetic Algorithm

The GA process, described in 12, begins by cre-

ating a population of individuals. An individual, or

genotype, is a set of genes, each of which represents a

SA-UNet hyper-parameter. The hyper-parameters we

select for optimisation are: depth, number of ﬁlters,

kernel sizer, pooling type, activation and optimizer.

Each set of genes produces the genotype, with each

unique genotype representing a unique model.

Algorithm 1: Genetic Algorithm.

Input: G = [g

,...,g

] // Genotype

Output: P = [p

, p

,..., p

] // Phenotype

1 I

← (G,P,S)

2 S = ∅

3 Q

t=0

← I

// Initial population

4 while t < m // m = max generations

5 do

6 Evaluate each phenotype P ∈ Q

t−1

7 S(I

) ← eval(P

) assign ﬁtness score

8 Select parents from Q

t−1

using S

9 Genetic operations on G

of selected parents

10 Q

← (G,P) offspring (new pop)

11 t ← t +1

12 Return I

from Q

with the best S.

3 EXPERIMENTAL SETUP

3.1 Dataset

The DRIVE (Digital Retinal Images for Vessel Ex-

traction) database (Staal, 2018) was created to al-

low for comparative research on blood vessel seg-

mentation in retinal pictures for the diagnosis, screen-

ing, treatment and evaluation of various diseases such

as diabetes. The morphological attributes of reti-

nal blood vessels, such as length, width, texture and

branching patterns, are identiﬁed and used by the ex-

perts. Automatic identiﬁcation and analysis of the

vasculature may help in DR detection methods, re-

search into the association between vascular deforma-

bility and hypertensive retinopathy, vessel diameter

measurement in relation to hypertension diagnosis

and computer-assisted laser surgery. Furthermore, the

retinal vascular branch has been shown to be unique

to each person and may be utilized for biometric iden-

tiﬁcation.

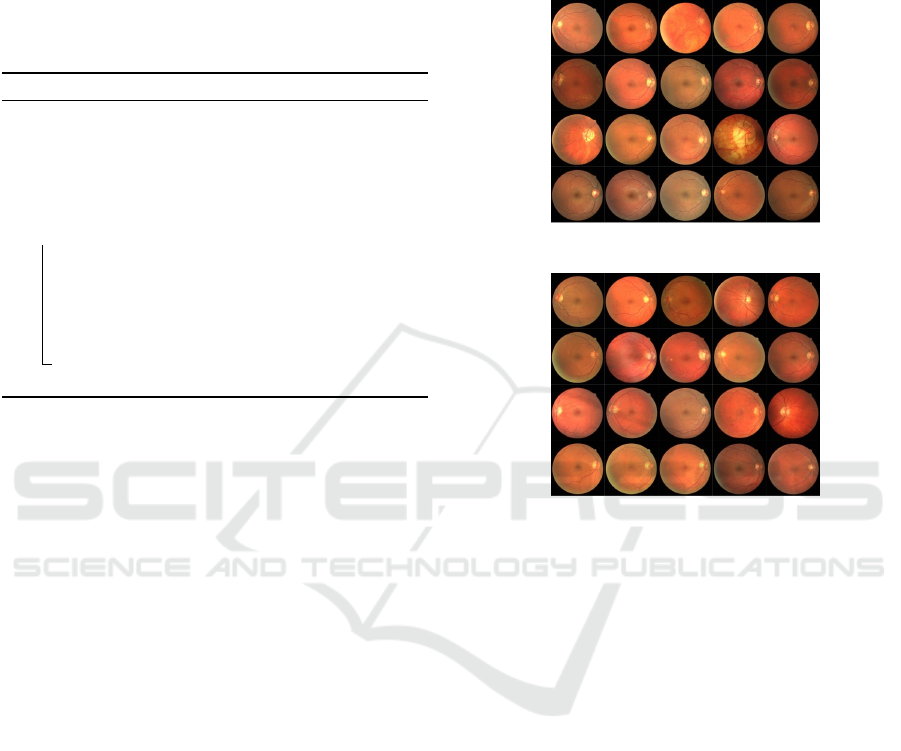
The 40 images were separated into two sets, each

with 20 images. A training set, Fig. 3, and a test set,

Fig. 4. The training set is further separated into a

validation set and a training set. A single manual seg-

mentation of the vasculature is provided for the train-

ing images. Two manual segmentations are provided

for the test cases. One works as a gold standard, while

the other may be used to compare computer-generated

segmentation to those of a human observer. In addi-

tion, for each retinal image, a mask image represent-

ing the area of interest is supplied. An expert ophthal-

mologist guided and trained all human observers who

manually segmented the vasculature.

Figure 3: DRIVE training images.

Figure 4: DRIVE testing images.

3.2 GA Parameters

Each experiment was run for 20 generations with a

population size of 15. This was repeated a total of

10 times. Each run used random initialisation to

create the initial population and employed one-point

crossover and bit-ﬂip mutation. Tournament selection

and generational replacement were also utilised.

Each individual was trained for 10 epochs, with

a batch size of 2, during the evolutionary run. At

the end of each run, the best performing model was

trained for a further 150 epochs.

The evolutionary parameters are summarised in

Table 1.

The ﬁtness function used was validation accuracy.

Validation accuracy helps prevent over ﬁtting, a key

concern given our small training dataset.

3.3 Genome

Our solutions are represented as genomes which are

then translated into a CNN architecture. Table 2 de-

scribes how each genome is constructed, with differ-

ent genes representing different hyper-parameters of

the SA-UNet. The number of bits for each hyper-

ECTA 2022 - 14th International Conference on Evolutionary Computation Theory and Applications

100

Table 1: List of the parameters used to run GA.

Parameter Value

Runs 10

Total Generations 20

Population Size 15

Crossover Rate 0.9

Mutation Rate 0.5

Epochs 10 (Training)

Epochs 150 (Best)

parameter depends on the number of choices avail-

able.

3.4 Hardware & Software

The experiments were run on a single machine with a

Nvidia Quadro RTX 8000 GPU. TensorFlow (Abadi

et al., 2016) was used to train the networks while the

GA framework used was DEAP (Fortin et al., 2012).

3.5 Evaluation Metrics

Each of test accuracy, sensitivity (the percentage of

true positives (TP) and which may also be considered

as the test’s sensitivity to noticing small changes),

speciﬁcity (the percentage of true negative (TN)),

Area Under the Curve (AUC), which refers to the re-

ceiver operating characteristic curve, a metric that as-

sesses how effectively predictions are scored, Positive

Predictive Value (PPV), Negative Predictive Value

(NPV) and F1 Score were used to evaluate our mod-

els.

Sensitivity =

T P

T P + FN

Speci f icity =

T N

T N + FP

PPV =

T P

T P + FP

NPV =

T N

T N + FN

F1Score =

T P

T P + 1/2(FP + FN)

In addition, we used Matthew’s Correlation Co-

efﬁcient (MCC), a technique useful for quantifying

the difference between expected and actual values

(Chicco and Jurman, 2020), which was also used in

the original SA-UNet (Guo et al., 2021) model. MCC

is a trustworthy statistical rate that delivers a high

score only if the prediction performed well in all four

confusion matrix areas (TP, FN, TN, and FP)

MCC =

T P × T N −FP × FN

(T P + FP)(T P + FN)(T N + FN)(T N + FN)

4 RESULTS

The full results from all 10 experiments can be seen

in Table 4. The hyper-parameters which yielded the

best model from each run are shown in Table 5. Each

individual, trained for 10 epochs, took approximately

5-7 minutes to train resulting in each run taking ap-

proximately 36 hours to complete (20 population *

(15+1) generations). It took a further 1 hour to train

the best-of-run individual for a further 150 epochs.

The 10 runs resulted in a mean AUC score of

0.9784. Average model weight was 14.29 M, however

interestingly, the best performing model was also the

lightest model at 8.3M

The best performing model, found in experi-

ment 2, achieved an AUC of 0.9855. A comparison of

this performance with other techniques on the DRIVE

benchmark dataset is shown in Table 3. We can see

that our GA-based approach achieves close to state-

of-the-art performance, slightly lower than RV-GAN,

which achieves an AUC of 0.9887. It outperforms

both of the well-known IterNet and VGN networks,

as well as two versions of the U-Net.

Our approach lags slightly behind the SA-UNet,

which achieves an AUC of 0.9864. However, both

our approach and the SA-UNet yield similar MCC

scores, 0.8054 and 0.8097, respectively. It is notewor-

thy that our model displays reduced overﬁtting when

compared to the SA-UNet and original U-Net, shown

in Fig. 5.

Our experimentation produced results which ex-

ceeded our previous approaches, GA-based U-Net

(AUC 0.9751) and HNAS-based (AUC 0.9749), both

of which used the UNet as a base model. Indeed,

nearly all runs found models which achieved better

performance, with the best performing models from

the GA-based U-Net only outperforming 2 runs from

10 of our latest experiments.

The hyper-parameters chosen for each model are

described in Table 5.

7 of the 10 models have depth 2, with 2 having

depth 4. Strikingly, the only model to chose depth

3 was also the best performing model, experiment 2.

Six models had ﬁlter size of 32, three models had ﬁlter

size 16 and a single best of run model had a ﬁlter size

of 64. All but one model had a kernel type of (3,3) and

all but two had a RMSprop optimizer. Sigmoid was

the most popular activation function, appearing in six

models, followed by softplus in three and relu in one.

Pooling type was roughly split evenly, with average

pooling appearing in six models and max pooling in

four models.

https://paperswithcode.com/sota/retinal-vessel-

segmentation-on-drive

Parameterising the SA-UNet using a Genetic Algorithm

101

Table 2: Genotype representation of the hyper-parameters.

Parameter Gens Choices Bit-Size

Depth D { 1, 2, 3, 4 } 2

Filter Size F { 16, 32, 64, 128 } 2

Pooling Type T { MaxPooling, AveragePooling } 1

Kernel Type K { (3,3), (5,5), (7,7), (9,9) } 2

Optimizer O { sgd, adam, adamax, adagrad, Nadam, Ftrl, Adadelta, RMSprop } 3

Activation A { relu, sigmoid, softmax, softplus, softsign, tanh, selu, elu } 3

Keep Probability P { 0.8, 0.9 } 1

Block Size B { 7, 9 } 1

(a) Our best model. (b) SA-UNet. (c) U-Net.

Figure 5: Different model’s training and validation plots for 150 epochs.

Table 3: Comparison of the AUC-ROC performance the

best model found during our experimentation with other

stat-of-the-art models. Two last models, GA-based UNet

and HNAS-based, are our previous GA-based optimisation

results.

Method AUC ROC

RV-GAN(Kamran et al., 2021) 0.9887

Study Group Learning (Zhou et al., 2021) 0.9886

SA-UNet (Guo et al., 2021) 0.9864

EXP2 0.9855

U-Net (Uysal et al., 2021) 0.9855

IterNet (Li et al., 2020) 0.9816

VGN (Shin et al., 2019) 0.9802

U-Net (Ronneberger et al., 2015) 0.9755

GA-based U-Net (Popat et al., 2020) 0.9751

HNAS-based (Houreh et al., 2021) 0.9749

DropBlock’s hyper-parameters showed equal us-

age, with keep probability of 0.8 appearing in six

models and 0.9 in four, while block sizes of 7 and

9 both appearing 5 times each.

5 CONCLUSION

A genetic algorithm was used to optimise the design

and hyper-parameters of a convolution neural network

used for image segmentation. Previously, the U-Net

was used as a base model to be optimised. How-

ever, due in part to the small training dataset used, the

model can have a high overﬁtting rate. Therefore, an

updated version of the U-Net, the SA-UNet was used

as the base model in our latest experimentation as it

has shown improved performance over the original U-

Net. The SA-UNet includes a spacial attention func-

tion in the middle of it’s model. We also extend the

previous experimentation by including DropBlock.

Our results showed improved performance over

previous GA-based methods, increasing the model

best founds AUC from 0.9751 to 0.9855. We also

achieved improved performance over the base U-Net.

The base SA-UNet model still marginally outper-

forms the best model we found, with an AUC of

0.9864.

The results show the addition of DropBlock and

spatial attention in U-Net architecture improves the

models prediction and the genetic algorithm can ef-

fectively be used to ﬁnd the best combination of

hyper-parameters for the model.

In future we plan to use other evolutionary algo-

rithm such as Grammatical Evolution (GE) to check

if we can improve the CNN models with more ﬂexi-

bility. Another potential work is using different data

augmentation techniques and let the evolutionary al-

gorithm to pick the best one.

ECTA 2022 - 14th International Conference on Evolutionary Computation Theory and Applications

102

Table 4: Hyper-parameters of the 10 Best models.

TestAcc Sensitivity Speci f icity NPV PPV AUC F1 MCC Weight

Exp1 0.9666 0.7800 0.9840 0.9790 0.8277 0.9805 0.8033 0.7855 10.8 M

Exp2 0.9689 0.8225 0.9830 0.9830 0.8224 0.9855 0.8225 0.8054 8.3 M

Exp3 0.9670 0.7725 0.9856 0.9783 0.8376 0.9677 0.8038 0.7865 10.8 M

Exp4 0.9679 0.7792 0.9860 0.9790 0.8422 0.9817 0.8095 0.7927 20.3 M

Exp5 0.9672 0.7962 0.9836 0.9805 0.8231 0.9799 0.8094 0.7916 10.6 M

Exp6 0.9658 0.7547 0.9861 0.9767 0.8390 0.9751 0.7947 0.7774 20.6 M

Exp7 0.9657 0.7420 0.9872 0.9755 0.8473 0.9771 0.7912 0.7746 19.9 M

Exp8 0.9651 0.7695 0.9838 0.9780 0.8205 0.9740 0.7941 0.7756 20.4 M

Exp9 0.9670 0.7763 0.9853 0.9787 0.8352 0.9811 0.8047 0.7873 10.6 M

Exp10 0.9663 0.8189 0.9804 0.9826 0.8010 0.9813 0.8099 0.7914 10.6 M

Table 5: Hyper-parameters of the 10 Best models.

D F T K O A P B

Exp1 2 32 2 (3, 3) adam sigmoid 0.9 7

Exp2 3 16 2 (3, 3) RMSprop sigmoid 0.8 7

Exp3 2 32 2 (3, 3) RMSprop relu 0.9 9

Exp4 2 32 1 (3, 3) RMSprop sigmoid 0.8 9

Exp5 2 32 2 (5, 5) RMSprop sigmoid 0.9 7

Exp6 4 16 1 (3, 3) RMSprop softplus 0.9 9

Exp7 2 64 2 (3, 3) RMSprop softplus 0.8 9

Exp8 4 16 1 (3, 3) Nadam sigmoid 0.8 9

Exp9 2 32 2 (3, 3) RMSprop softplus 0.8 7

Exp10 2 32 1 (3, 3) RMSprop sigmoid 0.8 7

ACKNOWLEDGEMENTS

This project was supported by the Science Foundation

Ireland (SFI) Centre for Research Training in Artiﬁ-

cial Intelligence (CRT-AI), Grant No. 18/CRT/6223,

and also the Irish Software Engineering Research

Centre (Lero), the research Grant No. 16/IA/4605.

REFERENCES

Abadi, M., Barham, P., Chen, J., Chen, Z., Davis, A., Dean,

J., Devin, M., Ghemawat, S., Irving, G., Isard, M.,

et al. (2016). {TensorFlow}: A system for {Large-

Scale} machine learning. In 12th USENIX sympo-

sium on operating systems design and implementation

(OSDI 16), pages 265–283.

Baldi, P. and Sadowski, P. J. (2013). Understanding

dropout. Advances in neural information processing

systems, 26.

Burks, A. W. (1986). A radically non-von-neumann-

architecture for learning and discovery. In Interna-

tional Conference on Parallel Processing, pages 1–17.

Springer.

Chicco, D. and Jurman, G. (2020). The advantages of the

matthews correlation coefﬁcient (mcc) over f1 score

and accuracy in binary classiﬁcation evaluation. BMC

genomics, 21(1):1–13.

Ciulla, T. A., Amador, A. G., and Zinman, B. (2003). Dia-

betic retinopathy and diabetic macular edema: patho-

physiology, screening, and novel therapies. Diabetes

care, 26(9):2653–2664.

Dietterich, T. (1995). Overﬁtting and undercomputing in

machine learning. ACM computing surveys (CSUR),

27(3):326–327.

Fortin, F.-A., De Rainville, F.-M., Gardner, M.-A. G.,

Parizeau, M., and Gagn

e, C. (2012). Deap: Evolu-

tionary algorithms made easy. The Journal of Machine

Learning Research, 13(1):2171–2175.

Ghiasi, G., Lin, T.-Y., and Le, Q. V. (2018). Dropblock:

A regularization method for convolutional networks.

Advances in neural information processing systems,

31.

Guo, C., Szemenyei, M., Yi, Y., Wang, W., Chen, B.,

and Fan, C. (2021). Sa-unet: Spatial attention u-net

for retinal vessel segmentation. In 2020 25th Inter-

national Conference on Pattern Recognition (ICPR),

pages 1236–1242. IEEE.

Holland, J. H. (1975). Adaptation in Natural and Artiﬁcial

Systems. University of Michigan Press, Ann Arbor,

MI. second edition, 1992.

Parameterising the SA-UNet using a Genetic Algorithm

103

Houreh, Y., Mahdinejad, M., Naredo, E., Dias, D. M., and

Ryan, C. (2021). Hnas: Hyper neural architecture

search for image segmentation. In ICAART (2), pages

246–256.

Kamran, S. A., Hossain, K. F., Tavakkoli, A., Zuckerbrod,

S. L., Sanders, K. M., and Baker, S. A. (2021). Rv-

gan: segmenting retinal vascular structure in fundus

photographs using a novel multi-scale generative ad-

versarial network. In International Conference on

Medical Image Computing and Computer-Assisted In-

tervention, pages 34–44. Springer.

LeCun, Y., Bengio, Y., et al. (1995). Convolutional net-

works for images, speech, and time series. The

handbook of brain theory and neural networks,

3361(10):1995.

Li, L., Verma, M., Nakashima, Y., Nagahara, H., and

Kawasaki, R. (2020). Iternet: Retinal image segmen-

tation utilizing structural redundancy in vessel net-

works. In Proceedings of the IEEE/CVF Winter Con-

ference on Applications of Computer Vision, pages

3656–3665.

Ogurtsova, K., da Rocha Fernandes, J., Huang, Y., Lin-

nenkamp, U., Guariguata, L., Cho, N. H., Cavan, D.,

Shaw, J., and Makaroff, L. (2017). Idf diabetes at-

las: Global estimates for the prevalence of diabetes

for 2015 and 2040. Diabetes research and clinical

practice, 128:40–50.

Popat, V., Mahdinejad, M., Cede

no, O. D., Naredo, E., and

Ryan, C. (2020). Ga-based u-net architecture opti-

mization applied to retina blood vessel segmentation.

In IJCCI, pages 192–199.

Ronneberger, O., Fischer, P., and Brox, T. (2015). U-net:

Convolutional networks for biomedical image seg-

mentation. CoRR, abs/1505.04597.

Shin, S. Y., Lee, S., Yun, I. D., and Lee, K. M. (2019). Deep

vessel segmentation by learning graphical connectiv-

ity. Medical image analysis, 58:101556.

Staal, J. (2018). DRIVE: Digital retinal images for vessel

extraction.

Turing, A. M. (1990). The chemical basis of morphogene-

sis. Bulletin of mathematical biology, 52(1):153–197.

Uysal, E. S., Bilici, M. S¸., Zaza, B. S.,

Ozgenc¸, M. Y.,

and Boyar, O. (2021). Exploring the limits of data

augmentation for retinal vessel segmentation. arXiv

preprint arXiv:2105.09365.

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones,

L., Gomez, A. N., Kaiser, Ł., and Polosukhin, I.

(2017). Attention is all you need. Advances in neural

information processing systems, 30.

Wang, B., Qiu, S., and He, H. (2019). Dual encoding u-net

for retinal vessel segmentation. In International con-

ference on medical image computing and computer-

assisted intervention, pages 84–92. Springer.

Winder, R. J., Morrow, P. J., McRitchie, I. N., Bailie, J., and

Hart, P. M. (2009). Algorithms for digital image pro-

cessing in diabetic retinopathy. Computerized medical

imaging and graphics, 33(8):608–622.

Woo, S., Park, J., Lee, J.-Y., and Kweon, I. S. (2018). Cbam:

Convolutional block attention module. In Proceed-

ings of the European conference on computer vision

(ECCV), pages 3–19.

Zhou, Y., Yu, H., and Shi, H. (2021). Study group learning:

Improving retinal vessel segmentation trained with

noisy labels. In International Conference on Medi-

cal Image Computing and Computer-Assisted Inter-

vention, pages 57–67. Springer.

Zhou, Z., Rahman Siddiquee, M. M., Tajbakhsh, N., and

Liang, J. (2018). Unet++: A nested u-net architecture

for medical image segmentation. In Deep learning in

medical image analysis and multimodal learning for

clinical decision support, pages 3–11. Springer.

ECTA 2022 - 14th International Conference on Evolutionary Computation Theory and Applications

104