Degree Centrality Algorithms for Homogeneous Multilayer Networks

Hamza Reza Pavel, Abhishek Santra and Sharma Chakravarthy

Computer Science and Engineering Department and, Information Technology Laboratory (IT Lab),

The University of Texas at Arlington, Arlington, Texas 76019, U.S.A.

Keywords:

Homogeneous Multilayer Networks, Degree Centrality, Decoupling Approach, Accuracy & Precision.

Abstract:

Centrality measures for simple graphs/networks are well-deﬁned and each has numerous main-memory al-

gorithms. However, for modeling complex data sets with multiple types of entities and relationships, simple

graphs are not ideal. MultiLayer Networks (or MLNs) have been proposed for modeling them and have been

shown to be better suited in many ways. Since there are no algorithms for computing centrality measures

directly on MLNs, existing strategies reduce (aggregate or collapse) MLN layers to simple networks using

Boolean AND or OR operators. This approach negates the beneﬁts of MLN modeling as these computations

tend to be expensive and furthermore results in loss of structure and semantics.

In this paper, we propose heuristic-based algorithms for computing centrality measures (speciﬁcally, de-

gree centrality) on MLNs directly (i.e., without reducing them to simple graphs) using a newly-proposed

decoupling-based approach which is efﬁcient as well as structure and semantics preserving. We propose mul-

tiple heuristics to calculate the degree centrality using the network decoupling-based approach and compare

accuracy and precision with Boolean OR aggregated Homogeneous MLNs (HoMLNs) for ground truth. The

network decoupling approach can take advantage of parallelism and is more efﬁcient compared to aggregation-

based approaches. Extensive experimental analysis is performed on large synthetic and real-world data sets of

varying graph characteristics to validate the accuracy, precision, and efﬁciency of our proposed algorithms.

1 INTRODUCTION

In graph-based applications, an important require-

ment is to measure the importance of a node/vertex,

which can translate to meaningful real-world infer-

ences on the data set. For example, cities that act

as airline hubs, people on social networks who can

maximize the reach of an advertisement/tweet/post,

identiﬁcation of mobile towers whose malfunction-

ing can lead to the maximum disruption, and so on.

Centrality measures include degree centrality (Br

odka

et al., 2011), closeness centrality (Cohen et al., 2014),

eigenvector centrality (Sol

a et al., 2013), stress cen-

trality (Shi and Zhang, 2011), betweenness centrality

(Brandes, 2001), harmonic centrality (Boldi and Vi-

gna, 2014), and PageRank centrality (Pedroche et al.,

2016), are some of the well-deﬁned and widely-used

local and global centrality measures.

These centrality measurements use a set of crite-

ria to determine the importance of a node or edge in

a graph. Degree centrality metric measures the im-

portance of a node in a graph in terms of its degree,

which is the number of 1-hop neighbors a node has in

the graph. Most centrality metrics are clearly deﬁned

for simple graphs or monographs or networks, and

there are numerous techniques for calculating them

on simple graphs. However, for modeling complex

data sets with multiple types of entities and relation-

ships, multilayer networks have been shown to be a

better alternative due to the clarity of representation,

ability to preserve the structure and semantics of dif-

ferent types of relationships for the same and different

sets of nodes, and support efﬁcient computation using

parallelism (Kivel

a et al., 2014; Santra et al., 2017b;

Fortunato and Castellano, 2009).

A multilayer network (De Domenico et al., 2013;

Santra and Bhowmick, 2017; Santra et al., 2020)

is made up of layers, each of which is a simple

graph or a network with nodes (that correspond to

entities) and edges (that correspond to relationships).

Nodes within a layer are connected (termed intra-

layer edges) based on a relationship between nodes.

Nodes in a layer may also be optionally connected to

nodes in other layers through inter-layer edges. As

an example, the diverse interactions among the same

set of people across different social media (such as

Facebook, LinkedIn, and Twitter) can be modeled

using a multilayer network (see Figure 1.) In this

Pavel, H., Santra, A. and Chakravarthy, S.

Degree Centrality Algorithms for Homogeneous Multilayer Networks.

DOI: 10.5220/0011528900003335

In Proceedings of the 14th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2022) - Volume 1: KDIR, pages 51-62

ISBN: 978-989-758-614-9; ISSN: 2184-3228

MLN, the entities in each layer are the same, but the

relationships in each layer are different (Facebook-

friends, Twitter-relationships, LinkedIn-connections),

this sort of MLN is referred to as homogeneous MLNs

(or HoMLNs). As and the edges between layers are

implicit, they are not shown. It is also feasible to build

MLNs with different types of entities and relation-

ships within and between layers. This form of het-

erogeneous MLNs (or HeMLNs) is required for mod-

eling, for example, the DBLP data set (dbl, ) with au-

thors, articles, and conferences (Kivel

a et al., 2014).

Hybrid Multilayer networks (HyMLNs) include both

types of layers.

Figure 1: Social Media HoMLN Example.

For a social-network HoMLN such as the one

shown in Figure 1, it will be interesting to ﬁnd out

the set of people who are the most inﬂuential in a

single network or across multiple (or a subset of) so-

cial networks. This corresponds to ﬁnding out the de-

gree centrality nodes of a MLN using one or more

layers. Since extant algorithms that calculate degree

centrality measures on networks are limited to sim-

ple graphs/networks, MLNs need to be converted (us-

ing aggregation or projection) to simple graphs which

leads to the loss of structure and semantics. This pa-

per presents heuristic-based algorithms for computing

degree centrality nodes (or DC nodes) on HoMLNs

directly with high accuracy/precision and efﬁciency.

Boolean OR composition of layers is used for ground

truth in this paper.

For comparing the accuracy and precision of the

decoupling-based algorithms, we use Boolean opera-

tors for aggregation of layers and use simple graph al-

gorithms on them for ground truth. Other types of ag-

gregations are also possible. The aggregation of lay-

ers using AND and OR Boolean operators for homo-

geneous MLNs are straightforward as the nodes are

the same in each layer and the Boolean operator se-

mantics are applied to the edges. Both AND and OR

operators are commutative and distributive. OR ag-

gregation is likely to increase the size of the graph

(number of edges) used for ground truth. Accuracy is

computed by comparing the ground truth results for

the graph with the results obtained by the decoupling-

based algorithm for the layers of the same graph. The

naive algorithm uses only the results of each layer for

the computation (in this case degree centrality) and

applies the Boolean operator to the individual results

during the composition step. Typically, the naive ap-

proach does not yield good accuracy requiring addi-

tional information from each layer to be retained and

used for the composition algorithm using heuristics.

As layers are processed independently (may be in par-

allel), no information about the other layer is assumed

while processing a layer.

We adapt the decoupling-based approach pro-

posed in (Santra et al., 2017a; Santra et al., 2017b)

for our algorithms. Based on this approach, we com-

pute centrality on each layer independently once and

keep minimal additional information from each layer

for composing. With this, we can efﬁciently estimate

the degree centrality (DC) nodes of the HoMLN. This

approach has been shown to be application indepen-

dent, efﬁcient, lends itself to parallel processing (of

each layer), and is ﬂexible for computing centrality

measures on any subset of layers. The naive approach

to which we compare our proposed heuristic-based

accuracy and precision retains no additional informa-

tion from the layers apart from the degree centrality

nodes and their values. Contributions of this paper

are:

• Algorithms for directly computing degree cen-

trality nodes of Homogeneous MLNs (HoMLNs.)

• Several heuristics to improve accuracy, preci-

sion, and efﬁciency of computed results

• Decoupling-based approach to preserve struc-

ture and semantics of MLNs

• Experimental analysis on large number of syn-

thetic and real-world graphs with diverse charac-

teristics

• Accuracy, Precision, and Efﬁciency compar-

isons with ground truth and naive approach

The rest of the paper is organized as follows: Sec-

tion 2 discusses related work. Section 3 introduces

the decoupling approach used for MLN analysis and

discusses its advantages and challenges. Section 4

discusses ground truth and naive approach to degree

centrality. Sections 5 and 6 describe composition-

based degree centrality computation for HoMLNs us-

ing heuristics for accuracy and precision, respectively.

Section 7.1 describes the experimental setup and the

KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval

data sets. Section 7.2 discusses result analysis fol-

lowed by conclusions in Section 8.

2 RELATED WORK

As complex and massive real-world data sets are be-

coming more popular and accessible, there is a press-

ing need to model them using the best approach

and analyze them efﬁciently in various ways. How-

ever, use of graphs for their modeling and especially

MLNs poses additional challenges in terms of com-

puting centrality measures on MLNs instead of sim-

ple graphs. Centrality measures including MLN cen-

trality shed light on various properties of the network.

Although there have been numerous studies on rec-

ognizing central entities in simple graphs, there have

been few studies on detecting central entities in mul-

tilayer networks. Existing research for ﬁnding central

entities in multilayer networks is use-case speciﬁc,

and there is no standard paradigm for addressing the

problem of detecting central entities in a multilayer

network.

Degree centrality is the most common and widely-

used centrality measure. Degree centrality is used to

identify essential proteins (Tang et al., 2013). It is

also used in identifying epidemics in animals (Can-

deloro et al., 2016) and the response of medication

in children with epilepsy (Wang et al., 2021). The

most common and prominent use of degree central-

ity is in the domain of social network analysis. Some

of the common use of degree centrality in social net-

work analysis is identifying the most inﬂuential node

(Srinivas and Velusamy, 2015), inﬂuential spreaders

of information (Liu et al., 2016), ﬁnding opinion lead-

ers in a social network (Risselada et al., 2016), etc.

Despite being one of the most common and widely

used centrality measures, very few algorithms or solu-

tions exist to directly calculate the degree centrality of

a MLN. In this study (Br

odka et al., 2011), the author

proposes a solution to ﬁnd degree centrality in a 10-

layer MLN consisting of the Web 2.0 social network

data set. Similar to the previous work, in (Rachman

et al., 2013), authors identify the degree centrality of

nodes using the Kretschmer method. The authors in

this study (Yang et al., 2014) proposed a node promi-

nence proﬁle-based method to effectively predict the

degree centrality in a network. In another study (Gaye

et al., 2016), authors propose a solution to ﬁnd the

top-K inﬂuential person in a MLN social network us-

ing diffusion probability. More recently there has

been some work in developing algorithms for MLNs

using the decoupling-based approach (Santra et al.,

2017b).

The majority of degree centrality computation al-

gorithms are main memory based and are not suit-

able for large graphs. They are also use-case spe-

ciﬁc. In this paper, we adapt a decoupling-based tech-

nique proposed in (Santra et al., 2017b) for MLNs,

where each layer can be analyzed individually and

in parallel, and graph characteristics (such as de-

gree centrality nodes) for a HoMLN can be cal-

culated utilizing the information gathered for each

layer. Our algorithms follow the network decoupling

methodology, which has been demonstrated to be efﬁ-

cient, ﬂexible, and scalable. Achieving desired accu-

racy/precision/recall, however, is the challenge. Our

approach is not strictly main-memory based as each

layer (which is likely to be smaller than the aggre-

gated graph) outputs results into a ﬁle which are used

for the decomposition algorithm. Also, as each layer

is likely to be smaller than the OR aggregation of lay-

ers, larger size MLNs can be accommodated in our

approach.

3 NETWORK DECOUPLING

APPROACH

Existing multilayer network analysis approaches con-

vert or transform a MLN into a simple graph

. Ag-

gregating or projecting the network layers into a sim-

ple graph accomplishes this. Edge aggregation is used

to bring homogeneous MLNs together into a simple

graph. Although aggregating a MLN into a simple

network enables the use of currently available tech-

niques for centrality and community discovery (of

which there are many), the MLN structure and se-

mantics are not retained, causing information loss.

We use the network decoupling strategy for MLN

analysis to overcome the aforementioned difﬁculties.

Figure 2 shows the proposed network decoupling

strategy. It entails determining two functions: one

for analysis (Ψ) and the other for composition (Θ).

Each layer is analyzed independently using the anal-

ysis function (and in parallel). The partial results (as

they are called) from each of the two layers are then

combined using a composition function/algorithm to

obtain the HoMLN results for the two layers. MLNs

with more than two layers can use this binary com-

position repeatedly. Independent analysis permits the

use of existing techniques for each layer. Decoupling,

on the other hand, increases efﬁciency, ﬂexibility, and

scalability along with extending the existing graph

A simple graph has nodes that are connected by edges

(optionally labeled and/or directed) with no loops or multi-

ple edges between same odes.

Degree Centrality Algorithms for Homogeneous Multilayer Networks

Figure 2: Overview of the network decoupling approach.

analysis algorithms to compute directly on MLNs.

As the network decoupling method preserves the

structure and semantics of the data, drill-down and vi-

sualization of ﬁnal results are easy to support. Each

layer (or graph) is likely to be smaller, consume less

memory than the whole MLN, and composition is

done as a separate step on the partial results. The

analysis function results are preserved and used in

the composition. The requirement to recompute is re-

duced because the result of analysis for a layer can

be reused by several composition functions, increas-

ing the efﬁciency of the decoupling-based approach.

Individual layers can be analyzed using any of the

available simple graph centrality algorithms. This

method is also application-independent. As a result,

the decoupling-based approach can be used to extend

existing centrality algorithms to MLNs. To compose

the outputs of analysis functions (partial results) into

the ﬁnal results, we only need to deﬁne the composi-

tion function.

The problem with a decoupling-based approach is

getting high accuracy when compared to the ground

truth. This translates to one of the major challenges

in determining the minimum additional information

to retain as part of the layer analysis step to be used

during composition to improve the overall accuracy

and precision with respect to the ground truth. For

many composition algorithms we have looked into,

there is a trade-off between using more information

from each layer and improving accuracy or precision.

This trade-off is demonstrated in this paper as well.

The decoupling approach’s layer-wise analysis

has a number of advantages. First, only a smaller

layer of the network needs to be loaded into memory,

rather than the whole network. Second, the analysis

of individual layers can be parallelized, reducing the

algorithm’s overall storage requirements and execu-

tion time. Finally, the composition function (Θ) relies

on intuition, which is built into the heuristic and takes

substantially less complex computationally than Ψ.

The accuracy of a MLN analysis algorithm is de-

termined by the information we keep (in addition to

the output) during individual layer analysis. The ba-

sic minimum information we may maintain from each

layer in terms of centrality measurements is the high

centrality nodes of that layer, as well as their central-

ity values. The accuracy should potentially improve

as we retain more relevant information for compo-

sition. However, determining what is relevant and

should be retained to improve accuracy or precision is

the main challenge of this approach. The key hurdles

are identifying the most beneﬁcial minimal informa-

tion and the intuition for their effectiveness.

4 DEGREE CENTRALITY FOR

MLNs

The degree of a node in a graph is the total number

of edges that are incident on it

. Degree hubs are

nodes in a network that have a degree larger than

or equal to the network’s average degree. Degree

hubs are speciﬁed for simple graphs. In (Santra et al.,

2017b), the authors have proposed three algorithms

to estimate degree hubs in AND composed multilayer

networks. However, there are no algorithms for cal-

culating degree hubs for OR composed HoMLNs.

If the HoMLN layers are composed of a Boolean op-

eration such as OR, we can expand the notion of a hub

from a simple graph to HoMLNs. In this paper, we

suggest various composition functions to maximize

accuracy, precision, and efﬁciency while estimating

degree hubs in OR composed multilayer networks.

The ground truth is used to evaluate the perfor-

mance and accuracy of our suggested heuristics for

detecting the degree hubs of a multilayer network.

The degree centrality of a vertex u in a network

is deﬁned as C

(u) = Number of adjacent or 1-hop

neighbors. This value is divided by the maximum

number of edges a vertex can have to normalize it.

The equation for normalized degree centrality is:

(v) =

degree(v)

n − 1

(1)

High centrality hubs or degree hubs are the ver-

tices with normalized degree centrality values higher

than the other vertices.

Even though there are different variants of degree

centrality such as the group degree centrality (Ev-

erett and Borgatti, 1999), time scale degree central-

ity (Uddin and Hossain, 2011), and complex degree

We use degree as 1-hop neighbors in this paper without

taking direction into account. However, for directed graphs,

in- or out-degree can be substituted for the heuristics pro-

posed. Hence, we discuss only undirected graphs.

KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval

centrality (Kretschmer and Kretschmer, 2007), in this

paper, we only address the normalized degree cen-

trality for Boolean OR composed undirected homo-

geneous multilayer networks. We propose several

algorithms to identify high centrality degree hubs in

Boolean OR composed MLNs. We test the accuracy,

precision, and efﬁciency of our algorithm against the

ground truth. With extensive experiments on data sets

of varying graph characteristics, we show that our ap-

proaches perform better than the naive approach and

are efﬁcient compared to the ground truth.

For degree centrality, the ground truth is calcu-

lated as follows:

• First, all the layers of the network are aggregated

into a single layer using the Boolean OR aggrega-

tion function.

• Degree centrality of the aggregated graph is cal-

culated and the hubs are identiﬁed.

We compare the hubs computed by our algorithms

against ground truth for accuracy and/or precision.

We use Jaccard’s coefﬁcient as the measure to com-

pare the accuracy of our solutions with the ground

truth.

Our aim is to design heuristics based on intuition

and algorithms using the network decouple approach

so that our accuracy for degree centrality is much bet-

ter than the naive approach and closer to the ground

truth. Efﬁciency is expected be better than that of the

ground truth. For the naive composition approach, we

estimate the degree hubs in OR composed layers as

the union of the degree hubs of the individual lay-

ers (for OR aggregation). Even though our solution

works for any arbitrary number of layers, we have fo-

cused on two layers which can be applied repeatedly

for more than two layers.

5 DEGREE CENTRALITY

HEURISTICS FOR ACCURACY

We measure accuracy with respect to ground truth us-

ing the Jaccard coefﬁcient. An accuracy of 1 indicates

an exact match with the ground truth without any false

positives or false negatives. The goal is to get accu-

racy as close to 1 as possible using the decoupling

approach. For most applications, high accuracy is de-

sired. In this section, we present two heuristic-based

composition algorithms with better overall accuracy

as compared to the naive approach.

5.1 Degree Centrality Heuristic

Accuracy 1 (DC-A1)

Intuitively, with the information from each layer, we

are trying to estimate the degree of a node when the

layers are aggregated. If we can do it effectively,

we can use the approximated average degree of the

OR aggregation to determine whether a node is a hub

when layers are combined. For layers x and y, based

on the OR operator semantics, the estimated degree

estDeg

xORy

(u) of a node u in the OR composed layer

can be max(deg

(u), deg

(u)). This happens when the

one-hop neighbor of the node u in layer x is a subset

of the one-hope neighbor of the same node in layer y

or vice-versa. We can use this estimated degree value

of the nodes to directly calculate the degree hubs of

the HoMLN in the OR composed layer. Algorithm 1

describes the steps of the composition or Θ step using

this heuristic.

Algorithm 1: Procedure for Heuristic DC-A1.

Require: deg

, deg

, DHxORy ←

1: for u ∈ x do

2: estDeg

xORy

(u) ← max(deg

(u), deg

(u))

3: end for

4: Calculate DH

xORy

using estDeg

xORy

(u)

As can be seen from Table 1 (details in Section 7.1)

and Figure 3, this heuristic improves accuracy for

data sets where the edge distribution is equal and fur-

ther accuracy improves as the data set size increases.

This is as expected as equal distribution of edges pro-

vides a better estimated degree for the combined lay-

ers. And for data sets with a larger number of edges,

even with non-equal distribution, the average degree

of the combined layers is smoother than for small data

sets. This observation holds for the other synthetic

data sets as well. For real-world data sets, both DC-

A1 and DC-A2 are uniformly signiﬁcantly better than

the naive and do not deviate much from synthetic data

sets with wider coverage of edge distributions and de-

gree distributions.

5.2 Degree Centrality Heuristic

Accuracy 2 (DC-A2)

In the DC-A1 heuristic, we assumed that the one-hop

neighbors of a node u in layer x are going to be a sub-

set of one-hop neighbors of the same node in layer y

or vice-versa. When we are estimating the degree of

a node u in the OR composed layer, there is a mini-

mum value and maximum value for the estimated de-

gree value of that node. The minimum of the esti-

mated degree value is max(deg

(u), deg

(u)). Sim-

Degree Centrality Algorithms for Homogeneous Multilayer Networks

Table 1: Summary of Synthetic Data Set-1 (Both layers with power-law degree distribution).

Base Graph

Edge Dist. % #Edges

#Nodes, #Edges in Layers L1 L2 L1 OR L2

100KV, 500KE

1 70,30 350000 150000 499587

2 60,40 200000 300000 499505

3 50,50 250000 250000 499505

100KV, 1ME

4 70,30 700000 300000 998303

5 60,40 600000 400000 998176

6 50,50 500000 500000 997998

100KV, 2ME

7 70,30 600000 1400000 1993608

8 60,40 1200000 800000 1992855

9 50,50 1000000 1000000 1992207

300KV, 1.5ME

10 70,30 1050000 450000 1499463

11 60,40 900000 600000 1499425

12 50,50 750000 750000 1499347

300KV, 3ME

13 70,30 2100000 900000 2997825

14 60,40 1800000 1200000 2997627

15 50,50 1500000 1500000 2997538

300KV, 6ME

16 70,30 4200000 1800000 5991761

17 60,40 3600000 2400000 5990599

18 50,50 3000000 3000000 5990044

500KV, 2.5ME

19 70,30 1750000 750000 2499344

20 60,40 1500000 1000000 2499238

21 50,50 1250000 1250000 2499166

500KV, 5ME

22 70,30 3500000 1500000 4997388

23 60,40 3000000 2000000 4996910

24 50,50 2500000 2500000 4997209

500KV, 10ME

25 70,30 7000000 3000000 9989402

26 60,40 6000000 4000000 9989190

27 50,50 5000000 5000000 9987447

ilarly, the maximum value of the estimated degree

could be min(((deg

(u) + deg

(u)), (n − 1)) when

there is no common one-hop neighbour among layer

x and y for node u. Here n is the number of

nodes in each layer of the HoMLN. Based on ob-

servations of various datasets, the estimated degree

of a node u in the OR composed layers is neither

the possible minimum nor possible maximum value,

rather somewhere close to the average of these val-

ues. Thus, we estimate the estimated degree of node

u in the OR composed layer, estDeg

xORy

(u), as the av-

erage of max(deg

(u), deg

(u)) and min(((deg

(u) +

deg

(u)), (n − 1)). We then use the estDeg

xORy

(u) of

the nodes to calculate the degree hubs of the OR com-

posed layer.

Note that in this heuristic, we are not using any

additional information than heuristic DC-A1, but

changing our estimation to a more intuitive, meaning-

ful, and realistic value than taking an extreme. With

this simple change in the heuristic, again from Table 1

and Figure 3, one can see a signiﬁcant improvement

in accuracy over DC-A1. In fact, some of the accu-

racy reach as high as 0.98 which is as good as 1. One

can also see that the edge distribution and data set

size differences no longer have the kind of impact seen

in DC-A1. also, real-world data sets match the syn-

thetic ones to some extent.

This heuristic validates the conjecture that both in-

KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval

Figure 3: Accuracy Comparison for Synthetic Data Set 1 (Refer to Table 1).

tuition and additional information play a signiﬁcant

role in identifying composition algorithms. Retaining

more information by itself is not sufﬁcient unless it is

combined with proper intuition!

6 DEGREE CENTRALITY

HEURISTICS FOR PRECISION

As mentioned in the previous section, we have used

accuracy to compare the effectiveness of our heuris-

tics (using the the Jaccard coefﬁcient.) Based on use

cases, accuracy might not be the only measure of in-

terest for many real-world applications. For example,

An airline is trying to expand its operation to a new

city based on the air routes and operation of other

competitors. This problem can be modeled as a prob-

lem to ﬁnd the degree hubs of a HoMLN where each

node of the HoMLN is a city and each layer repre-

sent the route of the competitors among these cities.

In this scenario, a high precision algorithm is pre-

ferred as a false positive in identifying a hub might

lead the airline to expand to a city without much traf-

ﬁc and incur loss due to the expansion. Advertising

on multiple social networks also has a similar need to

avoid false positives. Hence, in general, it is mean-

ingful to identify heuristics that do not produce any

false positives or any false negatives either depending

upon the application’s need. In this section, we pro-

vide two heuristics for composition algorithms to ﬁnd

the degree hubs of a HoMLN with high precision.

6.1 Degree Centrality Heuristic

Precision (DC-P1)

For the Boolean OR operator composed ground

truths, if a node is a degree hub (DH) in layer x or

layer y, then it is likely that the node is going to be a

degree hub in the OR composed ground truth. We use

this intuition as the basis for heuristic DC-P1 which is

used to develop the ﬁrst composition algorithm for the

Θ function to compute high precision degree hubs.

As we previously mentioned, in the analysis func-

tion (Ψ) of the decoupling approach we analyze the

layers of the HoMLN and use the partial results and

additional information to obtain the ﬁnal results for

the MLN. In DC-P1, after the analysis (Ψ) phase

of each layer (say layer x), we keep the set of de-

gree hubs DH

, the average degree avgDeg

, and the

set of one-hop neighbors of each degree hub (say, u)

NBD

(u)

During the Θ step, we use the stored partial re-

sults and additional information to estimate the hubs

for two layers (say layer x and layer y). As for

the OR composed ground-truth graph, the number

of edges for a node is likely to increase. We can

estimate the average degree of the OR composed

layer, avgEstDeg

xORy

, to be the maximum between

avgDeg

and avgDeg

. For each node present in ei-

ther DH

or DH

, if the union of their one-hop neigh-

bors set is more than avgEstDeg

xORy

, we consider that

node a degree hub in the OR composed layer of x and

y. Algorithm 2 shows the detailed steps of the com-

position algorithm (Θ.)

This is the additional information we retain from each

layer to improve precision as we have indicated earlier.

Degree Centrality Algorithms for Homogeneous Multilayer Networks

Figure 4: Precision Comparison for Synthetic Data Set 1 (Refer to Table 1).

Algorithm 2: Procedure for Θ using Heuristic DC-P1.

Require: DH

, avgDeg

, DH

, avgDeg

, NBD

NBD

, DH

xORy

←

1: avgEstDeg

xORy

← max(avgDeg

, avgDeg

)

2: for u ∈ DH

∪ DH

3: if |NBD

(u) ∪ NBD

(u)| >= avgEstDeg

xORy

then

4: DH

xORy

← DH

xORy

∪ u

5: end if

6: end for

Degree hubs and their values for each layer al-

low us to compute the higher bound of the average for

the aggregated graph. One-hop neighbor information

is used to reduce or eliminate false positives. How-

ever, as these are retained only for hubs, information

is still not complete. Even with this limited additional

information, as we will see in the experimental sec-

tion (Section 7.2), there is a signiﬁcant improvement

in precision over the naive for all data sets. For the

synthetic data sets, we get a precision of 100% (Fig-

ure 4) and for the real-world data sets we get a mean

precision of 96% (Refer to Section 7.2, Figure 8).

6.2 Degree Centrality Heuristic

Precision(DC-P2)

Based on how the edges are distributed in the lay-

ers of a MLN, the actual average degree of the OR

composed ground truth, avgDeg

xORy

, of layers x and

y might differ from the estimated avgEstDeg

xORy

DC-P1. If the avgEstDeg

xORy

is substantially greater

than avgEstDeg

xORy

, then a lot of nodes will not be

included as a hub in the OR composed layer despite

having enough common neighbors across both layers

x and y. Similarly, if avgEstDeg

xORy

is smaller than

avgEstDeg

xORy

, a lot of false positives will be gener-

ated as hubs in the OR composed layer.

To better estimate the avgEstDeg

xORy

, we keep the

degree of each node from each layer as additional in-

formation during the Ψ step. This allows us to esti-

mate the individual degree of a node u in the OR com-

posed layer from its degree information in layer x and

layer y. If the degree of a node u in layer x is deg

(u)

and degree of the same node in layer y is deg

(u), then

estimated degree of node u in the OR composed layer,

estDeg

xORy

(u), is going to be max(deg

(u), deg

(u)).

Using the estimated degree estDeg

xORy

(u) of each

node u, we calculate the avgEstDeg

xORy

. The rest of

the steps of the algorithm are same as 2. As can be

seen in Figure 8, this heuristic slightly increases fur-

ther the precision value for some data sets.

7 EXPERIMENTAL ANALYSIS

7.1 Data Sets and Environment

The NetworkX (Hagberg et al., 2008) package is used

in our Python implementation. All experiments were

carried out on a single node SDSC Expanse (Towns

et al., 2014). Each node in the cluster runs the Cen-

tOS Linux operating system using an AMD EPYC

7742 CPU with 128 cores and 256GB of RAM hard-

ware. Both synthetic and real-world data sets were

used to evaluate the proposed methodologies. PaR-

MAT (Khorasani et al., 2015), a parallel version of the

popular graph generator RMAT (Chakrabarti et al.,

2004), which uses the Recursive-Matrix-based graph

generation technique, was used to create the synthetic

data sets.

We use PaRMAT to produce three sets of synthetic

data sets for each base graph for experimentation. Our

synthetic data set consists of 27 HoMLNs with two

layers, each with a different edge distribution. The

base graphs start with 100K vertices with 500K edges

KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval

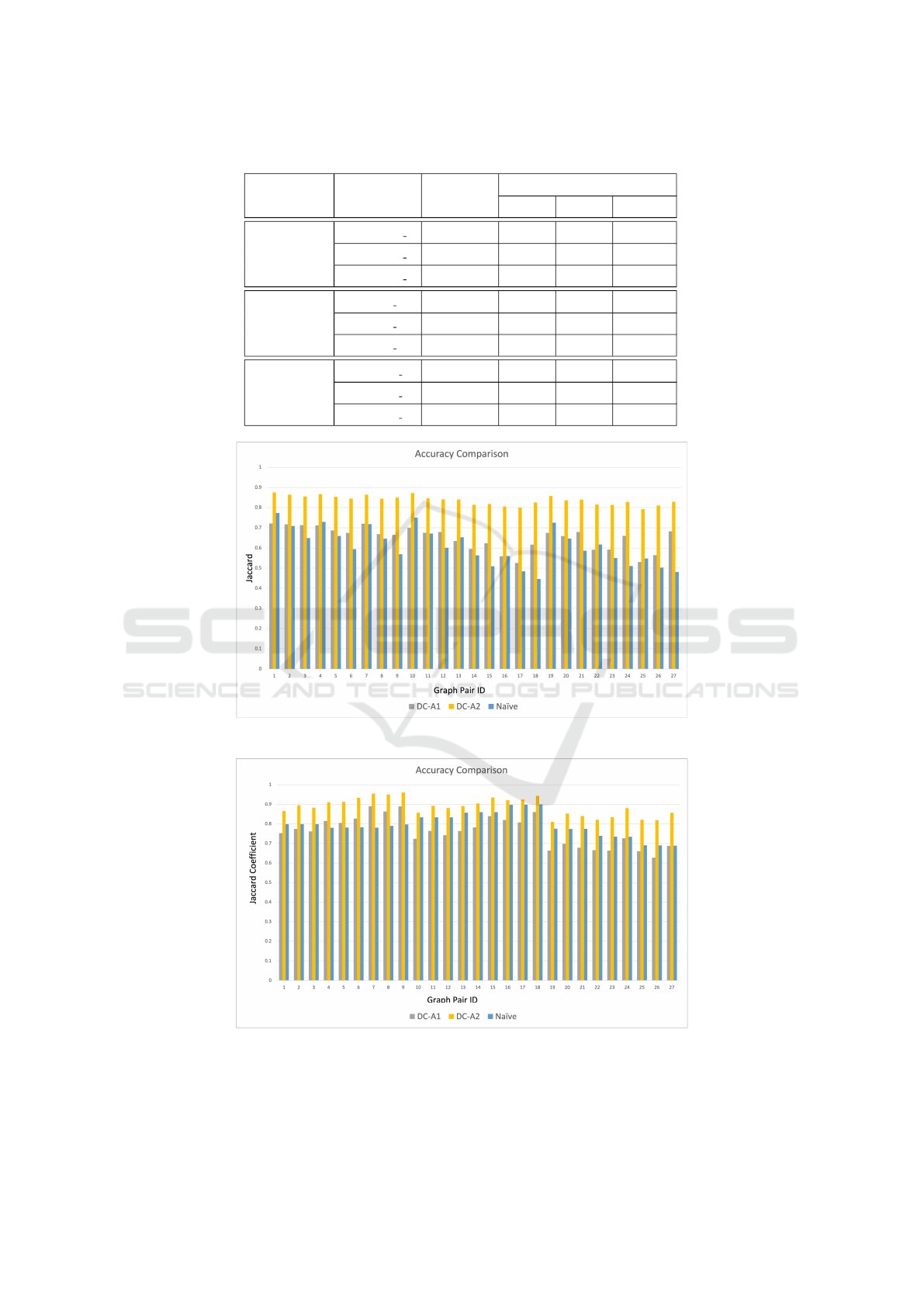
Table 2: Summary of Real World Data Set.

Base Graph

Edge Dist. % #Edges

#Nodes, #Edges in Layers L1 L2 L1 OR L2

735KV, 2.6ME

amazon-2008 1 50,50 1306357 1304863 1958865

amazon-2008 2 70,30 1828100 784552 2063141

amazon-2008 3 90,10 2349969 261133 2376256

325KV, 1.7ME

cnr-2000 1 50,50 876444 876383 1314919

cnr-2000 2 70,30 1226781 525244 1384962

cnr-2000 3 90,10 1577646 175236 1595367

100KV, 1.5ME

uk-2007-05 1 50,50 759899 761252 1141215

uk-2007-05 2 70,30 1065435 455957 1202326

uk-2007-05 3 90,10 1369767 152167 1385013

Figure 5: Accuracy Comparison for Synthetic Data Set 2.

Figure 6: Accuracy Comparison for Synthetic Data Set 3.

and go up to 500K vertices and 10 million edges. In

the ﬁrst synthetic data set (Table 1), both HoMLN lay-

ers have power-law degree distribution. In the second

synthetic data set (not shown, but similar to Table 1),

one layer (L1) follows power-law degree distribution

and the other one (L2) follows normal degree distri-

Degree Centrality Algorithms for Homogeneous Multilayer Networks

bution. In the ﬁnal synthetic data set, both layers have

normal degree distribution (again not shown, but sim-

ilar to Table 1).

For each of the aforementioned data sets, three

edge distributions (70, 30; 60, 40; and 50, 50) for a

total of 81 HoMLNs with varied edge distributions,

number of nodes, and edges are used for experimen-

tation and validation of the proposed heuristics. Ta-

ble 1 shows the different 2-layer HoMLN used in our

data set used in our experiments which are part of the

synthetic data set 1. The synthetic data set 1 consists

of HoMLN where both the layers have the power-

law distribution of edges (L1: Power-law, L2: Power-

law). The other two data sets, synthetic data set 2 and

3 have a similar number of nodes and edges in each

layer but have (L1: Power-law, L2: Normal) and (L1:

Normal, L2: Normal) edge distribution.

For our real-world-like data set (shown in Ta-

ble 2), the network layers are generated from real-

world like monographs using a random number gen-

erator. The real-world-like graphs are generated us-

ing RMAT with parameters to mimic real-world graph

data sets as discussed in (Chakrabarti, 2005). As a re-

sult, the graphs are not single connected components

and neither are their ground truth graph.

7.2 Result Analysis and Discussion

In this section, we present our experimental results.

We have tested our proposed heuristics on large real-

world and synthetic data sets. As a measure of accu-

racy, we use the Jaccard coefﬁcient and precision. We

compare the execution time of our heuristics against

the ground truth execution time as a measure of per-

formance. Figures 3, 5, and 6 show the Jaccard coef-

ﬁcient for accuracy of the proposed heuristics-based

approaches DC-A1, DC-A2, and the naive approach

for the synthetic data set 1, data set 2, and data set

3 respectively. While calculating the Jaccard coefﬁ-

cient, we consider the nodes with equal to or higher

than the average degree value in the ground truth as

degree hubs. The heuristic DC-A2 performs the best

when the accuracy metric is the Jaccard coefﬁcient.

It always shows higher accuracy than the naive ap-

proach. The heuristic DC-A1 performs better than

the naive approach in most cases. Figure 7 shows the

Jaccard coefﬁcient for the proposed heuristics in real-

world data set (Boldi and Vigna, 2004). Both heuris-

tics DC-A1 and DC-A2 perform better than the naive

approach for all the HoMLN in the data set. Table 3

shows the mean accuracy and average percentage gain

in accuracy for the synthetic and real-world data sets.

For all data sets, DC-A2 outperforms the naive ap-

proach. The DC-A1 heuristic performs poorly when

Figure 7: Accuracy Comparison for Real World Data Set

(Refer to Table 2).

both layers have a normal distribution of edges, but

performs better than naive in other cases. One reason

for the low percentage gain compared to the naive ap-

proach is, that for Boolean OR aggregated HoMLN,

the naive approach itself has relatively high accuracy.

Figure 8: Precision Comparison for real world data set (Re-

fer to Table 2).

When precision is used as the measure of accu-

racy, DC-P1 and DC-P2 outperform DC-A1, DC-A2,

as well as the naive approach. For the synthetic data

sets, the precision of DC-P1 and DC-P2 is always

100% (Figure 4) and more than 96% for the real-

world data sets (Figure 8.)

Figure 9: Comparison of Execution Time of the Heuristics

against Execution Time of Ground Truth.

Figure 9 shows the comparison of the execution

time of our proposed solutions against the ground

KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval

Table 3: Accuracy Improvement of DC-A1 and DC-A2 over Naive.

Data Set

Degree Distribution Mean Accuracy

L1, L2 DC-A1 DC-A2 DC-A1 vs. Naive DC-A2 vs. Naive

Synthetic-1 Power law, Power law 90.53% 96.01% +0.86% +6.96%

Synthetic-2 Power law, Normal 64.90% 83.74% +6.48% +37.38%

Synthetic-3 Normal, Normal 76.14% 88.72% -4.32% +11.47%

Real world Power law, Power law 93.11% 98.9% +10.03% +10.92%

truth time for 3 of the largest HoMLN of the syn-

thetic data set 1. The execution time of our approach

is calculated as maximum Ψ time of the layers + Θ

time. The ground truth time is computed as time re-

quired to aggregate layers into a single graph using

Boolean OR function + time required to ﬁnd the de-

gree hubs of the aggregated graph.

As we can see from Figure 9, ground truth exe-

cution time is more than an order of magnitude as

compared to our proposed approaches in all cases

(plotted on log scale).

As previously mentioned in Section 3, it is a chal-

lenge to identify and keep the minimum amount of

information required in the network decoupling ap-

proach. Theoretically, as more information is kept,

the accuracy should go up. It is also affected by

the use of retained information based on intuition or

understanding of aggregation method used. For this

demonstration, we used a HoMLN consisting of 100K

nodes from the synthetic dataset 2 where the ﬁrst layer

follows the power-law distribution and the second

layer follows the normal distribution. This HoMLN

was taken to minimize any similarity among the lay-

ers. The additional information kept is the one-hop

neighbors of the nodes in each layer.

Figure 10: Demonstration of increase in accuracy as more

information is kept in each layer for DC-A2.

In Figure 10 we show that as more information

is kept in each layer, the accuracy increases. If no

information is kept, we get the lowest accuracy. If we

keep one-hop neighbors of all the nodes, we get 100%

accuracy.

8 CONCLUSIONS AND FUTURE

WORK

In this paper, we proposed several heuristics-based al-

gorithms to compute degree hubs in a HoMLN di-

rectly using the decoupling approach. Some of the

heuristics (DC-A1 and DC-A2) achieve high accuracy

whereas others (DC-P1 and DC-P2) achieve a preci-

sion of 1. All proposed algorithms show more than

an order of magnitude improvement in efﬁciency

as compared to the traditional aggregation approach

used for ground truth. Our hypothesis with respect to

more information leading to higher accuracy is also

established. This heuristic-based approach has also

been applied for closeness centrality algorithms of ho-

mogeneous multilayer networks using the decoupling

approach with good results (Pavel et al., 2022).

Future work includes understanding the cascading

effects of accuracy and precision when more layers

are used. Also, how to identify and retain additional

information that can be used to improve the accuracy

of multiple layer centrality computation.

Acknowledgments: For this work, Drs. Sharma

Chakravarthy and Abhishek Santra were partly sup-

ported by NSF Grant CCF-1955798. Dr. Sharma

Chakravarthy was also partly supported by NSF Grant

CNS-2120393.

REFERENCES

DBLP Data Stats: https://dblp.uni-trier.de/statistics/

recordsindblp, Accessed: 24-May-2020.

Boldi, P. and Vigna, S. (2004). The WebGraph framework I:

Compression techaniques. In Proc. of the Thirteenth

International World Wide Web Conference (WWW

2004), pages 595–601, Manhattan, USA. ACM Press.

Boldi, P. and Vigna, S. (2014). Axioms for centrality. In-

ternet Mathematics, 10(3-4):222–262.

Brandes, U. (2001). A faster algorithm for betweenness

centrality. The Journal of Mathematical Sociology,

25(2):163–177.

odka, P., Skibicki, K., Kazienko, P., and Musiał, K.

(2011). A degree centrality in multi-layered social net-

Degree Centrality Algorithms for Homogeneous Multilayer Networks

work. In 2011 International Conference on Compu-

tational Aspects of Social Networks (CASoN), pages

237–242.

Candeloro, L., Savini, L., and Conte, A. (2016). A

new weighted degree centrality measure: The ap-

plication in an animal disease epidemic. PloS one,

11(11):e0165781.

Chakrabarti, D. (2005). Tools for large graph mining.

Carnegie Mellon University.

Chakrabarti, D., Zhan, Y., and Faloutsos, C. (2004). R-mat:

A recursive model for graph mining. In Proceedings

of the 2004 SIAM International Conference on Data

Mining, pages 442–446. SIAM.

Cohen, E., Delling, D., Pajor, T., and Werneck, R. F. (2014).

Computing classic closeness centrality, at scale. In

Proceedings of the Second ACM Conference on On-

line Social Networks, COSN ’14, page 37–50, New

York, NY, USA. ACM.

De Domenico, M., Sol

e-Ribalta, A., Cozzo, E., Kivel

a, M.,

Moreno, Y., Porter, M. A., G

omez, S., and Arenas,

A. (2013). Mathematical formulation of multilayer

networks. Physical Review X, 3(4):041022.

Everett, M. G. and Borgatti, S. P. (1999). The centrality

of groups and classes. The Journal of mathematical

sociology, 23(3):181–201.

Fortunato, S. and Castellano, C. (2009). Community struc-

ture in graphs. In Ency. of Complexity and Systems

Science, pages 1141–1163.

Gaye, I., Mendy, G., Ouya, S., Diop, I., and Seck, D.

(2016). Multi-diffusion degree centrality measure to

maximize the inﬂuence spread in the multilayer so-

cial networks. In International Conference on e-

Infrastructure and e-Services for Developing Coun-

tries, pages 53–65. Springer.

Hagberg, A., Swart, P., and S Chult, D. (2008). Explor-

ing network structure, dynamics, and function using

networkx. Technical report, Los Alamos National

Lab.(LANL), Los Alamos, NM (United States).

Khorasani, F., Gupta, R., and Bhuyan, L. N. (2015). Scal-

able simd-efﬁcient graph processing on gpus. In

Proceedings of the 24th International Conference on

Parallel Architectures and Compilation Techniques,

PACT ’15, pages 39–50.

Kivel

a, M., Arenas, A., Barthelemy, M., Gleeson, J. P.,

Moreno, Y., and Porter, M. A. (2014). Multilayer net-

works. Journal of Complex Networks, 2(3):203–271.

Kretschmer, H. and Kretschmer, T. (2007). A new central-

ity measure for social network analysis applicable to

bibliometric and webometric data. Collnet J. of and

Information Management, 1(1):1–7.

Liu, Y., Wei, B., Du, Y., Xiao, F., and Deng, Y. (2016). Iden-

tifying inﬂuential spreaders by weight degree central-

ity in complex networks. Chaos, Solitons & Fractals,

86:1–7.

Pavel, H. R., Santra, A., and Chakravarthy, S. (2022).

Closeness centrality algorithms for multilayer net-

works.

Pedroche, F., Romance, M., and Criado, R. (2016). A biplex

approach to pagerank centrality: From classic to mul-

tiplex networks. Chaos: An Interdisciplinary Journal

of Nonlinear Science, 26(6):065301.

Rachman, Z. A., Maharani, W., and Adiwijaya (2013). The

analysis and implementation of degree centrality in

weighted graph in social network analysis. In 2013

International Conference of Information and Commu-

nication Technology (ICoICT), pages 72–76.

Risselada, H., Verhoef, P. C., and Bijmolt, T. H. (2016). In-

dicators of opinion leadership in customer networks:

self-reports and degree centrality. Marketing Letters,

27(3):449–460.

Santra, A. and Bhowmick, S. (2017). Holistic analysis of

multi-source, multi-feature data: Modeling and com-

putation challenges. In Big Data Analytics - Fifth In-

ternational Conference, BDA 2017.

Santra, A., Bhowmick, S., and Chakravarthy, S. (2017a).

Efﬁcient community re-creation in multilayer net-

works using boolean operations. In International Con-

ference on Computational Science, ICCS 2017, 12-14

June 2017, Zurich, Switzerland, pages 58–67.

Santra, A., Bhowmick, S., and Chakravarthy, S. (2017b).

Hubify: Efﬁcient estimation of central entities across

multiplex layer compositions. In IEEE International

Conference on Data Mining Workshops.

Santra, A., Komar, K. S., Bhowmick, S., and Chakravarthy,

S. (2020). A new community deﬁnition for multilayer

networks and A novel approach for its efﬁcient com-

putation. CoRR, abs/2004.09625.

Shi, Z. and Zhang, B. (2011). Fast network centrality anal-

ysis using gpus. BMC Bioinformatics, 12(1).

Sol

a, L., Romance, M., Criado, R., Flores, J., Garc

ıa del

Amo, A., and Boccaletti, S. (2013). Eigenvector

centrality of nodes in multiplex networks. Chaos:

An Interdisciplinary Journal of Nonlinear Science,

23(3):033131.

Srinivas, A. and Velusamy, R. L. (2015). Identiﬁcation of

inﬂuential nodes from social networks based on en-

hanced degree centrality measure. In 2015 IEEE In-

ternational Advance Computing Conference (IACC),

pages 1179–1184.

Tang, X., Wang, J., Zhong, J., and Pan, Y. (2013). Pre-

dicting essential proteins based on weighted degree

centrality. IEEE/ACM Transactions on Computational

Biology and Bioinformatics, 11(2):407–418.

Towns, J., Cockerill, T., Dahan, M., Foster, I., Gaither, K.,

Grimshaw, A., Hazlewood, V., Lathrop, S., Lifka, D.,

Peterson, G. D., Roskies, R., Scott, J., and Wilkins-

Diehr, N. (2014). Xsede: Accelerating scientiﬁc

discovery. Computing in Science and Engineering,

16(05):62–74.

Uddin, S. and Hossain, L. (2011). Time scale degree cen-

trality: A time-variant approach to degree centrality

measures. In 2011 International Conference on Ad-

vances in Social Networks Analysis and Mining, pages

520–524. IEEE.

Wang, X., Hu, T., Yang, Q., Jiao, D., Yan, Y., and Liu, L.

(2021). Graph-theory based degree centrality com-

bined with machine learning algorithms can predict

response to treatment with antiepileptic medications

in children with epilepsy. Journal of Clinical Neuro-

science, 91:276–282.

Yang, Y., Dong, Y., and Chawla, N. V. (2014). Predicting

node degree centrality with the node prominence pro-

ﬁle. Scientiﬁc reports, 4(1):1–7.

KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval