A Simple Algorithm for Checking Pattern Query Containment under
Shape Expression Schema
Haruna Fujimoto and Nobutaka Suzuki
University of Tsukuba, 1-2 Kasuga, Tsukuba, 305-8550, Japan
Keywords:
RDF, Query Containment, Graph Data.
Abstract:
Query containment is one of the major fundamental problems for various kinds of data including RDF/graph,
and related to many important practical problems, e.g., determining independence of queries from updates and
rewriting queries using views. In this paper, we consider a query containment problem under Shape Expression
(ShEx), where query is defined as pattern graph with projection. We adopt a graph-theoretic approach to
cope with the containment problem, and propose a simple sound algorithm for solving the problem. In our
preliminary experiments, we first verified that the results of our algorithm are correct for all pairs of queries
generated in the experiments. We also show that types of ShEx schema can be used to reduce the search space
for checking pattern query containment.
1 INTRODUCTION
For over years, RDF/graph data has been used in a
wide variety of fields. For various kinds of data in-
cluding RDF/graph, query containment is one of the
major fundamental problems. Query containment is a
problem of determining if the result of a query is al-
ways included in the result of another query. In addi-
tion to being theoretically interesting in its own right,
query containment is related to many important prac-
tical problems, e.g., query optimization, determining
independence of queries from updates, and rewriting
queries using views.
In this paper, we consider a query containment
problem under Shape Expression (ShEx). Here, ShEx
is a novel schema language for RDF/graph data being
considered by Shape Expression Community Group.
ShEx is designed for capturing structural features of
RDF/graph data. A ShEx schema assigns types to the
nodes of an RDF/graph data and allows to define a set
of types that impose structural constraints on nodes
and their immediate neighborhood with regular bag
expression (RBE) (Staworko et al., 2015). ShEx is
useful in multiple contexts, e.g., model development,
regacy review, documentation of models and already
used in a variety of areas (Thornton et al., 2019).
ShEx shares many fundamental features with
Shapes Constraint Language (SHACL) (Gayo et al.,
2018), thus the result of this paper can also be applied
to SHACL as well. As for query language, we focus
on pattern graph with projection. For example, Fig. 1
depicts a tiny example consisting of three nodes but
only the value of circled node u
1
is output. Intuitively,
this query outputs any student taking a course taught
by his/her supervisor.
Figure 1: Example of pattern query with projection.
We adopt a simple graph-theoretic approach to
cope with the containment problem. If neither projec-
tion nor schema is considered, the problem is equiv-
alent to subgraph isomorphism; q
1
is contained in q
2
if and only if q
2
is a subgraph of q
1
. This no longer
holds, however, if projection is allowed and schema is
presented. That is, even if q
1
is not a subgraph of q
2
and vice versa, one of q
1
and q
2
may contain the other.
For example, consider Fig. 2, where u
1
,v
1
are student
nodes, u
2
,v
2
are course nodes, and u
3
,v
3
are profes-
sor nodes. Suppose that schema S asserts that “name”
is mandatory for students and courses, and that q
1
,q
2
are queries under S. Then q
1
* q
2
if the projections
and S are ignored, q
1
⊆ q
2
otherwise.
To cope with this problem, we devised a novel
simple algorithm for checking pattern query contain-
ment under ShEx schema. For given pattern queries
278
Fujimoto, H. and Suzuki, N.
A Simple Algorithm for Checking Pattern Query Containment under Shape Expression Schema.
DOI: 10.5220/0011536800003318
In Proceedings of the 18th International Conference on Web Information Systems and Technologies (WEBIST 2022), pages 278-285
ISBN: 978-989-758-613-2; ISSN: 2184-3252
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

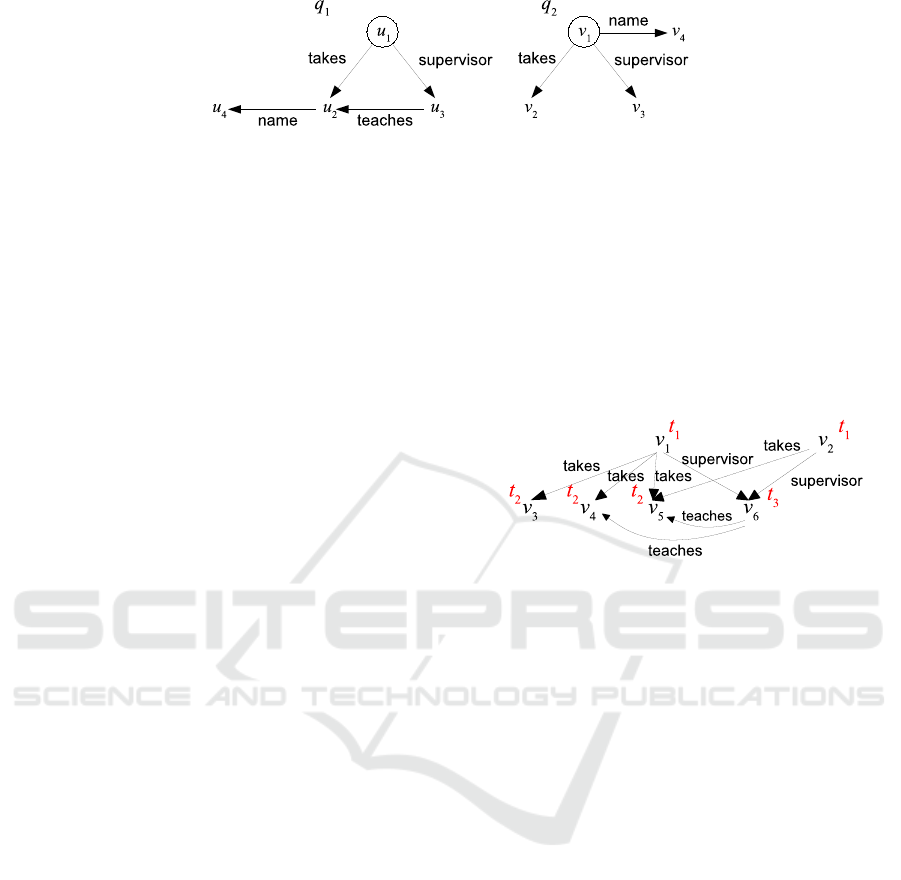
Figure 2: Queries q
1
and q
2
.
q
1
and q
2
, the algorithm firstly finds a correspondence
between the nodes of q
1
and q
2
, which is obtained
from a maximum common subgraph of q
1
and q
2
.
This problem is NP-hard, but the running time can
be reduced by using the types of ShEx schema which
can narrow the search space. Based on the correspon-
dence, we check if there is an edge e in q
2
but not in
q
1
such that e affects query containment w.r.t. q
1
. If
there is no such edge in q
2
, then the algorithm con-
cludes that q
1
is contained in q
2
. The algorithm is
shown to be sound but the proof of its completeness
is still ongoing. In our preliminary experiments, we
verified that the results of our algorithm are correct
for all pairs of queries generated in the experiments.
We also showed that types of ShEx schema can be
used to reduce the search space for checking pattern
query containment.
1.1 Related Work
Query containment has been a popular problem in
data management field including relational database
and XML (e.g. (Wood, 2003)). As for RDF/graph
data, Pichler and Skritek studied query containment
for a SPARQL fragment without schema (Pichler and
Skritek, 2014). Abbas et al. studied complexity
of SPARQL containment under ShEx without pro-
jection (Abbas et al., 2017). Saleem et al. pro-
posed a framework of SPARQL query containment
without schema (Saleem et al., 2017). Chekol et
al. studied complexity of query containment problem
for SPARQL fragments under RDF Schema (Chekol
et al., 2018). Mailis et al. proposed an index for RDF
query containment without schema (Mailis et al.,
2019). To the best of our knowledge, however, no
studies on pattern graph with projection containment
under ShEx has been made.
2 PRELIMINARIES
Let Σ be a set of labels. A labeled directed graph
(graph for short) over Σ is denoted G = (V,E),
where V is a set of nodes and E ⊆ V × Σ × V is a
set of edges. An edge labeled by l from a node v
to a node v
0
is denoted (v,l,v
0
). A pattern graph
(or query) is denoted q = (V (q), E(q),P), where
(V (q),E(q)) is a graph and P is a tuple of output
nodes. For example, the query in Fig. 1 is denoted
(V (q),E(q),P), where V (q) = {u
1
,u
2
,u
3
}, E(q) =
{(u
1
,supervisor, u
3
),(u
1
,takes,u
2
),(u
3
,teaches,u
2
)},
and P = (u
1
). By Ans(q,G), we mean the set of
answer tuples of q over G. For example, consider the
pattern query q in Fig. 1 and the graph G in Fig. 3.
Then Ans(q,G) = {(v
1
),(v
2
)}.
Figure 3: Example of valid graph G.
The content model of type in ShEx can be mod-
eled as regular bag expression (RBE) (Staworko et al.,
2015). RBE is defined similarly to regular expres-
sion except that RBE uses unordered concatenation
instead of ordered concatenation. Let Γ be a set of
types. Then RBE over Σ × Γ is recursively defined as
follows.
• ε and a :: t ∈ Σ × Γ are RBEs. ε denotes “empty
bag” having 0 occurrences of any symbol.
• If r
1
,r
2
,...,r
k
are RBEs, then r
1
|r
2
|···|r
k
is an
RBE, where | denotes disjunction.
• If r
1
,r
2
,...,r
k
are RBEs, then r
1
k r
2
k ··· k r
k
is an
RBE, where k denotes unordered concatenation.
• If r is an RBE, then r
∗
, r
+
, and r? are RBEs. Here,
‘∗’ indicates zero or more repetitions of r, r
+
= r k
r
∗
, and r? = ε|r.
For example, let r = (a :: t
1
|b :: t
2
) k c :: t
3
be an RBE.
Since k is unordered, r matches not only a :: t
1
c :: t
3
and b :: t
2
c :: t
3
but also c :: t
3
a :: t
1
and c :: t
3
b :: t
2
.
In the following, we assume that any RBE is single
occurrence, i.e., for any a :: t ∈ Σ × Γ and any RBE r,
a :: t occurs at most once in r.
A ShEx schema is denoted S = (Σ,Γ,δ), where
Γ is a set of types and δ is a function from Γ
to the set of RBEs over Σ × Γ. For example,
let S = (Σ, Γ, δ) be a ShEx schema, where Σ =
A Simple Algorithm for Checking Pattern Query Containment under Shape Expression Schema
279

{takes, supervisor,teaches}, Γ = {t
1
,t
2
,t
3
}, and
δ(t
1
) = (takes :: t
2
)
∗
k (supervisor :: t
3
)?,
δ(t
2
) = ε,
δ(t
3
) = (teaches :: t
2
)
∗
.
In RBE, a :: t matches an edge e if the label of e is a
and the target node of e is of type t. Thus, assuming
that each node in Fig. 3 is of the type colored in red,
the type of each node v
i
matches the outgoing edges
of v
i
. Thus G is a valid graph of S.
For queries q
1
,q
2
and a ShEx schema S, q
2
contains q
1
over S if for any valid graph G of S,
Ans(q
1
,G) ⊆ Ans(q
2
,G).
3 ALGORITHM
Our algorithm is essentially based on the node corre-
spondence between q
1
and q
2
. Such a correspondence
may already be known in some cases, e.g., compar-
ing an updated query and its original one. But this is
not always the case. Thus, our algorithm firstly finds
a node correspondence between q
1
and q
2
(Sec. 3.1)
if necessary, and then under the obtained node corre-
spondence, the algorithm checks the containment of
q
1
and q
2
(Sec. 3.2).
3.1 Finding Node Correspondence
We assume that the size of output tuples of q
1
and q
2
are identical (otherwise q
1
and q
2
are incomparable),
and thus we can identify the correspondence between
the output nodes of q
1
and q
2
. Thus, in the follow-
ing we consider finding a correspondence of between
their non-output nodes. This is done by the following
steps.
1. Let S be a ShEx schema. By using S, we identify
the type(s) of each node in q
1
and q
2
. This is done
by an extension of an algorithm for checking satis-
fiability of pattern queries (Matsuoka and Suzuki,
2020) (details are omitted because of space limi-
tations).
2. By comparing the type(s) of each node obtained
in step (1), we find correspondence(s) between
the nodes of q
1
and q
2
.
1
Their correspondences
are found from the output node of q
1
in the order
of connection. Two nodes do not correspond to
each other even if they are of the same type, when
there is no correspondence between their adjacent
1
If more than one type is associated with a node in step
(1), then we examine each of them one by one. Thus in each
correspondence every node is associated with one type.
nodes. For example, u
2
of q
1
corresponds to v
1
of
q
2
in Fig 4. This is because x
1
, an adjacent node
of u
2
, corresponds to y
1
, an adjacent node of v
1
.
On the other hand, u
2
of q
1
cannot correspond to
v
2
of q
2
in Fig 4 because there is no correspon-
dence between their adjacent nodes. For each ob-
tained correspondence, we compute a maximum
common edge subgraph of q
1
and q
2
under the
correspondence. The problem is NP-hard, but the
types of nodes obtain in step (1) can reduce the
search space of the problem.
3. Among the correspondences obtained in step (2),
output the correspondence that yields the maxi-
mum edge common subgraph of q
1
and q
2
.
Node correspondence is expressed by function
µ(). Let u ∈ V (q
1
). We write µ(u) = v (and we also
write µ(v) = u) if u corresponds to v ∈ V (q
2
), and
µ(u) = v
nil
if there is no node corresponding to u,
where v
nil
is a new node not in V (q
2
). For an edge
e = (v,a,v
0
) in q
2
, (µ(v), a, µ(v
0
)) is called the corre-
sponding edge of e in q
1
.
We explain the above steps (1) to (3) by an exam-
ple. Consider queries q
1
and q
2
shown in Fig. 4, and
suppose that in step (1) the type of each node is ob-
tained as shown in the figure. Consider step (2). By
the assumption, x
1
and x
2
of q
1
correspond to y
1
and
y
2
of q
2
, respectively, but no correspondence for the
other nodes is known. Since u
2
is of type t
2
, u
2
may
correspond to v
1
and v
2
. However, by checking edges
adjacent to u
2
it is impossible for u
2
to correspond to
v
2
, and we know that u
2
is able to correspond to only
v
1
. Since u
1
is of type t
3
but there is no node of type t
3
except y
2
, we know that there is no node correspond-
ing to u
1
. Similarly, there is no node corresponding
to v
2
. Therefore, we have µ(x
1
) = y
1
, µ(x
2
) = y
2
,
µ(u
2
) = v
1
, and µ(u
1
) = v
nil
(and µ(v
2
) = u
nil
). Based
on this correspondence, we create adjacency matri-
ces of q
1
and q
2
(Fig. 5). There are three elements
(colored red) appearing in both matrices at the same
position, meaning that we have three common edges
between q
1
and q
2
under the correspondence.
In this case we have only one correspondence, but
in general there may be more than one correspon-
dence between two queries. In such a case, for each
possible correspondence with each node associated
with one type, we compute the size of the common
edge subgraph under the correspondence, and choose
the maximum one among them.
3.2 Checking Containment
Let G be a graph. By u(G) we mean the undirected
graph obtained by replacing each directed edge of G
with an undirected one. A subgraph G
0
of G is weakly
WEBIST 2022 - 18th International Conference on Web Information Systems and Technologies
280

Figure 4: Queries q
1
and q
2
.
Figure 5: Adjacency matrices of q
1
and q
2
.
biconnected if any one node in u(G
0
) is removed, the
resulting undirected subgraph remains connected. A
subgraph G
0
of G is weakly biconnected component if
G
0
is a maximal weakly biconnected subgraph.
For queries q
1
,q
2
and a ShEx schema S, we check
if q
1
⊆ q
2
as follows.
1. For each edge e in q
2
, if e is not “answer-
reducing” for q
1
and its corresponding edge e
0
is
not in q
1
, then add e
0
to q
1
. Here, an “answer-
reducing” edge is an edge such that adding its cor-
responding edge to q
1
reduces the answer of q
1
, in
other words, the answer of q
1
is not preserved.
2. If q
2
is a subgraph of q
1
, then return “true” (i.e.,
q
1
⊆ q
2
), otherwise return “false.”
Next, we will explain the idea of “answer-
reducing” edge. Let q
1
,q
2
be queries shown in Fig. 6
with µ(v
1
) = u
1
, µ(v
2
) = u
2
, µ(v
3
) = u
3
, µ(v
4
) and
µ(v
5
) are new nodes, and let S = (Σ,Γ,δ) be a ShEx
schema, where Γ = {t
1
,t
2
,t
3
} and δ is defined as fol-
lows:
δ(t
1
) = a :: t
2
k (b :: t
3
)? k d :: t
2
,
δ(t
2
) = ε,
δ(t
3
) = c :: t
2
k (e :: t
2
)?
Then (v
1
,d, v
4
) is not answer-reducing, since any
node matched by u
1
must have an edge labeled by d
under any valid graph of S. Thus we can safely add
(u
1
,d, u
4
) to q
1
without reducing the answer of q
1
. On
the other hand, (v
5
,a,v
3
) is answer-reducing, since
(v
5
,a,v
3
) imposes an additional constraint that v
3
must be referenced by some edge labeled by a, mean-
ing that adding (u
5
,a,u
3
) reduces the answer of q
1
.
Then (v
3
,c,v
2
) is also answer-reducing, since adding
(u
3
,c,u
2
) to q
1
yields a new weakly biconnected com-
ponent (the triangle consisting of u
1
,u
2
,u
3
), which
imposes an extra constraint on q
1
that u
2
and u
3
must
be connected by an edge labeled by c.
Moreover, (v
3
,e,v
2
) is answer-reducing, since in
δ(t
3
) e :: t
2
is qualified by ?, meaning that every node
of type t
3
does not have an edge labeled by e. In
Fig. 6, a query obtained by adding (u
1
,d, u
4
) to q
1
does not contain q
2
as a subgraph, thus our algorithm
concludes that q
1
6⊆ q
2
.
Figure 6: Adding edges of q
2
to q
1
.
To define answer-reducing edge formally, we also
need min/max occurrences of label-type pair a :: t in
an RBE. Let r be an RBE over Σ ×Γ and a :: t ∈ Σ :: Γ.
The minimum occurrence and maximum occurrence
of a :: t, denoted minocc(r, a :: t) and maxocc(r, a :: t),
respectively, are defined as follows.
• If r = a :: t, then minocc(r, a :: t) = maxocc(r,a ::
t) = 1.
• If r = r
0∗
and a :: t is in r
0
, then minocc(r,a :: t) = 0
and maxocc(r, a :: t) = ∞.
• If r = r
0+
and a :: t is in r
0
, then minocc(r, a :: t) =
minocc(r
0
,a :: t) and maxocc(r,a :: t) = ∞.
• If r = r
0
? and a :: t is in r
0
, then minocc(r, a :: t) = 0
and maxocc(r, a :: t) = maxocc(r
0
,a :: t).
• If r = r
1
|r
2
|···|r
n
or r = r
1
k r
2
k ··· k r
n
, and a :: t
is in r
i
, then minocc(r, a :: t) = minocc(r
i
,a :: t)
and maxocc(r, a :: t) = maxocc(r
i
,a :: t).
By λ(u) we mean the type of node u. For example,
in Fig. 4 λ(x
1
) = t
1
, λ(u
2
) = t
2
, and so on. For an edge
e = (v
1
,a,v
2
) in q
2
, we say that e is answer-reducing
for q
1
if one of the following conditions holds:
(a) µ(v
1
) ∈ V (q
1
) and minocc(δ(λ(v
1
)),a :: λ(v
2
)) =
0, i.e., a :: λ(v
2
) is qualified by ? or ∗ in δ(λ(v
1
)),
A Simple Algorithm for Checking Pattern Query Containment under Shape Expression Schema
281

(b) µ(v
1
) ∈ V (q
1
), minocc(δ(λ(v
1
)),a :: λ(v
2
)) ≥ 1,
maxocc(δ(λ(v
1
)),a :: λ(v
2
)) = ∞, and q
1
already
has another edge (µ(v
1
),a,u
3
) such that λ(u
3
) =
λ(µ(v
2
)).
(c) The corresponding edge of e is a new “incoming”
one, i.e., µ(v
2
) is a new node and µ(v
1
) ∈ V (q
1
).
(d) Adding the corresponding edge of e to q
1
yields a
new weakly biconnected component.
(e) The corresponding edge of e is under a disjunctive
operator of δ(µ(v
1
)), and q
1
has no other edge un-
der the disjunctive operator.
For example, in Fig. 6 (a) applies to (v
3
,e,v
2
), (c) ap-
plies to (v
5
,a,v
3
), and (d) applies to (v
3
,c,v
2
).
Algorithm 1: Main.
Input: ShEx schema S = (Σ,Γ,δ), queries q
1
,q
2
Output: true or false
1: C(q
1
) ← FindWeaklyBiconnectedComponets(q
1
)
2: C(q
2
) ← FindWeaklyBiconnectedComponets(q
2
)
3: X(q
1
,q
2
) ← FindNodeCorrespondence(q
1
,q
2
)
4: for each x ∈ X(q
1
,q
2
) do
5: if ∀c ∈ C(q
1
) |c| < 3 and ∀c ∈ C(q
2
) |c| < 3
then
6: Resul t ← AddEdge(q
1
,q
2
,S,x)
7: else
8: M(q
1
) ← {c ∈ C(q
1
) | |c| ≥ 3}
9: M(q
2
) ← {c ∈ C(q
2
) | |c| ≥ 3}
10: Resul t ← IsInclude(M(q
1
),M(q
2
),q
1
,q
2
,S,x)
11: if Result = true then
12: break
13: return Result
Algorithm 2: AddEdge.
Input: ShEx schema S = (Σ,Γ,δ), queries q
1
,q
2
,
correspondence x between the nodes of q
1
and q
2
Output: true or false
1: for each e ∈ E(q
2
) do
2: Let e
0
be the corresponding edge of e in q
1
un-
der x
3: if e
0
/∈ E(q
1
) and e
0
is not answer-reducing for
q
1
then
4: add e
0
to q
1
5: if q
2
is a subgraph of q
1
then
6: return true
7: return false
We now present our algorithm (Algorithm 1). In
lines 1 and 2, biconnected components can be ob-
tained by linear-time depth first search (Hopcroft and
Tarjan, 1973). In line 3, our algorithm finds a set
X(q
1
,q
2
) of node correspondences between q
1
and
Algorithm 3: IsInclude.
Input: ShEx schema S = (Σ, Γ, δ), queries q
1
,q
2
, sets
of biconnected components M(q
1
),M(q
2
), corre-
spondence x between the nodes of q
1
and q
2
Output: true or false
1: if for some c ∈ M(q
2
), there is no c
0
∈ M(q
1
) s.t. c
is a subgraph of c
0
then
2: return false
3: Result ← AddEdge(q
1
,q
2
,S,x)
4: return Result
q
2
. For each correspondence x in X(q
1
,q
2
), the al-
gorithm checks if q
1
is contained in q
2
under x , as
follows (lines 4 to 12). If neither q
1
nor q
2
contains
any weakly biconnected component of size less than
three, we use AddEdge immediately (lines 5 and 6).
This adds, for each edge e in q
2
, its corresponding
edge e
0
to q
1
if e
0
is not in q
1
and not answer-reducing,
and then check if q
2
is a subgraph of the extended
q
1
. If this is true, then the algorithm returns true, i.e.,
q
1
⊆ q
2
. If q
1
or q
2
contains one or more weakly bi-
connected components of size three or more, we use
IsInclude (lines 8 to 10). This checks if q
2
contains a
weakly biconnected component c that is not contained
in any weakly biconnected component of q
1
(line 1 of
IsInclude). If so, the algorithm returns false since c
imposes an extra restriction to q
2
and thus q
2
cannot
contain q
1
. Otherwise, AddEdge is applied to q
1
,q
2
(line 3). We have the following.
Theorem 1. Let S be a ShEx schema and q
1
,q
2
be
queries. If the algorithm returns true, then q
1
⊆ q
2
under S. 
We are considering the completeness of the algo-
rithm. We expect that the completeness also holds at
least under certain restricted ShEx schema.
4 PRELIMINARY EXPERIMENTS
We present the result of our preliminary experiments.
The algorithm was implemented in Python 3.9.0, and
all the experiments were executed on a machine with
Quad-Core Intel Core i5 CPU, 8.00GB RAM, and
Mac OS Monterey 12.2.1.
We made two ShEx schemas for RDF data gen-
erated by SP2Bench (Schmidt et al., 2009) (consist-
ing of 11 types) and a fragment of Wikidata schema
(consisting of 6 types). Queries were created as fol-
lows. The number of edges in each query was be-
tween 3 and 7, and for each size (3,4,...,7) three pat-
tern graphs were created, where one contained more
than two biconnected components and the others not.
Thus we obtained 5 × 3 = 15 queries for each of the
WEBIST 2022 - 18th International Conference on Web Information Systems and Technologies
282

ShEx schemas. We examined all permutations of q
1
and q
2
from the 15 queries , i.e., we ran the proposed
algorithm for
15
P
2
= 210 pairs of queries. For ev-
ery pair, we assumed that the correspondence of non-
output nodes is unknown.
First, we verified the results of our algorithm, and
found that all the results of our algorithm for the 210
pairs were correct. This suggests that in most cases
our algorithm can solve the containment problem cor-
rectly, although only the soundness of our algorithm
has been shown by Theorem 1.
Second, we compare our algorithm and a base-
line algorithm. Here, the baseline algorithm finds the
correspondence of nodes without using schema types,
and the rest part is identical to that of our algorithm.
Thus, this experiment is to measure the effect of ShEx
types on the efficiency of our algorithm.
Table 1: The average execution time for the 210 pairs.
schema execution time (sec)
baseline our algorithm
SP2Bench 2.52 ×10
−1
4.83 ×10
−4
Wikidata 2.45 ×10
−1
6.36 ×10
−4
Figure 7: Scatter plot of the size of X (q
1
,q
2
) (y axis) and
the execution time of the algorithm (x axis) (SP2Bench).
Figure 8: Scatter plot of the size of X (q
1
,q
2
) (y axis) and
the execution time of the algorithm (x axis) (Wikidata).
Table 1 shows the average execution time for the 210
pairs for each ShEx schema. As shown in the table,
our algorithm is much faster than the baseline. The
SP2bench result shows that the execution time is re-
duced to about 1/520 by using ShEx types, while the
wikidata result shows that the execution time is re-
duced to about 1/385. These results show that the
types of nodes obtained by ShEx schema can reduce
the search space of finding node correspondences be-
tween queries.
Third, we investigated the execution time of our
algorithm further. Tables 2 and 3 show breakdowns
of the average execution time by the sizes of q
1
(row)
and q
2
(column). As shown in the tables, the algo-
rithm can check the containment of pattern queries
under ShEx schema in relatively short time, and the
execution time tends to increase with the size of
query.
Tables 4 and 5 show other breakdowns by the
number of weakly biconnected components contained
in the queries, for the following three cases: (a)
both q
1
and q
2
contain more than two weakly bicon-
nected components, (b) only q
1
contains more than
two weakly biconnected components, (c) only q
2
con-
tains more than two weakly biconnected components,
and (d) neither q
1
nor q
2
contains more than two
weakly biconnected components. Interestingly, these
suggest that the execution time tends to be smaller
when query q
2
contains weakly biconnected compo-
nents with more than two nodes. A possible reason
is that the algorithm can sometimes avoid executing
AddEdge if given pattern query contains weakly bi-
connected components with more than two nodes, i.e.,
when the if test in line 1 of IsInclude holds, the exe-
cution of AddEdge in line 3 is avoided.
Figures 7 and 8 plot the number of correspon-
dences, i.e., the size of X(q
1
,q
2
) (y-axis) and the ex-
ecution time of the algorithm (x-axis) for each pair
of queries. As shown in the tables, as the size
of X(q
1
,q
2
) becomes larger, the execution time in-
creases accordingly. This suggests that reducing the
size of X(q
1
,q
2
) is important to solve the problem
more efficiently.
5 CONCLUSION
In this paper, we proposed an algorithm for checking
containment of pattern queries under ShEx schema.
Our algorithm uses the ShEx schema to reduce
the search space of finding a correspondence between
nodes of queries. Then, the algorithm extends the pat-
tern graph using the ShEx schema. This allows us
to find containment that cannot be found by existing
A Simple Algorithm for Checking Pattern Query Containment under Shape Expression Schema
283

Table 2: Breakdown of average execution time by query size (SP2Bench).
3 4 5 6 7
3 2.24 × 10
−4
2.49 × 10
−4
3.20 × 10
−4
8.83 × 10
−4
4.77 × 10
−4
4 2.50 × 10
−4
2.35 × 10
−4
3.26 × 10
−4
3.28 × 10
−4
4.66 × 10
−4
5 3.11 × 10
−4
3.05 × 10
−4
4.56 × 10
−4
6.25 × 10
−4
8.07 × 10
−4
6 5.33 × 10
−4
3.07 × 10
−4
4.98 × 10
−4
5.71 × 10
−4
8.00 × 10
−4
7 3.07 × 10
−4
3.44 × 10
−4
4.36 × 10
−4
7.72 × 10
−4
1.40 × 10
−3
Table 3: Breakdown of average execution time by query size (Wikidata).
3 4 5 6 7
3 1.38 × 10
−4
2.73 × 10
−4
2.06 × 10
−4
5.44 × 10
−4
3.83 × 10
−4
4 2.20 × 10
−4
2.73 × 10
−4
3.15 × 10
−4
5.58 × 10
−4
8.64 × 10
−4
5 2.13 × 10
−4
3.07 × 10
−4
2.83 × 10
−4
3.77 × 10
−4
5.34 × 10
−4
6 4.36 × 10
−4
6.01 × 10
−4
4.33 × 10
−4
1.82 × 10
−3
1.91 × 10
−3
7 3.46 × 10
−4
6.34 × 10
−4
5.67 × 10
−4
1.78 × 10
−3
2.52 × 10
−3
Table 4: Breakdown of average execution time by the num-
ber of weakly biconnected components (SP2Bench).
# of pairs average execution time (sec)
(a) 20 3.66 ×10
−4
(b) 50 4.40 ×10
−4
(C) 50 3.62 ×10
−4
(d) 90 5.97 ×10
−4
total 210 4.83 ×10
−4
Table 5: Breakdown of average execution time by the num-
ber of weakly biconnected components (Wikidata).
# of pairs average execution time (sec)
(a) 20 2.75 ×10
−4
(b) 50 7.27 ×10
−4
(c) 50 5.45 ×10
−4
(d) 90 6.11 ×10
−4
total 210 6.36 ×10
−4
methods.
Since our algorithm is shown to be sound but the
proof of its completeness is still ongoing. In our pre-
liminary experiments, we verified that the results of
our algorithm are correct for all pairs of queries gener-
ated in the experiments. The results of another exper-
iment suggests that types of nodes obtained by using
ShEx schema can reduce the search space for finding
corresponding nodes between queries. In addition, we
showed that the weakly biconnected component and
the size of the queries are the main factors in the effi-
ciency of the algorithm.
However, this is still an ongoing work and we still
have a number of things to do. First, we need to con-
sider the inverse direction of Theorem3.1. Moreover,
ShEx has more functions not discussed in this paper
(e.g., negation). Thus we need to consider extending
our algorithm to adopt such functions.
ACKNOWLEDGMENTS
This work was partly supported by JSPS KAKENHI
Grant Number 21K11900.
REFERENCES
Abbas, A., Genev
´
es, P., Roisin, C., and Laya
¨
ıda, N. (2017).
SPARQL query containment with ShEx constraints.
In Proceedings of Advances in Databases and Infor-
mation Systems (ADBIS 2017), pages 343–356.
Chekol, M. W., Euzenat, J., Genev
`
es, P., and Laya
¨
ıda,
N. (2018). Sparql query containment under schema.
Journal on data semantics, 7(3):133–154.
Gayo, J. E. L., Prud’hommeaux, E., Boneva, I., and Kon-
tokostas, D. (2018). Validating RDF Data. Morgan &
Claypool.
Hopcroft, J. and Tarjan, R. (1973). Algorithm 447: Efficient
algorithms for graph manipulation. Commun. ACM,
16(6):372–378.
Mailis, T., Kotidis, Y., Nikolopoulos, V., Kharlamov, E.,
Horrocks, I., and Ioannidis, Y. (2019). An efficient
index for rdf query containment. In In Proceedings of
the 2019 International Conference on Management of
Data, pages 1499–1516.
Matsuoka, S. and Suzuki, N. (2020). Detecting unsatisfi-
able pattern queries under shape expression schema.
In Proceedings of the 16th International Conference
on Web and Information Systems and Technologies,
pages 285–291.
Pichler, R. and Skritek, S. (2014). Containment andequiv-
alence of well-designed SPARQL. In Proceedings
WEBIST 2022 - 18th International Conference on Web Information Systems and Technologies
284

of the 33rd ACM SIGMOD-SIGACT-SIGART Sympo-
sium on Principles of Database Systems, pages 39–50.
Saleem, M., Stadler, C., Mehmood, Q., Lehmann, J., and
Ngomo, A.-C. N. (2017). SQCFramework: SPARQL
query containment benchmark generation framework.
In Proceedings of the Knowledge Capture Conference,
K-CAP 2017.
Schmidt, M., Hornung, T., Lausen, G., and Pinkel, C.
(2009). SP2Bench: a SPARQL performance bench-
mark. In Proceedings of the 25th International Con-
ference on Data Engineering (ICDE 2009), pages
371–393.
Staworko, S., Boneva, I., Gayo, J. E. L., Hym, S.,
Prud’hommeaux, E. G., and Solbrig, H. R. (2015).
Complexity and expressiveness of ShEx for RDF.
In Proceedings of 18th International Conference on
Database Theory (ICDT 2015), pages 195–211.
Thornton, K., Solbrig, H., Stupp, G. S., Labra Gayo, J. E.,
Mietchen, D., Prud’hommeaux, E., and Waagmeester,
A. (2019). Using shape expressions (shex) to share rdf
data models and to guide curation with rigorous val-
idation. In In Proceedings of the European Semantic
Web Conference(ESWC 2019), pages 606–620.
Wood, P. T. (2003). Containment for XPath fragments un-
der DTD constraints. In Proceedings of the 9th Inter-
national Conference on Database Theory (ICDT’03),
pages 300–314.
A Simple Algorithm for Checking Pattern Query Containment under Shape Expression Schema
285