CAP-DSDN: Node Co-association Prediction in Communities in Dynamic

Sparse Directed Networks and a Case Study of Migration Flow

Jaya Sreevalsan-Nair

1 a

and Astha Jakher

Graphics-Visualization-Computing Lab, International Institute of Information Technology Bangalore, Bangalore, India

Department of Humanities and Social Sciences, IIT Kharagpur, Kharagpur, West Bengal 721302, India

Keywords:

Real-world Graphs, Directed Networks, Edge Sparsity, Dynamic Networks, Community Detection,

Community Evaluation, Migration Flows, Co-association, Prediction, Autoregressive Models, VAR Model,

ARMA Model.

Abstract:

Predicting the community structure in the time series, or snapshots, of a real-world graph in the future, is a

pertinent challenge. This is motivated by the study of migration ﬂow networks. The dataset is characterized

by edge sparsity due to the inconsistent availability of data. Thus, we generalize the problem to predicting

community structure in a dynamic sparse directed network (DSDN). We introduce a novel application of co-

association which is a pairwise relationship between the nodes belonging to the same community. We thus

propose a three-step algorithm, CAP-DSDN, for co-association prediction (CAP) in such a network. Given

the absence of benchmark data or ground truth, we use an ensemble of community detection (CD) algorithms

and evaluation metrics widely used for directed networks. We then deﬁne a metric based on entropy rate as

a threshold to ﬁlter the network for determining a signiﬁcant and data-complete subnetwork. We propose

the use of autoregressive models for predicting the co-association relationship given in its matrix format. We

demonstrate the effectiveness of our proposed method in a case study of international refugee migration during

2000–18. Our results show that our method works effectively for migration ﬂow networks for short-term

prediction and when the data is complete across all snapshots.

1 INTRODUCTION

The communities in the time series of directed net-

works (Malliaros and Vazirgiannis, 2013) enable us

to understand the change in the network topology in

real-world graphs. Let us take the example of the in-

ternational refugee migration network. Using the mi-

gration ﬂow data for n consecutive years, referred to

as snapshots, we get the time series of a directed net-

work, where the countries are nodes and the migrant

counts are the edge weights. Predicting a network at a

future time is difﬁcult as it involves predicting the oc-

currence of edges, i.e., pairwise relationship between

nodes, and their weights. This issue deteriorates in the

case of edge-sparse networks where there is no spe-

ciﬁc known model for the occurrence of edges. For

instance, in the case of migration networks, there are

socio-economic-political systemic dependencies, nat-

ural disasters, and other factors for the additions and

deletions of nodes and edges in the network which are

often complex to predict (Suleimenova et al., 2017).

https://orcid.org/0000-0001-6333-4161

At the same time, the data is not consistently avail-

able for any given pair of countries owing to lapses in

data curation and communication (Neumayer, 2005).

This inconsistency in the availability of edge data also

leads to inaccuracy in the study of network commu-

nity structures. Hence, we shift our focus to studying

the community behavior of nodes in the network in-

stead of the communities themselves. Thus, we focus

on using the persistent community behavior of nodes

in the time series to predict its community behavior

in the future. We propose an algorithm, CAP-DSDN

(Co-Association Prediction in Dynamic Sparse Di-

rected Network), for predicting the co-association be-

tween nodes in the (n+1)

year, using the data until

the n

year.

As an example, if the United States of America

(USA) and Mexico co-existed in a community over

most part of the n-year period, can we then use the

available data to predict their co-association in a com-

munity, i.e., membership to the same community,

in the (n+1)

year? Our proposed algorithm, CAP-

Pronounced as \kap-duhs-durn\.

Sreevalsan-Nair, J. and Jakher, A.

CAP-DSDN: Node Co-association Prediction in Communities in Dynamic Sparse Directed Networks and a Case Study of Migration Flow.

DOI: 10.5220/0011537600003335

In Proceedings of the 14th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2022) - Volume 1: KDIR, pages 63-74

ISBN: 978-989-758-614-9; ISSN: 2184-3228

DSDN (Figure 1) predicts such co-associations at a

future time instance, which in turn helps in inferring

the community structure. It must be noted that CAP-

DSDN does not predict the number of communities or

their constituencies. Instead, CAP-DSDN predicts the

likelihood of any two nodes being in the same com-

munity in the future.

Our novel contributions towards community anal-

ysis in DSDNs are:

• A three-step algorithm, CAP-DSDN, for co-

association prediction (CAP) for implicitly fore-

casting community behavior in real-world graphs

which are DSDNs.

• Deﬁnition of a metric of entropy rate H to be

used on the co-association matrices (CAM) for

determining persistent community behavior of the

nodes, and thus, a threshold τ

for node-ﬁltering

the network to address the issue of sparsity.

• A method of applying time series autoregressive

models to CAMs.

2 RELATED WORK

Recently, the communities in DSDNs have been mod-

eled as routed activity-driven networks for model-

ing its community structure (Bongiorno et al., 2019).

Here, starting from a set of existing community de-

tection (CD) algorithms, such as Louvain, Infomap,

etc., the communities are improved by using the pro-

posed characterization. A recent study on the state-

of-the-art CD algorithms for dynamic networks has

shown that the choice of algorithm is contextual and

is based on the nature of communities and commu-

nity events involved in such networks (Rossetti and

Cazabet, 2018).

In the classiﬁcation of different CD algo-

rithms (Rossetti and Cazabet, 2018), CAP-

DSDN falls in the category of instant optimal

CD approach that ﬁnds communities in each snapshot

and matches communities across snapshots. A known

disadvantage of this approach is that it is ambiguous

if the evolution in community structures is due to the

actual evolution of events or due to the instabilities of

CD algorithms in each timestamp.

There has been an empirical comparison of CD al-

gorithms for directed networks (Agreste et al., 2016),

which has studied the accuracy and time complex-

ity of selected state-of-the-art methods on real and

synthetic datasets. This work has concluded that

the WalkTrap algorithm (Pons and Latapy, 2006)

has the highest accuracy, but the worst time com-

plexity. The other key algorithms discussed in this

work are Infomap (IMAP) (Rosvall and Bergstrom,

2008), eigenvector algorithm or the modularity opti-

mization for directed networks (MODN) (Leicht and

Newman, 2008), and speaker-listener label propaga-

tion algorithm (SLPA) (Xie et al., 2011). The al-

gorithms are further classiﬁed as follows, based on

how they use the directionality information of the

networks: (i) directionality-preserving ones, e.g., In-

fomap and label propagation algorithm, and (ii)

directionality-discarding ones, e.g., eigenvector algo-

rithm and WalkTrap.

SLPA is based on directional propagation of la-

bels, whereas MODN deﬁnes a community based on

high and low densities of intra- and inter-community

edges, respectively; and IMAP uses random walks to

determine communities. Thus, these methods fall in

different categories of models used for CD, namely,

models based on dynamic processes on graphs, on a

null model, and on a ﬂow model, respectively (Agreste

et al., 2016). SLPA and IMAP are efﬁcient methods

and scalable to large graphs (Agreste et al., 2016).

SLPA and IMAP methods use the directionality infor-

mation, whereas MODN ignores the same by using a

symmetric adjacency matrix.

• Speaker Listener Label Propagation Algorithm

(SLPA) (Xie et al., 2011): is an extension of

the label propagation algorithm which initially as-

signs each node with a unique label and iteratively

updates labels to the most frequently occurring la-

bel in the neighborhood of the node. SLPA ex-

tends to overlapping communities, where nodes

can have multiple labels based on their role as a

listener or a speaker.

• Modularity Optimization for Directed Networks

(MODN) Algorithm (Leicht and Newman, 2008):

uses the variant of Girvan-Newman modularity

for directed networks, given by:

Q =

∑

i, j



i, j

−



δ(C

where A

i j

is an element of the adjacency matrix

A giving edge weight between nodes i and j,

i j

is the Kronecker delta, C

is the label of the

community to which node i belongs, k

is the

degree of node i, and 2m is the sum of degrees

of all nodes in the network. The algorithm is

implemented as an optimization problem, where

Q is maximized for community detection. The

maximum value of Q is considered as the best

approximation of the true communities in the

network.

• Infomap (IMAP) Algorithm (Rosvall and

Bergstrom, 2008): is based on information

theory, using the map equation. The entropy

of random walks within and between modules

KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval

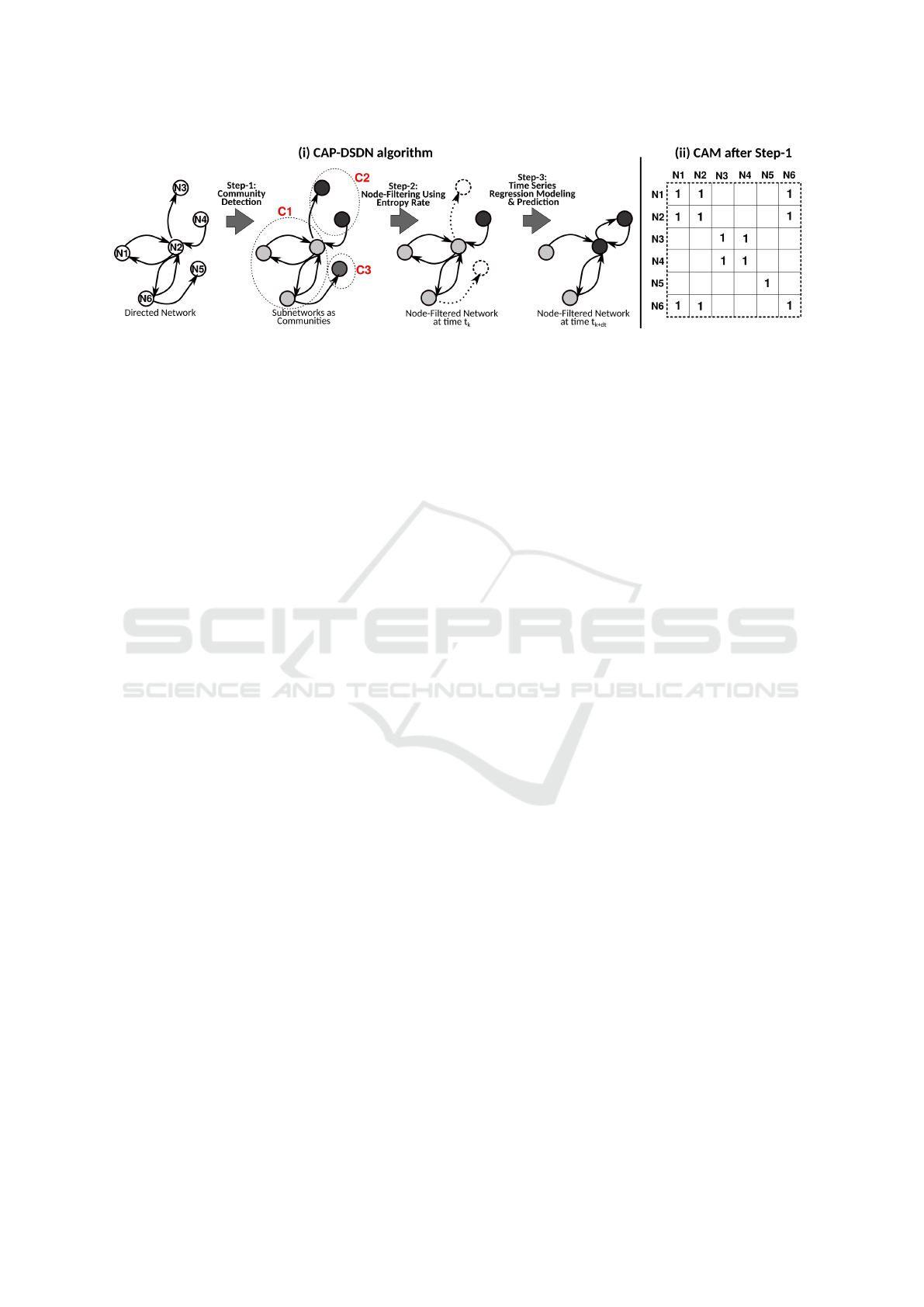
Figure 1: (i) Our proposed three-step algorithm, CAP-DSDN, for prediction of community behavior of nodes in a dynamic

sparse directed network (DSDN), where the node color indicates community ID. (ii) The co-association matrix (CAM) of the

network after community detection (CD) in Step-1.

is used in a cost function in the map equation.

This cost function is the expected description

length of a random walk, which is minimized.

Thus, the best node-partitioning occurs where the

probability ﬂow is the most cost-efﬁcient.

Community detection has been recently implemented

on sparse directed networks using a parameter-Sparse

Random Graph Model, that preserves the direction-

ality (Stein and Leng, 2021). This involves model-

ing using an estimator using an l

penalty to achieve

sparsity in parameter space to simulate a sparse net-

work. Previously, spectral methods have been used

extensively for sparse directed networks using the

spectrum of the non-backtracking matrix (Singh and

Humphries, 2015; Krzakala et al., 2013). Spec-

tral methods using non- and reluctant-backtracking

matrices have been successfully used for real-world

graphs (Singh and Humphries, 2015).

Perturbing and resampling network has been done

to aggregate information in large sparse undirected

networks (Mirshahvalad et al., 2012). This is simi-

lar to our proposed method of using an information-

theoretic metric of entropy rate for assessing the sta-

tistical signiﬁcance of communities. The size of a

controllable subnetwork for a node has been used to

determine the statistical signiﬁcance of the node in

sparse directed networks (Wang et al., 2012). This is

similar to how we use moving average smoothing for

ﬁnding signiﬁcant nodes.

There is limited work on community detection

in dynamic sparse directed networks (DSDNs). Re-

cently, a consensus method has been used to deter-

mine the state of clusters of nodes (Martin et al.,

2016). The rationale for tracking the state of the node

clusters is for reducing the dimensionality of DSDNs.

Our work is different, as we are focused on predicting

co-association values, so as to not limit our analysis

to the raw network data alone.

3 PRELIMINARIES

Here, we deﬁne the Co-association Matrix (CAM)

and persistent community behavior.

Deﬁnition 1. A Co-association Matrix (CAM) is a

symmetric matrix with rows and columns represent-

ing the same set of data items, say countries in the

migration ﬂow network, in the same order, and each

cell (i, j) indicates if the item in the i

row and that

in the j

column are associated with the same clus-

ter, i.e., belong to the same community in the case of

networks.

Deﬁnition 2. Persistent Community Behavior is a

property of a node of a dynamic network where it

has a high likelihood of non-zero co-association with

other nodes in a network across several snapshots.

4 CAP-DSDN: OUR PROPOSED

METHOD

Our three-step algorithm, CAP-DSDN, is as follows:

Step-1: Perform community detection in each snap-

shot of a DSDN using an ensemble of CD algorithms

and compute an aggregated CAM.

Step-2: Determine a subnetwork of nodes with

persistent community behavior using the aggregated

CAM, thus implementing node-ﬁltering the network.

Step-3: Perform time series autoregressive models

on the CAM of the ﬁltered network to predict the

community structure in the subnetwork in the future.

To handle the limitations of analysis stemming

from the sparsity in the networks, our approach is to

localize our analysis to a subnetwork that shows per-

sistent community behavior. Thus, we further analyze

a relatively denser subnetwork, which is determined

using the preprocessing steps Step-1 and Step-2. The

CAP-DSDN: Node Co-association Prediction in Communities in Dynamic Sparse Directed Networks and a Case Study of Migration Flow

requirement of a dense network also comes from the

insufﬁciency of data for a prediction algorithm.

We predict the co-association between nodes of

the network instead of the edge weight as the co-

association value has the property of being bounded

between 0 and 1, unlike the edge weight. The pre-

dicted co-association value is the probability or likeli-

hood of two nodes belonging to the same community

in the future using their past behavior. Since the com-

munity behavior is computed independently in each

snapshot with the information from the neighboring

snapshots, we now use the concept of moving aver-

age to compute the probability of co-association us-

ing a shorter time window, e.g., ﬁve snapshots, as

explained in Section 4.1.

We also do not pursue the idea of predicting the

likelihood of the occurrence of an edge in this work,

as the networks of interest are weighted networks and

not binary ones.

4.1 Step-1: Community Detection

In this step, we compute a CAM for each snapshot of

the network. The inputs to this step are a DSDN and

a CD algorithm, and the outputs are a time series of

community IDs for the nodes.

A community structure selected from an ensem-

ble of methods based on its performance is a reliable

choice in the absence of ground truth in real-world

graphs. Thus, the crux of this step is in identifying

an appropriate CD algorithm for DSDNs. Based on

a literature survey on widely used algorithms for CD

in directed networks (Agreste et al., 2016), we have

selected three algorithms, namely, Speaker-Listener

Label Propagation Algorithm (SLPA), modularity op-

timization for directed networks (MODN), and In-

fomap algorithm (IMAP). These algorithms are de-

signed using different approaches, as explained in

Section 2, which make them suitable for comparative

analysis in our work.

Choice of CD Algorithm: We choose a CD algo-

rithm for a DSDN using the following strategies:

• Community Quality Metrics: We compute the

quality of node-partitioning to form communities

using selected community quality metrics. We

then consider an algorithm to be better performing

when its outcomes are closer to the best quality.

• Characteristics of CD Outcomes in the Time Se-

ries: We consider an algorithm to be better per-

forming if it has consistently created more than

one community across snapshots. An algorithm

that leads to under- or over-fragmentation is not

preferred, which avoids scenarios of monolithic

and overly fragmented communities, respectively.

We identify widely used metrics using a literature

survey and use the following six metrics in this work,

namely, link modularity (LM) (Nicosia et al., 2009),

internal edge density (IED) (Radicchi et al., 2004),

average internal degree (AID) (Radicchi et al., 2004),

cut ratio (CR) (Fortunato, 2010), and Z-modularity

(ZM) (Miyauchi and Kawase, 2016). It is important

to use appropriate metrics for validation, given the

absence of benchmark datasets with ground truth in

real-world graphs. Hence, the ﬁnal set is identiﬁed

based on the better performance of the CD algorithm

on these metrics for our case study.

Computing CAMs: The CAM captures the ten-

dency of any two given nodes belonging to the

same community/cluster/node-grouping. The co-

association relationship between nodes i and j be-

longing to communities C

and C

, respectively, at

time instance T , is captured in the following matrix

element in CAM:

i j

(T ) =

(

1 , if (C

(T ) = C

(T )) and (i 6= j),

0 , otherwise.

(1)

Probability of Co-association Matrices (PCAMs):

For incorporating the temporal context, CAMs of con-

secutive snapshots can now be averaged to obtain a

probability matrix (or transition matrix), thus, giv-

ing the likelihood of each pair of nodes belonging

to the same community for those years. We refer to

this matrix as the probability of co-association matrix

(PCAM), which is computed by averaging the CAMs

in the moving time-window ∆

, and hence referred to

as P(T, ∆

). Thus, the probability of co-association

between nodes i and j at time instance T , using val-

ues backward in time, is:

i j

(T, ∆

) =

∆

∑

t=T −∆

i j

(t). (2)

Thus, CAM has binary values ‘0’ and ‘1’, and PCAM

has real values in [0,1]. We further use the PCAMs

for the prediction model in Step-3 (Section 4.3).

4.2 Step-2: Node-ﬁltering the Network

Given the quadratic complexity of CAM with an at-

tribute set of size N

, we observe that (N

 N

), for

time instances in real-world graphs. Hence, any

time series analysis runs into the risk of over-ﬁtting.

Thus, given the edge sparsity of the network, there

is a requirement to reduce N

. We achieve this by

retaining the signiﬁcant nodes with highly persistent

community behavior. Such nodes demonstrate a high

tendency to be part of a sufﬁciently large community

through most of the period of interest. We pay at-

tention to the size of the communities to which these

KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval

nodes belong so that we ﬁlter out overly fragmented

i.e., small communities. We choose node-ﬁltering

over edge-ﬁltering here because, though the ﬁltering

occurs in the CAM which represents relationships be-

tween nodes, it must also be simultaneously applied

to the original directed network. CAM is equivalent

to an undirected co-association network but uses the

same node-set as the original network. Thus, we ﬁl-

ter the nodes instead of the edges to simultaneously

apply it on both the CAM and the original DSDN.

Deﬁning a Metric for Threshold: Entropy Rate:

The persistence of the co-associations in a network

gives the temporal signiﬁcance of the relationship be-

tween nodes, which is computed using the time series

of the probability values in PCAMs. Here, we are

interested in the temporal signiﬁcance of the nodes

to decide if the node is to be ﬁltered out or retained.

Hence, we compute the signiﬁcance of the node using

the persistence of its co-associations in the network.

To compute the node-wise signiﬁcance, we ﬁrst

average the PCAMs over a speciﬁc period and then

average across either the rows or the columns, since

it is a symmetric matrix. Thus, for each node i in a

network of n nodes, its probability of associating with

other nodes in the window of time (T −∆

, T ], is:

(T, ∆

) =

(n − 1)

∑

j=1

i j

(T, ∆

). (3)

We use the averaging operator here instead of other

statistical operators, as the average gives us a likeli-

hood or probability value. We can now also see that

for each node i, the (N

− ∆

+ 1) instances of these

probability values is effectively the moving average

smoothing of the degree of the node in the CAM, for

a window of size ∆

. Hence, this operation is a mov-

ing average of order ∆

or ∆

-MA.

The ∆

-MA sequence is derived from a time se-

ries, and hence, is a stochastic process, by design. The

time series of edge weights of a real-world graph is a

stationary process (Cai et al., 2016), and hence the

∆

-MA sequence of PCAM elements is also a sta-

tionary process. For a stochastic process of n random

variables, its entropy rate gives us a measure of how

the entropy of the sequence grows with n (Cover and

Thomas, 2006). In our case, the entropy rate of the

sequence of probability values at each node gives us

the change in the tendency of the node to co-associate

with other nodes in communities.

The entropy rate of the stochastic process X is

given by the limiting value of the joint entropy of the

m members of the process {X

, X

, . . . , X

H(X ) = lim

m−>∞

H(X

, X

, . . . , X

)

For a discrete case of joint entropy, the joint en-

tropy of a set of random variables is bounded by the

sum of entropy of the individual variables (Cover and

Thomas, 2006):

H(X

, X

, . . . , X

) ≤

∑

i=1

H(X

) =

∑

i=1

(−p

log(p

)).

Thus, we get the upper bound of entropy rate at

each node i, for time sequence (t

, . . . , t

∆

, . . . , t

)

as a function of window size ∆

for moving average

smoothing:

(∆

) =

∑

k=∆

−(p

, ∆

)log(p

, ∆

)). (4)

Choice of Threshold for Node-ﬁltering: We observe

that the entropy rate of a node i, H

, is closer to 0 when

the node is highly likely to co-associate with other

nodes, i.e., p

, ∆

)≈1 across all snapshots. Thus,

the entropy rate for a node H

is inversely proportional

to the likelihood of its persistent community behavior.

Hence, we identify a threshold for H

, where nodes

with an entropy rate higher than the threshold are ﬁl-

tered out.

We propose to determine the threshold, τ

, using a

line plot of sorted entropy rates of all the nodes in the

network and the size of the node-ﬁltered network. A

steep increase in the entropy rate at a transition point

implies that the network maintains low entropy un-

til this point. We observe that the real-world graph

tends to have two groups of nodes that correspond to

low and high entropy rates, where the presence of any

node from the latter tends to sharply increase the size

of the node-ﬁltered network.

In the node-ﬁltered network of n

nodes, we now

have N

−1)

attributes. Since (N

< N

), we

reasonably reduce the gap between N

and N

, even

though (N

 N

). We also compute the reduced

PCAM, P

(T, ∆

), which is a submatrix of the origi-

nal PCAM, P, corresponding to the retained n

nodes.

4.3 Step-3: CAP using Autoregressive

Models

We now have time series of N

attributes in the re-

duced PCAMs, with N

time instances each, for the

network. In the case of real-world graphs, we ob-

serve that these attributes, which are the probabil-

ity of co-association values in PCAM, have constant

ﬁrst moments, i.e., mean, and ﬁnite second moments,

i.e., variance. Hence, we can now assume that each of

these N

attributes in PCAM forms a weakly station-

ary process. Autoregressive models (AR) (Box and

Jenkins, 1970) and their variants are widely used with

time series data for the prediction of weakly station-

ary stochastic processes.

Data Formats of PCAMs: Given that co-association

is a symmetric relationship, the PCAM stores

CAP-DSDN: Node Co-association Prediction in Communities in Dynamic Sparse Directed Networks and a Case Study of Migration Flow

Input : A sequence of snapshots of a dynamic sparse directed network (DSDN) in the form of sets {V, E(T

E(T

), . . ., E(T

)}

Input : Moving-average window ∆

, Choice of data format F (i.e., vector-format or independent-attribute-format)

Input : Parameters for the autoregressive model (i.e., p for VAR for vector-format, or (p, q) for ARMA for

independent-attribute-format)

Output: Probability of Co-association Matrix (PCAM) of signiﬁcant subnetwork P

+ 1, ∆

) (i.e., reduced

PCAM)

// Step-1

for method M in E

(an ensemble of community detection algorithms) do

for 1 ≤ T ≤ N

A community set C(M) ← Implement(M,{V, E(T )})

Compute the CAM, D(T ), from C, using Equation 1

end

for ∆

≤ T ≤ N

Compute the PCAM, P(T, ∆

), using Equation 2

for 1 ≤ i ≤ n do

Compute p

(T, ∆

) using Equation 3// Likelihood of a node to be co-associated

end

Select optimal CD method M

opt

based on quality of C(M), cardinality of kCk size of communities

// Step-2

for 1 ≤ i ≤ n do

Compute H

(∆

) using p

from M

opt

, using Equation 4

end

Sort H

for all nodes and determine transition point as threshold τ

V’ = {} // Node set of the node-filtered network

for 1 ≤ i ≤ n do

if H

< τ

then

← V

∪ {i}

end

for ∆

≤ T ≤ N

(T, ∆

) ← Submatrix of P(T, ∆

) for {V

,E(T − ∆

),E(T − ∆

+ 1), . . ., E(T )}// Reduced PCAM

end

// Step-3

if F is (vector-format) then

for ∆

≤ T ≤ N

v(T ) ← half-vectorization of P

(T, ∆

)

end

v(N

+ 1) ← Implement (VAR(p),{v(∆

), v(∆

+ 1), . . . v(N

)}), using Equation 5 // Predict for the

reduced PCAM

end

else if F is (independent-attribute-format) then

v(N

+ 1) ← []

for 1 ≤ i ≤ kV

k do

for ∆

≤ T ≤ N

Compute p

(T, ∆

) from P

(T, ∆

) using Equation 3

end

+ 1) ← Implement(AR(p,q),{p

(∆

, ∆

), p

(∆

+ 1, ∆

), . . . , p

, ∆

)}), using

Equation 6// Predict for each node

v(N

+ 1) ← Append(v(N

+ 1), v

+ 1))

end

+ 1, ∆

) ← Reverse-process of half-vectorization(v(N

+ 1))

Algorithm 1: The complete algorithm of CAP-DSDN for DSDNs for prediction of co-association of nodes in a subnetwork

with persistent community behavior.

KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval

n(n−1)

unique pairwise relationships in a network

of n nodes. We propose to use these co-association

values as attributes in a data model for the predic-

tion of community structure using the autoregressive

models. This leads to two possibilities of using the

attributes from the PCAM: (i) in the form of a vec-

tor, thus modeling a time series of N

-long vector, or

(ii) as independent attributes, thus, getting N

separate

time series. We use the upper or the lower triangular

part of the PCAM, without the diagonal for generating

(i) and (ii). Thus, we use half-vectorization of PCAM

for (i).

Prediction using Autoregressive Models: Here, we

choose two such models to suit the aforementioned

data formats, namely, (i) the vector auto-regressive

(VAR) model (Sims, 1980) for the vector format of

the attributes, and (ii) the auto-regressive-moving-

average (ARMA) model (Box and Jenkins, 1970) for

the format of the independent attributes.

In the VAR model, for a vector y of length k, con-

stants vector c, k × k matrices as coefﬁcients A

, a

vector ε as error term, and p as the order of auto-

regressive model, which is the number of time-lags,

the predicted value is given as:

y(T ) = c +

∑

i=1

y(T − i) + ε(T ). (5)

Since (N

 N

), we use low values of p, i.e., p =

1, 2, 3. Hence, we use VAR(1), VAR(2), and VAR(3)

models for our case study. Determining the optimal

choice of p values using the minimization of statistics

such as Akaike (AIC), Schwarz-Bayesian (BIC), etc.

is in the scope of future work.

Using both AR and moving-average (MA) models

together addresses a generalized structure. If we treat

the N

attributes independently, then we can use each

of their time series in an ARMA model for predictive

analysis. An ARMA(p,q) process has two parameters

– p is the order of the autoregressive model, and q is

the order of the MA, i.e, moving average part), which

gives the number of error terms considered. For time

series (scalar) values y at time instance T , constant

value c, coefﬁcients of AR model ϕ, coefﬁcients of

MA model θ, and error term ε(T ),

y(T ) = c +

∑

i=1

y(T − i) +

∑

i=1

ε(T − i). (6)

Since (N

 N

), we use low values of q also. Thus,

in our case study, we use p = 1, 2, 3 and q = 1, 2

in an ARMA(p,q) process. Thus, we implement six

ARMA(p,q) models with the selected (p, q).

Using the predicted values of the elements of the

reduced PCAM, P

, we reconstruct the matrix. The

complete step-by-step procedure of CAP-DSDN is as

given in Algorithm 1.

4.4 Prediction Evaluation

Given the absence of ground truth, we use the time se-

ries data for (N

−3) time instances for our analysis to

predict the remaining three time instances. Currently,

the value of three is conservatively chosen to indicate

short-term prediction and assuming that most of the

DSDNs have more than three snapshots.

We compare our predicted co-association values

with those values computed directly from the data

of these time instances for validation. For compari-

son, we use the metrics conventionally used in clus-

tering algorithms, especially in the absence of ground

truth. We use the Normalized Mutual Information

Score (NMI) (Studholme et al., 1998) and Rand In-

dex (RI) (Rand, 1971) here.

NMI is a measure of the similarity between two

label assignments of the same data, indicating mutual

agreement of labels between the assignments. NMI

values range from 0 to 1, implying the strength of

the agreement. While the bounded values of NMI are

an advantage for comparisons, NMI not adjusting for

chance is a disadvantage for our case study. For two

label assignments, U and V , with L and M classes,

respectively, mutual information (MI) and NMI are

computed, for N objects using entropy measure H, as:

H(U) =

|L|

∑

i=1

P(i)log(P(i));

H(V ) =

|M|

∑

i=1

( j)log(P

( j)),

where the probabilities P(i) and P

( j) are computed

using the number of instances in U and V in the i

and j

classes, respectively.

Thus, P(i) =

|Class(i)|

and P

( j) =

|Class( j)|

When comparing the two labeling assignments, there

may be some instances with both labels i and j. Thus,

the joint probability is:

P(i, j) =

|Class(i)∩|Class( j)|

Thus, MI(U,V ) =

|L|

∑

i=1

|M|

∑

j=1

P(i, j). log



P(i, j)

P(i).P

( j)



We normalize using the sum, i.e., the mean, as it is

considered a good trade-off when considering mini-

mum, mean, and maximum value as the normalizing

factor (Kvalseth, 1987). Thus, the normalized value

NMI(U,V ) =

MI(U,V )

mean(H(U),H(V))

We consider 0 and 1 in the (binarized) CAM as labels,

thus, giving |L| = |M| = 2.

RI is another similarity measure between the ac-

tual community distribution and the predicted com-

munity distribution by considering all pairs of objects,

and by counting the pairs that are assigned in the same

or different clusters in the predicted and true cluster-

ings. RI is the ratio of the number of common pairs

CAP-DSDN: Node Co-association Prediction in Communities in Dynamic Sparse Directed Networks and a Case Study of Migration Flow

to the total number of pairs. We use the unadjusted

RI, bounded in [0,1], as it provides the accuracy of

element pair labeling as given by the clustering.

4.5 Implementation

We have used Python for implementing our proposed

work. CDlib (Rossetti et al., 2019) has been used

for community detection algorithms and metrics. The

time series regression models VAR and ARMA have

been implemented using statsmodels (Seabold and

Perktold, 2010). The validation for prediction using

the metrics for clustering has been implemented us-

ing scikit-learn (Pedregosa et al., 2011). Shannon

entropy has been computed using scipy.stats (Vir-

tanen et al., 2020), using the default logarithm base e,

i.e., natural logarithm.

5 CASE STUDY: EXPERIMENTS

& RESULTS

In this section, we present the results of CAP-

DSDN (Figure 1) on a case study of international

refugee migration over an extended period.

International Refugee Migration Flow: We ana-

lyze the DSDN in a speciﬁc case study of inter-

national refugee migration ﬂow between countries.

The dataset, obtained from the United Nations Hu-

man Rights Commissioner (UNHCR)

.This publicly

available dataset has year-wise records of migrant

count from origin to destination (or asylum) coun-

tries, which are the ﬂow values. While the refugee

data in the UNHCR database is available from the

year 1951, the count of asylum seekers was ﬁrst avail-

able in 2000. Hence, we use the annual data starting in

2000 and thus, focus on the time period during 2000-

2018. In this time period, there are 208 countries of

origin and 186 countries of asylum. After pruning

nodes that have only zero-weighted edges for all the

snapshots, we reduce the node-set to 190 countries.

Thus, our DSDN has 190 nodes for 19 snapshots.

Given the absence of ground truth, we use 2000-

2015 data to predict the PCAM for 2016-2018 of the

signiﬁcant subnetwork, and the predicted values are

compared against the computed values from the orig-

inal data for validation.

Selection of CD Algorithm: The evaluation results

of the three selected community detection algorithms

are reported in Table 1 for a representative year, 2018,

Dataset: https://www.unhcr.org/refugee-statistics/

download/

which is the last year. For the link (LM) modular-

ity, SLPA and MODN show more similar values and

IMAP has a relatively lower value. For Z-Modularity

(ZM), MODN performs better than IMAP and SLPA.

The modularity values closer to zero indicate a sin-

gle large community (Fortunato, 2010), and higher

positive values, but less than one, indicate better par-

titioning. The LM values for the three algorithms

may be explained by the community characteristics

in the year 2018 (Figure 2, (i)-(ii)). We observe

that SLPA gives the highest count of communities

whereas IMAP gives the lowest, but all three gives

similarly sized largest community. Thus we observe

that IMAP has the lowest variation in community

sizes, and SLPA tends to have several smaller com-

munities, indicating a higher degree of fragmentation.

Since ZM is designed to address the issue of reso-

lution limit, we observe that MODN with a consider-

able number of communities, and with moderate vari-

ation in community sizes, performs well. The com-

munity characteristics in Figure 2 also explain the rel-

atively high values of IMAP for Internal Edge Den-

sity (IED), Average Internal Degree (AID), and Cut

Ratio (CR) metrics, indicating the best performance

by IMAP. Higher values of these metrics imply better

communities. SLPA has a distinct advantage in the

case of networks with overlapping communities (Xie

et al., 2011). We observe that SLPA does not per-

form as well as IMAP and MODN, with respect to

our chosen metrics, as our case study does not have

any relevance for overlapping communities.

Overall, we observe from Table 1 that there is

no single CD algorithm that distinctively or consis-

tently performs the best, with respect to our chosen

metrics. This can be explained by the known obser-

vation that these CD algorithms detect a large num-

ber of small and connected whisker-like communities

and a large core with several intermingled communi-

ties. Using the community structure characteristics

shown in Figure 2 (i)-(ii), we conclude that IMAP

performs the best as it demonstrates the community

structure with a large core (Figure 2 (ii)). Thus, IMAP

is an appropriate choice for community detection and

prediction of international refugee migration ﬂow in

our case study, as demonstrated in (Table 1 and Fig-

ure 2). It must be noted that algorithms that disregard

the edge directionality information, e.g., MODN, are

not considered to be accurate (Agreste et al., 2016).

Hence, even though MODN gives a moderate per-

formance, we have disregarded MODN here. With

respect to time complexity, SLPA is the fastest, fol-

lowed by IMAP closely, but MODN has the worst

performance (Agreste et al., 2016). Since time com-

plexity is also a critical factor for the choice of CD

KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval

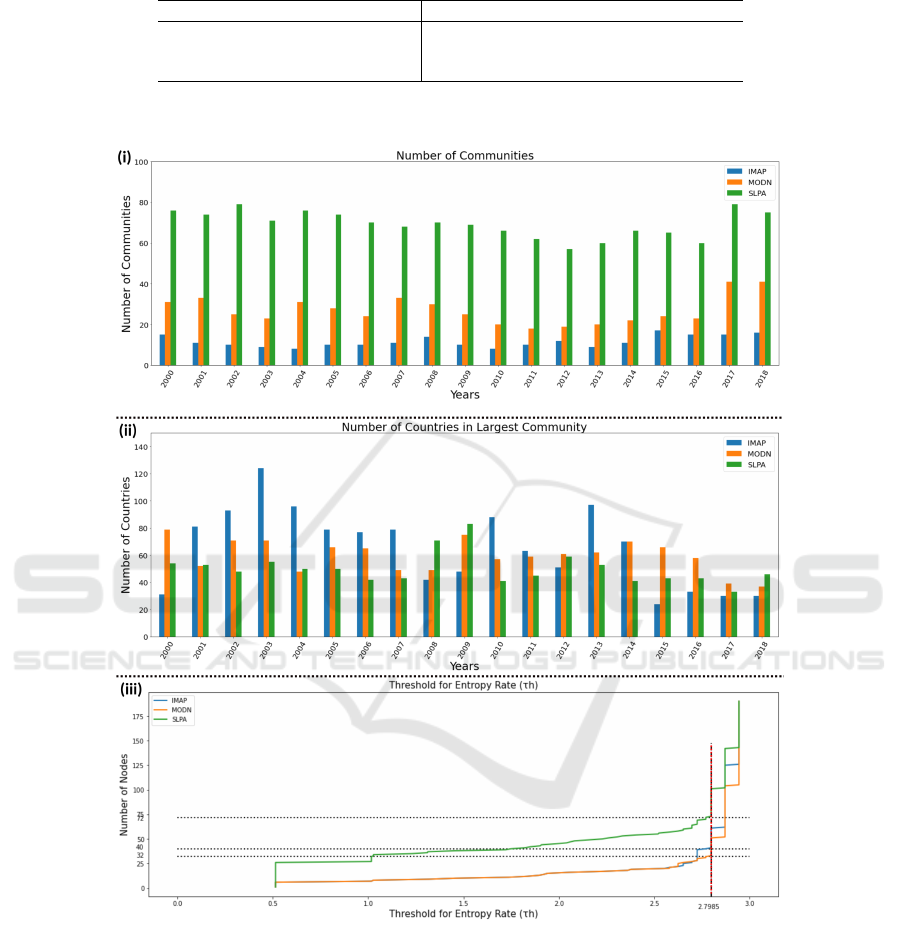
Table 1: Comparing communities in the international refugee migration ﬂow in the year 2018, in 190 countries, using different

algorithms, evaluated by different metrics.

Community Detection Algorithm LM IED AID CR ZM

SLPA 0.028 0.019 0.643 0.004 0.108

MODN 0.028 0.009 1.093 0.005 0.451

IMAP 0.019 0.114 3.647 0.048 0.207

SLPA: speaker-listener label propagation algorithm; MODN: modularity optimization in a directed network; IMAP: Infomap algorithm.

LM: link modularity; IED: internal edge density; AID: average internal degree; CR: cut ratio; ERM: Erd

os-R

enyi modularity; ZM: Z-modularity.

Figure 2: For the selected CD algorithms, (i)-(ii) characteristics of CD outcomes, and (iii) number of nodes retained for

different thresholds for determining entropy rate τ

(red dotted line), for the international refugee migration ﬂow in 190

countries (nodes of the DSDN).

algorithm, IMAP is the optimal choice here.

Node-ﬁltering the Network: Each CD algorithm can

independently have its own τ

. But, in this case study,

we observe that all three algorithms have the same

= 2.799 as the transition point for entropy rate in

their CD outcomes (Figure 2, (iii)). Using this value

as the threshold, we get node-ﬁltered networks of size

, i.e., 72, 32, and 40 nodes, in the case of SLPA,

MODN, and IMAP, respectively. This indicates that

IMAP is a conservative choice.

Time Series Modeling and Prediction: A summary

of the experiments for the IMAP algorithm (for both,

VAR and ARMA) for the network sizes upon ﬁlter-

ing, are given in Table 2. For each VAR experiment,

CAP-DSDN: Node Co-association Prediction in Communities in Dynamic Sparse Directed Networks and a Case Study of Migration Flow

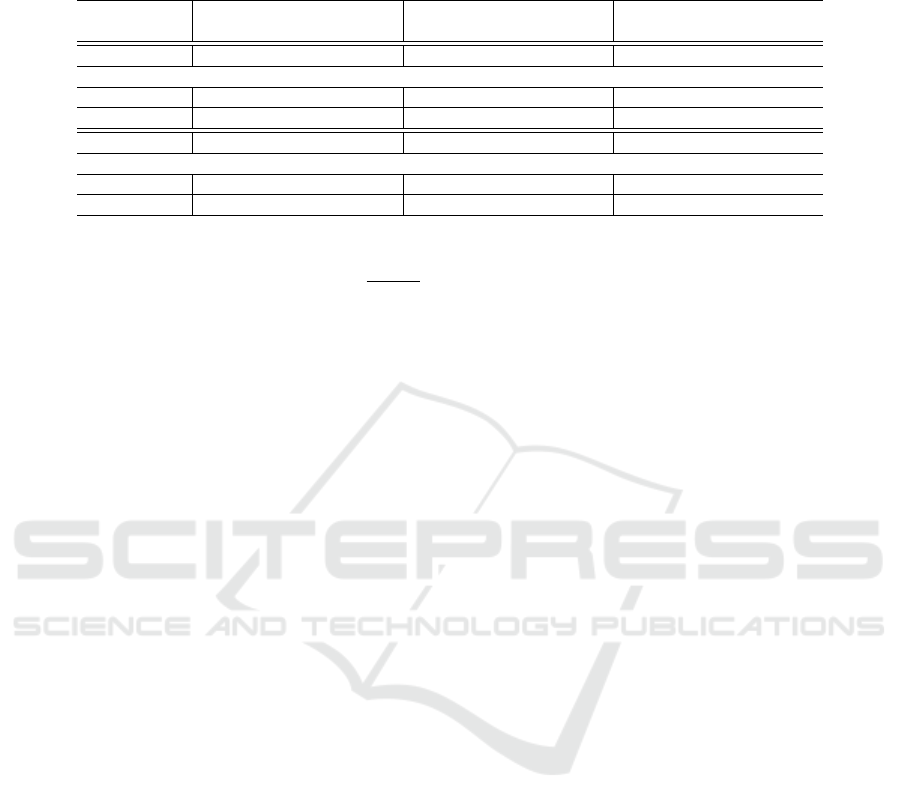
Table 2: Comparison of the predicted PCAMs using autoregressive models, i.e., VAR(p) and ARMA(p,1) models, for com-

munities detected using Infomap algorithm (IMAP), in the international refugee migration network with n = 190 nodes, giving

nodes after node-ﬁltering the DSDN using threshold τ

, in different prediction years (Pred. Yr.).

Pred. Yr. → 2016 2017 2018

Metric ↓

VAR(p) p = 1 p = 2 p = 3 p = 1 p = 2 p = 3 p = 1 p = 2 p = 3

= 2.799, n

= 40, Using IMAP

NMI 0.000 0.000 0.064 0.000 0.000 0.000 0.000 0.000 0.000

Rand-Index 0.943 0.943 0.945 0.982 0.982 0.980 0.992 0.992 0.990

ARMA(p,1) p = 1, p = 2, p = 3, p = 1, p = 2, p = 3, p = 1, p = 2, p = 3,

= 2.799, n

= 40, Using IMAP

NMI 0.039 0.039 0.039 0.015 0.015 0.015 0.008 0.008 0.008

Rand-Index 0.057 0.057 0.057 0.018 0.018 0.018 0.008 0.008 0.008

NMI: normalized mutual information; VAR: vector auto-regression; ARMA: auto-regressive moving average.

the time series of the vector v of size N

−1)

as the vector is obtained from the half vectorization

of the reduced PCAM (of n

nodes), after discarding

the zeros on the diagonal. On the other hand, ARMA

is implemented separately for the time series of N

different elements of v, used in the VAR model. We

make three major observations.

Firstly, the RI gives more variation in the results

than the NMI values, as the latter is a more stringent

validation metric than the former. This is because RI

compares pairwise similarities in the binary values in

the predicted and the original CAMs, whereas NMI

directly compares the matrix values in the CAMs.

Secondly, the VAR model gives better results

than the ARMA model, which can be explained by

the consideration of interdependence between the at-

tributes in the former than in the latter. Also, the dis-

parity N

 N

, for N

time instances, plays a role in

over-ﬁtting solutions for the ARMA model.

Thirdly, the AR parameter p value does not have

any impact on improving the ARMA model. p = 1, 2

show best results for the VAR(p) model. Given the

disparity, p = 1 may be considered the most conserva-

tive value for the VAR(p). We also found that the MA

parameter q = 2 showed the same results as q = 1,

in the ARMA(p,q) model. Hence, we consider only

AR(p,q) only for q = 1 in our experiments.

Overall, IMAP gives the best result for VAR(1)

for the year 2018. Given the political volatility of in-

ternational refugee migration, short-term predictions

are preferred over long-term ones. Thus, we conclude

that CAP-DSDN can be effectively used in interna-

tional refugee migration ﬂow analysis for conserva-

tive predictions of the community structure in the sig-

niﬁcant subnetwork over three years.

As an example of co-association available from

the dataset, the communities in the network in the

year 2015 show that the USA and Mexico are in

the same community. Based on the trend of the re-

duced number of migrations due to geopolitical cir-

cumstances over the years, our model predicts their

co-association to be zero in 2018. The actual co-

association value matches the same and correlates

with the fact that the proportion of the Mexican-born

population in the USA declined from 28% to 26% in

this duration (Krogstad and Radford, 2017).

Another example is that of Australia, where the

migration rates have continued to decline since 2004.

The CAM in 2015 shows that Australia belongs to

a community of 65 countries. The predicted CAM

shows that the community behavior has fallen steeply,

and Australia belongs to a community with 37 coun-

tries, which is reasonably close to the actual value of

29 (United Nations, Dept. of Econ. & Soc. Affairs,

Population Div., 2015).

6 CONCLUSIONS

It is important to note that in the previous litera-

ture while determining communities in DSDNs, the

community of nodes is seen as an entity rather than

its pairwise relationships. Instead of performing a

time series analysis of the network itself or its com-

munities, we have shifted our focus to the inter-

relationships between the network nodes which is

a novelty of CAP-DSDN. In this node-centric ap-

proach, we use the relationship of co-association in a

community, which we use for predictive analysis. We

use the co-association matrices (CAM) to represent

these relationships while representing the discovered

communities of nodes indirectly. When using a time

window, the moving average smoothing of the CAM

gives a likelihood value for the co-association rela-

tionship, which is the PCAM. Furthermore, we use

the elements of PCAM as attributes for the predictive

model for a time series dataset. Lastly, the outcome of

our study is in predicting the co-association value at a

KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval

future date, thus indirectly predicting the community

structure in a signiﬁcant subnetwork. This signiﬁcant

subnetwork retains only the nodes with a strong com-

munity forming tendency over time, determined using

our novel entropy rate metric. Overall, our results in

the case study of the international refugee migration

network demonstrate that the effectiveness of our pro-

posed method depends strongly on the completeness

of the time series data.

There are limitations in our work stemming from

the data quality and availability, concerning the mi-

gration ﬂow datasets. Finding datasets outside of mi-

gration ﬂow is non-trivial, given the nuanced proper-

ties expected of the dataset, i.e., directed networks,

sparse, and with time series. Further research can be

pursued for migration ﬂow data analysis itself in im-

proving the data quality using imputation and other

methods appropriate for the data.

ACKNOWLEDGEMENTS

The authors acknowledge the support of the IIIT Ban-

galore and the IIT Kharagpur summer internship pro-

gram for conducting this work. The authors are

grateful to the anonymous reviewers whose sugges-

tions have improved this paper. This publication

is supported by the grant by the Science and Engi-

neering Research Board (SERB), Government of In-

dia, under the Mathematical Research Impact Sup-

port (MATRICS). The authors are thankful to the help

provided by members of the Graphics-Visualization-

Computing Lab.

REFERENCES

Agreste, S., De Meo, P., Fiumara, G., and et al. (2016).

An empirical comparison of algorithms to ﬁnd com-

munities in directed graphs and their application in

web data analytics. IEEE Transactions on Big Data,

3(3):289–306.

Bongiorno, C., Zino, L., and Rizzo, A. (2019). A novel

framework for community modeling and characteri-

zation in directed temporal networks. Appl. Net. Sc.,

4(1):1–25.

Box, G. and Jenkins, G. (1970). Time Series Analysis: Fore-

casting and Control. Holden-Day, San Francisco.

Cai, D., Campbell, T., and Broderick, T. (2016). Edge-

exchangeable graphs and sparsity. Advances in Neural

Info. Processing Sys., 29.

Cover, T. M. and Thomas, J. A. (2006). Elements of Infor-

mation Theory (Wiley Series in Telecommunications

and Signal Processing). Wiley-Intersc.

Fortunato, S. (2010). Community Detection in Graphs.

Phys. Reports, 486(3-5):75–174.

Krogstad, J. M. and Radford, J. (2017). Key facts about

refugees to the US. Pew Rsrch. Cntr., 30.

Krzakala, F., Moore, C., Mossel, E., Neeman, J., Sly, A.,

Zdeborov

a, L., and Zhang, P. (2013). Spectral re-

demption in clustering sparse networks. Proceedings

of the National Academy of Sciences, 110(52):20935–

20940.

Kvalseth, T. O. (1987). Entropy and correlation: Some

comments. IEEE Transactions on Systems, Man, and

Cybernetics, 17(3):517–519.

Leicht, E. A. and Newman, M. E. (2008). Community

structure in directed networks. Phys. Rev. Letters,

100(11):118703.

Malliaros, F. D. and Vazirgiannis, M. (2013). Clustering and

community detection in directed networks: A survey.

Phys. Reports, 533(4):95–142.

Martin, S., Mor

arescu, I.-C., and Ne

c, D. (2016). Time

scale modeling for consensus in sparse directed net-

works with time-varying topologies. In 2016 IEEE

55th Conference on Decision and Control (CDC),

pages 7–12. IEEE.

Mirshahvalad, A., Lindholm, J., Derlen, M., and Rosvall,

M. (2012). Signiﬁcant communities in large sparse

networks. PloS one, 7(3):e33721.

Miyauchi, A. and Kawase, Y. (2016). Z-score-based modu-

larity for community detection in networks. PloS one,

11(1):e0147805.

Neumayer, E. (2005). Bogus refugees? The determinants

of asylum migration to Western Europe. International

studies quarterly, 49(3):389–409.

Nicosia, V., Mangioni, G., Carchiolo, V., and Malgeri,

M. (2009). Extending the deﬁnition of modular-

ity to directed graphs with overlapping communi-

ties. Jrnl. of Stat. Mech.: Theory and Experiment,

2009(03):P03024.

Pedregosa, F., Varoquaux, G., Gramfort, A., and et al.

(2011). Scikit-learn: Machine Learning in Python.

Journal of Machine Learning Research, 12:2825–

2830.

Pons, P. and Latapy, M. (2006). Computing communities in

large networks using random walks. Journal of Graph

Algorithms and Applications, 10(2):191–218.

Radicchi, F., Castellano, C., Cecconi, F., Loreto, V., and

Parisi, D. (2004). Deﬁning and identifying communi-

ties in networks. PNAS, 101(9):2658–2663.

Rand, W. M. (1971). Objective criteria for the evaluation of

clustering methods. Journal of the American Statisti-

cal Association, 66(336):846–850.

Rossetti, G. and Cazabet, R. (2018). Community discov-

ery in dynamic networks: A survey. ACM Computing

Surveys (CSUR), 51(2):1–37.

Rossetti, G., Milli, L., and Cazabet, R. (2019). CDLIB:

A Python Library to Extract, Compare and Evaluate

Communities from Complex Networks. Applied Net-

work Science, 4(1):1–26.

Rosvall, M. and Bergstrom, C. T. (2008). Maps of random

walks on complex networks reveal community struc-

ture. PNAS, 105(4):1118–1123.

CAP-DSDN: Node Co-association Prediction in Communities in Dynamic Sparse Directed Networks and a Case Study of Migration Flow

Seabold, S. and Perktold, J. (2010). statsmodels: Econo-

metric and statistical modeling with Python. In 9th

Python in Science Conference.

Sims, C. A. (1980). Macroeconomics and reality. Econo-

metrica: journal of the Econometric Society, pages

1–48.

Singh, A. and Humphries, M. D. (2015). Finding commu-

nities in sparse networks. Scientiﬁc reports, 5(1):1–7.

Stein, S. and Leng, C. (2021). A Sparse Random Graph

Model for Sparse Directed Networks. arXiv preprint

arXiv:2108.09504.

Studholme, C., Hawkes, D. J., and Hill, D. L. G. (1998).

Normalized entropy measure for multimodality image

alignment. In Medical Imaging 1998: Image Process-

ing, volume 3338, pages 132–143. Intl. Society for

Optics & Photonics.

Suleimenova, D., Bell, D., and Groen, D. (2017). A general-

ized simulation development approach for predicting

refugee destinations. Scientiﬁc reports, 7(1):1–13.

United Nations, Dept. of Econ. & Soc. Affairs, Population

Div. (2015). International Migration Flows to and

from Selected Countries: The 2015 Revision.

Virtanen, P., Gommers, R., Oliphant, T. E., et al., and SciPy

1.0 Contributors (2020). SciPy 1.0: Fundamental Al-

gorithms for Scientiﬁc Computing in Python. Nature

Methods, 17:261–272.

Wang, B., Gao, L., and Gao, Y. (2012). Control range: a

controllability-based index for node signiﬁcance in di-

rected networks. Jrnl. of Stat. Mech.: Theory and Ex-

periment, 2012(04):P04011.

Xie, J., Szymanski, B. K., and Liu, X. (2011). SLPA: Un-

covering overlapping communities in social networks

via a speaker-listener interaction dynamic process. In

IEEE 11th Intl. Conf. on Data Mining Workshops,

pages 344–349. IEEE.

KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval