A Novel Approach towards Gap Filling of High-Frequency Radar

Time-series Data

Anne-Marie Camilleri

, Joel Azzopardi

and Adam Gauci

Department of Artiﬁcial Intelligence, Faculty of ICT, University of Malta, Msida, Malta

Department of Geosciences, Faculty of Sciences, University of Malta, Msida, Malta

Keywords:

Time-series Analysis, Deep Learning, Machine Learning, Gap Filling, High Frequency Radar.

Abstract:

The real-time monitoring of the coastal and marine environment is vital for various reasons including oil spill

detection and maritime security amongst others. Systems such as High Frequency Radar (HFR) networks

are able to record sea surface currents in real-time. Unfortunately, such systems can suffer from malfunc-

tions caused by extreme weather conditions or frequency interference, thus leading to a degradation in the

monitoring system coverage. This results in sporadic gaps within the observation datasets. To counter this

problem, the use of deep learning techniques has been investigated to perform gap-ﬁlling of the HFR data.

Additional features such as remotely sensed wind data were also considered to try enhance the prediction ac-

curacy of these models. Furthermore, look-back values between 3 and 24 hours were investigated to uncover

the minimal amount of historical data required to make accurate predictions. Finally, drift in the data was also

analysed, determining how often these model architectures might require re-training to keep them valid for

predicting future data.

1 INTRODUCTION

The growth of the blue economy and maritime opera-

tions, and the importance given to sustainable oceans

has rendered the availability of real-time oceano-

graphic observation and forecast data to be crucial in

this day and age. Such data can be used in various

applications such as oil spill response, maritime se-

curity, and monitoring of the coast and marine envi-

ronments amongst others (Gauci et al., 2016). Obser-

vation data can be collected via in-situ methods (e.g.

buoys and ﬂoats), and also via remote sensing such as

High Frequency Radars (HFR).

HFR networks consist of a number of coastal radar

antennas, and the data from all the radars in the net-

works is aggregated together to provide real-time ob-

servations (maps) of oceanographic parameters, such

as sea surface currents (Gauci et al., 2016). One such

radar network is the Calypso HFR network, where the

antennas are distributed along the coasts of the Mal-

tese Islands and Southern Sicily providing real-time

observations in the Malta-Sicily channel, and in wa-

ters south of the Maltese Islands.

Observation data collected from such instruments

can be considered to be closer to reality than data gen-

erated from oceanographic hydrodynamical models,

and can have substantial spatial coverage (albeit with-

out providing data for different depth levels as hydro-

dynamic models). On the other hand, they are prone

to errors. Instruments and related electronics can mal-

function from time to time, and are prone to interfer-

ence from other sources of radio waves at frequencies

close to their operational frequencies. Such circum-

stances result in degraded outputs, limited spatial cov-

erage, and the occurrence of gaps (spatial areas within

the domain with missing or low quality data) (Gauci

et al., 2016). These gaps obviously hinder the effec-

tiveness of the applications that make use of this real-

time data. Therefore, gap-ﬁlling techniques would be

desirable to ﬁll such gaps with data close to reality.

Over the years many have obtained reasonably ac-

curate results using numerical techniques such as in-

terpolation. However, techniques such as regression

suffer in cases where gaps become substantial in size.

Good quality prediction is a difﬁcult task, especially

for areas such as the Mediterranean Sea, due to the

large temporal and spatial variability of wind and cur-

rents over this area. Therefore, more complex models

such as machine learning models, and especially deep

learning architectures, would be more suitable.

In this paper, we investigate the use of Artiﬁcial

Intelligence (AI) techniques to perform gap-ﬁlling on

Camilleri, A., Azzopardi, J. and Gauci, A.

A Novel Approach towards Gap Filling of High-Frequency Radar Time-series Data.

DOI: 10.5220/0011540400003335

In Proceedings of the 14th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2022) - Volume 1: KDIR, pages 229-236

ISBN: 978-989-758-614-9; ISSN: 2184-3228

229

observation data collected by the Calypso HFR net-

work. Our aim is to create an accurate, sea surface

current gap-ﬁlling model which uses machine learn-

ing techniques. This aim is attained through the fol-

lowing research objectives:

1. Identify the best-performing machine learning

model architecture;

2. Investigate the effect of external features such as

satellite wind data, which can be added to the cur-

rents data to enhance the prediction quality;

3. Attempt to identify the minimal amount of look-

back historical data required in order to train a

gap-ﬁlling model which gives accurate results;

and

4. Investigate how often the gap-ﬁlling models will

require retraining, in order to keep them valid for

predicting future data.

Research performed in this area generally resorts

to using numerical techniques and often times sim-

ple Feed-forward neural network models (Gauci et al.,

2016; Ren et al., 2018; Vieira et al., 2020). Although

relatively accurate results can be obtained, this re-

search is taken further by introducting other machine

learning models, and providing a more in-depth anal-

ysis on the use of external features, look-back re-

quired, and data drift.

2 RELATED WORK

This research builds mostly on the research performed

by Gauci et al., where they also performed gap-ﬁlling

of the HFR sea-surface currents data in the Malta-

Sicily Channel (Gauci et al., 2016). Due to the short-

comings of statistical methods, they considered using

Artiﬁcial Neural Networks (ANN) models in order to

ﬁll gaps in the radar maps. The ANN models were

built using previous observations of HFR data, in ad-

dition to satellite wind observations.

Ren et al. utilised different data sources to pre-

dict the coastal sea surface current velocity in the

Galway Bay area (Ren et al., 2018). Three-layer

Feed-Forward Neural Network (FFNN) models were

trained on different coordinates independently using

historical look-back data. Different experiments were

carried out, using tide elevation, wind speed and di-

rection and sea surface currents data to make predic-

tions (Ren et al., 2018).

Finally, Karimi et al. also applied ANN models to

try predict time-series sea level records for gap-ﬁlling

(Karimi et al., 2013). They found that using historical

data as inputs to the models gave better results, and

used six previous time-steps in order to make predic-

tions (Karimi et al., 2013).

2.1 Model Selection and

Hyper-parameter Tuning

A number of different statistical techniques have been

employed for this problem including interpolation

and linear regression amongst others (Gauci et al.,

2016; Karimi et al., 2013; Pashova et al., 2013). Ma-

chine learning models (most notably ANNs), have of-

ten been found to outperform statistical techniques.

Gauci et al. and Ren et al. both applied FFNNs to

HFR data to try ﬁll gaps in sea surface current radar

maps. Experiments were carried out to determine the

adequate amount of historical radar observations to

use as an input to the models (Gauci et al., 2016; Ren

et al., 2018). Song et al. applied multiple LSTM net-

works to predict sea surface height anomalies. Predic-

tions were made for 1 day ahead, using data from (L)

previous days (Song et al., 2020). RF models were

utilised by Kim et al. to perform gap-ﬁlling of eddy

covariance methane ﬂuxes (Kim et al., 2020). Finally,

Wolff et al. compared a number of different machine

learning models to predict sea surface temperature in-

cluding FFNNs, LSTMs, as well as RFs. To train the

models they used historical data (Wolff et al., 2020).

2.2 Feature Selection

Gauci et al. used a combination of radar data and

additional wind data and these two sources allowed

them to make more intelligent predictions in order to

ﬁll gaps in the radar maps (Gauci et al., 2016). Simi-

larly, Vieira et al. also tried experimenting by adding

wind speed and direction measurements to predict

gaps in the wave height (Vieira et al., 2020).

2.3 Temporal Historical Data

When dealing with time-series data, predictions can

be made in one of the following ways: using a single

previous time-step or multiple time-steps to make pre-

dictions. The reason for using historical data known

as look-back, depends on the variation of the data in

space and time (Ren et al., 2018).

Through experimentation, (Gauci et al., 2016) as

well as (Mahjoobi and Adeli Mosabbeb, 2009) found

that when more than six hours were used, the cor-

relation of data observations was not strong enough

(Gauci et al., 2016; Mahjoobi and Adeli Mosabbeb,

2009).

2.4 Data Drift

The concept of drift in time-series data is related to the

data changing over time (Vieira et al., 2020). Using

KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval

230

machine learning models is a good idea because they

are able to learn patterns and non-linearity in the data

(Vieira et al., 2020).

Gauci et al. and Pashova et al. trained their mod-

els on data collected over a couple of years, and ﬁlled

in the gaps in the data within the same time range

which were missing (Gauci et al., 2016; Pashova

et al., 2013). Mahjoobi et al. gathered data between

September and December from 2002 and 2004. The

data from 2002 was used to train the models, while

the data from 2004 was used to test and evaluate their

models (Mahjoobi and Adeli Mosabbeb, 2009). Al-

though different time ranges were used to train the

models for gap-ﬁlling in previous research, we did

not encounter previous works that investigate how of-

ten gap-ﬁlling models would require retraining when

trained on speciﬁc periods of time.

3 METHODOLOGY

This section starts with a system overview, followed

by a description of the data sources, and the prepro-

cessing techniques used. Subsequently, the method-

ology used to achieve each objective are presented.

3.1 System Overview

As mentioned in Section 1, the problem at hand re-

quires the ﬁlling of HFR sea surface currents for rea-

sons such as maritime security, among others.

Interpolation techniques were investigated to

achieve a baseline through ﬁlling artiﬁcially created

gaps of different sizes within the data domain. Three

machine learning models were considered according

to the literature found: FFNN, LSTM, and RF model

architectures. Hyper-parameter tuning of the model

architectures was carried out to determine the best

performing model. These investigations are linked to

Objective 1, and discussed further in Section 3.3.2.

The addition of wind data to the input data was

considered, related to Objective 2. The addition of

external features for environmental data prediction is

a common practice used in literature. Different ex-

periments were carried out to achieve an optimised

hyper-parameter conﬁguration for each model archi-

tecture, discussed further in Section 3.3.3.

An investigation was carried out to determine the

minimal amount of look-back time-steps used in or-

der to make predictions, related to Objective 3. Be-

tween 3 and 24 hours of look-back were considered,

discussed further in Section 3.3.4.

Drift in the data was also investigated in Sec-

tion 3.3.5. This investigation was related to Objec-

tive 4, and carried out to determine how often the

models would need re-training, to make predictions

on future data without losing accuracy. Finally, the

optimal gap-ﬁlling model conﬁguration was used to

train a model for each coordinate in the HFR map,

where independent models were trained on the U and

V data components.

3.2 Data Pre-processing

3.2.1 Sea Surface Current Radar Data

The HFR data used was obtained from the Calypso

Professional Data Interface. HFR data between the

Malta-Sicily channel is provided, which is recorded

with a temporal frequency of one hour. This hourly

data can be downloaded as is, or aggregated into daily

ﬁles readily available for download.

The data between 01/01/2018 T 00:00 GMT and

31/12/2019 T 23:59 GMT was obtained in the form

of hourly ﬁles, and contained the recorded HFR data

for coordinates within the radar map. The data for

each coordinate is recorded in the form of U and V

water velocity components, which together form the

sea surface current velocity matrices having dimen-

sions (time = 1, lat = 43, lon = 52). The values of

the longitude and latitude arrays have units ‘degrees

East’ and ‘degrees North’ respectively, while the U

and V velocity data is recorded in ‘m/s’.

3.2.2 Additional Data

The global ocean near real-time wind velocity data

was obtained from the Copernicus Marine website.

The data was obtained in the same date range as the

radar data, and stored in a single ﬁle. The U and

V wind velocity matrices had the following structure

(time = 2920, lat = 25, lon = 25), due to the fact that

the data was recorded at a temporal frequency of six

hours rather than one hour, and the data was recorded

at a different spatial frequency than the HFR data.

Due to the temporal and spatial frequencies of the

satellite wind data not correlating with the HFR data,

pre-processing had to be carried out on the wind data.

Bi-linear interpolation was applied to the U and V

raster grids to up-sample the data spatially and linear

interpolation was used to increase the temporal fre-

quency of the wind data from six hours to one hour

(Gauci et al., 2016).

3.2.3 Dataset Compilation

Once the datasets were pre-processed as mentioned

in the two previous sections, in order to train the

machine learning models, the data required compi-

A Novel Approach towards Gap Filling of High-Frequency Radar Time-series Data

231

lation before being inputted into the models. The

datasets were split into training, testing and valida-

tion data using k-fold cross validation. K-fold cross

validation is a commonly used technique in machine

learning for model selection (Mahjoobi and Adeli

Mosabbeb, 2009). The number of folds chosen for

experimentation was 10, as done by (Mahjoobi and

Adeli Mosabbeb, 2009).

3.3 Implementation

3.3.1 Baseline Interpolation Techniques

When dealing with gap-ﬁlling, one of the most com-

mon simple techniques which has been used through-

out literature has been interpolation, and more specif-

ically linear interpolation (Gauci et al., 2016; Ren

et al., 2018). The three interpolation techniques

considered in this research were: Bi-linear, Nearest

Neighbour and Inverse Distance Weighted (IDW). In

order to test how efﬁciently these techniques could ﬁll

gaps, the notion of ‘bounding boxes’ was adopted.

When analysing the HFR data, it was discovered

that more data is available in the centre of the do-

main. Therefore, a central coordinate at Longitude:

14.679

◦

East (30) and Latitude: 36.421

◦

North (25)

was chosen and bounding boxes having sizes: 3, 5,

7, 9, 11, 13, 15 and 21 were constructed around this

central coordinate.

For each available time-step in the data, the U and

V matrices were processed separately. For each time-

step, the values within the bounding box were set to

‘Nan’ values to create artiﬁcial gaps in the raster grid.

The different interpolation methods were then applied

to try ﬁll the values within the bounding box. The

reason increasing sizes of bounding boxes were used,

was to test how accurately these statistical techniques

could ﬁll in missing data when neighbouring data is

reduced.

3.3.2 Machine-learning Architecture Overview

More complex, but efﬁcient approaches which are

most commonly used for gap-ﬁlling, are machine

learning models. As seen in Section 2.1, one of the

most commonly used machine learning approaches

for gap-ﬁlling are FFNN models (Gauci et al., 2016;

Karimi et al., 2013; Pashova et al., 2013; Ren et al.,

2018; Vieira et al., 2020). Other commonly used ap-

proaches are LSTM models (Song et al., 2020; Wolff

et al., 2020) and RF models (Kim et al., 2020; Ren

et al., 2018; Wolff et al., 2020). Therefore, these three

different machine learning architectures were consid-

ered for gap-ﬁlling, in order to ﬁnd the best perform-

ing model through hyper-parameter optimisation, as

stated in Objective 1.

Feed-Forward Neural Network Model - FFNN

models are a commonly used machine learning tech-

nique because of their simple structure. The models

trained for gap-ﬁlling were 3-Layer FFNN models be-

cause these were commonly used in literature (Gauci

et al., 2016; Pashova et al., 2013; Ren et al., 2018;

Vieira et al., 2020), and have been known to produce

satisfactory results. In this model, the sum carried

out on a hidden neuron a

is calculated as follows

∑

i, j

1, j

, where x

represents the input val-

ues, w

i, j

represents the weight between the input and

hidden layers and b

1, j

represents the bias for the hid-

den layer (Vieira et al., 2020).

The size of the input layer was set according to

the number of look-back time-steps considered. The

look-back variable was initially set to 6, as done by

(Gauci et al., 2016; Pashova et al., 2013) who applied

FFNN models on oceanographic data for gap-ﬁlling.

The number of neurons h

used in the hidden layer

was set to 15 neurons, and the number of epochs was

set to 50, both determined through experimentation.

The size of the output layer was set to 1 neuron. The

ReLu activation function was applied to the input and

hidden layers as done by (Wolff et al., 2020). The

model was compiled using the Adam optimiser with

a learning rate α = 0.001 as done by (Sahoo et al.,

2019), also determined through experimentation. Fi-

nally, the loss function chosen was the Mean Squared

Error loss as done by (Sahoo et al., 2019).

Long Short-Term Memory Network Model - Al-

though less commonly used for gap-ﬁlling, the LSTM

model has been found in literature to perform better

than the classic FFNN model. The LSTM model net-

work block is composed of different gates, the input

, output o

and forget f

gates, where t represents the

prediction period (Sahoo et al., 2019). One or more

hidden layers were used with h

neurons in each layer

i, as done by (Wolff et al., 2020). Similar to the FFNN

implementation, the look-back variable was used to

deﬁne the input layer size, initially set to 6 and the

output layer was also set to 1. The size of the hidden

layer was set to 30 neurons and the number of epochs

used was set to 50, both determined through hyper-

parameter tuning. Finally, the model was compiled

using the same optimiser, loss function and activation

function applied to the FFNN model.

Random Forest Model - RF is not as commonly used

in literature for gap ﬁlling as the FFNN and LSTM

models, it has been used due its simplicity and rela-

tively good performance, as advised by (Kim et al.,

2020; Wolff et al., 2020).

Among the different parameters the RF model

accepts, the ‘n

estimators’ and Boolean ‘bootstrap’

KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval

232

variables were inputted into the model. The

‘n estimators’ variable represents the number of trees

to build in the RF, set to 50, while the ‘bootstrap’

Boolean variable determines if bootstrapping is used

or not. Bootstrapping is a process whereby, a random

sample from the original dataset is selected at random

with replacement when training each tree. This helps

with reducing over-ﬁtting within the model, and was

therefore set to ‘True’. These hyper-parameters were

determined through experimentation.

3.3.3 Feature Selection

Environmental data such as the sea surface currents

could be effected by external features such as wind,

tides and waves amongst others. Some researchers

which included the use of additional features in their

prediction models were (Gauci et al., 2016; Mahjoobi

and Adeli Mosabbeb, 2009; Ren et al., 2018; Vieira

et al., 2020; Wolff et al., 2020). The addition of ex-

ternal features was investigated in relation to Objec-

tive 2.

The input data for a particular time-step contained

6 hours of HFR data concatenated with 6 hours of

wind velocity data. After adding wind velocity as

features, the best performing FFNN model was found

(by experimentation) to have 25 neurons in the hidden

layers. The models in this phase were trained using

the same optimiser function, loss function, activation

function and number of epochs as described in Sec-

tion 3.3.2. The input layer now contained 12 neurons

as look-back observations (Gauci et al., 2016).

The LSTM model experiments carried out (after

adding the wind data) were similar to those carried out

on the FFNN model. The model architecture found to

produce the best results used 30 neurons in the hidden

layer. As done for the FFNN model, 12 neurons were

used in the input layer.

On the other hand, since the RF model did not re-

quire excessive hyper-parameter tuning, only a few

experiments were carried out on it. The models used

for these experiments were built using bootstrapping

and utilising 50 trees, since these were the best per-

forming hyper-parameters found.

3.3.4 Temporal Historical Data

The notion of a look-back variable was used to de-

termine the ideal minimum amount of historical time-

steps required in order to accurately predict the HFR

data, stated in Objective 3.

The look-back values taken into consideration

were: 3, 12, 18 and 24 hours, as the experiments car-

ried out for a look-back of 6 hours have already been

discussed in Section 3.3.2. For the FFNN model, ex-

periments on the different look-back values were car-

ried out using the same optimiser function, loss func-

tion, activation function and number of epochs used in

Section 3.3.2. The models were built using 15 in the

hidden layer, determined through experimentation.

For the LSTM model architecture, the same look-

back values used for the FFNN model were consid-

ered. For the look-back value of 3 hours, 20 neurons

were used in the hidden layer. For the look-back val-

ues of 12 and 18 hours, 50 neurons were used and for

24 hours, 52 neurons were found to produce the best

results.

For the RF model, the different look-back experi-

ments carried out used bootstrapping in order to train

the models. The experiments carried out on each of

the look-back values used 50 trees to build the mod-

els respectively, determined through experimentation.

3.3.5 Data Drift

When dealing with environmental data such as sea

surface currents data which is constantly changing

with time, prediction models might need re-training

to be able to predict data further away in the future.

Therefore, an investigation was carried out by train-

ing the different model architectures on data spanning

over different time ranges, related to Objective 4.

The experimentation carried out in order to inves-

tigate if there was any drift in the data was done by

splitting the 2018-2019 radar data into partitions. The

ﬁrst partition entailed the full two year dataset, while

the remaining partitions split the data into subsequent

6 month ranges. Then, the HFR data was obtained

from January to March of 2020, and used to evalu-

ate the models. Data from 2020 was used as this data

was unseen future data. The look-back value used for

these experiments was set to 6 hours, determined to

be an appropriate minimal amount of historical data

to use in Section 3.3.4.

3.3.6 Gap-ﬁlling System Overview

The ﬁnal step for the research carried out on the

gap-ﬁlling, was to use the best performing machine

learning prediction model with optimised hyper-

parameters, to train a model for the U and V HFR data

for each coordinate in the domain containing available

data. This was done by loading the required data be-

tween 2018 and 2019, pre-processing the data to ob-

tain the x and y data according to the look-back value

selected and shufﬂing the data randomly to avoid bias

in the models. Data from 2020 was then considered

for gap-ﬁlling prediction.

In order to make predictions, for the look-back

values of the ﬁrst prediction time-frame, the miss-

A Novel Approach towards Gap Filling of High-Frequency Radar Time-series Data

233

ing U and V values were ﬁlled using the bi-linear

interpolation method. This was done since, in or-

der to make a prediction for a particular coordinate,

each look-back time-step required available HFR ob-

servations. Bi-linear interpolation was chosen as it

performed best when compared to other interpolation

techniques.

4 EVALUATION

The error metric used to evaluate the models was

the Mean Squared Error (MSE), used by Wolff et al.

(Wolff et al., 2020).

4.1 Model Selection

As mentioned in Section 3.3.2, initial experimentation

on the different machine learning models was carried

out using a look-back of six hours, as this value was

found to be appropriate to make accurate predictions

in literature (Gauci et al., 2016; Mahjoobi and Adeli

Mosabbeb, 2009; Pashova et al., 2013).

4.1.1 Interpolation vs Machine Learning Models

The Bi-linear interpolation method was found to be

the best performing interpolation technique. When

comparing the machine learning models to the inter-

polation techniques, it was discovered that as the size

of the gap in the raster grid grew, the interpolation

techniques did not manage to ﬁll the gaps as well as

the machine learning models. The results achieved by

the machine learning models were found to be signif-

icantly better than those generated by simple interpo-

lation methods.

4.1.2 Machine Learning Model Comparison

Experiments were run on six selected coordinates in

the domain, for each machine learning model archi-

tecture using the best conﬁgurations discovered from

the hyper-parameter tuning carried out. The results of

the experiments carried out are presented in Tables 1

and 2. The results depict the averaged MSE over the

test data for the U and V component data, trained on

each of the machine learning models (for independent

coordinates in the raster grid).

When comparing the results, the LSTM model

was found to perform statistically better than the

FFNN and RF models, followed by the FFNN model.

Although the RF performed quite well, it did not man-

age to exceed the neural network model architectures.

4.2 Feature Selection

As an extension of the experiments carried out on the

three machine learning models, additional data was

also considered. The results from each model archi-

tecture using both wind and radar data, were statisti-

cally tested against the model conﬁgurations not using

the additional wind data. This was done to investigate

if adding the wind data to the HFR data, would im-

prove predictions, related to Objective 2.

For all three model architectures, although the ad-

dition of the wind data improved the prediction results

very slightly for some coordinates, the improvements

were very minor. This meant that accurate predictions

could still be made when only taking into considera-

tion the HFR sea surface currents data in order to ﬁll

gaps, as the difference in the MSE results was almost

negligible. Table 3 depicts the results obtained when

using the LSTM model.

4.3 Temporal Historical Data

An investigation was carried out in relation to the dif-

ferent amount of historical look-back data to use. The

minimum amount of look-back was desired since,

when making predictions to ﬁll gaps in the data for a

time-step, the previous consecutive look-back values

must all be available. This experimentation was done

as an extension of the experiments carried out using a

look-back value of six hours, presented in Section 4.1,

related to Objective 3.

Figure 1 depicts the average MSE results obtained

from each of the look-back experiments carried out on

the LSTM model. Although using longer look-back

sequences produced slightly better results overall, the

more look-back is used, the more training data would

be required in order to train these models, as men-

tioned previously. Therefore, using a look-back of

six was found to be an appropriate minimal amount

of historical data to use when training the different

model architectures.

4.4 Data Drift

Experimentation was carried out on the HFR data

used to train and test the neural network model archi-

tectures, in order to investigate any potential drift in

the data, related to Objective 4. The model architec-

tures used were the hyper-parameter tuned architec-

tures discovered through experimentation carried out

in Section 3.3.2.

Figure 2 depicts the experiment results on the

LSTM model. When comparing the results obtained,

no drift was detected in the data. The experiment

KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval

234

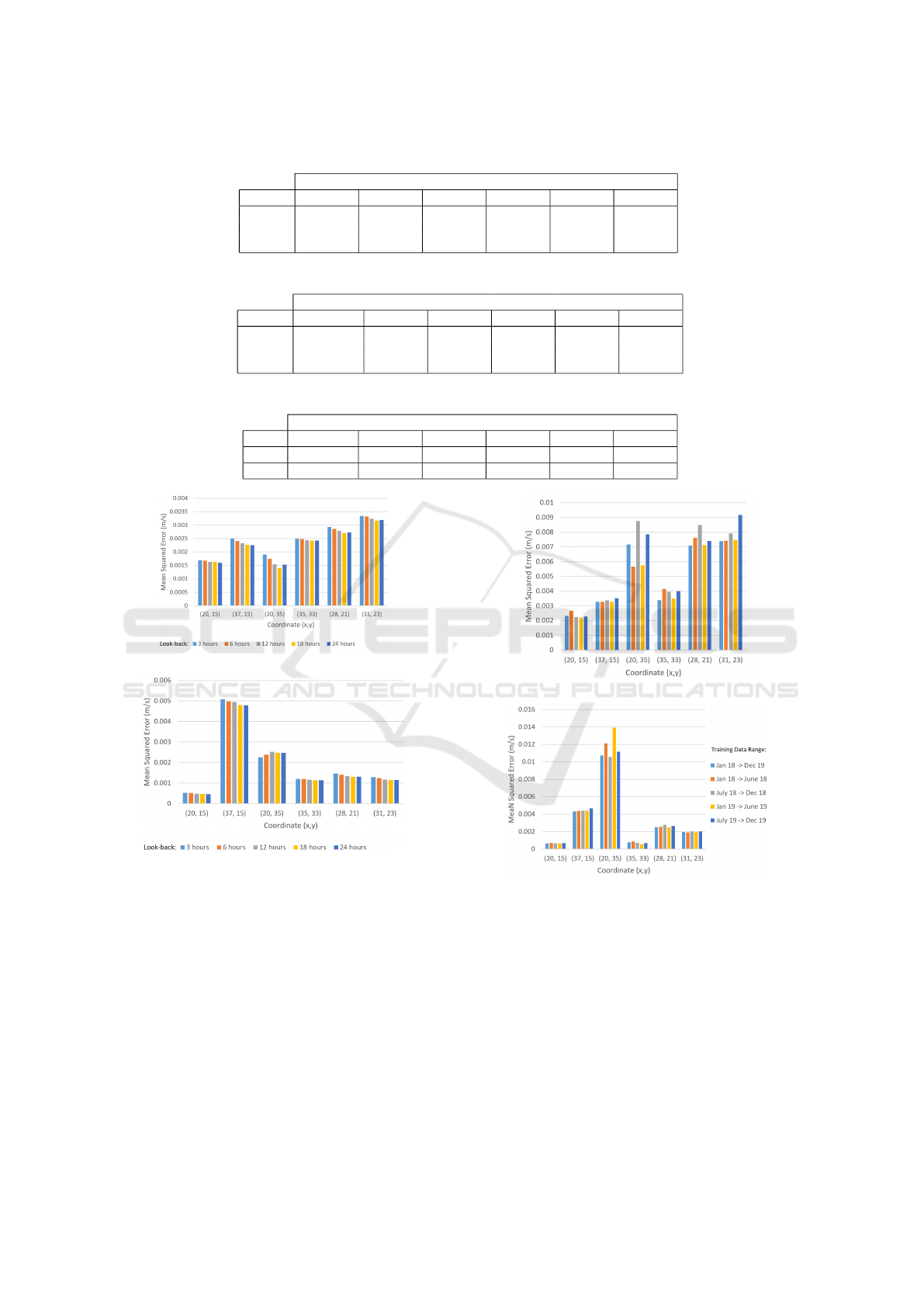
Table 1: Averaged Validation MSE for U Vector Data.

Coordinate

Model (20, 15) (37, 15) (20, 35) 35, 33) (28, 21) (31, 23)

FFNN 0.00176 0.00246 0.00153 0.00252 0.00297 0.00335

LSTM 0.00168 0.00241 0.00174 0.00249 0.00286 0.00332

RF 0.00186 0.00266 0.00148 0.00279 0.00319 0.00360

Table 2: Averaged Validation MSE for V Vector Data.

Coordinate

Model (20, 15) (37, 15) (20, 35) 35, 33) (28, 21) (31, 23)

FFNN 0.000520 0.00508 0.00261 0.00119 0.00144 0.00124

LSTM 0.000509 0.00498 0.00238 0.00120 0.00141 0.00124

RF 0.000562 0.00559 0.00247 0.00129 0.00152 0.00137

Table 3: LSTM Feature Selection Model Averaged Validation MSE.

Coordinate

Data (20, 15) (37, 15) (20, 35) 35, 33) (28, 21) (31, 23)

U 0.00167 0.00240 0.00230 0.00246 0.00283 0.00325

V 0.000506 0.00500 0.00240 0.00118 0.00140 0.00122

(a) U Data MSE Results.

(b) V Data MSE Results.

Figure 1: LSTM Look-Back Comparison Results.

using all data between 01/2018 and 12/2019 was se-

lected as the most appropriate amount of data in order

to train the models since, using all the data rather than

just a 6 month partition, performed slightly better for

most coordinates overall.

4.5 Gap-ﬁlling System Overview

The LSTM model conﬁguration having the follow-

ing architecture (6:30:1), obtained improved results

over the other models. This conﬁguration was used

(a) U Data MSE Results.

(b) V Data MSE Results.

Figure 2: LSTM Data Drift Experiment Results.

to train different models on the U and V component

HFR data between 2018 and 2019, for all coordinates

in the raster grid. Figure 3 depicts the gap-ﬁlling car-

ried out on data in July 2020. As can be seen from

the map plot, the prediction models manage to learn

trends in the data domain, such as the eddy currents.

When investigating the difference between the actual

and predicted vector values, the differences were al-

ways less than 1m/s which shows that the predictions

were very accurate.

A Novel Approach towards Gap Filling of High-Frequency Radar Time-series Data

235

Figure 3: LSTM Gap-Filling Hybrid Model Predictions.

5 CONCLUSION AND FUTURE

WORK

The aim of this research is concerned with achieving

accurate gap-ﬁlling of the HFR sea surface current

data through Objectives 1-4. It was discovered that in-

terpolation techniques are not be as accurate as using

machine learning models (Gauci et al., 2016). Fur-

thermore, when comparing the three machine learning

models, the LSTM model was found to be the most

effective.

Furthermore, the addition of external satellite

wind data to the training data did not improve the

results signiﬁcantly, as discovered by (Vieira et al.,

2020). An investigation was also carried out on the

amount of look-back historical data to use in order to

train the models. Through the experimentation car-

ried out, it was found that using a look-back of six

hours made more sense due to the constraints of the

dataset, as done by (Gauci et al., 2016).

Finally, an investigation was carried out related to

how often the gap-ﬁlling models would require re-

training in order to keep them valid for predicting

future data. It was found that there was no drift in

the data when being trained on certain periods. Fur-

thermore, training the models on the full two years

achieved the best results over-all and was able to make

accurate predictions on data in 2020.

5.1 Future Work

Although the wind velocity did not improve the pre-

diction results for gap-ﬁlling of the sampled data,

other external features could also be investigated fur-

ther. Tidal elevation and sea surface heights could be

investigated with regards to their effects on the HFR

sea surface current data.

Further investigations on the possibilities of sea-

sonal drift could be investigated further. Models

could be trained on data from different seasons to

test whether any trends in the data are found, and if

models trained per season could achieve more accu-

rate predictions. Finally, this research can be taken

further to achieve short-term forecasting of the HFR

data, which is already in the works.

REFERENCES

Gauci, A., Drago, A., and Abela, J. (2016). Gap ﬁlling of

the calypso hf radar sea surface current data through

past measurements and satellite wind observations.

International Journal of Navigation and Observation,

2016.

Karimi, S., Kisi, O., Shiri, J., and Makarynskyy, O. (2013).

Neuro-fuzzy and neural network techniques for fore-

casting sea level in darwin harbor, australia. Comput.

Geosci., 52:50–59.

Kim, Y., Johnson, M. S., Knox, S. H., Black, T. A., Dal-

magro, H. J., Kang, M., Kim, J., and Baldocchi, D.

(2020). Gap-ﬁlling approaches for eddy covariance

methane ﬂuxes: A comparison of three machine learn-

ing algorithms and a traditional method with prin-

cipal component analysis. Global Change Biology,

26(3):1499–1518.

Mahjoobi, J. and Adeli Mosabbeb, E. (2009). Prediction of

signiﬁcant wave height using regressive support vec-

tor machines. Ocean Engineering, 36:339–347.

Pashova, L., Koprinkova-Hristova, P., and Popova, S.

(2013). Gap ﬁlling of daily sea levels by artiﬁcial

neural networks. TransNav: International Journal on

Marine Navigation and Safety of Sea Transportation,

7:225–232.

Ren, L., Hu, Z., and Hartnett, M. (2018). Short-term

forecasting of coastal surface currents using high fre-

quency radar data and artiﬁcial neural networks. Re-

mote Sensing, 10:850.

Sahoo, B., Jha, R., Singh, A., and Kumar, D. (2019).

Long short-term memory (lstm) recurrent neural net-

work for low-ﬂow hydrological time series forecast-

ing. Acta Geophysica, 67.

Song, T., Jiang, J., Li, W., and Xu, D. (2020). A deep

learning method with merged lstm neural networks

for ssha prediction. IEEE Journal of Selected Topics

in Applied Earth Observations and Remote Sensing,

13:2853–2860.

Vieira, F., Cavalcante, G., Campos, E., and Taveira-Pinto,

F. (2020). A methodology for data gap ﬁlling in

wave records using artiﬁcial neural networks. Applied

Ocean Research, 98:102109.

Wolff, S., O’Donncha, F., and Chen, B. (2020). Statistical

and machine learning ensemble modelling to forecast

sea surface temperature. Journal of Marine Systems,

208:103347.

KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval

236