Using LSTM Networks and Future Gradient Values to Forecast Heart

Rate in Biking

Henry Gilbert, Jules White, Quchen Fu and Douglas C. Schmidt

Vanderbilt University, U.S.A.

Keywords:

Deep LSTM, Deep Neual Network, Heart Rate, Forecasting, Biking.

Abstract:

Heart Rate prediction in cycling potentially allows for more effective and optimized training for a given indi-

vidual. Utilizing a combination of feature engineering and hybrid Long Short-Term Memory (LSTM) models,

this paper provides two research contributions. First, it provides an LSTM model architecture that accurately

forecasts the heart rate of a bike rider up to 10 minutes into the future when given the future gradient values

of the course. Second, it presents a novel model success metric optimized for deriving a model’s accuracy

to predict heart rate while an athlete is zone training. These contributions provide the foundations for other

applications, such as optimized zone training and ofﬂine reinforcement models to learn fatigue embeddings.

1 INTRODUCTION

Monitoring intensity during exercise and training is

essential to optimize performance (Sylta et al., 2014).

Insufﬁcient intensity during training yields slower or

negligible performance progression. Excessive in-

tensity, however, yields over-training and the poten-

tial for injury or performance degradation (Collinson

et al., 2001).

There are several metrics for measuring exercise

intensity, including heart rate, V02 max, and power

output (Dooley et al., 2017). Heart rate can be consis-

tently measured across all types of athletics, whereas

power output is exclusive to cycling. Likewise, heart

rate can be used as a reliable indicator of exercise in-

tensity (Jeukendrup and Diemen, 1998). Our intensity

prediction efforts therefore focus on future heart rate.

Yet, predicting heart rate on a given cycling course

is a nuanced and difﬁcult problem. In particular, there

are various external factors that can not be accounted

for, even given the geographical data for a course. For

example, some materials require greater effort to ped-

dle across based on the material’s composition. More-

over, even excluding external course factors, there is

a need to account for cardiac drift, which is a contin-

ual rise or decline of heart rate after exercise due the

body’s internal temperature. (Dawson, 2005). In ad-

dition, there is inconsistency amongst humans, e.g.,

any data derived for training must account for the in-

evitable invariance caused by a person’s inability to

keep perfect pace or other intangible internal factors.

Research Question: Can deep Long Short-Term

Memory (LSTM) models be used to forecast biker

heart rates when given the future gradient val-

ues of the course? The ability for a model to accu-

rately forecast heart rate in the future can potentially

help improve the way athletes approach zone training.

Athletes today typically train reactively, i.e. if during

exercise their heart rate drops too low, they increase

intensity. If their heart rate becomes too high, they

decrease intensity (NEUFELD et al., 2019). This ap-

proach can be a sub-optimal and yield a constantly os-

cillating heart rate and a subsequently greater amount

of time spent outside the correct zone for training.

In contrast, if athletes can accurately predict their

heart rate minutes into the future, they can proactively

adjust their intensity to stay within the desired zone.

For example, if a model forecasts an athlete’s heart

rate will spike out of a given zone due to an upcom-

ing hill in two minutes, the athlete can proactively de-

crease their effort to lower their heart rate to prepare

for the increased effort of the hill. By limiting heart

rate oscillation, the time in the correct zone can in-

crease, thereby optimizing training performance.

Moreover, future heart rate prediction can be ap-

plied to an ofﬂine learning model when given enough

contextual data. For example, a model can learn the

embedding of intensity for a given athlete and apply

that learning to optimally indicate when the athlete

should speed up or slow down to ensure their heart

rate remains in a given zone. This is a novel ap-

proach that fundamentally contrasts with a coach re-

Gilbert, H., White, J., Fu, Q. and Schmidt, D.

Using LSTM Networks and Future Gradient Values to Forecast Heart Rate in Biking.

DOI: 10.5220/0011541800003321

In Proceedings of the 10th International Conference on Sport Sciences Research and Technology Support (icSPORTS 2022), pages 53-60

ISBN: 978-989-758-610-1; ISSN: 2184-3201

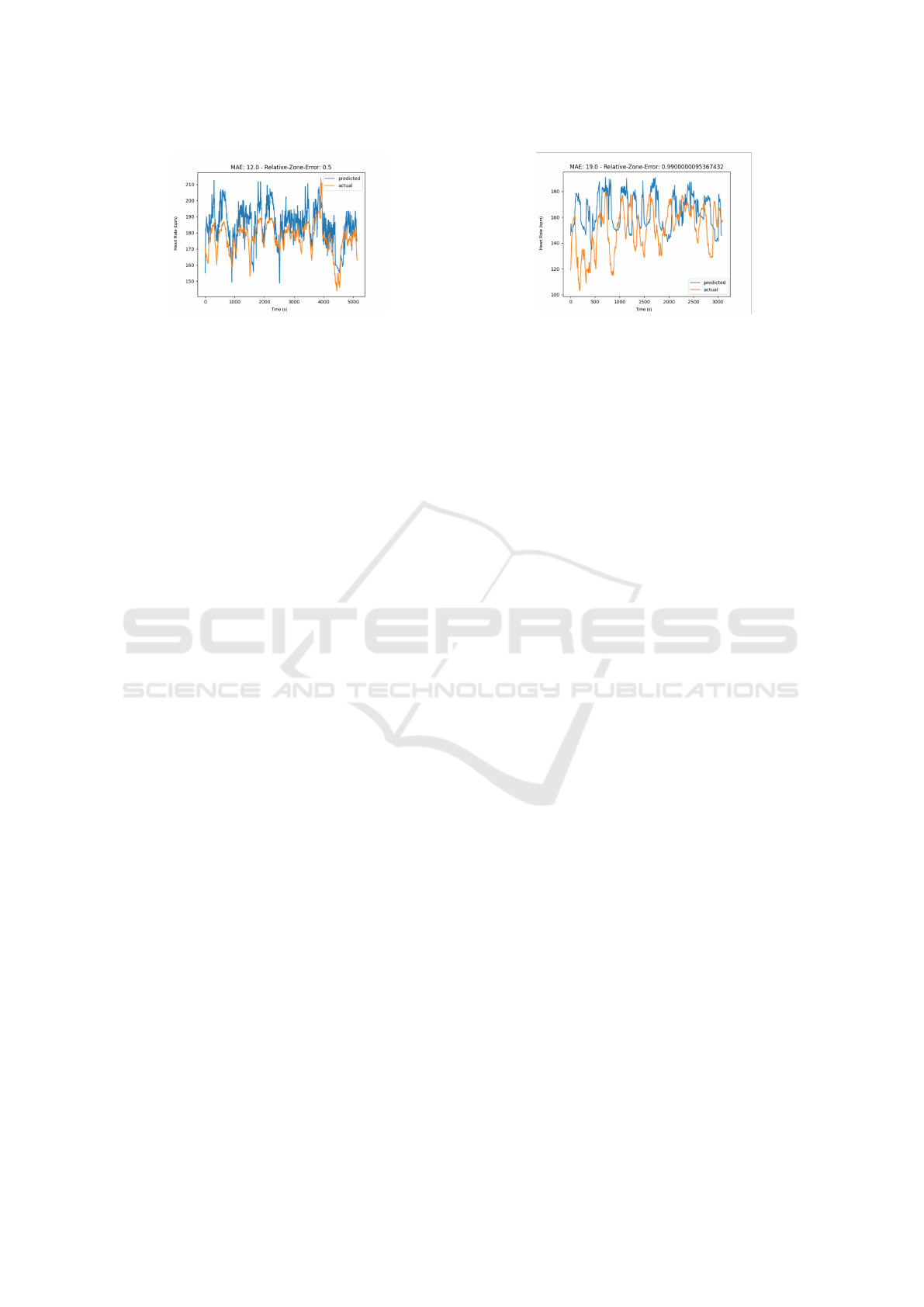
Figure 1: Model Results for 120’s Prediction on Validation

Run 0.

actively instructing an athlete. Therefore, an indepen-

dent model can optimally and proactively dictate an

athlete’s intensity. This information could be commu-

nicated to an athlete in the form of a [1,10] intensity

scale, with 1 being minimum effort and 10 being max-

imum effort, thereby potentially maximizing training

for an athlete’s speciﬁc intensity embeddings.

Key Contribution: A promising deep LSTM

Model for predicting heart rate Up to 600 seconds

in the future. This paper presents an architecture for

an LSTM model (Hochreiter and Schmidhuber, 1997)

that can predict heart rate up to 600 seconds (i.e., 10

minutes) in the future. This LSTM model achieves

this predictability via a mix of past historical heart

rate and velocity data with the future gradient values

of the course n minutes into the future.

The remainder of this paper is organized as fol-

lows: Section 2 summarizes related work and ex-

plores its relationship with the research described in

this paper; Section 3 illustrates the models underlying

architecture and the reasoning behind it; Section 4 ex-

plains the model’s performance in relation to the ex-

perimental data and analyzes the experiment results;

and Section 5 presents concluding remarks.

2 RELATED WORK

Prior work exploring heart rate prediction using ma-

chine learning can be categorized as focusing on (1)

predicting heart rate given noisy data and (2) forecast-

ing heart rate in the context of sports. This section

summarizes this related work and explores its rela-

tionship with the research described in this paper.

An important problem in the analysis of heart rate

is the quality of the data being collected. Unfor-

tunately, due to external factors (such as sweat and

excessive motion during exercise) common sensors

(such as PPG and ECG) fail to produce accurate read-

ings. Recent work has applied machine learning to

forecast heart rate more accurately, regardless of the

noise within the input data.

Figure 2: Model Results for 120’s Prediction on Validation

Run 1.

For example, (Yun et al., 2018) focused on fore-

casting heart rate variability via a Hidden Markov

model. Likewise, (Fedorin et al., 2021) compared

sequence-to-sequence models and deep LSTM mod-

els with integrated CNN layers for more accurate

heart rate forecasting and concluded that LSTM

model performed marginally better than the sequence-

to-sequence model. In contrast, our work focuses on

a related—but different—application, ı.e., ingesting

and forecasting using noisy data to predict heart rate

in the context of biking, rather than subjects at rest.

A recent paper (Stafﬁni et al., 2022) uses the past

n minutes of heart rate data to predict heart rate at

n + 1. Using only an auto-regressive model, this pa-

per achieved an mean absolute error (MAE) of 3 bmp.

However, once again, that paper’s data set consisted

entirely of subjects at rest. Thus, their model allowed

less variance in the external environment when com-

pared to heart rate forecasting in an exercise setting,

such as our focus on biking in this paper.

Yet another recent paper (Ni et al., 2019) com-

bined LSTM with sequence-to-sequence and encod-

ing layers to create a workout forecasting model,

a short-term heart rate forecaster, a linear projec-

tion embedding module, and a workout recommender

system. Given contextual information about the

user’s historical performance and sport type, they

constructed a model to forecast the user’s heart rate

for a given workout route at minute intervals. The

short-term forecasting model used a custom encoder-

decoder with temporal attention to forecast heart rate

10’s ahead with a resulting root means square error

(RMSE) of 7.025 heart beats. In contrast, our work

focuses on heart rate in the context of biking and

speciﬁcally applying future gradient values of a given

course for predictions up to 600 seconds ahead.

Finally, one of our earlier papers (Qiu et al., 2021)

is based on the same data set as this paper and also

forecasts heart rate at a one second interval using

several models, including Random Forest, a Feed-

Forward Neural Network (FFNN), a Recurrent Neu-

ral Network (RNN), and LSTM. That paper found

icSPORTS 2022 - 10th International Conference on Sport Sciences Research and Technology Support

Figure 3: Model Results for 120’s Prediction on Validation

Run 2.

Figure 4: Model Results for 120’s Prediction on Validation

Run 3.

the LSTM model exhibited the top forecasting per-

formance out of the aforementioned models. While

that paper shared a similar research question and the

same data set as our current paper, the papers differ

in two ways: (1) our current paper introduces a novel

forecasting performance metric to relate predictions

to their heart rate zone and (2) it also applies future

gradient values to increase the LSTM model’s predic-

tive power and ability to generalize.

3 MODEL ARCHITECTURE

This section describes the LSTM architecture that we

analyzed in our experiments to predict future heart

rate values given the future gradient values. Figure 5

shows the overall architecture for the LSTM model

that produced the best results, which consisted of 5

layers of 1000 neurons each. We experimented with

a variety of layers and neurons. Speciﬁcally, we ex-

perimented with models ranging from 2 layers of 50

neurons to models with 10 layers of 5,000 neurons.

Two additional dense layers were appended to the end

of the model to learn the output embedding from the

LSTM layers and apply it to forecast the heart rate.

Our experiments indicated that smaller models

were unable to capture the complexity of the rela-

tionships present in the data. Such models would

often end up converging to the average heart rate of

the training set, rather than a mapped relationship be-

tween gradient and heart rate. Conversely, models

larger than 5 layers of 1,000 neurons often had di-

minishing returns and struggled with over ﬁtting the

training data. Thus, they were not worth the exponen-

tial increase in compute time.

For heart rate prediction, our LSTM model used

three input vectors: past heart rate, past cadence, and

future gradient. All data was normalized between

[0,1]. Each of these vectors were bucketed and aver-

aged by chunks of ﬁve to reduce the input space and

limit the noise found in such granular data.

Chunk size was determined via grid search exper-

imentation, where we experimented with values in the

range of [1,2,5,10,50,100]. A chunk size of ﬁve con-

clusively performed the best. In particular, this chunk

size optimally balanced between retained information

density and noise reduction through smoothing.

These three vectors were then interwoven into

each other such that given vector heart rate =

], vector cadence = [c

] and vector

gradient = [g

]. The resulting vector was then

]. The heart rate and ca-

dence are historical values, while the gradient is the

future gradient of the route.

This interwoven list was subsequently segmented

into chunks of six, such that the model took a depth of

six steps for every feature vector x ∈ X. Given histor-

ical data h

, ... ,h

, c

, ... ,c

and g

, ... ,g

, the model

predicted the heart rate at time step 2n. Speciﬁcally,

for a prediction 120 seconds into the future, the in-

put was reformatted into chunks of the previous 120’s

of heart rate and cadence, along with the future 120’s

of the gradient. Given 120’s chunk of historical data,

120

] was used to make a singular prediction, 120’s

into the future at time step t

240

. Thus, given heart rate

= [h

,..., h

120

], cadence = [c

,..., c

120

] and gradient =

120

,..., g

240

], the model predicted the heart rate of

the athlete at time step t

240

Our approach interwove past heart rate, past ca-

dence, and future gradient together to enable the seg-

mentation of time steps when the data was fed to

the model. If heart rate, cadence, and gradient were

merely appended to the end of each other that data

could not be segmented into time steps because the

ﬁrst step would consist entirely of heart rate data, the

last step would consistent entirely of gradient values,

and the rest would be a mix of all three. To achieve

consistent and homogeneous time steps the three data

vectors must be interleaved.

Our LSTM model’s input layer took batch sizes of

one, where each time-step had a feature vector of size

of size 10. There were model − look − f orward −

amount/10 time-steps for each input into the model.

Using LSTM Networks and Future Gradient Values to Forecast Heart Rate in Biking

Figure 5: Model Architecture.

This part of the algorithm yielded a many-to-one

LSTM input architecture.

This input was then fed into four subsequent and

identical LSTM layers, each with 1,000 neurons. Ev-

ery one of these hidden LSTM layers had a 0.2 in-

tegrated drop layer. This portion of the algorithm

yielded a trainable 800 neurons, per layer, per pass.

The output of the deep LSTM model was then fed

into a densely connected layer of 800 neurons. The

subsequent output from this layer was next fed into

two further densely connected hidden layers with 300

neurons each. Finally, the output was condensed into

a ﬁnal single neuron with a linear activation applied

to forecast the heart rate.

Our LSTM model utilized a mean absolute error

loss function. Speciﬁcally, the absolute value of the

forecasting errors are summed together and used to

adjust the networks weights, as shown in Equation 1.

∑

i=1

− y

Equation 1: Mean absolute error function.

As described previously, the model also applied a

custom metric to determine model forecasting success

in relation to heart rate zones. Speciﬁcally, to calcu-

late the error between actual heart rate and predicted

heart rate, this metric created a relative error to the

size of the heart zone, which distinguished between

upper and lower bounds of a given zone and related

the distinction to the actual size of that zone.

For example, given a heart rate zone between 200

and 180 beats per minute the size of this heart rate

zone is 20 beats. Therefore, if the actual heart rate is

185 and the predicted heart rate is 190 the actual error

is 5 beats. Given this zone size 20, the adjusted error

is 5/20 or 0.25.

In contrast, for a heart zone between 200–190 with

a zone size of 10 the actual error is also 5 beats if the

actual heart rate is 195 and the predicted heart rate is

200. In this case, however, the adjusted error becomes

5/10 or 0.5. Since the zone is smaller, the relative dif-

ference between actual and predicted heart rate carries

a greater impact.

The difference in importance using the concrete

error cannot be captured in this scenario. However,

the relative adjusted error does capture this discrep-

ancy in importance. This distinction is shown by the

concrete error being 5 beats for both examples, but a

higher adjusted error of 0.5, rather than 0.25. This dif-

ference compensates for the narrower margins of the

smaller heart rate zone.

4 EXPERIMENT METHODS AND

RESULTS

This section gives an overview of our experiment data

and training method, analyzes the results from our ex-

periments, and explains threats to validity.

4.1 Overview of the Experiment

The data set used to train LSTM model comprised the

grade of the course, speed, heart rate, elevation, dis-

tance and cadence, all measured at one second inter-

vals. There were 110 overall rides, resulting in a data

set of 270,000 examples. We used both a validation

set of 30k examples and the same validation set de-

scribed in (Qiu et al., 2021) to directly contrast model

performance more accurately.

Our LSTM model was trained on a machine with

48GB of VRAM and 256GB RAM. This model uti-

lized early stopping with a patience of ﬁve and a min-

imum value loss variance of one. The model ran for

an average of eight epochs at a training time of four

minutes each, resulting in an average training time of

32 minutes.

icSPORTS 2022 - 10th International Conference on Sport Sciences Research and Technology Support

4.2 Analysis of Data

Understanding the nature and quality of the data is

essential before a full analysis of the results can be

given. Firstly, to give context to the model’s accuracy,

one must calculate the variance within the data.

Speciﬁcally, the variance of the heart rate data

is: 604.489, and the variance of the cadence data is:

1200.718. Both variance were derived using Formula

2. Naturally, variance relates to the scale of the data

it was derived from. However, even accounting for a

max heart rate of 219 and a max cadence of 225, both

data sets variance is relatively high. Cadence having

a high variance can be attributed to the the athlete’s

inability to hold a constant pace, along with the nat-

ural increase and decrease of effort in relation to the

course’s changing gradient. The high variance in the

heart rate can be attributed to an athlete’s imperfect

pace, along with the corresponding athlete’s ability

for physiological heart rate control. These factors are

echoed in the covariance between cadence and heart

rate, 221.204, and the correlation between cadence

and heart rate, 0.251. With correlation being calcu-

lated with Equation 3.

Thus, a large variance in both heart rate and ca-

dence helps form an upper ceiling for expected model

forecasting accuracy. The model will not only have

to model future heart rate for a given course, but also

account for the non-deterministic human divergence

from constant pace.

∑

i=1

− µ)

Equation 2: Variance equation.

r =

∑

i=1

− x)(y

− y)

∑

i=1

− x)

− y)

Equation 3: Pearson’s R equation.

4.3 Analysis of Results

A concrete example of the model’s performance on a

single ride is shown in Figure 6. Exact model perfor-

mance for each ride in the validation set is shown in

Table 1.

The corresponding run graph results are shown in

Figures 1, 2, 3, 4, 7, 8, 9, 10, 11 12. Given the valida-

tion set of 30k examples, the model achieves a mean

squared loss of 25.63, though there are outliers around

step 5,000 in the validation set. Regardless of the in-

herent noise in the data, the model continues to ﬁt

Figure 6: Model Results for 120’s prediction across valida-

tion set of 30,000 data points.

Table 1: Model Performance on Validation Rides.

Validation Ride MAE RZE

Run 0 13.82 0.47

Run 1 21.61 1.07

Run 2 23.23 1.04

Run 3 22.99 0.86

Run 4 32.34 1.52

Run 5 19.17 0.83

Run 6 14.84 0.58

Run 7 23.29 0.71

Run 8 22.67 1.02

Run 9 32.54 0.98

the general trend and not diverge to only predicting

the most recent heart rate. These results showcase the

model’s ability to learn the relationship between cur-

rent heart rate and future gradient values.

This same model can then be retrained to predict

10 minutes into the future. Even predicting so far into

the future, the model still generalizes to the correct

trend, as shown in Figure 13.

The 10 minute model’s predictions fail to contin-

ually match the trend of the users heart rate across

the entirety of the 2,000 time steps. However, this

result shows the model’s ability to learn the strong re-

lationship between past heart rate and cadence values

to future gradient values. Moreover, the divergence in

accuracy between time steps 750 and 1,250 can be ex-

plained by an analysis of the user’s cadence during the

same time period. As shown in Figure 14, the cadence

Figure 7: Model Results for 120’s Prediction on Validation

Run 4.

Using LSTM Networks and Future Gradient Values to Forecast Heart Rate in Biking

Figure 8: Model Results for 120’s Prediction on Validation

Run 5.

Figure 9: Model Results for 120’s Prediction on Validation

Run 6.

drops to 0, suggesting the athlete stopped during the

user’s ride.

Naturally, the model can not account for an un-

expected departure of the course and the subsequent

cardiac drift that ensues. However, the model was

quickly able to reﬁt the trend, as shown in Figure 13.

Moreover, Figure 15 depicts forecasting heart rate at

120’s intervals in relation to the associated heart rate

zones for the given athlete.

This model can therefore make valuable and ac-

tionable predictions if it is able to ﬁt the trend of heart

rate zones, which is not necessarily a direct trend

with the heart rate. It is also essential to consider the

model’s conﬁdence bounds, as shown in Figure 16.

Allowing for a certain margin of uncertainty in the

model’s predictions yields a better generalization to-

wards predicting zone relations. Speciﬁcally, this re-

lationship can be quantiﬁed to zone trends by taking

Figure 10: Model Results for 120’s Prediction on Validation

Run 7.

Figure 11: Model Results for 120’s Prediction on Validation

Run 8.

Figure 12: Model Results for 120’s Prediction on Validation

Run 9.

the absolute difference in a model’s prediction and the

ground truth and then scaling the difference to the size

of an individuals heart rate zone. For reference, the

model seen in 15 has an average relative zone error of

0.414, so it is accurate to within 60 percent of a given

heart zone for any x ∈ X. Figure 13 and Figure 17.

An example of the importance for generalized

zone forecasting instead of granularity heart rate is

shown in 13 It initially appeared the 10 minute model

was unable to ﬁt the validation set as well as as the

two minute model. However, the 10 minute model

sacriﬁced granular tracking for a more robust relation-

ship with the given zone for a heart rate. This trade off

allowed the model to achieve a lower relative zone er-

ror score of 0.37.

Figure 13: Model Results for 600’s Predictions.

icSPORTS 2022 - 10th International Conference on Sport Sciences Research and Technology Support

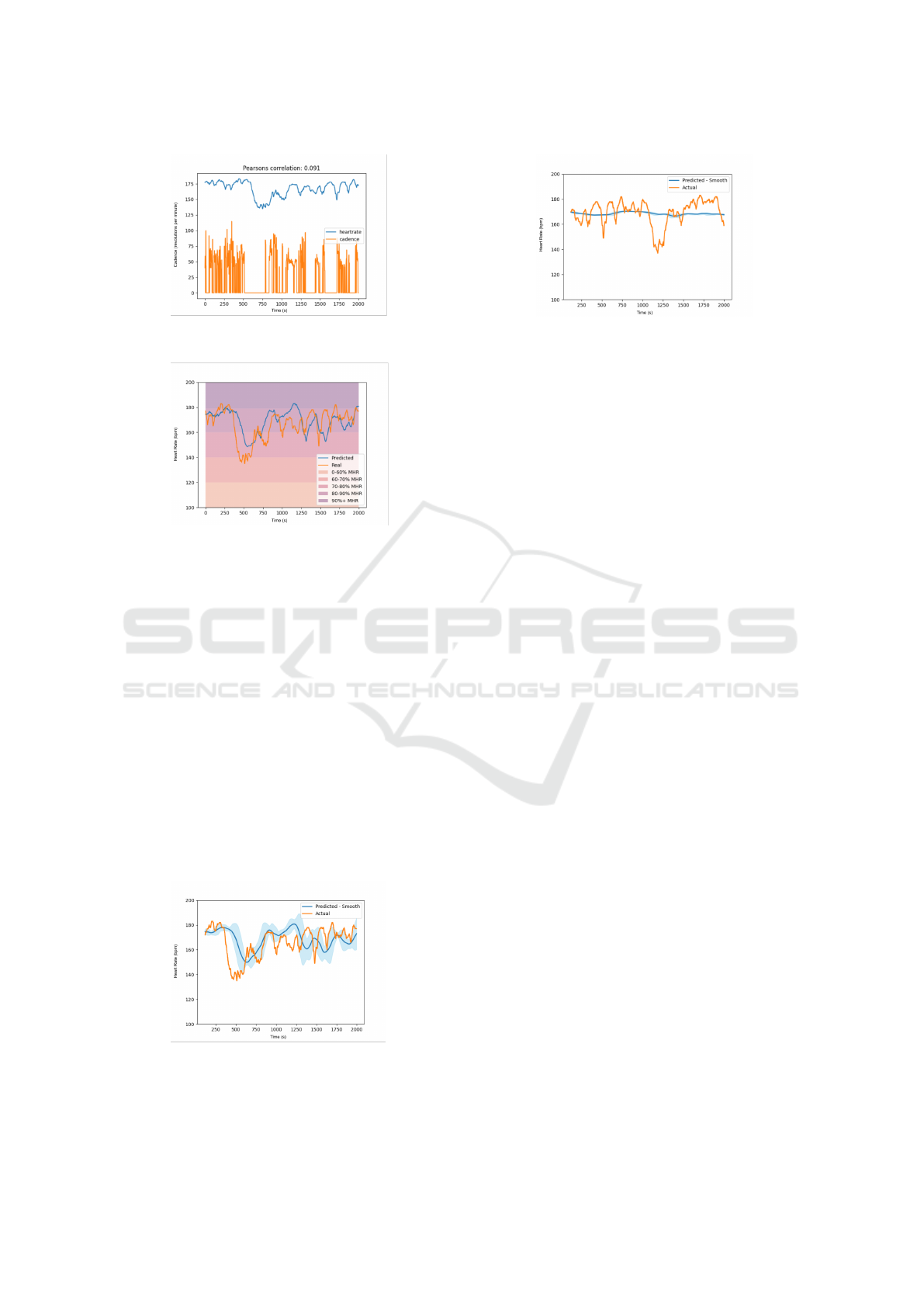
Figure 14: Cadence in Relation to Heart Rate.

Figure 15: 120’s Prediction for Single Ride in Reference to

Training Zones.

4.4 Threats to Validity

The results reported above show that our LSTM

model’s utility for optimized heart rate zone training

is promising and potentially actionable. However, the

current data set consists of only one athlete cycling

on a multitude of different routes and has not yet been

tested on other individuals cycling on more diverse

routes and in other sport types, such as running. Intu-

itively, this model should generalize to a greater pop-

ulation of subjects and contexts as the model’s inputs

are agnostic of the route, person or sport type. It also

remains an open research question if the model can

generalize across an entire population of athletes or if

each individual athlete will need a model ﬁne-tuned

to their internal exertion embeddings.

Figure 16: 120’s Prediction in reference to it’s conﬁdence

intervals.

Figure 17: 600’s Prediction in reference to it’s conﬁdence

intervals.

5 CONCLUDING REMARKS

Few papers have been published that provide deep

learning model architectures for forecasting heart rate

more than 60 seconds into the future. As discussed

in Section 2, even fewer proposed models attempt to

forecast heart rate in an athletic context.

This paper showed that a hybrid LSTM model in

conjunction with supplying future gradient values for

a given course allows prediction of actionable heart

rate forecasts up to 10 minutes into the future. Specif-

ically, by feeding a deep LSTM model into a densely

connected deep neural network, we are able to accu-

rately forecast the heart rate of an athlete biking in re-

lation to the gradient values of a given course. These

results suggest other potential applications for opti-

mized zone training and ofﬂine learning for athlete

intensity management through exertion embeddings.

Our research reported in this paper yield the fol-

lowing lessons regarding forecasting heart rate in an

athletic context:

1. LSTM Architecture for Heart Rate Forecast-

ing. As shown in this paper, the LSTM model

architecture is an effective choice for forecasting

future heart values.

2. Increased Forecasting Ability with Future

Gradient Values. Our LSTM model effectively

predicted the heart rate of an athlete up to 10 min-

utes into the future when using the future gradient

values of the course. This result demonstrated the

strong predictive relationship between the gradi-

ent of a course and heart rate.

3. Adjusted Model Success Metrics. We learned

that adjusting the model prediction error in rela-

tion to the size of a heart rate zone is a more de-

scriptive metric to deﬁne model success.

Our future work will continue evolving this re-

search by performing larger experiments with a more

diverse subject group to gain a greater breadth of

Using LSTM Networks and Future Gradient Values to Forecast Heart Rate in Biking

data. Speciﬁcally, we will increase our sample size by

studying 20 different athletes of an even distribution

of gender, as well as have each athlete cycle 10 differ-

ent routes and run the same 10 routes. We will then

use this data to retrain a larger version of the current

LSTM model and test whether this model can effec-

tively learn the relationship between future gradient

and current heart rate, irrespective of an athlete’s gen-

der, ﬁtness level, or sport.

All of the models and data that we presented in

this paper can be downloaded in open-source form

at the following GitHub repository URL: github

.com/henrygilbert22/RL-Human-Performance.

Please consult the repo’s ReadMe ﬁle for in-depth

instructions on replicating this paper’s results and a

more extensive description of the data used in the

experiments.

REFERENCES

Collinson, P. O., Boa, F. G., and Gaze, D. C. (2001). Mea-

surement of cardiac troponins. volume 38, pages 423

– 449.

Dawson, E. A. (2005). Cardiac drift during prolonged ex-

ercise with echocardiographic evidence of reduced di-

astolic function of the heart. volume 94, page 3.

Dooley, E. E., Golaszewski, N. M., and Bartholomew, J. B.

(2017). Estimating accuracy at exercise intensities:

A comparative study of self-monitoring heart rate and

physical activity wearable devices. JMIR Mhealth

Uhealth, 5(3):e34.

Fedorin, I., Slyusarenko, K., Pohribnyi, V., Yoon, J., Park,

G., and Kim, H. (2021). Heart rate trend forecasting

during high-intensity interval training using consumer

wearable devices. In Proceedings of the 27th Annual

International Conference on Mobile Computing and

Networking, MobiCom ’21, page 855–857, New York,

NY, USA. Association for Computing Machinery.

Hochreiter, S. and Schmidhuber, J. (1997). Long short-term

memory. Neural Comput., 9(8):1735–1780.

Jeukendrup, A. and Diemen, A. V. (1998). Heart rate moni-

toring during training and competition in cyclists. vol-

ume 16, pages 91–99.

NEUFELD, E., WADOWSKI, J., BOLAND, D., Dolezal,

B., and Cooper, C. (2019). Heart rate acquisition and

threshold-based training increases oxygen uptake at

metabolic threshold in triathletes: A pilot study. In-

ternational Journal of Exercise Science, 12:144–154.

Ni, J., Muhlstein, L., and McAuley, J. (2019). Modeling

heart rate and activity data for personalized ﬁtness rec-

ommendation. In The World Wide Web Conference,

WWW ’19, page 1343–1353, New York, NY, USA.

Association for Computing Machinery.

Qiu, X., White, J., and Schmidt, D. C. (2021). Analyz-

ing machine learning models that provide personal-

ized heart rate forecasting for elite cyclists.

Stafﬁni, A., Svensson, T., Chung, U.-i., and Svensson, A. K.

(2022). Heart rate modeling and prediction using au-

toregressive models and deep learning. volume 22.

Sylta, y., Tønnessen, E., and Seiler, S. (2014). From heart-

rate data to training quantiﬁcation: A comparison of 3

methods of training-intensity analysis. International

journal of sports physiology and performance, 9:100–

Yun, S., Son, C.-S., Lee, S.-H., and Kang, W.-S. (2018).

Forecasting of heart rate variability using wrist-worn

heart rate monitor based on hidden markov model. In

2018 International Conference on Electronics, Infor-

mation, and Communication (ICEIC), pages 1–2.

icSPORTS 2022 - 10th International Conference on Sport Sciences Research and Technology Support