
Evolving Analog Electronic Circuits for Fuzzy Membership
Functions Generation
P. H. G. Coelho, J. F. M. do Amaral, Y. C. Bacelar, E. N. Da Rocha and M. C. Bentes
State Univ. of Rio de Janeiro, FEN/DETEL, R. S. Francisco Xavier,524/Sala 5001E, Maracanã, RJ,20550-900, Brazil
Keywords: Fuzzy Systems, Genetic Algorithms, Artificial Intelligence Applications, Evolutionary Electronics.
Abstract: Recent research advances in fuzzy systems applications as controllers of increasingly complex systems
motivate the consideration of analog circuits capable of implementing fuzzy logic. The purpose of this paper
is to evolve the component values of known topologies of analog circuits to generate membership functions.
In order to accomplish that, a hybrid model is used for the evolution of electronic circuits, based on genetic
algorithms, using a fuzzy system to evaluate multiple objectives. The traditional fitness assessment of genetic
algorithms is modified, so that a fuzzy system is effectively responsible for the assessment, thus being able to
aggregate the different objectives of the electronic design and generating a fitness value for each circuit in the
population. The proposed model presents a simpler and more interpretable way of inserting preferences and
specifications, as it uses fuzzy logic. Such specifications are inserted before the evolution of the circuit,
ensuring that it is guided in the desired direction, preventing the designer from having to choose the most
appropriate solution at the end of the process. An implementation based purely on simulation of circuit models
was chosen, providing a flexible environment.
1 INTRODUCTION
Evolutionary Electronics was conceived in 1997 and
applies Evolutionary Algorithms in the development
of electronic circuits. It covers the developments and
issues related to the use of Evolutionary Computing
in the design of electronic circuits (Haddow and
Tyrrell, 2018). In addition, it enables the development
of practices, methods, algorithms and software and
hardware structures that allow evolving in the design
of more robust circuits. This terminology covers a
wide field of research on the use of evolutionary
algorithms in optimization and synthesis of electronic
circuits. Another point of interest is the growing
demand for the synthesis of more complex analog
circuits, to interact with the environment, and the
need to design them more quickly for the market
(Amaral et al., 2007). This imposes more dynamic
design practices that can generate products in less and
less time (Lohn et al., 1999).
Fuzzy systems are based on fuzzy logic and are
widely used, especially in control systems and
decision support models. There are several related
applications in the literature, such as, for example, in
the area of health and the study of human locomotion,
in speech signal processing, in the recognition of
information and emotions, in economics and in
routing systems (Luca et al.,2015). Its characteristic
of expressing human inference behavior enables a
high level of understanding, being interpretability a
strong point of fuzzy systems.
Among the points usually addressed in the area of
computational intelligence, optimization stands out,
which consists of the search for the best solution for
a given problem. At this point, evolutionary
algorithms are a commonly used computational
intelligence technique due to their great search
capability. Optimization in evolutionary algorithms
consists of trying several solutions and using the
information obtained in this process in order to find
better and better solutions. Initially, the great
concentration of efforts in the optimization area
consisted in understanding, developing and applying
methods for the optimization of a single objective
function. However, most real optimization problems,
such as in electronic design or component
adjustments in electronic systems, involve multiple
objectives and one cannot apply the idea of
optimizing each objective in isolation. Each objective
has its degree of importance and often the objectives
conflict with each other (Ajith et al., 2005). In
everyday situations it is common to find contexts that
Coelho, P., M. do Amaral, J., Bacelar, Y., N. Da Rocha, E. and Bentes, M.
Evolving Analog Electronic Circuits for Fuzzy Membership Functions Generation.
DOI: 10.5220/0011549800003332
In Proceedings of the 14th International Joint Conference on Computational Intelligence (IJCCI 2022), pages 175-182
ISBN: 978-989-758-611-8; ISSN: 2184-3236
Copyright © 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
175

have different objectives. For example, in an
industrial environment, generally, the aim is to
maximize the quality of a product while the cost must
be minimized.
Currently, there are several techniques and
computational algorithms developed for application
in multi-objective optimization (MOP) problems
motivated by the vast area of application (Coello
Coello, 2013). Many researches show good results
obtained over the years in this field for example
(Fonseca et al., 1995) (Altinoz et al., 2015) (Jiang et
al., 2016). The most used methodologies include the
use of genetic algorithms and are based on the Pareto
optimality concept. Such an approach comprises a
border with several solutions considered optimal in
relation to the analyzed objectives. This methodology
is characterized by having an a-posteriori articulation,
that is, the search process is performed autonomously,
and after obtaining the solutions, an expert must make
a choice to decide which is the best solution to be used
for the problem. The process of choosing the solution
considered acceptable, with a large number of
possibilities and variables involved, is not a trivial
task and requires experience and expert knowledge.
In this way, the articulation of the designer's
preferences made a-priori, that is, before the
execution of the algorithm, and the use of a technique
capable of translating the preferences in a simpler and
more understandable way are essential.
This article deals with the design of analog
electronic circuits to generate fuzzy membership
functions, in order to modify the traditional
evaluation form of a genetic algorithm to enable the
evaluation of multiple objectives. To this end, it was
chosen to use a fuzzy system that aggregates the
various objectives (Reiser at al., 2013), (Mardani et
al., 2015). The use of fuzzy systems makes it possible
to simultaneously evaluate all objectives, integrating
user preferences in relation to each objective and each
situation. This feature is an advantage over multi-
objective methods based on Pareto optimality, as this
type of model does not require user interference to
choose the best solution at the end of the process,
since preferences are entered before evolution, in a
more efficient way, simple and interpretable, through
fuzzy logic. Thus, the evolution process is guided
towards pre-established preferences or specifications.
The purpose of this work is to study the application
of an evolutionary model, which uses genetic
algorithms with the ability to evaluate multiple
objectives based on a fuzzy system, to optimize the
values of components of analog electronic circuits to
generate fuzzy membership functions. The technique
is evaluated in a purely simulation-based
environment that is used for the design of electronic
circuits.
From the recent literature, articles dealing with the
subject stand out (Marlen et. al, 2018) and (Rojec et.
al., 2022). The first deals with the implementation of
fuzzy membership function (MF), realized as an
analog electronic hardware with memristor. The other
one proposes an evolution of analog circuits,
including their topology, for general purposes,
considering the synthesis of robust and failure-
resilient electronics.
This paper is organized in four sections. The
second section describes the basic structure of the
evolutionary environment for generating the
membership functions. Section three discusses
examples and results in connection with the
evolutionary analog circuits. Finally, section four
ends the paper with the conclusions.
2 ELECTRONIC CIRCUITS
EVOLUTION
2.1 Basic Foundations
An electronic project can be developed in an intrinsic
or extrinsic way.
In the so-called intrinsic applications, the
evaluation is performed based on the behavior of the
circuits when loaded on programmable integrated
circuits or reconfigurable platforms. In this way the
real circuit is developed, although flexibility and
experimentation possibilities are more limited.
On the other hand, extrinsic applications are those
in which circuits are evaluated through their
equivalent models. For example, a linear analog filter
can be developed using its transfer function. It is also
possible to use circuit simulators, such as Spice, in
which case the evolutions tend to become very slow.
In this paper, we opted for the extrinsic evolution
based on models of analog electronic circuits to make
the experimentation of the multi-objective evaluation
method more flexible.
Evolutionary algorithms are efficient in solving
multicriteria optimization problems. A variety of
techniques using genetic algorithms have been
developed in recent decades.
The great advantage obtained in the use of genetic
algorithms is the fact that they simultaneously
evaluate a set of possible solutions that allows finding
the total set of solutions of the Pareto frontier in a
single round of the algorithm without the need to
FCTA 2022 - 14th International Conference on Fuzzy Computation Theory and Applications
176

carry out several iterations as in the other methods
(Coello Coello, 1999).
In addition, they present ease and flexibility of
modeling, are less susceptible to non-convex and
discontinuous Pareto frontier characteristics and can
work in search spaces that are intractable by
traditional approaches.
2.2 The Evolutionary Environment
The purpose of this work is the application of a hybrid
model to enable the evolution of electronic circuits,
based on a genetic algorithm and using a fuzzy system
to evaluate multiple objectives. The traditional fitness
assessment of genetic algorithms is modified, so that
a fuzzy system is effectively responsible for the
assessment, thus being able to aggregate the different
objectives of the electronic design and generating a
fitness value for each circuit in the population.
One of the most important advantages of fuzzy
systems is interpretability. This feature makes it
possible to insert preferences and adapt the system to
different situations using a natural and easy-to-
understand language. In this way, the evolutionary
environment presents a simpler and more
interpretable way of inserting preferences and
specifications, as it uses a fuzzy system. Such
specifications are inserted before the evolution of the
circuit, that is, a-priori, ensuring that it is guided in
the desired direction, preventing the designer from
having to choose the most appropriate solution at the
end of the process. The possibility of including
possibly conflicting inputs, but resulting in a single
output that aims to meet both, is also a strong point
that allows its use in solving problems with multiple
objectives.
An implementation based purely on simulation of
circuit models was chosen, providing a flexible
environment for case studies and enabling future
applications. Thus, a method for evaluation through
fuzzy systems has become attractive for the evolution
of electronic circuits. The search capability of genetic
algorithms motivated the choice of this intelligent
technique as a basis for use in this work. A genetic
algorithm was developed capable of obtaining a
solution, that is, the developed circuit, according to
preferences established according to the different
objectives of the problem, and, for this, a fuzzy
aggregation system is used. Comparing the model
with the algorithms that use the Pareto concept, this
fact is of great importance because it prevents several
solutions from being presented for later selection of
the best among them by the designer at the end of the
process.
The methodology used in the present work allows
the evolution of electronic circuits with
characteristics to be optimized, focusing on the
adjustment of the values of the components of pre-
defined topologies and whose model is available or
can be built. Basically, an evolutionary algorithm is
used to search for the best circuit that meets the
objectives. The evolutionary algorithm used is a
genetic algorithm based on GAOT (Genetic
Algorithm Optimization Toolbox) (Houck et al.,
1996) and executed in Matlab. For the simulations,
mathematical models of the circuits were used. The
genetic algorithm used in the work follows the model
presented in Figure 1. The algorithm starts with a
population normally generated randomly, but which
can also be generated from a seed with potentially
good solutions obtained from other methods. The
traditional fitness assessment is performed from a
fitness function defined by the designer.
Figure 1: Hybrid Model with Genetic Algorithm and Fuzzy
Aggregator.
Such a function generates a scalar number for
each evaluated individual, which corresponds to the
individual's aptitude in relation to the objective
established by the defined function. In this work, the
evaluation is performed by a fuzzy system, called
fuzzy aggregator. The fuzzy aggregator system makes
it possible to evaluate all objectives simultaneously,
integrating the user's preferences and specifications in
relation to each objective and each situation, in a
natural way. Figure 2 illustrates the proposed
evaluation model.
Evolving Analog Electronic Circuits for Fuzzy Membership Functions Generation
177
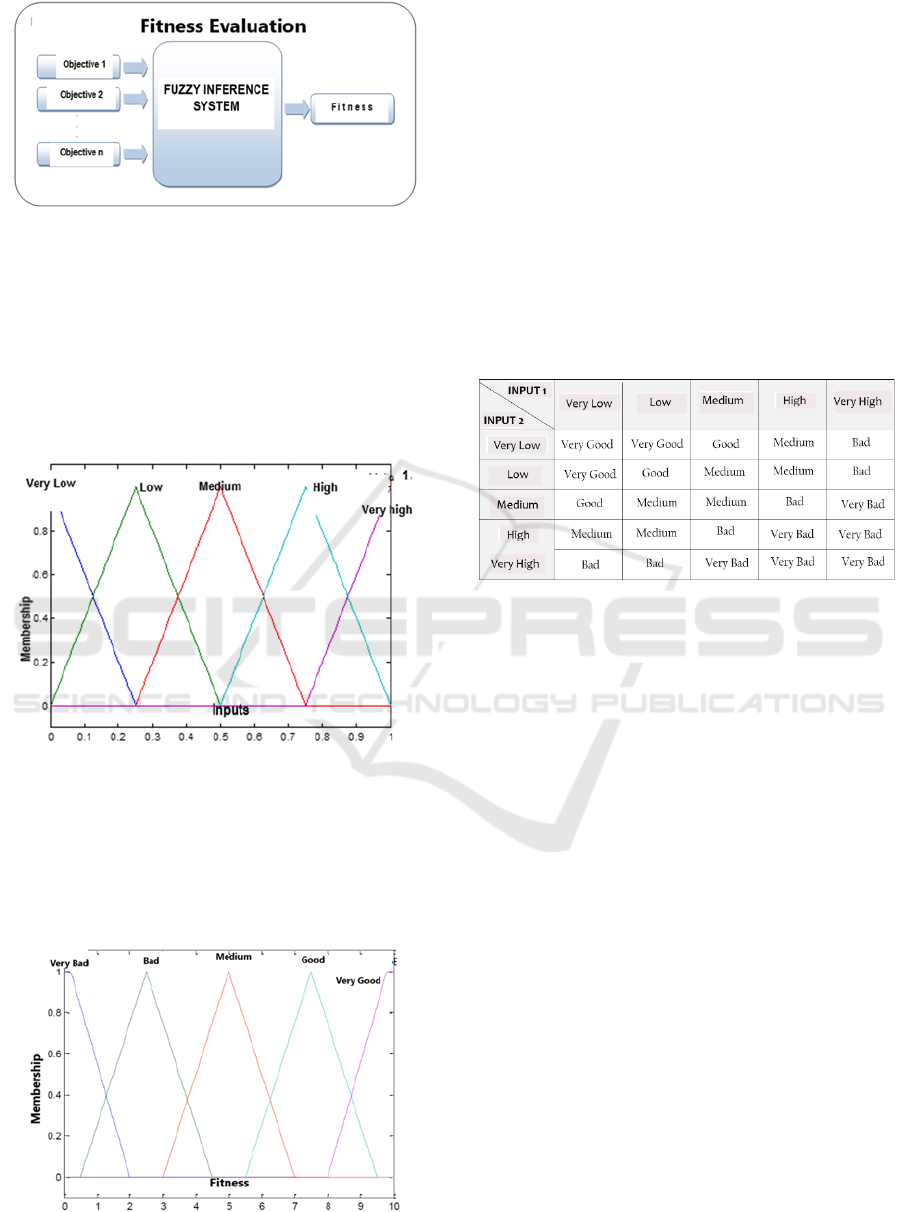
Figure 2: Fitness evaluation model with aggregator system.
A general model for aggregating two objectives
was developed, which can be used as a basis for
application to any problem. The model has five
triangular membership functions uniformly
distributed within the range from 0 to 1 for the inputs,
corresponding to the variation limits of each input
that must be normalized to facilitate and generalize
the application, as shown in Figure 3.
Figure 3: Base membership functions for inputs.
The defuzzified output of the fuzzy system
represents the general fitness assessment of the
individual being evaluated. For the membership
functions of the output, the format shown in Figure 4
is used as standard, consisting of five membership
functions.
Figure 4: Base membership functions for the output.
The fuzzy aggregator system is of the Mamdani
type, characterized by being simpler and more
interpretable than TSK-type systems and all rules
have the same degree of importance, that is, a weight
equal to one. The rules of the fuzzy aggregator system
are designed to meet the problem specifications
considering each of the objectives. To exemplify the
process of creating rules, Table 1 shows basic rules
for minimizing two objectives without preference
between their minimization, that is, the minimization
of both is sought equally. Thus, when the entries
correspond to a Very Low value, they generate a Very
Good aptitude assessment. Likewise, entries with a
Very High value have a Very Bad aptitude rating.
Table 1: Base model for minimization rules.
In case where it is desired to prioritize the
minimization of one objective in relation to the other,
the rules must be modified to meet this preference.
Likewise, if the problem involves maximization, the
same rules can be used by inverting only the linguistic
terms of the antecedents, or the designer can create a
new set of rules. The operators used in the system are
the minimum and maximum operators and
defuzzification is performed using the center of
gravity method. After the evaluation of all the
individuals of the population of the current
generation, the genetic algorithm continues the
evolution process in the traditional way, until the
evaluation of the next generation, where the
evaluation process through the fuzzy aggregator
system is executed again for all the individuals, until
the stopping criterion is reached. To carry out the
evolution of circuits with multiple objectives and the
fuzzy aggregator, the project must be carried out in a
simulated environment. Figure 5 shows a block
diagram of the proposal, illustrating in general the
interconnections between the components used.
An implementation based purely on simulation of
circuit models was chosen, providing a flexible
environment for case studies and enabling future
applications. Evolutions of analog electronic circuits
in different application areas are evaluated through
computer simulations.
FCTA 2022 - 14th International Conference on Fuzzy Computation Theory and Applications
178
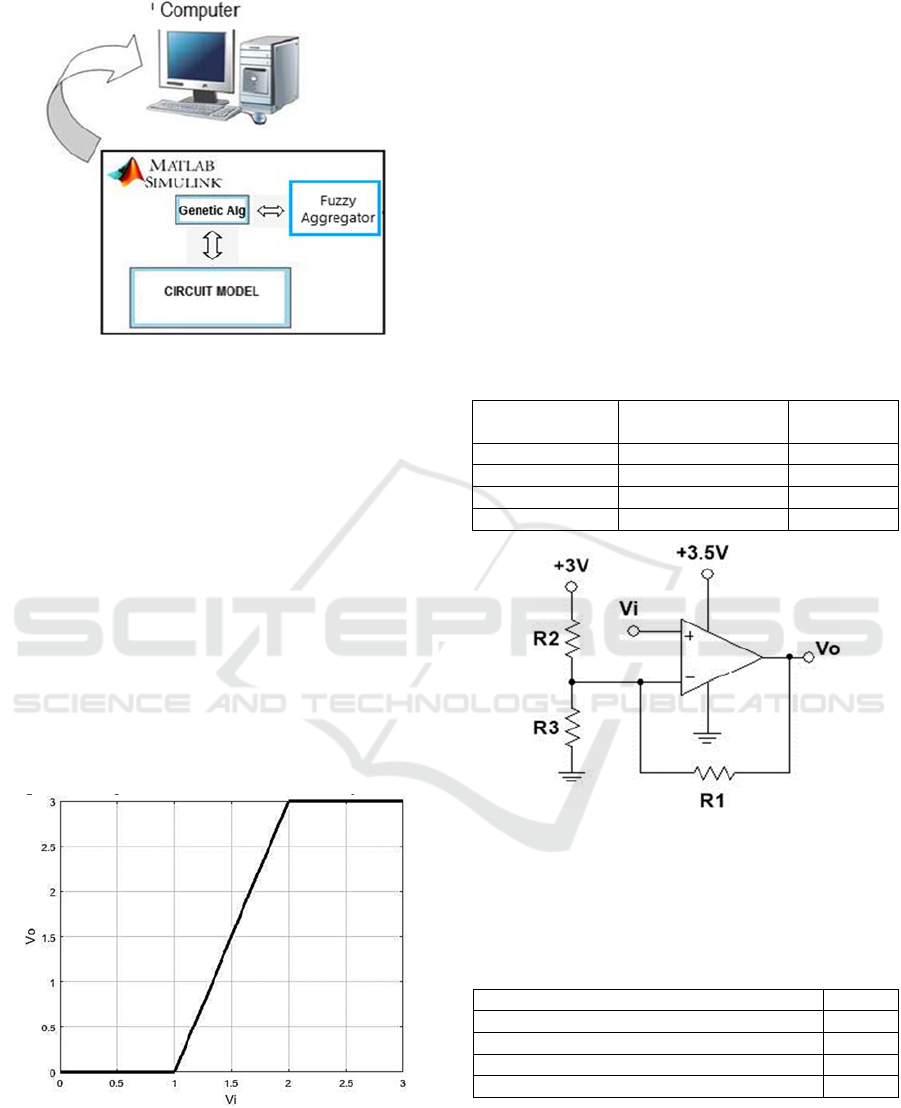
Figure 5: Basic Structure Used.
3 CASE STUDIES
With the great advance in research related to fuzzy
systems applications as controllers of increasingly
complex systems, it becomes interesting to enable the
production of analog circuits capable of
implementing fuzzy logic. The objective here was to
evolve the values of the components of topologies of
circuits known to perform membership functions.
3.1 Case Study 1:
S Membership Function (MF)
For the evolution of a S membership function circuit,
it is necessary a topology capable of generating at its
output a voltage similar to that shown in Figure 6.
Figure 6: Vo x Vi for the S Membership Function.
Thus, to proceed with the proposal, it was
necessary to use a circuit that behaves linearly when
its input was contained in the interval [ 1, 2 ], in
addition to providing 0V at the output when the
voltage applied to the input were at [ 0 , 1 ] and 3V in
the range [ 2 , 3]. A suitable circuit that has these
characteristics can be seen in Figure 7. One of the
objectives for the search for resistor values will be to
minimize the Root Mean Square Error (RMSE) in
relation to the straight line on figure 6, where Vi
varies from 1V to 2V. The other objective will be to
minimize the power consumption in the +3V source,
for that it is enough to maximize the value of resistor
R2, since the current supplied by the source is
inversely proportional to the value of R2.
Table 2 shows the possible values of resistors R1,
R2 and R3 as well as their ideal values, according to
the previously defined objectives.
Table 2: Range of values for Values of R1, R2, R3 and Vi
for the S Membership Function.
Parameters Range of Values
Ideal
Value
R1 1
k
Ω - 10
k
Ω 10
k
Ω
R2 1
k
Ω - 10
k
Ω 10
k
Ω
R3 1
k
Ω - 10
k
Ω 10
k
Ω
Vi 0V
–
3V ------
Figure 7: Selected topology for the S Membership
Function.
For this evolution, the used parameters are shown in
Table 3.
Table 3: Parameters of Genetic Algorithms.
Parameters Value
Number of Generations 100
Number of individuals
p
er
g
eneration 100
Crossover Probabilit
y
0.8
Probability of mutation 0.01
The rules were laid down so to minimize RMSE
and maximize R2. The matrix of rules is presented in
the Table 4. For the multi-objective Genetic
Algorithm with weighted aggregation, the following
fitness evaluation was adopted:
Evolving Analog Electronic Circuits for Fuzzy Membership Functions Generation
179
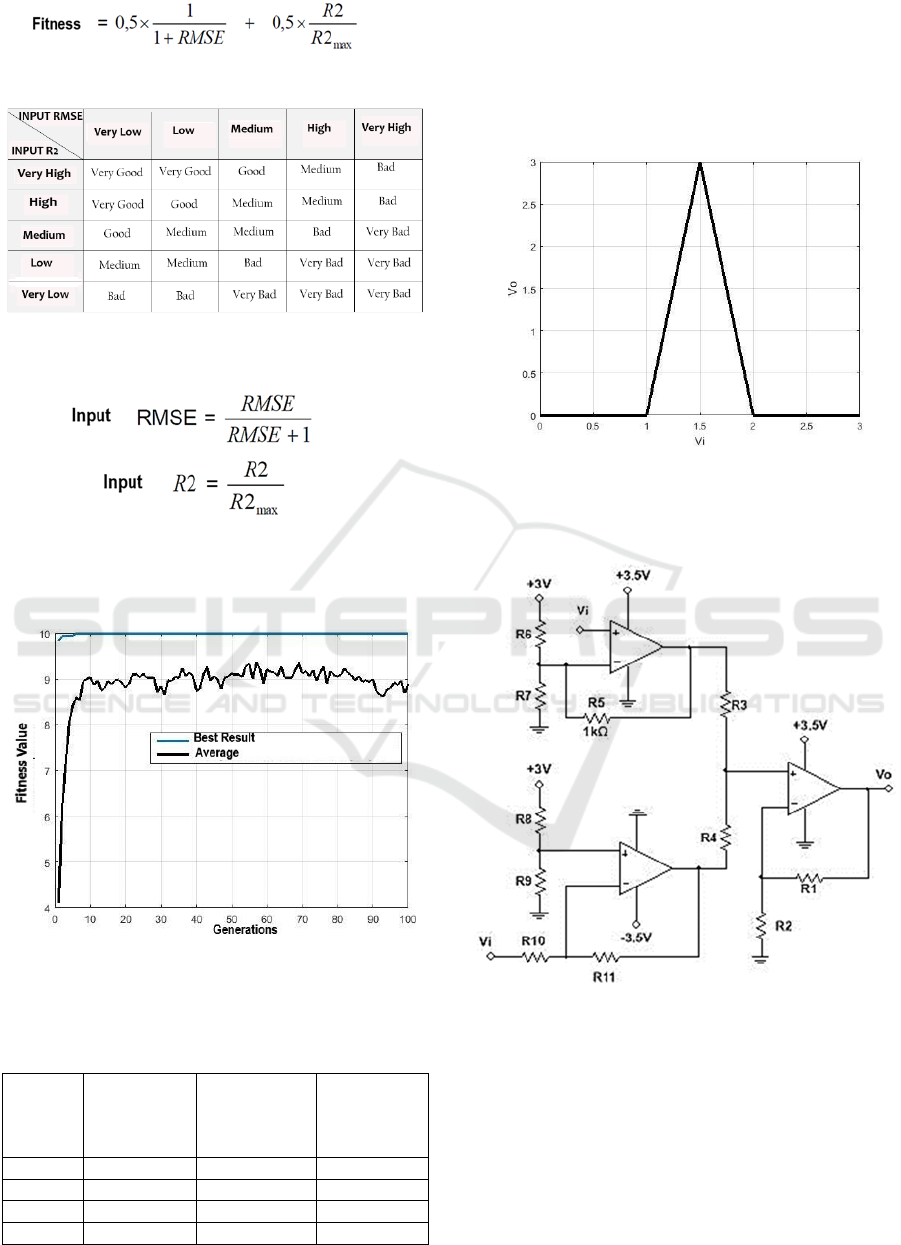
(1)
Table 4: Rules Matrix for S MF Circuit.
For the fuzzy aggregator system, the objectives were
normalized between 0 and 1 as follows:
(2)
(3)
Figure 8 depicts an evaluation graph of the best
individual and the average of individuals per
generation of the Multiobjective genetic algorithm
with fuzzy aggregator.
Figure 8: S MF circuit evolution.
The results of the evolutions are presented in Table 5.
Table 5: Results for the S membership function circuit.
Mono obj.
G.A.
Multi obj.
G.A.
Multi obj.
G.A. with
Fuzzy
A
gg
re
g
ato
r
RMSE 0 0 0
R1 3,3 kΩ 8,2 kΩ 10
k
Ω
R2 3,3 kΩ 8,2 kΩ 10
k
Ω
R3 3,3 kΩ 8,2 kΩ 10
k
Ω
3.2 Case Study 2: Triangular
Membership Function (MF)
The triangular membership function circuit topology
should provide an output voltage relative to the input
voltage as illustrated in Figure 9.
Figure 9: Vo x Vi for the triangular MF circuit.
A suitable circuit that has these characteristics is
depicted in Figure 10.
Figure 10: Topology for the evolution of the triangular
Membership Function.
The first objective of this evolution is to minimize
the RMSE of the voltage curve given by the circuit
that generates the triangular MF in relation to the
objective function that represents the target triangular
function. The second objective is to minimize the sum
of the resistor values in the circuit. The range of each
value of the 11 resistors in the circuit are between
FCTA 2022 - 14th International Conference on Fuzzy Computation Theory and Applications
180

1kΩ and 10 kΩ. The used parameters of the GA are
the same as in case study 1.
The configuration of the fuzzy aggregator system
was similar to that used for the S MF circuit but
following the rules according to Table 1. For this
system the objectives were normalized between 0 and
1 as follows:
(4)
(5)
For the multi-objective GA with weighted
aggregation, the following aptitude assessment was
used:
(6)
The obtained results are shown in Table 6:
Table 6: Results for the triangular MF circuit.
Mono obj.
G.A.
Multi obj.
G.A.
Multi obj.
G.A. with
Fuzzy
A
gg
re
g
ato
r
RMSE 0.16 0.21 0.13
51.7 kΩ 24.2 kΩ
9.02 kΩ
4 CONCLUSIONS
In this work, an evolutionary model was used for the
development of analog electronic circuits, which uses
a method for evaluation that considers more than one
objective and uses, for that, a process of aggregation
of objectives through a fuzzy system. This method
was called fuzzy aggregator and some circuits were
successfully evolved. The fuzzy aggregator was
applied in the evaluation process of genetic
algorithms, modifying the traditional method of these
algorithms and including, in this way, the feature of
multi-objective evaluation to such evolutionary
algorithms.
Case studies of MF circuit evolution were carried
out to analyze the effectiveness of the method. An
implementation based purely on simulation of circuit
models was chosen, providing a flexible environment
for case studies and enabling future applications.
Evolutions of analog electronic circuits are evaluated
through computer simulations. The work developed
for evolution, evaluation and implementation showed
good performance in the analyzed case studies, and
can be used as a basis for new applications and
implementations of other circuits. Compared to the
other methods studied, the evaluated method yielded
consistent results, with the advantages of inserting the
designer's preferences and specifications in a simple
and interpretable way at the beginning of the project,
in addition to not requiring the designer's
interference, either during or after the evolution
process. In this way, the work developed for the
evolution of analog electronic circuits with multi-
objective evaluation through a fuzzy system
constitutes a contribution to the design studies and
implementation of electronic systems that can be used
in several applications.
For future work, studies in different lines of action
may be suggested. It would be important to
implement the evaluation of circuits in a Spice-type
circuit simulator, thus facilitating the experimentation
and design of new circuits with models closer to the
real thing. The use of the GPGPU (General Purpose
Graphics Processing Unit) technique deserves to be
investigated because it will certainly contribute to
faster evaluations in the simulators and,
consequently, the evolved circuit will be obtained in
a shorter time. After implementing an evolutionary
platform with a Spice simulator that uses GPGPU, it
is worth investigating chromosomal representations
to enable the search for circuit topologies and not just
the values of the components.
In addition, comparisons with other algorithms
such as Coyote optimization algorithms, Particle
Swarm Optimization (PSO) (Mekhmoukh Taleb et al,
2022), Quantum Butterfly Optimization algorithm (Li
et al, 2022), etc. are anticipated possibilities in future
works.
ACKNOWLEDGEMENTS
This study was financed in part by the Coordenação
de Aperfeiçoamento de Pessoal de Nível Superior –
Brasil (CAPES) – Finance Code 001, and FAPERJ.
REFERENCES
Haddow, P. C.; Tyrrell, A. M., 2018. Evolvable Hardware
Challenges: Past, Present and the Path to a Promising
Future. Inspired by Nature, Emergence, Complexity
and Computation 28. Springer International Publishing.
Amaral, J. L. M., Amaral, J. F. M., Morin, D., Tanscheit,
R., 2007. An immune fault detection system with
automatic detector generation by genetic algorithms.
Seventh International Conference on Intelligent
Evolving Analog Electronic Circuits for Fuzzy Membership Functions Generation
181

Systems Design and Application (ISDA), 2007, p. 283
– 288.
Lohn, J. D., Colombano, S. P., 1999. A circuit
representation technique for automated circuit design.
IEEE Transactions on Evolutionary Computation, Vol.
3, No. 3, p. 205 – 219.
Luca, M., Luca, R., Bejinariu, Silviu-Ioan, Ciobanu, A.,
Paduraru, O., Zbancioc, M., Barbu, T., 2015. An
overview of several researches on fuzzy logic in
intelligent systems. 2015 International Symposium on
Signals, Circuits and Systems (ISSCS).
Ajith, A., Jain, L.C., Goldberg, R., (Eds.), 2005.
Evolutionary multiobjective optimization: theoretical
advances and applications. Springer Series on
Advanced Information and Knowledge Processing.
Coello Coello, C. A., 2013. Multi-objective evolutionary
algorithms in real-world applications: some recent
results and current challenges. Advances
inEvolutionary and Deterministic Methods for
Design, Optimization and Control in Engineering and
Sciences, Vol. 36 of the series Computational Methods
in Applied Sciences pp 3-18.
Fonseca, C. M., Fleming, P. J., 1995. Multiobjective
genetic algorithms made easy: selection, sharing and
mating restriction. First International Conference on
Genetic Algorithms in Engineering Systems:
Innovations and Applications, (Conf. Publ. No. 414).
Altinoz, O. T., Deb, K., 2015. Late parallelization and
feedback approaches for distributed computation of
evolutionary multiobjective optimization algorithms.
Second International Conference on Soft Computing
and Machine Intelligence.
Jiang, S., Yang, S., 2016. Evolutionary Dynamic
multiobjective optimization: benchmarks and algorithm
comparisons, IEEE Transactions on Cybernetics,
Volume: PP, Issue: 99, pp. 1-14.
Reiser, R. H. S., Bedregal, B., Baczyński, M., 2013.
Aggregating fuzzy implications. Information Sciences,
Volume 253, December 2013, pp. 126-146
Mardani, A., Jusoh, A., Zavadskas, E. K., 2015. Fuzzy
multiple criteria decision-making techniques and
applications – two decades review from 1994 to 2014,
Expert Systems with Applications, Volume 42, Issue 8,
pp. 4126-4148.
Marlen, A., Dorzhigulov, A., 2018. Fuzzy membership
function implementation with memristor. Computer
Science, Emerging Technologies, 1-4.
Rojec, Ž., Fajfar, I., Burmen, Á., 2022. Evolutionary
Synthesis of Failure-Resilient Analog Circuits.
Mathematics 10, no. 1: 156.
Coello Coello, C. A., 1999. A comprehensive survey of
evolutionary-based multiobjective optimization
techniques. Knowledge and Information Systems,
Volume 1, Issue 3, pp. 269–308.
Houck, C.R., Joines, J., Kay, M., 1996. A genetic algorithm
for function optimization: A Matlab implementation,
ACM Transactions on Mathematical Software.
Mekhmoukh Taleb, S., Meraihi Y., Gabis, A. B., Mirjalili,
S., Zaguia A., Ramdane-Cherif, A., 2022. Solving the
mesh router nodes placement in wireless mesh
networks using coyote optimization algorithm, IEEE
Access, vol. 10, pp. 52744-52759.
Li, M.W., Xu, D.Y., Geng, J., Hong, W.C., 2022. A ship
motion forecasting approach based on empirical mode
decomposition method hybrid deep learning network
and quantum butterfly optimization algorithm.
Nonlinear Dynamics 107, 2447–2467.
FCTA 2022 - 14th International Conference on Fuzzy Computation Theory and Applications
182
