
Towards Phenotypic Duplication and Inversion in Cartesian Genetic
Programming
Roman Kalkreuth
a
Natural Computing Research Group, Leiden Institute of Advanced Computer Science, Leiden University,
Keywords:
Cartesian Genetic Programming, Mutation, Duplication, Inversion, Boolean Function Learning.
Abstract:
The search performance of Cartesian Genetic Programming (CGP) relies to a large extent on the sole use of
genotypic point mutation in combination with extremely large redundant genotypes. Over the last years, steps
have been taken to extend CGP’s variation mechanisms by the introduction of advanced methods for recom-
bination and mutation. One branch of these contributions addresses phenotypic variation in CGP. Besides
demonstrating the effectiveness of various phenotypic search operators, corresponding analytical experiments
backed evidence that phenotypic variation is another approach for achieving effective evolutionary-driven
search in CGP. However, recent comparative studies have demonstrated the limitations of phenotypic recom-
bination in Boolean function learning and highlighted the effectiveness of the mutation-only approach. Espe-
cially the use of the 1+λ selection strategy with neutral genetic drift has been found superior to recombination-
based approaches in this problem domain. Therefore, in this work, we further explore phenotypic mutation
in CGP by the introduction and evaluation of two phenotypic mutation operators that are inspired by chro-
mosomal rearrangement. Our initial findings show that our proposed methods can significantly improve the
search performance of CGP on various single- and multiple-output Boolean function benchmarks by reducing
the number of fitness evaluations needed to find the ideal solution.
1 INTRODUCTION
Genetic programming (GP) can be considered as a
search heuristic for computer program synthesis that
is inspired by neo-Darwinian evolution. First work
on GP has been done by Forsyth (Forsyth, 1981),
Cramer (Cramer, 1985) and Hicklin (Hicklin, 1986).
Later work by Koza (Koza, 1990; Koza, 1992; Koza,
1994) significantly popularized the field of GP. GP
as proposed by Koza is traditionally used with trees
as program representation. In contrast, Cartesian Ge-
netic Programming is a well established graph-based
GP variants. First work towards CGP was done by
Miller, Thompson, Kalganova, and Fogarty (Miller
et al., 1997; Kalganova, 1997; Miller, 1999) by the
introduction of a graph encoding model based on
a two-dimensional array of functional nodes. CGP
can be seen as an extension to the traditional tree-
based GP representation model since its representa-
tion allows many graph-based applications such as
Boolean circuit design, image processing (Sekanina,
2002), and neural networks (Turner and Miller, 2013).
a
https://orcid.org/0000-0003-1449-5131
Even though standard CGP was introduced over two
decades ago, it is still predominantly used only with a
probabilistic point mutation operator for genetic vari-
ation.
The predominant use of the mutation-only CGP ap-
proach originates from failures of various geno-
typic crossover operators to improve its search per-
formance. This motivated the introduction of two
phenotypic approaches to recombination called sub-
graph crossover (Kalkreuth et al., 2017) and block
crossover (Husa and Kalkreuth, 2018). Although
initial experiments with phenotypic recombination
led to promising initial results, recent compara-
tive studies (Kaufmann and Kalkreuth, 2017; Husa
and Kalkreuth, 2018; Kalkreuth, 2020; Kalkreuth,
2021b) gave more evidence about the effectiveness
of mutation-only CGP for Boolean function learning.
However, the introduction of phenotypic recombina-
tion operators inspired later work on phenotypic mu-
tation in CGP and led to the introduction of two oper-
ators called insertion and deletion (Kalkreuth, 2019;
Kalkreuth, 2021a).
Considering recent findings on the limitations of re-
50
Kalkreuth, R.
Towards Phenotypic Duplication and Inversion in Cartesian Genetic Programming.
DOI: 10.5220/0011551000003332
In Proceedings of the 14th International Joint Conference on Computational Intelligence (IJCCI 2022), pages 50-61
ISBN: 978-989-758-611-8; ISSN: 2184-3236
Copyright © 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
combination in CGP and the fact that advanced vari-
ation is still underdeveloped when compared to the
number of contributions in tree-based GP, this work
aims to further exploration of phenotypic mutation.
We introduce two new operators called duplication
and inversion and evaluate these methods on a diverse
set of Boolean function problems. Boolean function
learning can be seen as one of the most popular prob-
lem domains of CGP since evolving solutions for this
kind of problem has been a major motivation for its
introduction (Miller, 1999).
The document is structured as follows: Section 2
of this work describes CGP. Related work on pheno-
typic variation in CGP is reviewed in Section 3. In
Section 4, we introduce our new methods. Section 5
is devoted to the formulation of the research question,
description of our experiments, and the presentation
of our results. Based on our experimental findings,
the formulated research question is analyzed in Sec-
tion 6. Points of criticism are discussed in Section 7.
Finally, Section 8 gives a conclusion and outlines our
future work.
2 CARTESIAN GENETIC
PROGRAMMING
In contrast to tree-based GP, CGP represents a genetic
program via genotype-phenotype mapping as an in-
dexed, acyclic, and directed graph. In this way, CGP
can be seen as an extension of the traditional tree-
based GP approach. The CGP representation model
is based on a rectangular grid or row of nodes. A def-
inition of a cartesian genetic program (CP) is given
in Definition 2.1. Each CP is encoded in the geno-
type of an individual and is decoded to its correspond-
ing phenotype. Originally, the structure of the graph
was represented by a rectangular grid of n
r
rows and
n
c
columns, but later work focused on a represen-
tation with one row. The CGP decoding procedure
processes groups of genes, and each group refers to
a node of the graph, except the last one, which rep-
resents the outputs of the phenotype. Each node is
represented by two types of genes that index the func-
tion number in the GP function set and the node in-
puts. These nodes are called function nodes and exe-
cute functions on the input values. A definition of a
function node is given in Definition 2.2. The number
of input genes depends on the maximum arity n
a
of
the function set.
Definition 2.1 (Cartesian Genetic Program). A carte-
sian genetic program is an element of the Cartesian
product N
i
× N
f
× N
o
× F :
1 0 1 2 2 1 0 3 2
2 3 4
OP
3
& ∥
¬
IP1
IP2
OP2 3 4
FunctionIndex Symbol
0
1
2
&
∥
Logical and
Logical or
⊕
Genotype
Phenotype
Function Lookup Table
¬
Negation
Decode
3
Exclusive or
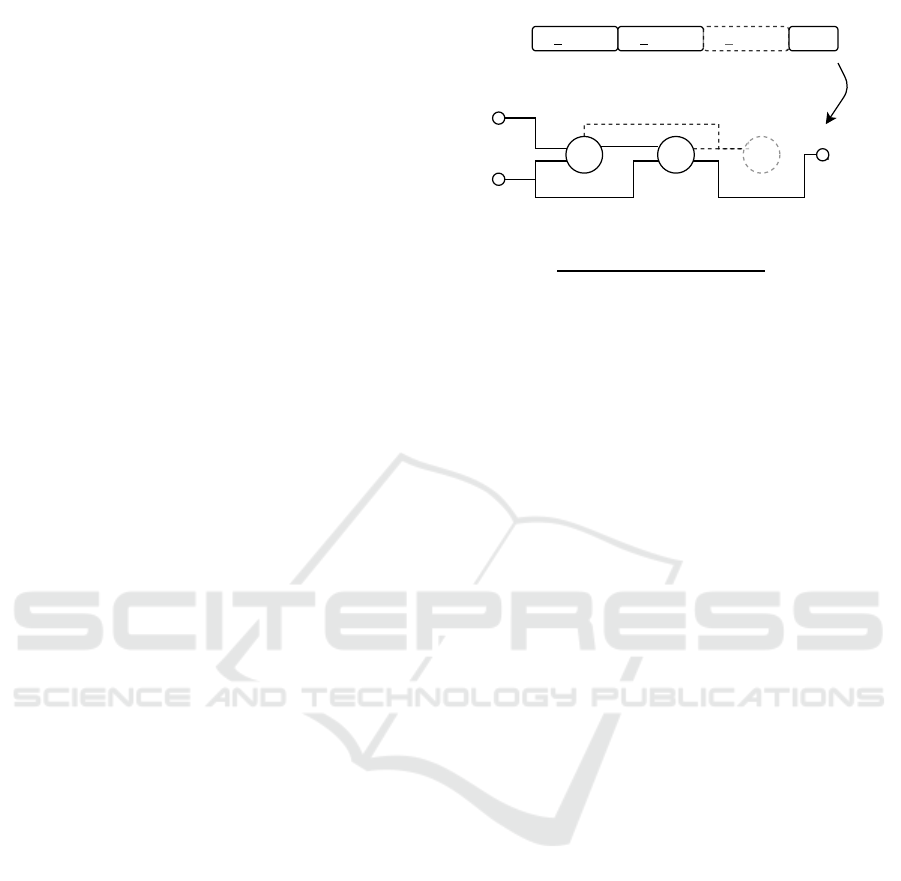
1
0
Figure 1: Example of the decoding procedure of a CGP
genotype to its corresponding phenotype. The identifiers
IP1 and IP2 stand for the two input nodes with node index
0 and 1. The identifier OP stands for the output node of the
graph.
• N
i
is a finite non-empty set of input nodes
• N
f
is a finite set of function nodes
• N
o
is a finite non-empty set of output nodes
• F is a finite non-empty set of functions
Definition 2.2 (Function Node). Given the number
of inputs n
i
, the number of function nodes n
f
, and the
maximum arity n
a
, a function node θ
f
is defined as a
tuple θ
f
= (x
f
, g
f
, g
0
c
, ..., g
n
a
−1
c
) of dimension n
a
+ 2:
• x
f
∈ {n
i
, . . . , n
i
+n
f
−1} is the number of the func-
tion node
• g
f
∈ {x ∈ N
0
| 0 ≤ x ≤ |F | − 1} is the function
gene
• g
0
c
, ..., g
n
a
−1
c
∈ {x ∈ N
0
| 0 ≤ x ≤ x
f
− 1} are the
connection genes
A backward search is conducted to decode the cor-
responding phenotype. The decoding procedure is
done for all output genes. An example of the back-
ward search of the most popular one-row integer rep-
resentation is illustrated in Figure 1. The backward
search starts from the program output and processes
all nodes which are linked in the genotype. In this
way, only active nodes are processed during evalu-
ation. The genotype in Figure 1 is grouped by its
function nodes. The first (underlined) gene of each
group refers to the function number in the correspond-
ing function set. The non-underlined genes represent
the input connections of the node. Inactive function
nodes are shown in gray color and with dashed lines.
Towards Phenotypic Duplication and Inversion in Cartesian Genetic Programming
51

The number of inputs n
i
, outputs n
o
, and the length
of the genotype is fixed. Every candidate program is
represented with n
r
∗ n
c
∗ (n
a
+ 1) + n
o
integers. Even
if the length of the genotype is fixed for each candi-
date program, the length of the corresponding phe-
notype in CGP is variable, which can be considered
as an advantage of the CGP representation. CGP is
traditionally used with a (1 + λ) evolutionary algo-
rithm (EA). The (1+λ)-EA is often used with a se-
lection strategy called neutrality, which is based on
the idea that genetic drift yields to diverse individuals
having equal fitness. The genetic drift is implemented
into the selection mechanism in a way that individuals
which have the same fitness as the normally selected
parent are determined, and one of these same-fitness
individuals is returned uniformly at random. The new
population in each generation consists of the best in-
dividual of the previous population and the λ created
offspring. The breeding procedure is mostly done by
a point mutation that swaps genes in the genotype of
an individual in the valid range by chance. Another
point mutation is the flip of the functional gene, which
changes the functional behavior of the corresponding
function node.
3 PHENOTYPIC VARIATION IN
CGP
Phenotypic variation in CGP can be described as a
type of chromosomal alteration whereby only the phe-
notype of an individual is varied by recombination or
mutation. It originates from an investigation of the
length bias and the search limitation of CGP (Gold-
man and Punch, 2013; Goldman and Punch, 2015).
In their work, Goldman and Punch presented a modi-
fied version of the point mutation operator which ex-
actly mutates one active gene. This so-called sin-
gle active-gene mutation strategy (SAGMS) has been
found beneficial for the search performance of CGP.
The SAGMS can be seen as a form of phenotypic vari-
ation since it mutates only active genes.
Phenotypic mutation inspired the introduction of
two phenotypic recombination operators called sub-
graph crossover (Kalkreuth et al., 2017) and block
crossover (Husa and Kalkreuth, 2018). The sub-
graph crossover exchanges and links subgraphs of ac-
tive function nodes between two selected parents and
the block crossover exchanges blocks of active func-
tion genes. In recent comparative studies, its use has
been found beneficial for several symbolic regression
benchmarks since it led to a significant decrease in
the number of fitness evaluations needed to find the
ideal solution (Kalkreuth, 2020; Kalkreuth, 2021b).
InversionDuplication
Figure 2: Exemplification of chromosomal duplication and
inversion in nature which served as inspiration for this work.
Duplication results in the formation of extra copies of a re-
gion within the chromosome. Inversion rearranges a seg-
ment of a chromosome by reversing it end-to-end.
However, the gain of the search performance was con-
siderably lower for the tested Boolean function prob-
lems. Moreover, the results of the experiments clearly
showed that the subgraph crossover failed to improve
the search performance on some of the tested Boolean
benchmarks when compared to the results of the tra-
ditional 1+λ selection strategy. Similar findings were
reported for the block crossover (Kalkreuth, 2021b).
Kalkreuth (Kalkreuth, 2019) adapted two phenotypic
mutation operators called insertion and deletion that
are inspired by frameshift mutation. Insertion se-
lects and activates one inactive function node of a CP,
where the inactive node is selected by chance. In con-
trast, deletion deactivates the first active function node
of a CP. Experiments with Boolean and symbolic re-
gression benchmarks demonstrated that the proposed
mutations can contribute to the search performance
of CGP on the tested problems.
ˇ
Ceška et al. (
ˇ
Ceška
et al., 2021) proposed a combination of the classical
single active gene mutation and a node deactivation
operation for circuit design called SagTree. The de-
activation operation of SagTree aims at eliminating a
part of the circuit and forming a tree from an active
gate.
Phenotypic mutation also led to the proposal of se-
mantic mutation in CGP. Manfrini et al. (Manfrini
et al., 2016) extended SAGMS to the so-called Biased
Single-Active Mutation, that records the frequencies
of beneficial function gene mutations during the evo-
lutionary run which are then used to calculate proba-
bilities for function transitions. Hodan et al. (Hodan
et al., 2020) proposed a semantically oriented form of
mutation that operates similar to the SAGMS but ad-
ditionally uses semantics to determine the best value
for each gene mutation.
ECTA 2022 - 14th International Conference on Evolutionary Computation Theory and Applications
52

4 THE PROPOSED METHODS
The proposed methods for phenotypic mutation in
CGP are inspired by two major single-chromosome
mutations which occur in nature and are studied in
the field of molecular evolution. Duplication is a form
of mutation that causes the generation of one or more
copies of a gene or section of a chromosome. Another
terminology that is common for this type of mutation
is gene amplification. Inversion means that the or-
der within a section of the chromosome is reversed.
Figure 2 exemplifies chromosomal inversion and du-
plication in nature on a part of a chromosome. Both
duplication and inversion count to the group of chro-
mosomal rearrangement mutations, and inversion was
originally adapted in the field of genetic algorithms
(GA) by Holland (Holland et al., 1975). For instance,
inversion in combination with the path representa-
tion for GA has been found useful for its application
to the traveling salesman problem (Larrañaga et al.,
1999). In CGP, gene duplication has been originally
adapted for a variant of the representation model by
Ebner (Ebner, 2012) to evolve sub-detectors for ob-
ject detection tasks. We adapt the two mutations for
CGP with phenotypic function variation which is also
utilized by the block crossover. This means that func-
tion genes of active function nodes are selected and
the values are rearranged by means of duplication and
inversion. To regulate the strength of both mutations
for the evolutionary process, the methods are utilized
with a respective duplication and inversion probabil-
ity. An implementation of both methods for the CGP
extension package of the Java Evolutionary Compu-
tation Research System (ECJ) (Scott and Luke, 2019)
is provided in the ECJ GitHub repository
1
.
4.1 Duplication
We adapt chromosomal duplication for CGP by se-
lecting an active function gene and replacing the
values of a sequence of successive active function
genes with the value of the selected gene. This
type of adaption does not cause any structural en-
largement as it happens in nature. The reason for
this is that such an operation is quite complex when
the CGP representation model is used. According
to Kalkreuth (Kalkreuth, 2021c), even the activation
of a single inactive node requires several rearrange-
ments of connection genes to ensure that other inac-
tive nodes are not affected by the operation. With our
adaption by replacement, we avoid this computational
effort but at the same time, increase the frequency of
the selected function within the phenotype. In this
1
https://github.com/GMUEClab/ecj
1 0 1 0 2 1 3 2 1 2 2 4Parent
Mutant
Duplication
2 3 4 5 OP
2 3 4 5
Parent
OP
Mutant
Duplication
1 0 1 0 2 1 1 2 1 2 2 4
& ⊕
¬
IP2
OP2
5
5
3 4 5
∥
& &
¬
IP1
IP2
OP2 3 4 5
∥
0
1
IP1
0
1
Node number
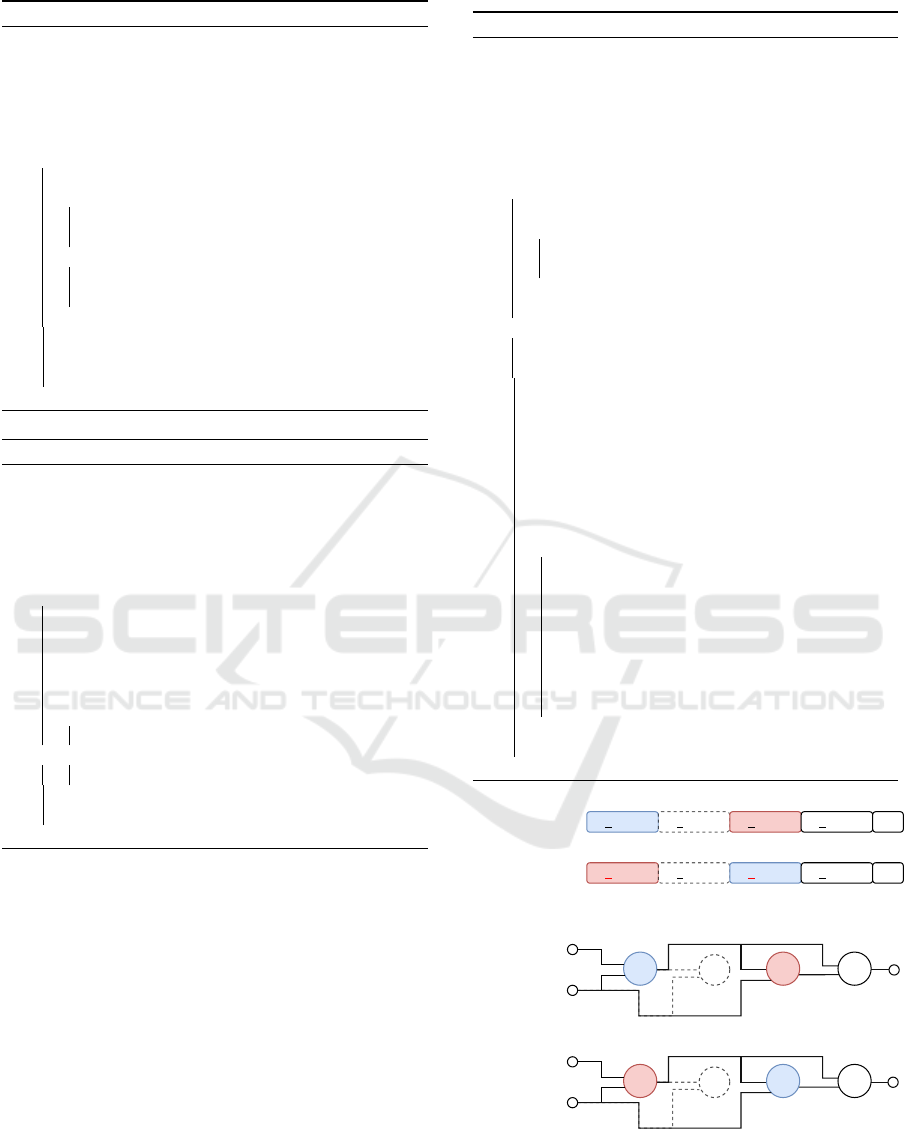
Figure 3: Exemplification of duplication in CGP: The value
of the function gene of node 2 is duplicated to node 4 by
the replacement of the function gene. In this example, the
duplication depth was set to one. The duplicated function
gene value is highlighted in red color.
way, we phenotypically amplify the occurrence of the
selected function. The procedure is discarded if the
CP has less than two active function nodes since at
least two active function nodes are necessary. Before
the duplication of the function gene is performed, a
duplication depth is determined in accordance with
the predefined maximum duplication depth and the
number of active function nodes. When the number
of active nodes is less than the predefined maximum
depth, the depth is adjusted to the number of active
function nodes. The maximum is then used to choose
the duplication depth by chance. Afterward, the in-
dex of an active function node, whose position allows
the duplication of its function gene of the determined
depth, is selected. The function gene is finally dupli-
cated and the altered genotype is returned.
A definition of duplication is given in Definition 4.1.
The algorithmic implementation of the determination
of the duplication depth and starting node is described
in Algorithm 1 and 2. The algorithmic implementa-
tion of the duplication procedure is described in Algo-
rithm 3. An exemplification is illustrated in Figure 3.
Definition 4.1 (Duplication). Let d be the duplica-
tion depth and let D = (g
0
f
, . . . , g
d
f
) be a tuple of active
function gene values which have been selected for the
duplication procedure. Let g
0
f
∈ D be the first active
function gene value and let
e
D = (g
0
f
0
, g
0
f
1
, . . . , g
0
f
d
) be
a tuple with duplicated function gene values which is
obtained after the duplication procedure. Duplication
is a variation operator for CGP that adapts chromoso-
mal duplication by replacing the active function genes
D by
e
D.
Towards Phenotypic Duplication and Inversion in Cartesian Genetic Programming
53
Algorithm 1: Determination of the stochastic depth.
Arguments
D: Maximum depth
|N
a
|: Number of active function nodes
Return
depth: Determined stochastic depth
1: function StochasticDepth(D, |N
a
|)
2: If the number of active nodes is less than the maximum depth
3: if |N
a
| ≤ D then
4: Adjust max to the maximum possible depth
5: max ← |N
a
| − 1
6: else
7: Set max to the predefined maximum depth
8: max ← D
9: end if
10: Determine the depth by chance in the interval [1, max]
11: depth ← RandomInteger(1, max)
12: return depth
13: end function
Algorithm 2: Determination of the start index.
Arguments
depth: Previously determined stochastic depth
|N
a
|: Number of active function nodes
Return
start: start index in the list of active function nodes
1: function StartIndex(depth, |N
a
|)
2: Set start initially to zero
3: start ← 0
4: Calculate the max possible start index
5: max ← |N
a
|− depth - 1
6: If the maximum is greater zero
7: if max > 0 then
8: Replace start index with a random one in the interval [0,
max]
9: start ← RandomInteger(0, max)
10: end if
11: return start
12: end function
4.2 Inversion
Inversion permutates the function gene values of a set
of successive active function nodes. The permutation
is performed by reversing the order of the function
gene values. The procedure is also discarded if the
CP has less than two active function nodes. Before the
inversion is performed, the inversion depth and node
index are determined in the same way as for the du-
plication procedure (Algorithm 1 and 2). A definition
of inversion is given in Definition 4.2 and the algo-
rithmic implementation is described in Algorithm 4.
An exemplification of the inversion procedure is il-
lustrated in Figure 4.
Definition 4.2 (Inversion). Let d be the inversion
depth and let I = (g
0
f
, . . . , g
d
f
) be a tuple of active
Algorithm 3: The duplication procedure.
Arguments
G: Original genome
N
a
: List of active function node numbers
D
d
: Maximum duplication depth
Return
e
G: Mutated genome
1: function Duplication(G, N
a
, D
d
)
2: If less than two active nodes are active
3: if |N
a
| < 2 then
4: Discard procedure by returning the orignal genome
5: return G
6: end if
7: Determine the depth stochastically and oriented with the maxi-
mum
8: depth ← StochasticDepth(D
d
, |N
a
|)
9: Determine start index in N
a
10: start← StartIndex(depth, |N
a
|)
11: Calculate endpoint for the iteration
12: end ← start + depth
13: Get first function gene value
14: func ← GetFunction(N
a
[start])
15: Initialize loop counter
16: i ← start + 1
17: Iterate over the duplication depth
18: while i ≤ end do
19: Get the next active function node number
20: node ← N
a
[i]
21:
Determine the genome position
22: pos ← PositionFromNodeNumber(node)
23: Duplicate the first function
24: G[pos] ← func
25: Loop counter increment
26: i ← i + 1
27: end while
28: return G
29: end function
1 0 1 0 2 1 3 2 1 2 2 4Parent
Mutant
Inversion
2 3 4 5 OP
2 3 4 5
Parent
OP
Mutant
Inversion
3 0 1 0 2 1 1 2 1 2 2 4
& ⊕
¬
IP2
OP2
5
5
3 4 5
∥
⊕ &
¬
IP1
IP2
OP2 3 4 5
∥
0
1
IP1
0
1
Node number
Figure 4: Exemplification of inversion in CGP: The func-
tion genes of node 2 and node 4 are inverted by a swap of
the gene values. In this example, the inversion depth was set
to one. The inverted function gene values are highlighted in
red color.
ECTA 2022 - 14th International Conference on Evolutionary Computation Theory and Applications
54

Algorithm 4: The inversion procedure.
Arguments
G: Original genome
N
a
: List of active function node numbers
D
i
: Maximum inversion depth
Return
e
G: Mutated genome
1: function Inversion(G, N
a
, D
i
)
2: If less than two active nodes are active
3: if |N
a
| < 2 then
4: Discard procedure by returning the orignal genome
5: return G
6: end if
7: Determine the depth stochastically and oriented with the maxi-
mum
8: depth ← StochasticDepth(D
d
, |N
a
|)
9: Determine start index in N
a
10: start← StartIndex(depth, |N
a
|)
11: Calculate endpoint for the iteration
12: end ← start + depth
13: Division by two and ceiling for the iteration
14: div ← d
depth
2
e
15: Initialize loop counter
16: i ← 0
17: while i < div do
18: Node number incremented from start
19: n
1
← N
a
[start + i]
20: Node number decremented from end
21: n
2
← N
a
[end - i]
22: Swap function gene values within the genome
23: G ← SwapFunctionGenes(G, n
1
, n
2
)
24: Loop counter increment
25: i ← i + 1
26: end while
27: return G
28: end function
function gene values which have been selected for the
inversion procedure. Let
e
I = (g
d−0
f
, g
d−1
f
, . . . , g
d−i
f
),
where i = d be a tuple of reversed function gene val-
ues which is obtained after the inversion procedure.
Inversion is a variation operator for CGP that adapts
chromosomal inversion by reversing the order of d +1
sequential active function genes I to
e
I .
5 EVALUATION
5.1 Formulation of Research Question
The experiments of this work focus on the examina-
tion of the following research question:
Research Question 1 (RQ1). Can the use of dupli-
cation and inversion significantly contribute to the
search performance of integer-based CGP for the
tested Boolean function problems?
5.2 Benchmarks
For our experiments, we composed a diverse set of
popular Boolean function problems. Since our ex-
periments focus on the Boolean function domain, we
want to ensure diversity for our evaluation. There-
fore, our benchmark set covers five categories of
Boolean functions which are often implemented in
digital circuits. The benchmark set is shown in Ta-
ble 1. In addition to the commonly used arithmetic
and parity problems, we also included combinational
and comparative problems such as the digital demul-
tiplexer and comparator. Moreover, besides merely
evaluating common single function problems, we also
included underrepresented multi-function problems
such as the adder/subtractor and the arithmetic logic
unit (ALU). The function set of the ALU benchmark
consisted of three logical and two arithmetic func-
tions and is shown in Table 2. Since the major-
ity of the problems are typically implemented with
XOR gates, we decided to use a reduced function
set F
= {AND, OR, NAND,NOR} which increases
the difficulty of these problems. An exception has
been made for the four-bit digital multiplier problem
for which we used an extended function set F
⊕
=
{AND, OR, NAND, NOR, NOT, XOR, XNOR}. All
benchmarks used in our experiments are implemented
for the ECJ CGP extension package and are available
in the ECJ GitHub repository
2
. For the generation
of the truth tables of the ALU benchmark, we devel-
oped a C++ based tool called Boolean Benchmark
Builder which is also available on GitHub
3
. With our
effort, we intend to promote the use of multi-function
benchmarks in the Boolean problem domain. Overall,
the emphasis of our benchmark set lies on multiple-
output problems since the graph representation model
of CGP is well-suited for this sort of problem. An-
other reason is the reported overuse of single-output
benchmarks such as the parity even problem (McDer-
mott et al., 2012; White et al., 2013). According to
White et al. (White et al., 2013) multiple-output prob-
lems are considered to be a suitable replacement in the
Boolean function domain.
5.3 Experimental Setup
To evaluate the search performance of the tested al-
gorithms, we measured the number of fitness eval-
uations until the CGP algorithm terminated (fitness-
evaluations-to-termination) as recommended by Mc-
Dermott et al. (McDermott et al., 2012). Termination
2
https://github.com/GMUEClab/ecj
3
https://github.com/RomanKalkreuth/boolean-
benchmark-builder/
Towards Phenotypic Duplication and Inversion in Cartesian Genetic Programming
55
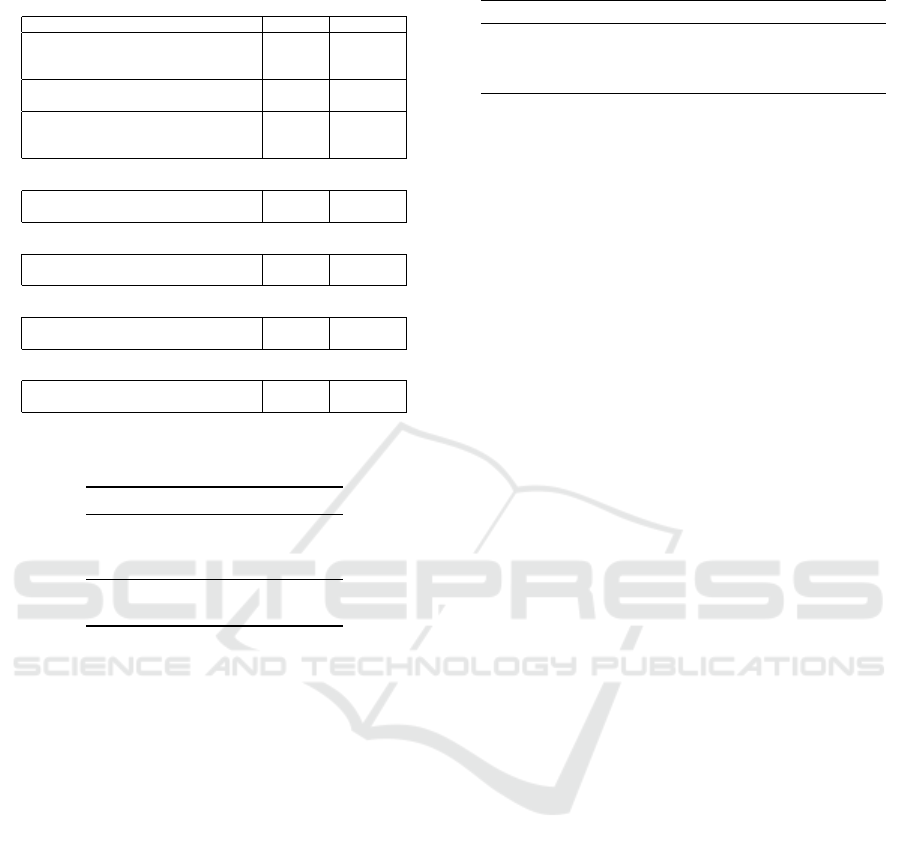
Table 1: Benchmark set used for the experiments.
Arithmetic
Problem # Inputs # Outputs
Adder 2-Bit 5 3
Adder 3-Bit 7 4
Adder 4-Bit 9 5
Subtractor 2-Bit 4 3
Adder/Subtractor 3-Bit 4 3
Multiplier 2-Bit 4 4
Multiplier 3-Bit 6 6
Multiplier 4-Bit 8 8
Combinational
Demultiplexer 1x8-Bit (DeMUX-1x8) 3 8
Demultiplexer 1x16-Bit (DeMUX-1x16) 4 16
Comparative
Comparator 3x1-Bit 3 9
Comparator 4x1-Bit 4 18
Parity
Parity-Even 8-Bit 8 1
Parity-Even 9-Bit 9 1
Arithmetic/Logical
Arithmetic Logic Unit 2-Bit (ALU 2-Bit) 7 3
Arithmetic Logic Unit 3-Bit (ALU 3-Bit) 9 4
Table 2: Function set of the arithmetic logic unit bench-
mark.
Opcode Function Description
000 & Logical and
001 || Logical or
010 ⊕ Exclusive or
011 + Addition
100 − Subtraction
was triggered when an ideal solution was found or a
predefined budget of fitness evaluation was exceeded.
For very complex problems, where it is likely that
an algorithm does not find the ideal solution within
a large budget of fitness evaluations, we additionally
calculated the success rate. To evaluate the fitness,
we defined the fitness value of an individual as the
number of different bits to the corresponding truth ta-
ble. When this number became zero, the algorithm
successfully terminated. In addition to the mean val-
ues of the measurements, we calculated the standard
deviation (SD), median (Q2) as well as lower and up-
per quartile (Q1 and Q3). The levels back parameter
l was set to ∞. We performed 100 independent runs
with different random seeds, except the complex and
computing-intensive four-bit digital multiplier prob-
lem for which we only performed 30 runs. Due to its
complexity, we defined a limit of 10
8
fitness evalua-
tions. Meta-optimization experiments have been per-
formed with the intention to compare the algorithms
fairly and are described in more detail in the follow-
ing subsection. All algorithms were compared on the
same number of function nodes and the same setting
of the λ parameter to exclude conditions, which can
distort the search performance comparison. All algo-
Table 3: Identifiers for the tested CGP algorithms.
Identifier Description
(1 + λ)-CGP 1 + λ selection strategy with neutral genetic drift
(1 + λ)-CGP-DP (1 + λ)-CGP with gene duplication
(1 + λ)-CGP-IN (1 + λ)-CGP with gene inversion
(1 + λ)-CGP-DP/IN (1 + λ)-CGP with duplication and inversion
rithms which used our proposed methods are tested
against the standard (1 + λ)-CGP which we declared
as the baseline algorithm for our experiments. In our
experiments, we exclusively used the single-row stan-
dard integer-based representation of CGP.
Since we cannot guarantee normally distributed val-
ues in our samples, we used the nonparametric two-
tailed Mann-Whitney U test (Mann and Whitney,
1947) to evaluate statistical significance. More pre-
cisely, we tested the null hypothesis that two samples
come from the same population (i.e. have the same
median). In addition to the p values, the average num-
ber of fitness evaluations is denoted with a
†
if the sig-
nificance level is p < 0.05 or a
‡
if the significance
level is p < 0.01.
5.4 Meta-optimization
We tuned relevant parameters for all tested CGP algo-
rithms on the set of benchmark problems. Moreover,
we used the meta-optimization toolkit of ECJ. The
parameter space for the respective CGP algorithms,
explored by meta-optimization, is presented in Ta-
ble 4. For the meta-level, we used a canonical GA
equipped with intermediate recombination and point
mutation. Since GP benchmark problems can be very
noisy in terms of finding the ideal solution, we ori-
ented the meta-optimization with a common approach
that has been used in previous studies (Kaufmann
and Kalkreuth, 2017; Husa and Kalkreuth, 2018;
Kalkreuth, 2021b). The meta-evolution process was
repeated several times, and the most effective settings
were compared to find the best setting. Finally, em-
pirical fine-tuning of the respective parameters was
performed.
5.5 Results
The results of our meta-optimization and search per-
formance evaluation are presented in Table 6 and it
is visible that either the use of duplication or inver-
sion reduces the number of fitness evaluations to ter-
mination for the majority of our tested problems. Vi-
olin plots are provided in Figure 5. Please note that
we evaluate the performance of the four-bit multiplier
problem by the respective success rates which are pre-
sented in Table 5. For this kind of problem, we are pri-
marily interested in how many solutions were found
ECTA 2022 - 14th International Conference on Evolutionary Computation Theory and Applications
56

Table 4: Parameter space explored by meta-optimization for
the tested CGP algorithms.
(1 + λ)-CGP
λ number of offspring [1, 16]
N number of nodes [10, 10000]
M
p
point mutation rate[%] [0.1, 5.0]
(1 + λ)-CGP-DP
M
p
point mutation rate[%] [0.1, 5.0]
M
d
duplication rate[%] [1.0, 20.0]
D
d
duplication depth [1, 20]
(1 + λ)-CGP-IN
M
p
point mutation rate[%] [0.1, 5.0]
M
i
inversion rate[%] [1.0, 20.0]
D
i
inversion depth [1, 20]
(1 + λ)-CGP-DP/IN
M
p
point mutation rate[%] [0.1, 5.0]
M
d
duplication rate[%] [1.0, 20]
D
d
duplication depth [1, 20]
M
i
inversion rate[%] [1.0, 20.0]
D
i
inversion depth [1, 20]
Table 5: Success rates of the evaluation of the four-bit mul-
tiplier problem.
Algorithm Success Rate [%]
(1 + λ)-CGP 37
(1 + λ)-CGP-DP 53
(1 + λ)-CGP-IN 40
(1 + λ)-CGP-DP/IN 23
at all by the tested algorithms since it has extraor-
dinary complexity when compared to other bench-
marks. The evolved parametrization pattern for the
(1+λ)-CGP are coherent with former findings (Kauf-
mann and Kalkreuth, 2017; Kalkreuth, 2021b). A
setting of λ = 1 turned out to be a general effec-
tive choice which is also coherent with former find-
ings (Kalkreuth, 2021b).
6 ANALYSIS OF RESEARCH
QUESTION
Our experiments demonstrate that the use of pheno-
typic inversion and duplication can significantly con-
tribute to the search performance of standard integer-
based CGP for our tested Boolean function problems.
Besides observing a reduced number of fitness eval-
uations to termination, we also observed a clearly in-
creased success rate on the complex four-bit multi-
plier problem for the duplication method. However,
on some of our tested problems we did not observe
a statistically significant result for a certain method
or combination. Moreover, on certain problems, only
the simultaneous use of our proposed methods led to
a significant result. But considered holistically, our
initial results demonstrate the effectiveness of phe-
notypic duplication and inversion for the tested prob-
lems since the use of at least one method led to a sig-
nificant reduction of the fitness evaluations or a clear
increased success rate on every problem.
7 DISCUSSION
The initial results of this work allow certain points
of criticism that are worthy of discussion. The first
point which should be addressed is that on some prob-
lems a certain method or the simultaneous use failed
to improve the search performance significantly. At
this point, we can only hypothesize that the underly-
ing semantics of certain problems are possibly suit-
able for one of our methods. For instance, duplica-
tion performed more effectively than inversion on the
demultiplexer and comparator problems. In contrast,
we achieved significant results with inversion on the
multi-function problems such as the adder/subtractor
and the ALU benchmark. Regarding the simultane-
ous use of our methods, we can only carefully hy-
pothesize that it may add too much mutation strength
to the evolutionary process of certain problems and
therefore leads to no significant improvement. These
points perhaps indicate the limitations of our meth-
ods but could open the opportunity to study and un-
derstand the search behavior of CGP on different
problems in more detail. Since our methods re-
quire further parametrization which seems to be very
problem-specific, a rule of thumb is difficult to de-
termine. However, based on the results of our meta-
optimization experiments we can narrow down the
parametrization pattern. We observed that higher mu-
tation rates greater than 12 % and depths greater than
6 function nodes were not successful on the tested
problems. Moreover, on the most complex problems
very low depths have been successful. Besides ensur-
ing fair conditions for our comparative experiments,
the motivation for the problem-specific tuning of the
parameters of our methods was also to achieve more
insight into the respective mutation strengths, com-
posed of mutation rate and depth, that are required to
achieve search performance enhancements. Another
major motivation for the chosen experimental setup
was to lay a foundation that can be used for further
analysis of the search behavior in the future.
As a first step, our experiments focused on the evalu-
ation of search effectiveness rather than runtime effi-
ciency. However, we considered computational com-
plexity for the design of our methods since the pheno-
type length is not altered. Consequently, our methods
can be used without redetermination of active func-
Towards Phenotypic Duplication and Inversion in Cartesian Genetic Programming
57

Table 6: Results of the meta-optimization and search performance evaluation measured by the number of fitness evaluations
(FE) to termination.
Parametrization Search Performance Evaluation
Problem Algorithm N λ M
p
[%] M
d
[%] D
d
M
i
[%] D
i
MFE SD 1Q 2Q 3Q p
Adder 2-Bit
(1 + λ)-CGP 3000 1 0.7 – – – – 42, 374 34, 431 22, 027 32, 662 50, 467 –
F
(1 + λ)-CGP-DP 3000 1 0.7 6.0 1 – – 36, 486 32, 141 17, 988 24, 167 45, 308 0.055446
(1 + λ)-CGP-IN 3000 1 0.7 – – 1.0 4 34, 754 23, 080 17, 332 26, 887 45, 691 0.083862
(1 + λ)-CGP-DP/IN 3000 1 0.6 5.0 1 1.0 2 31, 936
†
22, 104 16, 487 25, 255 43, 152 0.012563
Adder 3-Bit
(1 + λ)-CGP 5000 1 0.4 – – – – 200, 105 171, 364 106, 580 166, 913 237, 775 –
F
(1 + λ)-CGP-DP 5000 1 0.3 2.0 2 – – 164, 538
‡
131, 222 85, 697 134,631 183, 214 0.008644
(1 + λ)-CGP-IN 5000 1 0.3 – – 1.5 2 162, 874
†
110, 705 88, 534 145,333 196, 542 0.029721
(1 + λ)-CGP-DP/IN 5000 1 0.3 1.0 2 1.0 2 185, 788 163,019 98, 416 123, 169 210,512 0.109352
Adder 4-Bit
(1 + λ)-CGP 7000 1 0.3 – – – – 604, 729 471, 852 304, 067 473, 451 712, 748 –
F
(1 + λ)-CGP-DP 7000 1 0.3 5.0 1 – – 497, 716 298,933 334, 116 427,474 587, 760 0.330959
(1 + λ)-CGP-IN 7000 1 0.3 – – 4.0 1 459, 533
†
268, 773 288,186 374, 961 529,789 0.011349
(1 + λ)-CGP-DP/IN 7000 1 0.2 3.0 1 2.0 1 443, 801
†
292, 051 264,351 397, 726 545,033 0.035739
Subtractor 2-Bit
(1 + λ)-CGP 5000 1 0.6 – – – – 13,419 15, 619 5, 218 8, 995 15, 537 –
F
(1 + λ)-CGP-DP 5000 1 0.6 4.0 2 – – 9, 225
†
8, 218 3,967 6, 463 11, 093 0.010669
(1 + λ)-CGP-IN 5000 1 0.6 – – 7.0 2 10, 317
†
12, 996 4,395 6, 891 10, 617 0.024581
(1 + λ)-CGP-DP/IN 5000 1 0.6 4.0 2 1.0 2 10,477 10, 515 4, 451 6, 742 13, 262 0.069644
Adder/Subtr. 3-Bit
(1 + λ)-CGP 8500 1 0.3 – – – – 531,908 484, 390 300,633 422, 432 642,574 –
F
(1 + λ)-CGP-DP 8500 1 0.3 2.0 3 – – 452, 955 318,305 261, 270 359,154 526, 787 0.104550
(1 + λ)-CGP-IN 8500 1 0.3 – – 3.0 1 445, 812
†
303, 317 252,506 331, 591 507,720 0.044557
(1 + λ)-CGP-DP/IN 8500 1 0.3 2.0 1 3.0 1 444, 694 289,646 262, 952 346,882 519, 647 0.077479
Multiplier 2-Bit
(1 + λ)-CGP 4000 1 0.8 – – – – 8, 421 11, 306 3,945 5, 705 8, 814 –
F
(1 + λ)-CGP-DP 4000 1 0.8 10.0 1 – – 5, 224
‡
4, 598 2,825 4, 062 6, 241 0.000245
(1 + λ)-CGP-IN 4000 1 0.8 – – 10.0 2 5, 689
‡
5, 427 3, 027 4, 215 7, 025 0.005012
(1 + λ)-CGP-DP/IN 4000 1 0.8 10.0 1 2.0 1 5, 702
‡
4, 291 3, 004 4, 365 6, 662 0.007626
Multiplier 3-Bit
(1 + λ)-CGP 4000 1 0.3 – – – – 439,106 337, 382 229,458 317, 891 524,669 –
F
(1 + λ)-CGP-DP 4000 1 0.3 2.0 2 – – 346, 124
†
269, 190 193,182 282, 044 411,654 0.046687
(1 + λ)-CGP-IN 4000 1 0.3 – – 2.0 6 355, 625
†
240, 759 183,936 268, 791 470,502 0.023817
(1 + λ)-CGP-DP/IN 4000 1 0.3 2.0 2 1.0 5 361, 491 250,027 182, 755 293,246 462, 317 0.068831
Multiplier 4-Bit
(1 + λ)-CGP 8000 1 0.2 – – – – 89, 808, 385 19, 687, 510 89, 674, 939 100, 000,000 100, 000,000 –
F
⊕
(1 + λ)-CGP-DP 8000 1 0.2 2.0 1 – – 79, 153,688 25, 084, 937 65, 564, 659 94, 344, 994 100, 000, 000 0.078953
(1 + λ)-CGP-IN 8000 1 0.2 – – 1.0 2 86, 687,228 21, 810, 528 73, 410, 982 100, 000, 000 100, 000, 000 0.654324
(1 + λ)-CGP-DP/IN 8000 1 0.2 1.0 1 1.0 2 93, 499, 390 14, 98, 9673 100, 000, 000 100, 000,000 100, 000, 000 0.273819
DeMUX-1x8
(1 + λ)-CGP 5000 1 0.8 – – – – 30, 256 24, 829 16, 883 23, 553 34, 433 –
F
(1 + λ)-CGP-DP 5000 1 0.8 7.0 1 – – 19, 771
‡
11, 579 12, 074 17, 096 24, 473 0.000035
(1 + λ)-CGP-IN 5000 1 0.8 – – 7.0 3 21, 450
‡
13, 073 11, 914 18, 403 28, 081 0.001019
(1 + λ)-CGP-DP/IN 5000 1 0.8 5.0 2 5.0 3 20, 620
‡
12, 323 11, 974 18, 509 26, 172 0.000215
DeMUX-1x16
(1 + λ)-CGP 7000 1 0.5 – – – – 340,256 275, 806 159,293 252, 965 398,391 –
F
(1 + λ)-CGP-DP 7000 1 0.4 5.0 2 – – 273, 724
†
254, 154 116,691 186, 227 301,180 0.011269
(1 + λ)-CGP-IN 7000 1 0.4 – – 5.0 3 292, 079
†
265, 562 127,363 190, 456 366,133 0.047783
(1 + λ)-CGP-DP/IN 7000 1 0.4 5.0 3 1.0 3 259, 061
†
221, 916 131,296 193, 867 268,625 0.016808
Comparator 3x1-Bit
(1 + λ)-CGP 4000 1 0.6 – – – – 14, 734 11, 795 8,161 11, 005 18, 287 –
F
(1 + λ)-CGP-DP 4000 1 0.6 5.0 2 – – 10, 978
†
5, 011 7,043 9, 951 13, 796 0.049184
(1 + λ)-CGP-IN 4000 1 0.6 – – 3.0 2 11, 972
†
9, 196 6,369 10, 121 14, 628 0.044077
(1 + λ)-CGP-DP/IN 4000 1 0.6 1.0 2 1.0 2 11, 473
†
6, 194 6,908 9, 927 14, 541 0.027272
Comparator 4x1-Bit
(1 + λ)-CGP 6000 1 0.3 – – – – 80, 023 52, 598 49, 100 62, 841 89, 968 –
F
(1 + λ)-CGP-DP 6000 1 0.2 10.0 1 – – 64, 644
‡
45, 639 39, 321 55, 533 72, 831 0.008154
(1 + λ)-CGP-IN 6000 1 0.2 – – 7.0 4 68, 833
†
46, 017 39, 318 55, 320 86, 806 0.030281
(1 + λ)-CGP-DP/IN 6000 1 0.2 5.0 1 5.0 1 69, 710
‡
61, 338 37, 470 49, 211 71, 161 0.001747
Parity-Even 8-Bit
(1 + λ)-CGP 4000 1 0.5 – – – – 523,844 374, 044 289,856 419, 590 643,732 –
F
(1 + λ)-CGP-DP 4000 1 0.5 6.0 2 – – 438, 525
†
317, 747 233,748 362, 426 520,079 0.037735
(1 + λ)-CGP-IN 4000 1 0.5 – – 7.0 3 448, 418
†
371, 781 209,428 311, 644 591,727 0.019721
(1 + λ)-CGP-DP/IN 4000 1 0.5 4.0 2 3.0 3 474, 863 389,481 226, 027 362,221 577, 683 0.080760
Parity-Even 9-Bit
(1 + λ)-CGP 7000 1 0.3 – – – – 2, 706,718 2, 798, 332 1, 200, 713 1,803, 237 3, 367, 452 –
F
(1 + λ)-CGP-DP 7000 1 0.3 5.0 1 – – 2, 132, 412
†
2, 175,003 923, 679 1, 562,207 2,213, 686 0.018214
(1 + λ)-CGP-IN 7000 1 0.3 – – 2.0 3 2, 104, 790 1, 993,138 1, 006, 380 1, 532,286 2,390, 220 0.066980
(1 + λ)-CGP-DP/IN 7000 1 0.3 2.0 1 2.0 3 2, 226, 970
‡
2, 711,787 911, 135 1, 299,457 2,362, 052 0.007688
ALU 2-Bit
(1 + λ)-CGP 6000 1 0.3 – – – – 294,587 332, 068 126,606 192, 664 310,028 –
F
(1 + λ)-CGP-DP 6000 1 0.3 5.0 1 – – 233, 504 233,898 110, 430 159,325 264, 168 0.186220
(1 + λ)-CGP-IN 6000 1 0.3 – – 6.0 1 199, 940
†
154, 555 105,093 155, 823 237,044 0.031428
(1 + λ)-CGP-DP/IN 6000 1 0.3 4.0 1 2.0 1 236, 254 259,743 98, 382 171, 243 253,019 0.090671
ALU 3-Bit
(1 + λ)-CGP 8000 1 0.1 – – – – 1, 627,394 1, 743, 657 835,674 1,270, 141 1, 773,802 –
F
(1 + λ)-CGP-DP 8000 1 0.1 0.5 1 – – 1, 540, 866 1, 775,480 763, 535 1, 009,074 1,606, 575 0.121230
(1 + λ)-CGP-IN 8000 1 0.1 – – 0.6 1 1, 361, 882
†
1, 143,206 671, 365 1, 024,026 1,667, 233 0.048339
(1 + λ)-CGP-DP/IN 8000 1 0.1 0.2 1 0.2 1 1, 498, 320 1, 3224,62 753, 759 1, 160,890 1, 694, 086 0.368704
tion nodes after the backward search. However, run-
time studies are needed in the future to make more
significant statements.
8 CONCLUSIONS AND FUTURE
WORK
This work presented initial results of phenotypic du-
plication and inversion in CGP. The effectiveness of
these methods has been evaluated on a diverse set
of Boolean functions problems, covering single and
ECTA 2022 - 14th International Conference on Evolutionary Computation Theory and Applications
58
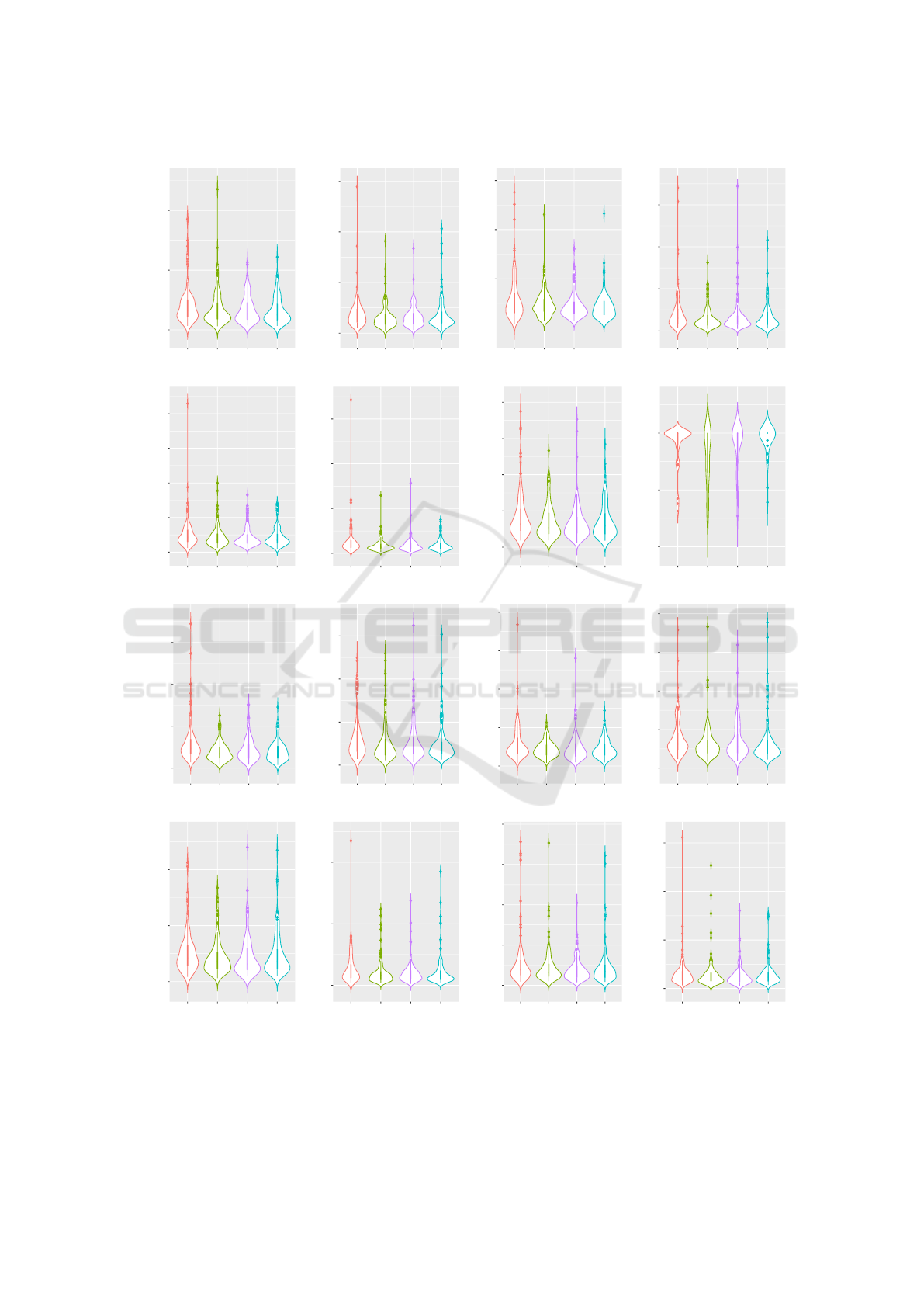
0e+00
1e+05
2e+05
1+λ 1+λ-DP 1+λ-IN 1+λ-DP-IN
Fitness Evaluations
Adder 2-Bit
0
500000
1000000
1500000
1+λ 1+λ-DP 1+λ-IN 1+λ-DP-IN
Adder 3-Bit
0e+00
1e+06
2e+06
3e+06
1+λ 1+λ-DP 1+λ-IN 1+λ-DP-IN
Adder 4-Bit
0
30000
60000
90000
1+λ 1+λ-DP 1+λ-IN 1+λ-DP-IN
Subtractor 2-Bit
0e+00
1e+06
2e+06
3e+06
4e+06
1+λ 1+λ-DP 1+λ-IN 1+λ-DP-IN
Fitness Evaluations
Adder-Subtractor 3-Bit
0
30000
60000
90000
1+λ 1+λ-DP 1+λ-IN 1+λ-DP-IN
Multiplier 2-Bit
0
500000
1000000
1500000
2000000
1+λ 1+λ-DP 1+λ-IN 1+λ-DP-IN
Multiplier 3-Bit
0e+00
5e+07
1e+08
1+λ 1+λ-DP 1+λ-IN 1+λ-DP-IN
Multiplier 4-Bit
0
50000
100000
150000
1+λ 1+λ-DP 1+λ-IN 1+λ-DP-IN
Fitness Evaluations
DeMUX-1x8
0
500000
1000000
1500000
1+λ 1+λ-DP 1+λ-IN 1+λ-DP-IN
DeMUX-1x16
0
25000
50000
75000
100000
1+λ 1+λ-DP 1+λ-IN 1+λ-DP-IN
Comparator 3x1-Bit
0e+00
1e+05
2e+05
3e+05
4e+05
1+λ 1+λ-DP 1+λ-IN 1+λ-DP-IN
Comparator 4x1-Bit
0e+00
1e+06
2e+06
1+λ 1+λ-DP 1+λ-IN 1+λ-DP-IN
Algorithm
Fitness Evaluations
Parity-Even 8-Bit
0e+00
1e+07
2e+07
1+λ 1+λ-DP 1+λ-IN 1+λ-DP-IN
Algorithm
Parity-Even 9-Bit
0
500000
1000000
1500000
2000000
1+λ 1+λ-DP 1+λ-IN 1+λ-DP-IN
Algorithm
ALU 2-Bit
0.0e+00
5.0e+06
1.0e+07
1.5e+07
1+λ 1+λ-DP 1+λ-IN 1+λ-DP-IN
Algorithm
ALU 3-Bit
Figure 5: Violin plots for all tested problems and algorithms of our experiments.
multiple output topologies as well as multi-function
problems. Overall, our results indicate that the use
of our proposed methods can be beneficial for learn-
ing Boolean functions. Since our experiments pri-
marily focused on the evaluation of the search per-
formance and ensuring fair conditions through meta-
Towards Phenotypic Duplication and Inversion in Cartesian Genetic Programming
59

optimization, the next step is to study and analyze our
methods with analytical experiments. Therefore, fu-
ture work will focus on phenotype space and semantic
analysis. Another part of our future work is devoted
to the development of self-adaptation mechanisms to
reduce parametrization and to increase effectiveness
further.
ACKNOWLEDGEMENTS
A large part of this work was carried out at the De-
partment of Computer Science of the Technical Uni-
versity Dortmund. We thank Paul Kaufmann from the
Westphalian University of Applied Sciences for pro-
viding the four bit digital adder and multiplier bench-
mark and sharing his empirical experience about the
complexity of both problems. We also thank Andre
Droschinksy, Marco Pleines and Fabian Ostermann
from the Technical University Dortmund for review-
ing the formalism and proofreading.
REFERENCES
Cramer, N. L. (1985). A representation for the adaptive
generation of simple sequential programs. In Grefen-
stette, J. J., editor, Proceedings of an International
Conference on Genetic Algorithms and the Applica-
tions, pages 183–187, Carnegie-Mellon University,
Pittsburgh, PA, USA.
Ebner, M. (2012). Evolving concepts using gene duplica-
tion. In Computational Modelling of Objects Repre-
sented in Images - Fundamentals, Methods and Appli-
cations III, Third International Symposium, CompIM-
AGE 2012, Rome, Italy, September 5-7, 2012, pages
69–74. CRC Press.
ˇ
Ceška, M., Matyáš, J., Mrázek, V., Sekanina, L., Vaší
ˇ
cek,
Z., and Vojnar, T. (2021). Sagtree: Towards effi-
cient mutation in evolutionary circuit approximation.
Swarm and Evolutionary Computation, page 100986.
Forsyth, R. (1981). BEAGLE a Darwinian approach to pat-
tern recognition. Kybernetes, 10(3):159–166.
Goldman, B. W. and Punch, W. F. (2013). Length bias and
search limitations in cartesian genetic programming.
In GECCO ’13: Proceeding of the fifteenth annual
conference on Genetic and evolutionary computation
conference, pages 933–940, Amsterdam, The Nether-
lands. ACM.
Goldman, B. W. and Punch, W. F. (2015). Analysis of
cartesian genetic programming’s evolutionary mech-
anisms. IEEE Trans. Evol. Comput., 19(3):359–373.
Hicklin, J. (1986). Application of the genetic algorithm to
automatic program generation. Master’s thesis, Uni-
versity of Idaho.
Hodan, D., Mrazek, V., and Vasicek, Z. (2020).
Semantically-oriented mutation operator in cartesian
genetic programming for evolutionary circuit design.
In Proceedings of the 2020 Genetic and Evolution-
ary Computation Conference, GECCO ’20, page
940–948, New York, NY, USA. Association for Com-
puting Machinery.
Holland, J., Mahajan, M., Kumar, S., and Porwal, R. (1975).
Adaptation in natural and artificial systems, the uni-
versity of michigan press, ann arbor, mi. 1975. In Ap-
plying genetic algorithm to increase the efficiency of a
data flow-based test data generation approach, pages
1–5.
Husa, J. and Kalkreuth, R. (2018). A comparative study
on crossover in cartesian genetic programming. In
Castelli, M., Sekanina, L., Zhang, M., Cagnoni, S.,
and Garcia-Sanchez, P., editors, EuroGP 2018: Pro-
ceedings of the 21st European Conference on Genetic
Programming, volume 10781 of LNCS, pages 203–
219, Parma, Italy. Springer Verlag.
Kalganova, T. (1997). Evolutionary approach to design
multiple-valued combinational circuits. In Proceed-
ings. of the 4th International conference on Applica-
tions of Computer Systems (ACS’97), pages 333–339,
Szczecin, Poland.
Kalkreuth, R. (2019). Two new mutation techniques for
cartesian genetic programming. In Guervós, J. J. M.,
Garibaldi, J. M., Linares-Barranco, A., Madani, K.,
and Warwick, K., editors, Proceedings of the 11th In-
ternational Joint Conference on Computational Intel-
ligence, IJCCI 2019, Vienna, Austria, September 17-
19, 2019, pages 82–92. ScitePress.
Kalkreuth, R. (2020). A comprehensive study on sub-
graph crossover in cartesian genetic programming. In
Guervós, J. J. M., Garibaldi, J. M., Wagner, C., Bäck,
T., Madani, K., and Warwick, K., editors, Proceedings
of the 12th International Joint Conference on Compu-
tational Intelligence, IJCCI 2020, Budapest, Hungary,
November 2-4, 2020, pages 59–70. SCITEPRESS.
Kalkreuth, R. (2021a). An Empirical Study on Insertion
and Deletion Mutation in Cartesian Genetic Program-
ming, pages 85–114. Springer International Publish-
ing, Cham.
Kalkreuth, R. (2021b). Reconsideration and extension of
Cartesian genetic programming. PhD thesis, Techni-
cal University of Dortmund, Germany.
Kalkreuth, R., Rudolph, G., and Droschinsky, A. (2017).
A new subgraph crossover for cartesian genetic pro-
gramming. In Castelli, M., McDermott, J., and Sekan-
ina, L., editors, EuroGP 2017: Proceedings of the
20th European Conference on Genetic Programming,
volume 10196 of LNCS, pages 294–310, Amsterdam.
Springer Verlag.
Kalkreuth, R. T. (2021c). Reconsideration and Extension of
Cartesian Genetic Programming. PhD thesis.
Kaufmann, P. and Kalkreuth, R. (2017). An empirical study
on the parametrization of cartesian genetic program-
ming. In Proceedings of the Genetic and Evolutionary
Computation Conference Companion, GECCO ’17,
pages 231–232, New York, NY, USA. ACM.
Koza, J. (1990). Genetic Programming: A paradigm for ge-
netically breeding populations of computer programs
ECTA 2022 - 14th International Conference on Evolutionary Computation Theory and Applications
60

to solve problems. Technical Report STAN-CS-90-
1314, Dept. of Computer Science, Stanford Univer-
sity.
Koza, J. R. (1992). Genetic Programming: On the Pro-
gramming of Computers by Means of Natural Selec-
tion. MIT Press, Cambridge, MA, USA.
Koza, J. R. (1994). Genetic Programming II: Automatic
Discovery of Reusable Programs. MIT Press, Cam-
bridge Massachusetts.
Larrañaga, P., Kuijpers, C. M. H., Murga, R. H., Inza, I.,
and Dizdarevic, S. (1999). Genetic algorithms for the
travelling salesman problem: A review of representa-
tions and operators. Artif. Intell. Rev., 13(2):129–170.
Manfrini, F. A. L., Bernardino, H. S., and Barbosa, H. J. C.
(2016). A novel efficient mutation for evolutionary de-
sign of combinational logic circuits. In Parallel Prob-
lem Solving from Nature - PPSN XIV - 14th Interna-
tional Conference, Edinburgh, UK, September 17-21,
2016, Proceedings, pages 665–674.
Mann, H. B. and Whitney, D. R. (1947). On a Test of
Whether one of Two Random Variables is Stochasti-
cally Larger than the Other. The Annals of Mathemat-
ical Statistics, 18(1):50 – 60.
McDermott, J., White, D. R., Luke, S., Manzoni, L.,
Castelli, M., Vanneschi, L., Jaskowski, W., Kraw-
iec, K., Harper, R., De Jong, K., and O’Reilly, U.-
M. (2012). Genetic programming needs better bench-
marks. In GECCO ’12: Proceedings of the fourteenth
international conference on Genetic and evolutionary
computation conference, pages 791–798, Philadel-
phia, Pennsylvania, USA. ACM.
Miller, J. F. (1999). An empirical study of the efficiency of
learning boolean functions using a cartesian genetic
programming approach. In Banzhaf, W., Daida, J.,
Eiben, A. E., Garzon, M. H., Honavar, V., Jakiela, M.,
and Smith, R. E., editors, Proceedings of the Genetic
and Evolutionary Computation Conference, volume 2,
pages 1135–1142, Orlando, Florida, USA. Morgan
Kaufmann.
Miller, J. F., Thomson, P., and Fogarty, T. (1997). Design-
ing electronic circuits using evolutionary algorithms.
arithmetic circuits: A case study. In Genetic Algo-
rithms and Evolution Strategies in Engineering and
Computer Science, pages 105–131. Wiley.
Scott, E. O. and Luke, S. (2019). ECJ at 20: toward a
general metaheuristics toolkit. In López-Ibáñez, M.,
Auger, A., and Stützle, T., editors, Proceedings of
the Genetic and Evolutionary Computation Confer-
ence Companion, GECCO 2019, Prague, Czech Re-
public, July 13-17, 2019, pages 1391–1398. ACM.
Sekanina, L. (2002). Image filter design with evolvable
hardware. In Applications of Evolutionary Comput-
ing, EvoWorkshops 2002: EvoCOP, EvoIASP, EvoS-
TIM/EvoPLAN, Kinsale, Ireland, April 3-4, 2002,
Proceedings, pages 255–266.
Turner, A. J. and Miller, J. F. (2013). Cartesian genetic
programming encoded artificial neural networks: a
comparison using three benchmarks. In GECCO ’13:
Proceeding of the fifteenth annual conference on Ge-
netic and evolutionary computation conference, pages
1005–1012, Amsterdam, The Netherlands. ACM.
White, D. R., McDermott, J., Castelli, M., Manzoni, L.,
Goldman, B. W., Kronberger, G., Jaskowski, W.,
O’Reilly, U.-M., and Luke, S. (2013). Better GP
Benchmarks: Community Survey Results and Propos-
als. Genetic Programming and Evolvable Machines,
14(1):3–29.
Towards Phenotypic Duplication and Inversion in Cartesian Genetic Programming
61
