Deep Learning of Structural Changes in Historical Buildings: The Case

Study of the Pisa Tower

Mario G. C. A. Cimino

1 a

, Federico A. Galatolo

1 b

, Marco Parola

1 c

Nicola Perilli

and Nunziante Squeglia

2 d

Dept. of Information Engineering, University of Pisa, 56122 Pisa, Italy

Dept. of Civil and Industrial Engineering, University of Pisa, 56122 Pisa, Italy

Keywords:

Structural Health Monitoring, Multi-sensor System, Transformer, LSTM, Leaning Tower of Pisa.

Abstract:

Structural health monitoring of buildings via agnostic approaches is a research challenge. However, due to the

recent advent of pervasive multi-sensor systems, historical data samples are still limited. Consequently, data-

driven methods are often unfeasible for long-term assessment. Nevertheless, some famous historical buildings

have been subject to monitoring for decades, before the development of smart sensors and Deep Learning

(DL). This paper presents a DL approach for the agnostic assessment of structural changes. The proposed

approach has been experimented to the stabilizing intervention carried out in 2000-2002 on the leaning tower

of Pisa (Italy). The data set is made by operational and environmental measures collected from 1993 to 2006.

Both conventional and recent approaches are compared: Multiple Linear regression, LSTM and Tansformer.

Experimental results are promising, and clearly shows a better change sensitivity of the LSTM, as well as a

better modeling accuracy of the Transformer.

1 INTRODUCTION

Structural health monitoring (SHM) plays an impor-

tant role in the diagnosis and evaluation of the sta-

bility and deformation of historical buildings. Over

the ages, such buildings have been subject to various

maintenance and renovations, using different materi-

als and construction techniques, leading to a complex

structural behavior.

Multi-sensor systems with high reliability and low

cost, small size and weight, low power consumption

and high rate data processing, are essential to SHM.

However, their pervasive application is still in its in-

fancy. As a consequence, long-term data are available

only for world famous historical buildings. For such

buildings, sensor systems gathering multiple parame-

ters for long time allow the experimentation of agnos-

tic techniques based on Deep Learning (DL) (Farrar

et al., 2006).

In the literature, according to the type of param-

eters acquired, SHM systems are classiﬁed into two

https://orcid.org/0000-0002-1031-1959

https://orcid.org/0000-0001-7193-3754

https://orcid.org/0000-0003-4871-4902

https://orcid.org/0000-0001-8104-503X

main categories: (i) static systems, which monitor the

temporal evolution of quantities that change slowly

over time (e.g., crack widths, wall slopes, relative dis-

tances, etc.) via periodic data sampling; (ii) dynamic

systems, which monitor dynamic parameters such as

velocities, accelerations, in order to gather informa-

tion on general dynamic properties such as natural

frequencies, mode shapes, and damping ratios.

Data pre-processing is also essential, because dif-

ferent sensing technologies can be employed over the

ages, as well as to distinguish any evolutionary trends

from seasonal and daily variations related to environ-

mental effects (Baraccani et al., 2017).

As a methodology of data analysis for SHM, DL

techniques have shown a signiﬁcant potential for their

capabilities of detecting implicit relationships in data,

by requiring less domain knowledge. Some DL archi-

tectures have been already experimented for speciﬁc

tasks on particular buildings (Mishra, 2021); e.g. a

convolutional architecture to solve the damage local-

ization task (Parola. et al., 2022). A relevant state-of-

the art review is provided in next section.

In this paper, the Transformer architecture is pro-

posed and compared with the Long-Short Term Mem-

ory (LSTM) for a speciﬁc SHM task. In the lit-

erature, it is well-known that a Transformer over-

396

Cimino, M., Galatolo, F., Parola, M., Perilli, N. and Squeglia, N.

Deep Learning of Structural Changes in Historical Buildings: The Case Study of the Pisa Tower.

DOI: 10.5220/0011551800003332

In Proceedings of the 14th International Joint Conference on Computational Intelligence (IJCCI 2022), pages 396-403

ISBN: 978-989-758-611-8; ISSN: 2184-3236

come an LSTM in the semantic capture of time-series

data. The different solutions are compared in order to

asses the structural changes in the Leaning Tower of

Pisa (Italy) (Burland et al., 2009), which has under-

gone many maintenance intervention over the epochs.

Speciﬁcally, the under-excavation intervention per-

formed between 2000 and 2001 is considered (Bur-

land et al., 2009) as a case study.

The SHM system installed on the Leaning Tower

of Pisa is a static system, with a conﬁgurable sam-

pling time period. Figure 1 shows some sensing sub-

systems installed inside the tower since 1993, deliver-

ing a synchronized Multivariate Time Series (MTS).

The data series hourly collected from 1993 to

2006, has been used for the assessment of the above

mentioned under-excavation effects, via both conven-

tional and recent approaches: Multiple Linear Regres-

sion, LSTM and Transformer.

The underlying strategy for the proposed approach

is to create a model of the structural behavior before

and after the maintenance intervention, exploiting the

large availability of data, via a general purpose pre-

processing, and without a knowledge-based supervi-

sion nor feature selection. This approach falls under

the regression task, whose goal is the agnostic model

of the relationship between input and output data. In

particular, prediction is a special type of regression

aimed to foresee the next values of a given time se-

ries. In the proposed approach, a multi input - multi

output prediction is considered.

(a)

(b)

(c)

Figure 1: Some sensing subsystems of the tower of Pisa:

(a) telecoordinometer - inclinometer and pendulum; (b) en-

vironmental parameters - wind speed and direction, solar

radiation and termometer; (c) deformometer.

Finally, the assessment of the structural change is

based on the differences in the prediction capability

of the model before and after the maintenance event.

Experimental results are promising, and clearly shows

the higher accuracy of Transformer, with respect to

LSTM and conventional Multi-Linear Regression, as

well as the better sensitivity of LSTM.

The paper is structured as follows. Section 2

presents an overview of the related works. Section

3 covers material and methods, whereas experimen-

tal results and discussions are covered by Section 4.

Finally, Section 5 draws conclusions and future work.

2 RELATED WORKS

A structural change of a building is measured via a

change of the materials and/or physical properties of

the structure. For example, an elastic material coef-

ﬁcient reduction and system connectivity, which ad-

versely affect the system’s current or future perfor-

mance (Farrar and Worden, 2007).

In the literature, the structural changes of a main-

tenance intervention can be detected via a two-phase

method: (a) to identify the stable key parameters of

a behavioral model of the structure, corresponding to

the periods before and after the intervention; (b) to

identify a persistent variation of such parameters by

comparing the two periods. The underlying idea is

that a change of behavior on the structure will occur

over time after the intervention in terms of deviation

from the condition before the intervention (Reynders

et al., 2014).

The main drawback of this approach is the knowl-

edge needed to set up a model, the key parameters,

and the baseline condition representing the state be-

fore the maintenance. A possible solution is to ex-

ploit multivariate clustering in feature space for the

identiﬁcation of the stable clusters/components that

describe the behavior of the structure (Figueiredo

et al., 2014). An alternative approach, requiring lit-

tle knowledge, is to exploit regression analysis, where

both environmental and operational properties are

taken into account to generate a predictive model of

the behavior before the maintenance, which can be

used for the behavior after the maintenance, in order

to assess a different deviation from the expected value

(Wah et al., 2021).

In this work, a regression-based approach is pro-

posed, by using the data provided by the multi-sensor

system in order to model the related Multivariate

Time Series (MTS). A MTS represents the evolution

of a group of variables partially independent. The pre-

diction of a MTS can be solved via a classical statis-

tical approach, such as an auto-regressive integrated

moving average method, which can be used to ana-

lyze the relationships between the different variables.

In the last decade, DL-based methods achieved

Deep Learning of Structural Changes in Historical Buildings: The Case Study of the Pisa Tower

397

widespread adoption, for their effectiveness. Dif-

ferent architectures have been experimented to solve

the MTS prediction problem, such as Recurrent Neu-

ral Network (RNN), Gated Recurrent Unit (GRU)

or Long short-term memory (LSTM). More recently,

Transformer have shown to perform better on both

synthetic and real datasets, due to their attention

mechanism (Li et al., 2019). In this research, both

conventional and recent approaches are compared:

Multiple Linear regression, LSTM and Tansformer.

3 MATERIALS AND METHODS

This section covers, on different subsections, the

multi-sensor system providing the MTS, the pre-

processing of the MTS samples, as well as the regres-

sion models adopted for MTS prediction.

3.1 Multi-sensor System and Data

Preprocessing

A complex system consisting of over 60 sensors is

available for the leaning tower of Pisa. In this re-

search, only a subsystem of sensors are considered to

address the structural change assessment occurred in

2000-2001. Such subsystem is deﬁned in Table 1: (i)

operational sensors, made of 25 deformometers and 2

telecoordinometers, which measure the physical con-

dition of the tower, such as rotations or displacements;

(ii) environmental sensors, which measure the exter-

nal conditions, such as temperature, wind, solar radia-

tion. Figure 2 shows the position on the tower of each

sensor. In particular, the most of the deformometers

(blue circles) are placed on the inclination side, on

bottom-right in ﬁgure, where the high load / stress is

located. Environmental sensors (yellow, red and pur-

ple circles) are placed on the top. Finally, the orange

long plumb wire of the telecoordinometer is clearly

visible in the middle.

Figure 3 and Figure 4 show a global plot over 13

years of the temperature and a deformometer time se-

ries. Series of samples related to very long periods

are normally affected by different artifacts: outliers,

missing samples, sensors re-calibration, sensors hard-

ware replacement/maintenance, and so on. As a con-

sequence, data preprocessing is of the utmost impor-

tance to avoid biases and false positives. Speciﬁcally,

outliers are due to electronic devices errors, which are

sometimes affected by sensor reading issues, resulting

in out-of-scale samples. On the other side, missing

data samples are due to hardware, power or network,

failures that sometimes occur. Finally, hardware re-

placement, maintenance and recalibration cause scal-

ing artifacts.

Figure 2: Multi-sensor system distribution on the tower, ac-

cording to the color legend in Table 1.

Figure 3: Global plot on 13 years of the temperature series.

Figure 4: Global plot on 13 years of a deformometer series.

The pre-processing pipeline is made by different

tasks:

1. out-of scale outliers detection, on the basis of

lower and upper thresholds;

2. z-score normalization, to reduce artifacts related

to scaling. Equations (1) shows the formula of the

z-score. Given a signal x = [x

, ..., x

], the nor-

malized signal z can be computed by subtracting

NCTA 2022 - 14th International Conference on Neural Computation Theory and Applications

398

from each element the mean value ¯µ

computed

on all elements as shown in Equation (2) and di-

viding by their standard deviation

as shown in

Equation (3);

3. statistical outliers detection, in which samples

having value of ±3 farther from the current mov-

ing average (window size, w=100) are selected;

4. outliers/ isolated missing samples reconstruction,

in which a linear interpolation between the near-

est neighbors is carried out for the outliers previ-

ously determined, and short sequences of consec-

utive missing samples (at most 4 elements). Long

sequences of missing values, e.g. due to device

failure, are not reconstructed at all.

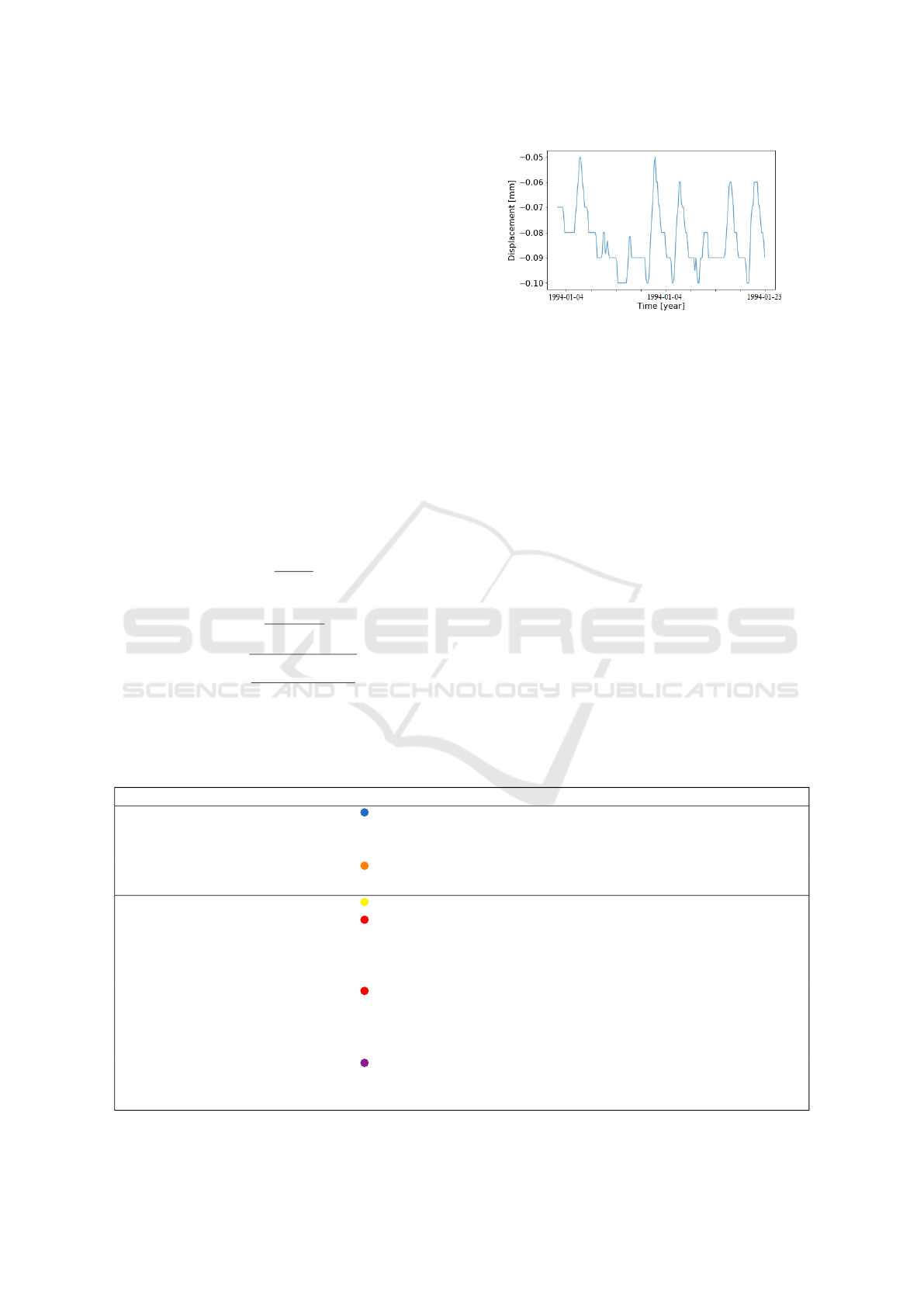
5. hourly data resampling. Figure 5 shows a two-

weeks plot of a deformometer time series. During

the considered period, as a consequence of main-

tenance, some changes in the frequency of device

reading activation occurred. To remove this type

of artifact, the entire time series is resampled with

one hour frequency.

− ¯µ

(1)

¯µ

∑

i−1

j=i−w

(2)

∑

i−1

j=i−w

− x

)

(3)

Figure 5: Two-weeks plot of a deformometer time series.

Figure 6 shows the distribution of samples for

each sensor in the considered period of observation,

separated in pre-maintenance (blue circles) and post-

maintenance (orange circles). Here, according to Ta-

ble 1, each sensor is identiﬁed by a letter and an in-

cremental number.

It is clear from the ﬁgure that the two distributions

highly overlap. As a consequence, statistical or data

mining approaches to structural change detection are

human knowledge driven. As a consequence, in this

paper, agnostic regression-based methodologies will

be applied and compared.

3.2 Multivariate Linear Regression

Model and Performance Metrics

In the proposed regression approach to structural

changes assessment three data sets are ﬁrst created:

1. pre-maintenance set (pre for short);

2. post-maintenance set (post);

3. pre- and post- maintenance (full).

Table 1: Subsystem of sensors installed on the leaning tower and used for the proposed research.

Sensor # Leg Thresholds Description

Deformometer (D) 25 [-0.5,0.5] mm Detects dimensional deformations of a struc-

ture subjected to mechanical or thermal

stresses.

Telecoordinometer (T) 2 [-2100,1800] ” Measures a small rotation by reading the posi-

tion of a plumb wire.

Termometer (TM) 1 [-10,42] °C Measures the atmospheric temperature.

Wind speed sensor (WS) 1 [0,45] m/s Measures wind speed; the wind drives the top

three wind cups to rotate, and the central axis

drives the sensing element to generate an output

used to calculate the wind speed.

Wind direction sensor (WD) 1 [0,360] degree Measure wind direction; it works through the

rotation of a wind vane arrow and transmits

its measurement information to the coaxial en-

coder board.

Solar radiation sensor (SR) 1 [0,1000] W/m

Measure broadband solar irradiance by detect-

ing the photons that impact a physical or chem-

ical device located within the instrument.

Deep Learning of Structural Changes in Historical Buildings: The Case Study of the Pisa Tower

399

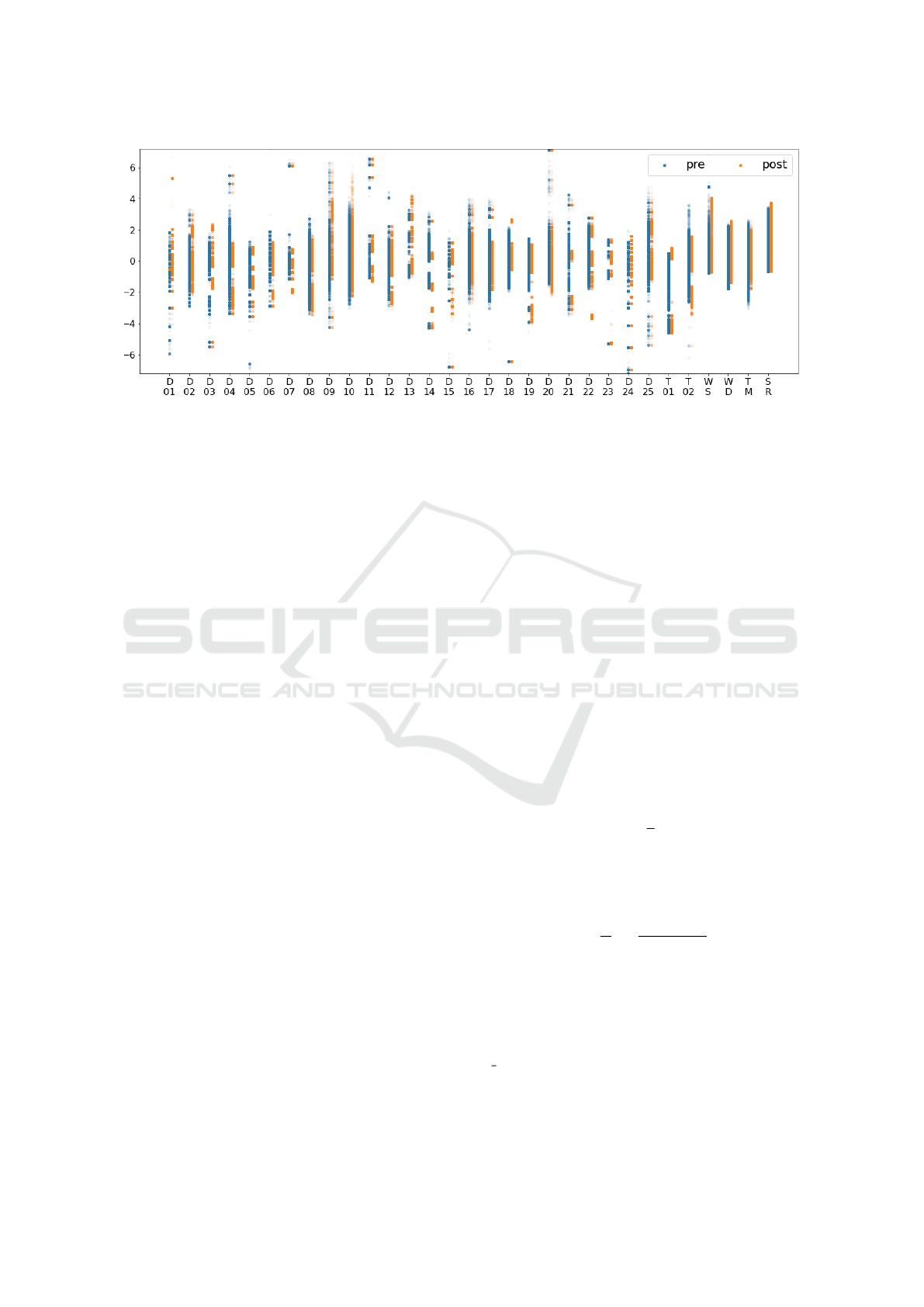
Figure 6: Values distribution (y-axis) for each separate sensor (x-asis), in the pre- and post- maintenance periods.

Speciﬁcally, the intervals of the pre, post and full

periods are, respectively: [Aug 1st, 1993 - Aug 31,

1999], [Jan 01, 2002 - Jun 30, 2006], [Jan, 08, 1993 -

June 30, 2006]. Then, three different prediction mod-

els are generated, using related subsets of the pre, post

and full sets, respectively, for training. Subsequently,

the generated models are tested on other subsets of

the pre, post and full sets.

Since a predictive model can be tested only on

future samples, there are four possible experiments

based on a combination of train and test sets: (a) full-

full; (b) pre-pre; (c) post-post; (d) pre-post.

Finally, the structural change assessment is carried

out by evaluating the difference in test performance

between the four experiments: roughly speaking, if

the test error is higher for the pre-post experiment

with respect to the other experiments, it means that

the model generated in the pre-maintenance period is

unable to accurately predict the behavior in the post-

maintenance period; and then, a structural change has

occurred between pre and post periods; otherwise, if

the error for the pre-post experiment is similar to the

others, no structural change has occurred.

More formally, let us consider a set of n synchro-

nized time series, X(t) = {X

(t) : j = 1, ..., n}, where

(t) is a time series of length m, X

(t) = {x

(t) : j =

1, ..., n; t = 1, ..., m}. An MTS predictive model takes

as an input a time window w extracted from the series,

(

t) = {x

w j

(t) : j = 1, ..., n; t =

t, ...,

t +w}, and pre-

dicts the next sample as an output The model can be

formally described by a function f : R

n×m

→ R

n×m

f (X

(

t)) = X

(

t + 1) (4)

where X

(

t + 1) = {x

w j

(t) : j = 1, ..., n; t =

t +

1, ...,

t + w + 1}.

A conventional machine learning method to per-

form this task is to calculate a Multivariate Linear

Regression, whose training is based on coefﬁcients

i j

and β

that are determined with n+1 equations, by

minimizing the error function via partial derivatives:

w j

(

t + 1) =

∑

j=1

∑

i j

w j

(i) + β

w j

(

t + 2) =

∑

j=1

t+1

∑

i j

w j

(i) + β

...

w j

(

t + w + 1) =

∑

j=1

t+w

∑

i j

w j

(i) + β

(5)

Given the set S of time series of length m, each

related to n sensors, in order to evaluate the model

error, trained and tested on related sets Tr ∈ S

and T s ∈ S, the overall forecasting performance is

measured via the Mean Relative Percent Difference,

MRPD(Tr; T s), i.e., the mean value of the Rela-

tive Percent Differences of each sensor (Botchkarev,

2018):

MRPD

(Tr; T s) =

∑

s∈S

RPD

(Tr; T s) (6)

The Relative Percent Difference between two values

is the absolute difference between the two values di-

vided by their absolute mean:

RPD

(Tr; T s) =

∑

k=1

− ¯y

| + | ¯y

; y

∈ T s

(7)

The aggregation in Formula (6) of different types

of sensors via the mean operator can be done under

the assumptions that the data follow a Gaussian dis-

tribution and are also normalized. For the data sets

used in this paper, this assumption is veriﬁed via a

Q Q plot, and via the z-score normalization applied

in the pre-processing phase, respectively.

Finally, by having the accuracy values of the pre-

dictive models via MRPD

(Tr; T s) on the test dataset,

NCTA 2022 - 14th International Conference on Neural Computation Theory and Applications

400

the following metric of structural change assessment

(SCA) can be derived:

SCA

(pre; post) =

2 · MRPD

(pre; post)

MRPD

(pre; pre)· MRPD

(post; post)

(8)

Assuming a good accuracy of the model on the

same period, the larger SCA is, the more the structural

behavior change assessment between pre and post pe-

riods is larger. Because if the model of the pre period

does not ﬁt the post period, the difference at the nu-

merator in Formula (8) is large with respect to the ac-

curacy at the denominator. In contrast, a small value

of the metric corresponds to a low structural change

assessment.

3.3 Deep Learning Models

Two DL models have been experimented to perform

the MTS regression task: (i) a Long-Short Term

Memory (LSTM) neural network, and (ii) a Trans-

former. The hyperparameters of the two models have

been set via grid-search, with intervals established to

keep a good accuracy and convergence. Table 2 and

Table 3 summarizes the search space and the optimal

values for each hyperparameter.

Table 2: LSTM hyperparameters optimization.

Hyperparameters

Search space Optimum

Layers [1,2,3] 2

Units [32,64,128, 256] 128

Linear layer - 31

Table 3: Transformer hyperparameters optimization.

Hyperparameters

Search space Optimum

Embedding type - Abs pos enc

Attention Head [4,5,6,7,8] 6

Layers per Head [5,6,7,8,9] 8

Neurons per layer [32,64,128] 128

In terms of parametric complexity, the Multivari-

ate Linear Regression (MLR) deﬁned in the previ-

ous section has 70 thousand trainable parameters. An

LSTM model is designed to overcome the explod-

ing/vanishing gradient problems that typically occur

when using too many layers (Van Houdt et al., 2020).

A common LSTM unit is composed of a cell that

remembers values over arbitrary time intervals and

three gate: an input gate, an output gate and a for-

get gate, which regulate the ﬂow of information into

and out of the cell. To model long-short term rela-

tionships, LSTM have a fairly complex internal struc-

ture, although it has been shown that similar but sim-

pler networks can achieve similar performance (Gala-

tolo et al., 2018). The LSTM architecture used has

210 thousand trainable parameters. Finally, a Causal

Transformer is a DL architecture that does not pro-

cess data in an ordered sequence, but analyzes the

entire sequence of data and exploits a self-attention

mechanisms to learn dependencies in the sequence,

achieving the potential of modeling complex dynam-

ics of time series (Vaswani et al., 2017). The Trans-

former architecture signiﬁcantly exceeds the other ar-

chitectures in terms of number of trainable parame-

ters: about 2.5 million.

The training process of both LSTM and Trans-

former has been performed for 2500 epochs, with

batch size 32, by setting the Adaptive Moment Es-

timation (Adam) as optimization algorithm to itera-

tively update the network weights.

4 EXPERIMENTAL RESULTS

The methodology has been developed on a python

open-source environment, which has been publicly

released (Galatolo, 2022), to foster collaboration and

application on various infrastructures. This section

summarizes and discusses the experimental results

achieved with the three considered architectures. To

this aim, Table 4 illustrates the results of the predic-

tion models. In particular, the MRPD is computed

aggregating each type of operational sensor (average

± standard deviation): 25 Deformometers (D*) or 2

Telecoordinometer (T*). Envirnomental sensors are

not considered as an output because they are not re-

lated to structural changes but to environmental vari-

ations.

Let us consider test performance, i.e.,

MRPD

D∗

test and MRPD

T ∗

test columns. In par-

ticular, let us focus on the values represented in

boldface style, i.e., the test performance on pre

and post sets for train and test, respectively. It can

be clearly observed that DL models, i.e., LSTM

and TRANS, perform better than MLR in pre-post

prediction, with LSTM model achieving the highest

score (.814 and 1.407). Furthermore, DL models are

more accurate in pre-pre and post-post prediction,

by having a lower score, especially TRANS model

(.256, .324 and .119, .145). Overall, TRANS is the

most accurate model whereas LSTM is the most

sensitive model to structural changes.

In order to analyze the contribution of each sen-

sor to the result, in Figure 7, the RPD value with

the related standard deviation on test set is repre-

sented, as a coloured circle with a vertical line, re-

spectively, for each DL model. Here, a horizontal red

line represents the MRPD already calculated in Table

Deep Learning of Structural Changes in Historical Buildings: The Case Study of the Pisa Tower

401

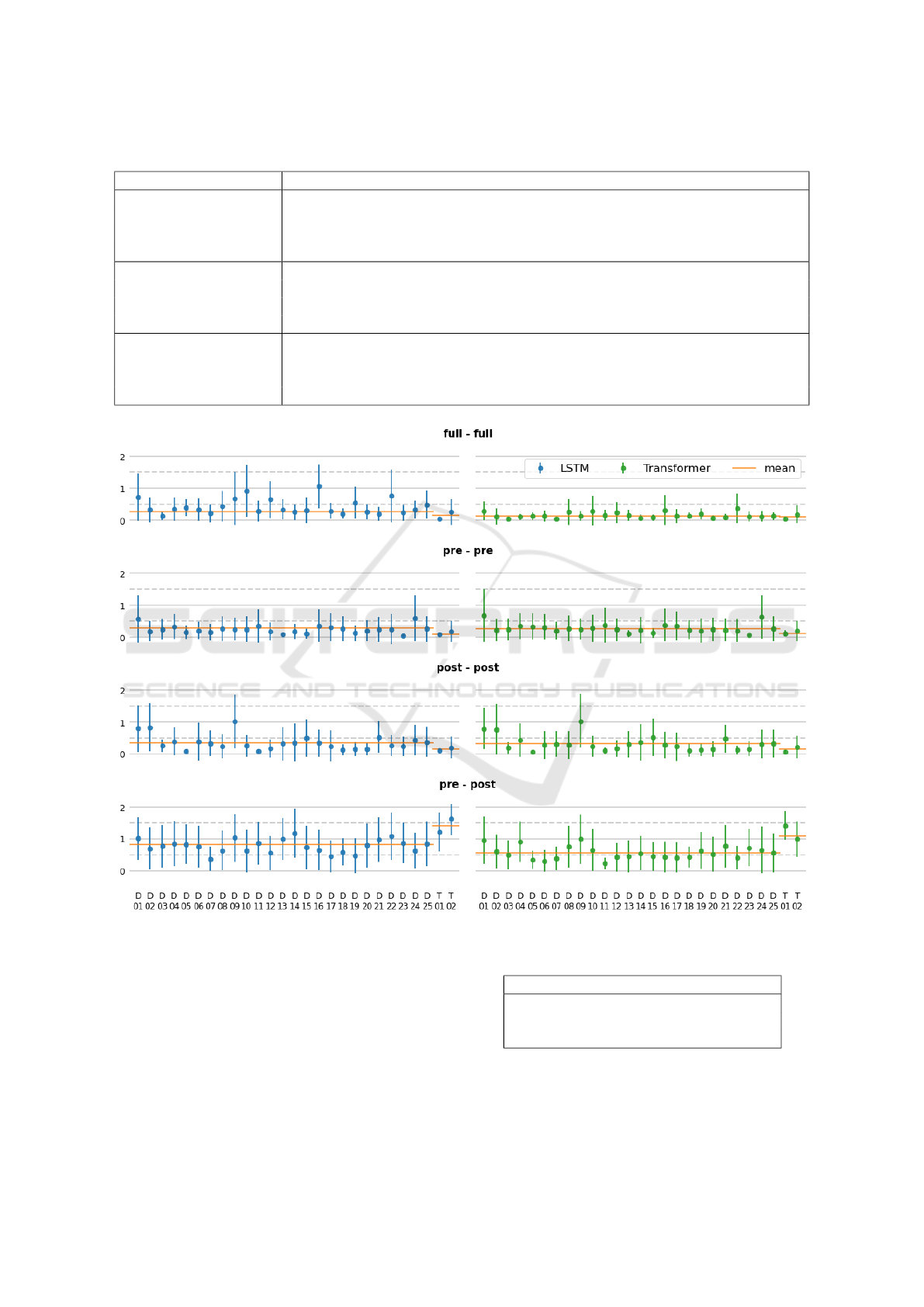
Table 4: MRPD on train and test set, for different models, using Deformometers (D*) or Telecoordinometers (T*) time series.

Model Train Test MRPD

D∗

train MRPD

D∗

test MRPD

T ∗

train MRPD

T ∗

test

MLR full full .234 ±.0081 .221 ±.0065 .276 ±.0068 .398 ±.0068

” pre pre .406 ±.0117 .435 ±.0114 .378 ±.0076 .277 ±.0072

” post post .393 ±.103 .434 ±.0118 .257 ±.0057 .212 ±.0041

” pre post .406 ±.0117 .522 ±.0122 .378 ±.0076 .605 ±.0161

TRANS full full .124 ±.0052 .141 ±.0050 .055 ±.0032 .112 ±.0038

” pre pre .219 ±.0077 .256 ±.0095 .070 ±.0032 .119 ±.0041

” post post .265 ±.0089 .324 ±.0096 .109 ±.0046 .145 ±.0044

” pre post .219 ±.0077 .573 ±.0125 .070 ±.0032 1.077 ±.0130

LSTM full full .113 ±.0051 .253 ±.0062 .045 ±.003 .144 ±.0010

” pre pre .230 ±.0086 .277 ±.0091 .091 ±.0040 .146 ±.0054

” post post .272 ±.0097 .356 ±.0103 .122 ±.0050 .151 ±.0045

” pre post .230 ±.0086 .814 ±.0149 .091 ±.0040 1.407 ±.0144

Figure 7: RPD values with the related standard deviation on test set, for each DL model and for each sensor.

4. Here, it can be clearly observed that the LSTM

model achieves better performance (i.e., larger RPD)

than Transformer on the pre-post test.

Finally, in Table 5, for each model, the

SCA

D∗,T ∗

(pre; post) is computed, i.e. aggregating

the contribution of both Deformometers and Teleco-

ordinometers. Not surprisingly, it can be clearly ob-

served that overall the most senstitive model to struc-

tural changes is LSTM, followed by the Transformer.

Table 5: SCA

D∗,T ∗

(pre; post) for each model.

Model SCA

D∗,T ∗

(pre; post)

MLR 1.20

TRANS 2.13

LSTM 2.86

NCTA 2022 - 14th International Conference on Neural Computation Theory and Applications

402

5 CONCLUSIONS

In this work, Deep Learning models for assessing

structural changes in historical buildings have been

compared, using a regression-based approach. As a

case study, a multi-sensors data set related to the mon-

itoring of the leaning Tower of Pisa from 1993 to 2006

has been used, for assessing a stabilizing intervention

of 2000-2002. First, a data preprocessing pipeline has

been developed and discussed. Then, the Multivari-

ate Linear Regression, the LSTM and the Transformer

models have been developed, together with modeling

accuracy and change sensitivity metrics.

Although a more in-depth exploration of the ap-

proaches, and an enrichment of the case studies are

needed, the experimental results are promising. In

particular, the LSTM model has proved to be more

sensitive to structural changes, whereas the Trans-

former model is more accurate in modeling. An ex-

tensive study in this direction can be a future work to

bring a contribution in the ﬁeld.

ACKNOWLEDGEMENTS

Work partially supported by (i) the Tuscany Region

in the framework of the ”SecureB2C” project, POR

FESR 2014-2020, Law Decree 7429 31.05.2017;

(ii) the Italian Ministry of University and Research

(MUR), in the framework of the ”Reasoning” project,

PRIN 2020 LS Programme, Law Decree 2493 04-11-

2021; and (iii) the Italian Ministry of Education and

Research (MIUR) in the framework of the CrossLab

project (Departments of Excellence).

REFERENCES

Baraccani, S., Palermo, M., Azzara, R. M., Gasparini, G.,

Silvestri, S., and Trombetti, T. (2017). Structural in-

terpretation of data from static and dynamic structural

health monitoring of monumental buildings. In Key

Engineering Materials, volume 747, pages 431–439.

Trans Tech Publ.

Botchkarev, A. (2018). Performance metrics (error mea-

sures) in machine learning regression, forecasting and

prognostics: Properties and typology. arXiv preprint

arXiv:1809.03006.

Burland, J. B., Jamiolkowski, M. B., and Viggiani, C.

(2009). Leaning tower of pisa: behaviour after sta-

bilization operations. ISSMGE International Journal

of Geoengineering Case Histories, 1(3):156–169.

Farrar, C. R., Park, G., Allen, D. W., and Todd, M. D.

(2006). Sensor network paradigms for structural

health monitoring. Structural Control and Health

Monitoring: The Ofﬁcial Journal of the International

Association for Structural Control and Monitoring

and of the European Association for the Control of

Structures, 13(1):210–225.

Farrar, C. R. and Worden, K. (2007). An introduction to

structural health monitoring. Philosophical Transac-

tions of the Royal Society A: Mathematical, Physical

and Engineering Sciences, 365(1851):303–315.

Figueiredo, E., Radu, L., Worden, K., and Farrar, C. R.

(2014). A bayesian approach based on a markov-chain

monte carlo method for damage detection under un-

known sources of variability. Engineering Structures,

80:1–10.

Galatolo, F. A. (2022). Github ncta2022 repository,

https://github.com/galatolofederico/ncta2022.

Galatolo, F. A., Cimino, M. G. C. A., and Vaglini, G.

(2018). Using stigmergy to incorporate the time into

artiﬁcial neural networks. In Groza, A. and Prasath,

R., editors, Mining Intelligence and Knowledge Ex-

ploration, pages 248–258, Cham. Springer Interna-

tional Publishing.

Li, S., Jin, X., Xuan, Y., Zhou, X., Chen, W., Wang, Y.-X.,

and Yan, X. (2019). Enhancing the locality and break-

ing the memory bottleneck of transformer on time se-

ries forecasting. Advances in Neural Information Pro-

cessing Systems, 32.

Mishra, M. (2021). Machine learning techniques for struc-

tural health monitoring of heritage buildings: A state-

of-the-art review and case studies. Journal of Cultural

Heritage, 47:227–245.

Parola., M., Galatolo., F., Torzoni., M., Cimino., M., and

Vaglini., G. (2022). Structural damage localization

via deep learning and iot enabled digital twin. In Pro-

ceedings of the 3rd International Conference on Deep

Learning Theory and Applications - DeLTA,, pages

199–206. INSTICC, SciTePress.

Reynders, E., Wursten, G., and De Roeck, G. (2014).

Output-only structural health monitoring in chang-

ing environmental conditions by means of nonlinear

system identiﬁcation. Structural Health Monitoring,

13(1):82–93.

Van Houdt, G., Mosquera, C., and N

apoles, G. (2020). A

review on the long short-term memory model. Artiﬁ-

cial Intelligence Review, 53(8):5929–5955.

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones,

L., Gomez, A. N., Kaiser, Ł., and Polosukhin, I.

(2017). Attention is all you need. Advances in neural

information processing systems, 30.

Wah, W. S. L., Chen, Y.-T., and Owen, J. S. (2021).

A regression-based damage detection method for

structures subjected to changing environmental and

operational conditions. Engineering Structures,

228:111462.

Deep Learning of Structural Changes in Historical Buildings: The Case Study of the Pisa Tower

403