A Multi-stage Multi-group Classification Model: Applications

to Knowledge Discovery for Evidence-based Patient-centered Care

Eva K. Lee

1,2 a

and Brent Egan

3,4 b

Center for Operations Research in Medicine and Healthcare, The Data and Analytic Innovation Institute, Atlanta, U.S.A.

Georgia Institute of Technology, Atlanta, U.S.A.

American Medical Association, Chicago, U.S.A.

Medical University of South Carolina, U.S.A.

Keywords: Multi-stage Classification, Multi-group Classification, Imbalanced Data, Discriminant Analysis via Mixed

Integer Program, Cardiovascular Disease, Multi-Site Knowledge Discovery, Best Practice, Alzheimer’s

Disease, Mild Cognitive Impairment, Early Diagnosis of Dementia, Machine Learning for Evidence-based

Practice, Branch-and-Bound.

Abstract: We present a multi-stage, multi-group classification framework that incorporates discriminant analysis via

mixed integer programming (DAMIP) with an exact combinatorial branch-and-bound (BB) algorithm and a

fast particle swarm optimization (PSO) for feature selection for classification. By utilizing a reserved

judgment region, DAMIP allows the classifier to delay making decisions on ‘difficult-to-classify’

observations and develop new classification rules in a later stage. Such a design works well for mixed (poorly

separated) data that are difficult to classify without committing a high percentage of misclassification errors.

We also establish variant DAMIP models that enable problem-specific fine tuning to establish proper

misclassification limits and reserved judgement levels that facilitate efficient management of imbalanced

groups. This ensures that minority groups with relatively few entities are treated equally as the majority

groups. We apply the framework to two real-life medical problems: (a) multi-site treatment outcome

prediction for best practice discovery in cardiovascular disease, and (b) early disease diagnosis in predicting

subjects into normal cognition, mild cognitive impairment, and Alzheimer’s disease groups using

neuropsychological tests and blood plasma biomarkers. Both problems involve poorly separated data and

imbalanced groups in which traditional classifiers yield low prediction accuracy. The multi-stage BB-

PSO/DAMIP manages the poorly separable imbalanced data well and returns interpretable predictive results

with over 80% blind prediction accuracy. Mathematically, DAMIP is NP-complete with its classifier proven

to be universally strongly consistent. Hence, DAMIP has desirable solution characteristics for machine

learning purposes. Computationally, DAMIP is the first multi-group, multi-stage classification model that

simultaneously includes a reserved judgment capability and the ability to constrain misclassification rates

within a single model. The formulation includes constraints that transform the features from their original

space to the group space, serving as a dimension reduction mechanism.

1 INTRODUCTION

Machine learning, using existing electronic medical

records (EMRs) (Lee et al., 2016; Rose, 2018) and

prospectively-collected population health data from

research programs, can identify patterns that predict

outcomes and potentially inform and improve clinical

care. However, most of these strategies must

compromise on data quality (e.g., the amount of

https://orcid.org/0000-0003-0415-4640

https://orcid.org/0000-0002-1470-5875

missing data from frontline workers and their

imputation by analysts) or breadth (the number of

examined parameters with acceptable missingness)

(Marlin et al., 2011; McDermott et al., 2018; Mohan

et al., 2013). While practice variances may occur

when and if tests are given to patients, missing data

may also reflect access and societal bias (Rajkomar et

al., 2018). Hence, understanding missingness and

certain actions and decisions and their dependencies

Lee, E. and Egan, B.

A Multi-stage Multi-group Classiﬁcation Model: Applications to Knowledge Discovery for Evidence-based Patient-centered Care.

DOI: 10.5220/0011557200003335

In Proceedings of the 14th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2022) - Volume 1: KDIR, pages 95-108

ISBN: 978-989-758-614-9; ISSN: 2184-3228

are critical. Since outcome can be defined and

interpreted differently among stakeholders, objective

outcome discovery is essential. Advances must be

made to accommodate heterogeneous data sources as

it facilitates the creation of a reliable outcome profile

(Lee et al., 2016, 2019; Lee, Yuan, et al., 2012;

Suresh et al., 2017).

Temporal data mining of longitudinal health data

cannot currently be achieved through statistically and

computationally efficient methodologies and is still

under-explored (Lee et al., 2019, 2021). This is a

particularly important issue when analyzing outcome,

health equity, and health conditions for patients with

chronic disease. To accommodate evolving data and

outcome trends, models must also be dynamic and

adaptable. Google Flu Trends’ overestimate

demonstrates this key modeling weakness (Lazer et

al., 2014). To ensure a model is robust, reliable, and

generalizable, independent multiple data sources

should be used to both train the model and to

independently validate its results (Ghassemi et al.,

2020). The model must also be able to be interpreted

by a diverse group of stakeholders for feedback and

refinement purposes.

We present a multi-stage, multi-group

classification framework that incorporates

discriminant analysis via mixed integer programming

(DAMIP) with an exact combinatorial branch-and-

bound (BB) algorithm and a fast particle swarm

optimization (PSO) for feature selection for

classification. By utilizing a reserved judgment

region, DAMIP allows the classifier to delay making

decisions on ‘difficult-to-classify’ observations and

develop new classification rules in a later stage. Such

a design works well for mixed (poorly separated) data

that are difficult to classify without committing a high

percentage of misclassification errors. We also

establish variant DAMIP models that enable

problem-specific fine tuning to establish proper

misclassification limits and reserved judgement

levels that facilitate efficient management of

imbalanced groups. This ensures that minority groups

with relatively few entities are treated equally as the

majority groups.

We apply the framework to two real-life

medical problems: (a) multi-site treatment outcome

prediction for best practice discovery in

cardiovascular disease and (b) early disease diagnosis

in predicting subjects into normal cognition, mild

cognitive impairment, and Alzheimer’s disease

groups using neuropsychological tests and blood

plasma biomarkers. Both medical problems involve

poorly separated data and imbalanced groups in

which traditional classifiers yield low prediction

accuracy. The multi-stage, BB-PSO/DAMIP

manages the poorly separable imbalanced data well

and returns interpretable predictive results with over

80% blind prediction accuracy.

Mathematically, DAMIP is 𝒩𝒫 − 𝑐𝑜𝑚𝑝𝑙𝑒𝑡𝑒

with its classifier proven to be universally strongly

consistent. Hence DAMIP has desirable solution

characteristics for machine learning purposes.

Computationally, DAMIP is the first multi-group

multi-stage classification model that simultaneously

includes a reserved judgment capability and the

ability to constrain misclassification rates within a

single model. The formulation includes constraints

that transform the features from their original space

to the group space, serving as a dimension reduction

mechanism.

2 DESIGN OF CLASSIFICATION

MODELS

Classification is a fundamental machine learning

problem of identifying the group status of new

observations, based on a set of observations of which

the group memberships are known. This technology

has wide-spread applications including marketing

and consumer sectors, agriculture, energy, finance,

psychology and behaviour science, social science,

criminology, electronics, internet-of-things, biology,

and healthcare, etc. (Cui et al., 2018; Dixon et al.,

2020; Hayward & Maas, 2021; Lei et al., 2020;

Myszczynska et al., 2020; Narciso & Martins, 2020;

Qu et al., 2019; Yarkoni & Westfall, 2017; Zhao et

al., 2021).

2.1 Multi-stage Multi-group

Classification Model

2.1.1 Discriminant Analysis via Mixed

Integer Program (DAMIP)

Let 𝜋



be the prior probability of group 𝑔 and 𝑓



(𝒙)

be the conditional probability density function of

group 𝑔, 𝑔∈ 𝒢 for the data point 𝒙∈ℝ



. Let 𝒪



denote the set of observations in group g, and 𝑛



denote the number of observations in group g ∈𝒢.

Let 𝛼



∈ (0, 1) , h, 𝑔∈𝒢 , ℎ≠𝑔 be the

predetermined limit on the misclassifications where

the observations of group 𝑔 are classified to group h.

The group assignment decisions of observations that

are classified into a reserved judgment region are

denoted by group g = 0. Let 𝑢



represent the binary

variable that indicates whether observation i in group

g is classified to group h, ℎ∈





∪𝒢. Thus, 𝑢



KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval

1 denotes a correct classification for observation i in

group g. The multi-group model with a reserved

judgement region is formulated as:

max   𝑢



∈𝒪



 ∈ 𝒢

subject to

𝐿



= 𝜋



𝑓



𝒙



−

∑

𝜆



𝑓



𝒙





∈𝒢,

, ∀ ℎ,𝑔 ∈ 𝒢,𝑗 ∈ 𝒪



(1)

𝑦



−𝐿



≤𝑀1−𝑢



, ∀ ℎ, 𝑔 ∈ 𝒢, 𝑗 ∈ 𝒪



(2)

𝑦



≤𝑀1−𝑢



, ∀ 𝑔 ∈ 𝒢, 𝑗 ∈ 𝒪



(3)

𝑦



−𝐿



≥𝜀1−𝑢



, ∀ ℎ, 𝑔 ∈ 𝒢, 𝑗 ∈ 𝒪



(4)

𝑦



≥𝜀 𝑢

,

∀ ℎ,𝑔 ∈ 𝒢, 𝑗 ∈ 𝒪



(5)

∑

𝑢

∈







∪𝒢

= 1, ∀ 𝑔 ∈ 𝒢, 𝑗 ∈ 𝒪



(6)

∑

𝑢

∈𝒪



≤𝛼



𝑛



, ∀ ℎ,𝑔 ∈ 𝒢,𝑔 ≠ ℎ (7)

𝑢



∈



0,1



∀ ℎ ∈





∪𝒢,𝑔∈𝒢,𝑗∈𝒪



(8)

𝑦



≥ 0, ∀ ℎ,𝑔 ∈ 𝒢, 𝑗 ∈ 𝒪



(9)

𝜆



≥ 0 ∀ ℎ, 𝑔 ∈ 𝒢,𝑔 ≠ ℎ (10)

Constraints (1) define the loss functions,

constraints (2)-(6) guarantee an observation is

uniquely assigned to the group with the maximum

value of 𝐿



(

𝒙

)

among all groups, and constraints (7)

set the misclassification limits. With the reserved

judgment region in place, the mathematical system

ensures that a solution that satisfies the preset errors

always exists.

2.1.2 Feature Selection via Particle Swarm

Optimization

Feature selection removes redundancy and selects

discriminatory features that can predict group status.

It can (a) improve the prediction performance, (b)

reduce over-fitting, (c) provide a faster predictor, and

(d) improve model interpretability.

There are three main categories of feature

selection algorithms: wrappers, filters, and embedded

methods. Wrapper methods use a search algorithm to

search through the space of features and evaluate the

subsets by running the classification models on them.

Filter methods are similar to wrapper methods, but

instead of evaluating by the classification models, a

simple filter that is independent of the classification

models is evaluated. Many filter methods provide a

feature ranking rather than the best subsets, where top

ranking features can be used in classification models.

Embedded feature selection algorithms (e.g., Lasso

and LAR (Efron et al., 2004; Tibshirani, 2011)) are

built in the classifier during the model construction.

Combinatorically, feature selection is intrinsically

𝒩𝒫 − ℎ𝑎𝑟𝑑 as there are exponential choices to

select among a given set of features. Numerous

algorithms and some of the earliest work including

branch-and-bound (Hocking & Leslie, 1967;

Tibshirani, 2011), greedy procedure and sequential

search (Pudil et al., 1994; Silva & Stam, 1994), and

random search (Siedlecki & Sklansky, 1989) have

been widely studied.

PSO (both continuous and binary) was originally

proposed by Kennedy and Eberhart (Kennedy &

Eberhart, 1997). Because of its computational speed,

numerous variant PSO-based algorithms have been

proposed for feature selection (Agrafiotis & Cedeño,

2002; Correa et al., 2006; Y. Hu et al., 2021; Jain et

al., 2018; Monteiro & Kosugi, 2007).

A Fast Modified PSO: We design a modified

PSO algorithm to solve the feature selection

algorithm where the number of selected features is

determined. We implement a PSO/DAMIP

framework that uses the modified PSO algorithm for

feature selection and the DAMIP model for

classification. For particle i, let 𝒗



denote the velocity

and 𝒙



represent a binary vector of length m, where m

is the number of features. Let 𝑥



denote whether the

jth feature is selected in particle i. In each iteration of

the modified PSO algorithm, a DAMIP model is

solved using the selected features in each particle.

Particle i records the current selected features 𝒙



and

the best achieved objective function value of DAMIP

thus far is denoted by 𝑦



. Then 𝒗



and 𝒙



in the next

iteration is determined by a random combination of

𝒗



, 𝒙



, 𝒑



, and 𝒑



(



)

in the current iteration where

𝑛

(

𝑖

)

is the set of particles in the neighbourhood of

particle i and 𝒑



is the best position of particle i thus

far. The von Neumann neighbourhood topology was

adopted to construct the particles.

A Combinatorial Exact BB Algorithm: To

compare the performance of the feature selection

heuristics, we also implemented the state-of-the-art

BB solver within DAMIP with an additional

constraint to limit the number of features that will be

selected during the solution process. We use this to

contrast the performance of the modified PSO

heuristics.

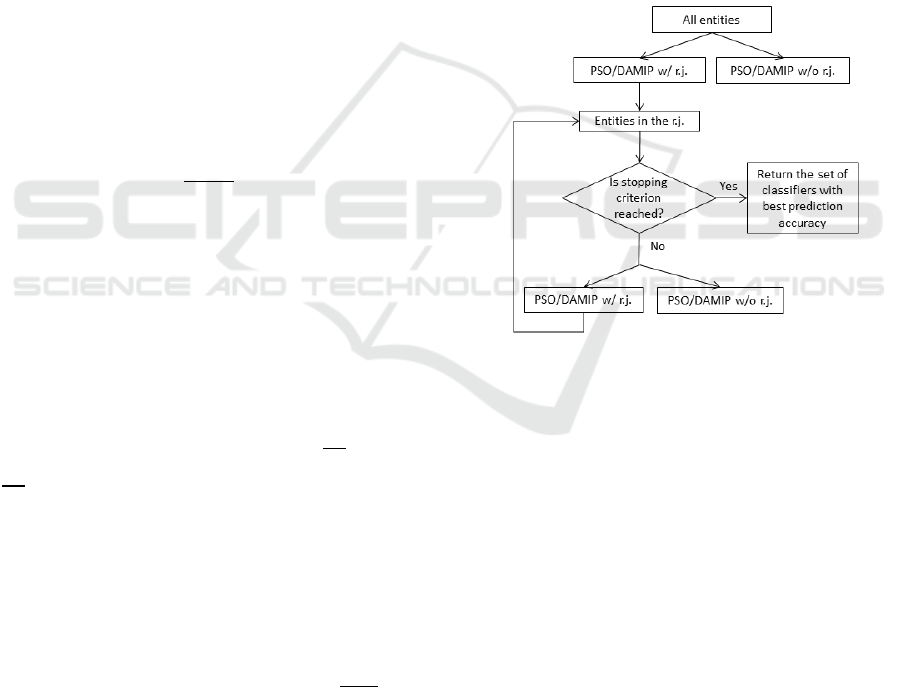
2.1.3 The Multi-Stage Classification Model

The multi-stage classification model aims to improve

the performance of the BB-PSO/DAMIP framework

by utilizing the reserved judgment region in DAMIP.

A DAMIP model bisects the data set into an ‘easy–

to-classify’ subset that it classifies to specific groups,

and a ‘difficult-to-classify’ subset that it classifies to

a reserved judgment region. It delays making a group

assignment decision to subjects that are difficult to

classify by the DAMIP with the selected features. In

the multi-stage model we propose, those subjects are

moved to the next stage where a new feature set is

selected and a new DAMIP classifier is developed. In

A Multi-stage Multi-group Classiﬁcation Model: Applications to Knowledge Discovery for Evidence-based Patient-centered Care

this way, the multi-stage framework constructs a

chain of successive classifiers using different subsets

of features. The classifier at the ith stage, denoted by

𝑓



, can be represented by a discriminant function

𝑓

(

𝒙



,𝝀

𝒊

)

, which is determined by the feature subset

𝒙



, and the decision variables 𝝀

𝒊

in DAMIP. More

stages do not necessarily produce a better model. At

each stage, the framework selects the better of two

models: a single-stage model that solves a DAMIP

model without a reserved judgment region and a

multi-stage model that solves a DAMIP model with a

reserved judgment region. The algorithm naturally

terminates when there are no observations in the

reserved judgment region. As more stages are

processed, fewer observations remain for DAMIP,

and the constructed model consists of too many

successive classifiers. This may result in over-fitting.

Hence, we propose two additional stopping criteria to

terminate the process: (a) the number of observations

is less than a pre-set minimum number, denoted by n,

and (b) the maximum allowed depth, denoted by d is

reached. The parameters n and d are pre-determined

according to the number of observations and the

number of input features in the given data.

2.2 Modified DAMIP Models

The size of the reserved judgment region is bounded

by the misclassification rates specified in constraints

(7). DAMIP is able to return good classification

results through problem-specific fine tuning of the

misclassification rates, especially when the groups

are unbalanced. To ease this fine-tuning process, we

envision that the classifiers in our multi-stage model

have the ability of balancing misclassifications and

‘difficult to classify’ observations in order to

maximize the prediction accuracy through a multi-

stage structure. For group g, let 𝛼



be the

misclassification rate, 𝛽



be the proper/correct

classification rate, and 𝛾



be the ‘difficult to classify’

rate, i.e., the percentage of observations placed in the

reserved judgment region. These three parameters can

be defined in DAMIP as follows:

𝛼









∑∑

𝑢

𝒪



𝒢,

(11)

𝛽









∑

𝑢

𝒪



(12)

𝛾









∑

𝑢

𝒪



(13)

Recall 𝒪



is the set of observations of group g and n

is the size of group g (i.e., n

= | 𝒪



|). The three

parameters satisfy that 𝛼



+ 𝛽



+𝛾



=1 for each

group g. We propose three modified DAMIP models

to (a) better utilize the reserved judgment region and

(b) handle imbalanced groups more efficiently.

2.2.1 Variant 1: The Base Model

V1: 𝑚𝑎𝑥 min

 ∈ 𝒢

𝛽

,

subject to constraints (1) - (6), (8)

- (10), and (12). This base model aims to generate an

optimal classification rule without using

misclassification limits and reserved judgment. The

objective is to maximize the minimum value of

correct classification rates 𝛽



among all groups. It

ensures that the minority groups are treated equally as

the majority groups, and hence it can perfectly deal

with imbalanced groups. It produces a lower bound of

the prediction accuracy of each group, and the

optimal values 𝛽



and the associated 𝛼



can be used

in the misclassification limits in DAMIP.

2.2.2 Variant 2: The β - α Model

𝑽𝟐: 𝑚𝑎𝑥 min

 ∈ 𝒢

𝛽



− 𝛼



 subject to constraints (1)

– (6), and (8) – (12). The 𝛽−𝛼 model maximizes the

minimum difference between 𝛽



and 𝛼



by moving a

small proportion of observations into the reserved

judgment region. Instead of using the

misclassification constraints, it incorporates both 𝛼

and 𝛽 into the objective function to keep the reserved

judgment region from getting too large that it

weakens the performance of the model.

2.2.3 Variant 3: The γ Model

𝑽𝟑: 𝑚𝑎𝑥

∑

𝛽

 ∈ 𝒢

subject to constraints (1) – (6),

(8) – (10), (12), and (13), plus the new constraint

∑

𝑢

∈𝒪



≤𝛾



𝑛



,∀𝑔 ∈ 𝒢.

The 𝛾 model maximizes the prediction accuracy

while limiting the size of the reserved judgment

region by adding constraints on the percentage of

reserved judgment 𝛾



for each group g. It provides

accurate control of the reserved judgment region to

avoid too many stages in the model. The maximum

percentage 𝛾



 for each group g is predetermined

according to the size of the problem. Thus the 𝛾

model resembles the original DAMIP model except it

constrains the reserved judgment region instead of

constraining the misclassification rates for each

group.

KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval

2.2.4 Special Case: Solutions for 2 Groups

For two groups, the modified DAMIP models can be

solved in polynomial time. The constraints that define

𝐿

(

𝑥

)

can be written as:

𝐿



=𝜋



𝑓



(

𝑥



)

−𝜆



𝑓



(

𝑥



)

∀ 𝑖 ∈ 𝒪

𝐿



=𝜋



𝑓



(

𝑥



)

−𝜆



𝑓



(

𝑥



)

∀ 𝑖 ∈ 𝒪,

where optimal 𝜆



and 𝜆



are determined in

DAMIP. We prove that the optimal 𝜆



and 𝜆



in a

two group DAMIP model that maximizes the total

correct classifications can be found by searching on

the sorted array 𝑓



/𝑓



where 𝑓



and 𝑓



are the density

functions in constraint (1) of group 1 and 2

respectively.

Briefly, when no reserved judgment region is used

in the modified DAMIP model, we define a partition

p on the sorted array 𝑓



/𝑓



such that observations

having 𝑓



(

𝑥

)

/𝑓



(

𝑥

)

≤ 𝑝 are classified to group 1,

and observations having 𝑓



(

𝑥

)

/𝑓



(

𝑥

)

>𝑝 are

classified to group 2. By searching on the sorted array

𝑓



/𝑓



, p* can be found such that the objective

function which is the minimum of the correct

classifications of the two groups in the base model is

maximized. An optimal solution of (𝜆

,

𝜆



) then

can be determined by

















=𝑝

∗

When a reserved judgment region is used in the

DAMIP models, we define two partitions 𝑝



and 𝑝



of the sorted array 𝑓



/𝑓



: observations having

𝑓



(

𝑥

)

/𝑓



(

𝑥

)

≤ 𝑝



are classified to group 1,

observations having 𝑝



<𝑓



(

𝑥

)

/𝑓



(

𝑥

)

≤𝑝



are

classified to the reserved judgment region, and

observations having 𝑓



(

𝑥

)

/𝑓



(

𝑥

)

> 𝑝



are

classified to group 2. By searching on the sorted array

𝑓



/𝑓



, (𝑝



∗

, 𝑝



∗

) can be found such that the objective

function is optimized. An optimal solution of

(𝜆

,

𝜆



) then can be determined by









=𝑝



∗

and









=𝑝



∗

The optimal partition may not be unique: any

partition 𝑝∈[𝑙



,𝑙



) results in the same objective

function value as 𝑝

∗

∈[𝑙



,𝑙



) where 𝑙



is the

maximum value of 𝑓



/𝑓



of observations that is less

than or equal to 𝑝

∗

and 𝑙



is the minimum value of

𝑓



/𝑓



of observations that is greater than 𝑝

∗

. A proper

way of determining 𝑝

∗

when searching on the sorted

array is to choose the mid-point 𝑝

∗





 





. The

complexity of this algorithm is O(nlogn): it takes

O(nlogn) to sort the array 𝑓



/𝑓



, and O(n) to search

through the array to find the partition that reaches the

optimal objective.

2.3 Running Multi-Stage

BB-PSO/DAMIP on Real-world

Problems

We apply the classification framework to real-world

problems, focusing on instances that challenge

existing classifiers where they perform poorly due to

imbalanced data and the very mixed nature of the

groups. By design, the DAMIP classifier partitions

the group space in a non-linear and segmented

manner, where observations belonging to the same

group could be classified under different conditions.

This is useful in medical applications. For example,

patients with the same outcome could have very

diverse sets of lab or treatment results. It is the entire

system that one must examine to classify properly.

Figure 1 shows the multi-stage DAMIP approach.

Figure 1: The algorithm selects the better of the two at each

stage to continue. Termination can be triggered by the

number of stages reached or the size of unclassified entities.

3 RESULTS FOR DISEASE

DIAGNOSIS AND TREATMENT

OUTCOME PREDICTION

For brevity, we discuss two applications:

cardiovascular disease and Alzheimer’s disease. The

cardiovascular disease analyses involve over 737

clinical sites of -patient data. They showcase the need

for unsupervised learning to uncover the group status

prior to machine learning, since the data were

originated from diverse sites with a heterogeneous

interpretation of outcome status. The Alzheimer’s

disease study distinguishes itself from other work as

our analyses involve raw neuro-psychological data

instead of the overall clinical scores. Furthermore, we

A Multi-stage Multi-group Classiﬁcation Model: Applications to Knowledge Discovery for Evidence-based Patient-centered Care

couple these low-cost non-invasive exams/tests with

the blood plasma biomarkers for comprehensive

analyses.

3.1 Cardiovascular Disease

“Cardiovascular diseases (CVD) are the leading

cause of death globally, taking an estimated 17.9

million lives each year. CVDs are a group

of disorders of the heart and blood vessels and include

coronary heart disease, cerebrovascular disease,

rheumatic heart disease and other conditions.”(World

Health Organization, 2022a) In the United States,

coronary heart disease is the leading cause of death

for men, women, and people of most racial and ethnic

groups, and affects about 20.1 million adults aged 20

and older (Tsao et al., 2022). Statistics show that

CVD affects nearly half of American adults

(American Heart Association News, 2019).

In our previous work, we have developed a

comprehensive, efficient “pipeline” for extracting,

de-identifying, and standardizing EMR data. The

system established interoperability for over 2.7

million patient data from the Care Coordination

Institute (CCI) covering = 737 clinical sites (Lee et

al., 2016, 2019, 2021). That prior work also

addressed challenges associated with temporal

laboratory time series data and unstructured text data

and described a novel approach for clustering

irregular Multivariate Time Series (MTS).

The CCI-health database contains 37,742

patients with CVD. Through our mapping, each

patient is eventually characterized by 11 raw features

including demographics, treatment duration, and co-

existing conditions, and 1,757 standardized features

described in Systematized Nomenclature of

Medicine-Clinical Terms (SNOMED-CT), including

laboratory tests, diagnosed problems, and

medications. These 1,757 standardized features were

mapped from 19,800 raw features from the database.

For each patient, treatment duration was determined

by calculating the elapsed time between diagnosis

(indicated by the first prescription of a medication)

and the last recorded activity (i.e., procedure, lab,

etc.).

Measurements of lipids and lipoproteins were

processed into time series since these are closely

related to cardiovascular conditions and can

potentially be used to characterize the severity of

CVD (Gordon et al., 1977). A low level of high-

density lipoproteins (HDL) is significantly associated

with the development of heart disease. A high level

of low-density lipoprotein (LDL) increases the risk of

heart disease. A high level of Triglycerides is also

associated with the incidence of heart disease but has

a less significant effect.

We used HDL, LDL, and Triglyceride

measurements to form an MTS containing three time

series for each patient. Each of these time series was

resampled to quarterly frequency. Gaps in the data

were filled by propagating the non-NaN values

forward first, and then backward, along each time

series. For each of the three types of laboratory

measurements, we removed patients with fewer than

three measurements after resampling from the

dataset. This produces a data set containing 450

patients. The global alignment kernel (GAK) distance

between each pair of corresponding time series was

calculated (Lee et al., 2021; Nwegbu et al., 2022).

The pairwise distance between each pair of MTS was

then obtained by averaging the three distances for

each pair of corresponding univariate time series.

Specifically, given two patients, P

and P

, each with

m lab measurement time series, their pairwise

distance was calculated using the following equation:

Distance (P

, P





(

∑

𝐷



(𝑃





𝑃





)





3.1.1 Clustering to Establish Treatment

Outcome Groups

K-medoids clustering performed on the CVD

distance matrix partitioned the patients into three

groups. The clinical experts examined the raw

laboratory records for each group and associated the

cluster characteristics as “Good,” “Medium,” or

“Poor” outcomes (blue, red, or green). We caution

that such interpretation by clinical experts is of

paramount importance. Figure 2 show the raw HDL,

LDL, and Triglyceride laboratory records by cluster.

The “Poor Outcome” group is well-segregated from

the other two groups, showing high variability in

HDL and LDL levels, which is a high-risk factor for

myocardial infarction. Although the ”Good” and

“Medium” outcome groups have similar trajectories

of cholesterol levels, the “Good” outcome group has

slightly higher HDL levels, lower LDL and

Triglyceride levels, and shows more consistency in

all three types of cholesterol levels. Table 1 shows the

patient partition for machine learning training and

blind prediction.

KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval

100

Figure 2: HDL, LDL, and Triglyceride laboratory records

for each patient cluster.

Table 1: Partition of CVD patients for machine learning

training and blind prediction.

Total Good Medium Poor

Training 314 60 158 96

Blind se

136 19 75 42

Total 450 79 233 138

3.1.2 Predicting Treatment Outcome Across

Multiple Sites

The goal of machine learning is to uncover

discriminatory features that can predict good

outcomes. This is critical for evidence-based, best

practice discovery and for the dissemination of good

clinical practice evidence across different sites. For

classification, we considered the “Good Outcome”

group versus the other two groups, the “Medium” and

“Poor” outcome clusters.

Table 2 summarizes the machine learning results

for the CVD patients using DAMIP, coupled with

either an exact combinatorial (BB) feature-selection

algorithm or the PSO feature-selection heuristic

described herein. We contrasted the accuracy of 10-

fold cross-validation and DAMIP blind prediction.

Table 2: BB-PSO/DAMIP classification rules in predicting CVD Treatment outcome.

Discriminatory feature

(chosen from 1,768 features)

Exact combinatorial branch-

and-bound search BB/DAMIP

Heuristics particle swarm

optimization PSO/DAMIP

Treatment Length X X X X X X X X X X

Glucose measurement, urine (procedure) X X X X X X X X

Synthetic steroid (substance) X X X X X X

Acute digestive system disorder (disorder) X

Inflammatory disorder of upper respiratory tract (disorder) X X X X X X

Calcium channel blocking agent (product) X X X

Neoplasm by body site (disorder) X X

Diabetic - poor control (finding) X X

Implantation (procedure) X X

Investigations (procedure) X X

Acute disorder of ear (disorder) X

Disorder of immune system (navigational concept) X

Allergen or pseudo allergen (substance) X

Oral form naproxen (product) X

Electrocardiogram finding (finding) X X

Disinfectants and cleansers (product) X X

Imaging (procedure) X X

Accuracy of 10-fold cross validation (%), Good Outcome 85.3 87.6 87.6 89.9 87.6 90.3 90.3 90.3 90.3 89.4

Accuracy of 10-fold cross validation (%), Medium Outcome 91.6 86.4 85.4 86.4 85.4 86.4 86.4 86.4 86.4 86.4

Accuracy of 10-fold cross validation (%), Poor Outcome 89.3 84.2 85.3 84.6 86.1 86.0 88.3 85.7 85.3 87.2

Accuracy of blind prediction (%), Good Outcome 89.3 91.4 91.4 93.6 91.4 91.9 93.6 92.5 92.5 92.5

Accuracy of blind prediction (%), Medium Outcome 97.6 92.8 92.8 90.4 92.8 92.5 90.4 90.4 95.2 97.6

Accuracy of blind prediction (%), Poor Outcome 91.2 88.3 90.6 89.7 90.8 91.0 92.1 89.7 94.9 92.5

A Multi-stage Multi-group Classiﬁcation Model: Applications to Knowledge Discovery for Evidence-based Patient-centered Care

101

DAMIP classified patients into “Good Outcome”

vs. “Medium” and “Poor” Outcomes by uncovering a

set of discriminatory features that yields a blind

prediction accuracy of 88.3% to 97.6%. Each rule (a

column) consists of 3-7 discriminatory features. The

multiple rules with relatively small subsets of

discriminatory features afford flexibility for different

sites (and different patient populations) to adopt

different policies for implementing the best practice.

BB/DAMIP and PSO/DAMIP produce similar

results, although results from BB/DAMIP tend to

have fewer features than those from PSO/DAMIP.

We contrasted the BB-PSO/DAMIP results with

eight commonly used classifiers: Logistic

Regression, SVM, K-nearest neighbours, Random

Forest, Decision Tree, Neural Network, Gradient

Boosting, and Bernoulli Naïve Bayes. Table 3 shows

the best two results among these eight classifiers.

Specifically, Decision Tree and Random Forest

yielded 10-fold cross-validation unbiased estimates

of 65% and 63% for the “Good Outcome” and 80%-

90% for the “Medium” and “Poor” outcome groups

respectively. The blind prediction fared worse, with a

roughly 50% predictive accuracy for the “Good

Outcome” group. The remaining six classifiers

suffered similarly from imbalanced data, and the

accuracy for “Good Outcome” was uniformly below

40%. In all cases, Randomized Lasso was used for

feature selection, and it selected twenty-five

discriminatory features. In contrast, the BB-

PSO/DAMIP results offer higher accuracy using

fewer discriminatory features.

Table 3: Performance of the top two classifiers among the

eight. All analyses used Randomized Lasso for feature

selection with 25 features selected.

10-fold Cross-Validation Blind Prediction

Goo

Medium Poo

Goo

Medium Poo

Extraclass results

65.1% 88.7% 82.9% 56.3% 91.5% 88.9%

Random Forest results

63.5% 90.3% 84.7% 50.0% 89.4% 81.5%

3.2 Alzheimer’s Disease

In 2019, Alzheimer's disease (AD) and other forms of

dementia ranked as the 7th leading cause of death,

affecting over 55 million people worldwide.

Globally, 65% of deaths from Alzheimer’s and other

forms of dementia are among women (World Health

Organization, 2022b). AD is a progressive and

irreversible brain disease which causes memory loss

and other cognitive problems severe enough to affect

daily life. Dementia is a collection of symptoms of

cognitive function problems, such as thinking,

remembering, or reasoning problems, and AD is the

most common cause of dementia. Mostly AD occurs

in people over 65, although familial AD has an earlier

onset. Currently, AD is incurable; drugs are used to

manage the symptoms or to prevent or slow the

progress of the disease.

Mild cognitive impairment (MCI) is a condition

that has clear evidence of cognitive problems, most

often involving short term memory, but normal day-

to-day functioning is preserved. MCI is a situation

between normal aging and dementia. People with

MCI may or may not develop dementia in the future,

but people with MCI are at higher risk of developing

dementia than those without.

The evaluation of AD or MCI is based on patient

information including a complete medical history,

neuropsychological exam, laboratory tests,

neuropsychological tests, brain scans (CT or MRI),

and information from close family members.

Neuropsychological changes in the expression of

cognitive declines are important to the diagnosis of

AD and MCI. Statistical analyses as predictive

analysis tools have been applied to

neuropsychological data to understand MCI patients

(Kluger et al., 1999; Lopez et al., 2006). In addition

to statistical analyses, classification models have been

applied to neuropsychological data for predicting

brain damage (Lee, Wu, et al., 2012; Lee & Wu,

2009; Stuss & Trites, 1977; Tabert et al., 2006) and

whether nondemented elderly patients declined to a

diagnosis of dementia or Alzheimer’s disease.

In addition to the traditional diagnosis, the clinical

diagnosis of MCI and AD is increasingly aided by

biomarkers predictive of underlying pathology.

Several recent studies generated additional

enthusiasm for a blood-based test to predict

nondemented controls and those with AD (W. T. Hu

et al., 2016; Palmqvist et al., 2020; Ray et al., 2007;

Reddy et al., 2011; Rocha de Paula et al., 2011;

Schindler & Bateman, 2021). However, identifying

MCI and AD remains challenging. Hu (W. T. Hu et

al., 2012) measured levels of 190 plasma proteins and

identified 17 analytes associated with the diagnosis of

MCI or AD.

We apply the multi-stage classification model to

predict the control, MCI, and AD groups, using two

data sets: The first one is de-identified

neuropsychological test data conducted by Emory

Alzheimer's Disease Research Center. The second

one is plasma biomarkers information collected by

two independent centers (University of Pennsylvania,

Philadelphia; Washington University, St. Louis,

MO).

KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval

102

3.2.1 Predictive Analysis using

Neuro-psychological Data

The neuropsychological tests conducted in this data

set include the Mini Mental State Examination

(MMSE), clock-drawing test, Word List Memory

tasks by the Consortium to Establish a Registry for

Alzheimer's Disease (CERAD), and Geriatric

Depression Scale (GDS). The MMSE is a screening

tool for cognitive impairment. It is brief, but covers

five areas of cognitive function, including orientation,

registration, attention and calculation, recall, and

language. The clock drawing test assesses cognitive

functions, particularly visuospatial abilities, and

executive control functions. The CERAD Word List

Memory tasks assess learning ability for new verbal

information. The tasks focus on repetition, word list

recall, and word list recognition. The GDS is a

screening tool to assess depression in the older

population.

Data of 267 subjects with known groups were

collected as shown in Table 4. Among the 267

subjects, two-thirds of the subjects in each group are

randomly selected as the training set for 10-fold

cross-validation, while the remaining subjects are

used for blind prediction. 107 features are included

for feature selection and classification. Among the

107 features are 3 features representing age, gender,

years of education, 15 features from the Clock

drawing test, 11 features from the GDS, 13 features

from the MMSE, and 65 features from the Word List

Memory tasks.

Table 4: Group information of 267 subjects in the

neuropsychological data set.

Total Control MCI AD

MCI or

Training 178 72 51 55 106

Blind se

89 36 26 27 53

Total 267 108 77 82 159

Table 5: Prediction accuracy of the best feature sets via

PSO/DAMIP.

10-fold Cross-Validation Blind Prediction

Ctrl MCI AD Ctrl MCI AD

87.8% 80.0% 88.3% 88.2% 80.6% 90.9%

89.2% 80.0% 86.7% 85.3% 80.6% 90.9%

464 discriminatory feature sets, each with no more

than 10 features that can correctly predict over 80%

of the subjects in both 10-fold cross-validation and

blind prediction, are found by the PSO/DAMIP

framework. We highlight two Pareto best prediction

accuracy results in Table 5. They are associated with

multiple feature sets. We list two sets here for the

purpose of explanation: “cClockNumbers4,

cClockCenter, GDS6, ‘Score for What is the year?’,

MMSE Total, cWL1Ar, cWL1Ticket, cWL2Ticket,

cWLrTotal. cWRyCabin”, and “cClockNumbers4,

cClockHands4, cClockCenter, ‘Score for What is the

month?’, ‘Score for Where are we?’, MMSE Total,

cWL1Ticket, cWLrTotal, cWRyButter,

cWRnVillage”.

The overall prediction accuracy of 10-fold cross-

validation and blind prediction are over 85%, with the

blind prediction accuracy of each group ranging from

80.6% to 90.9%. The prediction accuracy no

longer improves when more features are used in the

classification model. In Table 6, we highlight the

features that most frequently occur in the 464 feature

sets.

Table 6: Features with the highest occurrences in the 464

discriminatory feature sets.

Feature Test Occurrences

MMSE Total MMSE 100.0%

cWLrTotal Word List 94.4%

cWL1Ticket Word List 94.2%

cClockCenter Clock 76.1%

Score for What is the year? MMSE 59.5%

Score for What is the month? MMSE 53.4%

The features selected highlight the test modules or

specific questions/tasks that are most predictive. One

advantage in our findings is that they are easily

interpreted and understood by clinicians as well as

patients. Thus, these discriminatory features can

serve as an early detection tool that family members

and providers can use to monitor for disease in

patients.

3.2.2 Predictive Analysis using Plasma

Biomarkers

Data of 352 subjects with complete information are

collected as shown in Table 7. We use the same

partition strategy to establish the training set and the

blind prediction set. Thirty-one features for feature

selection are included: gender, age, education years,

MMSE, and 10 indicators and 17 analytes that were

identified by Hu (W. T. Hu et al., 2012).

Table 7: Group information of 352 subjects in plasma

biomarkers data set.

Total Control MCI AD

MCI

or AD

Training 250 35 133 82 215

Blind se

102 21 62 19 81

Total 352 56 195 101 296

A Multi-stage Multi-group Classiﬁcation Model: Applications to Knowledge Discovery for Evidence-based Patient-centered Care

103

92 discriminatory feature sets, each with no more

than 10 features that can correctly predict with

accuracy ranging from 82.9% - 91.5% in 10-fold

cross-validation and 81% to 94.7% in blind

prediction, are found by the PSO/DAMIP framework.

Table 8 presents the best prediction accuracy,

which associates with 3 feature sets: “MMSE,

ApoE_1, tTau, Ab42, BNP, Resistin, IGFBP2,

tTauG91, LoAbHiTau, SAP3”, “MMSE, ApoE_1,

tTau, Ab42, BNP, SAP, IGFBP2, TauG91,

LoAbHiTau”, and “MMSE, ApoE_1, tTau, Ab42,

IGFBP2, tTauG91, LoAbHiTau, BNP3, Resistin3,

SAP3.” Note that the 3 sets share 80% of the selected

features.

Table 9 highlights the features that most

frequently occur in the 92 feature sets.

Table 8: Prediction accuracy of the best feature sets via

PSO/DAMIP.

10-fold Cross-Validation Blind Prediction

Ctrl MCI AD Ctrl MCI AD

91.4% 82.9% 91.5% 81.0% 85.8% 94.7%

Table 9: Features with the highest occurrences in the 92

discriminatory feature sets.

Feature Occurrences

ApoE_1 100.0%

tTau 100.0%

Ab42 100.0%

IGFBP2 100.0%

tTauG91 100.0%

LoAbHiTau 100.0%

MMSE 100.0%

BNP 59.8%

Resistin 52.2%

SAP3 52.2%

The analyses using two independent patient sets

of data illustrate that MMSE can act as a low-cost

procedure to be added to annual physical exams for

the aged population. It offers good predictive power

for the brain’s cognition status. Early detection of

MCI offers the opportunity for treatment to slow

down the onset of AD.

4 CONCLUSIONS

Technological advances in prevention, diagnosis, and

treatment of diseases help predict disease, prolong

life, and promote health. However, with an increase

in the volume and complexity of data and evidence,

medical decision making can be a complex process.

Many decisions involve uncertainties and trade-offs

and can have profound consequences to patients and

the clinical practice. To make such complex

decisions, providers must balance the potential harm

and benefit of medical interventions. Computational

methods such as mathematical programming,

simulation, and classification have found broad

applications in these areas.

In this paper, we present a multi-stage, multi-

group classification framework that incorporates

particle swarm optimization (PSO) for feature

selection and discriminant analysis via mixed integer

programming (DAMIP) for classification. By

utilizing a reserved judgment region, it allows the

classifier to delay making decisions on ‘difficult-to-

classify’ observations and develop new classification

rules in a later stage. Such a design works well for

mixed (poorly separated) data that are difficult to

classify without committing a high percentage of

misclassification errors. We also establish variant

DAMIP models that enable problem-specific fine-

tuning to establish proper misclassification limits and

reserved judgement levels that facilitate efficient

management of imbalanced groups. By design,

DAMIP ensures that minority groups with relatively

few entities are treated equally as the majority groups.

We apply the framework to two real-life medical

problems: (a) multi-site treatment outcome prediction

for best practice discovery in cardiovascular disease,

and (b) early disease diagnosis in predicting subjects

into normal, mild cognitive impairment, and

Alzheimer’s disease groups using

neuropsychological tests and blood plasma

biomarkers. Both problems involve poorly separated

data and imbalanced groups in which traditional

classifiers yield low prediction accuracy. The multi-

stage PSO/DAMIP manages the poorly separable

imbalanced data well and returns interpretable

predictive results with over 80% blind prediction

accuracy. A note of comparison, the frequently used

Pap Smear test has an accuracy of roughly 70%.

Gallagher, Lee, and Patterson first established the

original DAMIP multi-group model (Gallagher et al.,

1997). They introduced a linear-programming

approximation to provide a rapid solution capability

(Lee et al., 2003). This study materializes the multi-

stage construct and integrates both an exact

combinatorial branch-and-bound algorithm and a fast

feature selection heuristic along with a systematic

multi-stage schema, with a set of problem-specific,

fine-tuning models to guide its practical usage.

Mathematically, DAMIP is 𝒩𝒫 − 𝑐𝑜𝑚𝑝𝑙𝑒𝑡𝑒 with

its classifier proven to be universally strongly

consistent. Hence DAMIP has desirable solution

characteristics for machine learning purposes.

KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval

104

Computationally, DAMIP is the first multi-

group, multi-stage classification model that

simultaneously includes a reserved judgment

capability and the ability to constrain

misclassification rates within a single model. Further,

Constraint (1) serves to transform the features from

their original space to the group space, serving as a

dimension reduction mechanism.

Nevertheless, the problem remains

computationally intractable. Although each iteration

of feature selection can be achieved rapidly when

heuristics are employed, the wrapper design

evaluation via DAMIP is computationally intensive.

For both the cardiovascular and Alzheimer’s disease

problems, the solution time to establish final

classification rules can take days of CPU time in a

cloud environment. Nonetheless, the high quality of

the blind predictive results is promising and usable

for clinical stakeholders who must carefully make

critical decisions.

For the multi-site cardiovascular study, the

ability to uncover a best practice that pinpoints a

specific clinical process, treatment regimen and

duration, and drug types helps to establish improved

clinical practice guidelines for adoption by other

sites. This accelerates patient-centered, evidence-

based care. For Alzheimer’s disease, an early

diagnosis of MCI can lead to proactive treatment that

can slow down or prevent the onset of Alzheimer’s.

The neuropsychological data features selected can

serve as an early detection tool for family members

and providers to monitor as they care for the elderly

population. All of which can have significant impact

on quality of life and medical outcome.

We remark that although balancing class size via

majority under-sampling, minority oversampling, and

synthetic minority oversampling techniques

(SMOTE) are commonly employed (Basha et al.,

2022; Fujiwara et al., 2020; Yi et al., 2022), these

approaches pose serious weaknesses (Gao et al.,

2020). Under-sampling of the majority class may

discard useful information about the data itself, which

could be necessary and important to establish an

unbiased classifier. It is also possible that the chosen

sample (after under-sampling) could be biased.

Oversampling may increase the likelihood of

overfitting, while synthetic patient data alters the

actual practice patterns, skews the classifiers, and

impedes implementation potential (Gao et al., 2020).

IBM Watson’s failure reinforces the premise that real

data and interoperability is of paramount importance

in driving machine learning technology (O’Leary,

2022; Sweeney, 2017).

In our two applications, the imbalanced data is

compounded further by the fact that they are poorly

separable. After the first stage classification, about

46% of “Good” outcome from the cardiovascular

disease were placed in the reserved judgement region.

And for the Alzheimer’s disease, about 54% MCI and

37% of AD were mixed together. We note that the

hardest and most critical knowledge is the earliest

diagnosis of mild cognitive impairment as it affords

early intervention to lower the risk of manifestation

to AD. These data underscore the poorly separable

concept and the advantage of a multi-stage approach,

In comparison, SMOTE approaches did not

yield improved predictive results on these

applications. There is no good way to generate

artificial patients that are representative of real

diseased patients. While we appreciate other

investigators’ efforts in creating data sets to mimic

real patients (for imbalanced data, or for increasing

the sample size), we cannot afford to do so since there

is a very serious danger of creating artificial patients

for actual clinical decision support. Our goal is to find

meaningful results that can be used in actual clinical

settings using real patient data that represent the

population. The multi-stage multi-group DAMIP

offers promising results.

Once the DAMIP classification rules are

established, the blind prediction process takes only

nanoseconds, making usage practical in real-time. In

our experience where we implemented the machine

learning toolkit for day-to-day use, many of the

predictive rules developed do not require constant

refinement or re-runs, rather they only need periodic

updates. Our goal is a high-quality robust

interpretable solution that can predict with

confidence. We are currently developing new

hypergraphic theoretical and computational results to

efficiently solve these intractable instances (Shapoval

& Lee, 2021).

ACKNOWLEDGEMENTS

A portion of the results from this project (the machine

learning advances, and the results obtained for

cardiovascular disease) received the first runner-up

prize at the 2019 Caterpillar and INFORMS

Innovative Applications in Analytics Award. This

work is partially supported by grants from the

National Science Foundation (IIP-1361532).

Findings and conclusions in this paper are those of the

authors and do not necessarily reflect the views of the

National Science Foundation. The authors would like

to acknowledge the participation of Fan Yuan and

Zhuonan Li on this project. The authors also thank Dr.

Allan Levey, Dr. Felicia Goldstein, and Dr. William

A Multi-stage Multi-group Classiﬁcation Model: Applications to Knowledge Discovery for Evidence-based Patient-centered Care

105

Hu of Emory Alzheimer's Disease Research Center

for their collaboration and clinical advice. We thank

the anonymous reviewers for their useful comments.

REFERENCES

Agrafiotis, D. K., & Cedeño, W. (2002). Feature selection

for structure-activity correlation using binary particle

swarms. Journal of Medicinal Chemistry, 45(5).

https://doi.org/10.1021/jm0104668

Basha, S. J., Madala, S. R., Vivek, K., Kumar, E. S., &

Ammannamma, T. (2022). A Review on Imbalanced

Data Classification Techniques. 2022 International

Conference on Advanced Computing Technologies and

Applications (ICACTA), 1–6. https://doi.org/10.110

9/ICACTA54488.2022.9753392

Cardiovascular diseases affect nearly half of American

adults, statistics show. (2019). American Heart

Association News, https://www.heart.org/en/news/

2019/01/31/cardiovascular-diseases-affect-nearly-half-

of-american-adults-statistics-show

Correa, E. S., Freitas, A. A., & Johnson, C. G. (2006). A

new discrete particle swarm algorithm applied to

attribute selection in a bioinformatics data set. GECCO

2006 - Genetic and Evolutionary Computation

Conference, 1.https://doi.org/10.1145/1143997.1144003

Cui, L., Yang, S., Chen, F., Ming, Z., Lu, N., & Qin, J.

(2018). A survey on application of machine learning for

Internet of Things. International Journal of Machine

Learning and Cybernetics, 9(8). https://doi.org/1

0.1007/s13042-018-0834-5

Dixon, M. F., Halperin, I., & Bilokon, P. (2020). Machine

learning in finance: From theory to practice. In Machine

Learning in Finance: From Theory to Practice.

https://doi.org/10.1007/978-3-030-41068-1

Efron, B., Hastie, T., Johnstone, I., Tibshirani, R.,

Ishwaran, H., Knight, K., Loubes, J. M., Massart, P.,

Madigan, D., Ridgeway, G., Rosset, S., Zhu, J. I., Stine,

R. A., Turlach, B. A., Weisberg, S., Johnstone, I., &

Tibshirani, R. (2004). Least angle regression. Annals of

Statistics, 32(2). https://doi.org/10.1214/009053604

000000067

Fujiwara, K., Huang, Y., Hori, K., Nishioji, K., Kobayashi,

M., Kamaguchi, M., & Kano, M. (2020). Over- and

Under-sampling Approach for Extremely Imbalanced

and Small Minority Data Problem in Health Record

Analysis. Frontiers in Public Health, 8. https://doi.o

rg/10.3389/fpubh.2020.00178

Gallagher, R. J., Lee, E. K., & Patterson, D. A. (1997).

Constrained discriminant analysis via 0/1 mixed integer

programming. Annals of Operations Research, 74.

https://doi.org/10.1023/a:1018943025993

Gao, L., Zhang, L., Liu, C., & Wu, S. (2020). Handling

imbalanced medical image data: A deep-learning-based

one-class classification approach. Artificial Intelligence

in Medicine, 108. https://doi.org/10.1016/j.artmed.

2020.101935

Ghassemi, M., Naumann, T., Schulam, P., Beam, A. L.,

Chen, I. Y., & Ranganath, R. (2020). A Review of

Challenges and Opportunities in Machine Learning for

Health. AMIA Joint Summits on Translational Science

Proceedings. AMIA Joint Summits on Translational

Science, 2020.

Gordon, T., Castelli, W. P., Hjortland, M. C., Kannel, W.

B., & Dawber, T. R. (1977). High density lipoprotein as

a protective factor against coronary heart disease. The

Framingham study. The American Journal of Medicine,

62(5). https://doi.org/10.1016/0002-9343(77)90874-9

Hayward, K. J., & Maas, M. M. (2021). Artificial

intelligence and crime: A primer for criminologists.

Crime, Media, Culture, 17(2). https://doi.org/10.117

7/1741659020917434

Hocking, R. R., & Leslie, R. N. (1967). Selection of the

Best Subset in Regression Analysis. Technometrics,

9(4). https://doi.org/10.1080/00401706.1967.10490502

Hu, W. T., Holtzman, D. M., Fagan, A. M., Shaw, L. M.,

Perrin, R., Arnold, S. E., Grossman, M., Xiong, C.,

Craig-Schapiro, R., Clark, C. M., Pickering, E., Kuhn,

M., Chen, Y., van Deerlin, V. M., McCluskey, L.,

Elman, L., Karlawish, J., Chen-Plotkin, A., Hurtig, H.

I., … Soares, H. (2012). Plasma multianalyte profiling

in mild cognitive impairment and Alzheimer Disease.

Neurology, 79(9). https://doi.org/10.1212/WNL.0b013

e318266fa70

Hu, W. T., Watts, K. D., Tailor, P., Nguyen, T. P., Howell,

J. C., Lee, R. C., Seyfried, N. T., Gearing, M., Hales, C.

M., Levey, A. I., Lah, J. J., & Lee, E. K. (2016). CSF

complement 3 and factor H are staging biomarkers in

Alzheimer’s disease. Acta Neuropathologica

Communications, 4. https://doi.org/10.1186/s40478-

016-0277-8

Hu, Y., Zhang, Y., & Gong, D. (2021). Multiobjective

Particle Swarm Optimization for Feature Selection with

Fuzzy Cost. IEEE Transactions on Cybernetics, 51(2).

https://doi.org/10.1109/TCYB.2020.3015756

Jain, N. K., Nangia, U., & Jain, J. (2018). A Review of

Particle Swarm Optimization. In Journal of The

Institution of Engineers (India): Series B (Vol. 99, Issue

4). https://doi.org/10.1007/s40031-018-0323-y

Kennedy, J., & Eberhart, R. C. (1997). Discrete binary

version of the particle swarm algorithm. Proceedings of

the IEEE International Conference on Systems, Man

and Cybernetics, 5. https://doi.org/10.1109/icsmc.1997

.637339

Kluger, A., Ferris, S. H., Golomb, J., Mittelman, M. S., &

Reisberg, B. (1999). Neuropsychological prediction of

decline to dementia in nondemented elderly. Journal of

Geriatric Psychiatry and Neurology, 12(4).

https://doi.org/10.1177/089198879901200402

Lazer, D., Kennedy, R., King, G., & Vespignani, A. (2014).

The parable of google flu: Traps in big data analysis. In

Science (Vol. 343, Issue 6176). https://doi.org/

10.1126/science.1248506

Lee, E. K., Gallagher, R. J., & Patterson, D. A. (2003). A

linear programming approach to discriminant analysis

with a reserved-judgment region. INFORMS Journal on

KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval

106

Computing,15(1). https://doi.org/10.1287/ijoc.15.1.23

.151 58

Lee, E. K., Li, Z., Wang, Y., Hagen, M. S., Davis, R., &

Egan, B. M. (2021). Multi-Site Best Practice

Discovery: From Free Text to Standardized Concepts to

Clinical Decisions. 2021 IEEE International

Conference on Bioinformatics and Biomedicine

(BIBM), 2766–2773. https://doi.org/10.1109/BIBM52

615.2021.9669414

Lee, E. K., Wang, Y., Hagen, M. S., Wei, X., Davis, R. A.,

& Egan, B. M. (2016). Machine learning: multi-site

evidence-based best practice discovery. Lecture Notes

in Computer Science (Including Subseries Lecture

Notes in Artificial Intelligence and Lecture Notes in

Bioinformatics), 10122 LNCS. https://doi.org/10.1

007/978-3-319-51469-7_1

Lee, E. K., Wang, Y., He, Y., & Egan, B. M. (2019). An

efficient, robust, and customizable information

extraction and pre-processing pipeline for electronic

health records. IC3K 2019 - Proceedings of the 11th

International Joint Conference on Knowledge

Discovery, Knowledge Engineering and Knowledge

Management, 1. https://doi.org/10.5220/0008071

303100321

Lee, E. K., & Wu, T. L. (2009). Classification and disease

prediction via mathematical programming. In Springer

Optimization and Its Applications (Vol. 26).

https://doi.org/10.1007/978-0-387-09770-1_12

Lee, E. K., Wu, T. L., Goldstein, F., & Levey, A. (2012).

Predictive model for early detection of mild cognitive

impairment and Alzheimer’s disease. Fields Institute

Communications, 63. https://doi.org/10.1007/978-1-

4614-4133-5_4

Lee, E. K., Yuan, F., Hirsh, D. A., Mallory, M. D., &

Simon, H. K. (2012). A clinical decision tool for

predicting patient care characteristics: patients

returning within 72 hours in the emergency department.

AMIA ... Annual Symposium Proceedings / AMIA

Symposium. AMIA Symposium, 2012.

Lei, Y., Yang, B., Jiang, X., Jia, F., Li, N., & Nandi, A. K.

(2020). Applications of machine learning to machine

fault diagnosis: A review and roadmap. In Mechanical

Systems and Signal Processing (Vol. 138).

https://doi.org/10.1016/j.ymssp.2019.106587

Lopez, O. L., Becker, J. T., Jagust, W. J., Fitzpatrick, A.,

Carlson, M. C., DeKosky, S. T., Breitner, J., Lyketsos,

C. G., Jones, B., Kawas, C., & Kuller, L. H. (2006).

Neuropsychological characteristics of mild cognitive

impairment subgroups. Journal of Neurology,

Neurosurgery and Psychiatry, 77(2). https://doi.org/

10.1136/jnnp.2004.045567

Marlin, B. M., Zemel, R. S., Roweis, S. T., & Slaney, M.

(2011). Recommender systems: Missing data and

statistical model estimation. IJCAI International Joint

Conference on Artificial Intelligence. https://doi.org/

10.5591/978-1-57735-516-8/IJCAI11-447

McDermott, M. B. A., Yan, T., Naumann, T., Hunt, N.,

Suresh, H., Szolovits, P., & Ghassemi, M. (2018).

Semi-supervised biomedical translation with cycle

Wasserstein regression GaNs. 32nd AAAI Conference

on Artificial Intelligence, AAAI 2018. https://doi.

org/10.1609/aaai.v32i1.11890

Mohan, K., Pearl, J., & Tian, J. (2013). Graphical models

for inference with missing data. Advances in Neural

Information Processing Systems.

Monteiro, S. T., & Kosugi, Y. (2007). Particle swarms for

feature extraction of hyperspectral data. IEICE

Transactions on Information and Systems, E90-D(7).

https://doi.org/10.1093/ietisy/e90-d.7.1038

Myszczynska, M. A., Ojamies, P. N., Lacoste, A. M. B.,

Neil, D., Saffari, A., Mead, R., Hautbergue, G. M.,

Holbrook, J. D., & Ferraiuolo, L. (2020). Applications

of machine learning to diagnosis and treatment of

neurodegenerative diseases. In Nature Reviews

Neurology (Vol. 16, Issue 8). https://doi.org/

10.1038/s41582-020-0377-8

Narciso, D. A. C., & Martins, F. G. (2020). Application of

machine learning tools for energy efficiency in

industry: A review. In Energy Reports (Vol. 6).

https://doi.org/10.1016/j.egyr.2020.04.035

Nwegbu, N., Tirunagari, S., & Windridge, D. (2022). A

novel kernel based approach to arbitrary length

symbolic data with application to type 2 diabetes risk.

Scientific Reports, 12(1). https://doi.org/10.1

038/s41598-022-08757-1

Palmqvist, S., Janelidze, S., Quiroz, Y. T., Zetterberg, H.,

Lopera, F., Stomrud, E., Su, Y., Chen, Y., Serrano, G.

E., Leuzy, A., Mattsson-Carlgren, N., Strandberg, O.,

Smith, R., Villegas, A., Sepulveda-Falla, D., Chai, X.,

Proctor, N. K., Beach, T. G., Blennow, K., … Hansson,

O. (2020). Discriminative Accuracy of Plasma

Phospho-tau217 for Alzheimer Disease vs Other

Neurodegenerative Disorders. JAMA - Journal of the

American Medical Association, 324(8). https://doi.org/

10.1001/jama.2020.12134

Pudil, P., Novovičová, J., & Kittler, J. (1994). Floating

search methods in feature selection. Pattern

Recognition Letters, 15(11). https://doi.org/10.

1016/0167-8655(94)90127-9

Qu, K., Guo, F., Liu, X., Lin, Y., & Zou, Q. (2019).

Application of machine learning in microbiology.

Frontiers in Microbiology, 10(APR). https://doi.org/1

0.3389/fmicb.2019.00827

Rajkomar, A., Hardt, M., Howell, M. D., Corrado, G., &

Chin, M. H. (2018). Ensuring fairness in machine

learning to advance health equity. Annals of Internal

Medicine, 169(12). https://doi.org/10.7326/M18-1990

Ray, S., Britschgi, M., Herbert, C., Takeda-Uchimura, Y.,

Boxer, A., Blennow, K., Friedman, L. F., Galasko, D.

R., Jutel, M., Karydas, A., Kaye, J. A., Leszek, J.,

Miller, B. L., Minthon, L., Quinn, J. F., Rabinovici, G.

D., Robinson, W. H., Sabbagh, M. N., So, Y. T., …

Wyss-Coray, T. (2007). Classification and prediction of

clinical Alzheimer’s diagnosis based on plasma

signaling proteins. Nature Medicine, 13(11).

https://doi.org/10.1038/nm1653

Reddy, M. M., Wilson, R., Wilson, J., Connell, S., Gocke,

A., Hynan, L., German, D., & Kodadek, T. (2011).

Identification of candidate IgG biomarkers for

A Multi-stage Multi-group Classiﬁcation Model: Applications to Knowledge Discovery for Evidence-based Patient-centered Care

107

alzheimer’s disease via combinatorial library screening.

Cell, 144(1). https://doi.org/10.1016/j.cell.2010.11.054

Rocha de Paula, M. R., Gómez Ravetti, M., Berretta, R., &

Moscato, P. (2011). Differences in abundances of cell-

signalling proteins in blood reveal novel biomarkers for

early detection of clinical Alzheimer’s disease. PLoS

ONE, 6(3). https://doi.org/10.1371/journal.pone.00174

Rose, S. (2018). Machine Learning for Prediction in

Electronic Health Data. In JAMA network open (Vol. 1,

Issue 4). https://doi.org/10.1001/jamanetworkopen.2018.

1404

Schindler, S. E., & Bateman, R. J. (2021). Combining

blood-based biomarkers to predict risk for Alzheimer’s

disease dementia. In Nature Aging (Vol. 1, Issue 1).

https://doi.org/10.1038/s43587-020-00008-0

Shapoval, A., & Lee, E. K. (2021). Generalizing 0-1

conflict hypergraphs and mixed conflict graphs: mixed

conflict hypergraphs in discrete optimization. Journal

of Global Optimization, 80(4). https://doi.org/

10.1007/s10898-021-01012-3

Siedlecki, W., & Sklansky, J. (1989). A note on genetic

algorithms for large-scale feature selection. Pattern

Recognition Letters, 10(5). https://doi.org/10.10

16/0167-8655(89)90037-8

Silva, A. P. D., & Stam, A. (1994). Second order

mathematical programming formulations for

discriminant analysis. European Journal of Operational

Research, 72(1). https://doi.org/10.1016/0377-2217

(94)90324-7

Stuss, D. T., & Trites, R. L. (1977). Classification of

neurological status using multiple discriminant function

analysis of neuropsychological test scores. Journal of

Consulting and Clinical Psychology, 45(1).

https://doi.org/10.1037/0022-006X.45.1.145

Suresh, H., Hunt, N., Johnson, A., Celi, L. A., Szolovits, P.,

Ghassemi, M., & Edu, M. (2017). Proceedings of

Machine Learning for Healthcare 2017 Clinical

Intervention Prediction and Understanding with Deep

Neural Networks. Ml4H, 68.

Tabert, M. H., Manly, J. J., Liu, X., Pelton, G. H.,

Rosenblum, S., Jacobs, M., Zamora, D., Goodkind, M.,

Bell, K., Stern, Y., & Devanand, D. P. (2006).

Neuropsychological prediction of conversion to

alzheimer disease in patients with mild cognitive

impairment. Archives of General Psychiatry, 63(8).

https://doi.org/10.1001/archpsyc.63.8.916

Tibshirani, R. (2011). Regression shrinkage and selection

via the lasso: A retrospective. Journal of the Royal

Statistical Society. Series B: Statistical Methodology,

73(3). https://doi.org/10.1111/j.1467-9868.2011.00771

Yarkoni, T., & Westfall, J. (2017). Choosing Prediction

Over Explanation in Psychology: Lessons from

Machine Learning. Perspectives on Psychological

Science, 12(6). https://doi.org/10.1177/17456916176

93393

Zhao, S., Zhang, S., Liu, J., Wang, H., Zhu, J., Li, D., &

Zhao, R. (2021). Application of machine learning in

intelligent fish aquaculture: A review. In Aquaculture

(Vol. 540). https://doi.org/10.1016/j.aquaculture.2021.

736724

KDIR 2022 - 14th International Conference on Knowledge Discovery and Information Retrieval

108