Construction of Absolutely Failure-free Minimal Data Transmission
Systems on Railway Transport
N. V. Medvedeva
a
and S. S. Titov
b
Ural State University of Railway Transport, Yekaterinburg, Russia
Keywords: Information protection, absolutely failure-free data transmission systems, perfect ciphers.
Abstract: One of the main tasks of the critical infrastructure process control system is information protection.
Information security is important for the transport system, including the railway one. The paper proposes a
graph approach to the construction of absolutely failure-free data transmission systems by creating ciphers
that do not disclose any information about encrypted texts. A class of minimal perfectly secure Shannon
ciphers is considered, in which for each pair of ciphertexts and ciphervalues,
),( yx
respectively, there are at
most two keys on which x is encrypted into
y
. For ciphers of this class, a graph is defined on a set of keys,
namely: two different keys are connected by an edge if there is such a pair
),( yx
that on both of these keys
the ciphertext
x
is encrypted into a ciphervalue
y
. Within the framework of this approach, the necessary and
sufficient minimality condition for the inclusion of perfect ciphers is proved. The minimality criterion for the
inclusion of perfect ciphers is formulated. Examples illustrating the concepts used and the theoretical
statements obtained are constructed. The tables of encryption of perfect ciphers are given, which ensure data
protection when they are transmitted over a communication channel on transport.
1 INTRODUCTION
The problem of transmitting short and important
messages that are absolutely resistant to a cipher-text
attack, due to the specifics of data transmission on
transport, is solved by using perfect (according to
Shannon) ciphers. In the continuation of research
(Medvedeva, 2015; Medvedeva, 2016; Medvedeva,
2019; Medvedeva, 2020; Medvedeva, 2021) of the
problem of describing Shannon-perfect ciphers in the
framework of the probabilistic cipher model
B
Σ
(Shannon, 1963), we consider an arbitrary perfect
cipher. According to (Alferov et al., 2001, Zubov,
2003), a cipher on a set of
 -grams is given by the
probability distribution of keys at
.1= Similarly
(Medvedeva, 2015; Medvedeva, 2016; Medvedeva,
2019; Medvedeva, 2020; Medvedeva, 2021), let
},...,2,1{},...,,{
21
λ
λ
== xxxX be the set of
ciphertexts;
== },...,,{
21 μ
yyyY
},...,2,1{ μ – a set of
ciphervalues with which some substitution cipher
operates; },...,,{
21 π
kkkK = – a set of keys. By
a
https://orcid.org/0000-0002-9736-5481
b
https://orcid.org/0000-0003-0427-9048
condition
,1>= λ X , λμ ≥=Y . μπ ≥=K
This means that open
,...
21 
iii
xxxx =
,...,2,1, =∈ jXx
j
i
and encrypted
...
21
ii
yyy =
,

i
y
Yy
j
i
∈
texts are represented by words ( -
grams, 1≥ ) in alphabets
X
and
Y
respectively. In
accordance with (Alferov, 2001; Zubov, 2003), a
cipher
B
Σ will be understood as a set of sets of
encryption rules and decryption rules with specified
probability distributions on sets of plain texts and
keys. Ciphers for which a posteriori probabilities
),|( yxp ,

Xx ∈

Yy ∈
of open texts coincide
with their a priori probabilities ),(xp are called
perfect (Alferov, 2001; Zubov, 2003).
In (Medvedeva, 2016) it is shown that the problem
of describing ciphers in a probabilistic model
B
Σ
leads to the problem of describing a convex
polyhedron (Nosov, 1983) in a
π -dimensional space
,
π
R where ),1(...)1(
max
+−⋅⋅−⋅== λμμμππ
Medvedeva, N. and Titov, S.
Construction of Absolutely Failure-free Minimal Data Transmission Systems on Railway Transport.
DOI: 10.5220/0011579100003527
In Proceedings of the 1st International Scientific and Practical Conference on Transport: Logistics, Construction, Maintenance, Management (TLC2M 2022), pages 73-77
ISBN: 978-989-758-606-4
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
73

each point is a probability distribution of the
k
P keys
Kk ∈
of a particular cipher. To solve this problem in
the work (Medvedeva, 2020) based on the
equivalence relation on the set of keys, sufficient
conditions are obtained for the absence of non-
endomorphic
),(
μ
λ
< endomorphic )(
μ
λ
= perfect
ciphers of Latin rectangles, squares, respectively, in
the encryption tables.
In this paper, the problem of constructing
(describing) ciphers that do not disclose any
information about open texts is investigated. A graph
approach to solving the problem is proposed. A
minimality criterion for the inclusion of non-
endomorphic (endomorphic) perfect ciphers is
obtained. Examples containing tables of encryption of
perfect ciphers are constructed, ready for use when
organizing a communication channel on transport.
2 MAIN RESULTS
Consider the definitions.
Definition 1 (Medvedeva, 2020). The keys
k
′
and
k
′′
are equivalent in ciphertext
i
x , if
i
x the keys
k
′
and
k
′′
are encrypted into the same ciphervalue,
i.e.
),()(
ikik
i
xexekk
′′′
=⇔
′′
≡
′
in this case, a bijection is used in the notation for the
equivalence of keys:
.
i
xi ↔
Definition 2 (Medvedeva, 2020). Pairwise
different keys
nn
kkkkk ,,...,,,
1321 −
form a cycle of
length
,n if the conditions are met
,...
11321
11432
kkkkkk
i
n
i
n
iiii
nn
≡≡≡≡≡≡
−
−
where
.,,...,,
114332
iiiiiiii
nnn
≠≠≠≠
−
We distinguish a class of minimal ciphers by
inclusion, in which for each pair
),( yx of ciphertext
x
and ciphervalue y there are at most two keys ,k
on which the ciphertext
x
is encrypted into y . Then,
in each column of the encryption tables of such
ciphers, each cipher value
y occurs, respectively, no
more than twice. For ciphers of this class, it is natural
to define a graph (Ore, 1980; Harari, 1973) on a set of
keys. According to (Medvedeva, 2021), two different
keys
k
′
and
k
′′
(corresponding to different injections
k
e
′
and
k
e
′′
encryption, where ,: YXe
k
→
Kk ∈
)
connect with an edge, if there is such a pair
),( yx of
ciphertexts
x
and cipher values y that on both of
these keys the ciphertext is
x
encrypted in ,y i.e.
equality
)()(
ikik
xexe
′′′
= is fulfilled.
Example 1. Consider an endomorphic cipher, for
which
}5,4,3,2,1{},,,,{
54321
== xxxxxX there is
a set of ciphertexts;
== },,,,{
54321
yyyyyY
}5,4,3,2,1{= – a set of cipher values; ,,{
21
kkK =
},,,,,,
9876543
kkkkkkk – a set of keys. Here in the
encryption table (Table 1) of a perfect endomorphic
cipher with
5==
μ
λ
and key probabilities 2,0
1
=P
and
1,0...
932
==== PPP there are no Latin
squares.
Table 1: Encryption table.
K
1
x
2
x
3
x
4
x
5
x
k
P
1
k
1 2 3 4 5 0,2
2
k
2 3 4 5 1 0,1
3
k
2 5 1 3 4 0,1
4
k
3 4 5 2 1 0,1
5
k
3 1 2 5 4 0,1
6
k
4 5 1 3 2 0,1
7
k
4 3 5 1 2 0,1
8
k
5 1 4 2 3 0,1
9
k
5 4 2 1 3 0,1
The graph corresponding to the cipher with the
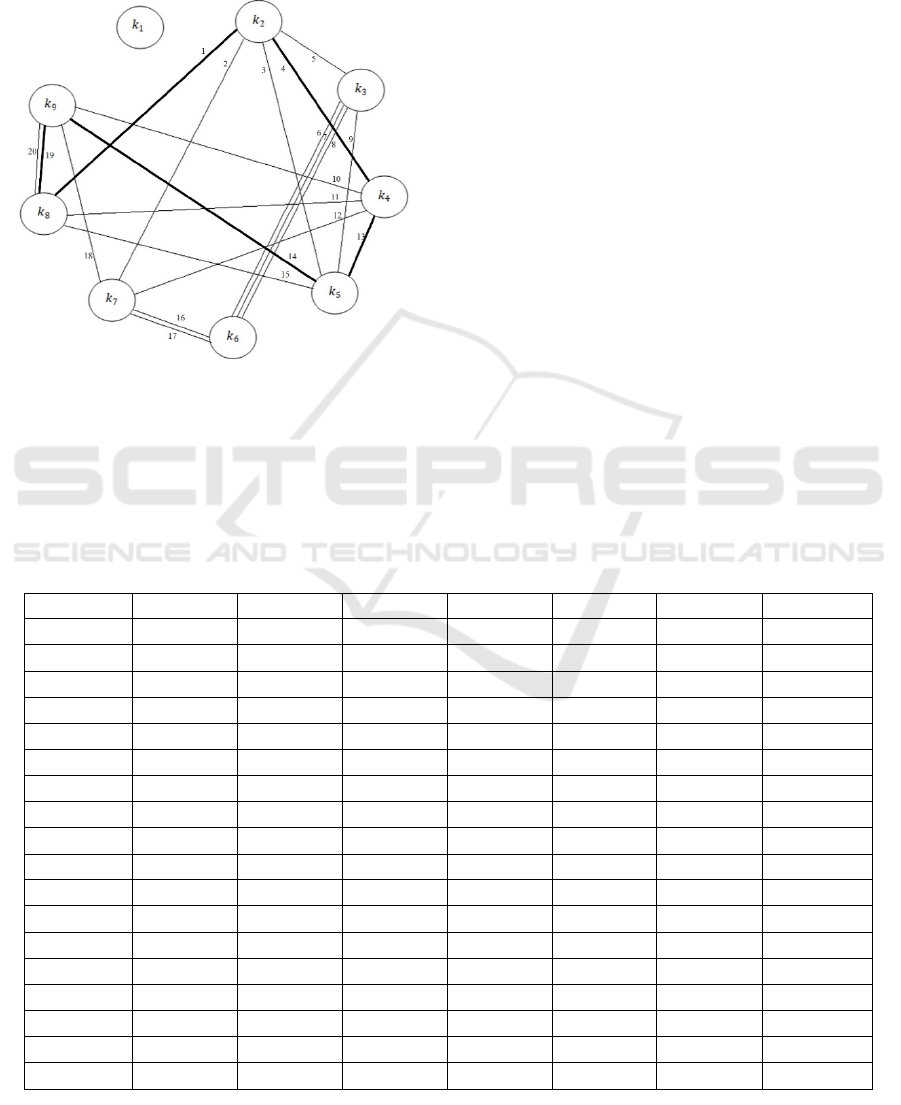
encryption Table 1 is shown in Figure 1. In this graph,
the key
1
k with probability 2,0
1
=Р is an isolated
vertex of the graph.
Note that in the graph shown in Figure 1, the keys
532
,, kkk form a cycle of length three:
,
2
4
5
5
3
1
2
kkkk ≡≡≡ and the keys
89542
,,,, kkkkk
form a cycle of length five:
5,1
9
3
5
1
4
5
2
≡≡≡≡ kkkk
.
2
3
8
5,1
kk ≡≡
The incidence matrix corresponds to this graph
(Ore, 1980, Harari, 1973), namely a binary matrix
I
of size 209 × :
.
11100010001000000000
11000100010000000001
00111000100000000010
00011000000011100000
00000111000100000100
00000001111000001000
00000000000111110000
00000000000000011111
00000000000000000000




























=
I
TLC2M 2022 - INTERNATIONAL SCIENTIFIC AND PRACTICAL CONFERENCE TLC2M TRANSPORT: LOGISTICS,
CONSTRUCTION, MAINTENANCE, MANAGEMENT
74

The necessary and sufficient condition for the
minimality of the cipher on inclusion is valid.
Statement. A cipher is minimal in inclusion if and
only if there is an odd-length cycle in some non-
element connected component of the graph
corresponding to it.
Figure 1: Graph.
Proof. Let the key k is not an isolated vertex of
the graph. This means that there is a partition
},...,,{
21 s
XXX of a set
X
and a set
},,...,,{
21
kkkk
s
of different keys such that
).,...,2,1()()( stXxxexe
tkk
t
=∈⇔=
It is clear that
2≥s . Since otherwise equality
would be fulfilled
)()(
1
xexe
kk
=
for all Xx ∈ .
Therefore, the valence
s
of each non-isolated vertex
is greater than one.
Let's assume that the cipher is not minimal, and
you can zero the probability
k
P of the key
.k
Then
the probabilities
t
k
P
of the keys ),...,2,1( stk
t
= in
the resulting (residual) cipher should be put equal
,/1
μ
since otherwise the transitivity of the cipher
will be violated. However, it follows that it is
necessary to put the probabilities of keys
,kk ≠
′
connected by an edge with one of the vertices
,,...,,
21 s
kkk equal to zero from the condition of
perfection of the cipher with equally probable cipher
values.
Continuing to track the probabilities of vertices
when moving along the edges of a connected
component containing
,k
we get: if ,,,
)2()1(
kkk
,......,
)(r
k – the path in this graph, then the
probabilities
,0=
k
P ,0
)2(
=
k
P and generally
0
)(
=
l
k
P for even ,l but
μ
/1
)1(
=
k
P , and
generally
μ
/1
)(
=
r
k
P for odd
,
r
since the sum of
Table 2: Encryption table.
K
1
x
2
x
3
x
4
x
5
x
6
x
k
P
1
k
1 2 3 6 5 4 1/18
2
k
1 4 6 3 2 5 1/18
3
k
1 6 2 5 4 3 1/18
4
k
2 4 1 5 3 6 1/18
5
k
2 1 6 4 3 5 1/18
6
k
2 5 4 3 1 6 1/18
7
k
3 5 4 1 2 6 1/18
8
k
3 4 6 2 1 5 1/18
9
k
3 2 5 4 6 1 1/18
10
k
4 5 3 1 6 2 1/18
11
k
4 1 5 6 3 2 1/18
12
k
4 6 1 2 5 3 1/18
13
k
5 1 3 6 2 4 1/18
14
k
5 6 4 3 1 2 1/18
15
k
5 3 2 1 6 4 1/18
16
k
6 3 2 5 4 1 1/18
17
k
6 3 5 2 4 1 1/18
18
k
6 2 1 4 5 3 1/18
Construction of Absolutely Failure-free Minimal Data Transmission Systems on Railway Transport
75

the probabilities of keys connected by an edge is
./1
μ
And since the probabilities of keys do not depend on
the path in the graph, we get that this component is a
bipartite graph, all cycles of which are of even length,
and the probabilities of vertices in the fraction
containing
,k
can be put equal to zero, and in the
other fraction equal
μ
/1 , i.e. we get a contradiction
with the fact that
k – an uninsulated vertex of the
graph.
The minimality condition formulated above for
the inclusion of a perfect cipher satisfies the criterion.
Minimality criterion for the inclusion of
perfect ciphers. Let be given an encryption table of
a perfect cipher
B
Σ with
,1>= λ X , λμ ≥=Y
. μπ ≥=K
1. Let's break each of
λ
columns
λ
xxx ,...,,
21
by
μ
columns, numbering all the resulting columns with
indexes
),,( ji where
,,...,2,1
λ
=i .,...,2,1
μ
=j
2. Let's construct
)1,0(
matrix
A
with
π
rows
and
λ
μ
columns corresponding to this encryption
table as follows: at the intersection of the row
k
),...,1(
π
=k and the column ),,( ji we will put one if
and only if,
,)(
jik
yxe =
i.e. if the ciphertext
i
x on
the key
k is encrypted into a cipher value
.
j
y
Otherwise, we set zero.
Table 3: Matrix .A
.
000100010000001000000001000010100000
000001001000000010010000000100100000
0000010010000100000000100001
00100000
001000100000000001000010000100010000
000010000001000100001000100000010000
001000000010100000000
100000001010000
000100010000000010000001100000001000
000010000100100000010000000001001000
00001010000000
0001000100010000001000
000001100000001000010000000010000100
010000000001000010100000001000000100
1000000
00010000001001000010000000100
100000000001000100001000010000000010
010000000100001000100000000001000010
100000000100010000000001001000000010
000100001000010000000010100000000001
01000000001000010010000000100
0000001
001000010000100000000100000010000001


























































=A
Table 4: Matrix
.A
.
000000000000010000000000000000000000
000000000000000001000000000000000000
0000000000000000000100000000
00000000
000000000000000000001000000000000000
000000000000000000000100000000000000
000000000000000000000
010000000000000
000000000000000000000001000000000000
000000000000000000000000010000000000
00000000000000
0000000000001000000000
000000000000000000000000000100000000
000000000000000000000000000010000000
0000000
00000000000000000000001000000
000000000000000000000000000000100000
000000000000000000000000000000010000
000000000000000000000000000000001000
000000000000000000000000000000000100
00000000000000000000000000000
0000010
000000000000000000000000000000000001


























































=A
TLC2M 2022 - INTERNATIONAL SCIENTIFIC AND PRACTICAL CONFERENCE TLC2M TRANSPORT: LOGISTICS,
CONSTRUCTION, MAINTENANCE, MANAGEMENT
76

Then the set of cipher keys is minimal if and only
if the rank of the matrix
A
maximal, equal to
π
.
Let us illustrate the application of this criterion to
the determination of minimality by the inclusion of a
given perfect cipher by an example.
Example 2. Consider an endomorphic cipher with
a set of six ciphertexts. Let
,,,,,{
54321
xxxxxX =
}6,5,4,3,2,1{}
6
=x – a set of ciphertexts; ,{
1
yY =
}6,5,4,3,2,1{},,,,
65432
=yyyyy – a set of cipher
values;
},...,,,{
18321
kkkkK = – a set of keys.
Encryption table of a given perfect endomorphic
cipher with
6==
μ
λ
and key probabilities
18/1=
k
P )18,...,2,1( =k – is this Table 2.
For this cipher, we will create a binary
)1,0(
matrix
A
of 18 rows and 36 columns (Table 3).
In the matrix
,A
for example, the first column
(column (1,1)) in the first three rows contains units
since in the encryption Table 2, the ciphertext is
1
1
=x encrypted on the keys
21
, kk and
3
k in the
cipher value 1. The remaining elements of the column
(1,1) are zero. The remaining columns of the matrix
A
are filled in the same way.
The matrix
A
is equivalent to the matrix
A
(Table 4) and its rank by rows (Gantmacher, 1967)
equal to 18, i.e. equal to the number of keys specified
in the encryption table. This, according to the
criterion, means that the cipher with the encryption
Table 2 is minimal in inclusion.
Consequences of the minimality criterion for the
inclusion of perfect ciphers:
1. For the minimality of the set of cipher keys, it
is necessary to perform an inequality
λ
μ
π
≤
.
2. For an endomorphic minimal perfect cipher, the
inequality holds
)1( −≤
λ
λ
π
.
3 CONCLUSIONS
Thus, the paper considers a graph approach to the
construction of absolutely failure-free data
transmission systems. Within the framework of this
approach, a necessary and sufficient condition for the
minimality of a perfect cipher by inclusion is proved.
A minimality criterion for the inclusion of non-
endomorphic (endomorphic) perfect ciphers is
obtained. Examples illustrating the concepts used,
obtained theoretical statements and constructions of
perfect ciphers are constructed. In addition, the paper
presents tables of encryption of perfect ciphers that
ensure the protection of the communication channel
in transport.
REFERENCES
Medvedeva, N. V., Titov, S. S., 2015. Non-endomorphic
perfect ciphers with two ciphertexts. Applied discrete
mathematics. Appendix. 8. pp. 63-66.
Medvedeva, N. V., 2016. On analogs of the Shannon's
theorem for perfect ciphers. CEUR Workshop
Proceedings. 1825. pp. 232-239.
Medvedeva, N. V., Titov, S. S., 2016. Geometric model of
perfect ciphers with three ciphertexts. Applied discrete
mathematics. Appendix. 12. pp. 113-116.
Medvedeva, N. V., Titov, S. S., 2020. Constructions of non-
endomorphic perfect ciphers. Applied discrete
mathematics. Appendix. 13. pp. 51-54.
Medvedeva, N. V., Titov, S. S., 2021. To the task of
describing the minimum on the inclusion of perfect
ciphers. Applied discrete mathematics. Appendix. 14.
pp. 91-95.
Shannon, K., 1963. Communication theory in secret
systems. Works on information theory and cybernetics.
pp. 333-402.
Alferov, A. P., Zubov, A. Yu., Kuzmin, A. S.,
Cheremushkin, A. V., 2001. Fundamentals of
Cryptography. p. 479.
Zubov, A. Yu., 2003. Perfect ciphers. pp. 160.
Nosov, V. A., Sachkov, V. N., Tarakanov, V. E., 1983.
Combinatorial analysis (Non-negative matrices,
algorithmic problems). Results of science and
technology. Ser. of Theor. of Prob. of Mat. Stat. Theor.
Cybernet. 21. pp. 120-178.
Ore, O., 1980. Graph Theory. pp. 336.
Harari, F., 1973. Graph theory. p. 300.
Gantmacher, F. R., 1967. Matrix Theory. pp. 575.
Construction of Absolutely Failure-free Minimal Data Transmission Systems on Railway Transport
77