Mathematical Modeling of the Management of the Processes of

Training Specialists of Transport Universities

Natalia Valeryevna Kalganova

and Nikolay Pavlovich Chuev

Ural State University of Railway Transport, Ekaterinburg, Russia

Keywords: Educational process, modeling, mathematical model, control matrix; management of the pro-cesses of training

specialists.

Abstract: The article presents scientific research in the field of mathematical modeling, namely the construction of a

mathematical model for managing the processes of training specialists. When formalizing this complex

process, problems arise that are explained by the presence of a large number of factors that ensure a high-

quality educational process. Therefore, great importance is attached to the use of the mathematical apparatus

in the implementation of quality management of the educational process in higher educational institutions.

The article presents the construction of mathematical models describing the most important links between the

characteristics of the educational process at the university. The considered mathematical models contribute to

the development and adoption of managerial decisions on the strategy of managing the processes of training

specialists.

1 INTRODUCTION

At the present stage of the socio-economic

development of Russia, the development of the higher

education system, the training of highly qualified

specialists depends on the achievements in all areas

of activity of each university in the country. This

requires: improving the system of effective

management of the processes of the university, the

introduction into the practice of developing

universities of new scientific and pedagogical

achievements that correspond to the subject of

management and the requirements of modern

education (Ansoff, 1989). To do this, it is necessary

to solve the following tasks:

1. Development and implementation of methods

and means of planning and management as a

complex of components of effective

management of high-quality training of

specialists.

2. Provision of qualified personnel: managerial,

managerial, scientific, pedagogical; including

their training, systematic professional

development and the effectiveness of forms of

work organization.

https://orcid.org/0000-0002-4117-8329

https://orcid.org/0000-0003-1549-3533

3. Development of methods and means for the

effective use of material and technical

resources in the organ-ization of the

educational process, ensuring the completeness

and reliability of resource support.

4. The use of modern methods of systems

analysis, strategic forecasting, effective

management and mathematical modeling.

Modeling as a universal method of cognition of

social and pedagogical problems, the tasks of

didactics today is an integral part of the study of the

educational process. The beginning of modeling is a

goal setting that takes into account modern

educational problems, the complexity of which

determines their complex nature. The key task of

building and applying a mathematical model is to

prepare a competent, qualified specialist.

The constructed mathematical model will allow

choosing the optimal control actions, as well as

making an objective forecast of the state of the control

system (Samarsky, Mikhailov, 2005; Neymark, Yu.

I., 2010).

The article (Solodova, 2005) considers a rather

simple from a mathematical point of view and a more

Kalganova, N. and Chuev, N.

Mathematical Modeling of the Management of the Processes of Training Specialists of Transport Universities.

DOI: 10.5220/0011579300003527

In Proceedings of the 1st International Scientiﬁc and Practical Conference on Transport: Logistics, Construction, Maintenance, Management (TLC2M 2022), pages 82-88

ISBN: 978-989-758-606-4

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

general conceptual model developed by the doctor of

philosophical sciences A.S. Panarin.

отраслмежотр

прикладфундам

работыучебы

(1)

These inequalities (1) can be interpreted as

follows: the first inequality indicates a higher growth

rate of cross-sectoral knowledge compared to sectoral

knowledge. The second inequality indicates an excess

of the growth rate of fundamental knowledge over the

growth rate of applied knowledge. In the third

inequality: the growth rate of study time must be

greater than the growth rate of working time

(Gianetto, Wheeler, 2005).

Projecting system (1) onto the educational process

of the university, the following conclusions can be

drawn: inequalities 1 and 2 determine the content of

education, thus, these inequalities organize the

activities of the university to develop qualification

requirements, curriculum, curriculum and thematic

plan. university plans; Inequality 3 expresses the

principle of lifelong education, the principle of self-

development, formalizes the system of additional

education.

The basis for the development of these

management models is the state standard, which not

only fixes the subject area, but also formulates the

learning objectives. Gosstandart sets the legal and

substantive basis for more detailed knowledge

models designed for a specific training course or part

of it (module), or sets the search vector for the optimal

knowledge acquisition process.

For an adequate choice of a mathematical

analytical model, it is necessary to formalize its

parameters:

− to consider educational texts of a textbook,

lecture notes, records of problem solutions, etc.

as information flows of a certain finite amount

of knowledge, taking into account the

sequential dynamics of their development and

memorization;

− to build and investigate the information flow as

a model of knowledge transfer "teacher-

learners" in order to determine the main

characteristics of their interactions,

connections, to identify the effectiveness of this

model in terms of adequate management of the

individual process of mastering professional

knowledge by each student, group, course;

− the mathematical model should form a finite set

of control parameters (components), with the

help of which control decisions can be made for

the further improvement of the educational

process at the university. The managerial

function of the regularity of the process,

contained in mathematical models, can help

management departments to make

scientifically sound decisions to improve it.

The problems of constructing mathematical

models of optimal control of the processes of training

qualified specialists have been considered by many

authors, for example (Vasiliev, 1997; Avetisov,

1998).

As you know, one of the management concepts

that emerged in the 80s of the last century is the

process approach. In accordance with this concept,

the entire activity of a higher educational institution

is a set of sequential and interrelated processes. The

process approach is one of the key elements of

improving the quality of training, therefore, effective

quality management is impossible without replacing

subjective descriptions with objective assessments of

the learning process by building appropriate

mathematical models (Kalganova, 2021; Golubeva,

2016).

1.1 Building a Mathematical Model for

Managing the Processes of Training

Specialists

Studying the content of the educational process,

analyzing statistical data, establishing cause-and-

effect relationships between the elements of the

process being studied, which can be described

quantitatively. This made it possible to formulate the

relationship between the parameters and build a

mathematical model in the form of equations between

the main objects of the model (Stepanov, 2006).

Let x(t) be the amount of knowledge accumulated

by the student at a certain point in time t, including:

the ability to reason, solve problems, understand the

material presented by the teacher. The unit is

important here. As a measure for x(t), you can enter

the sum of the exam grades, the number of

successfully passed credits, etc.

In this study, it is logical to consider the functions

introduced to build a mathematical model as

dimensionless quantities. Thus, the conventional

units (AU) act as a fixed number of credit units. A set

of conventional units is a system of theoretical

knowledge and practical skills formed in the process

Mathematical Modeling of the Management of the Processes of Training Specialists of Transport Universities

of implementing the educational process at a

university. Based on the results of examinations for

the differentiated assessment of student performance

in the learning process, it is possible to determine x1

– the minimum value of CU, but sufficient to

complete the training, x2 – the maximum value of

CU, for graduates who have received honors. degree

after graduation.

The task of constructing a mathematical model,

thus, acquires an additional condition: to find the law

of assimilation of knowledge during the period of

study by each student who has the initial amount of

knowledge upon entering the university x0 and who

completed training with the amount of knowledge x ≥

x2.

As a result, the inequality holds for the function

x(t):

x1 ≤ x(t) ≤ x2+d.

where d – is additional knowledge to the main

program (electives, courses, self-education according

to interests, etc.).

The model in this case will have the form:

()



=𝛼



𝑥

(

𝑡

)

 𝑥



𝑥

(

𝑡

)

, (2)

where dx(t)/dt – the speed of mastering conventional

units;

α1 – proportionality coefficient;

x(t) – the number of conventional units mastered

by students at a time t;

x2 – x(t) – the amount of knowledge on the

program required for successful completion of the

training.

The coefficient α1>0 depends on the individual

abilities of the student, his attitude to educational

work and the level of the previous one, up to the

moment t, of the qualitative development of the

educational material. The right side of equation (1)

depends only on previously acquired knowledge.

Please note that the value of x(t) with proper self-

organization of the student, tends to only increase;

therefore, it makes sense to apply model (1) on time

intervals: one semester or an academic year, a four-

year study for bachelors or a five-year period for

specialists..

Equation (1), known as the Verhulst equation,

originally arose from the study of population change.

This mathematical model is widely used not only in

various fields of natural science, but also plays an

important role in understanding the mechanisms of

applying nonlinear dynamics to socio-economic

models, in the tasks of introducing technological

innovations and developing science (Zhirkov, 2016;

Bagrinovsky, 1980).

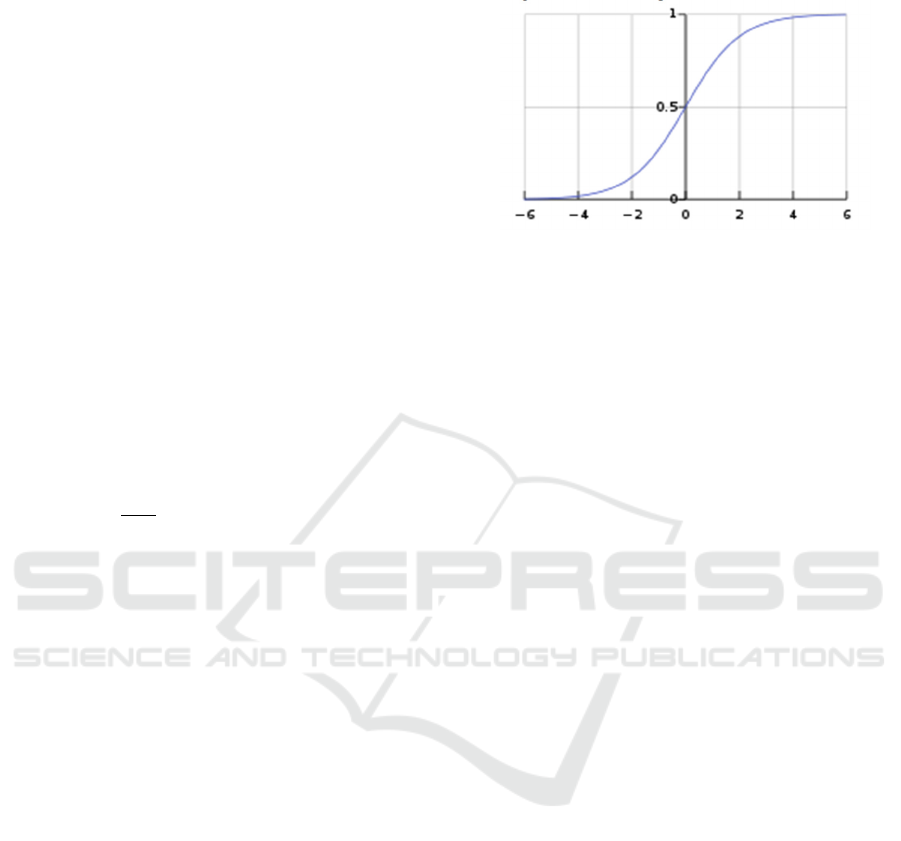
The dynamics described by the Ferhulst equation

is a logistic curve in Figure 1.

Figure 1: Logistic curve for x_2 = 1, x_0 = 0,5, α_1= 1.

The completeness and target volume of

knowledge necessary for the successful assimilation

of educational material during the period of study at

a university is a key component of the quality of

education, therefore, to study their dynamics, it is

advisable to use a logistic equation. However, other

parameters (directions) of the university's activity

also affect the successful assimilation of educational-

theoretical and practical material when studying at a

university.

Two important components are considered that

directly affect the quality of training of specialists.

This is the qualitative composition of the teaching

staff of the university and the presence of a modern

and fully material and technical base (Kalganova,

2020).

Let's consider the first component of the

pedagogical process and its influence on the quality

of training of specialists. The pedagogical activity of

the teacher is united by the main components of this

activity:

− transfer of knowledge through direct

interaction «teacher - student»;

− methodical work;

− scientific work;

− educational work.

In order to formalize a rather complex,

multifaceted activity of a teacher and reflect it in the

form of quantitative characteristics of numerical

assessments, it is necessary to find the criteria of

pedagogical work and the value of such assessments;

the methodology for calculating rating indicators is

partially presented in Table 1.

Thus, using the methods of organizing ratings at

the university using quantitative and qualitative

indicators of teachers' academic performance in

points, it is possible to introduce a numerical,

functional relationship with other parameters of the

mathematical model being developed.

TLC2M 2022 - INTERNATIONAL SCIENTIFIC AND PRACTICAL CONFERENCE TLC2M TRANSPORT: LOGISTICS,

CONSTRUCTION, MAINTENANCE, MANAGEMENT

Table 1: Methodology for calculating the rating indicators

of teachers.

Indicators The value

of the

indicator in

oints

Educational activities

Innovative pedagogical activity (online

courses; development of practice-

oriented technolo

ies; tests

)

0-3

Students' assessment of the teacher's

activities by factors: the availability of

material, the development of work

programs by disciplines, practices, - the

quality of classes

2-5

Professional development over the last

0-2

Availability of developed educational

and methodological documentation for

training courses

0-3

Preparation of students for international

and (or) republican Olympiads,

competitions

0-2

Research wor

Participation in research, research and

development work, in obtaining grants,

fulfillment of business contracts

0-3

Obtaining patents/certificates issued to

the universit

0-3

Scientific

ublications 0-2

References to the author's works

received in the reporting year

0-2

Reports at conferences 0-2

Defense of dissertations 0-2

Let us introduce the function y(t) – the rating

indicators of the teacher, as a measure of the

effectiveness of the influence of the teaching staff on

the quality of teaching. The numerical value of the

overall grade for each teacher will satisfy the

inequality:

y1 ≤ y(t)≤ y2,

where y1 – the lowest rating value in conventional

units (points), y2 – maximum rating value.

The function y(t) will be considered

dimensionless, which characterizes the direct effect

on the increase in the growth rate of the volume of

students' knowledge with the coefficient β1.

Coefficient β1 there is a function depending on

β11 – staffing with teaching staff, β12 – optimal ratio

of teachers with academic degrees of candidate and

doctor of sciences, β13 – the level of scientific and

scientific-methodical work of each teacher, β14 –

regular completion of refresher courses and other

ranking indicators.

Let us introduce the function z(t) – the relative

total cost of all scientific and educational equipment

The function z(t) will be considered

dimensionless in conventional units and will have a

direct impact on the increase in the growth rate of

students' knowledge with a coefficient of y1. The

effectiveness of the influence of educational and

material resources of the university on the quality of

training of specialists can be expressed using the

coefficient y1. This coefficient represents a certain

function depending on y11 – the full staffing of the

educational and material base of the university, y12 –

the optimal use of scientific and educational

laboratories in the educational process, y13 –

compliance with the modern level of scientific and

educational laboratories, y14 – the availability of

testing and training grounds, etc. Taking into account

the above, we finally come to the construction of the

following mathematical model for managing the

processes of training specialists.

)()(γ)(β))()((

)(

11121

tftztytxxtx

tdx

+++−=

)()(γ)(β

)(

222

tftzty

tdy

++=

)()(γ)(β

)(

222

tftzty

tdy

++=

(2)

where the functions fi(t) 𝑖 = 1,2,3, can act as

additional conditions due to additional sources of

knowledge, lectures by foreign scientists, the use of

research and testing laboratories of research

institutes, enterprises.

A preliminary analysis of the relationship

between the parameters included in the construction

of a mathematical model allows us to conclude that it

is possible to build a mathematical model for

managing the processes of training specialists using

systems of three linear differential equations.

Such a system, composed according to the same

principle as system (2), will have the following form.

)()(γ)(β)(

)(

1111

tftztytx

tdx

+++=

)()(γ)(β

)(

222

tftzty

tdy

++=

)()(γ

)(

tftz

tdz

(3)

We introduce the matrix А of coefficients of the

corresponding system of linear differential equations

(3):

A = 

𝛼



𝛽



𝛾



0𝛽



𝛾



00𝛾



. (4)

Mathematical Modeling of the Management of the Processes of Training Specialists of Transport Universities

Additionally, we introduce two matrices:

− matrix – a column of unknown functions

X = 

𝑥(𝑡)

𝑦(𝑡)

𝑧(𝑡)

; (5)

− matrix – a column of pivot members

F = 

𝑓



(𝑡)

𝑓



(

)

𝑓



(

𝑡

)

. (6)

Using the introduced matrices, system (3) can be

briefly written in matrix form:

XAXF

(7)

Please note that system (2) is nonlinear, and an

analytical solution in the form of a solution formula

is not possible. To study the solutions of this system,

the use of approximate or numerical methods is

required.

Therefore, let us consider in more detail the

solution of the linear system (3).

For systems (3), (7), we formulate the Cauchy

problem or the problem with initial conditions for t =

x(0) = x

, y(0) = y

, z(0) = z

(8)

1.2 Study of the Mathematical Model and

Solution of the Cauchy Problem for

Systems of Differential Equations (3)

Let us prove the existence and uniqueness theorem

for the solution of the Cauchy problem for system (3)

of differential equations with the initial conditions

(8).

Theorem.

Let the functions f1(t), i = 1, 2, 3 be continuous

on some interval t∈[0,T] then the Cauchy problem for

the inhomogeneous system of first-order differential

equations (3), (7), (8) with constants coefficients will

have the only solution.

Proof.

The third differential equation of system (3) is a

first-order linear equation with a solution (Stepanov,

2006):

𝑧

(

𝑡

)

= 𝑒







𝑧





𝑓



(

𝜏

)

𝑒







𝑑𝜏





=φ



(

𝑡

)

, (9)

where the function φ

(t) denotes the solution to the

third equation of the system (3).

Let us write the second equation taking into

account (9) as follows:

)()(γ)(β

)(

2122

tftty

++=

(10)

the resulting differential equation is also a first-

order linear equation, and its solution φ

(t) will have

the form:

𝑦

(

𝑡

)

= 𝑒







𝑦





(

𝛾





(

𝜏

)

+𝑓



(𝜏)

)

𝑒







𝑑𝜏





=



(𝑡), (11)

We continue to consistently perform similar

actions, we find the solution to the first equation:

𝑥

(

𝑡

)

= 𝑒







𝑥





(



(

𝜏

)

+ 𝑓



(𝜏)

)

𝑒







𝑑𝜏





 =



(𝑡). (12)

Suppose that the functions f (t), i=1, 2, 3 are

bounded,

𝑓



(

𝑡

)

<В, 𝑖=1,2,3.

Then for all 𝑡∈[0,𝑇] we obtain the inequalities:

].0[,

||||])([||)(|

γγ

3333

TtconstDxx

zdfztz

∈=<+≤+=

=+≤+=

−−







ττ

Finally:

|z(t)| ˂ D

Similar inequalities can be obtained for all

subsequent solutions of the systems of equations (3)

and (7).

Assume the existence of two x

(t) and x

(t)

solutions of system (3), (7) with initial conditions (8),

then the function X(t)=X

(t) - X

(t) will satisfy a

homogeneous equation fo f

= f

= 0 and zero

initial conditions.

Then from formula (9) follows z(t)=0, similarly,

formula (11) follows y¯(t)=0 and¯x (t)=0 Hence the

equality x

(t) = x

(t).

Thus, there is only one solution for problem (9) –

(10).

The theorem of existence and uniqueness of the

solution of the Cauchy problem for systems of

differential equations (3) and (7) with initial

conditions (8) is proved.

Based on the obtained solution of the Cauchy

problem for systems (2), (3), (7). it is possible to

develop proposals for managing the learning process

by choosing the values of the initial valuesx

, y

, z

and positive coefficients α

, β

, y

of the

matrices А and F, the elements of which are a set of

tunable parameters affecting the optimal control of

solutions of systems ordinary differential equations

(2), (3) or (7). By varying the elements of the matrix

А (coefficients of the system) and the function fi(t)

(free terms of the system), one can achieve an

TLC2M 2022 - INTERNATIONAL SCIENTIFIC AND PRACTICAL CONFERENCE TLC2M TRANSPORT: LOGISTICS,

CONSTRUCTION, MAINTENANCE, MANAGEMENT

increase or decrease in the rate of change of x(t) – the

amount of accumulated knowledge by a student.

Let's introduce a definition. The set of coefficients is

called α

, β

, y

and functions fi(t) of system

(2), matrices (4), (6) of systems (3), (7) control

matrices for solving systems of ordinary differential

equations (2), (4) or (6), i.e. this is a set of control

parameters from a set of matrix elements А and the

time functions of the matrix F, which have a direct

impact on the solutions of systems (2), (4), (6) –

systems that model the management of the future

development of the educational system of the

university and the processes of training specialists.

1.3 Verification of the Mathematical

Model

We will check the verification of mathematical

models, that is, the correspondence of the solutions of

systems of differential equations to the real

educational processes of the university, the optimal

control of the processes of training specialists.

Analysis of the construction of models, for

example, system (2), shows that in the process of

building the target value x

– the full amount of

knowledge for the formation of a specialist, is an

integral part of the system to which the function

aspires x(t) при t → ∞.

The members β

y(t), y

z(t), f

z(t), system (3) only

accelerate the achievement of the target value in a

limited time interval. This solution shows the

possibility of organizing training that is optimal for

all students at the same time. In this case, the

achievement of the target results depends on the

initial position and control matrices for solving the

systems of ordinary differential equations.

Let us give examples showing the role of the

control matrix А (4) for achieving target values in

managing the process of training specialists.

Example 1.

Consider a system of three equations and use the

MathCAD 15 software package (Makarov, 2009) to

obtain a numerical-graphic solution.

Given the system: (Given)

Here the steering matrix has the form:

A = 

0.1 0.008 0.034

0.027 0.27 0.024

0 0 0.67



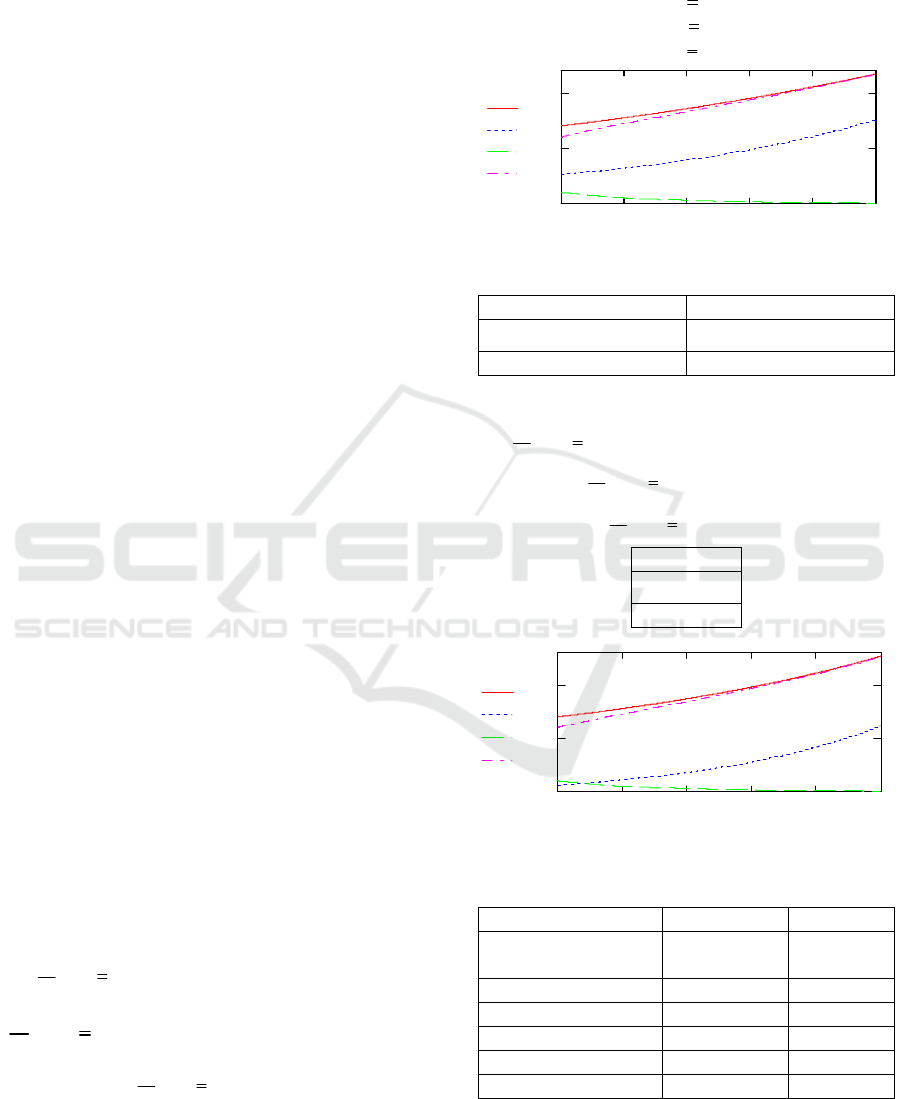
Figure: 2: Graphs of functions x(t),y(t), z(t) and x(t)-z(t).

(0) = 7.0

(5) = 11.698

y(0) = 2.6 y(5) = 7.572

(0) = 1

(5) = 0.035

Consider the case when some coefficients are zero

(0) = 7.0

y(0) = 0.6

(0) = 1

Figure: 3: Graphs of functions x(t), y(t) and z(t).

Let's make calculations

(0) = 7

(0) = 0,6

(0) = 1

x(5) = 12,712 y(1) =1,091

z(5) =

0,035

(1)

–

0,6 = 0,491

(2) = 1,788

(2)

–

(1) = 0,697

(3) = 2,776

(3)

–

(2) = 0,989

(4) = 4,179

(4)

–

(3) = 1,403

(5) = 6,17

(5)

–

(4) = 1,991

The graphs in Figures 2, 3 show an increase in the

volume of students' knowledge while improving the

xt()

0.1 x t()⋅ 0.008 y t()⋅+ 0.034 z t()⋅−

yt()

0.27 y t()⋅ 0.028 x t()⋅− 0.024 z t()⋅+

zt()

0.67− zt()⋅

x0( ) 7.0

y0( ) 2.6

z0( ) 1.0

0 1 2 3 4 5

xt()

yt()

zt()

xt() zt()−

xt()

0.1 x t()⋅ 0.08 y t()⋅+ 0.034 z t()⋅−

yt()

0.35 y t()⋅ 0.2+

zt()

0.67− zt()⋅

0 1 2 3 4 5

xt()

yt()

zt()

xt() zt()−

Mathematical Modeling of the Management of the Processes of Training Specialists of Transport Universities

quality of the educational process and educational and

material support.

Indeed, the results of analytical studies, the

examples given show that it is possible to develop

proposals for managing the learning process based on

the solutions of systems (3), (7), choosing for each t

the values of the initial values

, y

, z

the values of

the coefficients as a set of adjustable parameters

affecting the optimal control of the solution of the

systems of ordinary differential equations (3) or (7),

as well as the achievement of target values.

Thus, the models of the educational process

management process (2), (3) and (7) made it possible

to obtain a number of practical recommendations

expressed in numerical form. At the same time, there

was no need to clarify methods for measuring the

amount of knowledge available to students. It is

sufficient that these quantities satisfy the qualitative

relations leading to the systems of equations (2), (3),

and (7).

2 CONCLUSIONS

The article discusses mathematical models that

contribute to making managerial decisions about an

alternative choice of strategy for managing the

processes of training specialists.

The first mathematical model (2) allows you to

build an optimal acquisition strategy, taking into

account the initial state and the formulated target

value at the end of the training period (bachelor's,

specialist, master's degree) based on the logistic

function. obtained using a differential equation. This

model makes it possible to predict and implement

strategic programs of the educational process of the

university for a longer period.

Based on the analysis of the relationship between

the parameters included in the construction of a

mathematical model, a mathematical model for

managing the processes of training specialists using

systems of three linear differential equations with

constant coefficients has been built.

The matrices А and F of the coefficients of the

corresponding system of linear differential equations

and their free terms determine the control matrices for

the solution of the systems of ordinary differential

equations (3) and (7), which have a direct impact on

the process of managing the training of specialists.

The article conducts research on the verification

of mathematical models based on the consideration of

control matrices and the multivariance of parameters

included in the solution of differential equations that

form the basis of the mathematical models under

consideration.

REFERENCES

Ansoff, I., 1989. Strategic management. p. 358.

Samarsky, A. A., Mikhailov, A. P., 2005. Mathematical

modeling. p. 320.

Neymark, Yu. I., 2010. Mathematical modeling as a

science and art. p. 420.

Solodova, E. A., Antonov, Yu. P., 2005. Mathematical

modeling of pedagogical systems. p. 332.

Vasiliev, V. N., et al. 1997. On mathematical models of

optimal control of the system of training specialists. p.

136.

Avetisov, A. A., Kamyshnikova, T. V., 1998. Optimization

model for assessing and managing the quality of

student training at a university. pp. 105-109.

Kalganova, N. V., 2021. Mathematical modeling of the

process of sustainable development of the personnel

potential of industry universities. E3S Web of

Conferences. p. 296.

Golubeva, N. V., 2016. Mathematical modeling of systems

and processes. p. 192.

Zhirkov, A. M., 2016. Mathematical modeling of systems

and processes. p. 192.

Bagrinovsky, K. A., Busygin, V. P., 1980. Mathematics of

planning decisions. p. 224.

Kalganova, N. V., 2020. Mathematical models of optimal

management of the material support of educational and

scientific activities of industry universities. Bulletin of

USTU. 4, pp. 120-126.

Gianetto, K., Wheeler, E., 2005. Knowledge Management.

p. 192.

Stepanov, V. V., 2006. Course of differential equations. p.

472.

Makarov, E. G., 2009. MathCAD: training course. p. 384.

TLC2M 2022 - INTERNATIONAL SCIENTIFIC AND PRACTICAL CONFERENCE TLC2M TRANSPORT: LOGISTICS,

CONSTRUCTION, MAINTENANCE, MANAGEMENT