A Combinatorial Problem of Generating a Network of Routes of

Public Transport in Cities

Mikhail Yakimov

Russian Transport Academy, Moscow, Russia

Keywords: Public transport, route network, transport demand, correspondence matrix, transport model.

Abstract: The formulation and options for solving the problem of constructing a route network of public transport based

on information about the current transport demand are proposed. The ways of formalization of the transport

demand model based on the correspondence matrix are described. The statement and the first two iterations

of solving a part of the combinatorial-optimization problem of forming a route network of public transport,

which consists in the initial construction of a set of routes in the field of transport demand, are given. A

scheme for choosing the second and third stops on the generated routes is given. The results of the second

iteration of building a route network in the field of transport demand for the city of Berezniki in the Perm

Region (Russia) are presented. An assessment is given of the generalized characteristics of the found routes

and the entire network as a whole.

1 INTRODUCTION

With an increase in the level of motorization of the

population, and, accordingly, a significant increase in

the costs of the urban community for moving using

individual transport, the tasks of ensuring transport

accessibility of the population using public transport

come to the fore. The pattern of settlement of most

cities in the world, established in the middle of the

last century, has undergone significant changes in

recent decades.

The structure of transport mobility of the

population is changing radically due to changes in the

structure of employment of the population. The

global processes taking place in the economy,

affecting the employment of the able-bodied part of

the population and the subsequent change in the

structure of the settlement of people, require a serious

revision of the operation of public transport,

especially in large urban agglomerations.

The basis for the effective functioning of public

transport is determined, first of all, by the

configuration of its route network, as well as the types

of facilities operating on individual routes and

individual urban areas. The evolutionary process of

optimizing and adjusting the route network, created

https://orcid.org/0000-0002-7627-4791

decades ago, is not always able to meet the transport

needs of the population that are currently required for

public transport. In certain cases, when solving the

problem of constructing an optimal route network, it

is advisable to distance oneself from the

configurations of familiar routes, modes and types of

transport that have existed in a particular city for

many decades.

It seems interesting to solve the problem of

building a fundamentally new route network, based

only on knowledge of the current transport demand in

a particular city.

The object of the research is the system of public

transport. The subject of the study is the route

network of public transport.

2 MATERIALS AND METHODS

The initial data for solving the problem is a set of

elements that determine the structure and

characteristics of the transport demand that has

developed in the territory, everything that is called the

transport demand model in the process of transport

modeling. At the same time, it should be noted that,

in contrast to the creation of a transport demand

Yakimov, M.

A Combinatorial Problem of Generating a Network of Routes of Public Transport in Cities.

DOI: 10.5220/0011580700003527

In Proceedings of the 1st International Scientiﬁc and Practical Conference on Transport: Logistics, Construction, Maintenance, Management (TLC2M 2022), pages 151-155

ISBN: 978-989-758-606-4

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

151

model based on determining the study area to

transport areas, in the case of setting and solving the

combinatorial optimization problem of forming an

efficient city transport system, the initial data, and,

accordingly, the transport demand model should be

detailed not to the transport area, but to each stopping

point of public transport on the road network, as

places of generation and consumption of passenger

flows (Yakimov, 2017; Desaulniers, 2017; Buslaev,

2013; Buslaev, 2015).

In this regard, a set of initial data is presented as a

set of several matrices: a correspondence matrix, a

cost matrix for overhead lines, a cost matrix for a real

network, an adjacency matrix, and a matrix of paired

stops.

In addition, it is required to use geoinformation

tools that allow linking data on transport demand to

existing objects of the transport offer, namely, to the

road network existing in the city (Zhao, 2003; Baaj,

1995; Murray, 2003).

It is possible to carry out the primary generation

of the route network of public transport throughout

the city in several iterations, with different accuracy,

detail, and a set of initial data. The choice of the initial

stop on the route at all iterations is determined on the

basis of a set of data that represents an assessment of

the volume of passenger traffic at the stop, as well as

infrastructural opportunities for organizing the final

stopping point, such as settling and turning areas,

additional infrastructure that ensures a long stay of

the bus at the stopping point and crew replacement.

The more passenger traffic at a stop, as well as the

more developed the technological infrastructure for

servicing rolling stock, the more likely it is that this

stop will be chosen as the initial stop of the route.

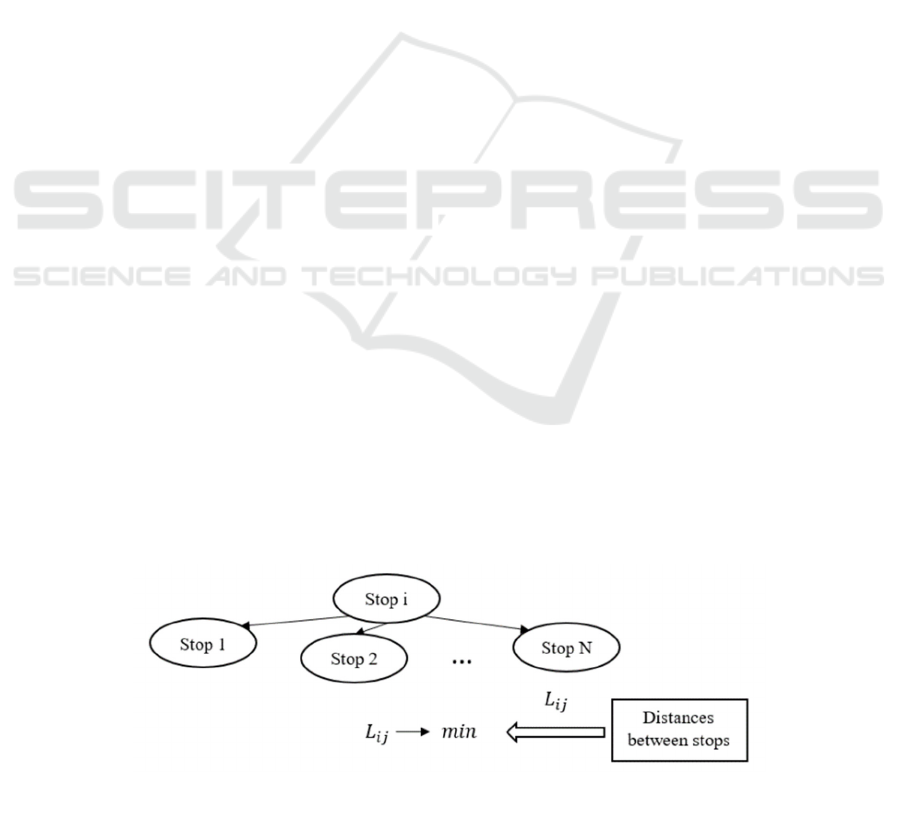
The first iteration is building routes based on

distances between stops. The initial data are the

coordinates of the stops and the distances between

them. The assumption is that the routes are built

without taking into account the road network, along

straight sections between stops, taking into account

the distances between stops (Figure 1).

The second iteration is the construction of routes

based on the cost matrix and the correspondence

matrix.

The initial data are the coordinates of the stops,

the matrix of correspondences. The assumption is that

the routes are built without taking into account the

road network, along straight sections between stops,

taking into account the correspondence matrix

between stops.

The choice of the initial stop on the route at all

iterations is determined on the basis of an estimate of

the passenger flow at the stops, i.e. the greater the

passenger flow at the stop, the more likely it is that

this stop will be selected. At the same time, routes

should start at stops with the appropriate

infrastructure, that is, settling and turning areas.

Route end: reaching the average route length in the

existing route network. Repeat stops in routes:

starting stops of routes are controlled, the starting stop

of a route cannot be the start of another route.

Duplication of routes is possible no more than two

stops in a row.

The algorithm is based on the choice of

subsequent stops of the route in such a way as to

minimize the costs of traveling to the end points of

transport correspondence routes starting from

previous stops. Let's consider the route construction

algorithm.

The first stop is selected from the list of stops that

are the final stops in the routes in the existing route

network. Next, from the entire list of stops, the stop

with the maximum volume of correspondence

between the first and second stops is selected.

Stops for which the distance to the previous stop

on the route is less than the distance to the last

selected stop on the route become inactive. This is

necessary so that the route does not change direction

to the opposite and is more straightforward. The

totality of such stops form an inactive zone.

Figure 1: Sequence of stops when building routes based on distances.

TLC2M 2022 - INTERNATIONAL SCIENTIFIC AND PRACTICAL CONFERENCE TLC2M TRANSPORT: LOGISTICS,

CONSTRUCTION, MAINTENANCE, MANAGEMENT

152

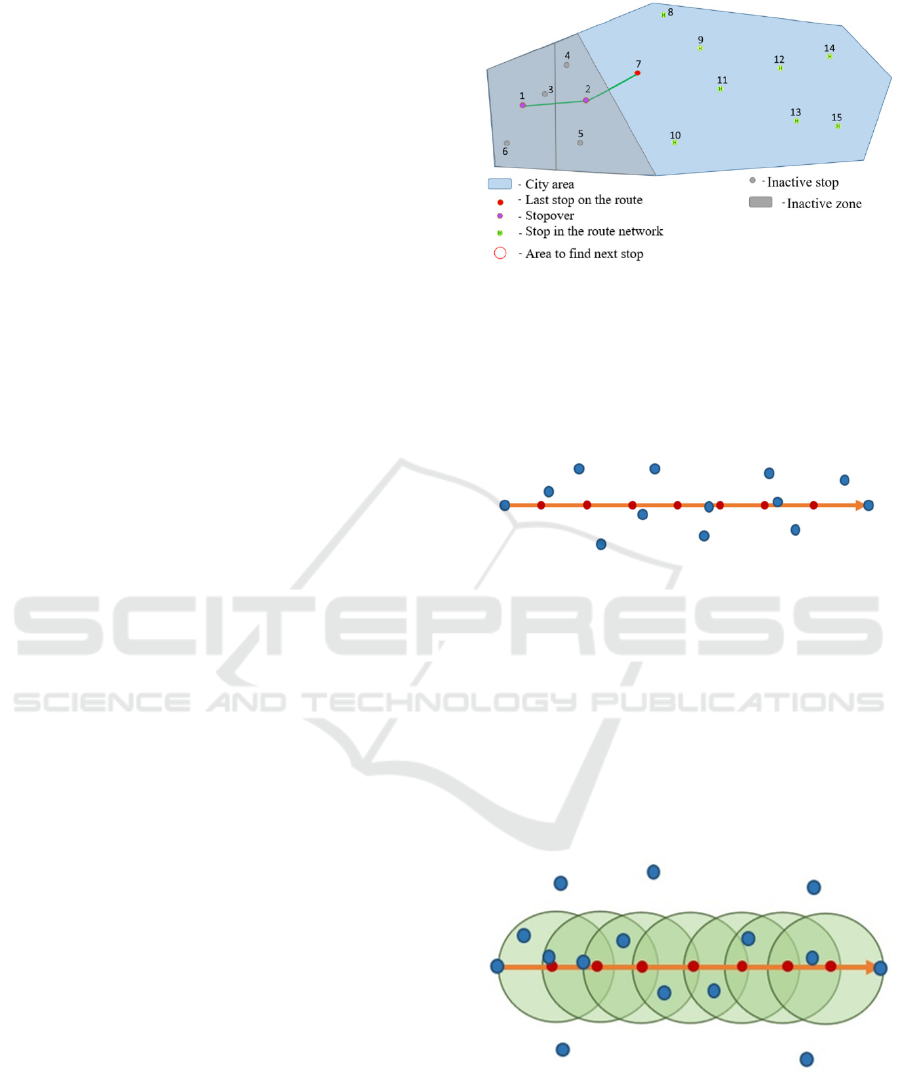
31 32

61 62

stop 3 is inactive

stop 6 is inactive

<→

(1)

where

- cost matrix value between stop i and stop

j, meters; i, j – stop number.

After adding each stopping point, the

correspondence matrix is adjusted. Those

accumulated correspondences that had an added

stopping point as a target are subtracted from the

correspondence matrix (zeroed).

For those accumulated correspondences for which

the targets are further away, the rows of the

correspondence matrix are added to the row of the

added stopping point, the original rows of the

correspondence matrix are reset to zero. Thus, when

building a route, the entrance and exit of passengers

on a real flight is simulated.

:0x =

(2)

where

- correspondence matrix values between

stop 1 and stop 2, people/day.

{

}

{}

221

4, 5,7,8,9,10,11,12,13,14,15

4, 5, 7, 8, 9,10,11,12,13,14

:0, ,15

iii

xxxi

+==

(3)

where

- correspondence matrix values between

stop i and stop j, people/day.

We also find the next stop within a radius of

500m. We count the plots for all suitable stops and

select the stop with the maximum plot value. When a

new stop is selected, the inactive zone also increases.

Adding subsequent stops is done in a similar way

(Figure 2).

42 47

52 57

stop 4 is inactive

stop 5 is inactive

<→

(4)

where

- cost matrix value between stop i and stop

j, meters.

:0x =

(5)

where

- correspondence matrix values between

stop 2 and stop 7, people/day.

{}

772

8,9,10,11,12,13,14,15

8, 9,10,11,12,1

3,14,1

:0, 5

iii

xxx

)

where

- correspondence matrix values between

stop i and stop j, people/day.

Figure 2: Choice of the fourth stop of the route.

With such a route construction, a case may arise

when the route passes in the vicinity of a stop, but

bypasses it. In this case, this stop is added to the route:

− The current section of the route is divided by n

equidistant points (Figure 3).

Figure 3: Example of splitting a route section to add

intermediate stops.

− Let's find the intermediate stops lying in the

vicinity of the route section at a distance r:

0, 25rL=⋅

(7)

where L - the length of the segment, meters.

To do this, circles with radius r are built from the

points of the route section. Belonging to the circle is

checked by comparing the distance from the stop to

the center of the circle (Figure 4).

Figure 4: Search for intermediate stops in the vicinity of a

route segment.

Stops that are inside the circle are added to the

route. If there are several stops in one circle, they are

added in ascending order of distance to the initial stop

of the considered section of the route.

A Combinatorial Problem of Generating a Network of Routes of Public Transport in Cities

153

3 RESULTS AND DISCUSSION

The city of Berezniki (Perm Region, Russia) was

chosen as one of the cities for testing scientific

research.

A typical set of initial data was formed, consisting

of:

− List of stopping points on the territory of

Berezniki (224 stops);

− Coordinates of stopping points on the territory

of Berezniki;

− List of starting and ending stopping points of

the existing network of municipal regular

transportation routes operating in the territory

of Berezniki;

− Correspondence matrix linked to stopping

points on the territory of Berezniki;

− Cost matrix linked to stopping points on the

territory of Berezniki;

− Matrix of connectivity of stopping points on the

territory of Berezniki.

On the basis of the above algorithms, on the basis

of the criterion of minimizing the time costs of

passengers, algorithms for generating a primary

population (set) of regular transportation routes were

developed and implemented.

Based on the generated standard set of initial data,

using the developed algorithms, the first iterations of

generating the primary population (set) of regular

transportation routes for the city of Berezniki were

made. As a result of the operation of the algorithm for

the automated construction of regular transportation

routes, the route network of the city of Berezniki was

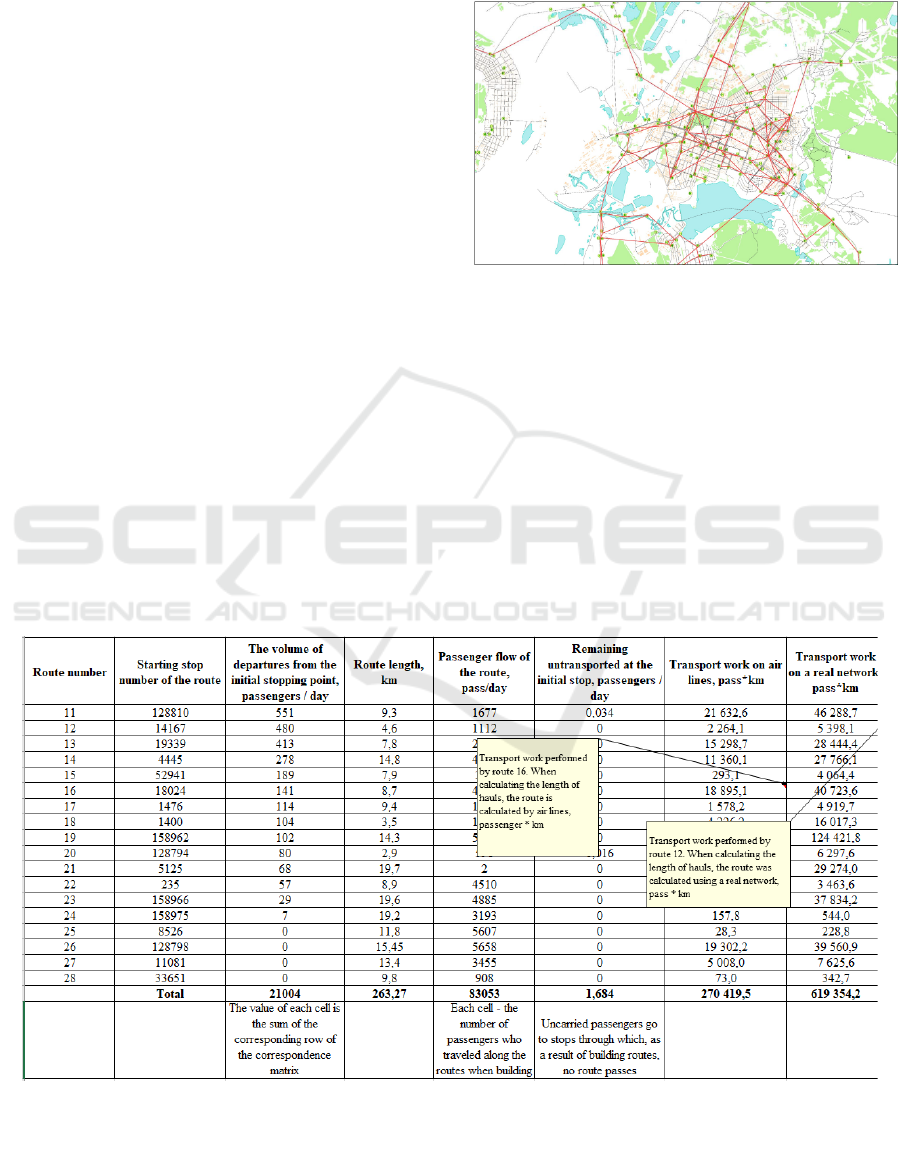
formed (Figure 5).

Figure 5: The route network of the city of Berezniki, formed

as a result of the algorithm for the automated construction

of regular transportation routes.

The main indicators of the generated routes turned

out to be good (Figure 6).

The length of all routes was 263,27 km. The total

passenger traffic on all routes amounted to 83 053

passengers per day. A rather small number of

uncarried passengers remained, the transport demand

for which is tied to stops through which no route

passed - only 1 person per day. In this set of generated

routes, a rather large transfer coefficient was obtained

- 1,9 (passengers quite actively use transfers from one

route to another route). Also, the transport work on

Figure 6: Fragment of the table with the main indicators of the generated routes.

TLC2M 2022 - INTERNATIONAL SCIENTIFIC AND PRACTICAL CONFERENCE TLC2M TRANSPORT: LOGISTICS,

CONSTRUCTION, MAINTENANCE, MANAGEMENT

154

overhead lines and the transport work of routes,

which are calculated on a real network, were

determined. Transport work on overhead lines

amounted to 270 419,5 pass*km, on the real network

– 619 354,2 pass*km. The indicators of the generated

route network for stopping points are also good. The

average volume of departures from the stopping point

is 197 passengers per day. The number of routes

passing through the stop was 1,52 routes.

4 CONCLUSIONS

The above algorithm for searching for a primary set of

routes in the field of transport demand represents the

solution of the first part of the combinatorial optimization

problem of constructing an efficient route network of a

large city. The presented algorithm implements only the

first two iterations of the search for the optimal set of routes.

The resulting set of routes for the city of Berezniki (Perm

Region, Russia) may be the necessary information for

further refinement and optimization with the choice of the

objective function when solving the problem of

mathematical programming. Such an objective function can

be a combination of time criteria for the implementation of

transport correspondence for all passengers of the route

network, as well as the efficiency of one unit of rolling

stock. At subsequent stages, it is possible to use a wide

range of optimization algorithms for solving problems of

mathematical programming, as well as algorithms for

changing the initial set of the parent route, called the general

word "genetic algorithms", the main task of which is to

modify the existing set by applying genetic operators

(copying, crossing, mutation) (Benn, 1995, Bunte, 2006;

Guan, 2003; Zhao, 2004; Zhao, 2006).

REFERENCES

Yakimov M. R., 2017. Optimal Models used to Provide

Urban Transport Systems Efficiency and Safety.

Transportation Research Procedia Сер. "12th

International Conference "Organization and Traffic

Safety Management in Large Cities", SPbOTSIC 2016",

pp. 702-708.

Desaulniers, G., Hickman, M., 2017. Public transit.

Handbooks in Operation Research and Management

Science, pp. 69-120.

Buslaev, A. P., Provorov, A. V., Yashina, M. V., 2013.

Mathematical Recognition Problems of Particle Flow

Characteristics by Video Sequence Images. In

Proceedings of the International Conference on Image

Processing, Computer Vision, and Pattern Recognition

(IPCV, WorldComp).

Buslaev, A. P., Yashina, M. V., Volkov, M., 2015.

Algorithmic and Software Aspects of Information

System Implementation for Road Maintenance

Management. In Theory and Engineering of Complex

Systems and Dependability, pp. 65-74.

Zhao, F., Gan, A., 2003. Optimization of transit network to

minimize transfers. Tech. Rep. BD015-02, Florida

Department of Transportation, Center for

Transportation Research, Florida International

University.

Baaj, M. H., Mahmassani, H. S., 1995. Hybrid route

generation heuristic algorithm for the design of transit

networks. Transportation Research Part, pp. 31-50.

Murray, A. T., 2003. A coverage model for improving

public transit system accessibility and expanding

access. Annals of Operations Research, pp. 143-156.

Benn, H. P., 1995. Bus route evaluation standards. Tech.

Rep., Transportation Research Board, Washington.

Bunte, S., Kliewer, N., Suhl, L., 2006. An overview on

vehicle scheduling models in public transport.

Proceedings of the 10th International Conference on

Computer-Aided Scheduling of Public Transport,

Leeds, UK. Springer-Verlag.

Guan, J. F., Yang H., Wirasinghe, S. C., 2003.

Simultaneous optimization of transit line configuration

and passenger line assignment. Transportation

Research Part B 40 (10). pp. 885-902.

Zhao, F., Ubaka, I., 2004. Transit network optimization -

minimizing transfers and optimizing route directness.

Journal of Public Transportation 7(1), pp. 67-82.

Zhao, F., Zeng, X., 2006. Simulated annealing-genetic

algorithm for transit network optimization. Journal of

Computing in Civil Engineering 20 (1), pp. 57-68.

A Combinatorial Problem of Generating a Network of Routes of Public Transport in Cities

155