Limit of Long-term Strength of Shells Operated in an Aggressive
Environment
I. G. Emel’yanov
1,2,3 a
1
Ural State University of Railway Transport, Yekaterinburg, Russia
2
Ural Federal University, Yekaterinburg, Russia
3
Institute of Engineering Science, Russian Academy of Sciences (Ural Branch), Yekaterinburg, Russia
Keywords: Shell, aggressive environment, mechanical characteristics of steel, stress state, long-term strength limit.
Abstract: The paper proposes a method for determining the limit of long-term strength of metal thin-walled structures
in contact with an aggressive hydrogen-containing medium. The method is demonstrated on a structure in the
form of a steel cylindrical pipe, which is used for wells and gas gathering pipeline networks. The indicator of
the long-term strength of typical structures proposed in the article will allow the consumer to better navigate
the market of the proposed pipes when choosing them.
1 INTRODUCTION
In various industries, including transport, the issues
of assessing the degree of degradation of the strength
properties of various materials during the operation of
structures are topical. The change in mechanical
properties leads to various types of destruction of
structures. In (Collins Jack, 1981), more than 20 types
of mechanical failure during operation are given.
It is known that many metals during operation in
various environments change their mechanical
properties in comparison with tests in air. The
environment can have both beneficial and harmful
effects on the material and affects the value of the
long-term strength of the structure. The ability of a
material to resist fracture under long-term static
loading is called long-term strength. The limit of
long-term strength of a material is the maximum
stress that causes destruction in a certain time at a
fixed temperature. It is designated
T
t
ult
σ
, where
ult
t
is the limiting time to failure, T is the temperature
(Troshchenko, 1994).
The calculation of the durability of materials
under long-term static loading can be carried out in
two ways. The first method develops methods for
predicting the time to failure using various parameters
depending on the level of acting stresses, i.e., it
models parametric long-term strength curves. The
a
https://orcid.org/0000-0002-9733-5485
second method is associated with the development of
methods for extrapolation of long-term strength
curves for a time exceeding the time for which the
initial curves were experimentally obtained.
Apparently, for standard structures loaded with a
known static load, it is possible to determine the limit
of long-term strength of the structure
T
t
ult
q
, where q
is the generalized force,
ult
t
is the limiting time
before the destruction of the structure, T is the
operating temperature of the structure. Therefore, the
introduced limit will depend on the operating
conditions causing the destruction of the structure in
a certain time. Such an entered value will be useful
when choosing the geometric parameters and
materials of typical structures (for example, pipes for
wells) based on their operating conditions.
At present, the issues of assessing the degree of
degradation of the strength properties of steels during
the operation of various structures in aggressive
environments are becoming relevant.
The effect of aggressive media, including
hydrogen-containing media, on the mechanical
characteristics of metals is actively studied by various
physical methods and by mechanical tests for samples
(Jemblie, 2017; Fassina, 2012; Miresmaeili, 2010;
Mironov, 2020; Gorkunov, 2008). A variety of
phenomenological effects that arise when exposed to
230
Emelâ
˘
A
´
Zyanov, I.
Limit of Long-term Strength of Shells Operated in an Aggressive Environment.
DOI: 10.5220/0011582100003527
In Proceedings of the 1st International Scientific and Practical Conference on Transport: Logistics, Construction, Maintenance, Management (TLC2M 2022), pages 230-234
ISBN: 978-989-758-606-4
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

hydrogen-containing media will determine the long-
term strength of steels.
Predicting the behavior of loaded metal structures
that are operated in an aggressive hydrogen-
containing environment is an important scientific
problem of great practical importance. One of these
problems is the problem of changing the strength of
steels for pipes that transport the so-called "sour gas".
This is natural gas with a high content of hydrogen
sulfide. Predicting the behavior of the material in such
metal structures is a very important and not
completely solved problem. The issue of assessing
the strength and durability of structures during their
operation in corrosive media containing hydrogen
sulfide remains very important.
In this paper, a method is proposed for
determining the ultimate strength of a typical
structure, which is operated in an aggressive
environment under static loading. The method is
demonstrated on a structure in the form of a steel
cylindrical pipe, which is used for wells and gas
gathering pipeline networks. The indicator of the
long-term strength of typical structures proposed in
the article
T
t
ult
q
will allow the consumer to better
navigate the market of the proposed pipes when
choosing them.
2 METHOD FOR SOLVING THE
PROBLEM AND BASIC
EQUATIONS
Statement of the problem and methods of solution.
The general problem of determining the long-term
strength limit of a metal structure in contact with an
aggressive environment consists of several
independent tasks:
− development of a model that allows
determining the stress state of the structural
element under study,
− determination of the mechanical parameters of
the material depending on the time of contact
with an aggressive environment,
− the choice of the interpolation method for
determining the mechanical parameters of the
material, depending on the operating time of
the structure,
− development of a model that determines the
limit of long-term strength of the structure.
Determination of the stress-strain state of the
shell.
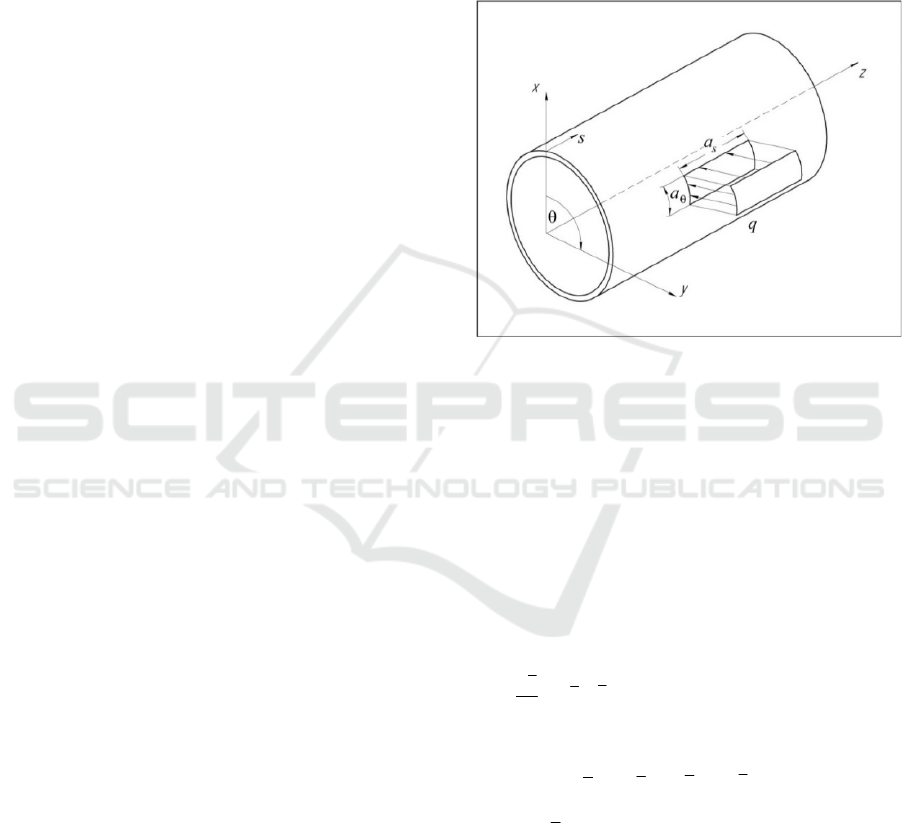
The investigated thin-walled structure is a shell
of revolution with variable geometric and mechanical
parameters along the generatrix. We will consider a
shell of thickness h using a continuous middle surface
with curvilinear orthogonal coordinates S,
θ
,
γ
.
Where s and
θ
are the meridional and circumferential
coordinates, and the
γ
( 2/2/ hh ≤≤−
γ
)
coordinate is in the direction of the outer normal to
the shell surface. A cylindrical shell loaded with a
distributed mechanical force q is shown in fig. 1.
Figure 1: Shell of revolution.
The inner surface of the shell is in contact with an
aggressive water-containing medium with an
overpressure p. The stress state of a thin-walled
structure will be determined using the classical theory
of shells based on the Kirchhoff–Love hypotheses
(Donnell, 1976). Given that the structure under study
is loaded only with pressure, its stress state will be
axisymmetric. Thus, the problem of determining the
stress-strain state of the shell will be described by a
system of ordinary differential equations in the
Cauchy normal form of the following form
(Shevchenko, 2001; Shevchenko, 2006)
, ( , 1,2,....6)
ij
dY
PY f i j
ds
=+ =
,
)(
0 L
sss ≤≤
(1)
with boundary conditions
()
101
bsYB =
,
()
22
bsYB
L
=
(2)
Here
{
}
,
,, ,,,
rz srzs
YNNMuu ϑ =
– vector–function
of the required solution
r
N
,
Z
N
– radial and axial
forces;
r
u
,
z
u
- displacement;
s
M
– meridional
bending moment;
S
ϑ
- angle of rotation of the normal
to the shell surface. Matrix elements
ij
P
depend on
the geometric and mechanical parameters of the shell,
Limit of Long-term Strength of Shells Operated in an Aggressive Environment
231

f
– the vector depends on the loads applied to the
shell.
i
B
– given matrices;
i
b
are the given vectors.
When solving the linear boundary value problem
(1), the Runge-Kutta method with discrete
orthogonalization and normalization of S.K.
Godunov is used [11].
Solution of a physically nonlinear problem for
a shell. When the plastic deformation of the material
is considered, the problem becomes physically
nonlinear. The problem will be described by the same
system (1), and the relationship between stress and
strain is presented in the form of Hooke's law, with
additional terms that consider the dependence of the
mechanical properties of the material on strain. In this
case, the volumetric stress state of the shell will be
compared with the uniaxial state in a simple tension
of the sample.
3
σ
=S
,
ε
μ
3
1
*
+
=H
(3)
where σ and ε are stresses and strains during simple
tension of the sample
ε
σ
μ
μ
E2
21
2
1
*
−
−=
(4)
In formula (4) E – young’s modulus,
*
μ
– Poisson’s
ratio
The intensities of the shear stress S and shear
strain H for the shell are determined as follows
)()3/1(
22
θθ
σσσσ +−⋅=
ss
S
(5)
]
)()()[()6/1(
222
ss
H εεεεεε
θθγγ
−+−+−⋅=
(6)
where
s
σ
and
θ
σ
are the meridional and
circumferential stresses, respectively, and
s
ε
,
θ
ε
,
γ
ε
are the components of deformations along the
meridian, circumference and normal to the shell
surface.
Determination of the mechanical parameters
of the material. Since an aggressive environment
usually has a negative effect on the metal of structures
and changes the mechanical characteristics,
experimental studies are needed to record changes in
the mechanical properties.
To demonstrate the method for determining the
ultimate strength of thin-walled structures, we will
investigate shells made of 12GB pipe steel (an
analogue of X42SS steel API).
The article (Gorkunov, 2008) presents the results
of measurements of the mechanical and magnetic
characteristics of samples of pipe steel 12GB,
exposed to hydrogen sulfide for 384 hours, directly
under the action of uniaxial tensile stresses up to the
destruction of the sample. Tests were also carried out
for samples in the initial state. The temperature during
testing is 20°С.
In (Gorkunov, 2008), stress-strain diagrams are
given for a given material at fixed times t=96 h, t=192
h and t=384 h of contact with an aggressive medium.
It can be seen from the above diagrams that they can
be approximated quite accurately by bilinear straight
lines with points of yield strength
Y
σ
,
Y
ε
, and
ultimate strength
ult
σ
,
ult
ε
both for the initial state
and after contact with an aggressive medium (where
ult
σ
and
ult
ε
are the maximum values of stress and
deformation upon failure). Table 1 shows the points
for plotting diagrams.
Table 1: The points for plotting stress-strain diagrams.
Time,
hou
r
point 1 point 2 point 3
0
ε
0
= 0
σ
0
= 0
ε
Y
=0,00187
σ
Y
=374 МPа
ε
ult
=0,23
σ
ult
=474 МPа
96
ε
0
= 0
σ
0
= 0
ε
Y
=0,00181
σ
Y
= 361 МPа
ε
ult
=0,22
σ
ult
=458 МPа
192
ε
0
= 0
σ
0
= 0
ε
Y
=0,00213
σ
Y
= 426 МPа
ε
ult
=0,14
σ
ult
=498 МPа
384
ε
0
= 0
σ
0
= 0
ε
Y
=0,00218
σ
Y
= 437 МPа
ε
ult
=0,12
σ
ult
=500 МPа
Approximation of stress state components.
After solving system (1), taking into account the
mechanical properties (Table 1), meridional and
circumferential stresses and strains
s
σ
,
θ
σ
, and
s
ε
,
θ
ε
, and invariant characteristics S and H will be
determined at each point of the shell. Considering that
the mechanical properties depend on time, these
characteristics will also depend on time of contact
with aggressive environment.
The criterion for the strength of structures is often
the condition when the intensity of shear stresses in
the shell (5) reaches the stress of the sample material
during its destruction. Therefore, the criterion for the
long-term strength of structures under fixed loading
(p=const) will be the condition
TLC2M 2022 - INTERNATIONAL SCIENTIFIC AND PRACTICAL CONFERENCE TLC2M TRANSPORT: LOGISTICS,
CONSTRUCTION, MAINTENANCE, MANAGEMENT
232

1
)3)(()(
−
≤ ttS
ult
σ
(7)
To determine the values of the intensity of shear
stresses
)(tS
within the time interval of saturation
with hydrogen sulfide, you can use the corresponding
approximating algebraic polynomial L
n
. Therefore,
the approximate value of the parameter of interest can
be represented in terms of its discrete value and time
),(
)( ii
tSS =
)(
)(
iin
StL =
ni ...1=
(8)
Here n is the number of experiments at different
times of sample saturation with hydrogen sulfide.
With a well-chosen polynomial
n
L
, the value of
the parameter of interest can be determined outside
the time of the experiment, i.e., at the time of interest,
such as
55
0
=
work
t hours.
The limit of long-term strength of the
structure. The value of the shear stress intensity
during operation can be represented as
i
n
i
i
taatS

=
+=
1
0
)(
(9)
Since the shell under study is loaded with internal
pressure p, therefore, the intensity of shear stresses
will be equal to
i
n
i
i
tbbptS

=
+=
1
0
),(
,
cons
t
p =
(10)
Considering the introduced criterion of long-term
strength of structures (7), we determine the limit of
long-term strength for a given shell structure
)(3),( tptS
ult
T
t
ult
σσ ≤=
,
при
constT =
(10)
3 CALCULATION EXAMPLE
Limit of long-term strength for a cylindrical shell.
Let us determine limit of long-term strength of a
cylindrical shell (pipe) operated in a hydrogen sulfide
environment. Pipe outer diameter D=0.114 m,
thickness h=0.013 m, material - steel 12GB.
During operation, the pipe experiences a plane
stress state from a variable internal pressure p.
Therefore, the shell can be investigated without edge
effects at a point far from the boundary conditions (2).
From table 1, the mechanical parameters change
depending on the time of exposure to hydrogen
sulfide. From physical considerations, the change in
these mechanical parameters should be monotonous,
since they should depend on the diffusion coefficient,
which characterizes the efficiency of the diffusion
movement of hydrogen sulfide into the metal and be
proportional to the time of contact with an aggressive
environment. Some solutions to the problems of
hydrogen diffusion into metal are considered in
(Emel’yanov, 2018; Emel'yanov, 2019). Considering
the physical monotony of the diffusion process, we
represent the change in the yield strength σ
Y
, ultimate
strength σ
ult
in the form of power functions. For
example, the change in ultimate strength σ
ult
with an
accuracy of 4% can be substituted as a quadratic
function
2
467.231 0.0869794 0.0000116704
ult
tt σ =+ +
(12)
According to the results of the calculation, it was
shown that at a pressure of p=80 MPa, the shell
material is in the region of elastic deformations. With
an increase in excess pressure to p=90 MPa, plastic
deformations occur at the most loaded point on the
inner surface of the shell. The problem becomes non-
linear and an iterative process is applied to achieve
the required accuracy of the problem solution.
Table 2 shows the values of the intensity of shear
stresses S = f(p) and shear strains H = f(p) for various
shell pressure p, when the structure is operated in an
environment of hydrogen sulfide t
work
= 550 hours.
Table 2: The intensity of shear stresses and shear
strains for various pressure.
p,
МП
а
100 110 120 130 131
S,
МП
а
224 244 269 294 299
H
0.0014
2
0.0015
6
0.0173
4
0.06
8
0.0782
8
By increasing the pressure, it is possible to
determine the limiting pressure at which the strength
condition is violated. For this design, the burst
pressure will be p = 132 MPa. Therefore, at
p = 131 MPa, it is possible to determine the limit of
long-term strength of the structure. Considering the
values
ult
σ
calculated by relation (12) at t=550 h and
the intensity of shear stresses for pressure p=131
(Table 2), we have
ult
ptS σ ≈3),(
≈3299
518.5 at
СT
0
20=
(13)
Limit of Long-term Strength of Shells Operated in an Aggressive Environment
233

Therefore, the limit of long-term strength of this
design for temperature T=20°С and pressure p=131
MPa is 550 h.
4 CONCLUSION
Thus, it is possible to determine the limits of long-
term strength of typical shell structures for various
combinations of material, temperature, operating
time, and internal pressure.
The proposed method will be useful in the design
and installation of various pipelines that operate in
contact with aggressive media.
REFERENCES
Collins Jack, A., 1981, Failure of Materials in Mechanical
Design. Analysis, Prediction, Prevention. The Ohio
State University. John Wiley & Sons. p. 624.
Troshchenko, V. T., Krasovsky, A. Ya, Pokrovsky, V. V.,
Sosnovsky, L. A., Strizhalo, V. A., 1994. Strength of
materials to deformation and destruction. Reference
manual, Part 2. Naukova Dumka, p. 703.
Jemblie, L., Olden, V., Akselsen, O., 2017. A coupled
diffusion and cohesive zone modelling approach for
numerically assessing hydrogen embrittlement of steel
structures. International Journal of Hydrogen Energy.
42 (16). pp. 11980-11995.
Fassina, P., Bolzoni, F., Fumagalli, G., Lazzari, L.,
Vergani, L., Sciuccati, A., 2012. Influence of hydrogen
and low temperature on mechanical behavior of two
pipeline steels. Engineering Fracture Mechanics. 81.
pp. 43-55.
Miresmaeili, R., Ogino, M., Nakagawa, T., Kanayama, H.,
2010. Accoupled elastoplastic-transient hydrogen
diffusion analysis to simulate the onset of necking in
tension by using the finite element method.
International Journal of Hydrogen Energy. 35 (3). pp.
1506-1514.
Mironov, V. I., Emelyanov, I. G., Vichuzhanin, D. I.,
Zamaraev, L. M., Ogorelkov, D. A., Yakovlev, V. V.,
2020. Effect of hydrogenation temperature and tensile
stress on the parameters of the complete deformation
diagram for steel 09G2S. Diagnostics, Resource and
Mechanics of materials and structures. 1. pp. 24-33.
Gorkunov, E. S., Zadvorkin, S. M., Veselov, I. N.,
Mitropol’skaya, S. Yu., Vichuzhanin, D. I., 2008.
Influence of Uniaxial Tension on Magnetic
Characteristics of the 12ÉÅ Pipe Steel Exposed to
Hydrogen Sulfide, Russian Journal of Nondestructive
Testing 44. 8. pp. 566–573.
Donnell, L. H. 1976, Beams, Plates and Shells. p. 453.
Shevchenko, Yu. N, Babeshko, M. E., 2001. The
thermoviscoelastoplastic state of shells of revolution
under axisymmetric deformation along various flat
paths. International Applied Mechanics, 37. pp. 967-
997.
Shevchenko, Yu. N., Babeshko, M. E., 2006. Numerical
Analysis of the Thermoelastoplastic Stress-Strain State
of Laminated Orthotropic Shells Under Axisymmetric
Loading. Journal of Thermal Stresses. 29. 12. pp. 1143-
1162.
Grigorenko, Ya. M., 2009. Using Discrete Fourier Series to
Solve Boundary-Value Stress Problems for Elastic
Bodies with Complex Geometry and Structure.
International Applied Mechanics, 45. 5. pp. 469-513.
Emel’yanov, I. G., Mironov, V. I., 2018. A
Thermodiffusion Problem of Hydrogenation of a Steel
Shell Structure. PNRPU Mechanics Bulletin, 3. pp. 27-
35.
Emel'yanov, I. G., Polyakov, A. A., Hodak, A. S., 2019.
Stressed state of a steel construction working in
hydrogen containing environment. 8th International
Conference on Mathematical Modeling in Physical
Science: Journal of Physics: Conference Series, 1391
012027.
TLC2M 2022 - INTERNATIONAL SCIENTIFIC AND PRACTICAL CONFERENCE TLC2M TRANSPORT: LOGISTICS,
CONSTRUCTION, MAINTENANCE, MANAGEMENT
234