Design of Foundations for Buildings and Bridges using Nonlinear Soil

Model

A. A. Alekhin

, G. S. Lobanova

and V. V. Orlov

Ural Federal University, Yekaterinburg, Russia

Ural State University of Railway Transport, Ekaterinburg, Russia

Keywords: Soil base of structures, soil, deformation, physical nonlinearity, mathematical model, model parameters,

determination of parameters.

Abstract: The article substantiates the need to design foundations of bridge supports on non-rocky soil base taking into

account physically and geometrically nonlinear features of soil deformation. Dusty-clayey soils (sandy loams,

loams, clays, and their older and stronger formations - saprolites) of semi-hard, hard, and often tough-plastic

consistency, serve as a reliable and economical soil basis for various structures, including bridges. According

to Article 16 of Technical Regulations on the Safety of Buildings and Structures (Federal Law № 384-FZ), as

well as paragraphs 5.1.11 of SP 22.13330.2016 ("Soil bases of Buildings and Structures") in this case design

must be carried out taking into account the nonlinear deformation of soils. The use in design of a theory

(design model) that corresponds to physical essence of soils instead of nominal for them, physically linear

(Hooke) model, makes it possible to increase radically reliability of structures and obtain at least a twofold

saving in the cost of foundations.

1 INTRODUCTION

Soils: hard rocks and non-hard soils (sands, sandy

loams, loams, clays) are the only solid natural

environment, one of four (except liquid, gaseous and

electromagnetic) natural environments at Earth and,

obviously, at other planets. From an engineering point

of view, soil base is bearing element of all structures,

as a rule, in natural, and sometimes in an artificially

improved state. If soil base consists of non-rocky

soils, then it turns out to be the most deformable load-

bearing element of the structure. But often due to

technical, economic, hydrological reasons, it is

impractical (for example, when dense soils or rocks

are very deeply buried) to pass through non-rock soil

by drilling or driven piles. In the case of using pile

foundations on friction piles (not resting on rocky

base), as well as non-piled foundations, it is necessary

to predict (calculate) their settlements and other

deformations of foundations (for example, their

incline and difference in settlement with neighboring

foundations, which is especially sensitive when

providing reliability and working capacity of bridge

spans. This situation imposes increased requirements

on resolving capabilities of soil base design model,

but in fact, on design soil model, in other words,

mechanical and mathematical deformation model of

non-rock soil (for rock soil at main positions it is

identical to deformation model of concrete, metal and

rubber, which means to Hooke-Young's linear

deformation theory) must corresponds as much as

possible to real mechanics of non-rocky soil,

determined in turn by its physical nature, which is so

complex and multifactorial that even generally

accepted in mechanics principle of replacement in

deformation theory of real soil structure by an ideal

continuous medium, which means introduction

instead of real forces between particles of stresses, as

forces acting on an infinitely small (idealization) area

and relative deformations in an infinitely small

(idealization) volume, creates an error in predicting

soil deformations by about 25...30% (for metals, for

example, as much more homogeneous formations, the

error of such replacement is up to 5%).

More serious errors arise in prediction of internal

forces (stresses) and, because of this, in external force

interactions of neighboring objects (for example, in

pressure of foundation on its soil base). But when

designing, not only quantitative values are important,

but even more important is character of their

distribution, for example, unevenness, and this is

determined the more reliably, the more adequate is

Alekhin, A., Lobanova, G. and Orlov, V.

Design of Foundations for Buildings and Bridges using Nonlinear Soil Model.

DOI: 10.5220/0011582300003527

In Proceedings of the 1st International Scientiﬁc and Practical Conference on Transport: Logistics, Construction, Maintenance, Management (TLC2M 2022), pages 239-244

ISBN: 978-989-758-606-4

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

239

mechanical and mathematical model to mechanics of

soil, by the way, in this case, quantitative values are

also more reliably determined due to decrease in

absolute terms of error from replacing real

environment in design with continuous one.

Approximately same assessment of the complexity of

geotechnical design belongs to famous Anglo-Polish

engineer and geotechnical scientist Zenkevich, a

specialist in computer-aided design of soil bases of

offshore oil platforms, who actually excluded an

accurate prediction of soil deformation during

loading even in the case of using the most advanced

soil model, but at the same time who pointed out the

need for ability of design specialists to model well the

mechanical properties of soil which are necessary to

solve the problem (Zienciewich, 1978).

Unfortunately, in the 1920s, when important problem

of reliable design of soil bases for large and complex

industrial and civil objects arose, no other

deformation theories except Hooke's theory (the

theory of linear, more precisely, linear elastic

deformation), especially for soil, did not exist

(Terzaghi, 1961). However, back in 1798, the Swiss-

Russian mathematician Fuss proposed an engineering

method for predicting depth of wheel rut of carriages,

carts and cannon carriages, which was important for

Petersburg soils (Fuss, 1798), implemented later, in

1872 (Fuss, 1798) by Saxon scientist Winkler in a

linear formula for predicting settlements of railway

sleepers and, accordingly, deflections of railway

tracks (Winkler, 1872) at the place of pressure

application P: S = P / C

(here C

= const is a

coefficient of proportionality, which Winkler called

“bed coefficient” on not quite correct analogy with

stiffness of sofa springs). But in the 1920s, after many

checks (Kurdyumov, 1894; Minyaev, 1916; Gerner's

experiments with a round pressure area, 1932;

Bernatsky, 1935), this formula was rejected as a

possible mechanical and mathematical deformation

soil model for design of structures (Terzaghi, 1961):

firstly, due to the absence of a relationship between

relative deformations εij and stresses σij for an

elementary but representative volume of soil medium

(sample), which reduces Fuss-Winkler formula to

some isolated boundary condition which is not in

agreement with mechanism of internal deformation of

soil massif, that, in turn, does not allow to carry out a

full-fledged analysis of its deformation, for example,

analysis of the effect of load influence on adjacent

sections of soil massif and on neighboring structures;

secondly, the hypothesis of constancy of the stiffness

coefficient C

was not confirmed, which is a

consequence of previous defect of Fuss-Winkler’s

formula. In this regard, the use of Fuss-Winkler’s

formula for calculating deformations of soil base in

some widely advertised and currently used programs

(for example, in programs "LIRA", "SCAD" and

others) for any method of determining the value of

stiffness coefficient C

contradicts to basic principles

of mechanics and is explained by failure of

developers of these programs in their attempts to

apply correct soil base model. The presence of this

formula in SP 22.13330.2016 ("Soil bases of

buildings and structures") (Gosstroyizdat of Russia,

2017) is some kind of temporary compromise, which,

however, for example, in Yekaterinburg has already

led to emergencies associated with incorrect

calculation of soil bases at several objects. In fact,

Fuss-Winkler formula, due to its purpose and method

of derivation, can be correctly used only for an

approximate, and therefore actually estimated

forecast of lateral displacement of a driven pile

(actually more is not required) and for approximately

same type of analysis of elastic work of soil under

action of a not very intensive dynamic load from

industrial equipment (but not from a much more

intensive train load). In general, and it should be well

known to engineers, that veracity and reliability of

geotechnical calculations as for any other mechanical

calculations, are ensured by using four groups of

resolving relations: 1) equilibrium-motion equations,

Newton, 1650; 2) geometric relations of compatibility

of deformations and displacements in the framework

of the theory of continuous medium, Cauchy, 1820s;

3) generalized physical relationships between relative

deformations and stresses, Genki, 1920s; and, most

importantly (Bell, 1984), 4) obtained from results of

special experiments (tests), relations between relative

deformations and stresses in a conventionally

elementary (small), but representative volume

(sample) of a solid formation, including for soil

medium. These relations in turn determine type and

value of rigidity of this solid formation, in this case of

soil. But Fuss-Winkler/s formula S = P / C

does not

belong to any of these four groups of resolving

relations, even as defining stiffness relation, despite

its outward likeness to Hooke-Young stiffness

relation ε = σ / E, including the constancy in both

formulas of coefficients of proportionality C

and E.

As indicated above, there is no in Fuss-Winkler

formula to contrast to Hooke-Young formula direct

connection between values included in Fuss-Winkler

formula and values included in other resolving

relations. It is for this reason that Austrian-American

geotechnician Terzagi, founder of International

Geotechnical Society, in absence of other

deformation theories, as well as in full absence at that

time devices for obtaining defining relationships

TLC2M 2022 - INTERNATIONAL SCIENTIFIC AND PRACTICAL CONFERENCE TLC2M TRANSPORT: LOGISTICS,

CONSTRUCTION, MAINTENANCE, MANAGEMENT

240

between relative deformations and stresses for soils

and effective computing means, has proposed in

1920s (Terzaghi, 1961) to apply for predicting

deformations of soils had being applied at that time

for all materials, Hooke's theory (now known as

theory of linear deformation), which mathematically

closed above mentioned system of resolving

relations. During that period of large-scale

development of industrialization and housing

construction all over the world, adoption of

mathematically correct design model for soil and soil

base has much intensified building design in all

directions. But contradiction that arose due to

insurmountable circumstances at the beginning of

XX-th century (primarily due to the lack of a

mechanical and mathematical design model adequate

to mechanical properties of soils) and turned into a

serious problem at the beginning of XXI-th century in

condition of construction of high-rise and other

uniquely complex objects, and especially bridges, is

that for calculating deformations of soils was adopted

mechanical and mathematical deformation model of

incompatible with them on physics and mechanics

metals, moreover, in many aspects this unreliable and

dangerous approach is still preserved, including, and

that is especially seriously threatens to technical

safety, in regulatory documents, including SP

35.13330.2011 "Bridges and Pipes", although since

2009 this unacceptable situation was actually blocked

by article 16 of Federal Law No. 384-FZ (Technical

Regulations on Safety of Buildings and Structures),

which requires the use in geotechnical design of

adequate for non-rocky soils physically nonlinear

deformation model (Federal Law № 384-FZ, 2010).

2 MAIN FEATURES OF

PHYSICALLY NONLINEAR

SOIL DEFORMATION

Obviously contradictory proposal of Terzaghi about

adoption for calculation of deformations of soils with

loose internal connections deformation theory of,

absolutely opposite to them in physical and

mechanical properties, dense materials (metals and

even rubber) could not but raise numerous questions

of geotechnical specialists, that even demanded later,

in 1948 year, when Terzaghi's proposal, again due to

insurmountable circumstances (absence, on one hand,

a proven, soil deformation model and accessible, with

the necessary power of computing means, and on

other hand, urgent need on prompt restoration of

destroyed by war and construction of new objects),

nevertheless, was adopted in USSR (Gersevanov,

1948), to apply this illogism, namely, having

identifying value of Young's modulus E, which is

consistent for materials, with inconsistent, as it was

later found out for soils (Lushnikov, 1969; Ruppeneit,

1973), value of modulus of deformation with same

designation E. although the physico-mechanical

essence of these two values is absolutely different

what is more, they are not even close analogs, as it

was actually assumed in 1948 (Gersevanov, 1948).

Young's modulus E by definition (according to the

technology of converting results of experiments of

Hooke and his folowers with metals and other similar

materials into mechanical and mathematical formula

of Young) reflects exclusively only direct

proportionality between applied unidirectional force

and resulting unidirectional deformation (and even

adopted later, more general in relation to Young's

formula, Genki's ratios with coefficient Poisson ν did

not change physical and mechanical essence of

Young's modulus E); modulus of soil deformation E

as a constant for any method of its determination, due

to the nonlinear features of deformation of soils,

inevitably includes an element of disproportionality

between applied forces and resulting deformation,

moreover, multidirectional, which just creates effects

of physical and geometric nonlinearity, and also

effects of contraction and dilatancy, one of a

manifestations of which is, for example, a multiple

difference in values of modulus of deformation

obtained from different methods of soil compression

testing (settlement plate, pressuremeter, odometr)

(Gersevanov, 1948; Lushnikov, 1969; Ruppeneit,

1973), which, in principle, cannot be when

determining Young's modulus, for example, for

metal. True, unreliable are formulas themselves

(Lame and Schleicher) for calculating the modulus of

soil deformation according to GOST 20276-2012

("Soils. Methods for in-situ determination of strength

and deformability characteristics") (GOST 20276–

2012, 2013), since they are derived from the

deformation theory not of soil, but of metal, that is,

from Hooke's theory of linear deformation, There are

also many other serious inconsistencies from

application of physically linear theory of deformation

to physically nonlinear soils, including, recently

noted even in textbooks, significant differences for all

types of buildings and for all types of soils between

calculated and actual values of deformations of soil

bases (Ukhov, 2002). At the same time, back in 1939

... 1940 Leningrad scientist Botkin, obviously

disagreeing with Terzagi's proposal to accept the

theory of deformation of metals and rubber for

calculating deformation of soils, performed tests on

Design of Foundations for Buildings and Bridges using Nonlinear Soil Model

241

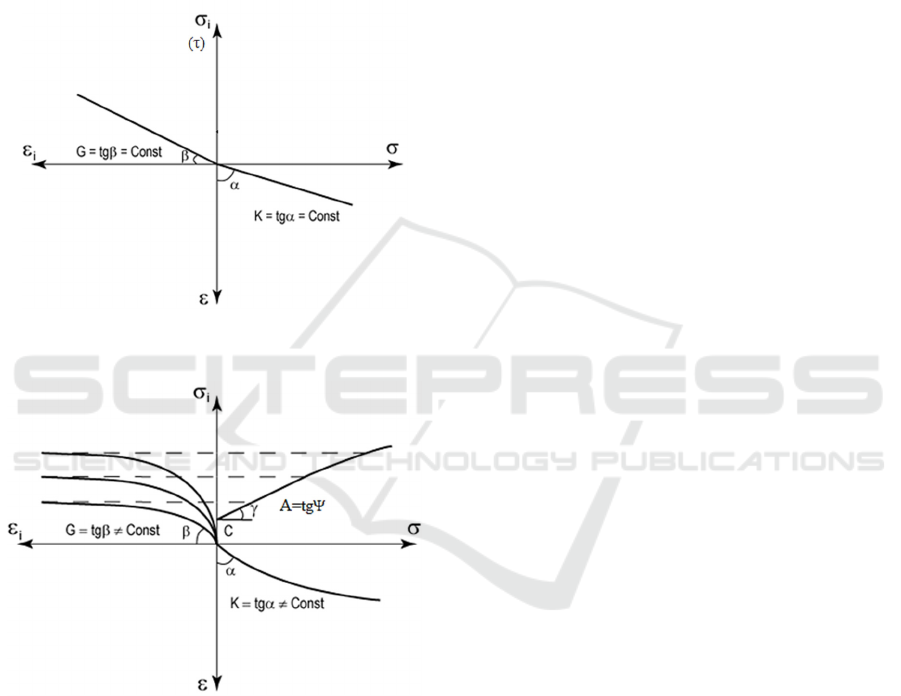
samples of sand and clay soils in a special triaxial

compression device recently created in Germany -

stabilometer, received deformation graphs of sandy

and clay soils (Botkin, 1939; Botkin, 1940), depicted

in the form of diagrams in Figure 1b (Botkin, 1939;

Botkin, 1940). Thus, firstly physically nonlinear type

of deformation of soils was investigated, which was

different from the physically linear type of

deformation proposed by Terzaghi, also shown

diagrammatically in Figure 1a.

a) physically linear (for structural materials

and rocks)

b) physically nonlinear (for non-rocky soils:

sands and clays)

Figure 1: Types of deformation.

Names of types of deformation (that time

physically nonlinear type of deformation was known

and was studied only for soils; for rocks, by analogy

with already studied concrete, metals and rubber, the

physically linear type of deformation was adopted)

were given in 1950s according to the form of given

diagrams, but physically, for example, physically

nonlinear deformation, consists in dependence of

rigidity (resistance to deformation) of a solid medium

or solid material on their internal stress-strain state

(herein after SSS) and decrease of this rigidity as

stress-strain state state approaches to the limit state

for a given solid formation, namely to it strength

(resistance to destruction). Physical essence of

physically linear (Hooke's) deformation, on the

contrary to nonlinear deformation, consists in

independence from internal stress-strain state, i.e., in

the constancy of the rigidity of a solid medium or

solid materials throughout the entire deformation

process due to density and strength of their internal

bonds. In fact, in deformations of all solid formations

(natural and artificially improved soils, as well as

solid materials, there is a factor of physical

nonlinearity to one degree or another, sometimes in

certain areas of deformation (for example, area of

yielding for steel). But only in soils, both in natural

and in artificially transformed states, due to the

fragility and looseness of internal bonds physically

nonlinear type of deformation, in its essential

understanding, is present at all stages of deformation

without exception. Thus, it is obviously that design

model for a soil should be at a minimum reflects

physical and geometric nonlinearities, which is quite

definitely declared by paragraphs 5.1.11, 5.1.12, 5.3.3

and paragraphs of Appendix C of SP 22.13330.2016

“Soil bases of buildings and structures

"(Gosstroyizdat of Russia, 2017), and especially by

Article 16 of Technical Regulations on Safety of

Buildings and Structures (Federal Law № 384-FZ,

2010), which excludes the use of formulas of the

theory of a linearly deformable soil with Young's

modulus (modulus of deformation) E for designing

soil bases, which from the standpoint of real soil

deformation as physically nonlinear medium and

hence requirements of above paragraphs of SP

22.13330.2016 and Federal Law № 384-FZ, cannot

be used at designing of soil bases, especially since

this value at different points of soil base, as in plan

and in depth due to the factor of physical nonlinearity

(dependence of stiffness on stress-strain state) is

significantly different: naturally, the question arises

about the localization of soil base section, for which

value of modulus of deformation E is given in

reports of geological engineers. There is no answer

within the framework of a nominal, and therefore

unreliable for soil, physically linear model (the theory

of a linearly deformable medium). But this answer

can be easily found within the framework of a

physically nonlinear model adequate to mechanical

properties of soil. Phenomenological formulas for

stiffness characteristics of this theory were first

derived by Botkin: for modulus of volume change

TLC2M 2022 - INTERNATIONAL SCIENTIFIC AND PRACTICAL CONFERENCE TLC2M TRANSPORT: LOGISTICS,

CONSTRUCTION, MAINTENANCE, MANAGEMENT

242

(bulk modulus) K = σ / ε = σ

1-α

and for modulus

of change of shape (shear modulus) G = σi /ε

= (σ

) / B = (Aσ+C) / (B+ (Here u = Aσ + C – strength

condition for soil according to Mises-Botkin version).

Thus, for soils, it is incorrect to determine values of

the parameters of the physically linear model E

(deformation modulus), which are different at

different points of the soil base and ν (Poisson's ratio,

which, by the way, for soils is almost impossible to

determine by direct measurements, but it is necessary

to determine values of parameters-constants of a

physically nonlinear model (for example, Botkin's

model: A0, α, A, B, C. Since values of these

parameters, as well as the parameters of any soil

model (and now there are quite a lot of them,

depending on the problems to be solved (Fedorovsky,

1985)), depend on the natural state of soil, including

its natural stress state, then their true significations

must be determined from the results of in-situ static

tests with the simplest scheme and the least disturbing

the natural state of soil. Brief mathematical

description of the algorithm of the method

(Fedorovsky, 1985) for Botkin soil model, as the most

verified in accordance with paragraph 5.1.12 of SP

22.13330.2016 ("Soil bases of buildings and

structures") (Gosstroyizdat of Russia, 2017) Using

true values of parameter stresses and strains of soil

masses and corresponding displacements of

foundations are determined. For rigid foundations of

columns and bridges supports, as well as for rigid slab

foundations, this problem has been completely

solved; it was also solved to determine the

deformations and stresses under the embankment,

which is important for analysis of karst problem. At

present, post-graduate students of Bridges and

Transport Tunnels Department are solving a similar,

but at the same time, due to computational features,

most difficult problem for slab foundations of any

rigidity. Comparison of results of geotechnical

calculations for bridge foundation using physically

nonlinear and physically linear (Hooke's)

deformation theories showed that at a pressure on soil

base of 400 kPa (40 t/m2), for first case average

settlement of foundation is 6.3 cm, and for second

case – 7. 7 cm. Thus, settlement according to

physically linear theory exceeded settlement

according to physically nonlinear theory by 20%,

which is explained by fact that at physically linear

case increase of soil stiffness with increasing depth is

not taken into account. Taking into account the still

unexplored uncertainty for soil on replacement of

granular soil medium to ideally continuous

(according to some data, it can be up to + 25%, and in

the case of using a linear model that is inadequate to

the soil, naturally more), the total difference in the

calculated settlements can reach 50% The nature of

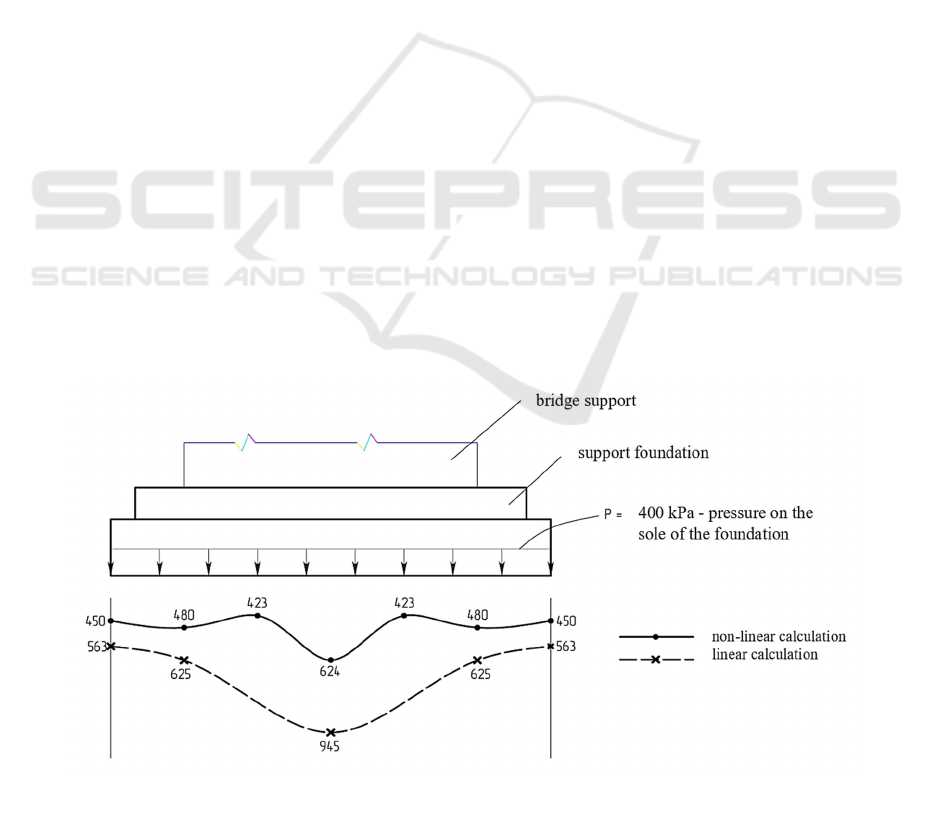
the distribution of contact pressures under foundation,

as well as in the soil mass differ significantly in

physically nonlinear and physically linear

calculations, and m in both cases, they are uneven and

not equal to average pressure under bridge support

(see Fig. 2). unequal to average pressure from the

bridge (see Fig.2). The unevenness of diagram at

nonlinear case is explained by the dependence of soil

stiffness on stress state, which is adequately reflected

by physically nonlinear model. Nonlinearity of the

Figure 2: Diagrams of contact pressures Pk under the base of the bridge foundation according to nonlinear (solid line) and

linear (dashed line) calculations at ground pressure P = 400 kPa.

Design of Foundations for Buildings and Bridges using Nonlinear Soil Model

243

diagram at linear case is at more significant values of

pressure along the edges than in the nonlinear case is

explained by increased distribution ability of linear

model, inadequate to soil, in entire space of acting

forces compared to nonlinear one (for analogy, one

can compare distribution ability of rubber and

plasticine). The unevenness of contact pressures

seriously affects at the roll of bridge supports, which

is sensitive for bridge spans, therefore, the most

accurate determination of contact pressures is

extremely important for design of bridges, especially

railway ones. At the same time, it must be mind that

it is the physically nonlinear deformation that is main

mechanical feature of non-rocky soils.

3 CONCLUSIONS

To improve traffic safety deformations of the soil

base of bridge supports must be calculated using

physically and geometrically nonlinear soil model, as

required by Federal Law № 384-FZ (Technical

Regulations on the Safety of Buildings and

Structures).

The use of a physically and geometrically

nonlinear soil model makes it possible to obtain the

most reliable prediction of deformation of ground

embankments and its soil bases in occurrence of karst

cavities and other defects in them.

REFERENCES

Zienciewich, O. C., Lewis, R. W., Stagg, K. G., 1978.

Numerical Methods in Offshore Engineering.

Terzaghi, K., 1961. Theory of soil mechanics. p. 507.

Fuss, N., 1798. Sur la résistance, de provoquer toutes sortes

de routes, aux quatre roues et deux roues des chariots /

écritures / universitaires de l'Académie Impériale.

Winkler, E., 1872. Neue Theorie des Erddruckes

(experiments Audé, reported by Winkler).

Kurdyumov, V. I., 1894. A short course on soil bases and

foundations.

Minyaev, P. A., 1916. On distribution of stresses in bulk

solids.

Gerner's experiments with a round pressure area, 1932.

Bernatsky, L. N., 1935. Applied Geotechnics, p. 258.

SP 22.13330.2016 ("Soil bases of buildings and structures".

– M.: Gosstroyizdat of Russia, 2017, 224 p.

Bell, J. F., 1984. Experimental foundations of the

mechanics of deformable solids. Part 1. Small

deformations: (translated from English), p. 600.

Federal Law of 30.12.2009. № 384-FZ “Technical

Regulations on Safety of Buildings and Structures". -

M.: "Collection of legislation of Russian Federation",

2010.

Gersevanov, N. M., Polshin, D. E., 1948. Theoretical

foundations of soil mechanics and their practical

application.

Lushnikov, V. V., 1969. To processing results of

pressuremeter studies of soil compressibility. In-situ

methods of soil research, pp.113-118

Ruppeneit, K. V., Bronshtein, M. I., Dolgikh, M. A., 1973.

Solution of axisymmetric elastoplastic problem for

anisotropic soil. Soil bases, foundations and soil

mechanics 4, pp. 26-29.

Alekhin, A. N., 1982. Non-linear analysis of stress-strain

state of soil mass under static loading: Thesis of cand.

techn. degree, p. 186.

GOST 20276–2012 Soils. Methods for in-situ

determination of strength and deformability

characteristics. – M.: Standartinform, 2013, p. 50.

Ukhov, S. B., Semenov, V. V. Znamensky, V. V., Ter-

Martirosyan, Z. G., Chernyshev S. N., 2002. Soil

mechanics, soil bases and foundations, p. 566.

Botkin, A. I., 1939. Investigation of stress state at

cohesionless and cohesive soils. Proceedings of RIIG.

24, pp. 153-172.

Botkin, A. I., 1940. On strength of loose and brittle

materials. News of VNIIG 26, pp. 205–236.

Fedorovsky, V. G., 1985. Modern methods for describing

mechanical properties of soils. Construction and

architecture, series 8: Building structures, 9.

Alekhin, A. N., 2015. Substantiation of the method for

determining parameters of nonlinear soil model from

in-situ test data. Academic Bulletin 1, pp. 57-62.

TLC2M 2022 - INTERNATIONAL SCIENTIFIC AND PRACTICAL CONFERENCE TLC2M TRANSPORT: LOGISTICS,

CONSTRUCTION, MAINTENANCE, MANAGEMENT

244