Assessment of the Operability of a Low-depth Concrete Anchor of

Overhead Line of Type AM using Modeling

Alexander Viktorovich Paranin

Ural State University of Railway Transport, Yekaterinburg, Russia

Keywords: Overhead line, anchor, deepening, soil, concrete, calculation, modeling, mechanical stress, pressure, finite

element method, elastic and plastic deformations.

Abstract: The article analyzes the design of a concrete low-depth anchor of overhead line of type AM. This design was

recently developed by Tolmachevsky Plant of Reinforced Concrete and Metal Structures. It is fundamentally

different from the design of widely used three-beam reinforced concrete anchors of the overhead line. To

assess the operability of the structure, a finite element model of the anchor itself placed in the ground was

created. This model is two-dimensional, taking into account plastic deformations of soil and concrete, as well

as mechanical contact of these materials. As a soil, sand is considered as weakly bearing: the worst conditions

during operation. According to the calculation results, the fields of equivalent mechanical stresses and

pressures arising in the soil and concrete are determined. The analysis of the results confirms the operability

of the AM anchor in the considered ground conditions with a force in the anchor cable of the overhead line

up to 90 kN inclusive.

1 INTRODUCTION

LLC Tolmachevsky Plant of Reinforced Concrete

and Metal Structures has recently developed a design

of a concrete low-depth anchor of the overhead line

of type AM. It is fundamentally different from the

design of widely used three-beam reinforced concrete

anchors of the overhead line. For example,

reinforcement is completely absent, its weight and

dimensions are significantly larger than the standard

existing anchors of the overhead line. The

manufacturer has applied for a patent for this design.

For this reason, the manufacturer does not provide the

results of calculation and physical tests of such a

design for the operating organization Directorate for

Energy Supply of JSC "Russian Railways". In this

regard, the anchor's operability was checked in a

calculated manner.

The calculation of such a structure by analytical

methods set out in regulatory documents (Standards

for the design of the overhead line STN CE 141-99,

2001; BSI Standards Publication, 2020) concerning

calculations and standards for the design of an

overhead line seems extremely complex and not fully

adequate, since all formulas are focused on the main

https://orcid.org/0000-0002-9522-3359

types of existing foundations with deep laying. In

addition, the top layer of soil up to 0.3 – 0.5 m is

usually considered non-bearing, i.e. conditionally not

resisting. Thus, the AM anchor is located almost

completely in a non-bearing layer.

Therefore, the calculation was performed using

simulation in the COMSOL Multiphysics software

package license number 9601577 in a two-

dimensional formulation.

2 MAIN PART

2.1 Materials and Methods

The calculation was performed on a two-dimensional

model. A concrete anchor with a steel eye for the

anchor guy is buried in the ground at 0.5 m. The

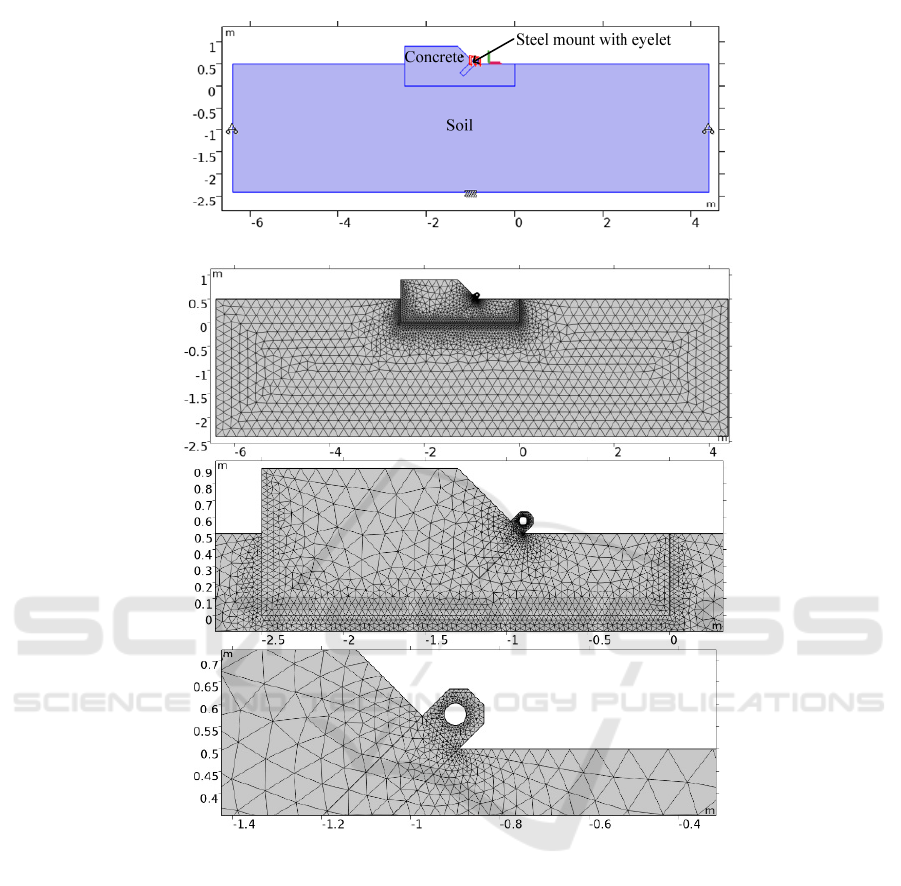
geometry of the computational domain with signed

materials is shown in Fig. 1. Sand was chosen as the

soil as a weak-bearing one, concrete was taken from

the B30 grade, carbon steel was used for mounting

with an eye.

300

Paranin, A.

Assessment of the Operability of a Low-depth Concrete Anchor of Overhead Line of Type AM using Modeling.

DOI: 10.5220/0011584100003527

In Proceedings of the 1st International Scientiﬁc and Practical Conference on Transport: Logistics, Construction, Maintenance, Management (TLC2M 2022), pages 300-304

ISBN: 978-989-758-606-4

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

The COMSOL Multiphysics software package

uses the principle of virtual operation to describe

continuum mechanics. This principle states that the

internal work performed by infinitesimal

deformations under the influence of internal stresses

is equal to the external work performed by the

corresponding virtual displacements under the

influence of external loads. For this purpose, Green-

Lagrange deformations and second Piola-Kirchhoff

stresses S (Pascon, 2013) are used. Such a

formulation is commonly called a complete

Lagrangian. The displacement field u is used as the

calculated variable (u is the horizontal component, v

is the vertical component). In the described two-

dimensional model, the hypothesis of plane

displacements is accepted.

A linear elastic model was chosen for steel, i.e.

there are no plastic deformations. Plastic deformation

models are set for concrete and soil. The model of

plastic deformation for soil was adopted by Drucker

— Prager (Wojciechowski, 2018; Liu, 2017) with the

calculation of its coefficients based on the adhesion c

and the angle φ of the internal friction of the soil

(Jiang, 2012). Plastic deformation is specified for

concrete according to the Ottosen model (Ottosen,

1996; Zhang, 2020).

Normal zero normal displacements are set on the

lateral boundaries of the soil: n · u = 0. The condition

of immobility u = 0 is set at the lower boundary of the

soil.

Figure 1: Geometry of the calculated area with signed materials.

Figure 2: The finite element grid used in the calculation.

Assessment of the Operability of a Low-depth Concrete Anchor of Overhead Line of Type AM using Modeling

301

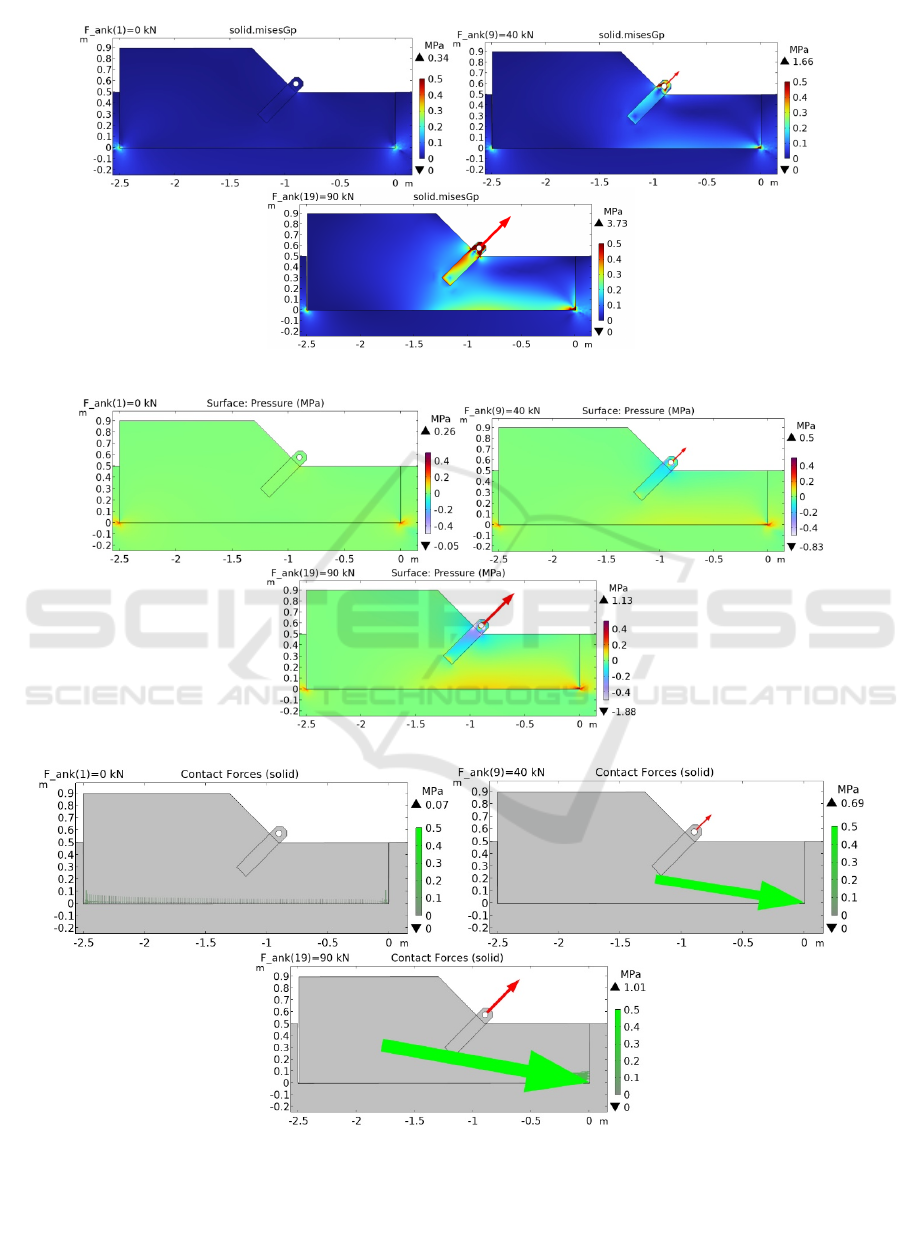
Figure 3: Plot of equivalent Mises stresses with a guyline force of 0, 40 and 90 kN (red arrow).

Figure 4: Plot of the pressure inside the material at a guyline force of 0, 40 and 90 kN (red arrow).

Figure 5: Plot of the pressure arrows on the contact surface (the color is the value of MPa, the size of the arrow is

proportional to the pressure value in a logarithmic scale with a base of 10) with a guyline force of 0, 40 and 90 kN (red

arrow).

TLC2M 2022 - INTERNATIONAL SCIENTIFIC AND PRACTICAL CONFERENCE TLC2M TRANSPORT: LOGISTICS,

CONSTRUCTION, MAINTENANCE, MANAGEMENT

302

A mechanical contact is used at the boundary of

the soil and concrete junction. In this case, the contact

pressure is calculated by the penalty method based on

the field of concrete and soil movements. On the

connection line of the steel fastening with the eye and

the concrete foundation, the condition of continuity

of the displacement field u. The upper boundary of

the eyelet is given by the force F

anc

. When

calculating, it incrementally increases from 0 to 90

kN.

The distributed volumetric force from its own

weight is set throughout the volume.

The finite element grid is shown in Fig. 2.

The type of finite element is quadratic

serendipitous. Since mechanical contact is assumed,

geometric nonlinearity is taken into account in the

model. In other words, the equilibrium conditions are

written taking into account the deformation.

The solution is in two stages by gradually

increasing the nonlinearity.

Stage 1: the strength of the anchor guy F

ank

= 0,

under the action of its own weight, there is a gradual

stabilization of the contact between the soil and

concrete. To do this, the lower limit of the contact

pressure gradually decreases from large values to zero

and the soil adhesion gradually decreases from 0.1 to

0.03 MPa. Below 0.03 MPa, the solution is not stable.

At the same time, the anchor sags slightly in the

ground, the contact pressure is distributed mainly

along the sole.

Stage 2. Starting from the final result of stage 1,

the strength of the anchor guy begins to increase step

by step from 0 to 90 kN. The anchor is shifted to the

right and slightly upwards. The contact pressure is

redistributed mainly to the lower right corner of the

anchor. At F

ank

> 93 kN, the solution is not found.

There are too large plastic deformations.

2.2 Results and Discussion

The main results are presented in the plot of

equivalent stresses according to Mises (Fig. 3), the

pressure inside the material (Fig. 4) and the contact

pressure (Fig. 5) at a force in the anchor tie F

ank

of 0,

40 and 90 kN. The magnitude of the stresses is

indicated by color, the color scale is on the right. The

red arrow indicates the force in the anchor tie.

The figure shows a graph of the horizontal and

vertical movement of the eyelet from the magnitude

of the force in the anchor tie F

ank

According to the results of the calculation on a

finite element mathematical model, it follows that the

specified anchor withstands the traction force in the

anchor tie at least 90 kN when 0.5 m is sunk into the

ground with characteristics close to sand. The density,

the angle of internal friction and Young's modulus

correspond to sand, and the adhesion of 30 kPa is

closer to loam. For sand, the adhesion is up to 8 kPa.

However, with a value less than 30 kPa, the

calculation cannot be performed.

Figure 6: A graph of the horizontal and vertical movement

of the eyelet from the magnitude of the force in the anchor

tie F

ank

The anchor weight is approximately 6.2 tons,

which is three times more than three-beam anchors.

The work of the AM anchor is provided by contact

pressure on the ground in the lower right part from the

side of the anchor guy. It can be said that the anchor

conditionally "cuts" the soil at this angle and thereby

perceives the force in the anchor tie, due to the

resistance of the soil.

The movement of the eyelet is no more than 7 mm

with a guyline force of 90 kN. This is three orders of

magnitude less than the length of the anchor guy and,

accordingly, the shift of the anchor under load will

not lead to a significant weakening of the guyline

force.

It follows from the pressure diagram inside the

concrete that the greatest compression (positive

pressure) occurs in the lower right part of the anchor.

Most of the left (protruding from the ground) side of

the anchor experiences a slight compression pressure

due to its own weight. The stretched area of concrete

with negative pressure is located near the metal

anchorage for the anchor guy. But there the modulo

negative pressure is not great. It should be noted that

the design of the steel fastening in the model is

reproduced approximately. From the point of view of

the strength of concrete, there are no large stretching

zones in it, which explains the lack of reinforcement.

The maximum compression stress occurs at the lower

right corner, where the greatest contact pressure with

the ground. It is not more than 0.5 MPa, which is

significantly lower than the calculated permissible

compression resistance of concrete B30 equal to 17

MPa.

Assessment of the Operability of a Low-depth Concrete Anchor of Overhead Line of Type AM using Modeling

303

3 CONCLUSIONS

Thus, it can be said that according to the simulation

results, the design of the AM anchor is operable under

the specified conditions of sinking even in a weakly

bearing sand-type soil.

It is worth noting that there remains the question

of the expediency of using such anchors and the

conditions for their use. It is hardly possible to install

them on embankments and recesses, only at zero

levels and with reasonable necessity. They have

relatively large dimensions, a larger amount of

excavation work will be required during installation

and a crane of the appropriate lifting capacity.

REFERENCES

2001. Standards for the design of the overhead line STN CE

141-99. M.:Transizdat. p. 176.

2020. EN 50119-2020. Railway applications - Fixed

installations - Electric traction overhead contact lines.

London, BSI Standards Publication, p. 196.

Pascon, J. P., Coda, H. B., 2013. Large deformation

analysis of elastoplastic homogeneous materials via

high order tetrahedral finite elements. Finite Elements

in Analysis and Design. 76. pp. 21-38.

Wojciechowski, M. , 2018. A note on the differences

between Drucker-Prager and Mohr-Coulomb shear

strength criteria. Studia Geotechnica et Mechanica.

40(3), pp. 163–169.

Liu, K., Chen, S. L., 2017. Finite element implementation

of strain-hardening Drucker–Prager plasticity model

with application to tunnel excavation. Underground

Space (China). 2(3). pp. 168-174.

Jiang, J. F., Wu, Y. F., 2012. Identification of material

parameters for Drucker-Prager plasticity model for FRP

confined circular concrete columns. International

Journal of Solids and Structures. 49(3–4). 445-456.

Ottosen N. S., Ristinmaa M., 1996. Corners in plasticity-

Koiter's theory revisited. Int. J. Solids and Struct. 33.

25. pp. 3697-3721.

Zhang, X., Wu, H., Li, J., Pi, A., Huang, F., 2020. A

constitutive model of concrete based on Ottosen yield

criterion. International Journal of Solids and

Structures. 193-194, pp. 79-89.

TLC2M 2022 - INTERNATIONAL SCIENTIFIC AND PRACTICAL CONFERENCE TLC2M TRANSPORT: LOGISTICS,

CONSTRUCTION, MAINTENANCE, MANAGEMENT

304