Planning of the Development of Indonesia's Transport Infrastructure

using Linear Programming Methods

Nikolay I. Kovalenko and Nina A. Kovalenko

Russian University of Transport, Moscow, Russia

Keywords: Indonesia's transport system, rail transport, National Transport Development Strategy (RIPNAS), simplex

method, canonical transport problem, combinatorial methods of solution, dynamic programming, integer

linear programming, industrial and economic relations, suppliers and consumers, contracting organizations.

Abstract: The article presents the results of a study of transport problems in Indonesia to solve the problems of

transportation of both passengers and cargo, to ensure energy savings, a high level of safety during

operation, environmental safety and greater efficiency compared to road transportation (in terms of mass

transportation). This task is assigned to rail transport, which is included in the program for the development

of transport on the islands of Sumatra, Sulawesi, Kalimantan and Papua, developed in the National Strategy

for the Development of Transport (RIPNAS) until 2030. The objective of the study is to apply linear

programming methods for the formation of municipal budgets for the construction or reconstruction of

railway infrastructure facilities in Indonesia, taking into account the production plan of contractors in

accordance with the comprehensive strategic plan for the development of infrastructure in the region of

Indonesia. Variants of the considered matrices are formed on the basis of the existing production and

economic relations between contractors and customers, for example, municipalities. They reflect not only

the current benefit, but also the stability of the interaction, which is ignored in the usual formulation of the

transport task. These matrices serve as the basis for obtaining a reference solution. For example, on the

island of Sumatra, it is planned to develop a suburban (between provinces) railway network to reduce the

traffic load on highways and are considered as a link of economic activity.

1 INTRODUCTION

Indonesia is an archipelago with more than 17,000

islands with a total area of 735,355 square miles.

Currently, Indonesia is the fourth of the 10 countries

with the largest population in the world, which is

about 269.6 million people. One of the problems of

Indonesia, as an archipelago country, is the

unification of all its territories by sustainable

transport links (Jakarta. 2011; Peraturan Presiden

Republik Indonesia Nomor 18, 2020; Peraturan

Presiden Republik Indonesia Nomor 38, 2015).

Therefore, transport is an important macroeconomic

aspect of the national, regional and local economy,

both in rural and urban conditions (Proyek KPBU

Kereta Api Makassar-Pare-pare, 2018; Jinca, 2009).

An important task in solving Indonesia's transport

problems is assigned to rail transport, which allows

transporting both passengers and cargo, ensuring

energy savings, having a high level of safety during

operation, being environmentally safe and more

efficient compared to road transportation (in terms

of mass transportation volumes). The beginning of

the development of railway transport in Indonesia

was the end of the 19th century. Currently, work on

the development and improvement in this area

continues and is included in the program for the

development of railway transport on the islands of

Sumatra, Sulawesi, Kalimantan and Papua

(Peraturan Daerah Provinsi Sulawesi Selatan Nomor

1, 2019; Peraturan Daerah Provinsi Sulawesi Barat

Nomor 8, 2017; Peraturan Daerah Provinsi Sulawesi

Utara Nomor 1, 2014). The development program is

laid down in the National Railway Development

Strategy (RIPNAS) until 2030. For example, the

goal of developing a railway network on the island

of Sumatra is to connect existing unrelated railway

lines in Aceh, North Sumatra, West Sumatra, South

Sumatra and Lampung into a single network of

interconnected railways (Provinsi Sulawesi Tengah

dalam Angka, 2018; Provinsi Sulawesi Barat dalam

Angka, 2021). By 2030, it is planned to stage-by-

Kovalenko, N. and Kovalenko, N.

Planning of the Development of Indonesiaâ

Zs Transport Infrastructure using Linear Programming Methods.

DOI: 10.5220/0011584300003527

In Proceedings of the 1st International Scientiﬁc and Practical Conference on Transport: Logistics, Construction, Maintenance, Management (TLC2M 2022), pages 305-311

ISBN: 978-989-758-606-4

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

305

stage construction of railway infrastructure,

including railway tracks and facilities (Jakarta. 2011;

Peraturan Presiden Republik Indonesia Nomor 18,

2020; Peraturan Presiden Republik Indonesia Nomor

38, 2015). According to the planned strategy

(Provinsi Sulawesi Tengah dalam Angka, 2018;

Provinsi Sulawesi Barat dalam Angka, 2021), the

development of a railway network, for example,

Sumatra Island, is planned in the capital of each

province, which includes the following cities:

Medan (North Sumatra) length – 230 km; Pekanbaru

(Riau) – 120 km; Padang (West Sumatra) – 330 km;

Palembang (South Sumatra) – 250 km; Bandar

Lampung (Lampung) - 170 km and Batam (Batam

Islands) – 330 km.

The authors express their deep gratitude to

Puspitasari Yu. and Nurdiane H. to students from

Indonesia who took an active part in collecting and

processing information on the state of Indonesia's

transport infrastructure.

2 MATERIALS AND METHODS

In accordance with Indonesia's National Strategy for

the Development of Railways (RIPNAS) until 2030,

it is necessary to develop the most effective

solutions to this task.

To analyze the factors affecting the construction

of railway transport infrastructure, the development

of the most effective plan for the distribution of

material and labor resources, a canonical transport

task can be considered. Two components are

considered as criteria for optimizing the solution of

the transport problem:

− minimum costs for the construction of new

lines and reconstruction of existing ones;

− minimum time for construction and

reconstruction.

In the classical view, the task is called transport.

The transport problem (Milovidov, 1982;

Borodinova, 2010) has an identical mathematical

model covering a wide range of tasks. Such

problems are considered and solved by linear

programming methods (Dantzig, 2016; Gass, 2004).

For the conditions of Indonesia as an island state, its

application goes beyond just the same type of

transport.

The classical transport problem can be solved by

the simplex method (Nelder, 1965; Tsvetkov, 2001),

but taking into account its features characteristic of

Indonesia, the result of the solution may be different.

As a rule, when solving transport problems, the

interests of only one market participant are taken

into account. For the conditions of Indonesia, such a

customer is the relevant municipality, on the

territory of which the construction of a railway

section is planned. This is a common disadvantage

of the formulation and solution of the transport

problem. Thus, it is not a market, as it represents the

interests of one market participant and is

characterized by its offer. In the conditions of

market planning, there are several options, both

applications and proposals, which are an additional

factor that are not taken into account in solving

transport problems.

The formulation of the transport problem in the

classical view has the following basic conditions:

− there are m – work producers (contractors)

(resource vector);

− there are n – construction objects

(consumption vector);

− * cost coefficients c

are set, that is, the cost of

a unit of construction operation from the i-th

manufacturer for the j-th construction object

(cost matrix).

Based on the results of solving the tasks, it is

necessary to determine (x

) the volume of

construction and installation works from the i-th

contractor) for the j-th municipality, which are

considered as the desired solution. In addition, it is

necessary to determine the most rational plan for the

volume of construction and installation work for

each contractor - customer pair, for which the

following conditions have been met:

1 - the capacities of the construction and

installation works involved in the implementation of

the project for contractors have been implemented;

2 - the applications for construction and

installation work of all involved municipalities

would be satisfied;

3 - the total costs of construction and installation

work would be minimal.

When setting a classical transport problem , the

features are:

− in canonical form , the system of constraints is

given in the form of equalities;

− with variable parameters, the coefficients of

the system are assumed to be equal to 1 or 0;

− each variable enters the constraint system

twice.

The system of restrictions has the form:



=М

(j = 1.....m) (1)

m - number of contractors (producers of works):

TLC2M 2022 - INTERNATIONAL SCIENTIFIC AND PRACTICAL CONFERENCE TLC2M TRANSPORT: LOGISTICS,

CONSTRUCTION, MAINTENANCE, MANAGEMENT

306



(i = 1.....n) (2)

n - the number of objects of construction and

installation works.

The linear function can be expressed as:





min (3)

When solving the problem of determining the

number of contractors to perform construction and

installation work, taking into account the set of

constraints presented in formulas (1, 2), it is required

to find a solution X in which the linear function F

(formula 3) will take a minimum value. In other

words, the construction and installation work will be

minimal. In solving the canonical form of the

transport problem, a sequential number of

contracting organizations has an arbitrary

distribution Х (х

, x

,...x

, x

,… x

, x

). Such

distribution should be considered as a plan of

applications (or proposals) for construction and

installation works.

The most convenient form of such distribution is

presented in the form of a table of applications (or

proposals) from contracting organizations to

customers (municipalities).

In the canonical form, it is considered that if the

total capacity to perform construction and

installation works of contractors is equal to the total

needs of municipalities, then this type of tasks is

called closed. Otherwise, the task has an open

character with the need to include a fictitious

contractor model in the algorithm.

In the canonical form, the solution of the

transport problem includes two stages. The first

stage is that the initial or basic solution is

determined. At the second stage, the initial solution

is adjusted and optimized in order to obtain an

optimal result.

After finding a basic solution to the construction

and installation work plan, it is necessary to apply

one of the algorithms for improving it and

approaching a rational plan.

A transport task taking into account the interests

of the customer and the competition of contractors.

In the practical activities of construction and

installation organizations in the construction of

railway infrastructure facilities in Indonesia, the

transport problem is solved taking into account the

experience of interaction between municipalities and

contracting organizations. The task is to take into

account the interests of contractors and the

requirements of municipalities.

When creating an algorithm for calculating the

model of interaction between municipalities and

contracting organizations, the interests of

contracting organizations can be reflected in the

form of a graph of proposals (matrix A in Figure 1)

on the one hand and a matrix of the capabilities of

contracting organizations to perform construction

and installation work (Figure 2). Conventionally, the

matrix of capabilities of contracting organizations is

designated as the matrix B.

The graph of proposals (Figure 1) shows that the

relationship between contractors is not

complimentary. There is competition between them

for their municipality. In the matrix, B sentences are

indicated by the v – tender symbol. The presence of

the symbol v in the matrix row qualitatively reflects

the contractor's interest in performing a certain

amount of construction and installation work,

quantified by the value of v for its municipality.

Figure 1: Graph of proposals for construction and

installation works of contractors.

…. …. …. А

v v v

…. v v

v v v

Figure 2 - Matrix for contractors: proposals A and

opportunities for their implementation B. v – compliance

of proposals and opportunities for their implementation.

For municipalities (or the customer), there is a

similar situation to meet their interests. The interests

of the municipality are reflected by the demand

graph (Figure 3), as well as the applicant matrix

(Figure 4).

Planning of the Development of Indonesiaâ

Zs Transport Infrastructure using Linear Programming Methods

307

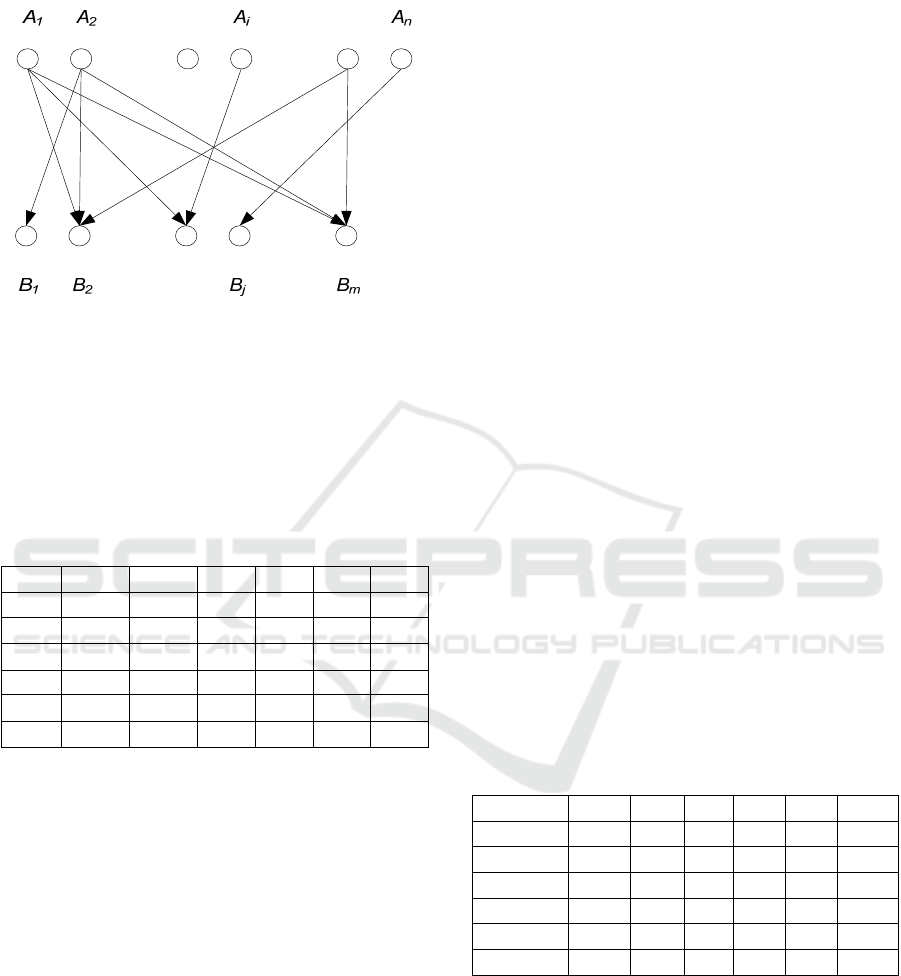
Figure 3: Graph of applicants' demand (for example,

municipalities).

Graphoanalytic interpretation of the interests of

municipalities can be conditionally represented in

the form of matrix A Figure 4. The demand graph

(Figure 3) shows that there is competition between

municipalities, as well as between contractors, and

the determination of preferences for their contracting

organization.

…. …. …. А

w w w

w w

…. w w

…. w w w

w w

Figure 4: Matrix of the customer (for example,

municipalities) A. w – correspondence of the contractor's

proposals and the possibilities of municipalities to meet

them.

In matrix A (Figure 4), the proposals are

indicated by the symbol w – request. The w symbol

in the matrix row reflects the municipality's interest

in this contracting organization. This interest can be

expressed quantitatively in the form of the cost of

construction and installation work or the volume of

such work, as well as the duration of construction

and installation work. The planned parameters of the

obtained results of the work are quantitatively

indicated by the value w.

The values w and v should have opposite signs,

due to the fact that the environment in question has a

market formation structure. In graphs, such a

statement of the problem is indicated by the opposite

directions of the vectors in Figure 1 and Figure 3.

As a rule, this formulation of the problem leads

to not one, but two matrices. These matrices reflect

not only the different interests of the customer (for

example, in the person of the municipality) and the

contracting organization, but also the internal

competition between the interests of the contracting

organization and the tasks of municipalities.

In the practical implementation of real objects,

matrices A and B differ from the mathematical

formulation of the problem, since they are formed on

the basis of real annual plans for the construction of

railway infrastructure facilities or investment plans

for the construction of facilities. The most

acceptable option is when the plan of the previous

year is repeated with adjustments made to it. In this

case, they can be used as a realistic reference plan.

The solution of the tasks in matrix form can be

obtained by superimposing vector schemes or

adding matrices A and B with elements having

opposite signs.

The optimal solution to the problem of a rational

relationship between the satisfaction of the interests

of the customer (for example, in the person of the

municipality) and contractors for construction and

installation works can be achieved ideally in a

balanced customer–contractor system (formula 4).

А + В = 0 (4)

In a real situation, as a rule, there is a

discrepancy (discrepancy Z), formula 5:

А + В = Z (5)

Where Z is defined as the residual matrix (Figure

5):

… … … А

w 0 w 0 0 w

v 0 0 0 0 v

…. 0 0 0 0 0 0

…. 0 0 0 w w 0

…. v v v w 0 0

w v 0 0 0 v

Figure 5: The residual matrix Z.

The elements of the matrix of inconsistencies

(inconsistencies) Figure 5, the values of the values w

(possibilities of municipalities) and v (proposals of

contracting organizations), as well as

w and

v are

accepted.

The values of the values

w and

v show the

presence of a partial discrepancy between the

TLC2M 2022 - INTERNATIONAL SCIENTIFIC AND PRACTICAL CONFERENCE TLC2M TRANSPORT: LOGISTICS,

CONSTRUCTION, MAINTENANCE, MANAGEMENT

308

capabilities of municipalities and the proposals of

contracting organizations. For example, with partial

financing of construction and installation works by

the municipality, or, on the other hand, only partial

production of construction and installation works by

a contractor.

The values of w and v are considered as a

complete discrepancy between the capabilities of

municipalities and the proposals of contracting

organizations. For example, on the one hand, there is

an excess of resources on the part of the work

producer, for example, contractor v, or, on the other

hand, there is a lack of resources w (lack of funding)

on the part of the customer, for example, the

municipality. When a variant of the problem arises

with the appearance of a matrix of residuals, the

solution of such a problem is reduced to minimizing

the base matrices by mutual absorption of its

elements (formula 6):

А + В = min (N) (6)

Such a problem (formula 6) is solved by methods

of combinatorial mathematics.

3 RESULTS

Combinatorial methods for solving Indonesia's

transport infrastructure. Matrix minimization (Figure

4 or Figure 5) can be considered as an integer

programming problem. The minimization problem is

called the "Knapsack Problem", which is always

solved. This problem is formulated as follows

(Rosenberg, 2019). There are n railway transport

infrastructure construction facilities in Indonesia (c

= 1,… n) and various production costs of cj works. It

is required to select such types of construction and

installation works that have a minimum total value

of no more than b

(the specified budget value). We

denote x

= 1 if the j – th variant of the organization

of work is selected. For the case of choosing another

solution option, x

= 0. For the considered problem

of the construction of railway transport

infrastructure in Indonesia, the task is to minimize

costs when organizing the construction of linear

transport infrastructure facilities (FL) (formula 7):

min......)()(

=



jjL

xcxF

(7)

Under linear constraints:

{}

1,0,)(

=≤



xbxс

(8)

To solve the problem of minimizing costs when

organizing the construction of linear transport

infrastructure facilities, algorithms based on the

dynamic programming method are mainly used

(Bellman, 1965).

In general, the listed tasks are reduced to the

parameters of integer linear programming.

Therefore, the variant of integer linear programming

will be the solution of the transport problem. For the

construction of railway infrastructure in Indonesia, it

is required to minimize the cost of construction and

installation works (f

njxcxf

jjr

,...1)()(



(9)

As restrictions for solving the tasks, the

following conditions are accepted:

{}

1,0 x1.....n;j m; 1.....i

,)(

===

≤



(10)

4 DISCUSSION OF THE

RESULTS

Gomori's research (Gomory, 1963; Gilmore, 1965)

proposed algorithms for solving integer linear

programming problems using additional secant

planes.

The developed software, conducted with these

algorithms (Teplitsky, 1968), showed that the

method of "secant planes" gives good results, mainly

for problems of small dimension. At the same time,

for such problems, there are cases when the

algorithms of "secant planes" either do not provide a

reliable solution in real time, or require a complete

search of calculations.

For problems of combinatorial type, as a rule,

two groups of solutions can be distinguished based

on the method of local optimization and the second

group using the method of step-by-step obtaining

solutions. The most common is the method of "step-

by-step obtaining solutions", which includes

iterative, incremental and spiral algorithms

(Tsvetkov, 2018). In the studies of Pyatetsky-

Shapiro A.B. (Pyatetsky-Shapiro, 1966), the

application of the random search method to solve the

integer programming problem is given under the

Planning of the Development of Indonesiaâ

Zs Transport Infrastructure using Linear Programming Methods

309

additional condition that all parameters a

, c

, b are

non-negative.

The formation of the budget of municipalities for

the construction and reconstruction of railway

infrastructure facilities in Indonesia, taking into

account the volume of production plans of

contracting organizations, is carried out sequentially,

starting from the linear level formed by the

production and technical department of the

contracting organization (Volkov, 2018; Volkov,

2019) in accordance with the comprehensive

strategic plan for the development of infrastructure

in the region of Indonesia.

Taking into account the interests of not only

contractors, but also the customer, for example,

municipalities, leads to the need to set a new type of

transport task.

In this task, instead of one matrix that takes into

account "supply and demand", two matrices are

used, independently reflecting the interests of both

contracting organizations for the construction of new

and reconstruction of the existing infrastructure of

railways in Indonesia, and the customer – customer,

for example, municipalities. Each of these matrices

is formed on the basis of the existing production and

financial relations between contractors and

customers represented, for example, by

municipalities. Together, these "matrices of

interests" reflect not only the current benefits of each

of the participants in the overall process, but also the

reliability of interaction, which is ignored in the

usual formulation of the transport task. When

considering the process of creating an algorithm for

the construction and reconstruction of railway

infrastructure facilities in Indonesia, these matrices

serve as the basis for obtaining a reference solution.

For example, on the island of Sumatra, it is the

development of a suburban (between provinces)

railway network to reduce the traffic load on

highways as a link of economic activity.

5 CONCLUSIONS

Further optimization is obtained by processing the

resulting matrix, and such a matrix can be

supplemented by new construction and repair

companies and new customers. One of the options

for solving general or resultant matrices, in which,

on the one hand, the interests of the customer, for

example, the municipality, are taken into account, on

the other – the interests of the contracting

organization, methods that are characteristic of the

"Dynamic transport problem with delays" or

combinatorial methods can be used.

To develop the suburban railway network on

Sumatra Island, it is planned to build a main

highway to connect the following cities: Banda Aceh

– Sigli – Bireun – Lokseumave (284 km);

Lokseumave – Langsa – Besitang (199.5 km); Binjai

– Besitang (156 km); Rantauprapat – Duri –Dumai

(251 km); Duri – Pekanbaru (100 km); Pekanbaru –

Muaro (297 km); Pekanbaru – Rengat – Jambi (274

km); Jambi – Betung (188 km); Betung – Simpang

(124 km); Tarahan – Bakauhen (70 km); Pematang

Siantar – Danau Toba (117 km); Shortest way

Rejosari – Tarakhan (37,752 km); The shortest route

is Indarung – Solok (36.2 km); Reconstruction of the

Belavan – Gabion line; Reconstruction of the

Padang – Pulo Aer line; Reconstruction of the Naras

– Sungai Limau line, and Reconstruction of the

Moiro Calaban – Logas line.

When using an integrated approach of planning

for the development of the railway infrastructure of

Indonesia based on linear programming methods, it

is possible to obtain a balanced version of the

financial and economic plan of expenditures and

expenditures for the development of the railway

infrastructure of Indonesia. And also determine the

components of the share of financing, both private

capital and the state. Thus, the development of the

suburban train network is impossible without state

financial support for infrastructure to achieve

maximum quality of service.

REFERENCES

Kementerian Perhubungan. Rencana Induk Perkeretaapian

Nasional. Ditjen Perkeretaapian. Jakarta. 2011. p. 86.

Peraturan Presiden Republik Indonesia Nomor 18 Tahun

2020 tentang Rencana Pembangunan Jangka

Menengah Nasional 2020-2024, 2020. p. 710.

Peraturan Presiden Republik Indonesia Nomor 38 Tahun

2015 tentang Kerjasama Pemerintah dengan Badan

Usaha dalam Penyediaan Infrastruktur, 2015. p. 37.

PT. Penjaminan Infrstruktur Indonesia. Proyek KPBU

Kereta Api Makassar-Pare-pare, 2018. p. 366.

Jinca, M. Yamin., 2009. Keterpaduan Sistem Jaringan

Antar Moda Transportasi di Pulau Sulawesi. Jurnal

Transportasi. p. 14.

Peraturan Daerah Provinsi Sulawesi Selatan Nomor 1

Tahun 2019 tentang Rencana Pembangunan Jangka

Menengah Daerah Provinsi Sulawesi Selatan Tahun

2018-2023. 2019. p. 655.

Peraturan Daerah Provinsi Sulawesi Barat Nomor 8 Tahun

2017 tentang Rencana Pembangunan Jangka

Menengah Daerah Provinsi Sulawesi Barat Tahun

2017-2022. 2017. p. 484.

TLC2M 2022 - INTERNATIONAL SCIENTIFIC AND PRACTICAL CONFERENCE TLC2M TRANSPORT: LOGISTICS,

CONSTRUCTION, MAINTENANCE, MANAGEMENT

310

Peraturan Daerah Provinsi Sulawesi Utara Nomor 1 Tahun

2014 tentang Rencana Pembangunan Jangka

Menengah Daerah Provinsi Sulawesi Utara Tahun

2014-2034. 2014. p. 114.

Badan Pusat Statistik Provinsi Sulawesi Tengah. Provinsi

Sulawesi Tengah dalam Angka. 2018. p. 607.

Badan Pusat Statistik Provinsi Sulawesi Barat. Provinsi

Sulawesi Barat dalam Angka. 2021. p. 651.

Milovidov, S. P., Kozlov, P. A., 1982. Dynamic transport

problem with delays in network formulation. Izvestia

of the USSR Academy of Sciences. Technical

cybernetics. 1. pp. 211-212.

12.Borodinova, I. A., Saraev L. A., 2010. Stochastic

transport problem. Bulletin of Samara State

University. 81. pp.16-23.

Dantzig, G., 2016. Linear programming and extensions.

Gass, S. I., 2004. Linear programming. Encyclopedia of

Statistical Sciences. 6.

Nelder, J. A., Mead, R. A., 1965. Simple method for

function minimization. The computer journal. 7. 4. p.

308-313.

Tsvetkov, V. Ya., 2001. Mathematical methods of analysis

in economics. p. 56.

Rosenberg, I. N., Tsvetkov V. Ya., 2019. Combinatorial

solution of the transport problem. Science and

Technology of Railways. 3. 1 (9). pp. 85-88.

Bellman, R., Dreyfus, S., 1965. Applied problems of

dynamic programming. Science.

Gomory, R. Е. 1963. An Algorithm for integer solutions to

linear programs. Recent Advances Math. Programm.

Gilmore, P. C., Gomory, R. E., 1965. Multi-Stage Gutting

Stock Problems of two and more dimensions. Opns.

Res. 13. 1.

Teplitsky, E. D., Finkelyptein, Yu. Yu., 1968 Machine

experiment for solving integer linear programming

problems. Economic and Mathematical Methods. IV.

Tsvetkov, V. Ya., Mordvinov V. A., 2018. Approach to

systematization of algorithms. Ontology of design. 7. 4

(26). pp. 388-397.

Pyatetsky-Shapiro, A. B. et al., 1966. About an interactive

method for solving integer programming problems.

Report of the USSR Academy of Sciences. 160. 169. 6.

Volkov, B. A., Kovalenko, N. I., Dobrin, A. Yu.,

Kovalenko, A. N. 2018. On the methodology of

planning expenses for the current operation of the

track. Path and track management. 5. pp. 23-26.

Volkov, B. A., Kovalenko, N. I., Dobrin, A. Yu.,

Kovalenko, A. N., 2019. Reduction of costs for the

current operation of the track depending on the

classification of railway lines. Path and track

management. 6. pp. 15-19.

Planning of the Development of Indonesiaâ

Zs Transport Infrastructure using Linear Programming Methods

311