Hybrid Fuzzy Classiﬁcation Algorithm with Modifed Initialization and

Crossover

Tatiana Pleshkova

and Vladimir Stanovov

Siberian Federal University, Krasnoyarsk, Russian Federation

Keywords:

Classiﬁcation, Fuzzy Logic, Genetic Algorithm.

Abstract:

The article proposes two modiﬁcations of initialization and crossover operations for the design of a genetic

fuzzy system. A fuzzy logic system is used to solve data classiﬁcation problems and is automatically generated

by a genetic algorithm. The paper uses a genetic algorithm to encode of several fuzzy granulations into a single

rule, while each individual encodes a rule base. The proposed algorithm uses several training objects of the

same class to create a single rule during initialization. The modiﬁed crossover creates a new rule base from

most efﬁcient rules selected from parents. To evaluate the effectiveness of the modiﬁcation, the computational

experiments were carried out on several datasets, followed by veriﬁcation using Mann-Whitney U test. The

proposed initialization modiﬁcation allows reducing the number of rules in a fuzzy rule base and increasing

the accuracy and F-score on some datasets. The crossover modiﬁcation shows higher efﬁciency only on one

dataset.

1 INTRODUCTION

In the modern world, data analysis is a necessary

process in all spheres. One of the popular methods

of knowledge systematization is classiﬁcation, which

implies the organization of data into categories for ef-

fective use. Various tasks are solved with classiﬁca-

tion methods, for example, the classiﬁcation of data

from satellite images or medical diagnosis and prog-

nosis of diseases (S¸tefan, 2012). There is no regular

method for solving data classiﬁcation problems. De-

pending on the formulated conditions, it is necessary

to select a method that would classify the data into

the appropriate categories. There are many methods

for solving data classiﬁcation problems that can be

divided into two groups, based on “black box” and

“white box” principles (Komargodski et al., 2017).

Depending on the problem, a suitable method is se-

lected before starting the classiﬁcation. First of all,

due to the fact that the user of the system that classi-

ﬁes data does not always have the opportunity to un-

derstand the decision-making process, there is a need

to create a system that allows the classiﬁcation pro-

cess to be performed while getting information about

which characteristics inﬂuence the classiﬁcations. In

https://orcid.org/0000-0001-7761-7808

https://orcid.org/0000-0002-1695-5798

other words, the users’ involvement is aimed at study-

ing the decision-making process, which gives them

the opportunity to use their knowledge of the subject

area to increase the reliability of data classiﬁcation.

To fulﬁll these conditions, it is necessary to use the

“white box” model when implementing the data clas-

siﬁcation method. If the solver type (neural network

and so on) is not important, then it makes sense to

use the data classiﬁcation method without providing

information about which characteristics inﬂuence the

classiﬁcation results.

In this study it was decided to use Fuzzy Rule-

Based System due to its ﬂexibility and interpretabil-

ity. Many researchers use Fuzzy Rule-Based System

to implement the “white box” model (Bodenhofer and

Herrera, 1997). L. Zadeh proposed a fuzzy logic in

1965 that was able to cope with the task of describing

vague deﬁnitions of human language (Zadeh, 1965).

And in 1974, I. Mamdani designed the ﬁrst function-

ing controller for a steam turbine (Mamdani, 1974),

which operated based on the L. Zadeh algebra. Mod-

ern researchers also continue to develop this area and

have achieved great success. For example, Y. Nojima,

H. Ishibuchi and F. Herrera are doing research with

the classiﬁcation of objects based on fuzzy rules. In

the current study, it was decided to use the method

discussed in the article (Ishibuchi et al., 2013) as base-

line, where H. Ishibuchi proposed a machine learn-

Pleshkova, T. and Stanovov, V.

Hybrid Fuzzy Classiﬁcation Algorithm with Modifed Initialization and Crossover.

DOI: 10.5220/0011587500003332

In Proceedings of the 14th International Joint Conference on Computational Intelligence (IJCCI 2022), pages 225-231

ISBN: 978-989-758-611-8; ISSN: 2184-3236

225

ing algorithm based on fuzzy logic. Our goal is to

improve the quality of fuzzy classiﬁers by proposing

new genetic operations, to make the algorithm work

more efﬁciently, that is, to ﬁnd better solutions faster,

but with the same level of complexity. In particu-

lar, the contributions of this study are: initializing

rules from several objects is more efﬁcient and select-

ing better rules during crossover may improve perfor-

mance.

This paper is organized as follows: Section II con-

tains related works. In Section III we brieﬂy ex-

plain the basic method and its features. Next we

explain proposed modiﬁcations for initialization and

crossover in Section IV. In Section V we present the

results. Finally we conclude this paper in Section VI.

2 RELATED WORKS

Genetic fuzzy systems have attracted considerable at-

tention in the artiﬁcial intelligence community in the

last decades. Since 2000 there was a growing need

to ﬁnd a compromise between interpretability and

accuracy in the tasks of linguistic fuzzy modeling.

First of all in (Ishibuchi and Nakashima, 2000) au-

thors introduce the effective use of rule weights in

fuzzy rule-based classiﬁcation systems. In (Alcal

et al., 2007) a new post-processing method was in-

troduced. This method was based on the well-known

SPEA2 algorithm. In (Fern

andez et al., 2010) evo-

lutionary approaches that help to search for a set of

rules were considered. The hybrid fuzzy genetics-

based machine learning (GBML) algorithm was pro-

posed in (Ishibuchi et al., 2013), where algorithm had

a Pittsburg-style framework in which a rule set is han-

dled as an individual. The operation of the algorithm

will be described in more detail in the next section.

Each of the works uses the representation of the

decision-making process in the language understand-

able for the expert. It is possible thanks to the use

of fuzzy rules in the classiﬁcation, which determine

whether an object with known characteristics belongs

to a particular class. A fuzzy rule consists of a con-

dition of the type “if... then...” with fuzzy terms in

the“if...” part and the corresponding class number in

the “then...” part (Herrera and Magdalena, 1997).

Rule R

: if x

is L

and...and x

is L

then Class C

with CF

, (1)

where n – number of rules in the rule base, v – number

of variables in the data sample, L – this is a linguistic

term, C – class label, CF – rule weight (which is a

real number in the unit interval [0, 1]).

3 GENETICS-BASED MACHINE

LEARNING

The method in (Ishibuchi et al., 2013) is based on the

search for the optimal rule base. This search is carried

out using evolutionary algorithms, where the main

idea is based on Charles Darwin’s theory of natural

selection (Bleckmann, 2006). The process of ﬁnding

the best solution begins with a set of individuals, i.e.

a population. The process of natural selection begins

with the choice of the individuals with better ﬁtness

from the population. The selected individuals pro-

duce an offspring that inherits the characteristics of

the parents. If the parents are better i.e. have a higher

ﬁtness than the others, there is an opportunity that

their offspring will be better than the parents and will

have a higher chance of survival. This process contin-

ues to be repeated for a certain number of generations,

and at the end of the generation the ﬁttest individual

is found (Mitchell, 1996). One individual consists of

n fuzzy rules, where upper limit is n ≤ 50. Each rule

is designed using linguistic terms L

, L

, ..., L

. One

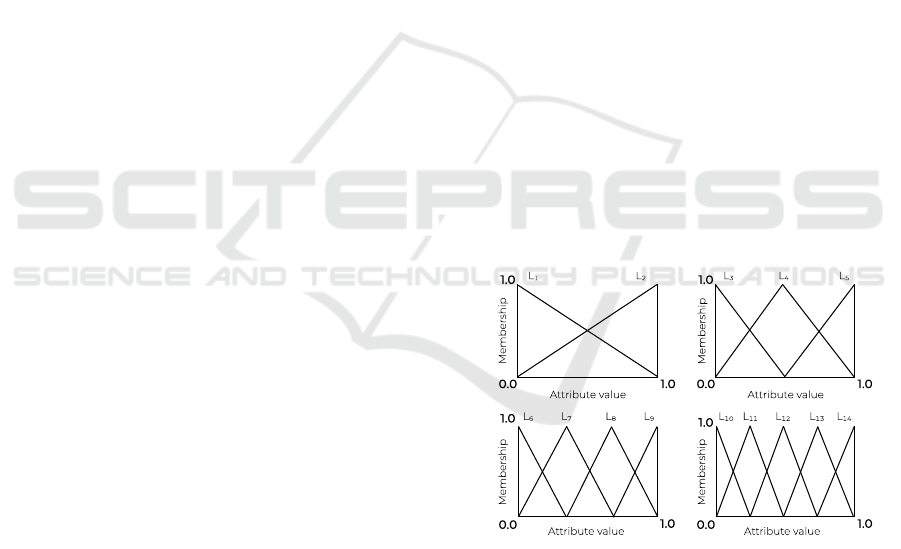
of the features of study (Ishibuchi et al., 2013) is the

use of several fuzzy granulations for each linguistic

variable. Figure 1 shows this concept. There are 14

linguistic variables and a “don’t care” condition (DC),

which means that for this variable in this rule there is

no difference what value the variable has. This is de-

scribed in (Ishibuchi et al., 2013).

Figure 1: Fuzzy granulations (L

, L

,...,L

After that, using the ﬁtness function, the ﬁtness

of the individual is determined, i.e. how well the

fuzzy rules base performs classiﬁcation. After receiv-

ing ﬁtness function value of each individual, we can

determine the probability of choosing a particular in-

dividual for following reproduction. The genetic al-

gorithm, which is one of the variations of the evolu-

tionary algorithm and is used in the study, consists

of several stages: initialization, selection, crossover,

mutation and formation of a new generation (Banzhaf

FCTA 2022 - 14th International Conference on Fuzzy Computation Theory and Applications

226

et al., 1998). The feature of the Ishibuchi algorithm

is that after the mutation, the Michigan-style part is

applied.

The ﬁrst stage is initialization, in which individu-

als are formed. When creating a rule, a random ob-

ject is ﬁrst selected from the training sample, then a

rule is formed based on the parameters of the selected

object, that is, the corresponding linguistic variable

is selected for each parameter. Then the conﬁdence

is calculated and applied in evaluating the rule class

number, which is the most corresponding to a partic-

ular rule. To specify the consequent class C

and the

rule weight CF

, we ﬁrst calculate the conﬁdence of

the association from the antecedent fuzzy vector L

each class k (k = 1, 2, ..., M) (Ishibuchi et al., 2013) as

follows:

Con f (L

⇒ Class k) =

∑

∈ Class k

)

∑

p=1

)

(2)

where µ

is the product of all memberships values of

the antecedent fuzzy set L

at the input value x

If the conﬁdence value for a particular class C

larger than 0.5 in eq. 2 in (Ishibuchi et al., 2013) com-

putational experiments, we generate a fuzzy rule with

the antecedent fuzzy rule and the consequent class C

Then the rule weight CF

in (Ishibuchi et al., 2013) is

speciﬁed as follows:

= 2 ∗Con f (L

⇒ Class C

) − 1. (3)

It is established that if CF

> 0, then the rule

is added to the fuzzy rule base. Fuzzy rules with

negative weights are not applicable for classiﬁcation.

One of the advantages of this work is the use of a

Michigan-style algorithm probabilistically applied to

each set of rules. The Michigan-style part is used as

local search after main genetic algorithm.

The ﬁtness of the main genetic algorithm was cal-

culated as shown in eq. 4, and the ﬁtness of the

Michigan-style part is the ﬁtness of the individual

rules at the selection stage, which was calculated

based on the number of correctly classiﬁed objects.

f itness = w

∗ f

+ w

∗ f

+ w

∗ f

(4)

where w

= 100, w

= 1, w

= 1 and f

– the error rate

on training patterns in percentage, f

– the number of

active fuzzy rules (rules that classiﬁed at least 1 object

correctly), f

– the length of the rule (the number of

variables other than 0 - don’t care).

The second stage is selection, in which from the

entire population, individuals are selected with the

same probability in an amount equal to the size of the

tournament, that is, the number pre-set by the user,

the number must necessarily be greater than 2 and less

than the population size. After the tournament is per-

formed, the individual with the highest ﬁtness in this

group is selected (Banzhaf et al., 1998).

The selected individuals enter the next stage –

crossover. Offspring is the random combination of

the genes (fuzzy rules) of two individuals. Two indi-

viduals are selected with tournament in the algorithm,

and the number of active rules for each of them is cal-

culated. Then an offspring is formed from these indi-

viduals (Poli et al., 2008). The offspring should not

have the number of active rules less than the number

of classes.

The last stage is mutation, where certain parts of

the rule base change in accordance with a given for-

mula:

min(

v ∗ f

, 1), (5)

where v is the number of variables in the dataset.

In the next section the proposed modiﬁcations is

described.

4 MODIFICATION

Due to the fact that the rule describes several objects,

the following modiﬁcation was proposed. Instead of

forming a fuzzy rule on one random object, the use of

several objects of the same class to create a rule was

implemented. To form a rule, a random object a is

ﬁrst selected, then several more objects b

of the same

class are selected, where k = 1...r and r is a number

of neighbors. The search is carried out for the nearest

several objects to the selected one using the Euclidean

distance, as shown in Figure 2. For example, based

on three objects a, b

, b

a fuzzy rule is generated.

The analysis of the best combination of the number of

objects to form the rule was also performed.

Figure 2: Visualization of fuzzy rules generation modiﬁca-

tion.

Hybrid Fuzzy Classiﬁcation Algorithm with Modifed Initialization and Crossover

227

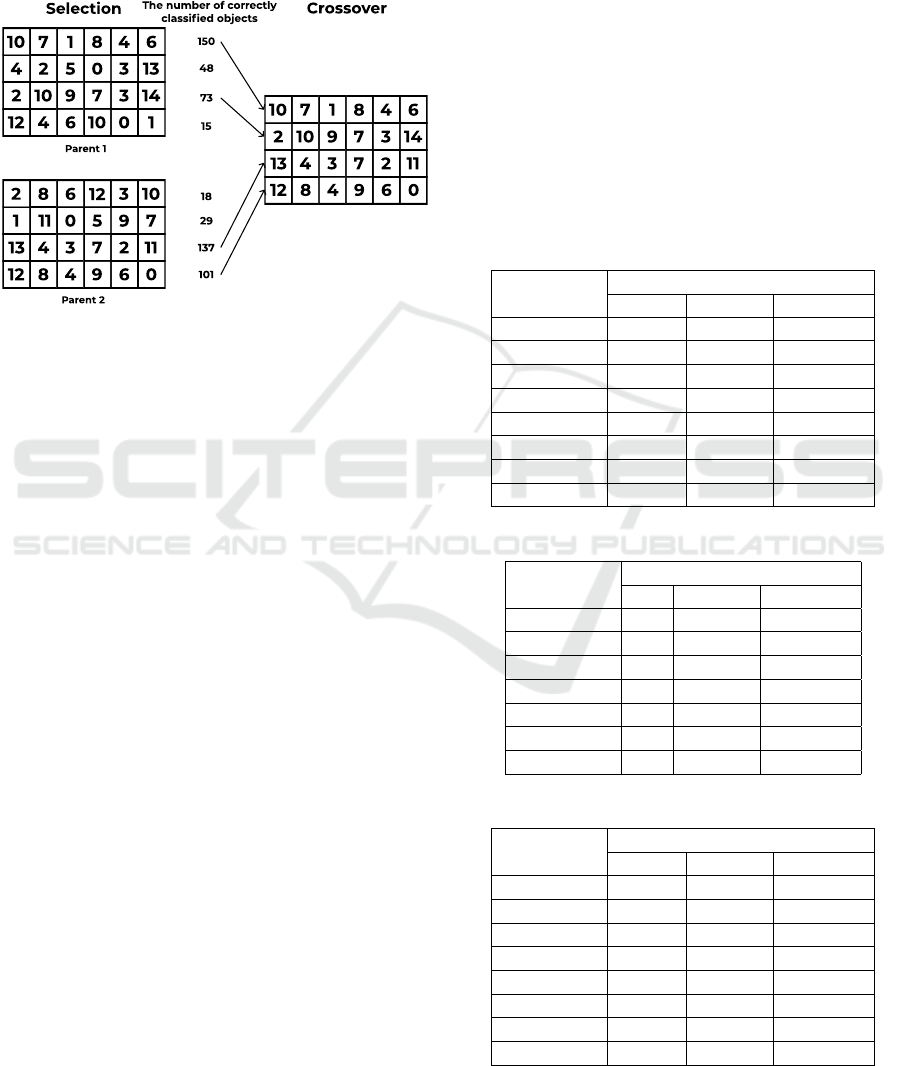
As for crossover modiﬁcation, we proposed to

change the choice of rules for the formation of an

offspring. The new method selects the most suitable

rules, then forms an offspring from these rules that

have the largest number of correctly classiﬁed objects.

An example is shown in Figure 3.

Figure 3: Visualization of crossover modiﬁcation.

We also made additional changes in the algorithm.

For instance, we used F-score in ﬁtness of the main

genetic algorithm. As we said before, one of the fea-

tures in (Ishibuchi et al., 2013) is the Michigan-style

part. Depending on the number of active rules of an

individual, the number of rules that will be formed

heuristically or genetically was calculated using for-

mula with one addition: if the value is 1, then the

number of rules generated by the genetic algorithm is

2, heuristic is 2. Heuristically, a rule was formed for

an object that was not correctly classiﬁed by any rule.

In addition, we set the minimum threshold parame-

ter for conﬁdence equal to 0.6. In our experiment

we checked the results of weak, average and strong

mutation and we came to the conclusion that average

mutation has better effect on accuracy.

5 RESULTS

Testing of the basic and the modiﬁed algorithms was

carried on several tasks taken from the UCI repository

(Asuncion, 2007). The algorithm was run with the

number of individuals set to 100.

In the ﬁrst experiment with selecting the best num-

ber of objects we used three tasks and 500 genera-

tions. In the second experiment we used four tasks

and we decided to increase the number of generations

to 1000 in order to check whether improvements are

noticeable when the number of generations is dou-

bled.

The 10-fold cross-validation procedure was iter-

ated three times using different data partitions into

ten subsets. Average results over 30 runs are sum-

marized in Table 1, Table 3 and Table 5, NR is the

number of rules. Since the average values are pre-

sented, in order to evaluate the efﬁciency of the mod-

iﬁcation, it is necessary to use the Mann-Whitney U

test (Mann and Whitney, 1947), popular nonparamet-

ric test to compare outcomes between two indepen-

dent groups. Table 2, Table 4 and Table 6 also show

the results of a statistical test accordingly, where the

symbol “=” shows that differences are insigniﬁcant,

the symbol “+” shows that differences are signiﬁcant

and the modiﬁcation is more efﬁcient and “–” means

that differences are signiﬁcant and the modiﬁcation is

worse than the original algorithm.

Table 1: Results on phoneme dataset, ﬁrst experiment.

Number of Values

objects NR F-score Accuracy

1 10.267 0.722 0.792

2 12.060 0.705 0.783

2 of 5 6.200 0.745 0.801

3 10.367 0.721 0.782

3 of 6 4.367 0.774 0.807

4 of 6 4.900 0.775 0.811

5 of 7 7.300 0.776 0.808

6 10.833 0.709 0.789

Table 2: Results Mann-Whitney U-test on phoneme dataset.

Number of Values

objects NR F-score Accuracy

2 – = =

2 of 5 + = =

3 = = =

3 of 6 + + +

4 of 6 + + +

5 of 7 + + +

6 = = =

Table 3: Results on ring dataset, ﬁrst experiment.

Number of Values

objects NR F-score Accuracy

1 20.107 0.831 0.831

2 20.300 0.825 0.825

2 of 5 20.100 0.832 0.834

3 20.000 0.829 0.829

3 of 6 18.000 0.832 0.833

4 of 6 19.900 0.828 0.829

5 of 7 19.333 0.829 0.829

6 19.533 0.830 0.831

FCTA 2022 - 14th International Conference on Fuzzy Computation Theory and Applications

228

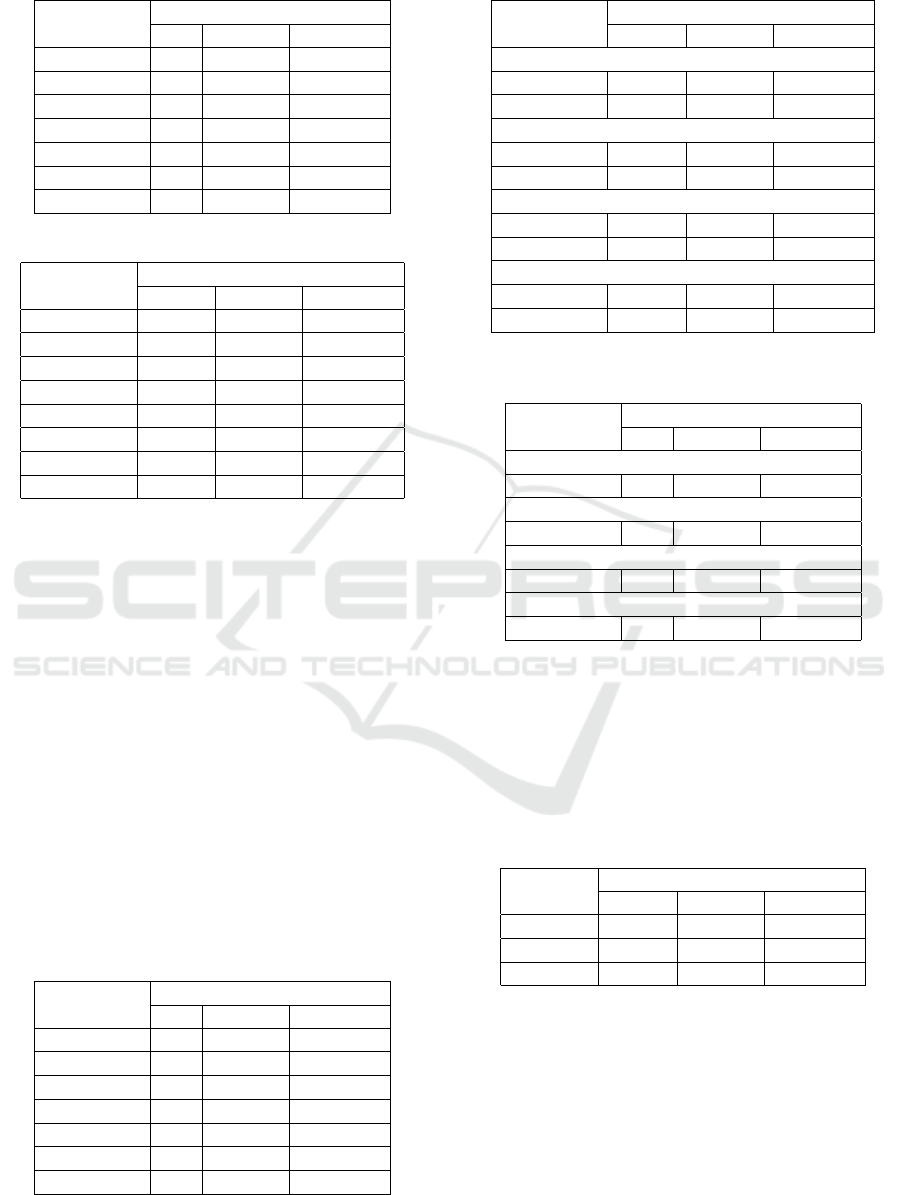
Table 4: Results Mann-Whitney U-test on ring dataset.

Number of Values

objects NR F-score Accuracy

2 = = =

2 of 5 = = =

3 = = =

3 of 6 + = =

4 of 6 + = =

5 of 7 = = =

6 + = =

Table 5: Results on segment dataset, ﬁrst experiment.

Number of Values

objects NR F-score Accuracy

1 22 0.903 0.903

2 22.567 0.898 0.899

2 of 5 22.600 0.904 0.905

3 21.767 0.903 0.904

3 of 6 17.933 0.905 0.905

4 of 6 22.700 0.907 0.908

5 of 7 21.100 0.903 0.903

6 21.567 0.907 0.907

Based on Tables 1, 3, 5, it can be seen that the

modiﬁcation with the design of a fuzzy rule on nearby

objects works more efﬁciently than on randomly se-

lected ones from the same class, regardless of their

number. For the second experiment, it was decided

to use 3 nearest objects selected from 6 objects of the

same class to form the rule as shown in Figure 3. It

can be seen from the results of the modiﬁcation that

the number of rules decreases, which has a positive

effect on interpretation, because the fewer rules, the

easier the rule base. The results are presented in Ta-

ble 7 and results from Mann-Whitney U-test is in Ta-

ble 8. Comparing the results of the ﬁrst and second

experiments, it can be seen that the changes are in-

signiﬁcant, which means there is no need to increase

the number of generations for the data used in the ex-

periment. The algorithm ﬁnds a high-quality rule base

in 500 generations, and therefore in less time.

Table 6: Results Mann-Whitney U-test on segment dataset.

Number of Values

objects NR F-score Accuracy

2 – = =

2 of 5 – = =

3 = = =

3 of 6 + = =

4 of 6 = = =

5 of 7 = = =

6 = = =

Table 7: Results of second experiment.

Number of Values

objects NR F-score Accuracy

Phoneme

1 10.833 0.721 0.789

3 of 6 4.933 0.766 0.825

Ring

1 20.567 0.832 0.832

3 of 6 18.533 0.828 0.828

Satimage

1 22.700 0.806 0.863

3 of 6 16.833 0.837 0.885

Page-blocks

1 9.900 0.435 0.909

3 of 6 9.000 0.440 0.910

Table 8: Results Mann-Whitney U-test of second experi-

ment.

Number of Values

objects NR F-score Accuracy

Phoneme

3 of 6 + + +

Ring

3 of 6 + = =

Satimage

3 of 6 + + +

Page-blocks

3 of 6 + = +

Based on Table 7, it can be noted that the proposed

method of generating fuzzy rules allows the modiﬁed

algorithm to signiﬁcantly reduce the number of rules

and at the same time improve the accuracy for some

data classiﬁcation problems.

The results of crossover modiﬁcations and Mann-

Whitney U test are presented in Table 9 and Table 10.

Table 9: Crossover modiﬁcation.

Data Values

set NR F-score Accuracy

Phoneme 11.400 0.731 0.786

Ring 23.133 0.833 0.834

Satimage 17.100 0.833 0.858

Based on the results in Tables 9-10, we can con-

clude that crossover modiﬁcation shows higher efﬁ-

ciency only on one dataset “Satimage”. That means

that there is a possibility that the modiﬁcation may

work in some cases. The difference between “Satim-

age” and other datasets is the number of classes and

range of numbers. Dataset “Satimage” has posi-

tive numbers, others have both (positive and nega-

tive numbers). The main contributions of this paper

Hybrid Fuzzy Classiﬁcation Algorithm with Modifed Initialization and Crossover

229

Table 10: Results Mann-Whitney U-test for crossover mod-

iﬁcation.

Data Values

set NR F-score Accuracy

Phoneme = = =

Ring – = =

Satimage + + +

are: 1) it is shown that initialization on several objects

works better than on one; 2) it is shown that modiﬁed

crossing can work better on some data. It is necessary

to conduct additional experiments on other datasets

to ﬁnd out what conditions inﬂuence the efﬁciency of

modiﬁed crossover.

We decided to test both modiﬁcations on the same

data in order to check if there will be improvements.

The results are presented in Table 11.

Table 11: Results of both modiﬁcations.

Data Values

set NR F-score Accuracy

Phoneme 5.833 0.747 0.797

Ring 23.200 0.833 0.835

Satimage 14.667 0.832 0.861

Segment 21.852 0.899 0.896

As we can see from the results of both modiﬁca-

tions, the differences are insigniﬁcant. In future ex-

periments, it will be necessary to try changing the pa-

rameters to test the efﬁciency.

The modiﬁed method was also compared with al-

ternative approaches: Decision Tree (DT), Support

Vector Machine (SVM), Logistic Regression (LR),

Neural Networks (NN). These methods were taken

from sklearn library, the standard parameters were

used. The accuracy are presented at Table 12.

Table 12: Results of alternative approaches.

Data Methods

set DT SVM LR NN

Phoneme 0.770 0.774 0.774 0.738

Ring 0.737 0.726 0.721 0.762

Satimage 0.772 0.869 0.867 0.789

Page-blocks 0.960 0.967 0.967 0.944

Segment 0.541 0.961 0.962 0.913

As can be seen from the table, the proposed modi-

ﬁcation with initialization is comparable classiﬁcation

quality to other known methods. For example, on the

“Satimage” and “Ring” tasks, it proved to be better

than neural networks and on the “Phoneme” task the

proposed modiﬁcation showed better results compar-

ing to others.

6 CONCLUSIONS

In this paper, the search for better way to ﬁnd accu-

rate and compact rule bases was investigated. In this

regard, the modiﬁcation with initialization was pro-

posed in this paper, and showed efﬁciency on several

datasets, decreasing number of rules and increasing

accuracy and F-score. The design of a rule on several

nearby objects from the same class showed higher ef-

ﬁciency compared to using a single object. As for the

modiﬁcation with crossover, the improved efﬁciency

of this approach was observed only on one dataset.

The proposed method shows similar accuracy com-

pared to alternative methods. In future studies, it is

possible to consider other modiﬁcations to improve

the quality of the algorithm. For instance, we want to

implement multi-objective optimization.

ACKNOWLEDGEMENTS

The work was carried out within the framework of the

state support program for leading scientiﬁc schools

(grant of the President of the Russian Federation NSh-

421.2022.4).

REFERENCES

Alcal

a, R., Gacto, M. J., Herrera, F., and Alcal

a-Fdez, J.

(2007). A multi-objective genetic algorithm for tun-

ing and rule selection to obtain accurate and compact

linguistic fuzzy rule-based systems. Int. J. Uncertain.

Fuzziness Knowl. Based Syst., 15:539–557.

Asuncion, A. U. (2007). Uci machine learning repository,

university of california, irvine, school of information

and computer sciences.

Banzhaf, W., Francone, F. D., Keller, R. E., and Nordin, P.

(1998). Genetic programming - an introduction: On

the automatic evolution of computer programs and its

applications.

Bleckmann, C. A. (2006). Evolution and creationism in sci-

ence: 1880–2000.

Bodenhofer, U. and Herrera, F. (1997). Ten lectures on ge-

netic fuzzy systems.

Fern

andez, A., Garc

ıa, S., Luengo, J., Bernad

o-Mansilla,

E., and Herrera, F. (2010). Genetics-based machine

learning for rule induction: State of the art, taxonomy,

and comparative study. IEEE Transactions on Evolu-

tionary Computation, 14:913–941.

Herrera, A. and Magdalena, L. (1997). Genetic fuzzy sys-

tems : A tutorial.

Ishibuchi, H., Mihara, S., and Nojima, Y. (2013). Parallel

distributed hybrid fuzzy gbml models with rule set mi-

gration and training data rotation. IEEE Transactions

on Fuzzy Systems, 21:355–368.

FCTA 2022 - 14th International Conference on Fuzzy Computation Theory and Applications

230

Ishibuchi, H. and Nakashima, T. (2000). Effect of rule

weights in fuzzy rule-based classiﬁcation systems.

Ninth IEEE International Conference on Fuzzy Sys-

tems. FUZZ- IEEE 2000 (Cat. No.00CH37063), 1:59–

64 vol.1.

Komargodski, I., Naor, M., and Yogev, E. (2017). White-

box vs. black-box complexity of search problems:

Ramsey and graph property testing. 2017 IEEE 58th

Annual Symposium on Foundations of Computer Sci-

ence (FOCS), pages 622–632.

Mamdani, E. H. (1974). Applications of fuzzy algorithms

for control of a simple dynamic plant. Proceedings of

the IEEE.

Mann, H. B. and Whitney, D. R. (1947). On a test of

whether one of two random variables is stochastically

larger than the other. Annals of Mathematical Statis-

tics, 18:50–60.

Mitchell, M. (1996). An introduction to genetic algorithms.

Poli, R., Langdon, W. B., and McPhee, N. F. (2008). A ﬁeld

guide to genetic programming.

S¸ tefan, R.-M. (2012). A comparison of data classiﬁcation

methods. Procedia. Economics and ﬁnance, 3:420–

425.

Zadeh, L. A. (1965). Fuzzy sets. Inf. Control., 8:338–353.

Hybrid Fuzzy Classiﬁcation Algorithm with Modifed Initialization and Crossover

231