Energy Consumption, CO2 Emissions and Economic Growth: A

Comparative Analysis in Guangdong, China

Hao Guo

School of Urban Planning and Design, Peking University Shenzhen Graduate School, Shenzhen, Guangdong, China

Keywords:

Energy Consumption, Carbon Dioxide Emissions, Environmental Kuznets Curve.

Abstract: Carbon dioxide (CO2) is the chief greenhouse gas causing global warming, and the relationship between

this gas and economic development is a major subject of research. This study uses panel data and models for

coastal cities in Guangdong province, China, from 2005 to 2017, as well as the robustness results obtained

using Driscoll-Kraay standard errors. The study finds that an inverted U-shaped relationship exists between

income and emissions in the Pearl River Delta region; the expected income per capita at the inflection point

on the U curve is between US$24,920 and 27,860, and the expected per capita CO2 emissions at the

inflection point are projected to be approximately 13 tons annually. However, the EKC hypothesis is not

verified in the non-Pearl River Delta area. Population agglomeration is found to benefit the reduction in per

capita CO2 emissions, and a population scale effect exists; however, the emissions reduction effect of

population agglomeration in the non-Pearl River Delta area is greater than that in the Pearl River Delta

region. This study also provides relevant policy recommendations and suggestions for future research.

1 INTRODUCTION

Climate change has become a major global issue,

and excessive greenhouse gas emissions pose a

threat and disaster to the survival of life on Earth.

Carbon dioxide (CO2) is the chief greenhouse gas

causing global warming and currently accounts for

approximately 75% of the earth's greenhouse effect

(Sirag, 2018). While CO2 emissions are tightly

linked with fossil fuel consumption, fossil fuels are

an important factor driving the rapid economic

development of numerous countries and areas. The

relationship between environmental quality and

economic development can be represented by what

is known as the environmental Kuznets curve

(EKC), which has become a major topic of research.

The Kuznets curve was first proposed by the

economist Simon Kuznets in 1955 while researching

per capita income and the fairness of income

distribution (Kuznets, 1955). Afterwards, during the

early 1990s, many scholars innovatively applied the

Kuznets curve in the field of environmental quality

and proposed that the relationship between per

capita income and environmental quality took the

form of an inverted U-shaped curve (Grossman,

1995). While numerous empirical studies have

supported the EKC hypothesis (Diao, 2009), other

scholars have reached different conclusions and

believe that there is no empirical support for EKC

(Sanchez, 2016). Some studies have reached

different conclusions concerning the shape of the

EKC curve due to differences in regional

characteristics (Churchill, 2018) or differences in the

pollutants studied (Kaika, 2013). As a result, doubts

still exist concerning the relationship between CO2

emissions and income that form the basis of the

EKC hypothesis, and further efforts must be made to

verify the hypothesis employing representative

geographical areas and methods.

This study takes CO2 emissions per capita as an

indicator of environmental degradation to analyze

and compare the EKC of the Pearl River Delta

region with other areas in Guangdong province,

during the period from 2005 to 2017.

2 METHODS

2.1 Data Sources and Variables

This study employs balanced panel data from 21

cities in Guangdong province from 2005 to 2017 as

Guo, H.

Energy Consumption, CO2 Emissions and Economic Growth: A Comparative Analysis in Guangdong, China.

DOI: 10.5220/0011731000003607

In Proceedings of the 1st International Conference on Public Management, Digital Economy and Internet Technology (ICPDI 2022), pages 99-104

ISBN: 978-989-758-620-0

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

a sample and obtains GDP per capita and population

density data from the Guangdong Statistical

Yearbook for various years. This paper takes 2005

as the base year for GDP per capita, corrected for

inflation, and converts all amounts into US dollars

from the average annual exchange rates. The cities’

energy consumptions are calculated from each city's

energy intensity and GDP, and CO2 emissions are

estimated by the energy and economic data. The

definitions of the variables involved are shown in

Table 1.

Table 2 provides a statistical description of the

panel sample data. The sample consists of balanced

panel data with a period of 13 years. The Pearl River

Delta region includes Guangzhou, Shenzhen,

Huizhou, Dongguan, Foshan, Zhaoqing, Zhuhai,

Zhongshan, and Jiangmen, and the overall sample

size is 117. This study classifies the remaining areas

of Guangdong province, including the eastern

region, western region, and mountain areas, as the

non-Pearl River Delta area. This area includes 12

cities and has an overall sample size of 156. From

this table, the CO2 emissions per capita, GDP per

capita, and population density of the Pearl River

Delta region are 2, 3, and 2.77 times greater than the

corresponding figures for the non-Pearl River Delta

area, respectively. This outcome indicates that

significant differences exist between these two areas.

The standard deviations of the research variables are

relatively small, which indicates that the fluctuations

in values of the variables around the mean values are

relatively small; this also shows that the data are

stable and suitable for further study.

Table 1: Summary of variable definitions.

Name of

variable

Abbreviation Description Units Source

CO2

emissions

per capita

CO2pc

Average per

capita CO2

emissions

Tons/person

Estimated from energy consumption,

GDP, and population data from the

Guangdong Statistical Yearbook

Income

level

GDPpc GDP per capita

US$10,000/pers

Guangdong Statistical Yearbook for

various years

Population

density

Popuden

Permanent

population/area

1,000

persons/km2

Guangdong Statistical Yearbook for

various years

Table 2: Descriptive statistics of variables.

Region Pearl River Delta Non-Pearl River Delta

Variable CO2pc GDPpc Popuden CO2pc GDPpc Popuden

Mean 9.336 0.975 1.729 4.694 0.32 0.624

St.d 2.912 0.509 1.53 2.216 0.146 0.618

Min 2.762 0.145 0.247 1.029 0.091 0.154

Max 13.972 2.122 6.272 10.899 0.675 2.55

Size 117 117 117 156 156 156

Figure 1: Scatter diagram of the GDP and CO2 emissions per capita.

ICPDI 2022 - International Conference on Public Management, Digital Economy and Internet Technology

100

Figure1 shows the results of the quadratic curve

fitting for GDP per capita and CO2 emissions per

capita in the Pearl River Delta and the non-Pearl

River Delta area. From this figure, the Pearl River

Delta region has a significantly higher income level

than that in the non-Pearl River Delta area, and CO2

emissions per capita display a slowing trend as the

income level increases. This very likely indicates

that the EKC inflection point has been reached,

while emissions per capita in the non-Pearl River

Delta area continue to increase rapidly.

2.2 Model Design

Equations used to test EKC models include

quadratic term equations and cubic term equations,

and linear equations are usually used for model

testing in the case of countries or areas that are not

fully industrialized. A quadratic polynomial model is

a very versatile means of assessing the form of an

EKC curve. To observe whether an inverted U-

shaped curve is present, and whether environmental

degradation continues as income increases, this

study uses per capita income as a quadratic term in

model testing. The equation used to test the EKC

model in this study is as follows:



= 𝛼



+ 𝛽



𝑋



+ 𝛽



𝑋





+ 𝛽



𝑍



+ 𝜀

,

(1)

Here, Y is the variable expressing the degree of

environmental degradation; X is the income level

(GDP per capita); Z consists of other explanatory

variables; ε

,

is an error term; i indicates different

entities; and t expresses time. The coefficients in

front of X and its quadratic term determine the form

of the curve. Accordingly, the following situations

can be used to judge whether the EKC hypothesis is

correct:

If β_1>0 and β_2=0, then X and Y have a

monotonically increasing relationship.

If β_1<0 and β_2=0, then X and Y have a

monotonically decreasing relationship.

If β_1>0 and β_2>0, then X and Y have a U-

shaped relationship

If β_1>0 and β_2<0, then X and Y have an

inverted U-shaped relationship.

All of these different curve shapes have different

implications. A monotonically decreasing curve

indicates that environmental quality improves as

income increases, while a monotonically increasing

curve indicates that environmental quality

deteriorates as income increases. A U-shaped curve

indicates that while environmental quality improves

as income increases, it begins to deteriorate after

reaching a certain point. When an inverted U-shaped

curve is present, this outcome indicates that

environmental quality first deteriorates steadily with

rising income but begins to improve with rising

income after reaching an inflection point.

The explained variable in this model is CO2

emissions per capita, and the explanatory variables

are GDP per capita and its quadratic term. Model 1.1

is used to determine whether the EKC hypothesis is

applicable to the study area. Degree of population

agglomeration is subsequently added to model 1.1 as

an explanatory variable, yielding model 1.2. This

study also establishes models 2.1 and 2.2 for the

non-Pearl River Delta area during the same period

and adopts a fixed effects model and the random

effects model to compare the results of other models.

These models' equations are as follows:

CO2pc



= 𝛼



+ 𝛽



𝐺𝐷𝑃𝑝𝑐



+ 𝛽



𝐺𝐷𝑃𝑝𝑐





+ 𝜀

,

(2)

CO2pc



= 𝛼



+ 𝛽



𝐺𝐷𝑃𝑝𝑐



+ 𝛽



𝐺𝐷𝑃𝑝𝑐





𝛽



𝑃𝑜𝑝𝑢𝑑𝑒𝑛



+ 𝜀

,

(3)

Here, the subscript i=1,⋯ ,n indicates cross-

sectional units, and the subscript t=1,⋯ ,T

indicates time.

While many factors influence CO2 emissions per

capita, this study adopts per capita income and

degree of urban population agglomeration as the two

chief research variables. One of the chief difficulties

affecting analysis is model selection because the

choice of model has a large effect on the analysis.

Apart from the ordinary least squares method (OLS),

the fixed effects and random effects models are used

to analyze the panel data. An F-test is used to

determine the importance of individual effects and

compares a mixed OLS model with the fixed effects

model. In addition, the Lagrange multiplier (LM)

test is used to compare the OLS regression model

with the random effects model. Finally, the

Hausman test is used to confirm whether to use a

random effects model or a fixed effects model.

Cameron and Trivedi suggested that the sigmamore

option is the best in Stata for the Hausman test

because this option indicates that the two covariance

matrices are based on an estimation variance by the

same effective estimator (Cameron, 2010). These

tests indicate that model 1.1, model 1.2, and model

2.2 are fixed effects models, while model 2.1 is a

random effects model. Diagnostic testing is

performed on all models. The Pesaran cross-

sectional dependence test (Pesaran CD) is employed

to determine whether the residual is relevant across

different cities (Pesaran, 2004). The revised Wald

test is used to determine the models'

heteroscedasticity. The Wooldridge test is used to

Energy Consumption, CO2 Emissions and Economic Growth: A Comparative Analysis in Guangdong, China

101

test the serial correlation of the panel data.

According to Hoechle, if models are heterogeneous,

autocorrelated, and cross-regionally dependent, the

Driscoll-Kraay standard errors method should be

used (Hoechle, 2007).

3 RESULTS

From the F statistic of model 1.1 in Table 3, the

results of the F-test are significant for a fixed effects

model (F (2, 106) = 441.819, p-value = 0.000).

Model fitting reveals that a regression estimate using

the CO2 emissions per capita function can explain

up to 89% of the variation in CO2 emissions per

capita (R-squared = 0.848). The fixed effects

modeling results also reveal that the coefficients of

all variables are significant to a level of 1%.

Furthermore, model 1.1 verifies the existence of an

inverted U-shaped curve. After the population

density variable is added, this study finds that the

fixed effects model is also applicable to model 1.2.

Based on the results of testing for heteroscedasticity,

autocorrelation, and panel dependence, this study

employs the Driscoll-Kraay standard errors method

to overcome and minimize these problems. The

results of the fixed effects estimation and Driscoll-

Kraay standard errors estimation are shown in Table

3. From the F statistic of model 1.2, the results of the

F-test are significant for a fixed effects model (F (3,

105) = 313.032, p-value = 0.000). Similarly, the

model estimation results indicate that the data and

model have a good fit, and the model can explain

62.7% of the variation in per capita CO2 emissions

(R-squared = 0.627). The coefficients of all variables

are significant in a fixed effects model. For

population density, each increase in population

density by 1,000 persons per square kilometer could

reduce per capita CO2 emissions by 0.734 tons.

4 DISCUSSION

This study consequently discovers that a significant

inverse correlation exists between population density

and CO2 emissions per capita. Furthermore, the

inverted U-shaped curve in the Pearl River Delta

region is also confirmed by this model. From the

results of the fixed effects model estimation

employing models 1.1 and 1.2 and Driscoll-Kraay

standard errors estimation in the table, the monomial

coefficient of GDP per capita is significantly

positive, while the second-order coefficient is

significantly negative. Model 1.1 indicates that per

capita income at the inflection point is US$24,920

while CO2 emissions per capita at the inflection

point are 12.922 tons, with a 95% confidence

interval of 12.178 to 13.667 tons.

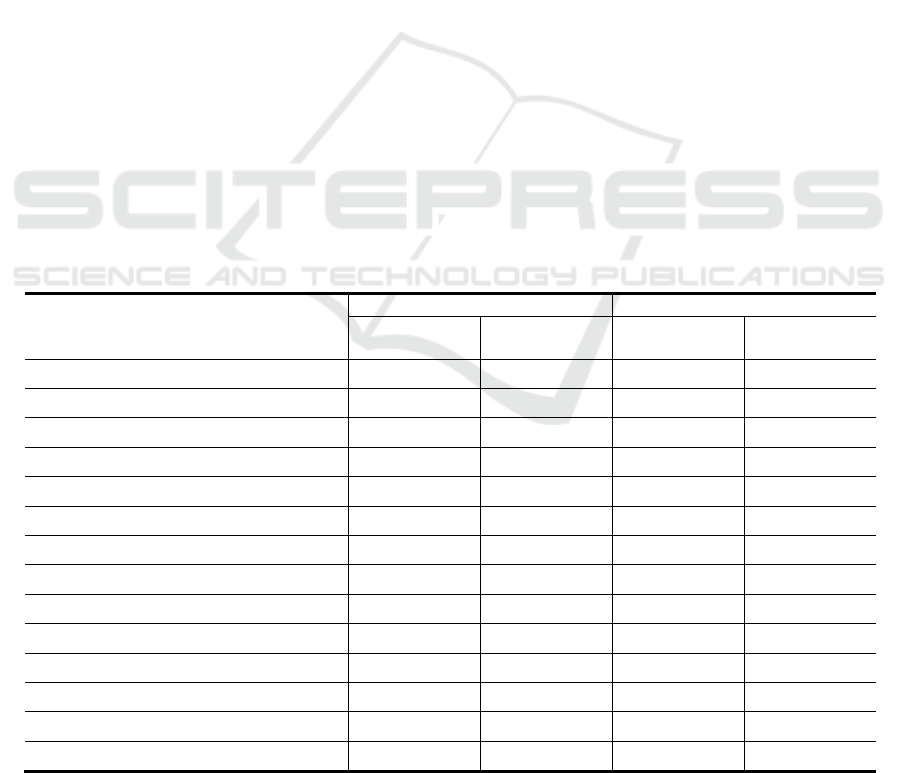
Table 3: Panel regression results for the pearl river delta region.

Model 1.1 FE Model 1.2 FE

Square FE

Driscoll- Kraay

Standard Errors

Square FE

Driscoll- Kraay

Standard Errors

GDPpc 6.983*** 6.983*** 7.020*** 7.020***

(-14.65) (-15.59) (-15.12) (-18.84)

GDPpc

-1.401*** -1.401*** -1.260*** -1.260***

(-7.09) (-7.35) (-6.31) (-8.10)

Popuden -0.734** -0.734***

(-2.61) (-6.60)

_cons 4.220*** 4.220*** 5.282*** 5.282***

(-17) (-19.33) (-11.17) (-16.78)

Observations 117 117 117 117

Cities 9 9 9 9

F-test or Wald chi2 441.819 415.713 313.032 606.414

R-square/ R-square within 0.848 0.893 0.627 0.899

EKC Holds Yes Yes Yes Yes

Turning points (real 2005 US$) 2.492 2.492 2.786 2.786

Note: ***, **, and * indicate 1%, 5%, and 10% levels of significance.

ICPDI 2022 - International Conference on Public Management, Digital Economy and Internet Technology

102

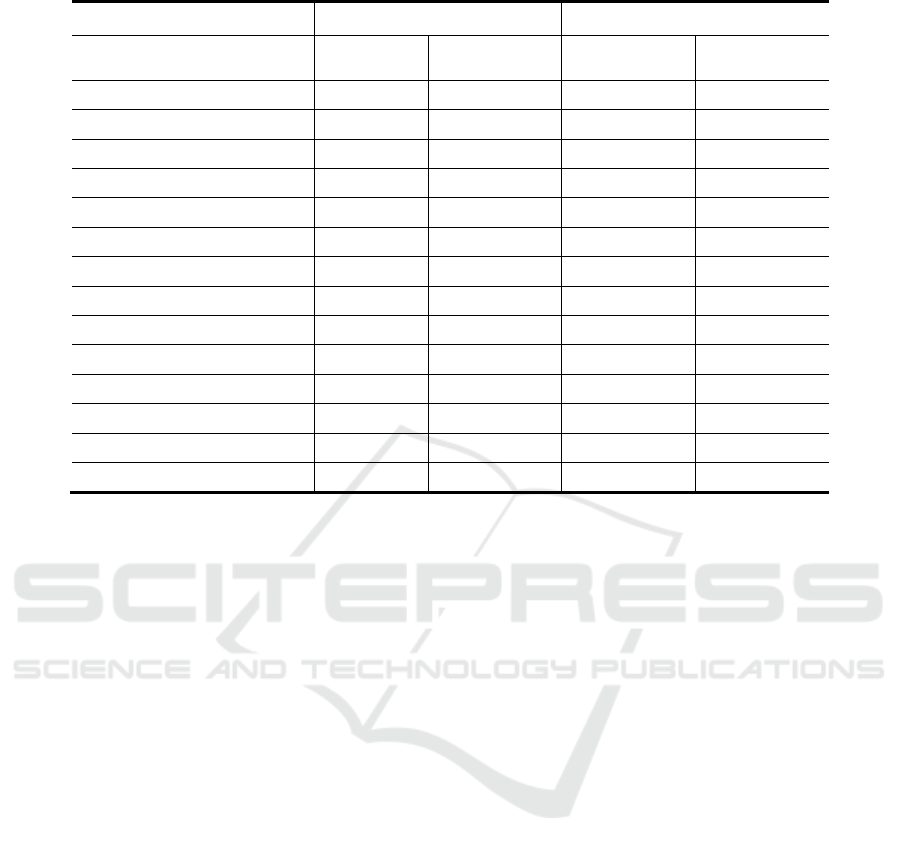
Table 4: Panel regression results for the non-pearl river delta region.

Model 2.1 RE Model 2.2 FE

Square RE

Driscoll- Kraay

Standard Errors

Square FE

Driscoll- Kraay

Standard Errors

GDPpc 9.654*** 9.654*** 10.808*** 10.808***

(-8.44) (-5.6) (-9.68) (-7.87)

GDPpc

-2.721 -2.721 -3.538** -3.538

(-1.64) (-1.04) (-2.24) (-1.69)

Popuden -5.811*** -5.811***

(-4.20) (-3.39)

_cons 1.939*** 1.939** 5.295*** 5.295***

(-3.58) (-2.38) (-6.49) (-5.48)

Observations 156 156 156 156

Cities 12 12 12 12

F-test or Wald chi2 921.321 394.165 347.441 165.244

R-squared 0.396 0.396 0.881 0.881

EKC Holds No No Yes No

Turning points (real 2005 US$) - - 1.527 -

Note: ***, **, and * indicate 1%, 5%, and 10% levels of significance.

The results of the LM test, the F test, and the

Hausman test reveal that while model 2.1 for the

non-Pearl River Delta area should be treated as a

random effects model, model 2.2 for the Pearl River

Delta region should be treated as a fixed effects

model. Similarly, after confirming the

heteroscedasticity, autocorrelation, and panel

dependence of these models, this study employs the

Driscoll-Kraay standard errors method to overcome

these problems. Table 4 displays the random effects

results for model 2.1 and the fixed effects results for

model 2.2. However, although the quadratic term for

GDP per capita in the fixed effects results for model

2.2 is significant (as indicated by two asterisks),

after employing the Driscoll-Kraay standard errors

to overcome the problems of heteroscedasticity,

autocorrelation, and panel dependence, this term is

not significant, which is consistent with

expectations. Based on the F test and the Wald chi-

squared values of the two models, this study finds

that these two models are significant, and there are

significant inverse correlations between increasing

population density and CO2 emissions per capita. In

the non-Pearl River Delta area, each increase in

population density by 1,000 persons per square

kilometer could reduce per capita CO2 emissions by

5.8 tons. However, an inverted U-shaped curve is

not verified for the non-Pearl River Delta area.

According to the standard errors estimation results

for models 2.1 and 2.2, the first-order coefficient of

GDP per capita is significantly positive, but the

second-order coefficient is not significant.

5 CONCLUSIONS

An inverted U-shaped relationship exists between

income and environmental degradation in the Pearl

River Delta region. This study finds that an income

per capita between US$24,920 and 27,860 is

expected at the EKC inflection point for the Pearl

River Delta region. Although economic growth

could cause pollution in the short run, it could

reduce emissions and pollution in the long term.

However, reductions in environmental degradation

may not spontaneously appear as per capita income

increases, and attention should be paid to the

specific mechanisms by which this positive effect

occurs. An inverted U-shaped relationship does not

exist in the non-Pearl River Delta area, but a

significant positive correlation exists between

income and environmental degradation. The reason

for this difference between the Pearl River Delta

region and the non-Pearl River Delta area lies in the

relatively high level of urbanization and

industrialization of the Pearl River Delta region;

even some cities in the Pearl River Delta region have

already reached the middle or late stage of

Energy Consumption, CO2 Emissions and Economic Growth: A Comparative Analysis in Guangdong, China

103

urbanization and industrialization. However, most

areas in the non-Pearl River Delta area are still in the

initial stage of rapid urbanization and

industrialization, and these processes will continue

in the future. Finally, we find that population

agglomeration can facilitate a reduction in the per

capita CO2 emissions in the Pearl River Delta and

the non-Pearl River Delta area. The population

agglomeration brings a population scale effect and

can significantly reduce the level of carbon dioxide

emissions.

Although the article has made some significant

findings, it still has certain limitations. Besides CO2

emissions, other pollutants such as sulfur dioxide,

methane and so on, could be also used to measure

environmental degradation. Furthermore, CO2

emissions data cannot be obtained directly, so the

carbon emissions data estimated by the energy and

economic data in this paper are not completely

accurate, so more precise data should be obtained

through more advanced tools and methods in the

future.

ACKNOWLEDGEMENTS

The authors would like to thank Shenzhen Low

Carbon City Big Data Engineering Laboratory for

providing with all the necessary support.

REFERENCES

Churchill S A, Inekwe J, Ivanovski K, et al. The

Environmental Kuznets Curve in the OECD: 1870–

2014 [J]. Energy Economics, 2018, 75: 389-399.

Cameron A C, Trivedi P K. Microeconometrics using stata

[M]. College Station, TX: Stata press, 2010.

Diao X D, Zeng S X, Tam C M, et al. EKC analysis for

studying economic growth and environmental quality:

a case study in China [J]. Journal of Cleaner

Production, 2009, 17(5): 541-548.

Grossman G M, Krueger A B. Economic growth and the

environment [J]. The quarterly journal of economics,

1995, 110(2): 353-377.

Hoechle D. Robust standard errors for panel regressions

with cross-sectional dependence [J]. The Stata Journal,

2007, 7(3): 281-312.

Kuznets S. Economic growth and income inequality[J].

The American economic review, 1955, 45(1): 1-28.

Kaika D, Zervas E. The Environmental Kuznets Curve

(EKC) theory—Part A: Concept, causes and the CO2

emissions case [J]. Energy Policy, 2013, 62: 1392-

1402.

Pesaran H. General diagnostic tests for cross section

dependence in panels[J], Cambridge Working Papers

in Economics, 0435, University of Cambridge, 2004.

Sirag A, Matemilola B T, Law S H, et al. Does

environmental Kuznets curve hypothesis exist?

Evidence from dynamic panel threshold [J]. Journal of

environmental economics and policy, 2018, 7(2): 145-

165.

Sanchez L F, Stern D I. Drivers of industrial and non-

industrial greenhouse gas emissions [J]. Ecological

Economics, 2016, 124: 17-24.

ICPDI 2022 - International Conference on Public Management, Digital Economy and Internet Technology

104