Dynamical Analysis for the Control of COVID-19: A Modified SEIR

Model

Chenhao Zhang

Department of Optical Science and Engineering, Fudan University, Shanghai, 200433, China

Keywords: Coronavirus Disease 2019, SEIR Model, Disease Consciousness, Isolation and Treatment.

Abstract: Objective: The paper of this research is to establish a new infectious disease dynamics model, which can be

used to evaluate the epidemic situation of covid-19 in 2019, and to evaluate the epidemic situation of covid-

19 in Hubei Province based on the SEIR model. Methods: Considering that covid-19 patients with latent

period have strong infectious ability, and the epidemic prevention information of the media has a positive

impact on mass epidemic prevention, an optimized SEIR epidemic dynamics model considering latent period

transmission ability, tracking and isolation intervention measures and mass disease awareness was

established. Referring to the official epidemic data of Hubei Province from January 23 to February 24, 2020

as the initial value of the dynamic system, the paper analyzes the epidemic situation in Hubei Province based

on the modified SEIR model to evaluate the impact of various measures and policies on the epidemic

transmission trend. Results: The theoretical analysis of the model shows that measures such as quarantine and

medical tracking can effectively inhibit the large-scale spread of the epidemic; centralized reception, layered

treatment and other important measures have played a key role in the rapid decline of the peak number of

infected people. Improving personal prevention awareness can curb the increase of infected people. In

addition, the publicity of news media can greatly increase people's disease awareness, so as to control the

development trend of epidemic situation and effectively reduce the peak number of infected people.

Conclusion: the modified SEIR model can be used for theoretical analyzing of covid-19 transmission and help

the government to formulate epidemic prevention policies.

1 INTRODUCTION

In recent decades, many infectious diseases are

constantly erupting, such as Ebora, swine flu, and

Chaga virus. At the end of 2019, an infectious disease

called New Coronavirus pneumonia (COVID 19) was

first launched in the world. The virus was highly

infectious and no vaccine was available at that time.

The COVID-19 has been responded very quickly

by China's government. In Hubei Province, where the

epidemic first broke out, the first level response to

major public health emergencies has been launched

since January 24, 2020. In order to control the spread

of the epidemic, the government has adopted isolation

measures based on past experience, such as stopping

performances and other activities, closing cinemas,

KTVs, schools and some workplaces to reduce crowd

gathering. In addition, the government has also

introduced policies to restrict the movement of people

to prevent the large-scale spread of the virus from

person to person. Hubei Province has also

implemented strict medical follow-up isolation, such

as a 14 day isolation observation of the people who

have been in contact with the infected people.

From the experience of China and other countries

in dealing with the epidemic situation, it can be found

that isolation measures are a very effective and

feasible anti-epidemic policy which has become the

first choice of many countries in facing the epidemic

situation. However, in the early stage of the epidemic,

some scholars did not consider the isolation factor in

the research on the development trend of covid-19

epidemic through dynamic model. For example,

according to the estimate results of the number of

infections by Jonathan et al. (Jonathan, 2020) on

January 24, 2020, as of February 4, the number of

COVID-19 infection cases in Wuhan will reach

190,000, far exceeding the actual number of

infections.

Also, with the development of technology,

communication software and news media, people

have more and more ways to obtain disease

information, which is conducive to timely taking

Zhang, C.

Dynamical Analysis for the Control of COVID-19: A Modiﬁed SEIR Model.

DOI: 10.5220/0011731600003607

In Proceedings of the 1st International Conference on Public Management, Digital Economy and Internet Technology (ICPDI 2022), pages 131-136

ISBN: 978-989-758-620-0

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

131

protective measures to reduce the occurrence of

diseases. Especially, how the behavior of people with

strong awareness of disease and the government

quarantine methods affect the spread of infectious

diseases is worthy of targeted research. Over the

years, many mathematical models have been proposed

to study the impact of disease awareness on infectious

diseases. These models can be divided into two

categories: Network model and mean field model

There are two ways about the influence of disease

awareness on infectious diseases: 1) The first way is

to reduce the contact infection rate and take preventive

measures. 2) The media area m of independent

storehouse is introduced to represent the change of

disease information

As for the second mode of influence, most of the

relevant studies did not consider the constant input

rate of media coverage. For example, The SIS model

established by Basir et al. (Basir, 2018) In 2018

studied the impact of disease awareness and time lag

on infectious disease control. In 2020, Kumar et al.

(Kumar, 2020) established a SVIR model based on an

independent rate equation, taking into account the

impact of vaccination coverage information. These

studies consider the second mode of disease

awareness, but the growth of media coverage is only

related to the infected people.

In addition, recent conditions have shown that

carriers of the virus in the incubation period have a

strong risk of virus transmission because they have not

yet shown symptoms. However, the dynamic model

of the epidemic spread established by researchers

previously ignored this risk. At the same time, in

previous studies, isolation and prevention have not

been considered as factors influencing the spread of

epidemics. Therefore, this paper studies the effect of

disease awareness, virus latency, and quarantine

measures on the dynamic model of infectious

diseases. Under the above assumptions, an infectious

disease model with certain rationality and research

value is established, which provides theoretical

support for the prevention and control of the current

COVID-19 and some other infectious diseases in the

future.

2 METHODS

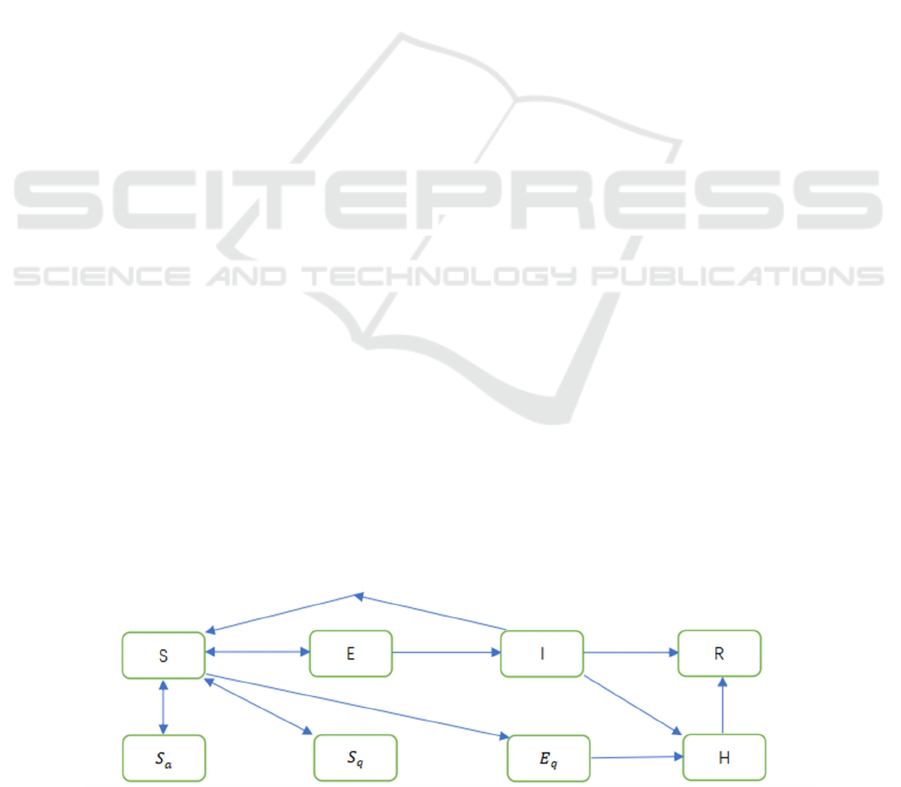
2.1 Improvement of SEIR Model

In the traditional SEIR model, S stands for the

susceptible population, I stands for the infected

population, E stands for the exposed population and R

stands for the recovered population. The model also

assumes because the infected individual will produce

antibodies after recovery. However, considering the

quarantine measures, quarantine susceptible [ S



quarantine exposed [E



] and quarantine infected [I



]

are taken into consideration. When it comes to the

impact of the disease awareness, a new population

group which stands for the awared susceptible [S



]

should also be added into the model. So that it will be

possible to estimate the impacts of both the disease

awareness and the quarantine measures on the spread

of a certain epidemic. In view of the fact that the

isolated infected people will beput into quarantine

treatment as soon as possible, all these people will

become hospitalized patients in this model [ H ].

Therefore, in the revised model [ S ], [ I ] and [ E ]

respectively refer to the susceptible, infected and

exposed persons who escape from the isolation

measures. In this way, the improved SEIR model in

this paper can be represented by figure 1.

2.2 Establishment of New Model

[q] is defined as isolation proportion, [β] is defined as

infection probability, [c] is defined as contact rate, [ρ]

is defined as effective contact coefficient (1 for

reference), Therefore, [ ρc ] refers to the effective

contact rate. Then we can give out the transmissive

relationship between susceptible people and other

Figure 1: The improved SEIR model.

ICPDI 2022 - International Conference on Public Management, Digital Economy and Internet Technology

132

groups of people:

• The conversion rate from susceptible

population to quarantine susceptible population

is ρcq(1 −β)

• The conversion rate of susceptible population

to isolated latent population is ρcqβ

• The conversion rate from susceptible

population to exposed population is ρcβ(1 − q)

The effective information density [M(t)] adopted

in the model is a time dependent function and includes

the following three terms:

• The input value of disease awareness [o], a

constant in the whole model which reprents the

publicity efforts of government officials and other

news media for epidemic prevention and control

• The generation rate of autonomous disease

awareness [η] , reporting how people’s disease

awareness develop naturely through the spread of

disease

• The disease awareness decay rate [ θ] ,

modeling how people’s disease awareness decay over

time

In this case the effective information density

[M(t)] can be written ito the following expression:

𝑑𝑀

𝑑𝑡

= 𝑜 + 𝜂𝐼 − 𝜃𝑀 (1)

At the same time, the influence of non quarantine

infected person and exposed person on the susceptible

population should be taken into consideration, and the

susceptible person whose quarantine has been

removed is changed into susceptible person again. In

addition, it is reasonable to assume that patients during

latent period has the same ability of infection as that

of patients with symptoms.

Therefore, the equation of the number of the

susceptible is:

𝑑𝑆

𝑑𝑡

= −

[

𝜌𝑐𝛽 + 𝜌𝑐𝑞

(

1 −𝛽

)

]

𝑆

(

𝐼 + 𝐸

)

+ 𝜆𝑆



−𝑀𝑆

+ 𝜔𝑆



(2)

In equation (2), λ stands for the quarantine

release rate. Since the quarantine time in China is 14

days, the value of λ can be taken as 1/14.

The equation of the number of the exposed is:

𝑑𝐸

𝑑𝑡

= 𝜌𝑐𝛽

(

1 −𝑞

)

𝑆

(

𝐼 + 𝐸

)

−𝜎𝐸 (3)

In equation (3), σ stands for the transformation

rate from exposed to infected. Since the average latent

period is about seven days according to the China

Health Inspection Commission,the value of σ can be

taken as 1/7.

The equation of the number of the infected is:

𝑑𝐼

𝑑𝑡

= 𝜎𝐸 −

(

𝛿



+ 𝛼 + 𝛾



)

𝐼 (4)

In equation (4), δ



, α, γ



respectively represent

the quarantine rate, the fatality rate and the recovery

rate of the infected.

The initial values of the dynamic system refer to

the official data (State Health Commission of the

people's Republic of China) of Hubei Province. The

specific parameters and their values are described in

Table 1.

Table 1: Parameters used in the system and their values.

aramete

descri

tion default value Reference

𝑞

isolation proportion

1×10



(Wang, 2020)

𝛽

infection probability

2.05 × 10



(Wang, 2020)

𝑐

contact rate

𝜌

effective contact coefficient

𝑜

disease awareness value

0.1

(Liu, 2018)

𝜂

autonomous disease awareness rate

0.01

(Gani, 2018)

𝜃

disease awareness decay rate

0.06

(Gani, 2018)

𝜆

quarantine release rate

𝜔

disease awareness loss rate

0.2

(Gani, 2018)

𝜎

transformation rate

𝛿



quarantine rate of the infected

0.13

(Wang, 2020)

𝛼

fatality rate

2.7 × 10



(Wang, 2020)

𝛾



recovery rate of the infected

0.007

(Wang, 2020)

Dynamical Analysis for the Control of COVID-19: A Modiﬁed SEIR Model

133

3 RESULTS

Based on the SEIR model, this paper makes a

retrospective study on the epidemic situation in Hubei

Province. Furthermore, the author analyzes the

development law of the epidemic under the impact of

different control measures as well as media publicity.

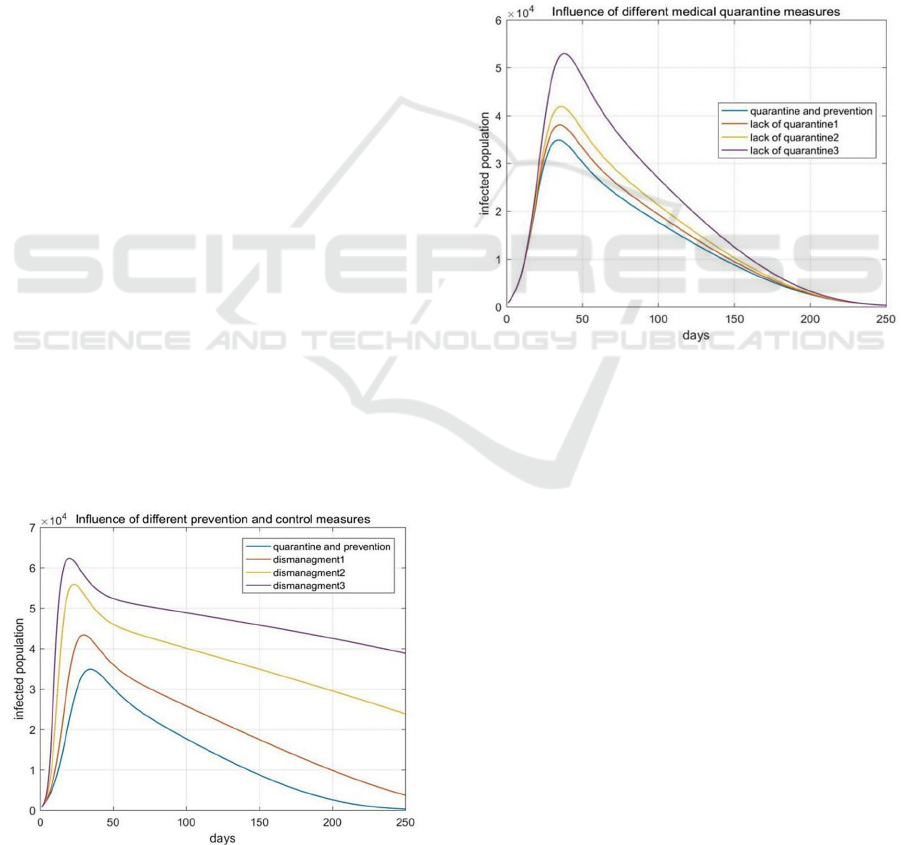
3.1 Estimation of The Impact

Quarantine on Epidemic Situation

In the numerical simulation analysis, it is assumed that

the initial contact rate under the current prevention

and control measures is 2. By increasing the exposure

rate to simulate the development trend of people

infected with covid-19 under the condition of

ineffective prevention and control measures, the effect

of different prevention and control measures can be

evaluated. Figure 2 shows the epidemic simulation

under higher exposure probability of susceptible

persons (the exposure rates under three kinds of poor

management and control are 3, 4 and 6 respectively).

The analysis found that strict prevention and control

measures can effectively contain the large-scale

spread of the epidemic. It is estimated that if the

government does not issue strict quarantine measures

on January 23, 2020, the number of infections in

Hubei Province may reach more than twice the actual

number of infections. In addition, if measures are not

taken to control the epidemic, the virus will spread

faster, which will cause greater loss of life and

property, and cause serious social panic. In particular,

in the extreme cases of ineffective prevention and

control (i.e. 2 and 3), the number of people infected

with the epidemic will drop very slowly after reaching

the peak, and the duration of the epidemic will be very

long.

Figure 2: Influence of different prevention and control

measures.

In this paper, the author simulated the effect of

tracking and isolation measures, that is, the decrease

of tracking and isolation ratio. As shown in the figure

3, the isolation ratio decreases to 0.9, 0.8 and 0.6 times

in case of lack of quarantine1, 2and 3. The peak

number of infected people and the rising rate largely

increased. Especially when the isolation rate was

taken as 0.6q, the peak number of the infected nearly

doubles. In the numerical simulation, the overall trend

of the epidemic development is basically consistent,

and the number of infected people drops to 0 in about

250 days, which means that the epidemic is basically

over. Therefore, strict medical tracking and isolation

is an effective means to control the development of the

epidemic.

Figure 3: Influence of different medical quarantine

measures.

With the increase of daily contact rate between

personnel, personal daily safety protection will be

particularly important. The effective contact rate is

‘

= ρc. Where c is the daily contact rate between

daily personnel, ρ is the effective contact coefficient.

Figure 4 reflects the impact of the reduction of

effective contact coefficient on the development of the

epidemic situation (assuming that the number of

infected people does not jump), and sets the contact

rate between personnel. When the effective contact

coefficient is 0.5, 0.25 and 0.1 respectively. Personal

daily protective measures will not only ensure

personal safety, but also play a vital role in curbing the

development of the epidemic. Strict daily safety

protection helps advance the peak time of infection

and reduce the peak number. Under strict personal

protection measures, the peak number of infected

people can be reduced by nearly 60%.

ICPDI 2022 - International Conference on Public Management, Digital Economy and Internet Technology

134

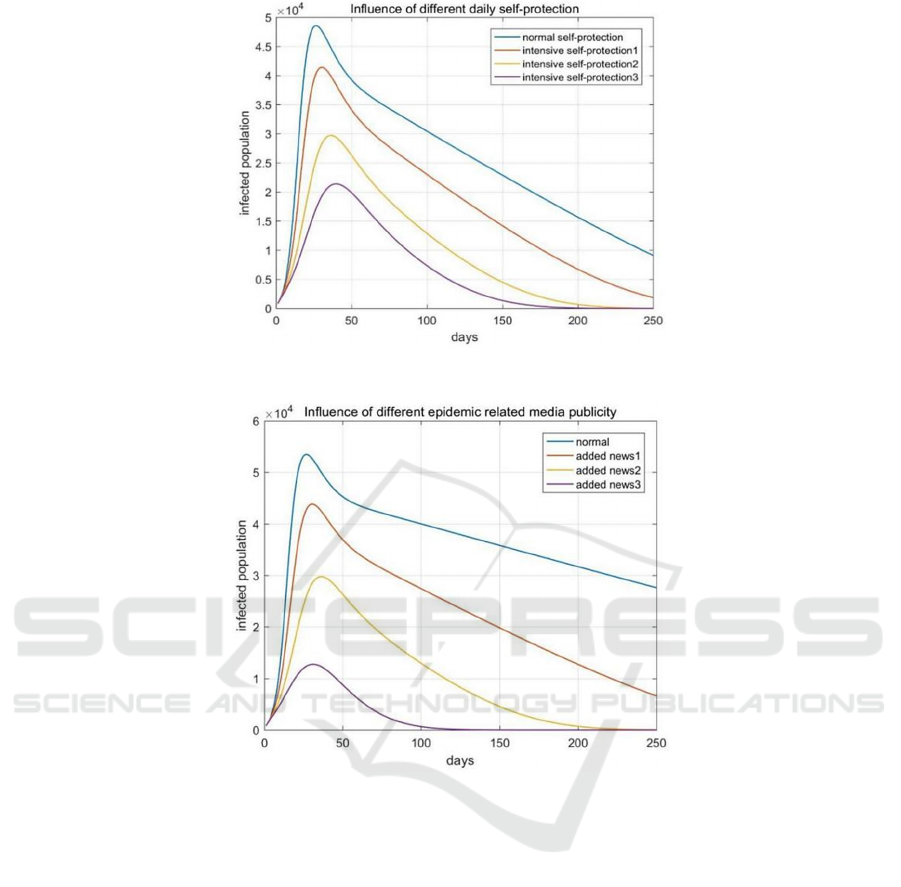
Figure 4: Influence of different daily self-protection.

Figure 5: Influence of different epidemic related media publicity.

3.2 Estimation of The Impact of

Disease Awareness on Epidemic

Situation

The broadcast of epidemic situation by TV news

media is one of the most important ways to obtain

people's disease awareness. Figure 4 simulates the

impact of different input rates of disease awareness on

the spread of epidemic situation in the early stage of

the epidemic when the media reports the epidemic

related information to different degrees. As shown in

figure 5, when the disease awareness input rate

reaches 10 times, 20 times and 50 times of the initial

value respectively, the rising rate of the number of

infected people decreases rapidly, and the peak of

infection also decreases greatly, and the number of

infected people decreases rapidly after experiencing

the peak, and soon reaches the disease-free

equilibrium point. Especially when the input rate of

disease awareness is 50, the peak number of infected

people is only one third of the original, and nearly half

of the time earlier to reach the disease-free

equilibrium. It can be seen that information factors

have a great impact on the prevention and control of

the epidemic, and the improvement of people's disease

awareness can effectively curb the development of the

epidemic.

4 CONCLUSION

In summary, the research results of this article show

that: First of all, prevention and control isolation and

medical tracking isolation can effectively curb the

spread of covid-19. Secondly, important measures

such as centralized reception and graded treatment can

Dynamical Analysis for the Control of COVID-19: A Modiﬁed SEIR Model

135

enable the infected people to receive better treatment,

and make the number of infected people drop rapidly.

Third, self-protection measures, such as wearing a

mask and paying attention to personal hygiene, can

also effectively reduce the infection rate. Finally,

when the epidemic just broke out, spreading

knowledge about epidemic prevention through

channels such as TV and the Internet can increase

people's awareness of the disease and cultivate good

hygiene habits for the public, thereby reducing the

severity of the epidemic.

What is more, the results of the optimized SEIR

model in this paper are in good agreement with the

actual development trend of the epidemic situation in

Hubei Province, thus confirming that the model is

reliable in the analysis of infectious disease

transmission situation. Furthermore, the result of this

research can provide theoretical support for relavant

policy making in the future.

REFERENCES

A. Kumar, K.S. Prashant, Y.P. Dong, et al. Optimal control

of infectious disease: information induced vaccinatine

and limited treatment. Physica A: Statistical Mechanics

and its Applications, 2020, 542(4): 1-17

F.A. Basir, S. Ray, E. Venturino. Role of media coverage

and delay in controlling infectious disease: A

mathematical model. Applied Mathematics and

Computation, 2018, 337: 372-385

G.R. Liu, Z.M. Liu, Z. Jin. Dynamics analysis of epidemic

and information spreading in overlay networks. Journal

of Theoretical Biology. 2018(444): 28-37

M.R. Jonathan, R.E.B. Jessica, A.T.C. Derek, etal. Novel

coronavirus 2019-nCoV: early estimation of

epidemiological parameters and epidemic predictions.

Medrxiv, 2020.

S.R. Gani, S.V. Halawar. Optimical control for the spread

of infectious disease: the role of awareness programs by

meida and antiviral treatment. Optimal Control

Applications and Methods, 2018 39(4): 1407-1430.

State Health Commission of the people's Republic of China

(nhc.gov.cn)

X. Wang, S. Tang, Y. Chen, et al. When will be the

resumption of work in Wuhan and its surrounding areas

during COVID-19 epidemic? A data-driven network

modeling analysis. Scientia Sinica Mathematica. 2020.

ICPDI 2022 - International Conference on Public Management, Digital Economy and Internet Technology

136