Analysis of Stability on the ERISA Humanoid Dance Robot

Bianca Surya Nobelia, Novian Fajar Satria, Eko Henfri Binugroho and Teuku Zikri Fatahillah

Politeknik Elektronika Negeri Surabaya, Jl. Raya ITS, Kampus PENS, Surabaya, Indonesia

Keywords: Humanoid Robot, Kinematics, ERISA, IMU Sensor, Analysis of Stability, Center of Mass.

Abstract: ERISA is a humanoid robot dancing developed by PENS students to participate in Indonesia Robot Contest

(KRI) on the humanoid dancing robot division. One of the main assessments in this contest is to keep the

robot stable until the finish zone. To analyze the stability of a humanoid robot, the Inertial Measurement Unit

(IMU) sensor namely GY-952 is applied to detect the slope of the robot body. To determine the stability

analysis variable of the robot, the Ground Projection of Center of Mass (GCoM) method is used by using the

simplification of the Five Link Models. the ERISA robot starts to fall if there is an error approach around ±

40 mm. For future work, it is possible to apply it as feedback for a balance control system.

1 INTRODUCTION

The Indonesia robot contest has been held annually

for more than a decade, one of the divisions in that

contest is the Indonesia Dance Robot Contest

(KRSTI). KRSTI is a competition for designing,

manufacturing, and programming robots

accompanied by elements of Indonesian art and

culture, especially traditional dance in Indonesia. The

purpose of this robot contest is to cultivate the

students’ creativity and interest in technological

advances, especially in the industrial robotic field and

traditional dance culture (KRI Committe, 2021).

One of the main assessments in this contest is to

keep the robot stable until the finish zone. The

difficult part is to keep the balance of the robot while

performing dance movements and walking

simultaneously. To overcome this, it is necessary to

know about parameters of the stability of the robot

before build a balancing system. Many studies were

already conducted in this area, but in this paper

present one of the easiest ways to analyze the stability

of biped humanoid robotics by using an IMU sensor

with a simplified Five-links model method. In order

to prove this approach, the system was tested in three

different conditions.

1.1 ERISA Robot Construction

The ERISA robot is designed using 29 servo motors

arranged on an aluminum frame, PLA+, and using an

ARM-type microcontroller as the main control

Figure 1: ERISA Robot Performance in KRSTI 2021.

system (Alasiry, Satria, & Sugiarto, 2018). The detail

of the construction is explained below.

1.1.1 Mechanical Structure

ERISA robot design has 29 DoF (Degree of Freedom)

consist of legs, body, hands, and head, as shown in

Table 1 (Alasiry, Satria, & Sugiarto, 2018). Figure 3

shows the isometric view of the mechanical skeleton

construction of the ERISA robot. Mechanical design

has been done by using Autodesk Inventor® software

and then the process of manufacturing parts is using

CNC machines and a 3D Printer.

182

Nobelia, B., Satria, N., Binugroho, E. and Fatahillah, T.

Analysis of Stability on the ERISA Humanoid Dance Robot.

DOI: 10.5220/0011738400003575

In Proceedings of the 5th International Conference on Applied Science and Technology on Engineering Science (iCAST-ES 2022), pages 182-187

ISBN: 978-989-758-619-4; ISSN: 2975-8246

Table 1: DoF Part Detail on ERISA Robot.

No. Bod

Part Amount of DoF

1. Hea

(

Neck

)

2. Stomach 1

(

Stomach

)

3. Waist 1 (Waist)

4. Hand

6 (Shoulder)

2 (Elbow)

4 (Wrist)

5. Feet

6 (Hip)

2 (Knee)

4 (Ankle)

Total 29 DoF

1.1.2 Electrical Design

To control the overall performance, ERISA utilizes

STM32F407VGT as a microcontroller, it has a clock

frequency up to 168MHz. The main controller runs

robot performance ranging from kinematics

calculations, accessing sensors, and communicating

with other devices, in addition to more details can be

seen in Figure 1. This microcontroller also performs

the computation of the IMU data to access the roll,

pitch, and yaw angle of the robot body (Alasiry,

Satria, & Sugiarto, 2018). The orientation data will be

received by the main microcontroller over UART

communication.

Figure 2: System Configuration Block Diagram.

Figure 3: IMU Sensor Installation in the Robot Body.

1.1.3 IMU Sensor

The GY-952 module shown in Figure 3 is utilized as

the IMU sensor in this research. The GY-952 module

has a request-response communication model, so to

get the tilt data, the microcontroller must send a

request command over UART communication and

then wait for the response data. The microcontroller

needs to parsing of the data packets that have been

sent by the GY-952 module sensor. The placement of

the IMU sensor is on the shoulder of the robot,

because the shoulder of the robot is still in one

connection with the trunk link of the robot.

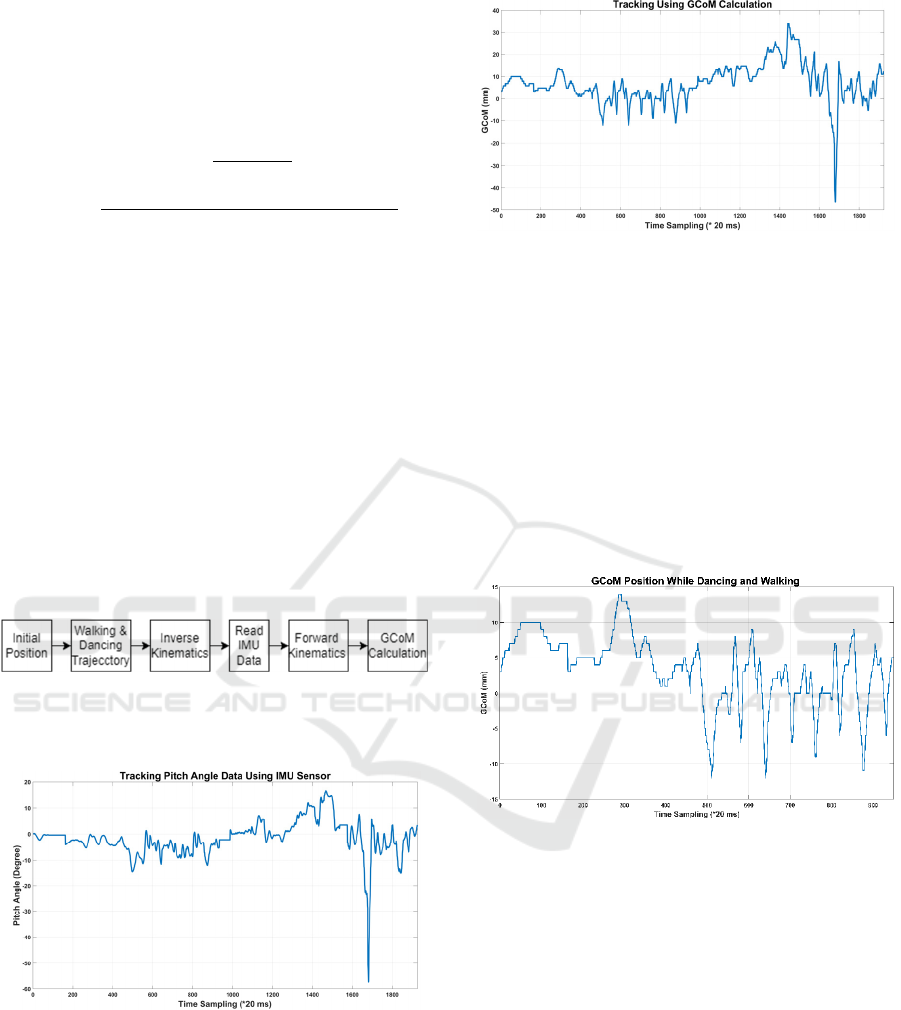
2 SYSTEM OVERVIEW

There are two types of kinematics applied to the

ERISA robot: forward kinematics and inverse

kinematics. The forward kinematics is applied to

control the movement of the hand servo and inverse

kinematics for the leg. The forward kinematics is also

used to enumerate the GCoM estimation.

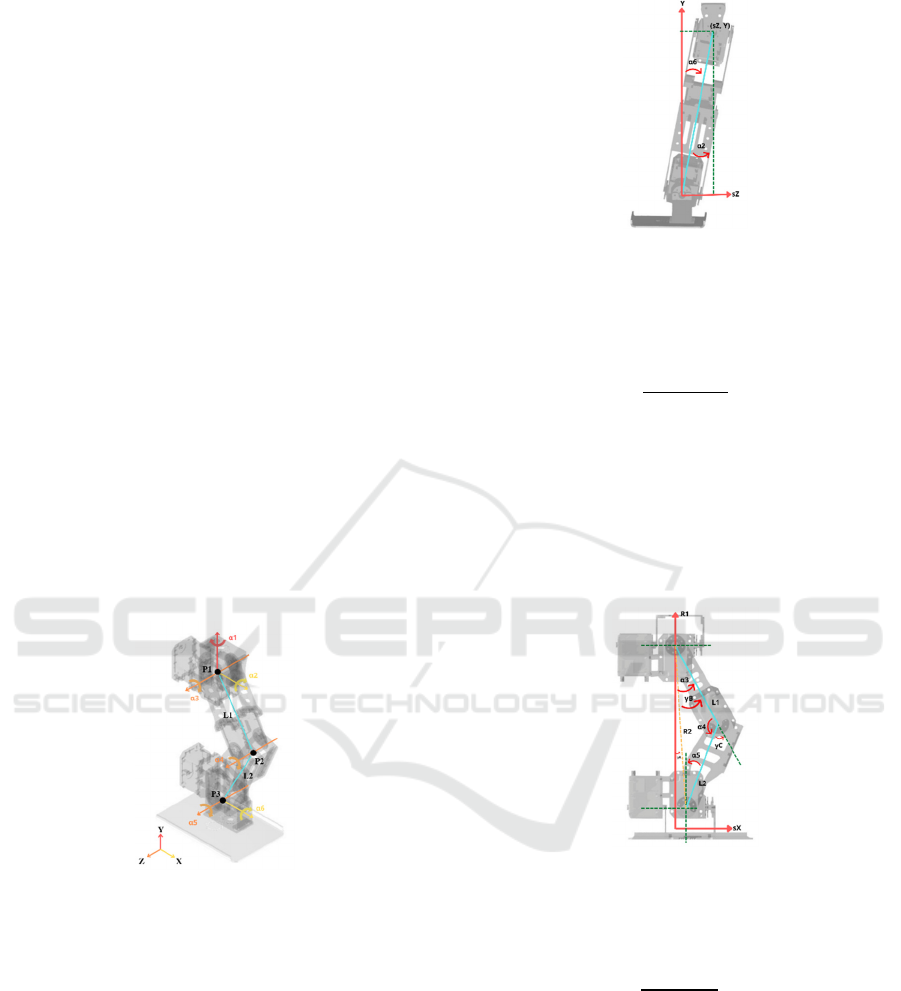
2.1 Forward Kinematics

In general, forward kinematics is applied to find the

End of Effector (EoE) position when all of the angle

values in every joint are given. In this research,

forward kinematics explanation will be focused to

enumerate the GCoM estimation on the sagittal plane.

The humanoid robot model is simplified to a Five-

links model (Haavisto & Hyötyniemi, 2004) based on

the link that has the most dominant mass. The

humanoid Five-links model is shown in the following

figure. The value of 𝛼

will be obtained from IMU

sensor. While 𝛼

, 𝛼

are the current angle of

the servo.

Figure 4: The Five-Links Model.

𝑝𝑥

= 𝑙

× sin(𝛼

)

(1)

𝑝𝑥

= 𝑙

× sin(𝛼

+ 𝜋 + 𝛼

)

(2)

𝑝𝑥

= 𝑝𝑥

+ 𝑙

× sin(𝛼

+ 𝜋 + 𝛼

+ 𝛼

)

(3)

𝑝𝑥

= 𝑙

× sin(𝛼

+ 𝜋 + 𝛼

)

(4)

GY-952

Analysis of Stability on the ERISA Humanoid Dance Robot

183

𝑝𝑥

= 𝑝𝑥

+ 𝑙

× sin(𝛼

+ 𝜋 + 𝛼

+ 𝛼

)

(5)

𝑝𝑦

= 𝑙

× cos(𝛼

)

(6)

𝑝𝑦

= 𝑙

× cos(𝛼

+ 𝜋 + 𝛼

)

(7)

𝑝𝑦

= 𝑝𝑦

+ 𝑙

× cos(𝛼

+ 𝜋 + 𝛼

+ 𝛼

)

(8)

𝑝𝑦

= 𝑙

× cos(𝛼

+ 𝜋 + 𝛼

)

(9)

𝑝𝑦

= 𝑝𝑦

+ 𝑙

× cos(𝛼

+ 𝜋 + 𝛼

+ 𝛼

)

(10)

Where :

𝑙

𝑖

Length of i

link

𝛼

𝑖

Joint angle of i

link

𝑐

𝑖

CoM position of i

link

𝑝𝑥

𝑖

EoE position of i

link in X axis

𝑝𝑦

𝑖

EoE position of i

link in Y axis

2.2 Inverse Kinematics

The Inverse Kinemtics used to resolve the walking

trajectory in 3-Dimensional cartesian form. This

inverse kinematic system is modeled on 6 DoF for

each robot's leg, where the hip is managed as the base

and the ankle as the End of Effector. The modeling

calculation applies the triangle geometry solution.

Cartesian coordinates are symbolized by the (x, y, z)

axis, and for joints symbolized by the (α

, α

) degree. Figure 5 has illustrated the isometric

shape of the robot leg configuration.

Figure 5: Joint Configuration on the Robot Leg (isometric

view).

𝛼

= 𝜃

𝐻

(11)

𝑅

0 =

√

𝑋

𝑍

Where :

𝜃

𝐻

= Heading direction

𝑅0 = Resultant between X and Z value

As shown in Figure 5, joint 1 is directly affected by

the heading direction.

Figure 6: Kinematics Model in Front View.

𝛽

=tan

−1

(

𝑍

∕

)

–

α1

𝑠𝑍 = 𝑍 +

(

𝑅0 × sin 𝛽

)

𝑠𝑋 = 𝑋 −

(

𝑅0 × cos 𝛽

)

𝛼

= tan

−1

(

𝑠𝑍

∕

𝛾

)

(12)

Where :

𝛽 = Distance between R0 and sX

𝑠𝑍 = Distance that occurs due to the angle 𝛽

𝑠𝑋 = Length of the hypotenuse of the triangles R0

and sZ

𝛼

= Angle between sZ and 𝛾

𝑅1 = Resultant between sZ and 𝛾

Figure 7: Kinematics Model in Side View.

The joint angle 2 can be obtained by referring to Figur

6. Where joint 2 is a plane that shows the side view,

so that the robot's legs look like human legs.

𝛼

= 0 − 𝛾𝐴 + 𝛾𝐵

(13)

𝛼

= 180 − 𝛾𝐶

(14)

𝛼

−

𝛼

(15)

𝛼

= 0 −

(

𝛾𝐴 + 𝛾𝐵

)

(16)

𝑅1 



𝛾

𝑠𝑍

𝑅2 



𝑅1

𝑠𝑋

𝛾𝐶  cos

1





𝐿1

𝐿2

𝑅2



2𝐿1𝐿2





𝛾𝐴  sin

1



𝑋

𝑅2





𝛾𝐵  sin

1



𝐿2  sin𝛾𝐶

𝑅2





iCAST-ES 2022 - International Conference on Applied Science and Technology on Engineering Science

184

Where :

𝐿1 = Length of the upper leg

𝐿2 = Length of the lower leg

R2 = Resultant between the R1 and sX

𝛾𝐴 = Angle between R2 and R1

𝛾B = Angle between R2 and L1

𝛾C = Angle between L1 and L2x

𝛼

= Angle from the sum of 𝛾𝐴 and 𝛾B

𝛼

= Angle of subtraction 180° and 𝛾C

𝛼

= Angle of the sum of 𝛼

and 𝛼

𝛼

= Reflection from angle 𝛼

After getting the values required for the calculations

in Figure 5, another joint angle can be computed.

From the inverse kinematics explanation above, eight

coordinate data are acquired for moving the robot's

legs, namely x, y, z, and headings, for the right foot

and left foot, respectively (Alamri, 2020).

2.3 Walking Gait

This system utilizes a parabolic function trajectory

pattern algorithm (walking path) with a set time

interval, where the time interval is a parameter that

can be changed (Alamri, 2020). The following

trajectory equation is shown in equations (17) and

(18).

∆S = PP − CP

(17)

(18)

Where :

∆S = Difference between start and end positions

PP = Previous Positions

CP = Current Positions

θ = Time Interval

= Output position at time (t)

Figure 8: Inverse Kinematics of ERISA Robot.

The gait trajectory applied by ERISA to perform its

walking sequence is 8 steps shown in Figure 8. The

red color represents the right leg, while the blue color

represents the left leg (Rahmawati, et al., 2021).

2.4 Motion Choreography

The dancing motion applied to the robot still uses trial

and error tuning, as shown in the following flowchart.

Figure 9: ERISA Robot’s Tuning Method Flowchart.

Because the ERISA robot is still using an open-loop

system, that’s why when the robot falls, the walking

trajectory must be corrected manually.

2.5 Ground Projection Center of Mass

(GCoM)

The Center of Mass (CoM) is the point where the

average mass of an object is equal to zero. All

external forces and momentum will have an effect on

the CoM of an object. Therefore in humanoid robots,

CoM is utilized as a reference point to see the slope

of the robot due to the force and momentum that

occurs, which can be used as the error value

(Nugroho, 2014). To keep the robot in balance the

Ground Projection of the Center of Mass (GCoM)

must be kept strictly inside the support polygon

(Goswami, 1999).

Figure 10: Center of Mass.

𝑆



(t)

Analysis of Stability on the ERISA Humanoid Dance Robot

185

𝑥

= 𝑐

× sin(𝛼

)

𝑥

= 𝑐

× sin(𝛼

+ 𝜋 + 𝛼

)

𝑥

= 𝑝𝑥

+ 𝑐

× sin(𝛼

+ 𝜋 + 𝛼

+ 𝛼

)

𝑥

= 𝑐

× sin(𝛼

+ 𝜋 + 𝛼

)

𝑥

= 𝑝𝑥

+ 𝑐

× sin(𝛼

+ 𝜋 + 𝛼

+ 𝛼

)

Where :

𝑚

𝑖

Mass of i

link

𝑥

𝑖

GCoM position of i

link in X-axis

3 RESULT

To analyze the stability of the robot using GCoM

estimation, there are three different conditions

applied to the robot, first is tracking GCoM position

while the robot dancing and walking, second is while

the robot dancing and doing one leg lifting motion,

third is while the robot dancing and walking on

obstacle. The data is taken by following the sequence

as shown below.

Figure 11: System Design.

3.1 Tracking GCoM Position

Figure 12: Tracking Pitch Angle Data using IMU Sensor.

Figure 13: Tracking GCoM Position.

Figure 12 and Figure 13 are a comparison between

tracking pitch data from the IMU sensor and tracking

the GCoM position. The most basic difference occurs

in GCoM calculation with Five-links model engaging

the consideration while doing leg motion, whereas

tracking pitch angle only uses data from the IMU

sensor. There is a moment when the robot's posture is

detected as an error, but it is still considered balanced

based on its GCoM value. And vice versa, there is a

moment when the robot's posture is detected as

balanced by the IMU, but the motions can cause the

robot to be unbalanced.

Figure 14: Graph of Tracking GCoM Position While the

Robot Dancing and Walking.

Figure 14 unveils the experimental result while doing

dance motions and walking. From the data above, the

magnitude of the GCoM error with the reference (0

mm) make a fluctuation, which is up to 10 mm and

less than -10 mm. This would cause the robot in an

unstable condition.

𝐺𝐶𝑜𝑀 

∑

𝑛

𝑖1

𝑚

𝑖

𝑥

𝑖

∑

𝑛

𝑖

1

𝑚

𝑖

𝐺𝐶𝑜𝑀 

𝑚

𝑥

𝑚

𝑥

𝑚

𝑥

𝑚

𝑥

𝑚

𝑥

𝑚

𝑚

iCAST-ES 2022 - International Conference on Applied Science and Technology on Engineering Science

186

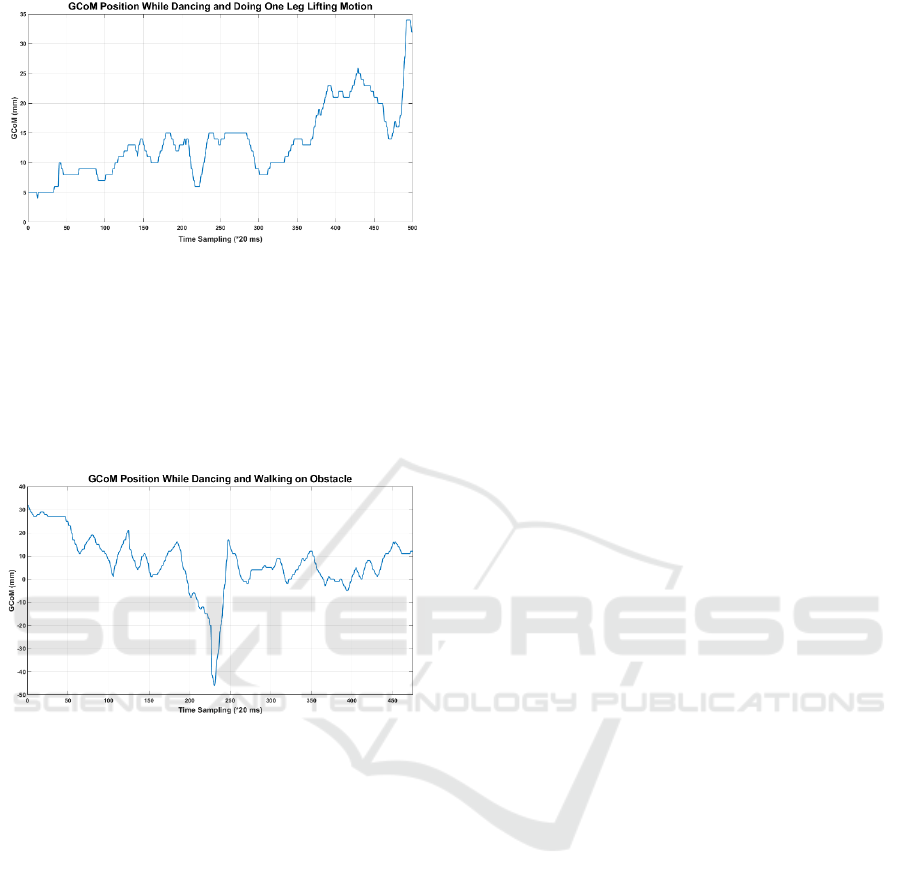
Figure 15: Graph of Tracking GCoM Position While the

Robot Dancing and Doing One Leg Lifting Motion.

From the second condition, it can be inferred that

carrying out one leg lifting motion will also cause the

robot's body to be unstable. Although the GCoM error

of the robot reaches 34 mm, it doesn’t cause the robot

fall. However, this situation make the robot easier to

fall if there is any other disturbance.

Figure 16: Graph of Tracking GCoM Position While the

Robot Dancing and Walking on Obstacle.

Figure 16 shows that walking on the obstacle will

cause the robot to fall backwards with a GCoM error

around -40 mm. In other word, if the error value

reaches approximately ± 40 mm, the robot no longer

maintain its stability.

4 CONCLUSIONS

This study reveals one method to analyze the stability

of a humanoid robot, which is by computing the

position of the Center of Mass projected directly to

the ground using a Five-links model. Calculating

GCoM has more advantage than only using the angle

value obtained from the IMU sensor, because it does

not only consider the tilt of the robot's posture, but

also the movements performed. Based on the

experiments, the ERISA robot began to fall when the

GCoM error reached the range of ± 40 mm. For future

works, it is possible to apply this analysis as feedback

for balance control.

ACKNOWLEDGMENTS

This research is supported by the ERISA robotics

team and Industrial Robotic Laboratory at Politeknik

Elektronika Negeri Surabaya (PENS) (Rahmawati, et

al., 2021).

REFERENCES

Alamri, R. D. (2020). Kontrol Keseimbangan Robot

Humanoid ERISA Menggunakan PID Dengan Sensor

Fusion. Surabaya: Politeknik Elektronika Negeri

Surabaya.

Alasiry, A. H., Satria, N. F., & Sugiarto, A. (2018). Balance

Control of Humanoid Dancing Robot ERISA while

Walking on Sloped Surface using PID. International

Seminar on Research of Information Technology and

Intelligent Systems (ISRITI) (hal. 577-581).

Yogyakarta: IEEE.

Goswami, A. (1999). Postural Stability of Biped Robots

and the Foot-Rotation Indicator (FRI) Point. The

International Journal of Robotics Research, 523-533.

Haavisto, O., & Hyötyniemi, H. (2004). Simulation tool of

a biped walking robot model. Helsinki: Helsinki

University of Technology.

KRI Committe. (2021). Buku 5 Kontes Robot Seni Tari

Indonesia (KRSTI) Daring 2021. Petunjuk

Pelaksanaan Kontes Robot Indonesia (hal. 65-78).

Jakarta: Pusat Prestasi Nasional Kementerian

Pendidikan RI.

Nugroho, A. T. (2014). Optimalisasi Pergerakan dan

Algoritma Robot Humanoid Sebagai Kiper. Salatiga:

Universitas Kristen Satya Wacana.

Rahmawati, M. S., Irwansyah, A., Binugroho, E. H.,

Alasiry, A. H., Satria, N. F., & Basuki, D. K. (2021).

ERISA Robot’s Walking Trajectory Control using Pixy

CMUcam5 to Locate the Target Position. International

Electronics Symposium (IES) (hal. 476-481). Surabaya:

IEEE.

Analysis of Stability on the ERISA Humanoid Dance Robot

187