The Assessment of Landslide Vulnerability Levels in Ponorogo,
Indonesia, Using Fuzzy Analytical Hierarchy Process: Natural Breaks
Arna Fariza, Annisa R. Kartika and Arif Basofi
Politeknik Elektronika Negeri Surabaya, Jl. Raya ITS, Kampus PENS, Surabaya, Indonesia
Keywords: Landslide, Spatial Mapping, Fuzzy Analytical Hierarchy Process, Natural Breaks.
Abstract: Landslide is a natural phenomenon that turns into a landslide natural disaster when the landslide causes both
losses of life and loss of property and human cultural products. Indonesia, which is partly hilly and
mountainous, has caused parts of Indonesia to become areas prone to landslides. Although landslides are
disasters that occur, repeated mitigation actions are often carried out spontaneously. This study proposes a
new model for determining the level of vulnerability in Ponorogo Regency based on rainfall, land slope,
elevation, land use, and soil type, using a fuzzy analytical hierarchy process (FAHP). FAHP produces priority
weight values in 318 villages. The natural breaks classification method is used to classify the weight values
into very low, low, medium, and high vulnerability values. The mapping results obtained were validated using
the calculation of FAHP analysis and showed better results than AHP.
1 INTRODUCTION
Landslide is one of the natural disasters that often
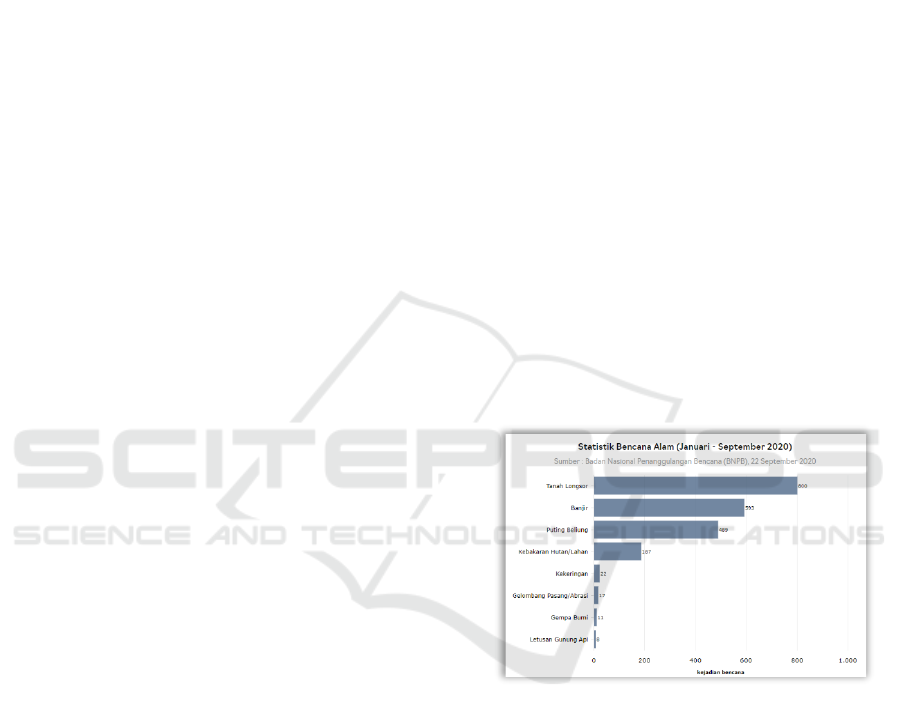
occur in Indonesia. The potential for landslides in
Indonesia is a disaster that ranks first, with as many
as 800 landslide events from January-September
2020. (Source: National Disaster Management
Agency). Figure 1 shows statistical data on natural
disasters that occurred in Indonesia from January –
September 2020. Landslides are the most common
disasters in Indonesia.
A landslide is a natural event that is currently
increasing in frequency. This natural phenomenon
turns into a landslide natural disaster when the
landslide causes both losses of life and loss of
property and human cultural products. Indonesia,
which is partly hilly and mountainous, has caused
parts of Indonesia to become areas prone to
landslides. Landslides occur due to shear failure
along the landslide, which is the limit of the
movement of the soil or rock mass (Hardiyatno, 2012)
Ponorogo Regency is one of the regencies in East
Java Province. This regency is located at
geographical coordinates between 111° 17' - 111° 52'
longitude and 7° 49' – 8° 20' latitude with an altitude
of 92 to 2,563 meters above sea level and has an
Source: Katadata.co.id
Figure 1: Statistical data on Natural Disaster Events from
January – September 2020.
area of 1,371.78 km². Ponorogo Regency is varied,
such as highlands and hills (Basofi et al., 2019).
Landslides in several villages in Ponorogo
Regency caused damage to houses and public
facilities and even claimed lives. The landslide
disaster was caused by heavy rains that occurred on
five consecutive days. The soil in the area results
from weathering of thick rocks that absorb air and
changes in land use from pine forests to agricultural
land (Yuniarta et al., 2015).
Assessment of the level of vulnerability to
landslides is needed as an effort for disaster early
warning and decision support systems for
194
Fariza, A., Kartika, A. and Basofi, A.
The Assessment of Landslide Vulnerability Levels in Ponorogo, Indonesia, Using Fuzzy Analytical Hierarchy Process: Natural Breaks.
DOI: 10.5220/0011739600003575
In Proceedings of the 5th International Conference on Applied Science and Technology on Engineering Science (iCAST-ES 2022), pages 194-199
ISBN: 978-989-758-619-4; ISSN: 2975-8246
Copyright © 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

stakeholders. The level of vulnerability to landslides
is influenced by several factors that depend on the
conditions of a particular area. The rainfall is the most
significant factor in landslides in Ponorogo, followed
by land slope, elevation, land use, and soil type
(Basofi et al., 2017; Basofi et al.).
The analytical hierarchy process (AHP) is a
decision support model developed by Thomas L.
Saaty. This decision support model will describe a
complex multi-factor or multi-criteria problem into a
hierarchy. However, in reality, the AHP method has
not been able to overcome vague or uncertain issues
and is very dependent on the subjectivity of experts.
This study proposes a new model for determining
the level of vulnerability in Ponorogo Regency based
on rainfall, land slope, elevation, land use, and soil
type, using a fuzzy analytical hierarchy process
(FAHP). FAHP produces priority weight values in
318 villages. The natural breaks classification method
is used to classify the weight values into very low,
low, medium, and high vulnerability values.
2 METHODOLOGY
2.1 Model Development
In model development, several models will be
developed using the FAHP method and carried out
several experiments with a combination of several
approaches. The development of the FAHP model
consists of several stages, such as preparing a dataset,
preprocessing, processing, and visualization.
A detailed description in Figure 2 of the system
design for landslide-prone areas is as follows:
1. Landslide Data
The data needed in this application to determine
landslide-prone areas are historical data from
previous landslides, rainfall, and rain duration. This
data is initial data in the form of raw data from related
agencies that have not been processed. The
information is from data obtained directly from the
relevant agency, including the Disaster Management
Agency of Ponorogo and the Department of Public
Works of Ponorogo.
• Data History of landslides in 2015 was obtained
from the Agency Ponorogo Disaster
Management.
Figure 2: System Design.
• Variable data in the form of rainfall, land use,
elevation, soil type, and land slope was obtained
from Dinas Ponorogo Regency Public Works.
2. Databases
Landslide history data that has been collected will be
prepossessed before being stored in the database.
Prepossessing is the process of sorting data that aims
to retrieve the required data. The database used is
PostgreSQL.
3. Fuzzy Analytical Hierarchy Process (FAHP)
Preprocessing data such as village data and variables
that affect landslide susceptibility will be processed.
Then the process of collecting data from the database
is carried out which is then carried out by the
Statistical Analysis process which aims to find the
correlation between the landslide history data and the
variables that affect landslide susceptibility. In this
application to produce flood-prone areas, calculations
are carried out using FAHP (Intan et al, 2018).
4. Landslide Prone Area Data
The results of this correlation serve as a weighting
reference to determine the ranking of priority
variables that can cause landslides. Then the data
processed from calculations using the FAHP method
will be grouped in detail, then processed in the API.
5. API
The risk analysis results are provided in the form of
an API that will be used on the mobile platform
(android) and the website. After the modeling process
The Assessment of Landslide Vulnerability Levels in Ponorogo, Indonesia, Using Fuzzy Analytical Hierarchy Process: Natural Breaks
195

is complete, a decision is made for landslide-prone
areas. The user can access the output from regions
that are prone to landslides.
6. Web Server
Information that has been processed regarding areas
prone to landslides will also be displayed in the form
of a spatial website that the admin will access.
7. Admin
In this application, the admin works on the server
side, where the admin has access to add, read, update,
and delete the data needed in this application.
8. Mobile
In this application, the user can use the application to
view landslide data, landslide soup, and information
about where the location is prone to landslides.
9. User
In this application, the user has a role on the client
side where the user can view a map of landslide
hazards, landslide history map, SOP for landslide
disasters, and mitigation suggestions.
2.2 Hierarchy of Criteria
Figure 3 below shows that five criteria determine
landslide-prone areas, namely land use, rainfall, land
slope, soil type, and elevation.
Figure 3: Hierarchy of criteria.
Each of the five criteria has sub-criteria: land use
consisting of forests, non-rice fields, agriculture, rice
fields, and settlements. Rainfall criteria consist of <
100 mm, 100-199 mm and > 200 mm. The land slope
criteria consist of class 1 (0-8 degrees), class 2 (9-15
degrees), class 3 (16-25 degrees), class 4 (26-45
degrees), and class 5 (more than 45 degrees). The soil
type or geology criteria consist of sub-criteria
Alluvium, Limestone, Quaternary Volcanic, Young
Quaternary Volcanic, Old Quaternary Volcanic,
Pliosine Deposits, and Diosit. Then the land height
criteria consist of 1000 mdpl, 1000-2000 mdpl, and >
2000 mdpl (Dzulkarnain et al., 2016).
2.3 FAHP Design
The flowchart of FAHP design for landslide
assessment is shown in Figure 4. The following is an
explanation of Figure 4 which consists of several
stages, which are as follows:
Figure 4: FAHP Flowchart.
1. Develop a comparison matrix (Pairwise Matrix
Comparison / PCM) between all criteria and sub-
criteria. Each element will be compared by giving
weight to each comparison.
2. Calculate the Consistency Ratio (CR) value from
the PCM calculation results to determine whether
the PCM weighting has been consistent or not
with the condition that the CR value is 0.1 by
using the following formula
CI = (λmax- n) / (n -1)
(1)
CR = CI / IR
(2)
where:
CI = Consistency Index
λmax = Maximum Eigen Value
n = Number of elements
CR = Consistency Ratio
IR = Index Ratio
3. The FAHP method uses a fuzzy ratio called
Triangular Fuzzy Number (TFN) and is used in
the fuzzification process. TFN consists of the
iCAST-ES 2022 - International Conference on Applied Science and Technology on Engineering Science
196
three membership functions, namely the lowest
value (l), the middle value (m), and highest value
(u). Change the results of the PCM weighting into
the form of TFN using the scale as shown in Table
1.
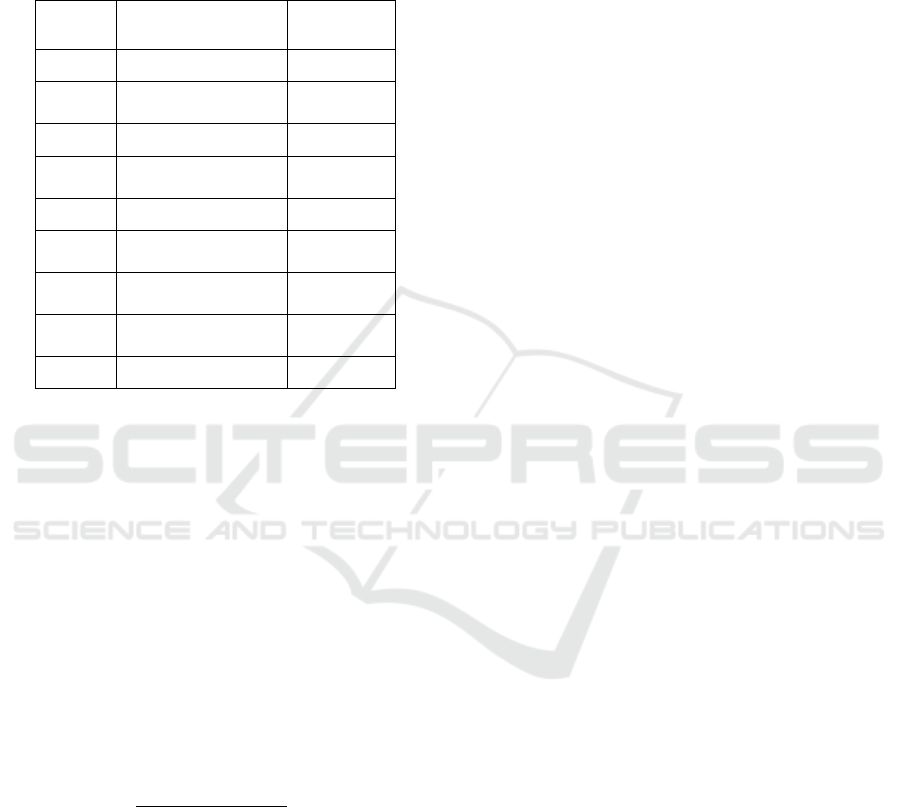
Table 1: Triangular fuzzy number (TFN) scale.
AHP
Scale
Linguistic Scale
TFN Scale
(l; m; u)
1
Equal important
(1; 1; 1)
2
Intermediate
important
(1/2; 1; 3/2)
3
Moderate important
(1; 3/2; 2)
4
Moderate plus
important
(3/2; 2; 5/2)
5
Strong important
(2; 5/2; 3)
6
Strong plus
important
(5/2; 3; 7/2)
7
Very strong
important
(3; 7/2; 4)
8
Very strong plus
important
(7/2; 4; 9/2)
9
Extreme important
(4; 9/2; 9/2)
4. Calculate the fuzzy geometric mean and fuzzy
weight of each element using the formula:
(3)
(4)
where:
= synthetic pairwise comparison fuzzy value
from element to i-n
= geometric mean of i-th element
= fuzzy weight of the i-th element
n = Number of elements
5. The process of defuzzification of all elements
(criteria and sub-criteria) using the Center of
Gravity (COG) method.
(5)
where:
BNP = Best Non-Fuzzy Performance
lR
i
= the lowest value of the fuzzy weight of the
i-th element
mR
i
= the middle value of the fuzzy weight of the
i-th element
uR
i
= the highest value of the fuzzy weight of the
i-th element
6. Determine the fuzzy priority for each alternative
property by using linguistic variables. Integrating
the weight of each criterion / sub-criteria and
fuzzy performance values with fuzzy number
calculations to get a fuzzy synthetic decision
matrix using the formula:
(6)
where:
R
i
= i-th alternative fuzzy synthetic decision
E
i
= alternative fuzzy performance value on the
i-th element
W
i
= total weight of fuzzy element i
7. Defuzzification of alternatives using the Center of
Gravity method. The COG calculation results will
be sorted based on the highest value to the lowest
value to get the final result, which means the
alternative that gets the highest value is the best
alternative to be an investment choice (Xiong et
al., 2017).
2.4 Natural Breaks Classification
The Natural Break method determines the points in
the data by looking at the grouping and patterns of the
data. The data used a range from the smallest to the
largest. The data is then divided by the limits
determined based on the value of the most extensive
range. This natural breaks method is designed to
select the best value settings for different classes
(Sujatha et al., 2012).
This method seeks to reduce the variance within
classes and maximize the variance between classes.
Natural Breaks is the only method that finds the best
ranges. The best ranges are the ranges where the area
is like a grouping, which doesn't give the low-level
areas the same color as the high-level areas. Natural
Breaks minimize the variation within each color, so
the areas within each color are as close to the same
value as possible each other (Basofi et al., 2015)
(Basofi et al., 2019).
Natural breaks iteratively calculate the squared
deviation between classes (SDCM) and the squared
deviation from the mean of each class (SDAM). After
examining each SDCM, a decision was made to move
one unit from the class with the largest SDCM to the
class with the lowest SDCM. To test this
classification method, the Goodness of Variance Fit
(GVF) was calculated. GVF ranges from 0 to 1, which
means from worst to very perfect.
The Assessment of Landslide Vulnerability Levels in Ponorogo, Indonesia, Using Fuzzy Analytical Hierarchy Process: Natural Breaks
197

3 RESULT
Experiments on 318 villages in Ponorogo regency
used the following five criteria:
C1 = Rainfall
C2 = Land slope
C3 = Elevation
C4 = Land use
C5 = Soil type
The comparison matrix for each criterion can be seen
in Table 2. Rainfall has the highest priority value,
followed by land slope, elevation, land use, and soil
type.
Table 2: Comparison matrix of each criterion.
C1
C2
C3
C4
C5
C1
1
3
5
7
9
C2
1
3
5
7
C3
1
3
5
C4
1
3
C5
1
The results of the FAHP calculation are in the
form of priority weight values for each alternative
value (village). The priority weight values must be
changed into high, medium, low, and very low
categories. These categories are produced using the
natural break classification. This method classifies
318 villages into four class categories. The GVF
value from the classification results can be seen in
Table 3. The GVF value analysis ranges from 0-1,
where a value close to number 1 indicates a better
classification result. The FAHP method produces a
GVF value of 0.75, more significant than the
classification results from the AHP priority weight
value of 0.69.
Table 3: GVF Calculation Table.
SDAM
SDCM 1
SCDM 2
SCDM 3
GFV
FAHP
3.97
1.73
0.99
1.29
0.75
AHP
4.50
2.00
1.38
1.46
0.69
The results of spatial mapping using FAHP and
natural breaks for 318 villages in Ponorogo district
can be seen in Figure 5. While spatial mapping using
AHP and natural breaks can be seen in Figure 6.
Areas in green indicate very low landslide
susceptibility levels, blue color indicates low, yellow
indicates medium, and red indicates high.
Figure 5: Result of FAHP Method.
Figure 6: Result of AHP Method.
Then, the significant value and accuracy value
were calculated using Pearson's Chi-squared test
method. This trial is based on historical data on the
number of villages with the number of landslide
points that occur and the number of villages with the
number of landslide points that do not happen in each
classification of landslide vulnerability levels.
Pearson's Chi-squared is used to calculate the
accuracy value or significant value of the method It
based on real area with landslide point data and area
without landslide event on each classification
category.
The formula used to get the Chi-squared value is
(7)
The value of Oi cell is the value derived from the
landslide point data that already exists in each village.
While Ei cell is a random value from the spatial
distribution obtained from the formula Ei = (Total Oi
× Total' Oi) / Oi. Then the Chi-squared cell is
obtained from the calculation using the formula (7).
The value from Pearson chi-square (χ2) 80,016
have higher value and critical values. It show that the
method has reasonably good accuracy in mapping
landslide susceptibility in Ponorogo.
iCAST-ES 2022 - International Conference on Applied Science and Technology on Engineering Science
198
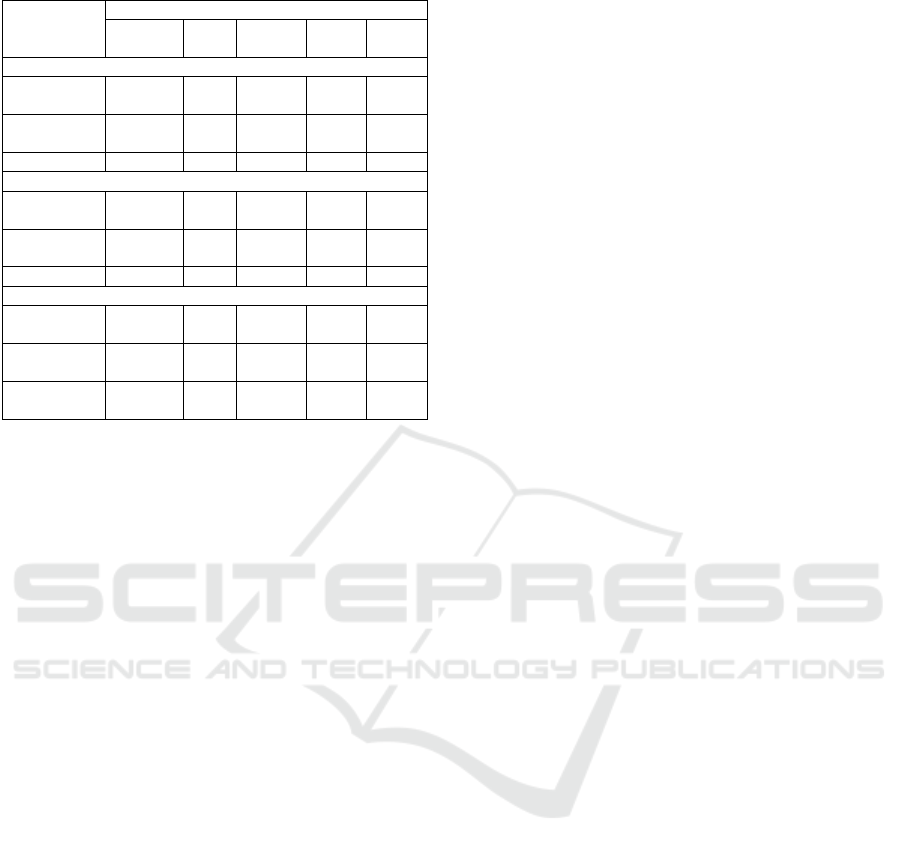
Table 4: Chi-Squared Result of FAHP Method.
Susceptibili
ty area
Class
Very
Low
Low
Mediu
m
High
Total
Observed Number Cell (Oi)
Without
Landslide
188
43
44
2
277
With
Landslide
3
8
24
6
41
Total
191
51
68
8
318
Expected Number Cell (Ei)
Without
Landslide
166,37
44,4
2
59,23
6,96
277
With
Landslide
24,62
6,57
8,76
1,03
41
Total
191
51
68
8
318
Chi-Squared Value
Without
Landslide
2,810
0,04
5
3,917
3,542
10,31
6
With
Landslide
18,991
0,30
8
26,466
23,93
3
69,69
9
Total
21,802
0,35
4
30,383
27,47
6
80,01
6
4 CONCLUSIONS
This study can determine the 318 Ponorogo village's
vulnerability to landslides using the Fuzzy Analytic
Hierarchy Process method based on five criteria,
including rainfall, land height, land slope, land use,
and soil type. The mapping results from the
calculation of the FAHP method can be classified into
four levels of vulnerability: areas with a level of
vulnerability, landslides are high, medium, low, and
very low.
The results of the landslide-prone areas are
validated using natural-break calculation with data
obtained when calculating FAHP and AHP. So the
results of Fuzzy AHP give the best value compared to
AHP, which shows a value of 0.75 rather than 0.69.
ACKNOWLEDGEMENTS
The authors would like to thank to Politeknik
Elektronika Negeri Surabaya for supporting this
research.
REFERENCES
Basofi, A., Fariza, A., Ahsan, A. S., Kamal, I. M. (2015). A
comparison between natural and Head/tail breaks in
LSI (Landslide Susceptibility Index) classification for
landslide susceptibility mapping: A case study in
Ponorogo, East Java, Indonesia. International
Conference on Science in Information Technology
(ICSITech).
Basofi, A., Fariza, A., Kamal, I. M. (2019). Mitigation and
Emergency Management System of Landslide in
Ponorogo District, Indonesia. JOIV: International
Journal on Informatics Visualization. Vol. 3 No. 2.
pp.100-107.
Basofi, A., Nailussa'ada, Fariza, A. (2017). Landslide
susceptibility mapping using ensemble fuzzy
clustering: A case study in Ponorogo, East Java,
Indonesia". 2nd International conferences on
Information Technology, Information Systems and
Electrical Engineering (ICITISEE).
Dzulkarnain, M.R., Fariza, A., Basofi, A. (2016). Mobile
based of mitigation and emergency system for landslide
in ponorogo, East Java, Indonesia, International
Electronics Symposium (IES).
Basofi, A., Rahmana, R., Fariza, A. (2019). Pencarian Jalur
Alternatif Sebagai Sistem Evakuasi Bencana Tanah
Longsor di Kabupaten Ponorogo Dengan Algoritma A-
Star Berbasis Perangkat Bergerak. SCAN-Jurnal
Teknologi Informasi dan Komunikasi. Vol. 13 No. 3.
pp.1-8.
Hardiyatno, C.H. (2012). Tanah Longsor dan Erosi
Kejadian dan Penanganan. Gajah Mada University
Press.
Intan, A., Shofie, A., Widi, S. (2018). Analytical Hierarchy
Process(AHP), Fuzzy AHP, and TOPSIS for
Determining Bridge Maintenance Priority Scale in
Banjarsari. Surakarta.
Sujatha, E. R., Rajamanickam, G. V., Kumaravel, P.
(2012). Landslide susceptibility analysis using
Probabilistic Certainty Factor Approach: A case study
on Tevankarai stream watershed, India. School of Civil
Engineering, SASTRA University.
Xiong, T., Indrawan, I.G.B., Prakasa, B. D. (2017).
Landslide Susceptibility Mapping Using AHP,
Statistical Index, Index of Enthropy, and Logistic
Regression Approaces In the Tinalah Watershed.
Yuniarta, H., Saido, A.P., Purwana, Y.M. (2015).
Kerawanan Bencana Tanah Longsor Kabupaten
Ponorogo. Universitas Sebelas Maret Surakarta.
The Assessment of Landslide Vulnerability Levels in Ponorogo, Indonesia, Using Fuzzy Analytical Hierarchy Process: Natural Breaks
199
