Simulation of Korea Composite Stock Price Index (KOSPI) for the

First 20 Years in the 21

Century Using Random Walk

Shaomin Yan and Guang Wu

National Engineering Research Center for Non-Food Biorefinery, State Key Laboratory of Non-Food Biomass and

Enzyme Technology, Guangxi Academy of Sciences, 98 Daling Road, Nanning, 530007, Guangxi, China

Keywords: KOSPI, Monte Carlo Simulation, Computational Finance, Random Walk.

Abstract: The Korea Composite Stock Price Index (KOSPI) can be regarded as a representative of the economic

development not only in South Korea but also in the emerging markets. Thus, the KOSPI and its derivatives

are the objective of many studies with models from

neural network model to stochastic model, whose

computation can be considered as a part of the computational finance,

in particular with the Monte Carlo

simulation. In this study, we apply the random walk model to simulate KOSPI for the first 20 years in the 21

century with division into five sub-periods because whether or not KOSPI follows a random walk is closely

related to the efficient market hypothesis (EMH). At first, we use the random walk in the 1/–1 format to

simulate KOSPI in a simplified format for 2020, and then we use the random walk in the decimal format to

simulate the real-life KOSPI for five different periods with increment of five-year data each. The simulation

is done using the Monte Carlo algorithm to generate random numbers with 100,000 seeds for each sub-period

of KOSPI simulation. The results show that the simulation can fit for short periods of time and can follow

KOSPI for a longer period of time.

1 INTRODUCTION

The Korea Composite Stock Price Index (KOSPI) is

an index, which represents the economic

development not only in South Korea but also in the

emerging markets. Consequently, it is the objective

of many studies (

Na, Sohn, 2011; Lee, Lim, 2011;

Kim, Kim, 2004; Kim, Bang, 2014

). Moreover, the

KOSPI derivatives are also the subject of studies (

Ko,

2012; Han, Guo, Ryu, Webb, 2012

Theoretically, the studies on KOSPI can help us

understand the human behaviour in stock market, the

underlined mechanisms for the KOSPI movement,

etc. Practically, the studies on KOSPI can help

investors and fund managers for better following

KOSPI and allocate their assets. Technically, various

mathematical and statistical models have been

applied to KOSPI studies, for example,

neural

network (Lee, Lim, 2011; Lee, Yoo, Jin, 2007) and

stochastic method (Kim, Kim, 2004). In this

context, we are particularly interested in the

random walk model, which was too used in KOSPI

studies (Aggarwal, 2018; Yoon, Kim, 2018).

To a broader sense, the issue of whether a stock

index follows a random walk is a disputing subject

for years with approval and disapproval in different

stock markets around the world (

Charles, Darné.

2009; Abraham, Seyyed, Alsakran, 2002; Gilmore,

McManus 2003

). As a matter of facts, most studies

using the statistical tests to determine the random

walk hypothesis, such as unit root tests (

Aggarwal,

2018

), but it is rare to use a random walk to simulate

a particular stock index. Nevertheless, both statistical

tests and real-life case simulation are equally

important because they reflect the same mechanism

from two different angles.

In this study, we use the random walk to directly

simulate the KOSPI for the first 20 years in the 21

century to add more pieces of evidence to this hot

debating issue from real-life simulation aspect.

2 MATERIALS AND METHODS

2.1 KOSPI Data

The daily KOSPI for the first 20 years in the 21

century is obtained from a branch of Yahoo Finance.

The KOSPI from 2001 to 2020 includes 4935 trading

days with open, high, low, close, adjusted close, and

Yan, S. and Wu, G.

Simulation of Korea Composite Stock Price Index (KOSPI) for the First 20 Years in the 21st Century Using Random Walk.

DOI: 10.5220/0011753200003607

In Proceedings of the 1st International Conference on Public Management, Digital Economy and Internet Technology (ICPDI 2022), pages 613-618

ISBN: 978-989-758-620-0

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

613

volume. We choose the daily close as our target for

random walk simulation. In order to get more

practical knowledge on the simulations, the 20-year

KOSPI are furthermore divided into five sub-groups:

there are 248 daily closes for 2020, 1220 for 2016-

2020, 2456 for 2011-2020, 3700 for 2006-2020, and

4935 for 2001-2020.

2.2 Random Walk Model

The classical random walk is a path obtained by

tossing a fair coin continuously (

Feller, 1968

): define

a side of coin and the other side of coin as 1 and –1,

record 1 or –1 for each tossing, and finally add the

recorded 1 and –1 together. In graphic presentation,

the x-axis is time (number of tossing of coin), and the

y-axis is the addition of recorded 1 and –1. As the

tossing of coin is a random event, its addition is a

series of random events, which construct a random

walk.

2.3 KOSPI in a Simplified Form

Similar to the consideration in random walk, the

KOSPI can also be presented in a similar way, i.e. if

KOSPI close in a day is higher or lower than that in

its previous day, we record 1 or –1 for the day, and

finally we add these 1 or –1 step-by-step along the

time course. Graphically, this operation will have the

x-axis as time and y-axis as the addition of recorded

1 or –1. Basically, this graph is a simplified KOSPI

when we consider only its up or down movement

daily. In this type of simulation studies, we use the

random walk to fit this simplified KOSPI profile.

2.4 Random Walk in Decimal Format

Although the classical random walk is just related to

1 or –1, we should expand its concept to decimals to

accommodate KOSPI because KOSPI is in decimal

form. Conceptually, this means that we toss an item

with many sides, each of which represents a number

in decimals. This is possible because we do not toss a

physical coin to generate a random walk but use a

computer to generate a series of random numbers,

which in fact are decimal numbers. Actually, we have

to round the decimal numbers to integer in order to

construct a classical random walk. Hence, we can

simply use a computer to generate a series of random

numbers, and then add them along the time course,

which is a random walk in decimal format useful to

compare with the real-life KOSPI.

2.5 Simulation

The simulation is done by means of computation with

random numbers generated by Monte-Carlo

algorism. The generated random numbers are

rounded to integers for simplified KOSPI and without

rounding for real-life KOPIS. Thereafter, the random

walk in both 1/–1 and decimal formats are compared

with the simplified and real-life KOSPI. This process

is continued until the random walks are very

approximate to the simplified and real-life KOSPI.

Because the Monte-Carlo algorism requires a seed to

generate a series of random numbers, 100 thousand

seeds ranging from 0 to 10 are used to find the best

simulation in this range.

3 RESULTS AND DISCUSSION

Table 1 explains how to perform the random walk

simulation in both 1/–1 and decimal formats.

Columns 1and 2 are the first 10 trading days in 2020

and their corresponding KOSPI close. Column 3 is a

list comparing whether a KOSPI close is larger or

smaller than that in its previous day in terms of the

1/–1 format. For example, 2176.46, the KOSPI close

on January 3, 2020 is larger than 2175.17, the KOSPI

close on January 2, 2020, so 1 is assigned to the

second cell in column 3. Column 4 is the addition of

each cell in column 3, resulting in a KOSPI in the 1/–

1 format. Column 5 is the random numbers generated

by Monte Carlo simulation using SigmaPlot (

SPSS

Inc., 1986-2001

) with a seed of 0.78654, which is the

best one of 100,000 seeds. Column 6 is the

comparison of whether the generated random number

is larger or smaller than its preceding random number

in the 1/–1 format. Column 7 is the classical random

walk by adding each number in column 6, and is

compared with column 4 for goodness-of-fit. The last

two columns describe how to perform a random walk

simulation in the decimal format. Column 8 is the

random numbers generated by Monte Carlo

simulation using SigmaPlot with one of the following

ten seeds: 7.30548, 7.30549, . . . 7.30557. The

command for generation of random numbers

generally includes the generated number of random

numbers, seed, upper and lower ranges, and we use

the standard deviation of the KOSPI close in 2020

upper and lower ranges. Column 9 is the random walk

in the decimal format by adding each random number

in column 8, and then we can compare the KOSPI

close value in column 2 with the random walk

simulation in column 9.

ICPDI 2022 - International Conference on Public Management, Digital Economy and Internet Technology

614

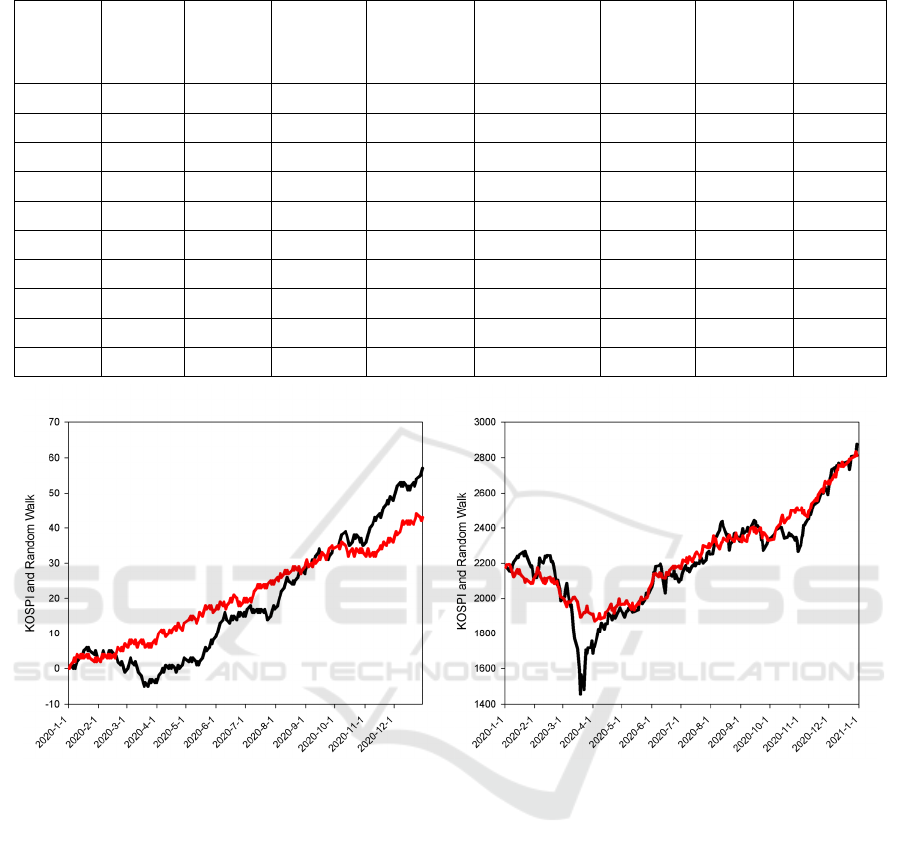
Table 1: Simplified KOSPI and random walks in 1/–1 and decimal formats.

Date

KOSPI

Compare

preceding

Random

alk in 1 or

–

1 format

Generated

random

number

Compare

preceding

random number

Random

alk in 1 or

–

1 format

Generated

random

number

Random

walk in

decimal

format

Jan 2, 2020 2175.17 –0.56759 18.76995

Jan 3, 2020 2176.46 1 1 0.10146 1 1 16.42251 2191.59

Jan 6, 2020 2155.07 –1 0 0.12706 1 2 0.70776 2192.3

Jan 7, 2020 2175.54 1 1 0.81422 1 3 –13.88377 2178.42

Jan 8, 2020 2151.31 –1 0 –0.32088 –1 2 –17.16913 2161.25

Jan 9, 2020 2186.45 1 1 0.03117 1 3 –16.45686 2144.79

an 10, 202

2206.39 1 2 0.66874 1 4 –22.7432 2122.05

an 13, 202

2229.26 1 3 –0.90877 –1 3 34.00345 2156.05

an 14, 202

2238.88 1 4 –0.33833 1 4 7.08048 2163.13

an 15, 202

2230.98 –1 3 –0.50799 –1 3 –20.66977 2142.46

Figure 1: KOSPI and random walk simulation. On the left panel, KOPIS in simplified format (black line) and random walk

in the 1/–1 format (red line) with a seed of 0.78654. On the right panel, KOSPI (black line) and random walk in the decimal

format with one of seeds: 7.30548, 7.30549, . . . 7.30557

Exactly following the steps demonstrated in Table

1, we can construct the random walk simulation of

KOSPI graphically for different periods of KOSPI

and its simulation..

The left panel of Figure 1 shows the simplified

KOSPI and its random walk simulation in the 1/–1

format. The initial several steps are exactly the same

as we show in from column 1 to column 6 in Table 1.

Because of simplification of KOSPI, the range in y-

axis is not as large as real-life KOSPI range. As seen

in the left panel, the random walk simulation

increases monotonically, but the simplified KOSPI

fluctuates largely for the first half year of 2020, which

marks the initial lockdown due to Covid-19

pandemic. Because the random walk goes either one

step up or one step down and there are 248 trading

days in 2020, the random walk theoretically has a

(½)

248

chance to fit the KOSPI without any difference

although this chance is extremely low.

The right panel of Figure 1 shows the real-life

KOSPI and its random walk simulation in decimal

format. Evidently, the random walk misses the big

fall of KOSPI in March 2020, which is totally due to

the unexpected Covid-19, on the one hand. On the

other hand, it does follow the uptrend from May 2020

until December 2020 although there is a small dip in

October. Interestingly, there are ten seeds, which can

produce the same results. This may suggest the

possibility that random number generator using

Monte Carlo algorism is not sensitive to the

increment at 0.00001. However, this possibility may

not be valid because the increment of 0.00001 does

Simulation of Korea Composite Stock Price Index (KOSPI) for the First 20 Years in the 21st Century Using Random Walk

615

Figure 2: KOSPI (black line) and random walk simulation (red line) for the period from 2016 to 2020 with seed of 1.32353

(left panel), and for the period from 2011 to 2020 with one of seeds: 7.73709, 7.73710, . . . 7.73718 (right panel).

have effects in other simulations. In fact, we used the

increment of 0.000001 in the past, but we frequently

find the same result from a series of seeds with

increment of 0.000001. Therefore, we choose the

increment of 0.00001 in our recent studies to reduce

the computational time.

Comparing two panels in Figure 1, we sometimes

feel that we can phase out the random walk

simulation in the 1/–1 format in the future because it

does have a certain chance to occur, i.e. (½)

248

, but

the random walk in decimal format also has a certain

possibility for a perfect fit. Technologically, we have

no need to pay great attention to the upper and lower

ranges in the random walk simulation in the 1/–1

format because the generated random numbers

should be rounded after comparison. In contrast, the

choice of upper and lower ranges becomes difficult

when there is an unexpected rise or fall in KOSPI

because these rises and falls do not rend a big change

in standard deviation, which are used in our studies.

The left panel in Figure 2 illustrates the random

walk simulation on KOSPI for five years. There are

two periods of uptrend, a slow one and a rapid one.

For the slow uptrend from 2016 to 2018, the random

walk simulation still can follow its paces step-by-

step. For the rapid uptrend from April 2020 to

December 2020, the random walk does not move fast

enough to catch up with the final phase of uptrend in

December 2020.

The right panel in Figure 2 depicts the random

walk simulation on KOSPI for ten years. As seen in

this panel, the KOSPI holds on the relatively small

fluctuations from 2011 to the middle of 2017. For this

period of time, the random walk simulation can

follow the trend moving horizontally, and even

follow the uptrend in 2018, but fails to follow the

sharp uptrend at the end of 2020. When looking the

three real-life random walk simulations from the right

panel in Figure 1 to left and right panels in Figure 2,

we can see a general tendency, that is, it becomes

harder and harder to catch up with the final uptrend

in the end of 2020.

Similar to what happens in the right panel in

Figure 1, there are also ten seeds in the right panel in

Figure 2, which generate the same result. More

importantly, there is no big difference between the

seeds for the right panel in Figure 1 and the seeds for

the right panel in Figure 2. These are very suggestive

because it implicates that there is a possibility to use

a seed to simulate two periods of KOSPI opening up

the possibility to predict the future KOSPI movement

using the same seed.

The left panel in Figure 3 pictures the random

walk simulation on KOSPI for fifteen years from

2006 to 2020. For this period of time, we can see that

KOSPI actually goes up although there are two big

falls in 2008, which is the financial crisis, and in

2020, which is the Covid-19 pandemic. Clearly, the

random walk cannot reach as deep as the real-life

KOSPI in these two big falls.

The right panel in Figure 3 describes the random

walk simulation on KOSPI for twenty years from

2001 to 2020. For this longest period of simulation in

this study, the KOSPI goes up from 500 approaching

to 3000. The small fluctuations appear insignificant

in such a long scale, however, their contribution to

the statistical description is large because they

significantly decrease the standard deviation.

Therefore, it is impossible for Month Carlo algorithm

to generate very large random numbers to cope with

the two great falls in 2008 and 2020, and

subsequently the biggest jump at the end of 2020.

Indeed, the simulation in the right panel of Figure 3

is encouraging because it does follow the KOSPI

trend for 20 years.

ICPDI 2022 - International Conference on Public Management, Digital Economy and Internet Technology

616

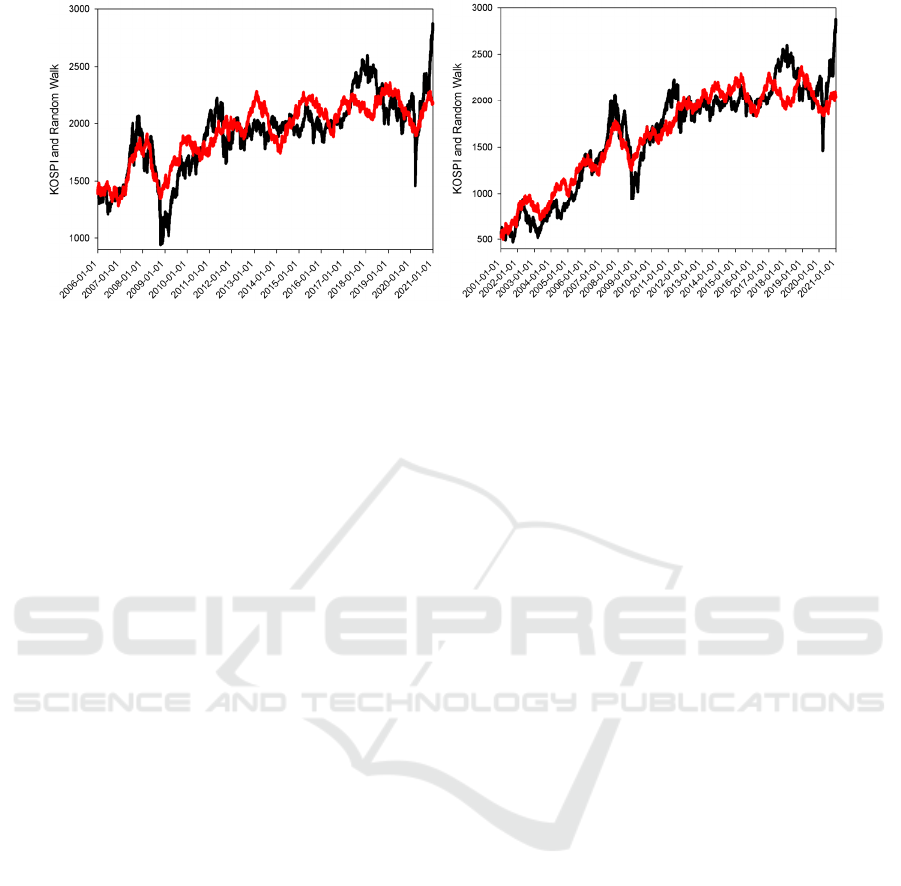
Figure 3: KOSPI (black line) and random walk simulation (red line) for the period from 2006 to 2020 with a seed of 2.62207

(left panel), and for the period from 2001 to 2020 with a seed of 0.03275 (right panel).

The issue of whether or not a stock market index

or an individual stock follows a random walk is the

objective in many studies, but the difficulty is that

random walk cannot reveal the underlined

mechanism in stock market. Nevertheless,

randomness can be the underlined mechanism for

stock movement, not only because various known

and unknown factors affect the movement of stock

market, but also randomness is considered to stay at

the heart of nature (

Everitt, 1999

). However, the

simulation actually does a phenomenological job. In

fact, regression is also a phenomenological tool to

build a possible and potential cause-effect

relationship, but random walk does link any cause to

the effect. Yet, the random walk has few parameters,

i.e. seed, upper and lower ranges, so it may

encompass uncountable known and unknown factors,

which can be considered random because we cannot

define their cause-effect relationship.

Oftentimes, the issue of whether or not a stock

index can be described by a random walk model is

related closely to the efficient market hypothesis

(EMH), especially, the weak form market efficiency.

The knowledge gap is progressively filled up with

various statistical tests as well as the real-life random

walk simulations. The issue of whether or not the

simulation is dependent on time length is yet to be

proved because simulations for different period of

time result in different results.

In foreseeable future, we hope to solve several

problems with random walk simulation, for example,

how to choose suitable upper/lower ranges, whether

to use a percentage will be more helpful than the real-

life data, etc, At any rate, much work needs to be done

in the future.

4 CONCLUSION

In this study, we use the random walk model to

simulate KOSPI for the first 20 years in the 21

century because the hypothesis of whether a stock

index can be described using a random walk model is

still unsolved. Therefore, it is necessary to conduct

this type of studies to different stock indices and

different individual stock. In fact, statistical tests on

random walk go along this way. Our results

demonstrate that the random walk model can simulate

at least the general trend of KOSPI, but far from

accurately and precisely follow the real-life KOSPI

although there is an extremely small possibility to do

so. We wish to continue our studies along this line in

near future.

ACKNOWLEDGMENTS

The study was supported by the Scientific

Development Fund of Guangxi Academy of Sciences

(2021YFJ1203).

REFERENCES

Abraham, A., Seyyed, F.J., Alsakran, S.A. (2002)

Testing the random walk behavior and efficiency of

the Gulf stock markets. Finan. Rev., 37: 469-480.

Aggarwal, D. (2018) Random walk model and

asymmetric effect in Korean composite stock price

index. Afro-Asian J. Finan. Account., 8: 85-104.

Charles, A., Darné. O. (2009) The random walk

hypothesis for Chinese stock markets: evidence from

variance ratio tests. Econ. Syst., 33: 2.

Simulation of Korea Composite Stock Price Index (KOSPI) for the First 20 Years in the 21st Century Using Random Walk

617

Everitt, B.S. (1999) Chance Rules: An Informal Guide to

Probability, Risk, and Statistics. Springer, New York.

Feller, W. (1968) An Introduction to Probability Theory

and Its Applications. 3

Edition, John Wiley, New

York.

Gilmore, C.G., McManus G.M. (2003) Random walk

and efficiency tests of central European equity

markets. Manag. Finan., 29: 42-61.

Han, Q., Guo, B., Ryu, D., Webb, R.I. (2012)

Asymmetric and negative return-volatility

relationship: The case of the VKOSPI. Invest.

Analysts J., 41: 69-78.

Kim, W., Bang, S. (2014) Regime-dependent

characteristics of KOSPI return.

Commun Stat Appl

Methods., 21:

501-512.

Kim, I.J., Kim, S. (2004) Empirical comparison of

alternative stochastic volatility option pricing

models: Evidence from Korean KOSPI 200 index

options market. Pacific-Basin Finan. J., 12: 117-142.

Ko, K. (2012) Who wins in the money game? The case

of KOSPI 200 futures. Pacific-Basin Finan. J., 20:

843-856.

Lee, S.H., Lim, J.S. (2011) Forecasting KOSPI based on

a neural network with weighted fuzzy membership

functions. Expert Syst. Appl., 38: 4259-4263.

Lee, K., Yoo, S., Jin, J.J. (2007) Neural network model

vs. SARIMA model in forecasting Korean Stock

Price Index (KOSPI). Issues Inform. Syst., 8: 372-

378.

Na, S.H., Sohn, Y.S. (2011) Forecasting changes in

Korea Composite Stock Price Index (KOSPI) using

association rules. Expert Syst. Appl., 38: 9046–9049.

SPSS Inc., (1986-2001) SigmaPlot 2002 for Windows

Version 8.02.

Yoon, I.H., Kim, Y.M. (2018) A study on weak-form

efficiency of KOSPI stock market after the recent

expansion of daily price limits. J. Int. Trade

Commerce, 14: 73-88.

ICPDI 2022 - International Conference on Public Management, Digital Economy and Internet Technology

618