The Modeling of Fire Scenario Deduction in Commercial Complexes
by Bayesian Network
Jianyu Zhao
1
and Linghan Meng
2
*
1
Pengbo Operating Company, Tianjin Branch of CNOOC Ltd, Tianjin 300459, China
2
School of Engineering and Technology, China University of Geosciences, Beijing 100070, China
Keywords: Commercial Complex Buildings, Scenario Rehearsal, Bayesian Network.
Abstract: The fire evolution process in commercial complex buildings is complicated, and it is often difficult for
firefighters to take targeted emergency measures when a disaster occurs. In order to solve this problem
effectively, this paper combines Bayesian network with scenario deduction to deduce the evolution path of
fire accidents in commercial complex buildings. On the basis of specifying the scenario deduction elements,
the Bayesian network joint probability distribution is used to calculate the scenario state probability, so as to
obtain the current state of the accident and the possible future evolution trend. The example results show that
the model can directly show the fire evolution process of commercial complex, and provide a reliable basis
for fire emergency decision-makers to take timely and effective emergency plans.
1 INTRODUCTION
The rise of commercial complex buildings has
brought convenience to people's lives, but the
complex architectural structure of the commercial
complex and the dense combustible materials in these
buildings also lurk a huge fire hazard. The unique
regional environment of the commercial complex
makes the evolution of fire highly uncertain and
chain dynamic, and once a fire occurs in the area,
people's lives and property safety will be greatly
threatened. Therefore, how to quickly predict the fire
evolution path based on the fire information and take
early measures to reduce disaster losses after a
commercial complex fire has become the focus of
current research.
In recent years, scenario deduction model has
been used to predict disaster accident trends in a wide
range of fields, including natural disasters (Zhu, Li
and Wang 2016), food safety (Song, Liu, Jiang and
Yang 2018), production accidents (Wang, Zhang, Ji
2020, Li, Xia, WU 2014), and electrical safety (Lin,
LYU, Wang, Peng 2019). Therefore, if the
evolutionary path of fire in commercial complexes
can be predicted by scenario deduction model, the
result of this model can be used to design effective
measures to control the growth and spread of fire in
complex buildings, so as to improve the safety of life
and property damage. In the earlier studies, the
Bayesian network (BN) (Wu, Tan, GAI 2016),
multidimensional scenario space methods (Qian, Liu,
Jiao 2015) and knowledge meta-model (Zhang, Wang,
Chen 2016) were combined with scenario deduction
model. After analyzing the fire evolution law of
commercial complex, this paper used the Bayesian
network and scenario deduction model to construct
the fire scenario evolution network, and then used the
joint probability distribution of Bayesian network to
calculate the scenario occurrence probability to
realize the extrapolation of fire accidents in
commercial complex.
2 FUNDAMENTALS OF
SCENARIO DEDUCTION
MODEL
Scenario evolution is used to provide an objective
description of the current and possible future
evolution of a disaster incident. Scenario deduction is
a dynamic process, and after the initial event, other
secondary events are often chained due to human
interference and external environmental factors.
Therefore, when the fire scenario evolution process
of a commercial complex is extrapolated, the
evolution of the fire scenario will be more intuitively
796
Zhao, J. and Meng, L.
The Modeling of Fire Scenario Deduction in Commercial Complexes by Bayesian Network.
DOI: 10.5220/0011767900003607
In Proceedings of the 1st International Conference on Public Management, Digital Economy and Internet Technology (ICPDI 2022), pages 796-801
ISBN: 978-989-758-620-0
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

grasped. To describe the process of scenario
evolution, firstly, it is necessary to clarify the current
state of the disaster event and the information of the
accident scene, and then infer the evolution route and
possible consequences of the event by objective and
scientific means.
2.1 Elements of Scenario Deduction
Model
To reflect the real situation of disaster evolution,
emergency decision makers should first extract the
key scenarios of a disaster that can describe the
disaster situation in a certain time period. In the
deduction of fire scenarios in commercial complex
buildings, the key scenarios are the real fire situations
faced by fire fighting and rescue decision makers. In
the scenario evolution process, in addition to
identifying the key scenarios in an accident, the
emergency environment in which the scenarios are
located and the measures taken by emergency
decision makers for each scenario are also identified.
Therefore, the commercial complex fire scenario
evolution process contains four main elements:
situational state, emergency measures, emergency
environment, and evolution of the situation. The
evolutionary network is established using a symbolic
language to characterize the relationship between the
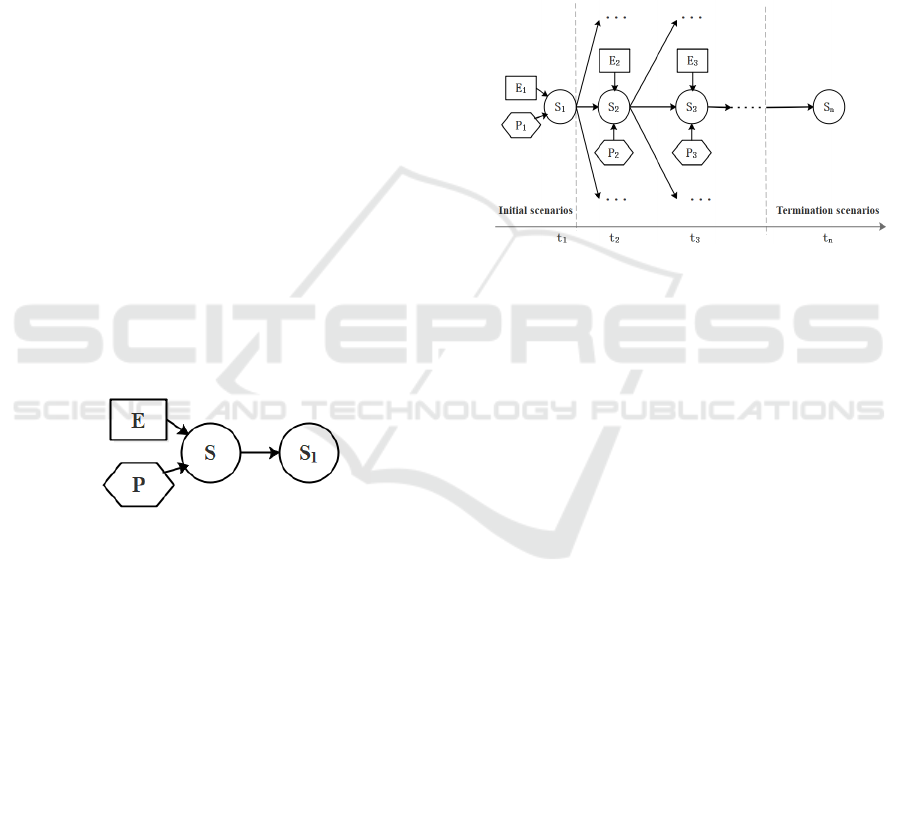
elements, as shown in Figure 1.
Figure 1: Basic units of scenario evolution.
S denotes the current situational state; P denotes
the emergency measures to be taken in this situational
state S; and E denotes the current environmental
situation of the fire, i.e., the emergency environment.
Under the influence of fire emergency measures and
the emergency environment, scenario S will change
and then jump to scenario S
1
, which is a scenario unit
of scenario evolution.
2.2 The Law of Scenario Deduction
The complexity of the fire disaster evolution process
is determined by the specificity of the regional
system of commercial complexes. In addition to the
evolution of the fire accident scenario itself, the
correlation between the systems, the complexity of
the emergency environment, the effectiveness of
emergency measures and other factors often cause the
chain evolution of other secondary hazards,
eventually forming an evolutionary network of
multiple paths. As shown in Figure 2, the scenario S
1
appears in the commercial complex building at the
moment t
1
, and S
1
evolves to S
2
under the joint action
of the emergency environment E
1
and emergency
measures P
1
. As time advances, the dynamic
evolution of the scenario goes from the initial
scenario S
1
through a series of evolutionary scenarios
S
2
, S
3
… S
n-1
and finally reaches the termination
scenario Sn.
Figure 2: Scenario deduction rule.
3 FUNDAMENTALS OF
BAYESIAN NETWORK
A Bayesian network is a directed acyclic graph
representing probabilistic dependencies among
variables, consisting of nodes representing variables
and directed edges connecting these nodes. Bayesian,
as a probability-based uncertainty inference method,
is an important tool for dealing with uncertain
information. Due to the complex building
environment of commercial complexes and the
changeable path of fire evolution process, it is more
practical to use Bayesian network to simulate the fire
evolution process.
3.1 Construction of Bayesian Network
When a fire broke out in a commercial complex, the
current scenario of the incident was identified.
However, the real scenario of the fire keeps changing
over time. This paper extracts key scenarios and
influencing factors by combining the experience of
experts in the field and the law of fire evolution in
commercial complexes, and then the evolution
network is established by symbolic language. In this
paper, nodes are used to represent the key elements in
the evolution process, and directed edges are used to
The Modeling of Fire Scenario Deduction in Commercial Complexes by Bayesian Network
797

represent the influence of each element on the
scenario state and the scenario evolution, so as to
construct the Bayesian network of the fire scenario
evolution process of commercial complex. As shown
in Figure 3, the nodes S
1
, S
2
, S
3
respectively denote
different situations, 𝑃

𝑆


represents the prior
probability of the occurrence of node S
1
,
𝑃

𝑆


represents the prior probability of the
occurrence of node S
2
, 𝑃

𝑆

, 𝑆


and
𝑃

𝑆

, 𝑆


respectively represent the conditional
probability of node S3 occurrence when scenarios S
1
and S
2
occur.
Figure 3: Sketch of Bayesian networks.
3.2 Determination of Bayesian Network
Probabilities
Determining the Bayesian network also identifies
various scenarios that may occur in the future, but it’s
also necessary to know the probabilities of
occurrence of these scenarios in order to achieve
inference about the evolution of the scenarios. The
Bayesian network inference is based on Bayesian
probability theory. Firstly, the prior probability of the
initial scenario should be determined based on the
local historical statistics of this type of accident and
the expert’s own experience, and then synthesize
each expert's opinion to analyze the degree of
association between nodes. Finally, the conditional
probability is derived according to the pessimistic
decision criterion. Then, the state probabilities of the
nodes in the network are calculated using the
Bayesian network joint probability formula.
The joint probability formula of Bayesian
network is as follows:
𝑃

𝑆

, 𝑆

, ⋯ , 𝑆


=
𝑃

𝑆

|
𝑆

, 𝑆

, ⋯ , 𝑆


⋯𝑃

𝑆

|
𝑆


𝑃

𝑆


=
∏
𝑃

𝑆

|𝑃

(𝑆

)



(1)
In the form,
()
ai
P
S
is denote the prior probability of
the parent node of
i
S
,
1, 2,in= 
.
4 CASE STUDY
In 2013, a commercial complex was affected by an
underground natural gas pipeline leak, which caused
a fire and explosion on the first basement and first
floor of the building, which quickly spread to the roof
and nearby buildings. In this paper, scenario
deduction and analysis of the accident were
conducted by using the above-mentioned method.
4.1 Analysis of the Evolutionary
Process of Accident Scenarios
Based on the information of the commercial complex
Table 1: Scenario elements of the fire accident in commercial complex.
Situational state (S) Emergency environment € Emergency measures (P)
A fire broke out on the first underground
floor (S
1
)
gas pipelines leakage (E
1
) Emergency treatment of employees
(P
1
)
The fire was controlled without spreading on
the first under
g
round floo
r
(S
2
)
There were many combustibles in the
b
uildin
g
(E
2
)
Firefighters put out the fire (P
2
)
The end of the fire accident (S
3
)
Fire spread to upper floors (S
4
) Surrounding roads were blocked (E
4
) Request support to stop the fire from
spreading (P
4
)
Fire was basically stable under control (S
5
) Sending more people to rescue (E
5
) Firefighters put out the fire (P
5
)
The end of the fire accident (S
6
)
Open flame extinguishe
d
(S
7
) Large fire smoke (E
7
) Firefighters put out the fire (P
7
)
The end of the fire accident (S
8
)
The whole building was in fire and
endangered the surrounding buildings (S
9
)
Smaller spacing between surrounding
buildings (E
9
)
Firefighters put out the fire (P
9
)
Surrounding buildings fire extinguished
(S
10
)
Open flame in the complex continues
to s
p
read outward (E
10
)
Adding large equipment to
extin
g
uish fire (P
10
)
Open flame in the complex extinguished
(S
11
)
Large fire smoke (E
11
) Firefighters put out the fire (P
11)
The end of the fire accident (S
12
)
ICPDI 2022 - International Conference on Public Management, Digital Economy and Internet Technology
798

Figure 4: Schematic diagram of the Bayesian network scenario deduction path.
Table 2: Network nodes prior probability and conditional probability table (partial data).
Node
p
rior
p
robabilit
y
conditional
p
robabilities
S
1
()
1
0.95PE T==
()
1
0.15PP T==
()
111
,0|.70PS T E TP T====
()
111
,0|.95PS T E TP F====
()
111
,0|.40PS T E FP T====
()
111
,0|.60PS T E FP F====
S
2
()
2
0.95PE T==
()
2
0.45PP T==
()
2122
,, 5|0.0PS T S TP TE T=====
()
2122
,, 6|0.0PS T S TP TE F=====
()
2122
,, 1|0.0PS T S TP FE T=====
()
2122
,, 1|0.5PS T S TP FE F=== ==
()
222
1, , 0.75|PS T S FP TE T=====
()
222
1, , 0.90|PS T S FP TE F=====
()
222
1, , 0.65|PS T S FP FE T=====
()
222
1, , 0.70|PS T S FP FE F=====
fire accident scene, the accident was sorted out
according to the time line. Through the
communication with experts, the key Situational
State (S), emergency environment (E) and
Emergency measures（P）were extracted from each
key period in the accident development process, as
shown in Table 1. After each node of the Bayesian
network were determined, the nodes could be
connected by directed edges to form the accident
scenario deduction path, as shown in Figure 4.
According to the fire environment and the
effectiveness of firefighting and rescue measures, the
fire evolution of commercial complex is divided into
optimistic and pessimistic paths. The horizontal
arrow indicates that the firefighting and rescue is
more effective, and the scenario evolves in the
optimistic direction. The vertical arrow represents the
opposite meaning. In the figure, S
1
→S
4
→S
9
is the
most optimistic direction in the evolution path of fire
scenarios, and S
1
→S
4
→S
9
is the most pessimistic
path.
4.2 Calculating the Probability of Each
Scenario
To deduct the fire accident of the commercial
complex, it is necessary to determine the probability
of each scenario. The prior probability of network
The Modeling of Fire Scenario Deduction in Commercial Complexes by Bayesian Network
799

Figure 5: Fire accident dynamic Bayesian network situation deduction diagram.
nodes were scored by experts in the field based on
historical statistics of complex fires and their own
experience, then combined with the accident scenario
evolution model described above, and finally the
conditional probabilities were derived based on
pessimistic decision criteria (Table 2).
Bayesian network joint probability formula is
used to calculate the state probability of each scenario.
For example, the state probability P (S
1
= T) = P (E
1
= T) * P (P
1
= T) * P (S
1
= T | E
1
= T, P
1
= T) + P (E
1
= T) * P (P
1
= F) * P (S
1
= T | E
1
= T, P
1
= F) + P (E
1
= F) * P (P
1
= T) * P (S
1
= T | E
1
= F, P
1
= T) + P (E
1
= F) * P (P
1
= F) * P (S
1
= T | E
1
= F, P
1
= F) = 0.895,
and state probability of other scenarios can be
calculated by analogy with this method. This paper
used the Bayesian network software Netica to obtain
the Bayesian network scenario deduction diagram of
fire accident in the commercial complex, as shown in
Figure 5.
4.3 Analysis of Inference Results
(1) It can be seen from Figure 4 that the scenarios
with a higher probability of occurrence were S
1
, S
4
and S
9
, with the occurrence probability of 89.5%,
79.3% and 72.5% respectively. It could be seen that
the probability of the accident scenario evolution in
an adverse direction was higher than that of the
optimistic direction. However, this does not mean
that fire emergency measures were ineffective. To
some extent, these measures had played a role in
delaying the spread of fire.
(2) After the occurrence of disaster, taking
effective measures in time has a certain inhibitory
effect on the evolution of the disaster. While other
conditions remained unchanged, when the
probability of P
1
was increased to 95%, the
probability of S
1
was reduced from 89.5% to 69.7%;
the probability of S
2
has been reduced from 79.3% to
69.9%. In the early stage of the commercial complex
fire accident, if the managers took effective
emergency measures immediately, such a big disaster
loss would not have been caused.
5 CONCLUSION
In this paper, the derivation of the evolutionary path
of fire accidents in commercial complexes includes
three processes: (1) analyzing the evolutionary law of
accident scenarios; (2) constructing a Bayesian
scenario network; (3) calculating the scenario state
probabilities. According to the example results, it can
be found that the calculation results are basically
consistent with the actual situation of the fire scene,
which verifies the validity of the model.
This paper provides a new perspective for
firefighters to develop scientific emergency response
plans by using scenario extrapolation models to
predict fire evolution paths. The method can provide
a more intuitive response to the effect of emergency
measures and facilitate timely adjustment of the plan
by firefighters. However, due to the complex fire
environment of commercial complex buildings and
the uncertainty of path development, this paper only
considers the evolution path with fire development as
the main line, and a more comprehensive, systematic
ICPDI 2022 - International Conference on Public Management, Digital Economy and Internet Technology
800

and reasonable analysis of evolution path needs
further study.
REFERENCES
Li JH, Xia DY, WU XP. (2014) Scenario analysis of
unconventional emergency disaster accidents based on
the knowledge elements and dynamic Bayesian
networks. J. Journal of Safety and Environment,
14(04):165-170.
Lin D, LYU ZQ, Wang HF, Peng DG. (2019) Research on
Electric Power Emergency Scenario Deduction Method
Based on Bayesian Network. J. Zhejiang Electric
Power, 38(07):86-91.
Qian J, Liu Y, Jiao YY. (2015) Study on case analysis and
scenario deduction based on multi-dimensional
scenario space method. J. Systems Engineering-Theory
& Practice, 35(10):2588-2590.
Song YH, Liu HX, Jiang XY and Yang LJ. (2018) Research
on Scenario Evolution of Food Safety Incidents Based
on Knowledge Element and Bayesian Network. J.
Journal of the China Society for Scientific and
Technical Information, 37(7): 712-720.
Wang JN, Zhang YH, Ji SS. (2020) Probability prediction
of the controller＇s status- in -situ alertness based on
the Markov chain Monte Carlo. J. Journal of Safety and
Environment, 20(04):1420-1426.
Wu Q, Tan W, GAI WM. (2016) Study on scenario analysis
of civil aviation emergency based on dynamic Bayesian
network. J. Journal of Safety Science and Technology,
12(03):169-174.
Zhu XH, Li XY and Wang SY. (2016) Scenarios
Combination Deduction Method of Natural Disaster. J.
Management Review, 28(08):143-151.
Zhang L, Wang YZ, Chen XL. (2016) Fuzzy inference
method for unconventional events scenarios based on
knowledge unit. J. Journal of Systems Engineering,
31(06):729-738.
The Modeling of Fire Scenario Deduction in Commercial Complexes by Bayesian Network
801