Design of Cradle as a Tool for Inserting Shaft in New Shipbuilding

Using Finite Element Methods

Budianto

, Rachmad Tri Soelistijono and Shihabuddin Afghoni

Shipbuilding Department, Politeknik Perkapalan Negeri Surabaya, Jalan Teknik Kimia, Surabaya, Indonesia

Keywords: Cradle, Inserting Shaft, New Shipbuilding, Design, Finite Element Method.

Abstract: The shipbuilding industry in Indonesia has experienced very rapid development. Innovation methods in

development have been improvised in time. In Indonesia, many shipyards have implemented the Full

Outfitting Block System (FOBS) methods. This method, especially in the machinery outfitting process in the

inserting shaft stage, takes a long time because it uses conventional methods with chain block tools. At PT.

PAL Indonesia has historically carried out inserting shafts using a cradle on the Missile Destroyer Ship project

(PKR) by recommendation from a foreign company and was able to minimize production time and costs. In

supporting the sustainability of the work efficiency of new shipbuilding, cradle design is very much needed

in the Inserting Shaft process on ships. The design process begins by making a design of 6 models of cradle

variations that are tailored to the needs of the shipyard. All these design variations were then subjected to a

strength analysis with the limits of allowable stresses and deflections from American Association of State

Highway and Transportation Official (AASTHO). The stress and deflection values obtained from each

variation of the design concept with all design concepts included in the allowable category.

1 INTRODUCTION

The shipbuilding industry in Indonesia has

experienced very rapid development. Innovation

methods in development have been improvised in

time. In Indonesia, many shipyards have

implemented the Full Outfitting Block System

(FOBS) methods. This method, especially in the

machinery outfitting process in the inserting shaft

stage, takes a long time because it uses conventional

methods with chain block tools. At PT. PAL

Indonesia has historically carried out inserting shafts

using a cradle on the Missile Destroyer Ship project

(PKR) by recommendation from a foreign company

and was able to minimize production time and costs.

In supporting the sustainability of the work

efficiency of new shipbuilding, cradle design is very

much needed in the Inserting Shaft process on ships,

where improvement and proper engineering are

needed for the inserting shaft process, this is very

important to escalate and ensure safety, quality

fulfilment, timely delivery. This will further reduce

the production cost of shipbuilding. Design and

analysis of the strength of the cradle construction in

https://orcid.org/0000-0002-4155-5008

supporting the load of the ship's shaft in the Inserting

Shaft process by paying attention to the position of

the shaft bearing that supported the cradle. This

analysis uses the finite element method using

Fusion360 software to determine the maximum stress

and maximum deflection that occurs in the cradle.

Where the structure of the cradle must comply with

the American Association of State Highway and

Transportation Official (AASHTO).

2 INITIAL DESIGN

At the initiation stage of the cradle design, several

reviews are needed of the components to be worked

on.

2.1 Cradle

The cradle consists of two parts, namely train sled and

shoes sled. A train sled or often referred to as a trolley

is a type of conveyance whose operation method is

pushed or handled by workers or operators manually

Budianto, ., Soelistijono, R. and Afghoni, S.

Design of Cradle as a Tool for Inserting Shaft in New Shipbuilding Using Finite Element Methods.

DOI: 10.5220/0011806800003575

In Proceedings of the 5th International Conference on Applied Science and Technology on Engineering Science (iCAST-ES 2022), pages 381-387

ISBN: 978-989-758-619-4; ISSN: 2975-8246

381

in industrial plants or similar agencies. In general, a

shoes sled shipyard is a tool used for the docking

process (moving) the ship from the waters to the land

for repairs. Skates or often referred to as sliding ways

according to Meriam-Webster's Dictionary and

Thesaurus are the bottom part of the cradle on which

the ship is built and which slides over the ground

when launched or raised (Dictionary, 2006).

2.2 Stress

Stress can be interpreted as the intensity of the force

on the structural elements which is a reaction to the

deformation that arises due to the work of external

loads. Broadly speaking, stress is the magnitude of

the force acting on each unit of cross-sectional area

(Asroni 2017). So that stress can also be referred to as

a force that can withstand a load (Macdonald 2002).

2.3 Deflection

Deflection is a condition of changes in the shape of

the beam in the y-direction due to vertical loading

given to the beam or rod. Deformation in the beam is

very easily explained by the deflection of the beam

from its position before being subjected to loading.

The deflection is measured from the initial neutral

surface to the neutral position after deformation. A

structural system that is placed horizontally and

which is mainly intended to carry lateral loads namely

loads that act perpendicular to the axial axis of the rod

(Hariandja, 1996). The maximum allowable

deflection according to the American Association of

State Highway and Transportation Official

(AAHSTO) is the maximum deflection of the bridge

construction (Restrepo 2002), not more than:

2.4 Deflection

The moment is the result of multiplying the force with

the distance from the force to the point (Widiyanto

2013). The moment equation can be written in this

Equation as refer rule regulation.

In the condition of the force that has a different

capture point, where the point of capture of the force

with each other has a distance so that the moment

occurs. Then the number of moments at one point

equal to zero can be seen in this equation as follows

actual maximum bending moment.

2.5 Safety Factor

Safety Factor is a factor that shows the level of ability

of an engineered material from external loads to

handle pressure loads and tensile loads. The safety

factor can be determined in equation 3 as follows

(Budianto, Strength Structure Analysis of Main Gate

Graving Dock Using 2018).

The value of the safety factor must be greater than

1.0 in order to avoid failure. If the factor of safety is

very low, the probability of failure will be high, and

the structure will not be acceptable. If the factor of

safety is too large, the structure will be wasteful of

materials and may not be suitable for its function, e.g.,

too heavy. Due to this complexity and uncertainty, the

factor of safety must be determined probabilistically.

The following is the Typical Overall Factor of Safety

table according to the Mechanical Engineer's Data

Handbook as follows (Carvill 1993).

Figure 1: Typical factor of safety for various materials.

Figure 2: Typical factor of safety for various components.

2.6 Load

Loading is a load that burdens a construction in the

form of object weight, wind strength, and wind

weight (Priambodo, 2011). These charges have

magnitude, direction, and line of action. In the cradle

construction that has been made, there is only one

loading, namely vertical loading (M.Gere and

S.P.Timoshenko 1994).

2.7 Finite Element Method

The finite element method was originally used to

solve complex problems in the field of Civil

iCAST-ES 2022 - International Conference on Applied Science and Technology on Engineering Science

382

Engineering and Aeronautical Engineering,

especially on elasticity problems and structural

analysis (Budianto, Analisis Kekuatan Struktur pada

Kapal Wisata Sungai Kalimas 2015). This is much

more practical and economical when designing a

design before making it a physical prototype (Naruto,

2019). The finite element method is a numerical

method used in solving problems in various

engineering fields such as the geometry, loading, and

properties of very complex materials. In addition, this

method can also be used to solve structural, thermal,

and electromagnetic problems (Morna 2012).

Problem-solving in the finite element method is a

solution approach to find the displacement of the

element's discrete nodes and the strength of the

structure (Budianto, Strength Structure Analysis of

Main Gate Graving Dock Using 2018).

In this method, all complex problems such as

variations in shape, boundary conditions, and loads

are solved by an approximation method. The finite

element method approach uses the information at the

node. In the process of determining the node points

called discretization, a system is divided into smaller

parts, then problem-solving is carried out on these

parts and then recombined to obtain a comprehensive

solution (Logan 2005). The descriptions carried out

can be in the form of one-dimensional elements (line

elements), two-dimensional (shell field elements), or

three-dimensional (solid elements or continuum)

(Budianto, 2018). In structural analysis, the finite

element method analysis can be used to solve

deflections and stresses in complex structures that

receive certain loads at appropriate boundary

conditions (Asmara and Budianto 2016)

3 CONCEPT DESIGN

Collecting data to support the design process is a

General Arrangement of Shaft Line design drawing

of the highest weight ever produced by PT. PAL

Indonesia (Persero). In addition, in planning the

cradle design, comparative design data is needed as a

basis for planning dimensions for making a new

design on the cradle where this data is taken from the

cradle design that has been used before by the

company. The data that has been collected will be

used as a basis for designing and planning the shape

of the cradle. The general arrangement of the Shaft

Line is used to determine the load borne by the

planned Cradle.

In this case, because the load supported by the

cradle is a shaft that has a relatively heavy weight, the

cradle is designed with materials that can be found on

the market and are also economical in price so that the

material is obtained in the form of plate-shaped steel

with ASTM 36 type with specifications as shown in

the following table.

Table 1: Specification of ASTM 36 steel.

ASTM A36 Steel

Mechanical

Properties

Ultimate Tensile

Strength

400–550

MPa

Yield Tensile Strength 250 MPa

Elongation at Break

(200cm)

20,0 %

Modulus of Elasticity 200 GPa

After obtaining supporting data, the next step is

planning from the cradle shape. In this planning, the

sled design is made with almost the same shape as the

sled that has been used before because the shape

adjusts to the shape of the pedestal of the shaft that

has been planned by the vendor and for the skates,

variations are made with different girder shapes and

construction patterns as shown in the following table.

Table 2: Variations of design.

From these variations, a model will be made with the

following scheme.

Figure 3: Design Variation Relationship Patter.

The cradle consists of a train sled and shoes sled with

cradle modeling done using Fusion 360 software as

follows.

Figure 4: Design of the Shoes Sled Variations.

Part 1 2 3

Girder

(G)

I Shape

Hollow

Patterm

(P)

Triangle

Cross X

Square

Box

Design of Cradle as a Tool for Inserting Shaft in New Shipbuilding Using Finite Element Methods

383

Figure 5: Design of the Train Sled.

In the assembly of the cradle, it is necessary to plan

the positioning of the pedestal of the cradle, where it

is planned that one cradle has three supports which

are placed at both ends and the middle position of the

cradle as shown in the following schematic image.

Figure 6: Cradle Leg Arrangement Sketch.

This cradle has a load in the form of a shaft placed on

a sled with a configuration that adjusts to the bearing

position that has been planned by the maker of the

shaft in the shaft dimension drawing and the

following shaft bearing arrangement.

Figure 7: Shaft Dimensions and Shaft Bearing Arrangement.

It is necessary to calculate the load at each point

of the shaft bearing to obtain the load value that will

be used as a reference for strength analysis. From the

dimension and arrangement data, it can be used as a

reference in calculating the load that will be borne by

the cradle at each point of the shaft bearing by

carrying out the calculations illustrated in the

following sketch.

Figure 8: Shaft Load Distribution Sketch.

This calculation can be done using the equation of

moment and balance. The moment is the result of

multiplying the force with the distance from the force

to the point (Widiyanto, 2013), which can be written

with equations 1 and 2 with the following

calculations.

∑M

= 0

(-3.026 ton × 1.5200 m) - (0.564 ton × 0.3710 m) +

(4.527 ton × 2.9753 m) – (RVB × 5.9570 m)

= 0

8.6749055 – 5.957 RVB

= 0

∑M

= 0

(4.527 ton × 2.978 m) - (RVA × 5.957 m) + (0.564

ton × 6.328 m) + (3.026 ton × 7.477 m)

= 0

39.6758 – 5.957 RVB

= 0

∑M

= 0

(4.286 ton × 2.820 m) - (RVC × 5.640 m)

= 0

12.08652 – 5.640 RVC

= 0

∑M

= 0

(4.286 ton × 2.820 m) - (RVB × 5.640 m)

= 0

12.08652 – 5.640 RVB

= 0

∑M

= 0

(2.580 ton × 1.697 m) - (RVD × 3.395 m) + (1.445

ton × 4.3455 m)

= 0

10.6575075 – 3.395 RVD

= 0

∑M

= 0

(-1.442 ton × 0.9505 m) + (2.580 ton × 1.697 m) -

(RVC × 3.395 m)

= 0

3.0047875 – 3.395 RVC

= 0

= 1,456254871

= 6.660365456

= 2.143 ton

= 2,143 ton

= 3,139177467

= 0.885062592

iCAST-ES 2022 - International Conference on Applied Science and Technology on Engineering Science

384

After calculating the value of the reaction force,

correction is made by comparing the values of q

, q

, and q

with RV

, RV

, and RV

equal to one with the following calculations.

Correction = (3.02642 + 0.56392 + 4.52732 +

4.2864 + 2.5802 + 1.44475) /

(6.660365456 + 3.599254871 +

3.02806392 + 3.139177467)

= 16.43 / 16.43

= 1 (accepted)

From the calculation of the value of the reaction

force, the shaft load point can be taken for simulating

cradle loading with the summary in the following

table.

Table 3: Summary of Shaf Load Value.

Pos. Load Value

A 6.660365456 ton

B 1.456254871 + 2.143 = 3.599254871 ton

C 2.143 + 0.885062592 = 3.028062592 ton

D 3.139177467 ton

Total 16.43 ton

After obtaining the load value at each supported

point, then the highest load value is taken, namely

6.66 tons, as the load value for the simulation.

Because this is a design process, it is necessary to

carry out further calculations to determine the design

load value as in equation 4 with the following

calculations.

design

= 6.660 kg × 1,25

= 8.325 kg

design

= 8.325 kg × 9,81

= 81668.25 N

After obtaining the Fdesign value, then a strength

analysis is carried out. To obtain accurate finite

element analysis results, it is necessary to adjust the

element size by conducting a meshing convergence

test. So that the element size is 150mm as shown in

the following graph.

Figure 9: Meshing Convergence Graph.

4 RESULT AND DISCUSSION

After obtaining the F design value, a meshing

convergence test was carried out and the element size

was obtained at 150mm, then a simulation of each

design concept was carried out with a perfect circuit

together with the train sled. The maximum stress

results from the simulation are compared to the

maximum allowable stress value that occurs in

structures having a Safety Factor (SF) of 5.0 in the

typical overall safety of factor table (referring to

Tables 1 & 2) so that the bending stress value is

obtained. The maximum of the cradle is.

The maximum deflection results from the

simulation are compared to the maximum allowable

deflection value in accordance with the regulations of

the American Association of State Highway and

Transportation Official (AAHSTO) as in equation 1

is shown below.

The simulation can be done with Fusion 360

software by inputting the type of material, the

constraints on the cradle legs, and also the size of the

elements according to the convergence results of 150

mm. so that the simulation results are obtained in each

of the following six models.

Figure 10: (a) Stress Result of Model 1; (b) Displacement

Result of Model 1.

0,000

1,000

2,000

3,000

4,000

5,000

6,000

7,000

8,000

9,000

0 200 400 600 800 1000 1200

Design of Cradle as a Tool for Inserting Shaft in New Shipbuilding Using Finite Element Methods

385

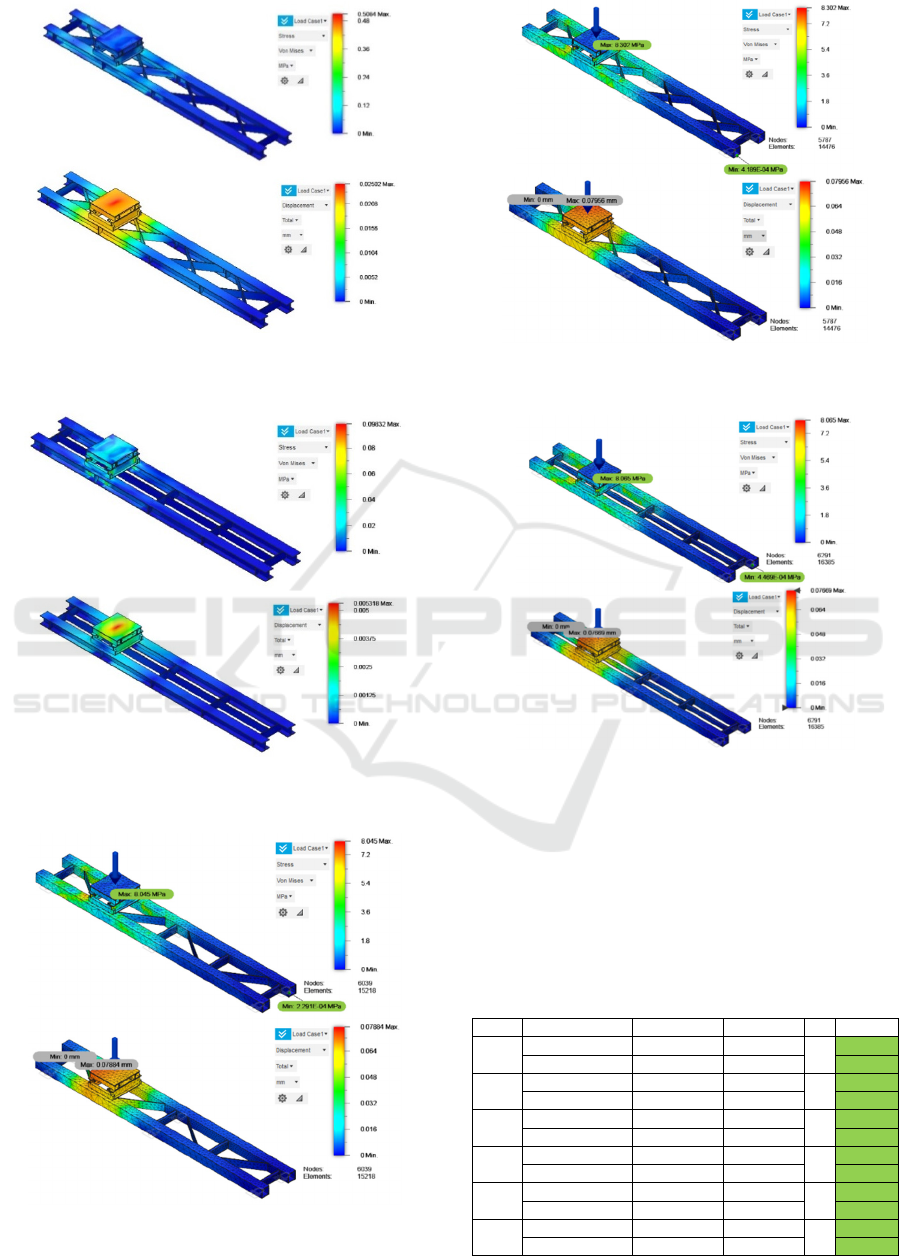
Figure 11: (a) Stress Result of Model 2; (b) Displacement

Result of Model 2.

Figure 12: (a) Stress Result of Model 3; (b) Displacement

Result of Model 3.

Figure 13: (a) Stress Result of Model 4; (b) Displacement

Result of Model 4.

Figure 14: (a) Stress Result of Model 5; (b) Displacement

Result of Model 5.

Figure 15: (a) Stress Result of Model 6; (b) Displacement

Result of Model 6.

From all simulation results, each stress and

displacement value is obtained, then validation is

carried out with the allowable stress and permit

displacement which have been calculated according

to regulations and the results are obtained in the

following table.

Table 4: Strength analysis results.

Model Type of Analysis Maximum Allowable SF Status

Stress 0.526 N/mm

110 N/mm

Allowed

Displacement 0.026 mm 1.586 mm Allowed

Stress 0.508 N/mm

110 N/mm

Allowed

Displacement 0.025 mm 1.586 mm Allowed

Stress 0.098 N/mm

110 N/mm

Allowed

Displacement 0.005 mm 1.586 mm Allowed

Stress 8.045 N/mm

110 N/mm

Allowed

Displacement 0.079 mm 1.586 mm Allowed

Stress 8.302 N/mm

110 N/mm

Allowed

Displacement 0.080 mm 1.586 mm Allowed

Stress 8.065 N/mm

110 N/mm

Allowed

Displacement 0.077 mm 1.586 mm Allowed

iCAST-ES 2022 - International Conference on Applied Science and Technology on Engineering Science

386

5 CONCLUSIONS

The cradle is designed with ASTM 36 Steel material

with 6 different models, where in the analysis results

the six models are in the conditions allowed by

regulation. of the six models, model 3 has a relatively

lower stress value than all models with a value of

0.098 N/mm

and also has a relatively lower

displacement value than all models with a value of

0.005 mm. So that model 3 has a tendency to be used

as a reference model in making the cradle because it

has a higher strength than all the models made.

The 3rd concept cradle is made in the form of a

girder I shape. This concept shoes sled is given a

reinforcement construction with a square box pattern

made of 12 mm thick plate and for the middle

reinforcement made of 10mm thick plate, both of

which have been adjusted to the position of the welder

during welding.

ACKNOWLEDGEMENTS

The author is grateful to the lecturers colleague of the

Shipbuilding Institute of Polytechnic Surabaya for all

the knowledge sharing, especially in the design and

analysis of finite elements to carry out this research

work.

REFERENCES

Asmara, I Putu Sindhu, and Budianto. (2016). "Analisa

Kekuatan Deck Crane pada Kapal Tol Laut Nusantara."

Seminar Nasional Maritim, Sains, dan Teknologi

Terapan 29-34.

Asroni, A. (2017). Teori dan Desain Balok Plat Beton

Bertulang Berdasarkan SNI 2847-2013. Surakarta:

Muhammadiyah University Press.

Budianto. (2015). “Analisis Kekuatan Struktur pada Kapal

Wisata Sungai Kalimas.” Kapal 8-18.

Budianto. (2018). "Strength Structure Analysis of Main

Gate Graving Dock Using." Makara J. Technol 109-

114.

Carvill, James. (1993). Mechanical Engineer's Data

Handbook. Oxford: Elsevier Science Ltd.

Hariandja, Binsar. (1996). Analisis Lanjut Sistem Struktur

Berbentuk Rangka. Jakarta: Penerbit Erlangga.

Logan, DL. (2005). A First Course in The Finite Element

Method. Platteville: University of of Wisconsin.

McCreary, D. R., & Amacker, E. (2006). Experimental

Research on College Students' Usage of Two

Dictionaries: A Comparison of the Merriam-Webster

Collegiate Dictionary and the Macmillan English

Dictionary for Advanced Learners, 871-885.

Dictionary, M. W. (2006). The Merriam-Webster

Dictionary. Merriam-Webster, Incorporated.

Priambodo, G. (2011). Technical and social impacts of

wastewater from fish processing industry in Kota

Muncar of Indonesia. Journal of Applied Technology in

Environmental Sanitation, 1(1), 1-7.

MacDonald, M. P., Paterson, L., Volke-Sepulveda, K., Arlt,

J., Sibbett, W., & Dholakia, K. (2002). Creation and

manipulation of three-dimensional optically trapped

structures. Science, 296(5570), 1101-1103.

Restrepo, L., Wityk, R. J., Grega, M. A., Borowicz Jr, L.,

Barker, P. B., Jacobs, M. A., ... & McKhann, G. M.

(2002). Diffusion-and perfusion-weighted magnetic

resonance imaging of the brain before and after

coronary artery bypass grafting surgery. Stroke, 33(12),

2909-2915.

Widiyanto, A. (2013). Agroforestry dan peranannya dalam

mempertahankan fungsi hidrologi dan konservasi. Al-

Basia, 9, 55-68.

Naruto, H., & Togo, H. (2019). Preparation of 2-

arylquinolines from β-arylpropionitriles with

aryllithiums and NIS through iminyl radical-mediated

cyclization. Organic & Biomolecular Chemistry,

17(23), 5760-5770.

Morna, A. (2012). Research on contribution of agriculture

to economic growth of the North-West region. Analele

Universității din Oradea, Fascicula: Protecția

Mediului, 19, 129-132.

Design of Cradle as a Tool for Inserting Shaft in New Shipbuilding Using Finite Element Methods

387