Fuzzy Information Based Vehicle Routing Problem with Improved

Hybrid Intelligent Algorithm

Junjie Shen

Wuhan Industrial Holding Group Industrial Technology Research Institute Co.,Ltd.,

No. 26, Jiangda Road, Jiang-an District, Wuhan, China

Keywords: Fuzzy Information Vehicle Routing Problem, Hybrid Intelligent Genetic Algorithms, Roulette Heuristic

Algorithm.

Abstract: Vehicle routing problem is one of the most popular supply chain management problems, which are at the

heart of most decision support systems for real-life distribution problems. The traditional vehicle routing

problem (VRP) is often constrained to some specific terms. But in actual situations, the procedure of the travel

is full of uncertain elements (i.e. traffic jams et al.). In this paper, an improved hybrid intelligent genetic

algorithm is designed to solve fuzzy information constrained VRP. The roulette heuristic algorithm is adopted

to create the initial chromosomes with great efficiency. A numerical experiment is presented at the end of this

paper to show the efficiency and effectiveness of the hybrid intelligent genetic algorithm under the given

condition. Some critical parameters of this algorithm are discussed and some suggestions are proposed in the

paper to guide the use of this model in practice.

1 INTRODUCTION

With the development of modern manufacturing

technology, engineers and researchers begin to

improve all technologies to increase efficiency and

qualities of the manufacturing process. As an

important part of this procedure, vehicle routing

problem (VRP) plays a crucial role in it. VRP was

proposed by Dantzing G, Ramser J in 1959 firstly

(G.B.Dantzig et al., 1959). The traditional methods

pay attention to the specific information (include the

workstation information, travel time information and

so on), this cannot describe the real problem

precisely. After that the Stochastic demands and

stochastic travel times were considered to simulate

the case, F.Tillman proposed a model which has

several depots (F. Tillman, 1969). These problems are

called stochastic vehicle routing problems (SVRP).

Stewart andGolden contributed to the problem too (Jr.

Stewart, W.R. et al., 1983). Teodorovic and Pavkovic

gave many models and algorithms to SVRP models

(D.Teodorovic et al., 1992).

In real situation, we cannot describe the problems

with those random variables either for there are not

enough information for use to analyze. As a result, the

fuzzy variables were adopted to simulate the actual

situation. Teodorovic and Pavkovic used fuzzy

programming to deal with the uncertain parameters

(Teodorovic et al., 1996). In their model, fuzzy

customer’s demands were used to solve VRP problem

with single central depot. All other information

(travel time, cargo capacity et al.) is given certain. Lai

et al, also contributed to this problem by a fuzzy

model with possibility measure (K.K.Lai, B.Liu et al.,

2003). Chen and Gen solve the problem with genetic

algorithm under fuzzy due time to meet the multiple

purposes including minimize the fleet size of

vehicles, maximize the average grade of satisfaction

over customers, minimize the total travel distance and

total waiting time (Chen, R. et al., 1995). Zheng and

Liu depicted the fuzzy information with triangular

fuzzy number to describe the preferences of

customers (Zheng, Y. et al., 2006). Zhang et al

analyze the problem under the fuzzy customer’s

demands (Jianyong, Z. et al., 2004) and fuzzy travel

time (ZHANG Jianyong et al., 2006). Cao et al

discussed the problem with fuzzy customer’s

demands either (Cao Erbao et al., 2007).

All these papers mentioned above discussed about

the one of many elements that affects the whole

process. But as we all know, in the real delivering

process, none of these elements show its influence

respectively. Anyone factor interacts with others. So

researches on the multiple fuzzy variables in VRP are

totally necessary and important.

Shen, J.

Fuzzy Information Based Vehicle Routing Problem with Improved Hybrid Intelligent Algorithm.

DOI: 10.5220/0011820300003612

In Proceedings of the 3rd International Symposium on Automation, Information and Computing (ISAIC 2022), pages 5-11

ISBN: 978-989-758-622-4; ISSN: 2975-9463

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

2 MAIN FUZZY INFORMATION

2.1 Fuzzy Requirements

Fuzzy requirements mean that each workstation’s

cargo requirements are not certain. In modern

workshop, the products in one workshop often need

to be changed, such as agile manufacturing. In that

case, different products may be manufactured in one

machine to meet the different needs of customers.

That demands the travel vehicle carry different raw

materials to meet the need. After serving the previous

stations, the vehicle needs to find out whether it has

the ability to serve the next station. The

is the

cargo demand of

workstation.

2.2 Fuzzy Travel Time

When the vehicle is on the way to the next station,

there are plenty of uncertain elements (such as traffic

jam, the speed of vehicle is not constant and so on)

preventing the cargo to be delivered just on time. As

a result, the fuzzy variables are used to describe the

fuzzy travel time. The

is the distance between the

workstation i and j.

2.3 Fuzzy due Time

The actual reservation time will also be an uncertain

element. The traditional time window use rectangle

frame to depict the tolerance of the workstation. This

cannot describe the preferences of each station. Chen

and Gen (Chen R et al., 1996)brought forward the

tolerance of interval time for workstation as triangular

fuzzy window (TFW). The preferences of

workstation were naturally represented by triangular

fuzzy number (TFN) with respect to the grade of

satisfaction for service time. Two windows are listed

in figure 1. Where

and

is the earliest and latest

tolerance of the workstation which is waiting to be

served. The

means the grade of satisfaction is 1.

The function

()

is used to represent the degree of

satisfaction, which is zero when the arrival time falls

out of [

Figure 1: Contrast of fuzzy time window and traditional

time window.

3 MODEL DESIGNING

In order to describe the problem, some parameters are

introduced to help designing the model. We assume

that,

 Each vehicle has a container with a physical

capacity limitation and the total loading of each

vehicle cannot exceed its capacity.

 A vehicle can only be assigned for only one

route.

 A workstation will be visited by one and only

one vehicle.

 Each vehicle begins at central depot and ends

at it.

For the triangular fuzzy window

ii i

iii

etu

utl





−



≤≤

 −



−



≤≤



−



≥



(1)

Auxiliary decision parameters

－

when workstation i is served by

vehicle k, otherwise 0;

ijk

－

ijk

x =

when vehicle k travels from

workstation i to j, otherwise 0;

Optimal goals

max ( )



)

11 1

min

mnn

ij ijk

ki j

== =



)

ISAIC 2022 - International Symposium on Automation, Information and Computing

() 0,

ut i>∀

(4)

iik k

ay C k

≤∀



(5)

=∀



(6)

ijk ik

yik

=∀



(7)

ijk ik

yik

=∀



(8)

||1,

ijk

≤−∀



(9)

01,,,

ijk

or i j k=∀

(10)

01,,

yorik=∀

(11)

ti≥∀

(12)

and

ijk

are auxiliary decision parameters,

is cargo capacity of each vehicle. Objective (2)

maximize the credibility of satisfaction over each

workstation. Objective (3) minimize total travel cost

of all vehicles. Constraint (4) ensures that each

desired time is within the tolerable interval of time.

Constraint (5) ensures each vehicle is assigned to

serve the workstation without exceeding its freight

restriction. Constraint (6) ensures that each

workstation is served by one and only one vehicle.

Constraints (7) and (8) ensures that each station

connect to only one station traveled to itself and only

one it will travel to, that means each station has two

neighbor stations. Constraint (9) show the

relationship between vehicles and workstations for

each journey of each vehicle, that means each vehicle

should start from central depot and end at this depot

after finishing the journey. (10), (11) and (12) is

auxiliary decision parameters constraint.

4 INTELLIGENT ALGORITHM

DESIGNING

Hybrid intelligent algorithm was a kind of intelligent

algorithm which was proposed by Baoding Liu (Liu

Baoding et al., 2003)in 2003 for solving the problems

under uncertain condition (including random and

fuzzy). The main idea of this algorithm is to express

uncertain information by using the characteristics of

neural network and to search the approximate optimal

solution by genetic algorithm (GA). Because the main

function of optimization is GA, how to design GA

directly affects the efficiency and precision of this

algorithm.

4.1 Representation of Genetic

Chromosomes

Assume workstations encoding in natural number

from 1 to n, as a result, the chromosomes are designed

as natural denote.

0, ...... ,0, ,...... , 0,......,0, ,...... , 0

jkm n s t

iii i i i

one of the chromosome means that there are k

vehicles in total, which carry the raw material. The

symbol 0 represents the central depot,

is the

workstation that the specific vehicle serves.

4.2 RHA Algorithm

In this paper, the roulette heuristic algorithm (RHA)

is adopted to generate the first population for the

genetic algorithm. The steps are listed below:

Step 1:

()

ϕξ

is the membership degree function.

is a credibility number. Workstation demand and

transportation time can be drawn from

()

inf( ) sup( )

αα

ξξξ

∈

. The fuzzy due time window

can be simplified into certain traditional time window

which using

and

as up and down

boundaries and satisfaction degree always equals 1.

Step 2: Select current all workstations at first. If

there isn’t any station satisfying the demands, select

the distribution center as current node. Draw lines

between the select node and other unselected stations.

Erase those incompatible constraint lines. Use

evaluation function which considers the distance as

important weight to give a score to each existing line.

If there is no line remains, this path is arranged over.

Choose another vehicle to arrange again. At this time,

we choose distribution center as current node, repeat

what we have done above.

Step 3: If all remained lines with scores were

available. Roulette selection is used to select the best

line of all. After we getting a line by this method,

delete others and decide the downstream station as the

current node.

Step 4: If all of workstations have been arranged

well, RHA method selection is finished. Otherwise go

to step2 to repeat the loop.

Apparently, we can get one feasible chromosome

after the RHA selection is used once. Repeat that

Fuzzy Information Based Vehicle Routing Problem with Improved Hybrid Intelligent Algorithm

method by n times, the number of n chromosomes can

be created. These chromosomes can be used as initial

population of the genetic algorithm. In this way of

choosing the initial population of the algorithm, we

can easily get some chromosomes that are closer to

the shortest solution that we expect. The result of the

demo can prove that the convergence iterations are

less than ordinary methods.

4.3 Crossover Designing

Because of the specialty of the vehicle routing

problem, traditional method of crossover cannot be

used directly. In this paper, the PMX crossover (Li

Renan et al., 2004) is adopted to solve the VRP

problem.

Assume that A and B is two chromosomes of the

initial population, the PMX choose a part of route

from A randomly, then the part is hand over to its next

generation A1. Find the same route in chromosome

B, and then delete it. Arrange the rest parts of routes

of B to A1. After that, we get a new chromosome of

next generation. Repeat the same procedure to B and

we can get B1 too. Do the procedure by crossover

probability. All chromosomes of next generation are

available.

4.4 Mutation Designing

In this paper, the reverse mutation (Zhang Jing et al.,

2004) is adopted to mutate each chromosome. The

main idea of this method is to reverse the part of the

route of chromosomes. Certainly, this reverse should

ensure that the new chromosome is better than the old

one. Assume L13 represents the length of route

between workstation 1 and 3, so do L28, L34, and

L56. If L13 +L28< L12 +L38, then the exchange of 3

and 2 is valid.

After crossover and mutation, there may be

unreasonable chromosomes. If the there is no central

depot in head and tail position, or there are two

neighborhood depots among the chromosomes,

exchange any non-depot station to central depot

randomly. Then check the feasibility of each

chromosome.

4.5 General Hamming Similarity

Degree

Standard genetic algorithm has two weak characters.

One is local convergence and the other is lower

efficiency in later evolution period. This paper

proposes general hamming similarity degree to

distinguish chromosomes from each other and

establishes double-selection and double-mutation

operations in the evolution period.

This paper proposes general hamming similarity

degree, which refers to the concept of general

hamming distance mentioned by Wang Jie et al

(Wang Jie et al., 2008). The definition is listed below:

Definition 1: Generalized Hamming similarity

is the ratio of the number of the same routes

between two chromosomes i and j to the number of

routes which are less than the other one.

For instance, chromosome 015403206780 and

0320154060780 both concludes the same two routes

01540 and 0320. The first chromosome has the three

routes which are less than the second one. According

to the definition we mentioned before, the

2/3

GL =

. If two different chromosomes have the

same number of routes and all route have the same

contents with each other, like 0123057068940 and

0570123068940, then

GL =

It can be concluded that

GL =

only if the two

chromosomes represent the same solution of the

problem (Li Jinhang et al., 2009).

4.6 Improved Hybrid Intelligent

Algorithm

Improved hybrid intelligent algorithm more efficient

than traditional algorithm for it uses neural network

to train an approximate function to help looking for

the solution of problems, which refers to Baoding Liu

et al. The steps of this algorithm are listed below:

Step 1: Use fuzzy simulation function to create

input and output data for the following uncertain

functions.

{

}

{

}

: ( , ) 0, 1, 2,...,

:min|{(,)}

Ux Posgx j p

Ux fPosfx f

ξβ

→≤=

→≥≥

Step 2: According to the data generated by step 1,

train a neural network to approximate to the uncertain

functions.

Step 3: Create

{

}

inf (α) sup(α)

ξξ,ξ∈

randomly and

use roulette heuristic algorithm to create initial

population. Use the neural network mentioned above

to check the feasibility of each chromosome.

Step 4: Mutate and intersect chromosomes by

genetic algorithm with double-selection and double-

mutation operations. In this process, general

hamming similar degree is used to distinguish similar

genes from each other to avoid inbreeding.

ISAIC 2022 - International Symposium on Automation, Information and Computing

Step 5: Evaluate all chromosomes by neural

network that has been prepared well.

Step 6: Evaluate the fitness of each chromosome

according to their value.

Step 7: Select healthy chromosomes as the next

generation under roulette wheel selection.

Step 8: Do not stop repeating step 4 and step 7

until the ultimate number of loops is reached.

Step 9: Find the best chromosome as the solution

of the problem.

5 APPLICATIONS

Central depot to seven workstations (denote from 1 to

7). Each vehicle has a maximum load of 8 units. The

freight volume of each workstation is listed below in

Table 1. The travel time and cost between

workstations is listed in Table 2 (the travel time is

triangular fuzzy number, and the coefficient matrix is

symmetric). Given that overload is not allowed and

each workstation’s cargo requirements are met, it’s

important and crucial to arrange a vehicle routing

with a lowest total mileage.

Table 1: Reservation time and cargo demand of each workstation.

Position Number 1 2 3 4 5 6 7

Demand [unit] (3,3.5,4) (2.6,3,3.5) (1.8,2,2.1) (2.1,2.5,2.5) (3.6,4,4.1) (3,3.5,4)

(2.6,3,3.4）

Due time[min] (30,40,43) (50,70,80) (90,110,117) (45,50,67) (66,80,100) (85,100,110) (120,150,160)

Table 2: Travel time and mileage between workstations.

Travel-time[s]

Distance[m]

Position Number

0 1 2 3 4 5 6 7

Position

Number

0 0 (30,36,38) (27,31,35) (12,14,20) (5,10,14) (15,20,25) (17,22,30) (26,31,34)

1 17 0 (30,30,30) (21,22,28) (20,28,30) (30,50,65) (50,58,64) (35,41,50)

2 29.22 22.09 0 (24,28,31) (17,22,30) (28,31,34) (40,50,60) (50,56,59)

3 5.83 11.18 32.37 0 (9,10,11) (24,31,41) (30,36,40) (23,27,32)

4 26.4 7.07 18.38 31.18 0 (15,22,29) (29,31,38) (31,36,40)

5 20.25 24.6 13 5 18.03 0 (19,22,28) (45,51,60)

6 5 31.54 6.32 24.44 19.85 19.1 0 (38,41,50)

7 16.76 6 25.06 19 29.43 37 18.87 0

Algorithm parameters are configured as below.

The first selection probability is set to 0.8, second

probability is 0.8, local mutation probability is 0.1,

global mutation probability is 0.2, population size is

40, Hamming similarity degree is not larger than 0.5,

iterations is set to 200. For the fuzzy number’s

credibility, we set reservation time to 0.2, travel time

to 0.8, workstation volume to 0.8.

Program the hybrid intelligent algorithm on PC,

after 31 iterations, the best solution of the problem

was found. The best chromosome is 067014025030.

Decode the chromosome to the VRP problem, we get

the following routes:

Routes 1: central depotworkstation

6workstation 7central depot

Routes 2: central depotworkstation

1workstation 4 central depot

Routes 3: central depotworkstation

2workstation 5 central depot

Routes 4: central depotworkstation 3central

depot

The total distance is 165.23.

Traditional genetic algorithm is also used to solve

the problem for comparison. Initial population size is

set to 40, selection probability is set to 0.8, crossover

probability is set to 0.8, and mutation probability is

set to 0.1. For the selection of fuzzy number’s

credibility, we set reservation time to 0.2, travel time

to 0.8, and workstation volume to 0.8. This algorithm

converges to the same result as the hybrid intelligent

algorithm after 170 iterations.

Fuzzy Information Based Vehicle Routing Problem with Improved Hybrid Intelligent Algorithm

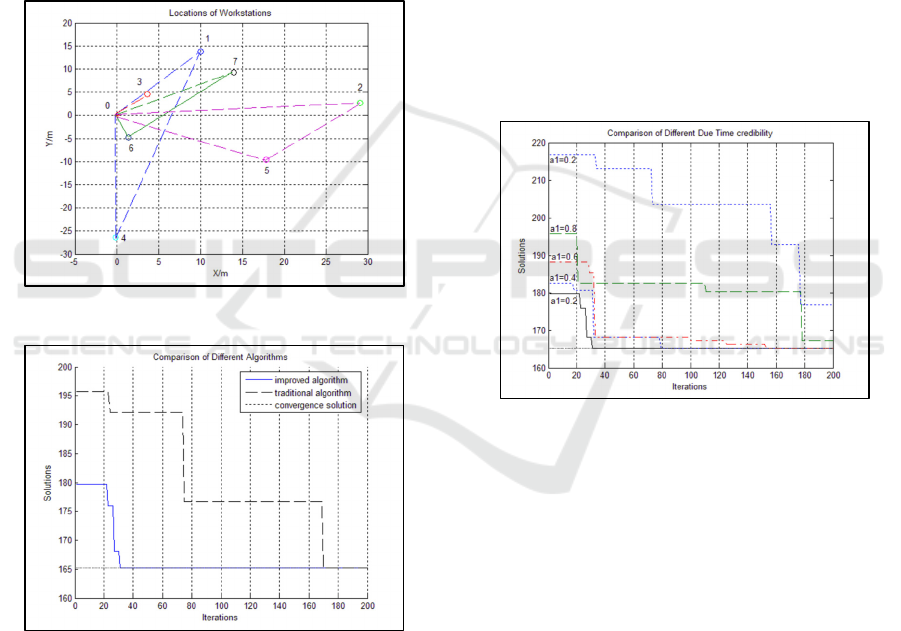
In order to test and verify the solution of the

problem, the same problem was programmed on

MATLAB 7.0. The problem was solved by genetic

algorithm tool and neural network tool in MATLAB,

we got the same solution showed in figure 2. In figure

3, we find that the hybrid intelligent algorithm used

in this paper got the best solution after 31 iterations,

the traditional genetic algorithm found the same

solution after 170 iterations. Besides that, the hybrid

intelligent algorithm created a better chromosome

which is 179.71, approaching the final solution which

is 165.23. Because the traditional genetic algorithm

creates the first population randomly, the best

solution of the traditional algorithm is 195.71, which

is larger than 179.71.

Figure 2: Result of MATLAB simulation.

Figure 3: Comparison of different algorithms.

In this case, it can be concluded that the improved

hybrid intelligent algorithm is more efficient than the

traditional algorithm on the fuzzy VRP problem, and

the convergence speed of improved algorithm is

faster too.

6 RESULTS ANALYSIS AND

CONCLUSIONS

In this model, there are three important fuzzy

variables: credibility of fuzzy reservation time

credibility of fuzzy travel time𝛼



, and credibility of

fuzzy cargo requirements 𝛼



. In the following part,

the selection of these variables will be introduced.

The parameters are listed bellow: population size

is set to 40, the first and second selection probability

are set to 0.8, both crossover probabilities are set to

0.8, local mutation probability is 0.1, global mutation

probability is 0.2, Hamming similarity degree is not

larger than 0.5, iterations is set to 200. The credibility

of fuzzy travel time 𝛼



is set to 0.8, the fuzzy cargo

requirements 𝛼



𝛼



is set to 0.8. The credibility of

fuzzy reservation time 𝛼



is set to 0.2, 0.4, 0.6, 0.8,

and 1.0 separately. The solution of the problem is

showed in figure 4.

Figure 4: Comparison of different credibility of fuzzy due

time.

As it’s shown in figure 4, the value of credibility

of fuzzy reservation time plays a significant part in

the algorithm. Different values lead to different

results. It can influence the best solution of first

population and the convergence speed of the

algorithm. The larger 𝛼



means workstations ask

vehicles to deliver the goods in need much stricter. In

other words, the larger credibility of fuzzy reservation

time is, more narrower time window is. As a result,

there are less feasibility solutions satisfying the

requirements of workstations.

When the credibility is larger than 0.8, the

algorithm converged to different solutions rather than

the best solution we got. That means the vehicles can

only satisfy the reservation time requirements whose

credibility is smaller than 0.8.

Credibility of Fuzzy Travel time 𝛼



and Cargo

Requirements 𝛼



ISAIC 2022 - International Symposium on Automation, Information and Computing

Set population size to 40, the first and second

selection probability are set to 0.8, both crossover

probabilities are set to 0.8, local mutation probability

is 0.1, global mutation probability is 0.2, Hamming

similarity degree is not larger than 0.5, iterations is set

to 200. The credibility of fuzzy due time 𝛼



is set to

0.8, the fuzzy cargo requirements 𝛼



is set to 0.8. The

credibility of fuzzy travel time 𝛼



is set to 0.2, 0.4,

0.6, 0.8, and 1.0 separately. Then set the credibility of

fuzzy travel time 𝛼



to 0.8, the credibility of fuzzy

cargo requirements 𝛼



to 0.2, 0.4, 0.6, 0.8, and 1.0

separately. The results are listed in table 3.

Table 3: Comparison of results under different 𝛼



and 𝛼



Credibility value

Initial

solution

Convergence

generation

Optimal

solution

α0.2

α0.8







＝

0.2 179.71 180 165.23

0.4 179.71 153 165.23

0.6 182.6 98 165.23

0.8 184.4 38 165.23

1 195.71 42 165.23

α0.2

α0.8







＝

0.2 182.6 165 165.23

0.4 195.71 123 165.23

0.6 191.2 80 165.23

0.8 194.85 39 165.23

1 195.71 41 165.23

As the table shown, different values of credibility

of fuzzy travel time and fuzzy cargo requirements

have less influence on the solution of the VRP

problem. The larger these two variables are, the more

constant travel time and cargo requirements are. It

leads to faster convergence of the algorithm.

The result shows that different variables play

different roles in the algorithm. The changes of these

variables can lead to different results. If we want to

increase the grades of satisfaction, we should increase

the credibility of fuzzy reservation time 𝛼



. If the

traffic condition and workstation’s demands are more

stable, values of 𝛼



and 𝛼



should be increased in

order to speed up the convergence.

The fuzzy vehicle routing problem has several

kinds of fuzzy information. Those uncertainties make

the problem more complex and difficult to be solved.

The improved hybrid intelligent algorithm shows its

advantages over the traditional genetic algorithm.

This can be used to associate decision makers to solve

these problems more efficiently.

REFERENCES

Chen, R. and M. Gen, 1995. vehicle routing problem with

fuzzy due time using genetic algorithm, Japanese

Journal of Fuzzy Theory and Systems, 7(5), 1050-1061.

Cao Erbao, Lai Mingyong and Zhang Hanjiang, 2007. On

the Routing Problems of Vehicle with Fuzzy Demands,

Systems Engineering, 25(11).

Chen R, and Gen. M, 1996. Fuzzy vehicle routing and

scheduling problem using genetic algorithms. Japan

Journal of Fuzzy Theory System, 1996, 683-709.

D.Teodorovic and G.Pavkovic, 1992. A simulated

annealing technique approach to the vehicle routing

problem in the case of the stochastic, Transportation

Planning and Technology 16 261–273.

F. Tillman, 1969. The multiple terminal delivery problem

with probabilistic demands, Transportation Science 3

192–204.

G.B.Dantzig and J.H.Ramser, 1959. “The truck dispatching

problem”, Management Science, 6 80–91.

Jr. Stewart, W.R. and B.L. Golden, 1983. Stochastic vehicle

routing: A comprehensive approach, European Journal

of Operational Research, 14(4), 371-385.

Jianyong, Z., G. Yao-huang and L. Jun, 2004. Research of

vehicle routing problem under condition of fuzzy

demand, Journal of Systems Engineering, 1.

K.K.Lai, B.Liu and J.Peng, 2003. Vehicle routing problem

with fuzzy travel times and its genetic algorithm,

Technical Report.

Liu Baoding et al 2003. Uncertain programming with

applications, Tsinghua University Press, 8p.

Li Renan and Yuan Jijun, 2004. Research on the

Optimization of Logistics Distribution Routing Based

on Improved Genetic Algorithm, Journal of Wuhan

University of Technology, 12, 99-101.

Li Jinhang, Huang Gang and Jia yan, 2009. Vehicle routing

problem in material distribution under condition of

much fuzzy information, Chinese Journal of

Mechanical Engineering.

Teodorovic and Pavkovic, 1996. The fuzzy set theory

approach to the vehicle routing problem when demand

at nodes is uncertain. Fuzzy Sets and System, 82, 307-

317.

Wang Jie, Ma Yan and Wang Fei, 2008. Study of improved

genetic algorithm based on dual mutation and its

simulation, Computer Engineering and Applications,

44(3), 57-59.

Zheng, Y. and B. Liu, 2006. Fuzzy vehicle routing model

with credibility measure and its hybrid intelligent

algorithm, Applied Mathematics and Computation,

176(2), 673-683.

ZHANG Jianyong and LI Jun, 2006. A Hybrid Genetic

Algorithm to the Vehicle Routing Problem with Fuzzy

Traveling Time, Journal of Industrial

Engineering/Engineering Management, 20(4).

Zhang Jing and Zhou Quan, 2004. Study on the

Optimization of Logistics Distribution VRP Based on

Immune Clone Algorithm, Journal of Hunan University

(Natural Sciences), 31(5), 54-58.

Fuzzy Information Based Vehicle Routing Problem with Improved Hybrid Intelligent Algorithm