Discharge Coefficient Analysis for Sluice Gates Set in Weirs

Agostino Lauria

, Antonino D’Ippolito

, Francesco Calomino

and Giancarlo Alfonsi

Department of Civil Engineering, Università della Calabria, Rende (CS), Italy

Keywords: Sluice Gates, Weir, Discharge Coefficients, Channel Inlet, CFD, RANS.

Abstract: Experimental tests and computational tests were performed to analyse discharge coefficients when gates are

placed into weir walls. Gate slope and side contraction effect have been considered. A great number of

experiments were conducted by considering three angles of inclination of the weir, three shape ratio and three

values of the relative opening. Two mathematical equations were obtained, relating the discharge coefficient

to the parameters that characterize the phenomenon. Furthermore, computational tests were performed

following the Reynolds-Averaged Navier-Stokes (RANS) approach in conjunction with a turbulence closure

model. In order to track the fluid surface, the Volume of Fluid algorithm being used. Numerical results have

been validated against the experimental showing a good agreement. The validated numerical fluid flow can

help to better understand the phenomenon not caught by the experiments.

1 INTRODUCTION

Sluice gates are efficient devices for flood control

purposes and active defence against flooding. Despite

sluice gates devices are commonly used, the

hydraulic phenomena that occur their operation are

not yet clear enough. Overall, the previous studies on

sluice gates are not focused on the lateral contraction

that can play a key role. By analysing the literature

some experimental papers are present about sloping

and vertical sluice gates (Montes, 1997, Sinniger and

Hager, 1988). In the case of sluice gates forming an

angle smaller than 90° with the horizontal plane, the

discharge coefficient, C

, decreased as the angle

increased (Sinniger and Hager, 1988). The discharge

coefficient decreases as the angle increases when this

one is less than or equal to 90° (Gentilini, 1941).

Other experimental works shows how the values of

against the relative opening range between 0.64

and 0.48 and decrease with the relative gate opening

(Roth and Hager, 1999, Rajaratnam, 1967). The

authors carried out one of the most complete studies

on the topic, by means of tests on a rectangular flume

and scale effect analysis. The authors showed the

presence of a ridge upstream to the gate, moreover,

https://orcid.org/0000-0003-4608-3684

https://orcid.org/0000-0003-3265-2196

https://orcid.org/0000-0002-6103-180X

https://orcid.org/0000-0001-5510-6708

they observed a recirculation zone upstream to the

gate, affecting the contraction of the vein, and two

oblique stationary waves at the channel inlet. In the

numerical field, many researchers reported a state-of-

art review on the potential flow theory-based model,

where the problem is described by a two-dimensional,

irrotational, inviscid flow (Fangmeier and Strelkofff

1968, Larock 1969, Belaud and Litrico 2008). Some

researchers carried out numerical simulations to study

, the distribution of the flow pressure and the flow

contraction past a sluice gate (Kim, 2007, Akoz,

2010). Recently the Volume of Fluid (VoF) algorithm

(Hirt et al., 1981), coupled with the Reynolds-

Averaged Navier-Stokes equations, were used in

several simulations of sluice gate flow (Cassan and

Belaud, 2012, Lauria et al. 2020). Phenomena

occurring during the underflow of sluice gates placed

in weirs are not properly investigated. In this work,

the phenomenon of the side contraction and gate

slope, that should affect the results in terms of C

have been considered.

Lauria, A., Dâ

ZIppolito, A., Calomino, F. and Alfonsi, G.

Discharge Coefﬁcient Analysis for Sluice Gates Set in Weirs.

DOI: 10.5220/0011884900003536

In Proceedings of the 3rd International Symposium on Water, Ecology and Environment (ISWEE 2022), pages 11-14

ISBN: 978-989-758-639-2; ISSN: 2975-9439

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

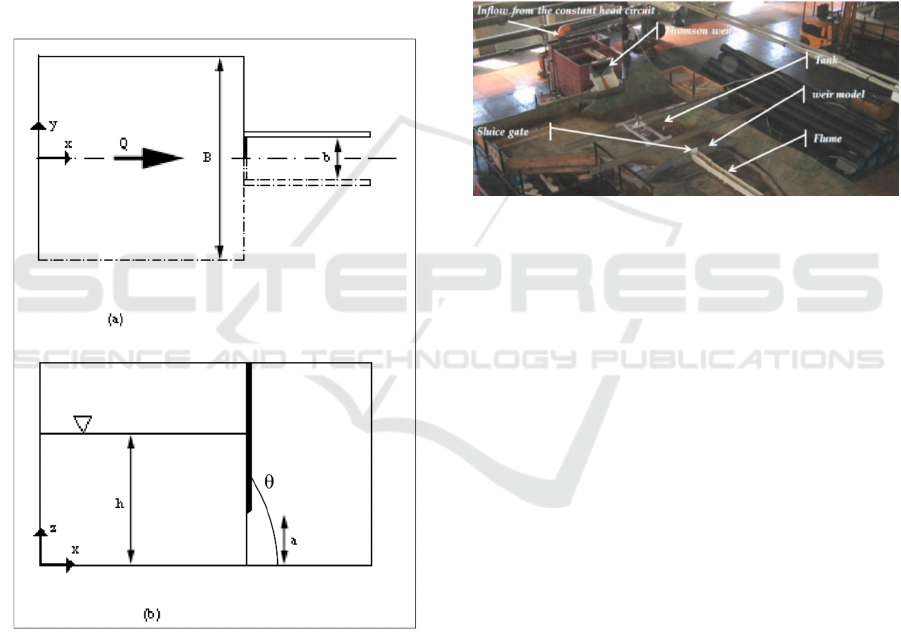
2 MATERIALS AND METHODS

By considering the definition sketch (Figure 1), the

discharge Q can be expressed as a function of ϴ, a, b,

h, g (gravity), ρ (water density), ν (kinematic

viscosity) and σ (surface tension):

F (Q, a, b, h, ϴ, g, ρ, ν, σ) = 0 (1)

After assuming Q=C

ab(2gh)^0,5, and by selecting,

a, g and ρ as basic variables, by applying the Π

theorem and by following the procedure reported in

Lauria et al. (2020), one has:

= (a/h, b/a, ϴ) (2)

Figure 1: Definition sketch: (a) up and (b) lateral view.

2.1 Experimental Tests

Experimental campaigns were conducted in a

physical model representing a structural device for

flood control purposes (see Figure 2). In the model

the weir is located into the riverbed causing a

backwater effect, and consequently the storage of a

flood volume in the upstream area (Lauria et al.,

2020). The dimensions of the rectangular tank were

120 cm along the span-wise, 400 cm along the

stream-wise, and 25 cm along the stream-normal

direction. The weir physical model, 18 cm high and

120 cm wide, was placed at its downstream end.

Vertical planes have been used to divide the weir in

two parts and therefore create an orifice of dimension

b (Lauria et al., 2020). A rectangular channel of width

b was placed downstream of the gate opening (see

Figure 1). Different values b = 8,6, 10,6 and 14,2 cm

(gate widths) has been considered. Experiments were

conducted with different values of a (gate opening)

and at different values of ϴ = 0,78, 1,11 and 1,57 rad

(weir inclination) and at different values (see Table 1

in Lauria et al. 2020).

Figure 2: Downstream view of the physical model

The flow from the laboratory circuit fed the tank and

the discharge values were collected by means of an

ultrasonic flowmeter and by means of a Thomson

weir (Figure 2). During experimental tests, the water

level was measured by means of a pressure transducer

and by means of an electric point gauge. The pressure

measurements were obtained by means of a dedicated

system able to get data in 12 different points of the

tank (Lauria et al., 2020).

2.2 Numerical Simulations

To extending the investigation field computational

tests were performed by solving the system of the

three‐dimensional Reynolds‐averaged Navier-Stokes

(RANS) equations, not reported here for brevity. A

two – equation (Wilcox, 1998) turbulence closure

model has been used. Reynolds stresses and the mean

flow field has been related by means of the k- ε model

(Launder and Spalding, 1974). For the execution of

the 27 tests chosen for the calculations (see Table 3 in

Lauria et al., 2008), the Flow‐3D

software has been

used. The model equations, together with the

turbulence model equations, are discretized with the

finite-volume method (FVM). As for the

discretization of the solution domain, a structured

mesh has been built, where the dependent variables

are stored at the centre of each cell space domain in a

ISWEE 2022 - International Symposium on Water, Ecology and Environment

co-located arrangement. To describe the free-surface

behaviour the Volume of Fluid (VoF) method (Hirt,

1975) has been used. The algorithm has been used by

other authors, always giving satisfactory results (see

Alfonsi et al., 2012, 2013, 2015 and D’Ippolito et al.,

(2019)). The computational domain was composed by

a three-dimensional geometry 49,6 cm along the

streamwise direction and 40,0 cm along the spanwise

direction and a rectangular one 30,0 cm along the

stream-normal direction. The computing space

dimensions spans respectively 79,6 cm along the

streamwise 40,0 cm along the spanwise, and 30,0 cm

along the stream-normal directions. The

computational mesh was refined increasing points in

all the directions. The considered mesh configuration

was composed of about 1,9 million cells. Wall

boundary condition was imposed at the bottom plane

and at the model geometry. Symmetry boundary

condition was imposed at the geometric symmetry

plane and outflow conditions had been set on the y–z

end‐plane of the computing domain. On the inflow

section, the experimentally measured fluid depth has

been set. As initial condition, experimentally

measured fluid depth was set in the area of domain

localized upstream of the gate. A multi-core

computational system has been used for the

computational runs (Alfonsi et al., 2012).

3 RESULTS AND DISCUSSION

Table 1 provides information about the experimental

data, where different inclinations (ϴ) of the weir

equal to 0,78 rad, 1,11 rad, and 1,57 rad, of the

channel widths b = 8,6, 10,6 and 14,2 cm, and of the

gate opening a = 5,0, 6,0 and 7,0 cm, were

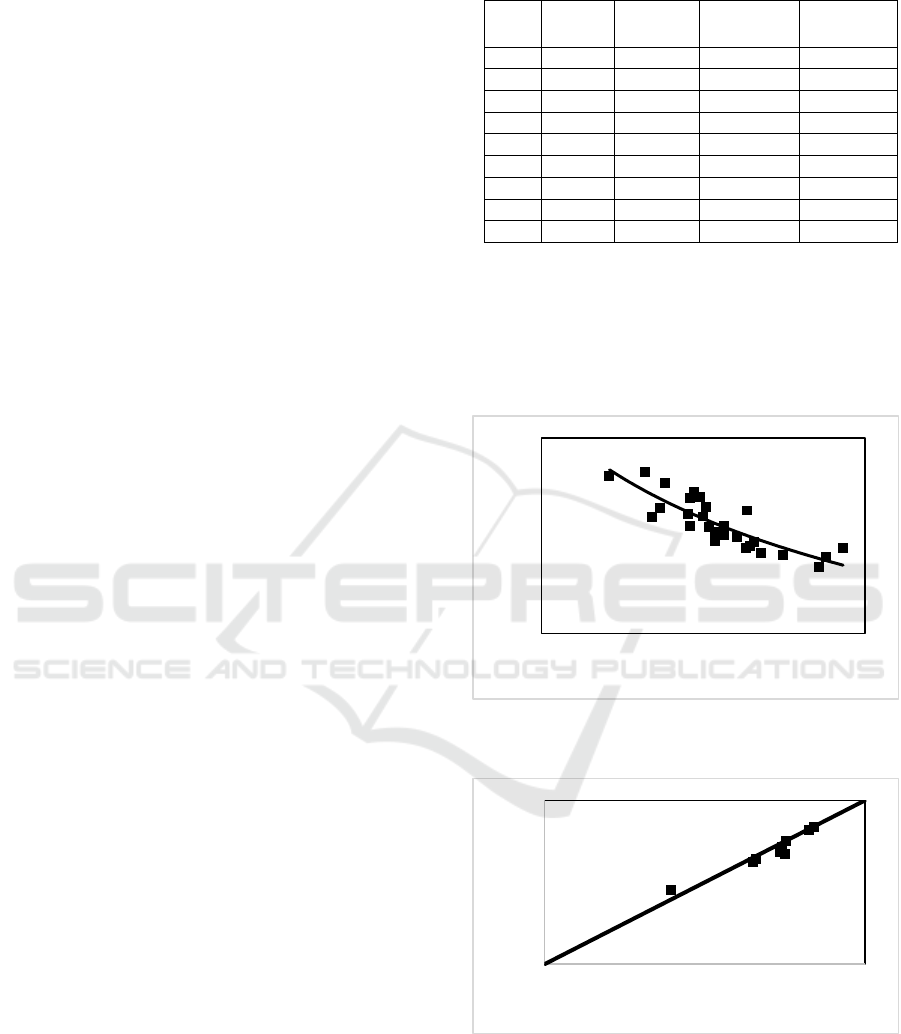
considered. The values of discharge coefficients as a

function of a/h (relative opening) for the angle ϴ =

0,78, 1,11 and 1,57 rad (weir inclination), for b/a =

1,23 and 2,84 (aspect ratio) and taking into account

only the openings a ≥ 50 mm, are shown in Figure 3.

After identifying the value of the gate opening above

which the role of viscosity is negligible a regression

analysis was carried out using all the experimental

data, and the following equation was obtained:

= 0,388 * (a/h)

-0,30

0,06

(3)

valid in the range 0,29 ≤ a/h ≤ 0,59, 1,23 ≤ b/a ≤ 2,84

and 0,78 ≤ ϴ ≤ 1,57 (in rad), with determination

coefficient R

= 0,97.

Table 1: Laboratory tests.

(°)

(mm)

b (mm) h (mm) Q (l/s)

45 50 86 - 142 109 - 125 3,4 -5,2

45 60 86 - 142 136 - 144 4,2- 7,2

45 70 86 - 142 125 - 145 4,8

–

7,4

63,4 50 86 - 142 131 - 149 3,6

–

6,3

63,4 60 86 - 142 145 - 156 4,3

–

7,6

63,4 70 86 - 142 129 - 153 5,1

–

7,4

90 50 86 - 142 142 - 176 4,2

–

7,4

90 60 86 - 142 149 - 152 4,8

–

7,7

90 70 86 - 142 122 - 180 4,9

–

7,6

Figure 4 shows the comparison between the

numerical values of the computed discharge

coefficients versus the observed ones, valid in the

range 0,29 ≤ a/h ≤ 0,59, 1,23 ≤ b/a ≤ 2,84, for ϴ = 90°

, and the results show a very good agreement. The

validated numerical tool can help to investigate

deeply the phenomena.

Figure 3: Experimental values of C

versus a/h and

regression line.

Figure 4: Numerically computed vs observed discharge

coefficients for the case ϴ = 90°.

Considering the case ϴ = 45°, figure 5 shows the

numerically computed discharge coefficients versus

a/h. A regression analysis was carried out using the

0,4

0,45

0,5

0,55

0,6

0,2 0,3 0,4 0,5 0,6

a/h

0,4

0,5

0,6

0,4 0,5 0,6

(observed)

(computed)

Discharge Coefﬁcient Analysis for Sluice Gates Set in Weirs

numerical results, and the following equation was

obtained:

= 0,370 * (a/h)

-0,356

(4)

valid in the range 0,20 ≤ a/h ≤ 1,00, 1,23 ≤ b/a ≤ 2,84

and for ϴ = 45°, with determination coefficient R

0,97.

Figure 5: Numerical values of C

versus a/h (ϴ = 45°).

4 CONCLUSIONS

Experimental tests and computational tests were

performed to analyse discharge coefficients when

gates are placed into weir walls. Gate slope and side

contraction effect have been considered. Two

mathematical equations have been obtained, relating

the discharge coefficient to the parameters that

characterize the phenomenon. The first one (equation

(3)), was valid in the range 0,29 ≤ a/h ≤ 0,59, 1,23 ≤

b/a ≤ 2,84 and 0,78 ≤ ϴ ≤ 1,57 (with ϴ in rad). The

second expression (equation (4)) is valid in a more

extended range (0,20 ≤ a/h ≤ 1,00, 1,23 ≤ b/a ≤ 2,84)

and for ϴ = 45°. The proposed results and the

validated numerical model, obtained by following a

RANS approach, can help to better understand the

phenomenon not caught by the experimental tests.

REFERENCES

Montes, R., (1997). Irrotational flow and real fluid effects

under planar sluice gates. J. Hydraul. Eng. 123, 219-

232.

Sinniger, R., Hager, W.H. (1988). Constructions

Hydrauliques. Ecoulements Stationnaires; Presses

Polytechniques Romandes; Traité de Génie Civil de

l’Ecole polytechniques fédérale de Lausanne:

Lausanne, Switzerland, Volume 15.

Gentilini, B. (1941). Efflusso dalle luci soggiacenti alle

paratoie piane inclinate e a settore. L’Energia Elettrica,

18, 361–380.

Roth, A., Hager, W.H. (1999). Underflow of standard sluice

gate. Exp. Fluids, 27, 339–350.

Rajaratnam, N. (1977). Free flow immediately below sluice

gates. J. Hydraul. Div. ASCE, 103, 345–351.

Fangmeier D., Strelkoff T. (1968) Solution for gravity flow

under a sluice gate. J. Engrg. Mech. Div. 94(EM1),

153–176.

Larock B. (1969). Gravity-affected flow sluice gate. J.

Hydr. Div. 95(HY4), 153–176.

Belaud G., Litrico X. (2008). Closed-form solution of the

potential flow in a contracted flume. Journal of Fluid

Mechanics 599, 299–307.

Kim D.G. (2007). Numerical analysis of free flow past a

sluice gate. KSCE Journal of Civil Engineering 11,

127–132.

Akoz M.S., Kirkgoz M.S., Oner A.A. (2010). Experimental

and numerical modelling of a sluice gate flow. Journal

of Hydraulic Research 47(2), 167–176.

Hirt, C.W., Nichols, B.D. (1981). Volume of fluid (VOF)

method for the dynamics of free boundaries. J. Comput.

Phys., 39, 201–225.

Cassan L., Belaud G. (2012). Experimental and numerical

investigation of flow under sluice gates. Journal of

Hydraulic Engineering 138(4), 367–373.

Lauria, A., Calomino, F., Alfonsi, G., D’Ippolito, A.

(2020). Discharge coefficients for sluice gates set in

weirs at different upstream wall inclinations. Water

2020, 12, 245.

Wilcox, D.C. (1998). Turbulence modelling for CFD;

DCW Industries: La Cañada, CA, USA.

Launder, B.E., Spalding, D.B. (1974). The numerical

computation of turbulent flows. Comput. Methods

Appl. Mech. Eng., 3, 269–289.

Alfonsi, G., Lauria, A., Primavera, L. (2012). Flow

structures around a large-diameter circular cylinder. J.

Flow Visual. Image Process., 19(1), 15–35.

Alfonsi, G., Lauria, A., Primavera, L. (2013). On evaluation

of wave forces and runups on cylindrical obstacles. J.

Flow Visual. Image Process., 20, 269–291

Alfonsi, G., Lauria, A., Primavera, L. (2015). The field of

flow structures generated by a wave of viscous fluid

around vertical circular cylinder piercing the free

surface. Procedia Eng., 116, 103–110.

D’Ippolito, A., Lauria, A., Alfonsi, G., Calomino, F. (2019)

Investigation of flow resistance exerted by rigid

emergent vegetation in open channel. Acta Geophys.,

67, 971–986.

Alfonsi, G., Lauria, A., Primavera, L. (2012). A study of the

vortical structures past the lower portion of the Ahmed

car model. J. Flow Visual. Image Process., 19, 81–95.

0,2

0,3

0,4

0,5

0,6

0,7

0,1 0,6 1,1

a/h

ISWEE 2022 - International Symposium on Water, Ecology and Environment