Robust Optimization for Climatological Emergency Evacuation

Yasmany Fernández-Fernández

, Sira M. Allende-Alonso

, Ridelio Miranda-Pérez

Gemayqzel Bouza-Allende

and Elia N. Cabrera-Alvarez

Department of Computing, Universidad Politécnica Estatal del Carchi, Tulcán, Ecuador

Department of Mathematics-Computation, Universidad de La Habana, La Habana, Cuba

Department of Economical Sciences, Universidad de Cienfuegos, Cienfuegos, Cuba

gema@matcom.uh.cu, elita@ucf.edu.cu

Keywords: Emergency, Robustness, Uncertainty, Scenarios.

Abstract: Natural disasters are very common nowadays. Therefore, human lives are lost, and economical resources are

destroyed, so, it is important to plan actions to mitigate these unwanted effects. The uncertainty associated to

these phenomena is large. The solution shall somehow be robust, for instance the value of the losses shall be

relatively small for a sufficient large set of possible cases. This contribution will provide an overview on the

scenarios based robust mathematical model for the treatment of climatological emergencies models to assist

in the task of decision making for natural disasters with emphasis on evacuation work.

1 INTRODUCTION

Mathematical modelling of complex logistics

systems in the context of climatological emergencies

management is currently an difficult problem because

the uncertainty inherent to data received from an

emergency. (Behl and Dutta 2019; Beresford and

Pettit 2021; Rodríguez-Espíndola, Albores, and

Brewster 2018; Yáñez-Sandivari, Cortés, and Rey

2021; Zhang and Liu 2021).

Climatological phenomena (Clarke, E. L. Otto,

and Jones 2021) cause great physical damage and

material losses due to natural events or phenomena

such as earthquakes, hurricanes, floods, landslides,

tsunamis, and others.

A classic humanitarian logistics (HL) model

envisages pre-emergency and post-emergency stages

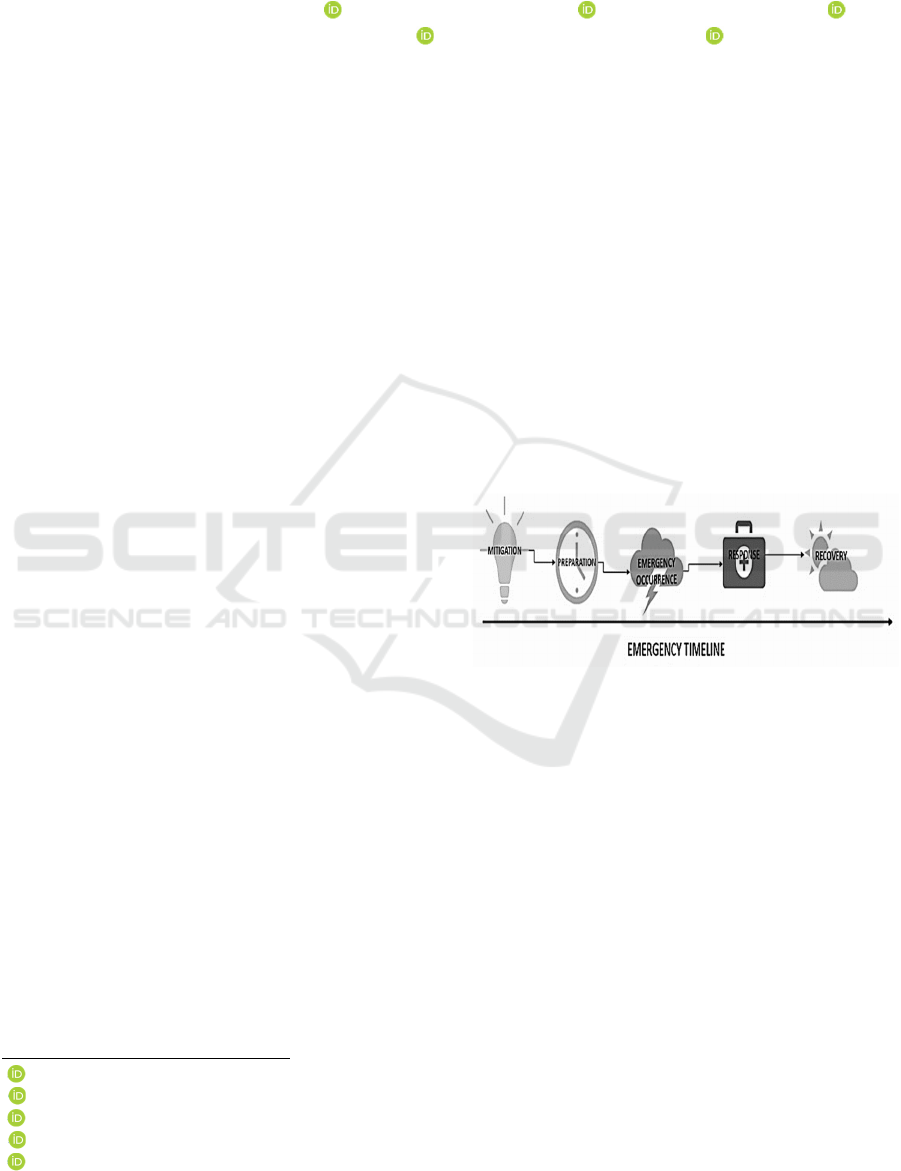
(Yáñez-Sandivari et al. 2021) (See Figure 1 ).

https://orcid.org/0000-0002-9530-4028

https://orcid.org/0000-0002-6803-5010

https://orcid.org/0000-0001-5344-9950

https://orcid.org/0000-0003-4457-9360

https://orcid.org/0000-0001-7661-5894

Figure 1: Emergency stages.

Prior to an emergency, mitigation; consist in the

idea of help reduce the risks of large-scale events.

Preparedness requires having a clear idea of what

actions need to be taken once an emergency occurs.

Response and recovery are post-emergency stages.

This paper will focus pre-emergency stages.

The problem of evacuation has recently been

addressed mainly in hurricane and flood

emergencies, see for example (Dalal and Uster

2021). A robust approach to problem 𝑃 entails a

robust optimization model which may even be non-

linear, which would lead to greater complexity at

the time of being solved.

FernÃ ˛andez-FernÃ ˛andez, Y., Allende-Alonso, S., Miranda-PÃl’rez, R., Bouza-Allende, G. and Cabrera-Alvarez, E.

Robust Optimization for Climatological Emergency Evacuation.

DOI: 10.5220/0011902600003612

In Proceedings of the 3rd International Symposium on Automation, Information and Computing (ISAIC 2022), pages 63-68

ISBN: 978-989-758-622-4; ISSN: 2975-9463

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

Considering any optimization problem 𝑃 such

that (See eq. 1).



𝑷



: 𝐦𝐢𝐧



𝒇



𝒙





𝒔.𝒕. 𝑭



𝒙



≤𝟎

𝒙∈𝑿

(1)

Where 𝐹: ℝ



→ℝ



represents the problem

constraints, 𝑓: ℝ



→ℝ is the objective function

and the variable space is such that 𝑋⊆ ℝ



Starting from the problem 𝑃, the uncertainty

can be formalized by considering a family of

uncertain scenarios 𝑃



𝑢



such that (See eq. 2):

𝑷



𝒖



: 𝐦𝐢𝐧



𝒇



𝒙,𝒖





𝒔.𝒕. 𝑭



𝒙,𝒖



≤𝟎

𝒙∈𝑿

(2)

Where 𝐹



∙,𝑢



: ℝ



→ℝ



, 𝑓



∙,𝑢



: ℝ



→

ℝ ∀ 𝑢 ∈ ℝ



, which describes that a scenario 𝑢 is

permitted to occur.

The formalization discussed in (Goerigk 2012),

suggests that it is at this point that the values that 𝑢

can take in the optimization problem 𝑃



𝑢



, are not

known but; it is assumed that 𝑢 is known to be in a

given uncertainty set 𝒰⊆ ℝ



representing the

probable scenarios of the analysis and the uncertainty

optimization problem.

Some authors (Akbari, Valizadeh, and

Hafezalkotob 2021; Ben-Tal, Ghaoui, and

Nemirovski 2009; Cao et al. 2021; Dönmez et al.

2021; Fakhrzad and Hasanzadeh 2020; Goerigk 2012;

Mahtab et al. 2021; Seraji et al. 2021) revived the

conceptual approach of robust modelling (Goerigk

and Schöbel 2011) given around the 1960's (Gupta

and Rosenhead 1968; Rosenhead, Elton, and Gupta

1972).

Figure 2. Basic procedure for detecting the robust approach

in a problem

Roughly speaking, this research aims to propose

a generic linear robust optimization model for

climatological emergencies with emphasis on the

evacuation task with the vulnerable population as an

unknown or uncertain parameter with the

particularity using scenarios in climatological

management considering the specific case of

evacuation.

2 APPROACHES FOR

REPRESENTING

UNCERTAINTY

Mathematical models describing emergency

situations have been presented in the literature, for

example;(Cao et al. 2021), proposes a post-disaster

relief model considering sustainability, multi-period,

hierarchical relationships, equity, diffuse and

insufficient supplies, split and unsplit demand, multi-

repository and multi-destination. (Seraji et al. 2021)

presents a two-stage multi-objective mathematical

programming model for resource location and

distribution.

In (Mahtab et al. 2021) is proposed a robust

stochastic humanitarian logistics model to assist

decision-makers in pre- and post-disaster

management.

(Zhang and Liu 2021) proposes a mathematical

simulation model based on the vehicle routing

problem with uncertain transport time for a post-

emergency period.

(Akbari et al. 2021) proposes a mathematical

simulation model based on the vehicle routing

problem with uncertain transport time for a post-

emergency period.

(Dönmez et al. 2021) proposes a comprehensive

review of the research conducted on the problems of

locating facilities under uncertainty in a humanitarian

context.

(Yáñez-Sandivari et al. 2021) conducts a

comprehensive review of recent literature on

humanitarian logistics and disaster response

operations.

In (Fakhrzad and Hasanzadeh 2020), the author

analyzes the importance of logistics networks in

strategic decisions for emergency relief distribution

using a mathematical model for stock shortages and

pre-disaster decision support.

Other approaches use fuzzy optimization,

neutrosophic solutions and even the modeling of

these events with possibilistic optimization

(Mohammadi et al. 2020; Özceylan and Paksoy 2014;

Paydar and Saidi-Mehrabad 2014; Saati et al. 2015).

However, with the searches performed, there is no

model that integrates the various robust uncertainty

management approaches.

One of the fundamental problems detected in the

previous contributions continues to be the uncertainty

ISAIC 2022 - International Symposium on Automation, Information and Computing

and quality of the model as we seek an integral

mathematical model that can absorb a humanitarian

logistics problem under various approaches.

2.1 Scenarios for Robust Optimization

The concept established by Ben-Tal (Ben-Tal et al.

2009) show feasibility for all scenarios as

conservative in nature. This conceptualization is not

always possible to apply given the complex data

structure of a system (Goerigk and Schöbel 2011).

In (Kouvelis and Yu 1997) a framework for

working with scenarios is formalized.

In (Kouvelis and Yu 1997) a clear definition of the

case of discrete scenarios with the different types of

robustness for mathematical optimization models is

proposed.

It is important to note the importance of the

concept of robustness referred to by (Kouvelis and Yu

1997) from (Mulvey, Vanderbei, and Zenios 1995)

perspective:

 A mathematical program solution is robust with

respect to optimality (it is called a robust

solution) if it remains close to the optimum for

any input data scenario to the model.

 A solution is robust with respect to feasibility if

it remains close to feasible for any realization

scenario (it is called model robust).

For a better theoretical understanding of this

approach, see (Goerigk and Schöbel 2011; Kouvelis

and Yu 1997).

2.2 Robust Stochastic Optimization

In (Mulvey et al. 1995) an attempt is made to give a

robust answer to the issue of stochasticity through

(RSO) so, let 𝑃 be any (LP) with an uncertainty

coefficients constraint (eq. 3.ii) such that (see eq. 3).



𝑷



: 𝐦𝐢𝐧



𝑪

𝑻

𝒙+𝒅

𝑻

𝒚



∀𝒙∈

ℝ

𝒏

𝟏

,𝒚∈

ℝ

𝒏

𝟐



𝒊



𝒔.𝒕.

𝑨

𝒙=𝒃



𝒊𝒊



𝑩𝒙 +𝑪𝒚 = 𝒆



𝒊𝒊𝒊



𝒙 ≥ 𝟎,𝒚 ≥ 𝟎

(3)

For a set of Ω=



1,2,..,𝑠



scenarios are

associated another set



𝑑



,𝐵



,𝐶



,𝑒





of coefficients

of the control constraints where the probability of the

occurrence of the scenario 𝑝



is such that

∑

𝑝







Thus, the optimal solution of (eq. 3) may be

robust with respect to "optimality" or robust with

respect to "feasibility", in the first case; if it remains

close to the optimum for any realization of the

scenario 𝑠∈Ω and it´s called “Robust Solution”. In

the second case, if the solution remains "almost

feasible" for any realization of the scenario 𝑠∈Ω

and it´s called “Robust Model” solution.

The model proposed in (Mulvey et al. 1995) then

seeks to use an alternative through the stochastic

solution of linear programming, introducing a set of

control variables



𝑦



,𝑦



,…𝑦





∀ 𝑠 ∈Ω and another

set of error vectors



𝑧



,𝑧



,….,𝑧





∀ 𝑠 ∈Ω to

measure the infeasibility contained in the control

constraints considering the following formulation

𝑃



𝜉



of the model of (RO) ( eq. 4).

𝐏



𝝃



:𝐦𝐢𝐧

𝝈



𝒙,𝒚

𝟏

,𝒚

𝟐

,…,𝒚

𝒔



+𝝎𝝆



𝒛

𝟏

,𝒛

𝟐

,…,𝒛

𝒏







𝒊



𝒔.𝒕. 𝑨𝒙 = 𝒃



𝒊𝒊



𝑩

𝒔

𝒙+𝑪

𝒔

𝒚

𝒔

+𝒁

𝒔

=𝒆

𝒔

∀𝒔 ∈𝛀



𝒊𝒊𝒊



𝒙≥𝟎,𝒚

𝒔

≥ 𝟎 ∀𝒔 ∈𝛀

(4)

where the first term 𝜎



𝑥,𝑦



,𝑦



,…,𝑦





of the

objective function measures the optimality of

robustness, the penalty term being a measure of

model robustness, the second term for

𝜌



𝑧



,𝑧



,…,𝑧





is a function for penalizing violations

of control constraints in some scenarios, and 𝜔

represents the goal programming weight used to

derive a range of compensatory responses for model

robustness. P



𝜉



prevents there being a single option

for an aggregate objective function with multiple 𝜉

scenarios such that 𝜉 = 𝐶



𝑥 + 𝑑



𝑦 becomes a

random variable taking the value 𝜉



= 𝐶



𝑥+ 𝑑





𝑦



with probability 𝑝



𝝈



∙



=𝒑

𝒔

𝒔∈𝛀

𝝃

(5)

In summary, this is the point of the author's

contribution and where it is suggested to use the mean

value function of stochastic linear programming 𝜎



∙



as the aggregation function of the model (see eq. 5).

3 ROBUST MODEL FOR

CLIMATOLOGICAL

EMERGENCY

To model the process, we will consider the stochastic

problem for two stages according to the two

operational moments described above and the

following five scenarios:

1. Precipitation and intensity increases.

2. Precipitation and decreasing intensity.

3. Winds and increasing intensity.

4. Winds and decreasing intensity.

Robust Optimization for Climatological Emergency Evacuation

5. Sea penetrations.

The estimated probabilities of each of these

scenarios are input data. N possible evacuation

centers, the location and capacity of each are known.

Model and Notation:

Let J={1,...,N} be the set of possible evacuation

candidate center (CC).



: Cost of conditioning the (CC) considering

𝐶



: Capacity of candidate center j (CC), j ∈ J).

I: Set of localities with vulnerable affected

population.

𝑝𝑒𝑙



: Population of locality a vulnerable to rainfall,

a ∈ I.

𝑝𝑒𝑙𝑙



: Population of locality a vulnerable to intense

rainfall, a ∈ I.

𝑝𝑒𝑣



: Population of locality a vulnerable to wind,

a ∈ I.

𝑝𝑒𝑣𝑓



: Population of locality a vulnerable to strong

wind, a ∈ I.

𝑝𝑣𝑝



: Population of location a vulnerable to

penetrations, a ∈ I.

S={1,...,5}: Set of described scenarios.

Decision variables:

𝑥





: Number of people from location a to be in 𝐶𝐶



if scenario s in stage t.

Model for each scenario:

Restrictions: Evacuate all vulnerable. At least 20%

in case of heavy rain and at least 10% in case of non-

heavy rain. Similarly in case of winds. All vulnerable

in danger of penetration.

Objective: For each scenario s decide how many

people from each location are evacuated in stage 1

and 2 (mitigation and preparation):

Rainfall:

∑

𝑥





∈

≥𝑝𝑟𝑜𝑏



∙ 𝑝𝑒𝑙𝑙



𝑎∈𝐼

∑

𝑥









∈

≥ 𝑝𝑟𝑜𝑏

𝑙



𝑝𝑒𝑙



−𝑝𝑒𝑙𝑙





(6)

By wind:

∑

𝑥





∈

≥𝑝𝑟𝑜𝑏



∙ 𝑝𝑒𝑣𝑓



𝑎∈𝐼

∑

𝑥





∈

≥ 𝑝𝑟𝑜𝑏



∙



𝑝𝑒𝑣



−

𝑝𝑒𝑣𝑓





𝑎 ∈ 𝐼

(7)

Sea penetration:

∑

𝑥





∈

= 𝑝𝑣𝑝



𝑎 ∈ 𝐼

(8)

Capacity constraints at the centers:

∑∑

𝑥







∑∑

𝑥







≤ 𝐶



(9)

Objective Function:

min 

∑∑∑

𝐾



𝑋



∈

∈







 (10)

3.1 Case Simulation

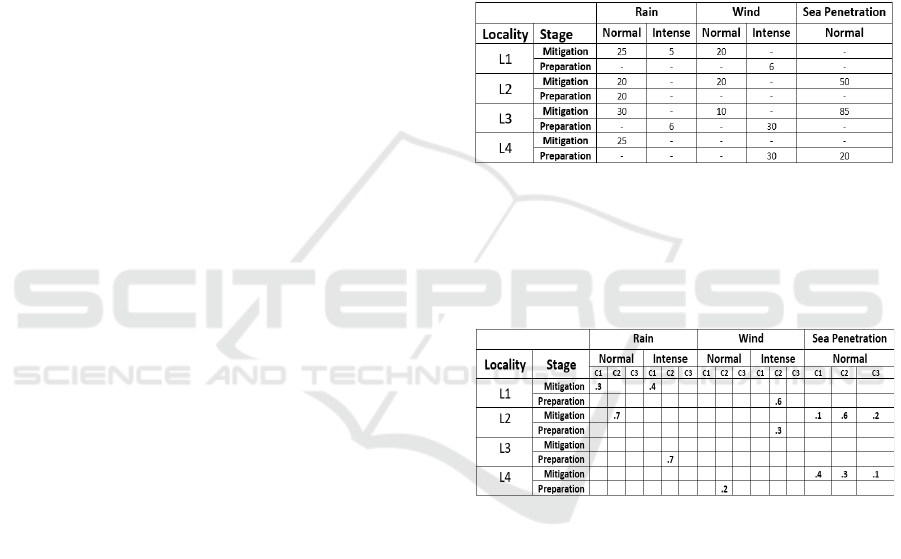
It is considered a cyclonic type of emergency in

which there are 4 localities affected by this entity

(Table 1) with their respective probabilities for each

scenario at each stage and a possible candidate

evacuation center for each location.

Table 1: Data locality vulnerable people.

The affected localities have people vulnerable to

rains, winds, and sea penetration (probable scenarios

of the emergency) and some occurrence probability

for some scenarios (Table 2).

Table 2: Probability assigned when scenario happen.

The response seeks to minimize the costs of

evacuating vulnerable people in each locality by

considering the likely scenarios.

AIMMS version 4.89.2.5 under community

license was used to emulate the following results.

(Table 3) shows the set of decisions that the decision-

maker must make to mitigate the effects of the

example problem, while reducing evacuation costs

for the planned centers a relationship can be

visualized between the scenario that occurred and the

people to be evacuated considerer Center Evacuation

Capacity as { C1 : 175, C2 : 90, C3 : 312 } with the

unitary person evacuation costs { C1 : $ 50, C2 : $

48, C3 : $ 72 }.

A robust solution is sought for all scenarios, to

exemplify the random case selected, in the case of sea

penetration, an affected population of 85 people is

visualized in L3 (Table 1); however, there is no

ISAIC 2022 - International Symposium on Automation, Information and Computing

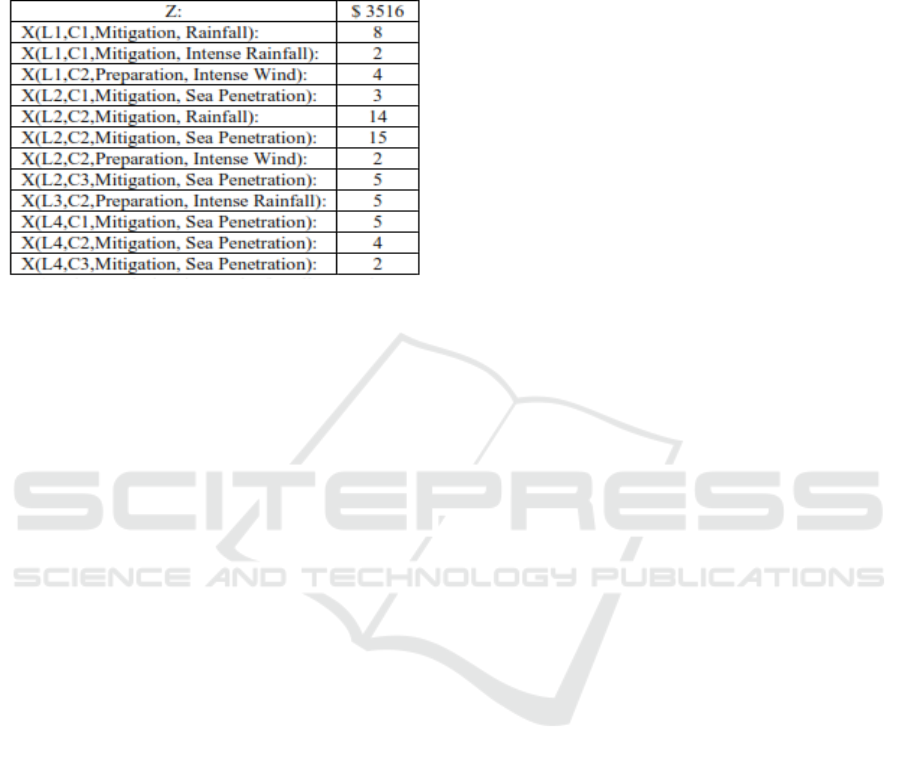
probability of sea penetration for this location, which

is contemplated in the decision not to evacuate people

in L3 due to sea penetration.

Table 3: Decision Variable and objective results.

The contributions of this research are moderate

and are in full development with the aim of using

applied robust optimization models to mitigate the

effects of a climate catastrophe.

4 CONCLUSIONS AND FUTURE

WORK

This contribution shows partial theoretical results on

robust optimization models applied to the

management of climatological emergencies related to

doctoral research in progress at the University of

Havana, Cuba.

It is expected soon to obtain specialized

simulations for the construction of a decision tool for

climatic catastrophes with uncertainty management

with different approaches.

ACKNOWLEDGEMENTS

The present paper tributes to the following research

projects:

• “Proyecto: PN223LH010-005: Desarrollo de

nuevos modelos y métodos matemáticos para la toma

de decisiones” of the Department of Mathematics and

Computation of the University of Havana, Cuba.

• “Proyecto: Smart Data LAB, para la aplicación

de la Ciencia de Datos” of the Department of

Computation of the Universidad Politécnica Estatal

del Carchi, Ecuador.

REFERENCES

Akbari, Foad, Jaber Valizadeh, and Ashkan Hafezalkotob.

2021. “Robust Cooperative Planning of Relief Logistics

Operations under Demand Uncertainty: A Case Study

on a Possible Earthquake in Tehran.”

Https://Doi.Org/10.1080/23302674.2021.1914767.

doi: 10.1080/23302674.2021.1914767.

Behl, Abhishek, and Pankaj Dutta. 2019. “Humanitarian

Supply Chain Management: A Thematic Literature

Review and Future Directions of Research.” Ann Oper

Res 283:1001–44. doi: 10.1007/s10479-018-2806-2.

Ben-Tal, A., and A. Nemirovski. 1998. “Robust Convex

Optimization.” Mathematics of Operations Research

23(4):769–805. doi: 10.1287/MOOR.23.4.769.

Ben-Tal, Aharon, Laurent El Ghaoui, and Arkadi

Nemirovski. 2009. Robust Optimization. Princeton

University Press.

Beresford, Anthony, and Stephen Pettit. 2021.

“Humanitarian Aid Logistics: A Cardiff University

Research Perspective on Cases, Structures and

Prospects.” Journal of Humanitarian Logistics and

Supply Chain Management 11(4):623–38. doi:

10.1108/JHLSCM-06-2021-0052/FULL/XML.

Cao, Cejun, Yang Liu, Ou Tang, and Xuehong Gao. 2021.

“A Fuzzy Bi-Level Optimization Model for Multi-

Period Post-Disaster Relief Distribution in Sustainable

Humanitarian Supply Chains.” International Journal of

Production Economics 235:108081. doi:

10.1016/J.IJPE.2021.108081.

Clarke, Ben J., Friederike E. L. Otto, and Richard G. Jones.

2021. “Inventories of Extreme Weather Events and

Impacts: Implications for Loss and Damage from and

Adaptation to Climate Extremes.” Climate Risk

Management 32. doi: 10.1016/J.CRM.2021.100285.

Dönmez, Zehranaz, Y. Kara, Özlem Karsu, and Francisco

Saldanha-Da-Gama. 2021. “Humanitarian Facility

Location under Uncertainty: Critical Review and

Future Prospects R.” Omega 102:102393. doi:

10.1016/j.omega.2021.102393.

Fakhrzad, M. B., and H. Hasanzadeh. 2020. “A New

Mathematical Modelling for Relief Operation Based on

Stochastic Programming.” International Journal of

Process Management and Benchmarking 10(2):224–

39. doi: 10.1504/IJPMB.2020.106141.

Goerigk, Marc. 2012. “Algorithms and Concepts for Robust

Optimization.” Universit¨at G¨ottingen, Berlin.

Goerigk, Marc, and Anita Schöbel. 2011. “A Scenario-

Based Approach for Robust Linear Optimization.”

Lecture Notes in Computer Science (Including

Subseries Lecture Notes in Artificial Intelligence and

Lecture Notes in Bioinformatics) 6595 LNCS:139–50.

doi: 10.1007/978-3-642-19754-3_15.

Gupta, Shiv K., and Jonathan Rosenhead. 1968.

“Robustness in Sequential Investment Decisions.”

Http://Dx.Doi.Org/10.1287/Mnsc.15.2.B18 15(2):B-

18-B-29. doi: 10.1287/MNSC.15.2.B18.

Kouvelis, Panos, and Gang Yu. 1997. Robust Discrete

Optimization and Its Applications. Springer.

Robust Optimization for Climatological Emergency Evacuation

Mahtab, Zuhayer, Abdullahil Azeem, Syed Mithun Ali,

Sanjoy Kumar Paul, and Amir Mohammad Fathollahi-

Fard. 2021. “Multi-Objective Robust-Stochastic

Optimisation of Relief Goods Distribution under

Uncertainty: A Real-Life Case Study.”

Https://Doi.Org/10.1080/23302674.2021.1879305.

doi: 10.1080/23302674.2021.1879305.

Mohammadi, S., Soroush Avakh Darestani, Behnam

Vahdani, and A. Alinezhad. 2020. “A Robust

Neutrosophic Fuzzy-Based Approach to Integrate

Reliable Facility Location and Routing Decisions for

Disaster Relief under Fairness and Aftershocks

Concerns.” Computers and Industrial Engineering 148.

doi: 10.1016/J.CIE.2020.106734.

Mulvey, John M., Robert J. Vanderbei, and Stavros A.

Zenios. 1995. “Robust Optimization of Large-Scale

Systems.” Https://Doi.Org/10.1287/Opre.43.2.264

43(2):264–81. doi: 10.1287/OPRE.43.2.264.

Özceylan, Eren, and Turan Paksoy. 2014. “Interactive

Fuzzy Programming Approaches to the Strategic and

Tactical Planning of a Closed-Loop Supply Chain

under Uncertainty.”

Http://Dx.Doi.Org/10.1080/00207543.2013.865852

52(8):2363–87. doi: 10.1080/00207543.2013.865852.

Paydar, Mohammad Mahdi, and Mohammad Saidi-

Mehrabad. 2014. “Revised Multi-Choice Goal

Programming for Integrated Supply Chain Design and

Dynamic Virtual Cell Formation with Fuzzy

Parameters.”

Https://Doi.Org/10.1080/0951192X.2013.874596

28(3):251–65. doi: 10.1080/0951192X.2013.874596.

Rodríguez-Espíndola, Oscar, Pavel Albores, and

Christopher Brewster. 2018. “Disaster Preparedness in

Humanitarian Logistics: A Collaborative Approach for

Resource Management in Floods.” European Journal

of Operational Research 264(3):978–93. doi:

10.1016/J.EJOR.2017.01.021.

Rosenhead, Jonathan, Martin Elton, and Shiv K. Gupta.

1972. “Robustness and Optimality as Criteria for

Strategic Decisions.”

Https://Doi.Org/10.1057/Jors.1972.72 23(4):413–31.

doi: 10.1057/JORS.1972.72.

Saati, Saber, Madjid Tavana, Adel Hatami-Marbini, and

Elham Hajiakhondi. 2015. “A Fuzzy Linear

Programming Model with Fuzzy Parameters and

Decision Variables.” International Journal of

Information and Decision Sciences 7(4):312–33. doi:

10.1504/IJIDS.2015.074129.

Seraji, Hasti, Reza Tavakkoli-Moghaddam, Sobhan Asian,

and Harpreet Kaur. 2021. “An Integrative Location-

Allocation Model for Humanitarian Logistics with

Distributive Injustice and Dissatisfaction under

Uncertainty.” Annals of Operations Research. doi:

10.1007/S10479-021-04003-5.

Yáñez-Sandivari, Luis, Cristián E. Cortés, and Pablo A.

Rey. 2021. “Humanitarian Logistics and Emergencies

Management: New Perspectives to a Sociotechnical

Problem and Its Optimization Approach Management.”

International Journal of Disaster Risk Reduction

52:101952. doi: 10.1016/J.IJDRR.2020.101952.

Zhang, Yutong, and Jing Liu. 2021. “Emergency Logistics

Scheduling under Uncertain Transportation Time Using

Online Optimization Methods.” IEEE Access 9:36995–

10. doi: 10.1109/ACCESS.2021.3061454.

ISAIC 2022 - International Symposium on Automation, Information and Computing