Computer Modeling of the Equilibrium Position Magnetization
Precession in the Ferrite Plate
V. S. Vlasov
1a
, D. A. Suslov
2b
, V. G. Shavrov
2c
and V. I. Shcheglov
2
1
Syktyvkar State University, Syktyvkar, Russia
2
Kotel’nikov Institute of Radio Engineering and Electronics, Russian Academy of Sciences, Moscow, Russia
Keywords: Nonlinear Magnetization Precession, Computer Modelling, Ferrite Plate.
Abstract: Nonlinear equilibrium position magnetization precession in a normally magnetized ferrite plate is modeled in
the Matlab system. The magnetization motion equations for 3 cases are given: the isotropic plate, the plate
with uniaxial anisotropy and the plate with cubic anisotropy. Differential equation system for magnetization
vector relative to magnetization components is solved by Runge-Kutta method in the Matlab. The code of the
program for modeling the magnetization dynamics is given. The program allows to build parametric portraits
of the magnetization and study their features under various types of the plate anisotropy. The features of
parametric portraits for these three cases of the anisotropy are considered.
1 INTRODUCTION
There is the great interest in modeling the dynamics
of nonlinear magnetic systems (Vlasov et al., 2022;
Vlasov et al., 2020). It is caused by promising
applications of magnetic nanostructures in
spintronics and nanoelectronics (Shelukhin et al.,
2022; Barman et al., 2020). Computer modeling is
also relevant due to the impossibility of analytical
solution of the magnetization dynamics nonlinear
problems (Shavrov and Shcheglov, 2021). One of the
interesting types of the magnetization vector
precession in planar structures is the equilibrium
position precession. Such precession can be observed
in the perpendicular magnetized plate (Shavrov and
Shcheglov, 2021). In this case, the DC field is smaller
than the demagnetization field and the magnetization
vector is deviated from the direction of the field in the
equilibrium state. When the alternating field is turned
on, the precession of the magnetization vector
appears relative to the equilibrium position.
Moreover, the equilibrium position moves along the
"big circle" of the precession portrait and we see the
rings filled the "big circle". So, the realization of
"precession in precession" is obtained (Shavrov and
Shcheglov, 2021; Vlasov et al., 2011).
a
https://orcid.org/0000-0001-6902-608X
b
https://orcid.org/0000-0002-1962-1195
c
https://orcid.org/0000-0003-0873-081X
The magnetization dynamics for the equilibrium
position precession cannot be found by using
analytical formulas. Therefore, the only theoretical
way to study the equilibrium position precession is
the computer modeling using numerical solution
methods (Shavrov and Shcheglov, 2021; Vlasov et
al., 2012; Vlasov et al., 2013). Matlab package
solution methods are used to simulate the motion of
the magnetization vector in the present paper.
The paper is devoted to modeling the equilibrium
position precession with the symmetric and
asymmetric DC fields orientation in the isotropic
ferrite plate and for cases of the uniaxial and cubic
anisotropy (Shavrov and Shcheglov, 2021).
2 GEOMETRY AND BASIC
EQUATIONS
2.1 Geometry of the Problem
Let’s consider the normally magnetized ferrite plate.
The 3 cases of equilibrium position precession for
different types of the plate anisotropy are studied: 1.
the isotropic plate; 2. the plate with uniaxial
Vlasov, V., Suslov, D., Shavrov, V. and Shcheglov, V.
Computer Modeling of the Equilibrium Position Magnetization Precession in the Ferrite Plate.
DOI: 10.5220/0011906700003612
In Proceedings of the 3rd International Symposium on Automation, Information and Computing (ISAIC 2022), pages 115-120
ISBN: 978-989-758-622-4; ISSN: 2975-9463
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
115

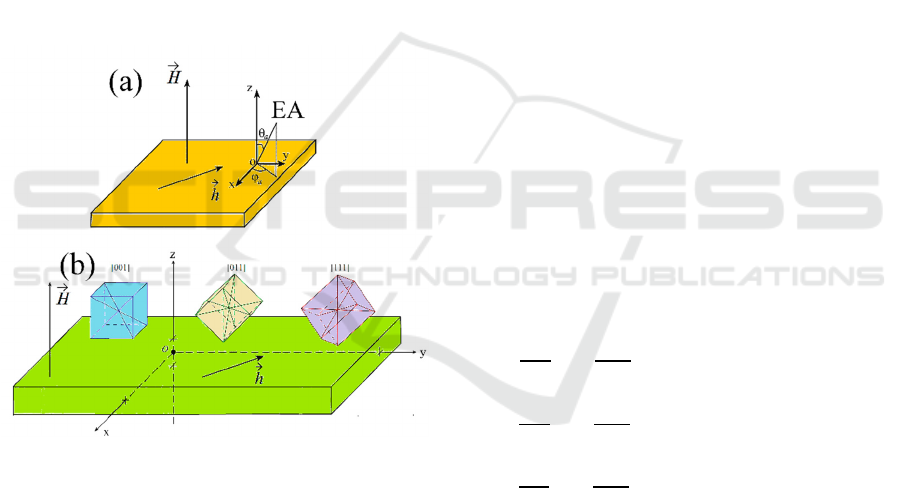
anisotropy; 3. the plate with cubic magnetic
anisotropy. The general geometry of the problem is
illustrated in Figure 1. Figure 1a shows the plate with
uniaxial anisotropy. Figure 1b illustrates the plate
with cubic anisotropy. The ferrite plate is magnetized
by the DC field perpendicular to its plane, the
alternating field is applied in the plane of the plate.
The xOy plane of the Cartesian coordinate system
Oxyz coincides with the plane of the plate. The z axis
is perpendicular to the plate plane. For the case of the
isotropic ferrite plate, the DC field may also have
weak components in the plane of the plate.
Firstly, let us consider in detail the geometry of
the problem for the ferrite plate with uniaxial
magnetic anisotropy (Shavrov and Shcheglov, 2021).
The easy axis (EA) is deviated from the normal to the
plate plane by the arbitrary angle. Such geometry of
the problem is shown in Figure 1a. The direction of
the EA is given by 2 angles in the spherical coordinate
system 𝜃

, 𝜑

.
Figure 1. Geometry of the problem.
For the case of the plate with cubic anisotropy,
three variants of the orientation of the cubic
crystallographic cell are considered in Figure 1b:
1) ORIENTATION [001]: one of the crystallographic
axes of the type [001] which is the edge of the cube is
directed along the normal from the plate plane;
2) ORIENTATION [011]: one of the axes of the type
[011] is directed along the normal from the plate
plane, i.e. the diagonal of the cube face;
3) ORIENTATION [111]: one of the axes of type
[111], i.e. the spatial diagonal of the cube, is directed
along the normal from the plane of the plate (Vlasov
et al., 2013).
2.2 Basic Equations
The problem of the magnetization vector dynamic
behavior is solved in the coordinate system associated
with the DC field, i.e. Oxyz. The expressions for the
energy and the uniaxial anisotropy field for the case
of the easy axis rotated by angles 𝜃

, 𝜑

are obtained
in the work (Shavrov and Shcheglov, 2021). The
expressions for the energy and fields of the cubic
anisotropy, for orientations [001], [011], [111] are
obtained similarly in work (Vlasov et al., 2013).
We further assume that the DC field 𝐻


⃗
is not
sufficient to align the magnetization vector in the
equilibrium state perpendicular to the plane of the
plate. The components of the alternating field have
the form:
ℎ

=ℎ

𝑠𝑖𝑛
(
2𝜋𝐹𝑡
)
, ℎ

=−ℎ

𝑐𝑜𝑠
(
2𝜋𝐹𝑡
)
(1)
where F – the alternating field frequency, h
0
– its
amplitude.
The magnetization equilibrium position
precession is possible to observe for such magnetic
fields orientation relative to the plate plane, in certain
circumstances. This precession type is the
equilibrium position motion around the direction of
the DC field with the frequency significantly lower
than alternating field frequency.
To solve the problem of the magnetization vector
dynamic behavior we use the Landau–Lifshitz
magnetization motion equations with the dissipative
Gilbert term (LLG) (Shavrov and Shcheglov, 2021):



=−



𝑚

+𝛼𝑚

𝑚

𝐻

−𝑚

−
𝛼𝑚

𝑚

𝐻

−𝛼𝑚


+𝑚


𝐻

 , (2)



=−



𝑚

+𝛼𝑚

𝑚

𝐻

−𝑚

−
𝛼𝑚

𝑚

𝐻

−𝛼
(
𝑚


+𝑚


)
𝐻

, (3)



=−



𝑚

+𝛼𝑚

𝑚

𝐻

−𝑚

−
𝛼𝑚

𝑚

𝐻

−𝛼𝑚


+𝑚


𝐻

, (4)
where 𝑚


⃗
=𝑀


⃗
𝑀

 – the normalized magnetization
vector, 𝑚

– its components in the Cartesian
coordinate system, 𝑀

– the saturation
magnetization, 𝛾 –the gyromagnetic ratio (𝛾 > 0), 𝛼 –
magnetic dissipation parameter, 𝐻

– the
components of the effective field. In the case of the
isotropic plate, the components of the effective field
included in equations (2-4) have the form:
𝐻

=ℎ

+𝐻

, (5)
𝐻

=ℎ

+𝐻

, (6)
ISAIC 2022 - International Symposium on Automation, Information and Computing
116

𝐻

=𝐻

−4𝜋𝑀

𝑚

. (7)
For the cases of the plate with uniaxial and cubic
anisotropy, the components of effective fields have
the following form:
𝐻

=ℎ

+𝐻

+𝐻

, (8)
𝐻

=ℎ

+𝐻

+𝐻

, (9)
𝐻

=𝐻

−4𝜋𝑀

𝑚

+𝐻

. (10)
Let's look at the components of the anisotropy
field included in expressions (8-10). For the case of
uniaxial anisotropy with angles 𝜃

, 𝜑

the
expressions for the anisotropy field components have
following form (Shavrov and Shcheglov, 2021):
𝐻

=𝐻

=



(−𝑚

(
𝑐𝑜𝑠

𝜃

𝑐𝑜𝑠

𝜑

+
𝑠𝑖𝑛

𝜑

)
+𝑚

𝑠𝑖𝑛

𝜃

𝑠𝑖𝑛𝜑

𝑐𝑜𝑠𝜑

+
𝑚

𝑠𝑖𝑛𝜃

𝑐𝑜𝑠𝜃

𝑐𝑜𝑠𝜑

, (11)
𝐻

=𝐻

=



(𝑚

𝑠𝑖𝑛

𝜃

𝑠𝑖𝑛𝜑

𝑐𝑜𝑠𝜑

−
𝑚

(
𝑐𝑜𝑠

𝜃

𝑠𝑖𝑛

𝜑

+𝑐𝑜𝑠

𝜑

)
+
𝑚

𝑠𝑖𝑛𝜃

𝑐𝑜𝑠𝜃

𝑠𝑖𝑛𝜑

, (12)
𝐻

=𝐻

=



(𝑚

𝑠𝑖𝑛𝜃

𝑐𝑜𝑠𝜃

𝑐𝑜𝑠𝜑

+
𝑚

𝑠𝑖𝑛𝜃

𝑐𝑜𝑠𝜃

𝑠𝑖𝑛𝜑

−𝑚

𝑠𝑖𝑛

𝜃

), (13)
where 𝐾 – the uniaxial anisotropy constant.
In the case of the cubic anisotropy and the
orientation [001], the components of the anisotropy
field can be written as follows:
𝐻

=𝐻

()
=




𝑚

(𝑚


+𝑚


), (14)
𝐻

=𝐻

()
=




𝑚

(𝑚


+𝑚


), (15)
𝐻

=𝐻

()
=




𝑚

(𝑚


+𝑚


). (16)
In the case of cubic anisotropy and orientation [001],
the components of the anisotropy field have the
following form:
𝐻

=𝐻

()
=




𝑚

(𝑚


+𝑚


), (17)
𝐻

=𝐻

()
=




𝑚

(2𝑚


+𝑚


−𝑚


), (18)
𝐻

=𝐻

()
=




𝑚

(2𝑚


−𝑚


+𝑚


). (19)
The cubic anisotropy fields for orientation [111] look
like this:
𝐻

=𝐻

()
=




(𝑚


+𝑚

𝑚


−
√
2𝑚


𝑚

+
√
2
𝑚


𝑚

), (20)
𝐻

=𝐻

()
=




(𝑚


+𝑚


𝑚

+
2
√
2
𝑚

𝑚

𝑚

), (21)
𝐻

=𝐻

(

)
=
=




(


𝑚


−
√


𝑚


+
√
2𝑚

𝑚


). (22)
where 𝐾

– the first constant of cubic anisotropy.
3 SOLUTION ALGORITHM
Let's consider the algorithm for solving the problem
in the Matlab system. The LLG equations system (2-
4) is solved by the 4-5 orders Runge-Kutta method
into the Matlab package with the accuracy control at
each step. Firstly, parameters are entered in the task.
The right part of the LLG equations system is
designed as the separate function. Next, the numerical
solution of the system is implemented. The results of
the numerical solution are output in the magnetization
precession portraits graphs form m
x
(m
y
), which are
projections of the magnetization phase trajectories.
The content of the main program for the Matlab is
shown in Listing 1.
Listing 1: The listing of the main program.
close all
clear all
global alf h F1 Hx Hy H0 M0 Ku teta_a
fi_a K1
neq=3;
M0=280/(4*pi);
gamma=1.756e7;
H0=252;
alf=0.3;
h=3;
F1=1e8/(gamma*M0);
Hx=0.1*0;
Hy=0;
Ku=0;
teta_a=10*pi/180;
fi_a=0;
K1=8;
for i=1:neq
abt(i)=5e-6;
end;
teta0=acos(H0/(4*pi*M0));
ink(1)=sin(teta0);
ink(2)=0;
ink(3)=cos(teta0);
tras=1000;
Computer Modeling of the Equilibrium Position Magnetization Precession in the Ferrite Plate
117

options = odeset('RelTol',5e-
6,'AbsTol',abt);
[T,Y] = ode45(@y_m2022_2,[0
tras],ink,options);
Nt=length(T);
T1=T(round(Nt/2):Nt);
mx1=Y(round(Nt/2):Nt,1);
my1=Y(round(Nt/2):Nt,2);
figure(1)
plot(mx1,my1,'LineWidth', 2);
set(gca,'FontSize',36,'LineWidth', 4);
xlabel('m_x','FontSize',48);
ylabel('m_y','FontSize',48);
Let's describe the text of the main program. First
of all, the global parameters are set. The
alf – the
magnetic dissipation parameter,
h – the alternating
field amplitude,
F1 – the alternating field frequency,
Hx, Hy – components of the weak DC field applied
in the plate plane, H0 – the main DC magnetizing
field applied along the normal from the plate plane,
M0 – the saturation magnetization of the plate,
Ku –
the uniaxial anisotropy constant, teta_a, fi_a –
angles 𝜃

, 𝜑

, K1 – the first constant of the cubic
anisotropy.
Next, the program introduces the
parameter
neq=3 corresponding to the number of
differential equations in the system and the values of
the listed system parameters. The absolute accuracy
is introduced in the for loop for the 3 components of
magnetization corresponding to the variables
abt(i)=5e-6 for the system of differential
equations LLG solution.
teta0 is the deviation angle
of the magnetization from the normal to the plate
plane, which is calculated by the formula taken from
work (Vlasov et al., 2011). The initial values of the
unit magnetization vector components
ink(1),
ink(2), ink(3) are calculated by using this angle.
tras=1000 is the final time for the dynamics of
magnetization calculation (in relative units). The set
of parameters
options gives the relative and
absolute accuracy of the solution of the LLG system.
The
ode45 function implements the solution of the
LLG system by the Runge-Kutta 4-5 orders method.
After the numerical solution of the LLG equations
system, the arrays
mx1, my1 are determined in the
program. The steady-state values of the
magnetization components 𝑚

, 𝑚

are written in the
arrays. The
plot function implements the plotting of
the magnetization precession portrait.
The right part of the differential equations system
is described as the separate function in the Matlab
system. 2 different functions are introduced to
describe the right side of the LLG system for all three
cases of the anisotropy. The function corresponding
the LLG system for the case of the isotropic plate and
the case of uniaxial anisotropy (case 1) is shown in
Listing 2.
Listing 2: The LLG system function. Case 1.
function f=y_m2022_1(t,m)
global alf h F1 Hx Hy H0 M0 Ku teta_a
fi_a K1
cg=-1/(1+alf*alf);
neq=3;
f=zeros(neq,1);
mx=m(1);
my=m(2);
mz=m(3);
Heu_x=2*Ku/M0*(-
mx*(cos(teta_a)^2*cos(fi_a)^2+sin(fi_a)
^2)+...
my*sin(teta_a)^2*sin(fi_a)*cos(fi_a)+
mz*sin(teta_a)*cos(teta_a)*cos(fi_a));
Heu_y=2*Ku/M0*(mx*sin(teta_a)^2*sin(fi_
a)*cos(fi_a)-...
my*(cos(teta_a)^2*sin(fi_a)^2+cos(fi_a)
^2)+mz*sin(teta_a)*cos(teta_a)*sin(fi_a
));
Heu_z=2*Ku/M0*(mx*sin(teta_a)*cos(teta_
a)*cos(fi_a)+...
my*sin(teta_a)*cos(teta_a)*sin(fi_a)-
mz*sin(teta_a)^2);
hx=(h*sin(2*pi*F1*t)+Hx+Heu_x)/M0;
hy=(-h*cos(2*pi*F1*t)+Hy+Heu_y)/M0;
hz=(H0-4*pi*mz*M0+Heu_z)/M0;
fx=my*hz-mz*hy;
fy=mz*hx-mx*hz;
fz=mx*hy-my*hx;
fhx=my*fz-mz*fy;
fhy=mz*fx-mx*fz;
fhz=mx*fy-my*fx;
f(1)=cg*(fx + alf*fhx);
f(2) = cg*(fy + alf*fhy);
f(3)= cg*(fz + alf*fhz);
end
The function implements the assignment of the right
side of the LLG system (2-4) in the case of the
isotropic plate or the uniaxial anisotropy. Moreover,
the solution of the system is carried out in relative
units: time is normalized by the value 1(𝛾𝑀

)
⁄
, the
alternating field frequency is normalized by the value
𝛾𝑀

(in the main program).
ISAIC 2022 - International Symposium on Automation, Information and Computing
118

The function of the LLG system for the case of the
cubic anisotropy plate (case 2) is given in Listing 3.
Listing 3: The LLG system function. Case 2.
function f=y_m2022_2(t,m)
…
a_orient = '111';
switch a_orient
case '001'
Ha_x=2*K1/M0*mx*(my^2+mz^2);
Ha_y=2*K1/M0*my*(mz^2+mx^2);
Ha_z=2*K1/M0*mz*(mx^2+my^2);
case '011'
Ha_x=2*K1/M0*mx*(my^2+mz^2);
Ha_y=2*K1/M0*my*(2*mx^2+my^2-
mz^2);
Ha_z=2*K1/M0*mz*(2*mx^2-
my^2+mz^2);
case '111'
Ha_x=2*K1/M0*(mx^3+mx*my^2-
sqrt(2)*mx^2*mz+sqrt(2)*my^2*mz);
Ha_y=2*K1/M0*(my^3+mx^2*my+2*sqrt(2)*mx
*my*mz);
Ha_z=2*K1/M0*(4/3*mz^3-
sqrt(2)/3*mx^3+sqrt(2)*mx*my^2);
end
hx=(h*sin(2*pi*F1*t)+Hx+Ha_x)/M0;
hy=(-h*cos(2*pi*F1*t)+Hy+Ha_y)/M0;
hz=(H0-4*pi*mz*M0+Ha_z)/M0;
…
The listing is given from the end of the line mz=m(3)
to the definition of the variable fx. The fragments of
the
function y_m2022_2(t,m) before the end of
the line
mz=m(3) and after determining the variable
fx, completely repeat the listing of the previous
function
function y_m2022_1(t,m). To separate
the different cases of orientation of the
crystallographic cell the text variable
a_orient is
introduced, for which one of 3 values must be set:
'001', '011', '111'.
4 RESULTS OF NUMERICAL
SOLUTION OF THE LLG
SYSTEM
Let's have a look at the main results of the numerical
solution of the LLG system obtained using the
described calculation program. The plots of all 3
cases of the solution (1. Isotropic plate; 2. Plate with
uniaxial anisotropy; 3. Plate with cubic anisotropy)
are shown in Figure 2. The values of the parameters
given in Listing 1 are used for constructing
calculations Figure 2. The parameters are given in the
CGS system of units. The frequency of the alternating
field is F=100 MHz and corresponds to the variable
F1. This value is divided by the value gamma*M0 due
to the transition to the relative times and frequencies
in the program text.
Let's consider the features of precession portraits
in Figure 2. In the case of the symmetric DC field and
the isotropic plate, small rings uniformly fill the
precession portrait along the generatrix of the large
circle. Such precessional portrait is shown in Figure
2a. The presence of the rings accumulations and
sparsities on the precessional portrait is visible in the
other sub-drawings. The mechanism of formation of
the ring accumulations and sparsities was described
in works (Shavrov and Shcheglov, 2021; Vlasov et
al., 2011; Vlasov et al., 2012; Vlasov et al., 2013) on
the basis of energy and vector models.
Figure 2: Precession portraits of magnetization for different
cases of the anisotropy: (a) the isotropic plate with the
symmetric DC field; (b) the isotropic plate with the weak
asymmetric field applied along x-axis; (c) the case of the
uniaxial anisotropy; (d) the cubic anisotropy with the
orientation [001]; (e) the cubic anisotropy with the
orientation [011]; (f) the cubic anisotropy with the
orientation [111].
The ring accumulations occur at the angle of 90
degrees to the weak DC field applied in the plane for
the isotropic plate. The such case is shown in Figure
2b. The additional weak DC field is directed along the
x axis and equal to 𝐻

=0.1 Oe. Therefore, the rings
Computer Modeling of the Equilibrium Position Magnetization Precession in the Ferrite Plate
119

accumulation in this portrait is located at the angle of
90 degrees with respect to the x axis and
counterclockwise rotated. The polar and azimuthal
angles that correspond to the orientation of the easy
axis are 𝜃

= 10°, 𝜑

=0 for the case of uniaxial
anisotropy (Figure 2c). Thus the projection of the
anisotropy axis onto the plate plane is parallel to the
x coordinate axis. The axis is 10° angle with the
normal from the plate. The similar rings
accumulations and sparsities are observed in Figure
2c, as in the case of the asymmetric DC field (Figure
2b) directed along the x axis. The number of ring
accumulations and sparsities depends on the number
of minima and maxima of the anisotropy energy in
the projection onto the plate plane for the case of
cubic anisotropy (Figure 2d, e, f). Figure 2d is
constructed for orientation [001]. The value of the
cubic anisotropy constant is 𝐾

=160 erg/cm
3
. 4 ring
accumulations are visible in Figure 2d. The
accumulations correspond to the presence of 4
minima and maxima along the precession forming the
large circle. Figure 2e is constructed for orientation
[011]. The value of the cubic anisotropy constant is
𝐾

=5 erg/cm
3
. 2 ring accumulations are visible in Fig.
2e corresponding to 2 minima and maxima along the
generatrix of the large circle. Figure 2f is constructed
for orientation [111]. The value of the cubic
anisotropy constant 𝐾

=8 erg/cm
3
. 3 thickenings are
visible in Figure 2f, corresponding to 3 minima and
maxima along the generatrix of the large circle.
5 CONCLUSIONS
The calculation computer program has been
developed in the Matlab system. The computer
simulation of the equilibrium position precession in
the ferrite plate has been carried out in 3 cases. The
first case is the isotropic plate, the second case is the
plate with uniaxial anisotropy, the third case is the
plate with cubic anisotropy. The listing of the
calculation program text is given. The program
consists of the main module and two auxiliary
functions to describe the right-hand side of the
Landau-Lifshitz-Gilbert system of differential
equations. The explanations for the features of the
obtained magnetization precession portraits based on
the presence of maxima and minima of anisotropy
energy along the large precession circle are given.
ACKNOWLEDGEMENTS
This work has been supported by the Russian Science
Foundation, project no. 21-72-20048.
REFERENCES
Vlasov, V. S., Makarov, P. A., Shavrov, V. G. and
Shcheglov, V. I. (2022). Impact excitation of magnetic
oscillations by an elastic displacement pulse. Journal of
Communications Technology and Electronics, 67(7):
876–881.
Vlasov, V. S., Lomonosov, A. M., Golov, A. V., Kotov, L.
N., Besse, V., Alekhin, A., Kuzmin, D. A., Bychkov, I.
V. and Temnov, V. V. (2020). Magnetization switching
in bistable nanomagnets by picosecond pulses of
surface acoustic waves. Phys. Rev. B, 101(2): 024425.
Shelukhin, L. A., Gareev, R. R., Zbarsky, V., Walowski, J.,
Münzenberg, M., Pertsev, N. A. and Kalashnikova, A.
M. (2022). Spin reorientation transition in
CoFeB/MgO/CoFeB tunnel junction enabled by
ultrafast laser-induced suppression of perpendicular
magnetic anisotropy. Nanoscale, 14: 8153-8162.
Barman, A., Mondal, S., Sahoo, S. and De, A. (2020).
Magnetization dynamics of nanoscale magnetic
materials: a perspective. J. Appl. Phys. 128: 170901.
Shavrov, V. G. and Shcheglov, V. I. (2021). Ferromagnetic
resonance in orientational transition conditions, CRC
Press. Boca Raton, 1
st
edition.
Vlasov, V. S., Kotov, L. N., Shavrov, V. G., and Shcheglov,
V. I. (2011). Forced nonlinear precession of the
magnetization vector under the conditions of an
orientation transition. Journal of Communications
Technology and Electronics, 56(1): 73–84.
Vlasov, V. S., Kotov, L. N., Shavrov, V. G., and Shcheglov,
V. I. (2012). Asymmetric excitation of the two-order
magnetization precession under orientational transition
conditions. Journal of Communications Technology
and Electronics, 57(5): 453–467.
Vlasov, V. S., Kirushev, M. S., Kotov, L. N., Shavrov, V.
G., and Shcheglov, V. I. (2013). The second-order
magnetization precession in an anisotropic medium.
Part 2: The cubic anisotropy. Journal of
Communications Technology and Electronics, 58(9):
847–862.
ISAIC 2022 - International Symposium on Automation, Information and Computing
120