Cooperative Trajectory Optimization for Long-Range Interception

with Terminal Handover Constraints

Zhengda Cui

, Mingying Wei

1,2

, Yunqian Li

and Pengfei Zhang

Beijing Institute of Electric System Engineering, Beijing 100854, China

Beijing Simulation Center, Beijing 100854, China

Keywords: Cooperative Handover Guidance, Long-range Interception, Cooperative Feasible Region, RBF Neural

Network.

Abstract: Motivated by the requirement of consistency engagement of long-range interceptors, a time cooperative

guidance method based on feasible region is proposed. First, the multi-missile cooperative trajectory planning

problem is established, considering the constraints in energy, heat protection and interception capacity. We

transform the problem into subproblems of determination of coordinated time and trajectory optimization

under time constraint. Based on the hp-adaptive pseudo-spectral method, the feasible region is analyzed and

solved under different initial conditions. The RBF neural network was used to realize the online negotiation

and prediction of cooperative cost. Numerical simulation shows the optimal cooperative trajectories can meet

the constraint on cooperative rendezvous.

1 INTRODUCTION

The conflict between air threat and interceptors is

becoming increasingly fierce in modern warfare, with

the range of precision-guided weapons getting farther

and farther. Interceptor missiles must also have the

ability to intervene quickly in remote areas and

accurately intercept various air targets (Wei, M, Cui,

Z, & Li, Y, 2020; Wang, F. B, & Dong, C. H, 2013;

Farooq, A, & Limebeer, D. J, 2002).

Unlike stationary or slow-moving targets, the

target set of long-range air-defense missiles also

includes high-mobility targets. Considering the long-

range and target maneuvers, the handover area

between midcourse and final interception is

inevitably expanded. In order to realize information

closure, it is used to add a trajectory planning phase

at the end of the midcourse phase, so that the positions

of multiple interceptors can meet the conditions of

cooperative detection field splicing, and improve the

capture probability of the seeker to the target.

The end stage of midcourse trajectory planning

problem for long-range air-defense missiles is often

described as a multi-constrained optimal control

problem under finite feasible regions (

GUO M,YANG

F,LIU K,XIA G,YANG J, 2022

); Because the

collaborative detection constraints are involved, it is

necessary to restrict the whole terminal state of the

interceptor, including position, velocity, velocity

angle and time. Meanwhile, the flight capability

boundary of each interceptor should be considered

comprehensively to find the cooperative trajectory

that meets the state and terminal constraints. With the

increase in the number of targets and interceptors,

finding such a trajectory under multiple constraints

via traditional method is time-consuming.

Considering the target movement, it is difficult to

meet the actual requirements of rapid response of

interceptors online.

There are nonlinear coupling among time,

speed, trajectory, constraint, and the horizontal and

longitudinal plane in the energy descent phase.

Nonlinear programming (NLP) tools can be used to

solve these problems (Lv, S, Cai, M, & Zhou, D,

2019). Besides, the numerical trajectory optimization

method can consider a variety of constraints and

directly use the dynamic model of interceptors, which

more truly reflects the mutual coupling between states

and the restraint relationship of air defense missiles

(Taub, I, & Shima, T, 2013).

In this paper, we study the coordination

rendezvous problem of long-range air-defense

missiles and trying to give a generalized structure to

realize the online negotiation and prediction of

cooperative cost. The key idea of this paper is to

divide the negotiation and optimization of the

trajectory into two subproblems: a) determination of

coordinated time and b) trajectory optimization under

Cui, Z., Wei, M., Li, Y. and Zhang, P.

Cooperative Trajectory Optimization for Long-range Interception with Terminal Handover Constraints.

DOI: 10.5220/0011917200003612

In Proceedings of the 3rd International Symposium on Automation, Information and Computing (ISAIC 2022) , pages 169-176

ISBN: 978-989-758-622-4; ISSN: 2975-9463

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

169

time constraint. And solve by nonlinear programming

tools. Based on the hp-adaptive pseudo-spectral

numerical optimization method, the properties of

feasible region are analyzed and fit the established

database with RBF neural network. Numerical

simulation shows the effeteness of the proposed

method.

2 PROBLEM STATEMENT

2.1 Dynamic Model

Assuming the vehicle is a point of mass, the kinetic

model of the

interceptor in the collaborative

mission is:

sin

cos

cos cos

sin

cos sin

ii i

ii i i

ii i

iiii

mV V

θθ

=− −

=−



(0.1)

Where:

m ,

, V ,

, y , z are the mass, local

gravitational acceleration, velocity, position

components in the interceptor, respectively. The

local trajectory inclination angle

is the angle

between the velocity vector and the local level, and

the heading angle

, that is, the angle between the

velocity vector and the local north direction.

Y ,

are the lift, lateral force and resistance of the

interceptor; the control parameters

[

]

Uaa= is the

normal acceleration instruction in two directions, can

be expressed as follows:

，

= (0.2)

2.2 Boundary Conditions and

Constraints

Different from the re-entry trajectory planning

problem for hypersonic gliding vehicles, the main

feature of the long-range air-defense missile

collaborative trajectories planning problem lies in the

different constraints. Long-range air-defense missiles

use light body and axisymmetric layout, with lower

energy, smaller lift-drag ratio, thinner cylinder wall,

poorer heat resistance than the glide vehicle, and the

interception targets are high mobile aircraft targets.

Their unique constraints can be summarized as

follows:

I) Overload Constraints

Due to the axisymmetric layout of the air-defense

missiles, its high-altitude overload capability is very

limited, and the acceleration constraint of

aerodynamic steering missile can not be simply

considered as constant, but limited by the shell

structure and the aerodynamic capacity. The

maximum overload

maxT

for the shell structure can

be considered as the constant value, but the maximum

aerodynamic overload capacity is subject to

substantial aerodynamic pressure variation due to

altitude and speed change. So, it is coupled together

with speed, height and trajectory, it cannot be solved

analytically (Cho, S. B, & Choi, H. L, 2022). The

coupling relationship between overload constraints,

control history, and terminal constraints can be

expressed as the following formula:

[

]

,(,)

VfUt

= (0.3)

[

]

2lim

(, , ,)

Uf Ut= xx (0.4)

[

]

lim 3

(,)

UfV

= (0.5)

Where

refer to the state parameters,

lim

the time varying control limitation.

II) Detection Constraints

The multi-missile cooperative detection of long-

range air-defense missiles needs to create good

detection conditions for the seeker. It has strict

constraints on the position, difference in search time,

difference in speed, speed angle and lower bounds of

speed. They form the terminal constraints of long-

range air-defense missiles. In addition, the

interception object of air-defense missile interception

is the aircraft-class high dynamic maneuver target.

After the interceptor arrives in the handover area and

the seeker is started, the target may maneuver at any

time. The interceptor is required to have strong

maneuverability and the final speed as much as

possible, to reserve sufficient speed advantages and

overload capacity for the final guidance.

2.3 Optimization Problem

Transforming the problem of collaborative guidance

into optimal control is described as follows:

() ( )

min

()

Ut U

∈Ω

=−

ISAIC 2022 - International Symposium on Automation, Information and Computing

170

min

lim

max

lim

max

s.t.

1, 2

ifi

nn i N

TT T





≥



≤



≤=





≤



≤



==…=









(0.6)

()

,, ,,,

iiiiiii

XYZV

θψ

Because of the nonlinearity aforementioned, the

optimization problem has no analytic solution. It can

only be solved via numerical methods.

3 FEASIBLE REGION FOR

COLLABORATIVE

DETECTION

As the number of interceptors in the bomb group

increases, the dimension explosion phenomenon will

appear, and it takes too long to solve the above

collaborative planning problem directly by numerical

methods. In order to give a general solution scheme

suitable for the arbitrary number of interceptors, this

paper divides the collaborative search problem into

two subproblems: solving the collaborative search

feasible region and constrained trajectory planning.

The difference between the collaborative search

feasible domain and the aircraft accessible

/recoverable region is that the former focuses on the

state-space boundary when the aircraft arrives at the

predicted handover point and focuses on its efficiency

on the subsequent mission; the latter focuses on the

space boundary of the aircraft, such as the hypersonic

aircraft foot print problem and the interceptor

interception area problem.

The Initial conditions are:

(0) 0X = ,

(0) 35 kmY =

(0) 0Z =

(0) 2000 /Vms=

(0) 0

=°

(0) 0

=°

; The terminal conditions are:

() 200km

Xt = , ( ) 20km

Yt = , () 0

Zt = ,

() max

Vt V= , () 0

= , () 0

=°. For the

reason of retain the destruction ability to the target

after detection, the minimum value of the final speed

is limited as

( ) 1200 /

Vt m s≥ .

3.1 Unconstrained Feasible Region

The trajectory obtained without constraints is the

ideal scenario of the flight profile. Reflects the best

capability of the aerodynamic design of the aircraft.

In this paper, the maximum final speed trajectory and

the unconstrained feasible region are shown in Figure

1-4.

Figure 1: Unconstraint optimal trajectory for different

arrival time.

Figure 2: Height history.

Figure 3: Velocity history.

-20

-15

-10

-5

x 10

-1

-0.5

0.5

x 10

Height

Traj ec tory

0 50 100 150

2.5

3.5

4.5

x 1 0

H / m

t / s

Height

0 50 100 150

1300

1400

1500

1600

1700

1800

1900

2000

V / (m/s)

t / s

Velocity

Cooperative Trajectory Optimization for Long-range Interception with Terminal Handover Constraints

171

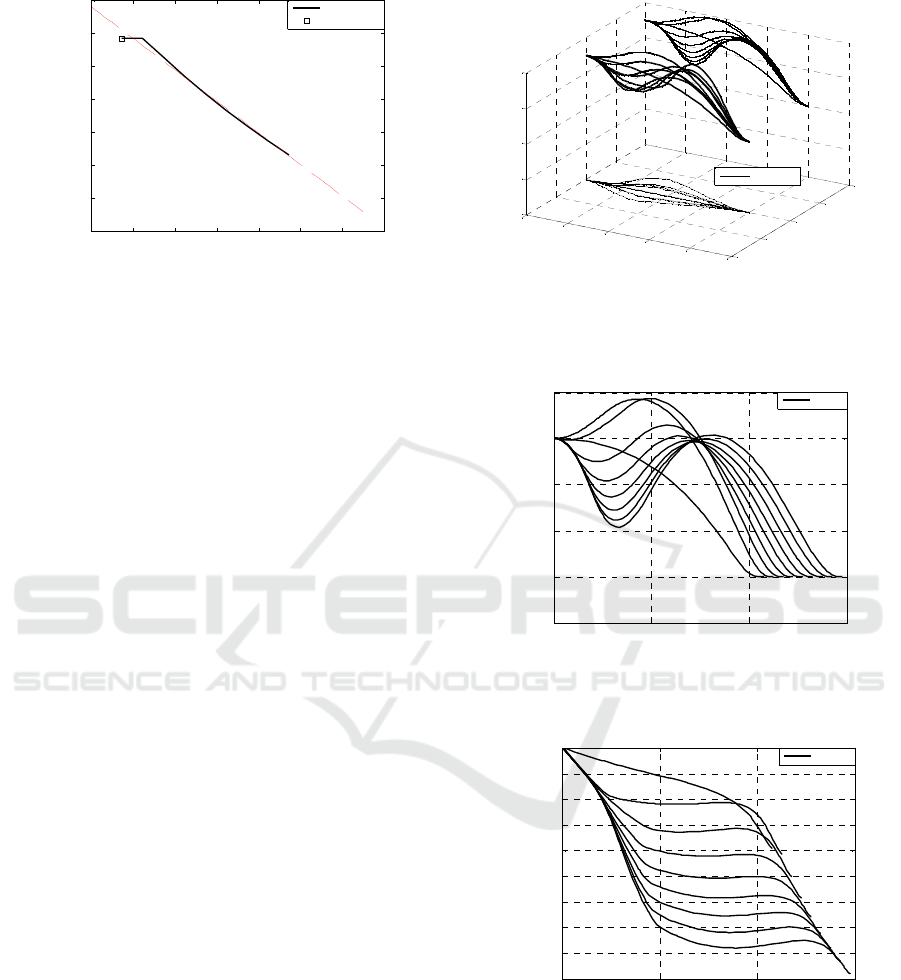
Figure 4: Maximum speed varies with time.

The simulation results show that after considering

the passive decay characteristics, the unconstrained

trajectory is only maneuver in the longitudinal plane.

The trajectories seem to be in the form of parabolic

trajectory. The former accomplishments related

mostly concentrate on the maximum terminal speed,

which is a critical factor for interception.

Nevertheless, this paper further points out through

simulation that the parabolic trajectory also can delay

the arrival time with minimum velocity cost. It has

certain reference significance for the subsequent

design of long-range air-defense missile coordinated

trajectories.

In addition, it can be seen that, after the maximum

speed can afford from parabolic trajectory, the speed

decreases while arrive time increases, and the linear

characteristics appear within a certain range. The

linear slope has obvious physical meaning: the

velocity cost of delay per second. This linear

correspondence will be further analyzed later.

3.2 Constrained the Feasible Region

After considering all the constraints of the long-range

air-defense missiles, the adjustable range of the shift

state is affected by the constraints, and it is reduced

accordingly. As shown in Figure 5~8:

Figure 5: Constrained optimal trajectory for different

arrival time.

Figure 6: Height history.

Figure 7: Velocity history.

100 110 120 130 140 150 160 170

1100

1200

1300

1400

1500

1600

1700

1800

t/s

V/ m/s

Upper bound

Minimum Time

-20

-15

-10

-5

x 10

-1

-0.5

0.5

x 10

Height

Trajectory

0 50 100 150

1.5

2.5

3.5

x 10

H / m

t / s

Height

0 50 100 150

1100

1200

1300

1400

1500

1600

1700

1800

1900

2000

V / (m/s)

t / s

Velocity

ISAIC 2022 - International Symposium on Automation, Information and Computing

172

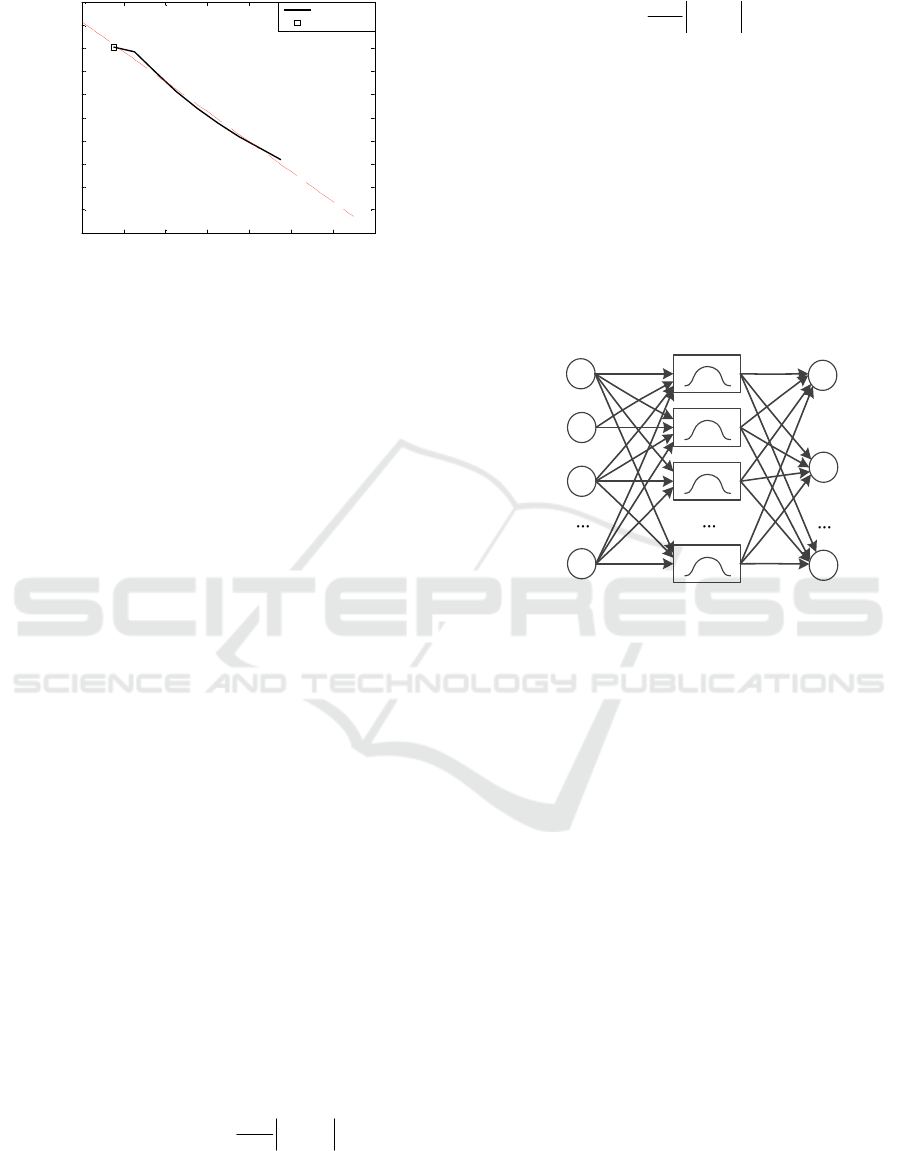
Figure 8: Maximum speed varies with time.

Compared with the unconstrained trajectory

above. It can be found that a) the trajectory changes

not only in the longitudinal plane, but also in the

horizontal plane. b) Because of the overload

limitation, the trajectory is in the form of double-

parabolic in the longitudinal plane, where only have

once in unconstrained scenario. c)

Maximum speed

varies with time still shows linear feature.

Furthermore, it is worth noticing that numerous

simulations show that it is unsensitive to the

disturbance on lift and drag coefficients, so it is

reasonable to fit the relationship linearly.

4 RBF NEURAL NETWORK

The Radical Basis Function (RBF) is one of the

multidimensional spatial interpolation techniques

proposed by Powell in 1985. In 1989, Jackson

demonstrated that RBF neural networks constructed

by RBF function as hidden layer neurons have the

ability to consistently approximate any nonlinear

continuous function. The RBF neural network has the

advantages of simple structure, explicit training

algorithm, and fast learning convergence. It is widely

used in the field of pattern recognition (Lampariello,

F, & Sciandrone, M, 2001) and nonlinear control

(Yang, H., & Liu, J, 2018)

The function commonly used in RBF neural

networks is Gaussian function, so the activation

function in a radial basis function neural network can

be expressed as:

()

exp

pi pi

Rx c x c



−= − −





(4.1)

The neural network structured as Figure 9 can

get the output as:

exp

ii pi

yw xc



=−−







12in=…，

(4.2)

Where,

()

xx x∈ 

is the p

input

sample,

is the node center of hidden layer,

is the

connection weight between the hidden layer to the

output layer,

is the actual output of the i

node.

The solution of the feasible domain of the long-

range air-defense missile can be transformed into a

nonlinear function regression problem with six inputs

and three outputs. The input variables are: speed,

height, range, lateral deviation and two initial

deviation Angle, and the output variables are the

maximum speed, corresponding time and the slope K.

Input Layer Hidden Layer Output Layer

Figure 9: Schematic diagram of the RBF neural network.

The learning algorithm of the RBF neural

network needs to solve the problem having three

aspects, the center of the basis function, the variance,

and the weights between the hidden layer to the

output layer. using self-organized selection center

method as the training method for RBF neural

network. It can be divided into two stages, one is the

self-organized learning stage, this stage using K-

average clustering method determine the center

and variance

, it is a nonlinear optimization

process; In second stage, in order to find the

appropriate weight for the output neurons, using

gradient descent method for training neurons in

output layer.

4.1 Training and Validation of RBF

Neural Network

Optimize 2700 sets of data points offline over the

possible range of initial conditions. The convergence

criteria of the loss function is set to be 4e-7, the

100 110 120 130 140 150 160 170

800

900

1000

1100

1200

1300

1400

1500

1600

1700

1800

t/s

V/ m/s

Upper bound

Minimum Time

Cooperative Trajectory Optimization for Long-range Interception with Terminal Handover Constraints

173

training and the testing result is shown in Figure

10~12:

Figure 10: RBF neural network fitting result.

Figure 11: Fitting error in RBF neural network.

Figure 12: Generalization capability of RBF neural

network.

4.2 Cooperative Guidance Strategy

Based on RBF Neural Network

The negotiation and optimization process of

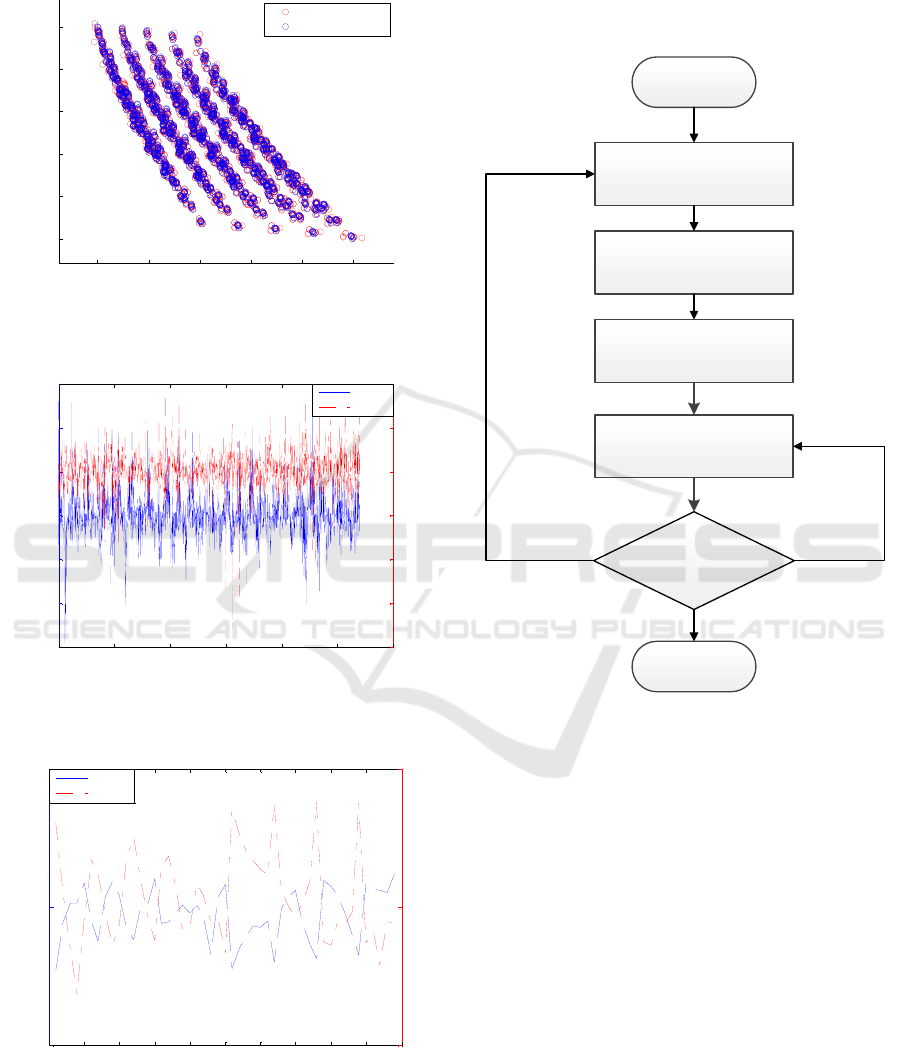
consistency engagement as shown in Figure 13.

Trajectory tracking In cons ider

of modeling inaccuracies

Initial Conditons

Feasi ble region forecasting

based on RBF neural network

trajectory optimization under

time constraint

The tracking error is

within the allowable range

End

Solve the cost of collaboration

and judg e whe ther it is

necessary to collaborate or not

Figure 13: Negotiation and optimization based on RBF

neural network.

5 SIMULATION RESULTS

The typical trajectory simulation of SM-6 missile is

given as an example, which satisfies all the

constraints and requirements on consistency

engagement. The initial parameters of the three

interceptors are shown in Table 1. And the forecast

results obtained through the neural network are

shown in Table 2. Because the time can only be

extended but not shorten, the coordination time is set

as (4.3), and the multiple interceptors plan their own

feasible trajectory. The planning results are shown in

Figure 14~16:

()

ma x , ,

ffi

ttt=…

(4.3)

0 0.2 0.4 0.6 0.8 1

0.2

0.4

0.6

0.8

Data Point

RBFNN Prediction

Training Value

0 500 1000 1500 2000 2500 3000

-3

-2

-1

Time fitting error

0 500 1000 1500 2000 2500 3000

-40

-30

-20

-10

Velocity fitting error

Time

Velocity

0 5 10 15 20 25 30 35 40 45 50

-0.5

0.5

Precision of time prediction

0 5 10 15 20 25 30 35 40 45 50

-5

Precision of velocity prediction

Time

Velocity

ISAIC 2022 - International Symposium on Automation, Information and Computing

174

Table 1: Initial conditions of the interceptors.

Trajectory

Parameter

Missile

Number

240km

1°

35km 2000m/s 300m

2°

200km

1−°

37km 1930m/s 500m

2−°

220km

2−°

33km 2070m/s 0m

0°

Table 2: Forecast results of the RBF neural network

Trajectory Parameter

Missile Number

131.1 s 1558.9 m/s -9.25

111.2 s 1541.2 m/s -12.6

117.1 s 1586.9 m/s -10.4

According to the formula (4.3), we can get

131.1

ts=

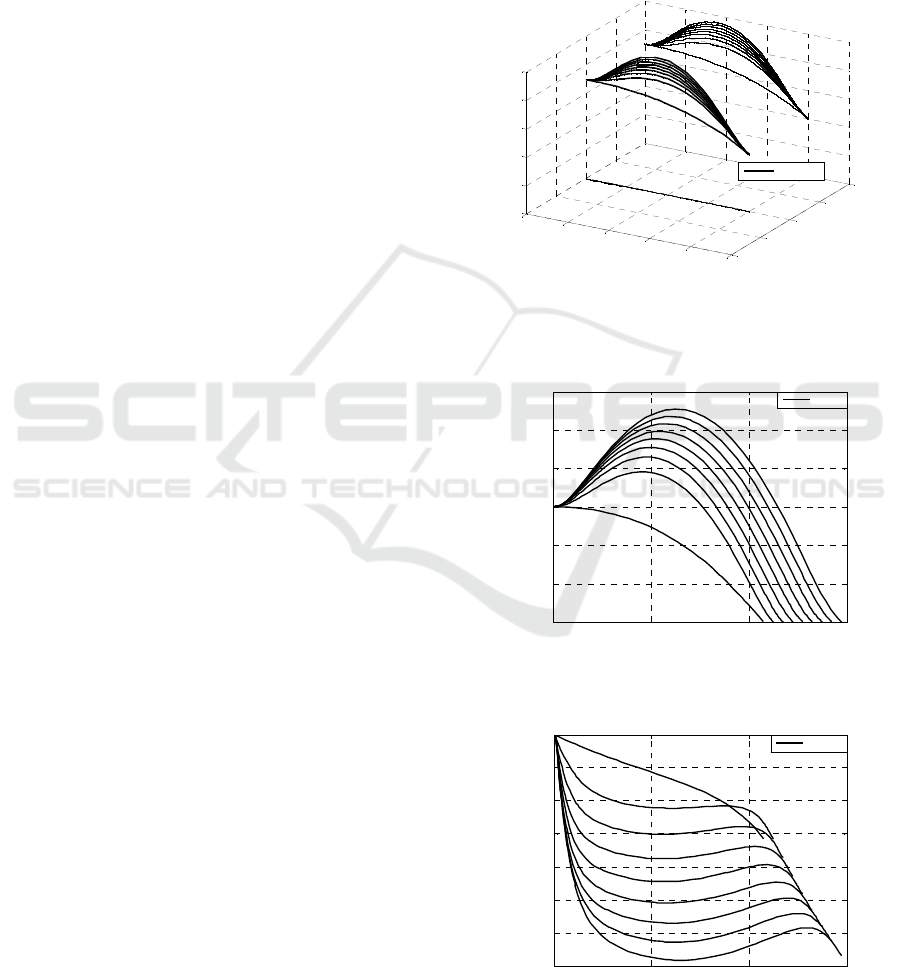
Figure 14: Cooperative trajectory for different interceptors.

Judging by the trajectory, all the interceptors

can reach the target with terminal constraints. And

they maneuver in both the horizontal and

longitudinal planes.

Figure 15: Height varies with time.

In longitudinal planes,

’s trajectory is in

the form of single high-parabolic ballistics, and

’s is in the form of double-parabolic. They both

extend the encounter time while reducing terminal

speed losses.

Figure 16: Velocity varies with time.

The optimal cooperative trajectories and can

satisfied the constraints and can adjust the terminal

time to realize the collaborative rendezvous of all

interceptors.

6 CONCLUSIONS

This paper proposes a method of time cooperative

guidance method based on feasible region to meet the

collaborative rendezvous problem for long-range air-

defense missile. First, the trajectory optimization

problem is decomposed into two subproblems of

determination of the coordinated time and trajectory

optimization under time constraint. Based on hp-

adaptive pseudo-spectral based solution, RBF neural

networks were trained to realize the online

negotiation and prediction. Trajectory simulation

shows that the proposed method can quickly negotiate

the terminal conditions and realize the multi-missile

cooperative planning for long-range air-defense

missiles.

REFERENCES

Wei, M., Cui, Z., & Li, Y. (2020). Review and future

development of multi-missile coordinated interception.

Acta Aeronautica et Astronautica Sinica, 41(suppl 1)),

29-36.

-2.5

-2

-1.5

-1

-0.5

0.5

x 10

-1

-0.5

0.5

x 10

Height

Trajectory

0 20 40 60 80 100 120 140

2.5

3.5

4.5

x 10

H / m

t / s

Height

0 20 40 60 80 100 120 140

1200

1300

1400

1500

1600

1700

1800

1900

2000

2100

V / (m/s)

t / s

Velocity

tf=131.1 s

Vf=1464 m/s

tf=131.1 s

Vf=1557 m/s

tf=131.1 s

Vf=1286 m/s

Cooperative Trajectory Optimization for Long-range Interception with Terminal Handover Constraints

175

Wang, F. B., & Dong, C. H. (2013). Fast intercept trajectory

optimization for multi-stage air defense missile using

hybrid algorithm. Procedia Engineering, 67, 447-456.

Farooq, A., & Limebeer, D. J. (2002). Trajectory

optimization for air-to-surface missiles with imaging

radars. Journal of guidance, control, and dynamics,

25(5), 876-887.

GUO Mingkun,YANG Feng,LIU Kai,XIA

Guangqing,YANG Jingnan. (2022). Research progress

of collaborative guidance technology of hypersonic

aircraft[J].Aerospace Technology, (02):75-84.

Shoukun, L. V., Mingchun, C. A. I., Di ZHOU, Z. H. O. U.,

& Zicai, W. A. N. G. (2019, July). Trajectory

optimization for Long-Range Air-Defense Missile with

a Constraint on Capability of Error Correction. In 2019

Chinese Control Conference (CCC) (pp. 3804-3808).

IEEE.

Taub, I., & Shima, T. (2013). Intercept angle missile

guidance under time varying acceleration bounds.

Journal of Guidance, Control, and Dynamics, 36(3),

686-699.

Cho, S. B., & Choi, H. L. (2022). A Convex Programming-

Based Approach to Trajectory Optimization for

Survivability Enhancement of Homing Missiles.

International Journal of Aeronautical and Space

Sciences, 1-17.

Wang, X., Zhang, Y., Liu, D., & He, M. (2018). Three-

dimensional cooperative guidance and control law for

multiple reentry missiles with time-varying velocities.

Aerospace Science and Technology, 80, 127-143.

Wen, L. I., Teng, S. H. A. N. G., Yinwei, Y. A. O., & Qilun,

Z. H. A. O. (2020). Research on time-cooperative

guidance of multiple flight vehicles with time-varying

velocity. Acta armamentarii, 41(6), 1096.

Liu, Z., Zheng, W., Wang, Y., Wen, G., Zhou, X., & Li, Z.

(2020, November). A cooperative guidance method for

multi-hypersonic vehicles based on convex

optimization. In 2020 Chinese Automation Congress

(CAC) (pp. 2251-2256). IEEE.

Zhou, H., Wang, X., & Cui, N. (2020). Glide guidance for

reusable launch vehicles using analytical dynamics.

Aerospace Science and Technology, 98, 105678.

Huang, G. B., Saratchandran, P., & Sundararajan, N.

(2005). A generalized growing and pruning RBF

(GGAP-RBF) neural network for function

approximation. IEEE transactions on neural networks,

16(1), 57-67.

Yingwei, L., Sundararajan, N., & Saratchandran, P. (1998).

Performance evaluation of a sequential minimal radial

basis function (RBF) neural network learning

algorithm. IEEE Transactions on neural networks, 9(2),

308-318.

Lampariello, F., & Sciandrone, M. (2001). Efficient

training of RBF neural networks for pattern

recognition. IEEE transactions on neural networks,

12(5), 1235-1242.

Yang, H., & Liu, J. (2018). An adaptive RBF neural

network control method for a class of nonlinear

systems. IEEE/CAA Journal of Automatica Sinica,

5(2), 457-462.

ISAIC 2022 - International Symposium on Automation, Information and Computing

176