BLCR: Block-Level Cache Replacement for Large-Scale In-Memory

Data Processing Systems

Yingcheng Gu, Yuanhan Du, Huanyu Cheng, Kai Liu and Tuo Cao

Information and Telecommunication Branch, State Grid Jiangsu Electric Power Co. Ltd., Nanjing, China

Keywords:

Cache Replacement, In-Memory Computing Systems, Big Data Processing.

Abstract:

To reduce the completion time of big data processing applications, in-memory computing has been widely

used in today’s systems. Since servers’ memory capacities are typically limited, there is a need to decide

which data should be cached in memory, namely the cache replacement problem. However, existing works

fall insufﬁcient in analysing the directed acyclic graphs of applications. Moreover, they optimize cache re-

placement in the resilient distributed data level, which is coarse-grained. In this paper, we investigate the

block-level cache replacement problem and formulate it as an integer programming problem. Since it has

the optimal substructure property, we develop the algorithm BLCR based on the dynamic programming tech-

nique. Trace-driven simulations are conducted to evaluate the performance of BLCR and the results show its

superiority over the state-of-the-art alternatives.

1 INTRODUCTION

Due to their superior performance, big data process-

ing systems based on large-scale clusters and in-

memory computing have been widely used in indus-

trial practice. Among these systems, a representative

and popular example is Spark (Zaharia et al., 2010),

which is also chosen as the target system of this paper.

To avoid repeated computation in data processing, the

memory cache technique is used. Speciﬁcally, instead

of ﬂushing intermediate result data to disks or simply

discarding them, Spark caches them in memory. In

this way, there is no need to reload data from the disks

and the completion time could be reduced.

However, since the memory capacities of com-

puting servers are typically limited and the amount

of data (including both raw and intermediate data) is

very large, to simply cache all data becomes impracti-

cal and needless. In other words, one has to determine

which data should be cached in memory and which

should not. Such problem is called the cache replace-

ment problem and has drawn many researchers’ atten-

tion. Currently, there exist many works investigating

the cache replacement problem from several different

perspectives, such as (Yang et al., 2018; Duan et al.,

2016; Yu et al., 2017; Wang et al., 2018).

Unfortunately, existing works fall insufﬁcient in

handling this problem for the following two reasons.

Firstly, to support complex data processing applica-

tions, Spark processes data based on the speciﬁca-

tion of directed acyclic graphs (DAGs), which may

contain guidance information for cache replacement.

Nevertheless, existing works usually assume tasks are

sequentially executed and fail to take advantage of the

parallelism of DAGs. That is to say, they lack a sufﬁ-

cient analysis for the DAG or only leverage the statis-

tical information obtained from the DAG.

Secondly, these works focus on RDD-level cache

replacement, where RDD is short for Resilient Dis-

tributed Dataset, but block-level cache replacement is

rather less studied. When the computing resources

of servers are limited, task scheduling has to satisfy

the computing resource constraint and the start times

of different tasks in the same phase are usually dif-

ferent, which results in different ﬁnish times. In this

case, it is intuitive to cache only some parts of a RDD

(namely, data blocks), rather than a whole RDD, in

memory, since it could improve the memory utiliza-

tion and accelerate data processing.

Therefore, in this paper, we investigate the block-

level cache replacement problem for large-scale in-

memory data processing systems, with the applica-

tion’s DAGs into consideration. Speciﬁcally speak-

ing, we strike to make block-level data cache deci-

sions, with the aim of minimizing the application’s

completion time while satisfying the memory re-

source constraint and the requirements of the applica-

tion’s DAG. To the best of our knowledge, this is the

256

Gu, Y., Du, Y., Cheng, H., Liu, K. and Cao, T.

BLCR: Block-Level Cache Replacement for Large-Scale In-Memory Data Processing Systems.

DOI: 10.5220/0011920800003612

In Proceedings of the 3rd International Symposium on Automation, Information and Computing (ISAIC 2022), pages 256-260

ISBN: 978-989-758-622-4; ISSN: 2975-9463

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

Stage 53 <Time, CPU>

RDD A

block 1

block 2

block 3

<3, 3>

RDD B

block 1

block 2

block 3

RDD C

block 1

block 2

block 3

Stage 54

RDD E

block 1

block 2

block 3

Stage 55

RDD G

block 1

block 2

block 3

RDD H

block 1

block 2

block 3

Stage 56

RDD F

block 1

block 2

block 3

Stage 57

RDD I

block 1

RDD D

block 1

block 2

block 3

<1, 4>

<1, 6>

<3, 2>

<1, 2>

S53 1

S53 2

S53 3

S55 3

S55 2

S55 1

Cache

Space

. . .

Memory Cache Space is full!

block 1

A1 B1 C1

A2 B2 C2

A3 B3 C3

G3 H3

G1 H1

G2 H2

E1 B2 E3 F3

Schedule

time

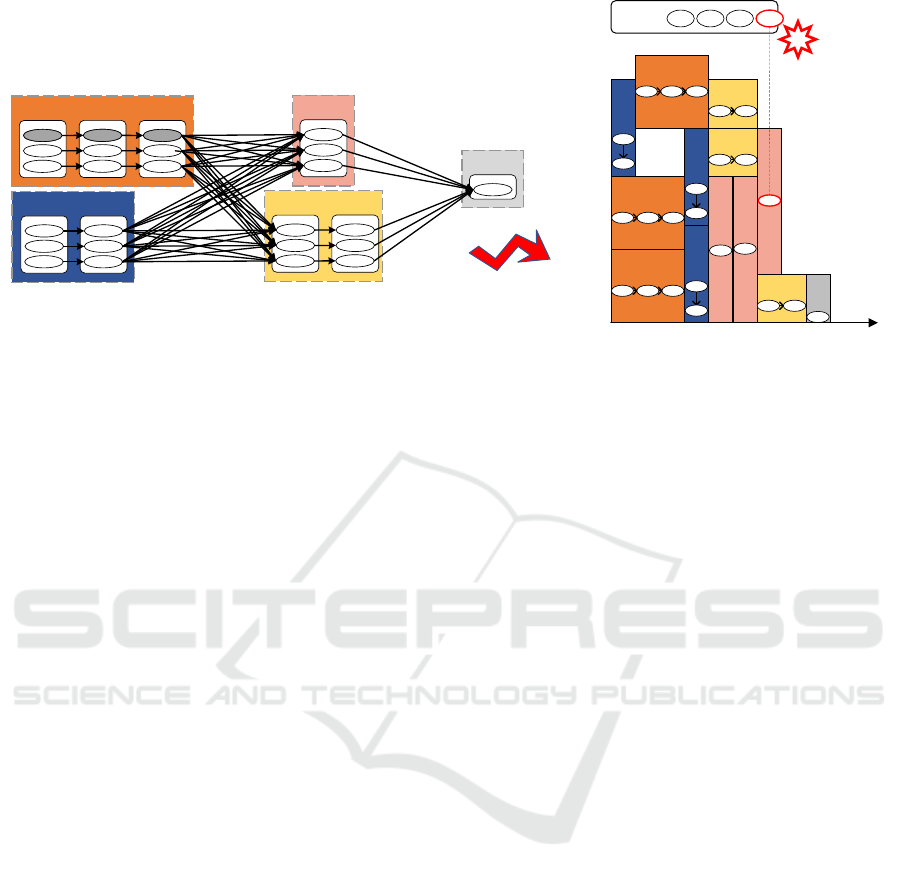
Figure 1: Block-level cache replacement for large-scale in-memory data processing systems.

ﬁrst work studying this problem. We ﬁrst formulate it

as an integer programming problem. To solve it, we

then develop the algorithm BLCR based on the dy-

namic programming technique, since it possesses the

optimal substructure property. At last, we conduct ex-

tensive trace-driven simulations to evaluate BLCR’s

performance and to measure the impact of scenario

parameters. The result shows that BLCR outperforms

the state-of-the-art alternative algorithms.

The remainder of this paper is organized as fol-

lows. We review the related works in Section 2 and

formulate the target problem in Section 3. Section 4

presents the proposed algorithm BLCR. We evaluate

it in Section 5 and conclude this paper in Section 6.

2 RELATED WORK

With the development of big data, cache replacement

for in-memory data processing has been a hot re-

search topic. According to the prior knowledge used,

existing works could be clariﬁed into two categories.

The ﬁrst one optimizes cache replacement decisions

based on history information. Most in-memory com-

puting systems use the LRU policy (Mattson et al.,

1970) to cache RDDs. For example, Yang et al. (Yang

et al., 2018) and Duan et al. (Duan et al., 2016) use the

historical information of computing times and mem-

ory consumption. They intend to cache RDDs with

higher ratios of time to memory. (Zaharia et al., 2010;

Li et al., 2014; Saha et al., 2015) are similar works.

However, historical information only reﬂects data’s

historical popularity, but not for the future.

The other one leverages the DAG information

since it could be obtained once the application is sub-

mitted. Perez et al. (Perez et al., 2018) design MRD

to evict the RDDs with the most reference instance,

which is deﬁned as the subtraction of stage indexes.

NLC uses the non-critical path to express the pop-

ularity of RDDs and evict the RDDs with the most

non-critical-path (Lv et al., 2020). Besides, Yu et al.

propose LRC to evict cached data with the least refer-

ence count, which is deﬁned as the out-degree in the

DAG (Yu et al., 2017). LCRC (Wang et al., 2018) is

similar but considers two types of reference counts,

i.e., intra-stage and inter-stage.

There are also works combining the information

of histories and DAGs, such as (Gottin et al., 2018;

Nasu et al., 2019; Park et al., 2021; Geng et al., 2017;

Zhao et al., 2019; Abdi et al., 2019). However, all

these works cache data in memory in the RDD-level,

which is rather coarse-grained. This paper innova-

tively focuses on the block-level cache replacement

problem and develops an algorithm, based on the dy-

namic programming technique, to solve it.

3 SYSTEM MODEL

We illustrate the block-level cache replacement prob-

lem for large-scale in-memory data processing sys-

tems in Figure 1. In the left side, it shows the DAG

of some data processing application, which is com-

posed of stages, tasks, RDDs and data blocks and is

aware of the computing resource requirements of the

tasks. These tasks are afterwards scheduled and the

scheduling result is shown in the right side. To reduce

the completion time, big data processing systems usu-

ally cache the data blocks generated at runtime in the

memory space. Since the memory resources are rel-

atively limited, there inevitably raises the cache re-

placement problem to be considered. For example,

when the third task of stage 56, i.e., S56 3, generates

data block F3 to be cached and the memory space is

BLCR: Block-Level Cache Replacement for Large-Scale In-Memory Data Processing Systems

257

exhausted, one has to decide which data blocks should

be cached in the memory space and which should be

dropped from the memory space.

Speciﬁcally, we investigate this block-level cache

replacement problem for large-scale in-memory data

processing systems in this paper. We strike to decide

the set of data blocks to be cached in the memory

space when a task is ﬁnished and a new data block

is generated. The objective is to minimize the total

completion time of the application. At the same time,

we have to satisfy the following constraints: 1) the to-

tal size of the cached data blocks is upper bounded by

the memory capacity; 2) the task execution process

follows the DAG of the application. Mathematically,

such problem is formulated as P1:

max

∑

i=1

V (x

, z

)

s.t. x = {x

, x

, . . . , x

= {b

i,1

, b

i,2

, . . . , b

i,Z

}, i = 1, 2, . . . , W

0 ≤ z

≤ Z

, i = 1, 2, . . . , W

∑

i=1

∑

j=1

s(b

i, j

) ≤ L

var. z

, z

, . . . , z

In P1, W is the number of the RDDs involved in

the application and x

is the set of data blocks of the i-

th RDD. Z

is the cardinality of x

, i.e., the number of

data blocks of the i-th RDD. Moreover, b

i, j

is the j-th

data block of x

, s(b

i, j

) is its size and L is the memory

capacity. Furthermore, we take z

, z

, . . . , z

to rep-

resent the decision variables, implying that we cache

the ﬁrst z

data blocks of the i-th RDD in memory.

Finally, V (x

, z

) in the objective function is the per-

formance gain (regarding computing time) of caching

the ﬁrst z

data blocks of x

in memory.

4 ALGORITHM DESIGN

Now we develop algorithms to solve P1. We could

reduce the bounded knapsack problem (BKP), which

is a NP-hard problem, to P1 and prove that P1 is also

a NP-hard problem. However, it is widely believed

that one can not solve a NP-hard problem optimally

in polynomial time unless P = NP. Fortunately, we

ﬁnd that P1 has a desirable property, namely the opti-

mal substructure property. There, based on the dy-

namic programming technique, we design an algo-

rithm, which is named BLCR. BLCR works as fol-

lows, where the details are also shown in Algorithm

1. It ﬁrst initializes the auxiliary variables d p and the

decision variables C (Line 1). Then it follows the dy-

namic programming framework to search optimal de-

cisions (Lines 2-18). At last, it converts and returns

the optimal decisions found (Lines 19-20).

Algorithm 1: BLCR (Block-level cache replacement for

large-scale in-memory data processing systems)

Require: Data blocks {x

| i = 1, 2, . . . , W }, Memory ca-

pacity L, Performance gain function V (x

, z

);

Ensure: Block-level cache decisions {z

| i = 1, 2, . . . , W };

1: d p ← [0]

W ×L

, C ←

2: for i ← 1, 2, . . . , W do

3: for j ← 1, 2, . . . , L do

4: c ← 0, k ← 1, d p

i, j

← d p

i−1, j

;

5: while j − k × s(b

i,1

) ≥ 0 do

6: k ← k + 1;

7: if d p

i−1, j−k×s(b

i,1

)

+V (x

, k) ≥ d p

i, j

then

8: d p

i, j

← d p

i−1, j−k×s(b

i,1

)

+V (x

, k);

9: c ← k;

10: end if

11: end while

12: if c == 0 then

13: C

i, j

= C

i−1, j

;

14: else

15: C

i, j

= C

i−1, j−c×s(b

i,1

)

∪ {b

i,1

, b

i,2

, . . . , b

i,c

};

16: end if

17: end for

18: end for

19: Convert C

W,L

to {z

| i = 1, 2, . . . , W };

20: return {z

| i = 1, 2, . . . , W }.

5 EXPERIMENTS

5.1 Experiment Setup

Table 1: Spark applications used as traces.

Type Name

Machine

Learning

Logistic Regression (LoR)

Linear Regression (LR)

Supported Vector Machine (SVM)

Matrix Factorization (MF)

Decision Tree (DT)

K-means Cluster (Kms)

Principal Component Analysis (PCA)

Label Propagation (LP)

Graph

Computing

Page Rank (PR)

SVD Plus Plus (S++)

Triangle Counting (TC)

Strongly Connected Component (SCC)

Connected Component (CC)

Pregel Operation (PO)

SQL Query RDD Relation (RR)

Others

Shortest Path (SP)

Tera Sort (TS)

Application traces. In order to better evaluate the

performance of BLCR, we leverage the real-word

traces obtained from a well-known Spark benchmark

system, i.e., SparkBench (Li et al., 2015). The traces

cover many applications types, ranging from machine

learning and graph computing to SQL query and oth-

ers. Some representative applications among them in-

ISAIC 2022 - International Symposium on Automation, Information and Computing

258

clude logistic regression, supported vector machine,

decision tree, principal component analysis, page

rank, strongly connected component and so on. We

list the applications used in the experiment in Table 1.

应用Trace

Job

Generator

Stage

Submitter

Task

Scheduler

Task Runner 1

Task Runner 2

Task Runner N

应用Trace

Application

Trace

Application Submit Module Application Runtime Module

Task

Submitter

Figure 2: Framework of Spark simulator with the block-

level cache replacement mechanism.

Spark simulator. We have designed and imple-

mented a Spark simulator with the block-level cache

replacement mechanism inside. As illustrated in Fig-

ure 2, it has four components: Job Generator, Stage

Submitter, Task Scheduler and Task Runner. Job Gen-

erator parses the necessary information from the used

traces. Besides, Stage Submitter is responsible for re-

ceiving the data processing jobs from Job Generator

and submitting executable data processing stages. It

is similar to DAG Scheduler in Spark. Task Sched-

uler receives the executable stages and then allocates

tasks to computing nodes for execution. At last, Task

Runner runs the tasks. More speciﬁcally, it invokes

BLCR and updates the cached data blocks.

Performance benchmarks. To evaluate BLCR,

the following benchmark algorithms are used:

• LRU: when the memory space is full, the least re-

cently used data block in cache is replaced.

• LRC: when the memory space is full, the data

block that has the smallest out-degree in the ap-

plication’s DAG is replaced.

• MRD: when the memory space is full, the data

block that has the longest reference distance in the

application’s DAG is replaced.

• DLCR: make cache replacement decisions via the

dynamic programming technique, but at the RDD

level, rather than the data block level.

5.2 Experiment Results

For any involved application, we take M to denote the

total memory size of all data blocks and take P to de-

note the maximum number of concurrent computing

tasks. Based on that, we set the memory capacity L to

{0.1M, 0.2M, . . . , M} and the number of CPU cores

to {0.25P, 0.5P, 0.75P, P}, which generates 40 conﬁg

combinations. Afterwards, for any cache replacement

algorithm, we perform each application for 40 times,

Figure 3: Averaged Results over 40 Conﬁg Combinations.

where each run corresponds to a unique conﬁg combi-

nation. Figure 3 shows the averaged normalized com-

pletion time and the averaged cache hit ratio. For most

applications, our algorithm BLCR achieves the lowest

completion time and the highest hit ratio.

Figure 4: Performance under Different Memory Capacities.

Figure 5: Performance under Different CPU Core Numbers.

We further conduct experiments to evaluate the

impact of the memory capacity and the available CPU

core numbers on these algorithms. On the one hand,

we set the CPU core number to 0.5P and perform

applications under different memory capacities. On

the other hand, we set the memory capacity to 0.3M

and perform applications under different CPU core

numbers. Their results for Strongly Connected Com-

ponent are shown in Figure 4 and Figure 5, respec-

BLCR: Block-Level Cache Replacement for Large-Scale In-Memory Data Processing Systems

259

tively. As expected, an increase of memory or com-

puting resources reduces the application completion

time. Meanwhile, more memory resources result in

a high cache hit ratio but computing resources have

little inﬂuence on it. We conclude that for most con-

ﬁg combinations, our algorithm BLCR achieves the

lowest completion time and the highest hit ratio.

6 CONCLUSIONS

In this paper, we investigate the block-level cache

replacement problem for large-scale in-memory data

processing systems, with the application’s DAG taken

into consideration. To solve the problem, we develop

the algorithm BLCR based on the dynamic program-

ming technique. At last, trace-driven simulations are

conducted to evaluate the performance of BLCR and

measure the impact of scenario parameters. The result

shows its superiority over the state-of-the-art alterna-

tives. In the future work, we will further study the

block-level cache replacement problem and strike to

design a near-optimal approximation algorithm that

has the polynomial time complexity.

ACKNOWLEDGEMENTS

This work is supported by State Grid Jiangsu Tech-

nic Project “Research on Cloud Native Data Pro-

cessing Architecture based on Data Lake” (No.

SGJSXT00SGJS2200159).

REFERENCES

Abdi, M., Mosayyebzadeh, A., Hajkazemi, M. H., Turk, A.,

Krieger, O., and Desnoyers, P. (2019). Caching in the

Multiverse. In 11th USENIX Workshop on Hot Topics

in Storage and File Systems, HotStorage 2019.

Duan, M., Li, K., Tang, Z., Xiao, G., and Li, K. (2016). Se-

lection and replacement algorithms for memory per-

formance improvement in Spark. Concurrency and

Computation: Practice and Experience, 28(8):2473–

2486. Publisher: Wiley Online Library.

Geng, Y., Shi, X., Pei, C., Jin, H., and Jiang, W. (2017). Lcs:

an efﬁcient data eviction strategy for spark. Interna-

tional Journal of Parallel Programming, 45(6):1285–

1297. Publisher: Springer.

Gottin, V. M., Pacheco, E., Dias, J., Ciarlini, A. E., Costa,

B., Vieira, W., Souto, Y. M., Pires, P., Porto, F., and

Rittmeyer, J. G. (2018). Automatic caching decision

for scientiﬁc dataﬂow execution in apache spark. In

Proceedings of the 5th ACM SIGMOD Workshop on

Algorithms and Systems for MapReduce and Beyond,

pages 1–10.

Li, H., Ghodsi, A., Zaharia, M., Shenker, S., and Stoica, I.

(2014). Tachyon: Reliable, memory speed storage for

cluster computing frameworks. In Proceedings of the

ACM Symposium on Cloud Computing, pages 1–15.

Li, M., Tan, J., Wang, Y., Zhang, L., and Salapura, V.

(2015). Sparkbench: a comprehensive benchmark-

ing suite for in memory data analytic platform spark.

In Proceedings of the 12th ACM international confer-

ence on computing frontiers, pages 1–8.

Lv, J., Wang, Y., Meng, T., and Xu, C.-Z. (2020). NLC: An

Efﬁcient Caching Algorithm Based on Non-critical

Path Least Counts for In-Memory Computing. In

Cloud Computing - CLOUD 2020, pages 80–95.

Mattson, R. L., Gecsei, J., Slutz, D. R., and Traiger, I. L.

(1970). Evaluation techniques for storage hierarchies.

IBM Systems journal, 9(2):78–117. Publisher: IBM.

Nasu, A., Yoneo, K., Okita, M., and Ino, F. (2019). Trans-

parent In-memory Cache Management in Apache

Spark based on Post-Mortem Analysis. In 2019 IEEE

International Conference on Big Data (Big Data),

pages 3388–3396. IEEE.

Park, S., Jeong, M., and Han, H. (2021). CCA: Cost-

Capacity-Aware Caching for In-Memory Data Analyt-

ics Frameworks. Sensors, 21(7):2321.

Perez, T. B., Zhou, X., and Cheng, D. (2018). Reference-

distance eviction and prefetching for cache manage-

ment in spark. In Proceedings of the 47th Interna-

tional Conference on Parallel Processing, pages 1–10.

Saha, B., Shah, H., Seth, S., Vijayaraghavan, G., Murthy,

A., and Curino, C. (2015). Apache tez: A unifying

framework for modeling and building data process-

ing applications. In Proceedings of the 2015 ACM

SIGMOD international conference on Management of

Data, pages 1357–1369.

Wang, B., Tang, J., Zhang, R., Ding, W., and Qi, D. (2018).

LCRC: A dependency-aware cache management

policy for Spark. In 2018 IEEE Intl Conf on Parallel

& Distributed Processing with Applications, Ubiq-

uitous Computing & Communications, Big Data &

Cloud Computing, Social Computing & Network-

ing, Sustainable Computing & Communications

(ISPA/IUCC/BDCloud/SocialCom/SustainCom),

pages 956–963. IEEE.

Yang, Z., Jia, D., Ioannidis, S., Mi, N., and Sheng, B.

(2018). Intermediate Data Caching Optimization for

Multi-Stage and Parallel Big Data Frameworks. In

11th IEEE International Conference on Cloud Com-

puting, CLOUD 2018, pages 277–284.

Yu, Y., Wang, W., Zhang, J., and Letaief, K. B. (2017).

LRC: Dependency-aware cache management for data

analytics clusters. In IEEE INFOCOM 2017-IEEE

Conference on Computer Communications, pages 1–

9. IEEE.

Zaharia, M., Chowdhury, M., Franklin, M. J., Shenker, S.,

and Stoica, I. (2010). Spark: Cluster computing with

working sets. In 2nd USENIX Workshop on Hot Top-

ics in Cloud Computing (HotCloud 10), volume 10,

page 95. Issue: 10-10.

Zhao, C., Liu, Y., Du, X., and Zhu, X. (2019). Research

cache replacement strategy in memory optimization of

spark. Int. J. New Technol. Res.(IJNTR), 5(9):27–32.

ISAIC 2022 - International Symposium on Automation, Information and Computing

260