An Auto-Paired Two-Dimensional DOA Estimation Method for Two
Uniform Linear Arrays
Jun Luo
a
ZTE Communication and Information Collage, Xinyu University, Xinyu, Jiangxi Province, China
Keywords: Propagator Matrix, Uniform Linear Arrays, DOA Estimation, Linear Transformation Matrix.
Abstract: In this paper, an auto-paired two-dimensional DOA estimation method is proposed. This method uses two
nonparallel uniform linear arrays to construct three cross-correlation matrices, and between these cross-
correlation matrices there exists some linear transformation matrices which can be used for obtaining a special
matrix with the paired azimuth and elevation angles information. Then, the propagator method principle will
be used to obtain the special matrix, and by calculating the eigenvalues of the matrix, the auto-paired DOA
can be estimated. The simulations show that the proposed method has better estimation performance with a
good paring manner than two other methods for two parallel uniform linear arrays, and greater advantage in
computational complexity.
1 INTRODUCTION
The direction of arrival (DOA) estimation is an
import problem in array signal processing technology
and widely used in wireless communication, sonar,
and other fields (Fayad et al., 2017 and Wen et al.,
2020). In decades, many liner space processing
methods have been used in DOA estimation for the
parallel array structure, such as multiple signal
classification method (MUSIC) (Liu et al., 2018),
estimation of signal parameters via rotational in
variance techniques method (ESPRIT) (
Herzog and
Habets, 2019
), propagator method (PM) (Xia et al.,
2015), DOA matrix method (Dai et al., 2019), etc. To
solve the non-positive-definite problem of direction
matrix caused by the parallel array structure, such as
coprime array (Li et al., 2018 and Chen et al., 2021),
nested array (Liu et al., 2021 and Zheng and Mu,
2020), many methods have been proposed in recent
years by combing the compressed sensing methods
with liner space processing methods. Besides, for the
radio signal is propagated in three-dimensional space,
the DOA estimates generally contain two angles, such
as azimuth and elevation angles, which should be
correct paired in the DOA estimation progress.
For two uniform linear arrays, an auto-paired
two-dimensional (2-D) DOA algorithm based on PM
method is proposed in this paper. Unlike the array
structure considering in many methods, the structure
a
https://orcid.org/0000-0002-9096-0464
of the two uniform linear arrays is not parallel
structure, and it will be used for constructing three
cross-correlation matrices between which there exists
some linear transformation matrices with auto-paired
angles information. The proposed method makes use
of the PM method principle to obtain the linear
transformation matrices, and then completes the
paired DOA estimation by performing eigenvalue
decomposition of the linear transformation matrix.
For the method proposed in this paper only uses the
cross-correlation matrix of the array output to
perform the DOA estimation, it will have a lower
computational complexity.
2 SYSTEM AND SIGNAL MODEL
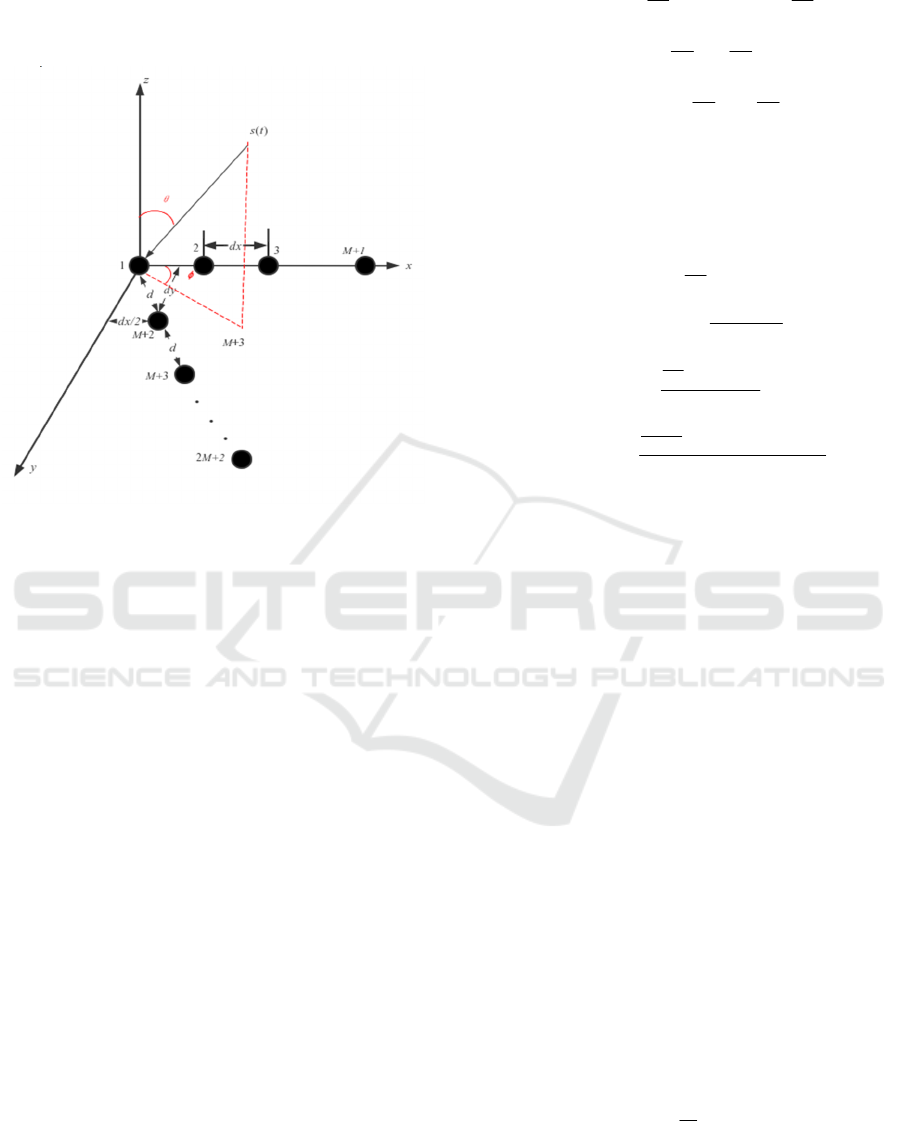
The two uniform linear arrays structure is shown in
Figure 1, and the spacing of horizontal array located
in the X axis is d
x
, and the spacing of the uniform
array located in the X-Y plane is d of which the
horizontal spacing is d
x
/2 and the vertical spacing is
d
y
. Then the position coordinates of the two uniform
linear arrays are (i×d
x
, 0) and (j×d
x
/2, j×d
y
), 0≤i≤M,
1≤j≤M+1, respectively. The K far-field narrowband
plane radio waves impinge on the arrays shown in
Figure 1 with angles (θ
1
, ϕ
1
), (θ
2
, ϕ
2
), …, (θ
K
, ϕ
K
)
where θ
i
and ϕ
i
are the elevation and azimuth angles
Luo, J.
An Auto-Paired Two-Dimensional DOA Estimation Method for Two Uniform Linear Arrays.
DOI: 10.5220/0011921400003612
In Proceedings of the 3rd International Symposium on Automation, Information and Computing (ISAIC 2022), pages 261-265
ISBN: 978-989-758-622-4; ISSN: 2975-9463
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
261

of ith incident signal and 0≤θ
i
<π/2, -π/2≤ϕ
i
<π/2. In
this paper, the number K of radio source signal and
the wavelength λ is assumed as known, and K<M,
d
x
=d
y
=λ/2.
Figure 1: The two uniform linear arrays structure and
direction of arrival of signal.
Then, let X
11
(t), X
12
(t), X
21
(t) and X
22
(t) are the
output of the first M components and last M
components of the two uniform linear arrays,
respectively, which can be written as:
)()(
)](),.....,(),([)(
11
2111
tt
txtxtxt
T
M
nSA
X
+=
=
(1)
)()(
)](),.....,(),([)(
211
13212
tt
txtxtxt
T
M
nSΦA
X
+=
=
+
(2)
)()(
)](),.....,(),([)(
32
123221
tt
txtxtxt
T
MMM
nSA
X
+=
=
+++
(3)
)()(
)](),.....,(),([)(
422
224322
tt
txtxtxt
T
MMM
nSΦA
X
+=
=
+++
(4)
n
1
(t), n
2
(t), n
3
(t) and n
4
(t) are the
M×1dimensional white Gaussian noise vectors with
zero means and variance σ
2
, S(t) is the
M×1dimensional source signal vector with zero
means, A
1
and A
2
are the direction matrices, Φ
1
and
Φ
2
are the diagonal matrices, which are:
)],(),.......,,(),,([
12211111 KK
φ
θ
φ
θ
φ
θ
aaaΑ =
(5)
)],(),.......,,(),,([
22221122 KK
φ
θ
φ
θ
φ
θ
aaaΑ =
(6)
)]2exp(),...,2[exp(
11 K
xx
d
j
d
jdiag
α
λ
πα
λ
π −−=Φ
(7
)
))]
2
(2exp(
)),...,
2
(2[exp(
112
K
y
K
x
y
x
d
d
j
d
d
jdiag
β
λ
α
λ
π
β
λ
α
λ
π
+−
+−=Φ
(8
)
iiiiii
φ
θ
β
φ
θ
α
sinsin ,cossin ==
(9
)
a
1
(θ
i
, ϕ
i
) and a
2
(θ
i
, ϕ
i
) are the direction vectors
of the ith source signal respectively, which are:
)]
)1(
2exp(,
),...2exp(,1[),(
1
k
x
k
x
kk
dM
j
d
j
α
λ
π
α
λ
πφθ
−
−
−=a
(10
)
)]
)1(
2
1
2exp(,
),...
2
2[exp(),(
2
λ
βα
π
λ
βα
πφθ
kykx
kyk
x
kk
dMd
M
j
d
d
j
++
+
−
+
−=a
(11
)
3 THE AUTO-PAIRED DOA
ESTIMATION METHOD
3.1 The DOA Estimation Method
Based on PM
It is clear from Equations (5), (6), (10) and (11) that
both the direction matrices A
1
and A
2
are the
Vandermonde matrices. Thus, A
1
and A
2
can be
assumed as the non-singular matrices, and let A
c
be
the first K rows of A
1
, and A
d
be the other M-K rows.
According to the propagator method, A
c
is a full rank
square matrix, and for the matrices A
c
and A
d
, there
exists a propagator matrix P which have:
dc
H
AAP =
(12
)
Then the cross-correlation matrices of X
11
(t),
X
12
(t), X
21
(t) and X
22
(t) can be written as:
[]
[]

−
=
×
≈==
==
==
1
0
*
1121112
22
12
*
11211
)()(
1
)]()([
N
i
c
H
c
KK
H
c
H
d
H
c
H
ii
N
ttE
XXPRPARA
PIARAAARA
ARAXXR
S
SS
S
(13
)
ISAIC 2022 - International Symposium on Automation, Information and Computing
262

()

−
=
−
≈=
==
==
1
0
*
11222
12
1
2122
122
*
11222
)()(
1
)]()([
N
i
c
H
c
H
c
H
c
H
c
H
ii
N
ttE
XXPR
PAΦAARAPAΦRA
ARΦAXXR
SS
S
(14
)
()

−
=
−
≈
==
==
1
0
*
1222
3112
1
2
1122
*
12223
)()(
1
)]()([
N
i
c
H
c
HH
c
H
c
HH
ii
N
ttE
XX
PRPAΦΦAARA
AΦRΦAXXR
S
S
(15
)
where R
c
is the sub-matrix of R
1
with the first K
columns, R
s
is the covariance matrix of source signal
vector S(t) and I
K×K
is the K×K dimensional identity
matrix. For the snapshot number N of output is finite,
only the approximate matrices of cross-correlation
matrices R
1,
R
2
and R
3
can be obtained which can be
still used for the DOA estimation.
The matrices P
1
, P
2
and P
3
in Equations (13), (14)
and (15) can be obtained by the the minimization
problem as:
1
1
11
)( RRRRRRP
H
cc
H
cc
−+
==
(16
)
2
1
22
)( RRRRRRP
H
cc
H
cc
−+
==
(17
)
3
1
33
)( RRRRRRP
H
cc
H
cc
−+
==
(18
)
where
R
c
+
is the pseudo-inverse matrix of R
c.
Then using Equations (13), (14) and (15), an
estimation matrix Ψ can be obtained as:
()
2/)(
2/)()(2/)(
122
1
1
11132132
H
c
HH
c
HH
AΦΦΦA
PPPPPPPPΨ
+=
+=+=
−
−+
(19)
where the diagonal matrix
Φ
2
+Φ
2
Φ
1
H
in
Equation (19) can be written as:
)]2exp()cos(2..., ,
)2exp()cos(2[
11122
K
y
K
x
y
x
H
d
j
d
d
j
d
diag
β
λ
πα
λ
π
β
λ
πα
λ
π
−
−=+ ΦΦΦ
(20)
It is clear from Equations (19) and (20) that the
eigenvalue matrix of matrix Ψ is a diagonal matrix
which contains the paired angles information.
Therefore, by performing the eigenvalue
decomposition and calculating the magnitude and
phase terms of eigenvalues, the azimuth and elevation
of source signal can be auto-paired and estimated
without extra pairing progress which means the
complexity can be reduced. Let ω
k
be the kth
eigenvalues of matrix Ψ, then the azimuth and
elevation can be estimated by:
()
















+








=
2
2
)(arg
arccos*2
arcsin
ˆ
π
ω
π
ω
θ
k
k
k
(21)
()








=
k
k
k
ω
ω
φ
arccos*2
)(arg
arctan
ˆ
(22)
The major steps of the proposed method can be
summarized as follows:
Al
g
orithm 1: Estimate the 2-D DOA of source si
g
nal
Require: the N output snapshot of all array
components
Obtain the cross-correlation matrices via
Equations (13), (14) and (15), and let R
c
be the sub-
matrix of R
1
with the first
K
columns
Calculate the matrices P
1
, P
2
and P
3
via
Equations (16), (17) and (18).
Obtain the estimation matrix Ψ via Equation
(19).
Perform eigenvalue decomposition of matrix
Ψ, and estimate the azimuth and elevation via
Equations (21) and (22).
3.2 Complexity Analysis
Since the matrix multiplication is much more
complicated than matrix addition, the complexity of
the DOA estimation method almost depends on the
matrix multiplication operation. For the proposed
method, the complexity of cross-variance matrices
calculation is O(3M
2
N), the complexity of the
matrices P
1
, P
2
and P
3
calculation is O(K
3
+2MK
2
+3M
2
K), the complexity of matrix Ψ is O(2MK
2
+2K
3
),
and the complexity of eigenvalue decomposition is
O(K
3
), then the total complexity is O{4K
3
+4MK
2
+3M
2
K+2M
2
N}. For comparison, Li’s method (Li et
al., 2012) and Luo’s method (Luo et al., 2017) are
considered, both of which are based on PM method
and suit for two parallel uniform linear arrays without
extra pairing progress. The complexity of Luo’s
method is O{4K
3
+4MK
2
+(2M)
2
K+MK+(2M)
2
N}, and
the complexity of Li’s method is O{3K
3
+(8M-
1)K
2
+(4M-1)K+(2M+1)
2
(N+K)}. Table 1 shows the
complexity comparison with different snapshot
number N where M is set as 8 and K is set as 3. It is
clear that the complexity of the proposed method is
nearly half of two other methods, and it means the
An Auto-Paired Two-Dimensional DOA Estimation Method for Two Uniform Linear Arrays
263

proposed method has much more advantage in
complexity.
Table 1: The total complexity of three estimation method
with different snapshot number N.
Proposed
metho
d
Luo’s
metho
d
Li’s method
N=100
O(13772) O(26788) O(30508)
N=200
O(26572) O(52388) O(59408)
N=300
O(39372) O(77988) O(88308)
N=500
O(64972) O(129188) O(146108)
N=1000
O(128972) O(257188) O(290608)
4 SIMULATION
In this section, the simulations of proposed method
are given. The carrier frequency f
c
is set as 1GHz, the
source signals are the independent Gaussian random
signals, d
x
and d
y
are set as half of wave length, and
the total number of arrays is 2M+2=18. For each
simulation, there are 500 Monte Carlo simulation
trails. The
root mean square error (RMSE) of
azimuth and elevation estimation which can be
used for the estimation performance comparison is
defined as:

==
−=
500
11
2
,
)
ˆ
(
500
1
l
K
k
klk
K
RMSE
θθ
θ
(23)

==
−=
500
11
2
,
)
ˆ
(
500
1
l
K
k
klk
K
RMSE
φφ
φ
(24)
Figure 2 shows the RMSE of angles estimation
and the comparison of three estimation methods
versus different signal-noise ratio (SNR), where the
snapshot number is 200, the azimuth and elevation
angles of three source signal are (35°,25°), (40°,10°),
(20°, -5°),
respectively.
(a) Elevation estimation performance
(b) Azimuth estimation performance
Figure 2: The estimation RMSE of three methods versus
different SNR.
It is clear in Figure 2 that the estimation RMSE of
the proposed method decrease when SNR increase,
which means the estimation performance of proposed
method improves. With the comparison of Luo’s
method and Li’s method which are suite for two
parallel array structure generally used for 2-D DOA
estimation, when SNR is 8dB, the RMSE of proposed
method is below 1°, and that of the other two methods
is above 1°, and when SNR is below 8dB, the RMSE
of proposed method is still below the other two
methods, and it is clear that the proposed method has
much better estimation performance while the array
structure used in this proposed method is two uniform
linear arrays unlike Luo’s method and Li’s method.
Figure 3 shows the DOA estimation results when
there are four source signals with angles (35°, -40°),
(55°,10°), (15°,10°), and (45°,30°),
respectively,
where the SNR is set as 10dB and the snapshot
number N is 200. It is clear in Figure 3 that the DOA
estimates are very close to the true DOA which are
marked in red in Figure3, and that indicates the
proposed method can estimate the azimuth and
ISAIC 2022 - International Symposium on Automation, Information and Computing
264

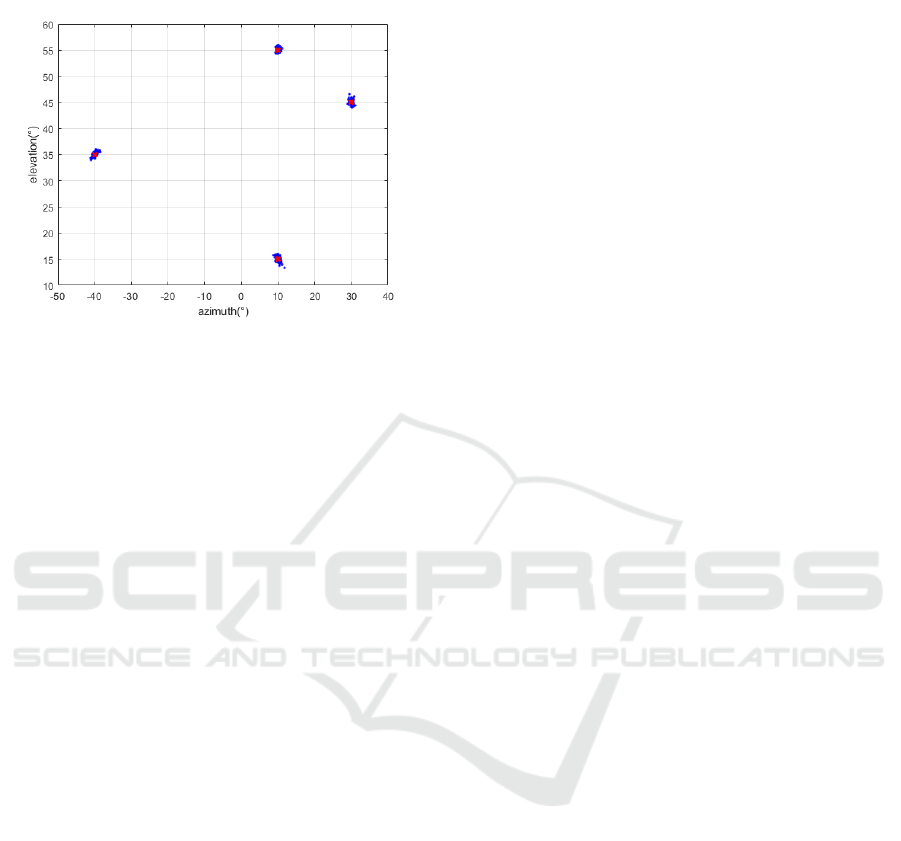
elevation angles with a good pairing manner while the
complexity is reduced.
Figure 3: Distribution of DOA estimates with four source
signals.
5 CONCLUSIONS
In this paper, an auto-paired 2-D DOA estimation
method based on PM method has been proposed for
two uniform linear arrays. The two uniform linear
arrays is not parallel which can be used for
constructing a linear transformation matrix
containing the auto-paired angles information by
using PM method principle and the cross-correlation
matrices of array output. Then, by calculating the
eigenvalue of the linear transformation matrix, the
proposed method can obtain the paired DOA
estimates. The simulations show that the proposed
method have a better DOA estimation performance
and lower complexity.
ACKNOWLEDGEMENTS
This work was financially supported by the Project
for Science and Technology of Jiangxi Education
Department (no. GJJ191048, GJJ202313 and
GJJ212322).
REFERENCES
Fayad, F., Wang, C., Wang, and Cao, Q. (2017). Temporal-
spatial subspaces modern combination method for 2D-
DOA estimation in MIMO radar. Journal of Systems
Engineering and Electronics, 28(4):697-702.
Wen F., Wang J., Shi J., and Gui G. (2020). Auxiliary
vehicle positioning based on robust DOA estimation
with unknown mutual coupling. IEEE Internet of
Things Journal, 7(6):5521-5532.
Liu, Y., Fu, J., Ran, X., and Ming, L. (2018). An improved
MUSIC algorithm for DOA estimation of non-coherent
signals with planar array. In Proceedings of 2018 2nd
International Conference on Data Mining,
Communications and Information Technology, volume
1060. IOP.
Herzog, A., Habets, E. (2019). Eigenbeam-ESPRIT for
DOA-vector estimation. IEEE Signal Processing
Letters, 26(4):572-576.
Xia, L., Zhang, X., and Qiu, X. (2015). Two-dimensional
DOA estimation in monostatic MIMO radar with
double parallel uniform linear arrays using propagator
method. In Proceedings of the 2015 International
Symposium on Computers & Informatics, pages 1416-
1423.
Dai, X., Zhang, X., Wang, Y. (2019). Extended DOA-
matrix method for DOA estimation via two parallel
linear arrays. IEEE Communications Letters,
23(11):1981-1984.
Li, J., Li, D., Jiang, D., and Zhang, X. (2018). Extended-
aperture unitary root MUSIC-based DOA estimation
for coprime array. IEEE Communications Letters,
22(4):752-755.
Chen, L., Lin, X., Zhu, B., and Zhang, X. (2021).
Generalized parallel coprime array for two-dimensional
DOA estimation: a perspective from maximizing
degree of freedom. China Communications, 18(4):14-
26.
Liu, S., Zhao, J., Zhang, Y. (2021). Array manifold
matching algorithm based on fourth-order cumulant for
2D DOA estimation with two parallel nested arrays.
International Journal of Computational Science and
Engineering, 24(2):109-115.
Zheng, Z., Mu, S. (2020). Two-dimensional DOA
estimation using two parallel nested arrays. IEEE
Communications Letters, 24(3):568-571.
Li, J., Zhang, X., Chen, H. (2012). Improved two-
dimensional DOA estimation algorithm for two-parallel
uniform linear arrays using propagator method. Signal
Processing, 92(12):3032-3038.
Luo, J., Zhang, G., Yu, K. (2017). An automatically paired
two-dimensional direction-of-arrival estimation
method for two parallel uniform linear arrays. AEU -
International Journal of Electronics and
Communications, 72:46-51.
An Auto-Paired Two-Dimensional DOA Estimation Method for Two Uniform Linear Arrays
265