Singing Voice Detection Based on a Deeper Convolutional Neural

Network

Wenming Gui

, Zeyu Xia

, Rubin Gong

, Gui Wang

, Bingxu Chen

and Donghui Zhang

Jinling Institute of Technology, Nanjing 211169, Jiangsu, China

Queensland University of Technology, Brisbane City QLD 4000, Australia

{gongrubin, wanggui}@jit.edu.cn, traveller_cbx@163.com, zdh20211025@gmail.com

Keywords: Singing Voice Detection, Deeper Convolutional Neural Network, Recurrent Neural Network, Squeeze and

Excitation Residual Convolutional Network.

Abstract: Singing voice detection is a fundamental task in music information retrieval, which benefits other tasks such

as singing voice separation. We propose a new algorithm based on a deeper convolution neural network, fed

with the logarithmic and mel-scaled spectrogram, to exact and integrate the features of the different layers of

the network and to discriminate the singing voice finally. We demonstrate that this deeper network can

produce good performances and be designed efficiently to some extent. The experiments are based on the

public datasets: Jamendo, Mir1k, RWC pop, and their combined dataset. We also studied what depth of the

network is suitable for this task. The experiments show that the optimal depth on the four public datasets is

152.

1 INTRODUCTION

Singing Voice Detection (SVD) discriminates

whether an audio segment contains a singer’s voice.

It is a frame-level task in the field of music

information retrieval (MIR), which is also

fundamental and crucial for various other tasks

(Krause et al., 2021), such as singing voice separation

(Lin et al., 2021), singer identification (Hsieh et al.,

2020) and lyrics alignment (Gupta et al., 2019).

Generally, the task is mainly associated with two

key steps: feature extraction and classification. From

early works to current methods, as an essential step,

researchers concentrated on developing features.

Earlier features were directly inspired by Voice

Detection (VD), a speech recognition task. These

features include such as Linear Prediction

Coefficients (LPC), Perceptual LPC (PLPC), Zero-

Crossing Rate (ZCR), Spectral Flux (SF), Harmonic

Coefficient (HC), and Mel-Frequency Cepstral

Coefficients (MFCCs). More recent ones have been

designed to capture particular musical characteristics,

such as Fluctogram, Spectral Flatness, and Spectral

Contraction (SC) (Lehner et al., 2018). For the

https://orcid.org/0000-0002-1230-1631

https://orcid.org/0000-0003-0234-5857

classification, several classifiers have been employed

from the earlier ones, such as Hidden Markov Models

(HMM), Gaussian Mixture Models (GMM), Support

Vector Machines, and Random Forest, to the modern

Deep Neural Networks, such as Convolution Neural

Networks (CNN) (Huang et al., 2018; Lehner et al.,

2018; Schlüter, 2016; Schlüter & Grill, 2015; Zhao et

al., 2022a; Zhao et al., 2022b; Zhao et al., 2022c), and

Recurrent Neural Networks (RNN) (Leglaive et al.,

2015).

If we can find a suitable feature to discriminate

voice segments from audio, it would be

straightforward to resolve the problem. However, it

has been challenging to design such a feature so far.

Since some instruments are made following the

frequency characteristics of the human voice, it

would be challenging to distinguish them from voice

using the audios containing these kinds of

instruments. Even state-of-the-art methods still need

help to detect voice while concatenating many

advanced features (Lehner et al., 2018). Fortunately,

we can compensate for this difficulty using

sophisticated classifiers, Random Forests, and DNN-

based algorithms. For example, CNN (Huang et al.,

336

Gui, W., Xia, Z., Gong, R., Wang, G., Chen, B. and Zhang, D.

Singing Voice Detection Based on a Deeper Convolutional Neural Network.

DOI: 10.5220/0011924600003612

In Proceedings of the 3rd International Symposium on Automation, Information and Computing (ISAIC 2022), pages 336-341

ISBN: 978-989-758-622-4; ISSN: 2975-9463

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

2018; Lehner et al., 2018; Schlüter, 2016; Schlüter &

Grill, 2015; Voigtlaender et al., 2019) and RNN (Lee

et al., 2018; Leglaive et al., 2015) are reported to

obtain better performances than the traditional

classifiers.

DNN-based algorithms can learn different levels

of features (Zeiler & Fergus, 2014) by the different

layers of neurons from the input. In (Schlüter, 2016;

Schlüter & Grill, 2015), the input feature of a CNN

with four layers was the Logarithmic and Mel-scaled

Spectrogram (LMS), without any other sophisticated

features. In (Leglaive et al., 2015), the author claimed

to learn higher-level features using Bi-directional

Long Short-Term Memory units (Bi-LSTM) and kept

only the LMS input feature. However, they employed

pre-processing with the Harmonic-Percussive Source

Separation (HPSS) (Nobutaka et al., 2008) algorithm.

Since the shallower CNN (SCNN) can learn higher-

level features, can the Deeper CNN (DCNN) learn

more to obtain better performance?

In this paper, we propose a novel algorithm based

on DCNN with only LMS as the feature, whose depth

usually is larger than ten and can even reach hundreds

of layers. Instead of designing a delicate feature

extractor, we expected the deeper network could

automatically find and integrate the different level

features. Experiments on publicly available datasets

show that the DCNN outperformed the SCNN and

RNN and even surpassed state-of-the-art algorithms

using concatenated advanced features.

2 RELATED WORKS

In the earlier works of SVD, most features came from

speech recognition due to a lack of enough music

information research. As far as we know, the first

work related to SVD is (Berenzweig & Ellis, 2001),

in which speech features, including LPC and its

variants, were employed to locate singing voice

segments from the instrumental accompaniment.

Other speech features such as Spectral Power, Short

Time Energy, ZCR, and MFCC were also used in

some literature (Rocamora & Herrera, 2007).

Although the characteristics of the singing voice

are similar to the speech voice to some extent, there

are some significant differences between

distinguishing the singing voice from

accompaniments and the spoken voice from

background noise (Rocamora & Herrera, 2007). The

elaborated features have been focused on to

discriminate singing voices from accompaniments.

The SF and HC were once taken into account, but

they could have been better features for

discriminating against singing voices because

accompaniments usually had the same characteristic.

In recent years, the Fluctogram, Spectral Flatness,

and SC (Lehner et al., 2018) demonstrated well-

designed features for SVD. A good performance

comparison for different features in earlier works was

conducted (Rocamora & Herrera, 2007). It showed

that MFCCs plus their first-order differences

outperformed the other features in which SVM was

the standard classifier.

Regarding the development of classifiers, the

typical speech classifiers, HMM (Berenzweig &

Ellis, 2001) and GMM were proposed for SVD in the

earlier works. Recently, some classifiers were

reported to be more suited to the SVD task.

Particularly we mention some works based on DNN.

Due to their excellent learning capabilities, DNNs

have significantly improved various tasks, such as

image classification, speech recognition, and natural

language processing. When applied to SVD, they

have succeeded as well. For example, one method

based on a CNN with four layers (Schlüter & Grill,

2015), and another based on a Bi-LSTM (Leglaive et

al., 2015), have shown much better capabilities than

previous approaches (Lehner et al., 2018). They have

become state-of-the-art methods for SVD.

For different classifiers comparison, the same

paper (Rocamora & Herrera, 2007) mentioned above

also evaluated MFCC as the standard feature, and the

results showed that SVM surpassed all the other

classifiers. More recently (Lee et al., 2018), a good

review of SVD research, including DNN-based

algorithms, was presented.

3 PROPOSED METHOD

As mentioned above, SCNN had an excellent

performance on SVD. Can the DCNN learn the better

feature to improve the performance? Can we increase

the number of layers so that SCNN turns out to be

effective DCNN? The first question is just on which

this paper focuses, while for the second question, the

answer is NO due to the well-known problems, the

vanishing and exploding gradient, which lead to

CNN’s learning capabilities stopping to increase with

the number of layers increasing. As for RNN, for

example, LSTM has already extended its depth by the

time dimension. Also, it can increase its depth by

adding layers, as the paper (Leglaive et al., 2015) did.

However, we would pay higher computation costs to

train a deeper RNN with the whole connection layers.

Inspired by the fact that the Squeeze-and-

Excitation network (SENet) was immensely

Singing Voice Detection Based on a Deeper Convolutional Neural Network

337

successful on the recent image classification task (Hu

et al., 2018), we propose a novel SVD algorithm

using a SENet-based DCNN, looking at the LMS

feature as the concatenated images.

3.1 Squeeze-and-Excitation Residual

Neural Network

In order to increase the depth of CNN, some workers

have successfully done, from VGG (Simonyan &

Zisserman, 2014), Inception series (Szegedy et al.,

2015), to Residual Neural Network (Resnet) (He et

al., 2016). Especially Resnet, with identity-based skip

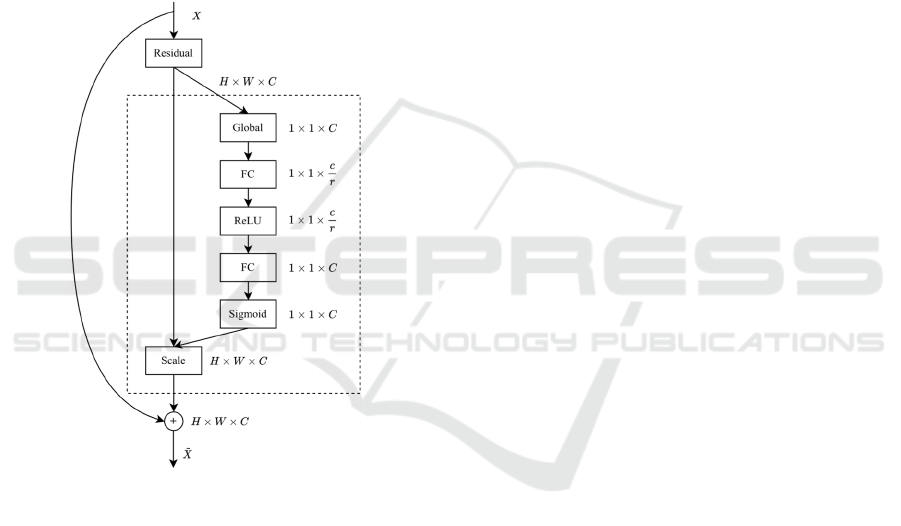
connections (see the arc in Figure 1), significantly

solved the vanishing and exploding gradient problem.

Figure 1: Resnet and SE-ResNet Block Structure.

While the SENet can be integrated into Resnet so

that we can get deeper SE-ResNet for our task. The

SENet ranked as the best performance in the ILSVRC

2017 image classification competition (Hu, Shen et

al. 2018). Besides investigating the spatial structure

of CNN, the SENet strengthened its learning

capabilities by using the relation among channels. Se-

Block is the core structure of the SENet. See the

dashed rectangle in Figure 1. The first step squeezes

the global spatial information into a channel

descriptor using global pooling. In the second step, a

gating mechanism is carried out on the descriptor

aiming at the limitation and generalization of the

model, which comprises three units, a full connection

layer for reducing the dimension, a ReLU, and a full

connection layer for increasing the dimension. A

sigmoid function is employed in the third step to

extract the channel-wised dependencies. Finally, this

dependency information is rescaled to the input

channels.

In CNN, channels represent the feature maps, i.e.,

the different levels of learned features. With more

layers, more features should be learned from the

network. The integrated features would be more

beneficial because some features would take effect

under some circumstances, and others would do

under other circumstances. Intuitively, can the

network learn the different importance of features to

take effect automatically when it is helpful for the

SVD?

As discussed, the SENet could answer this

question by modelling the channel relation. That is

why we employed SE-ResNet in this paper.

To conclude, we would like to employ Resnet

with various depths to extract the different levels of

features and then use Se-Block to choose the suitable

features to discriminate between the voice and the

non-voice segment.

3.2 Input Feature

As discussed, we computed only the kind of essential

feature, LMS, as the input. Ordinarily, the original

music signal was resampled at 22050Hz, and then we

calculated the spectrogram. After applying the Mel

scale to the spectrogram, we made the amplitude

logarithmic. We cut off the frequency band from 27.5

Hz to 8kHz. The frame length was 1024, and the hop

size was 315, i.e., 14.3ms. We segmented the LMS

feature into the 80  80 images and then fed them

into the SE-ResNet, with the hop size 5. So, the total

hop size was 71.5ms, and every image length was

1144ms.

3.3 SE-ResNet with Various Depth

To find the suitable depth for the task, we designed

the SE-ResNet with the depths 14, 18, 34, 50,

101,152, and 200, of which the majorities were by the

typical depths of Resets (He, Zhang et al. 2016),

except the first and last one. The networks with

depths 18 and 34 were piled up with the basic block,

while the bottleneck block was for depths 50, 101,

and 152 (He, Zhang et al. 2016). The SE-Blocks were

embedded into the primary or bottleneck block to

recalibrate the channel-wised weight. As examples,

we demonstrate three different layers of network

structure in Table 1.

Since the input size is 80  80, the output image

sizes are 40, 20, 10, 5, and 3, respectively. The lines

ISAIC 2022 - International Symposium on Automation, Information and Computing

338

“FC” represent SE-Blocks, where the reduction

parameter was 16. The block scale parameters of the

34-layer, 101-layer, and 152-layer network are [3, 4,

6, 3], [3, 4, 23, 3], and [3, 8, 36, 3]. We added depths

14 and 200 in case the best performance would exist

on them. For the 14-layer network, we just modified

the 18-layer network by deleting the last layer. For the

200-layer network, the block scale parameter is [3,

12, 48, 3].

Table 1: SE-ResNet structure examples.

3.4 Training Configuration

We implemented the network on the PyTorch

framework with the help of the Homura package. We

employed the step-wise learning rate scheduler with

step size 10. The cross-entropy was used as the loss

function, and Adam was the optimizer with the

weight decay 110



. We also had the early

stopping mechanism, and the patience was set to 5.

We usually could reach the early stopping around ten

epochs from the experiments, although we set the

maximum epoch as 100.

4 EXPERIMENTS AND RESULTS

This section presents experiments and results based

on SE-ResNet, showing better performance on public

datasets.

4.1 Datasets

We chose three publicly available datasets for

experiments. The first dataset is the Jamendo corpus

(JMD), which contains 93 songs with 371 minutes of

total length. The second is the RWC pop, which

contains 100 songs with 407 minutes of total length.

The third is the Mir1k. Relatively minor, it contains

133 minutes of total length and 1000 song clips with

durations ranging from 4 to 13 seconds.

We kept the original division of train, validation,

and test datasets for JMD (Leglaive et al., 2015; Lee

et al., 2018; Lehner et al., 2018) unchanged, i.e., 61

songs for train, 16 for validation, and 16 for the test.

We divided the RWC dataset by which the songs

ending with the numbers 0-4 were picked up as the

training dataset, 5 and 6 as the validation dataset, and

7-9 as the test dataset. We separated the Mir1k

datasets by which the songs starting with a-g were

chosen as the parts for the training dataset, h-k

(including K) as the validation dataset, and l-z as the

test dataset.

Finally, we combined all three datasets into a

whole dataset by integrating the corresponding

training, validation, and test datasets. Hence, we got

a new dataset called the JRM dataset.

4.2 Comparison of Results

In this paper, we compare the performances based on

the pure models without data augmentation and other

processing, such as HPSS (Lee et al., 2018). Since the

state-of-the-art performances are conducted by

SCNN and RNN (Lee et al., 2018; Lehner et al.,

2018), we designed the experiments to compare our

algorithm and theirs. To some extent, it is fair to

demonstrate the capabilities of the networks in this

way.

Table 2: Network Performances on datasets. The Avg

denotes the average accuracy on RWC, Mir1k, and JMD.

The bold accuracies are the best of SE-ResNets (SERN is

the abbreviation in the table) on the same datasets.

RWC Mir1k JMD Avg JRM

SCNN 0.879 0.876 0.868 0.874 0.873

Bi-LSTM 0.875 0.865 0.875 0.872 0.878

SERN-14 0.899 0.880 0.890 0.890 0.890

SERN-18 0.895 0.882 0.877 0.885 0.890

SERN-34 0.891 0.881 0.897 0.890 0.891

SERN-50 0.912 0.869 0.877 0.886 0.899

SERN-101 0.910 0.870 0.846 0.875 0.897

SERN-152 0.901 0.880 0.885 0.888 0.901

SERN-200 0.900 0.873 0.881 0.884 0.887

LSTM Gain 0.025 0.015 0.01 0.016 0.022

SCNN Gain 0.022 0.004 0.017 0.014 0.027

In (Lee et al., 2018), as a third-party evaluation,

SCNN and Bi-LSTMs-based methods were

developed for revisiting. For SCNN, it only fed the

LMS feature, just the same as our approach.

Therefore, we directly used their results on Jamendo.

To obtain the results of SCNN on the databases RWC,

Mir1k, and JRM, we just run the train and test

programs on the respective datasets. For Bi-LSTMs,

we have tried two versions. One was done without

Singing Voice Detection Based on a Deeper Convolutional Neural Network

339

HPSS, and the other with HPSS as the original

version did. However, the performances without

HPSS were always worse than their counterparts from

experiments. For example, the accuracy was only

0.8003 on JRM. Hence, we did not put it on the table.

On the other hand, we run our algorithm

implementation on the datasets with various depths to

get the performances. We show all the results in terms

of accuracy in Table 2.

From the results, if we used the SE-ResNet with a

depth of 152, the improvement for SCNN and Bi-

LSTM would be on the “SCNN Gain” and “LSTM

Gain” lines, respectively. On the more

comprehensive dataset JRM, which is more

convincing, the accuracies are improved by 2.73%

and 2.29%, respectively. The best performance on

JMD is better than the state-of-the-art method, in

which the five different features were concatenated to

feed to the RNN.

4.3 Results of SE-ResNet with Different

Depths

Due to the amount and diversity of the data for

different datasets, the different depths would lead to

different performances. We show the results in terms

of accuracy on the four mentioned datasets with the

different depths of SE-ResNet in Figure 2.

Figure 2: Accuracy with different depths of SE-ResNet.

The performance on the combined dataset JRM

reaches the highest accuracy of 0.9012 at the depth

152, whereas the others reach the peaks at the mid-

depths (50, 18, 34) on (RWC, Mir1k, Jamendo). It

proves that if there is enough data, the deeper SE-

ResNet would be more potential to get better

performance. Otherwise, the best performance could

end with relatively shallower networks. The deeper

networks tend to be overfitting on the small datasets,

so they cannot obtain the best performance.

It is also worthwhile to note that the performance

on JRM is better than the Avg line. It means the

combination of the three fundamental datasets can

strengthen the overall learning capability of the

network.

4.4 Computation Cost

The network determines the number of parameters

(NoP). Although the Bi-LSTM has the minimum

NoP, it consumes the maximum CC. At the same

time, the computation cost (CC) depends on many

factors, such as the network scale, the network

converging mechanism, and the implementation

method. We ran the programs on the TITAN XP with

12G memory and evaluated CC by minutes per

training, including validation epoch on dataset JRM.

Table 3:

NoP

and CC of the networks on JRM. SERN is

the abbreviation for

SE-ResNet

in the table.

Networ

NoP (M) CC (min)

SCNN 1.4 7

Bi-LSTM 0.1 97

SERN-14 2.8 8

SERN-18 11 10

SERN-34 21 14

SERN-50 26 18

SERN-101 47 24

SERN-152 65 29

SERN-200 118 41

5 CONCLUSIONS

In this study, we proposed a novel SVD algorithm

based on SE-ResNet, which can be very deep.

Furthermore, we investigated the effect of the

different depths of SE-ResNet on the datasets. If we

had a more comprehensive and significant data

dataset, the deeper the network, the better the

performance. The experimental results demonstrated

that we obtained better results than published

systems.

ACKNOWLEDGEMENTS

This research was funded by the Major Program of

Natural Science Foundation for Jiangsu Higher

Education Institutions of China, grant number

22KJA520001, by the Jiangsu Overseas Visiting

Scholar Program for University Prominent Young &

Middle-aged Teachers and Presidents, and by the

Jiangsu Province Modern Education Technology

Research Project, grant number 2022-R-105945.

ISAIC 2022 - International Symposium on Automation, Information and Computing

340

REFERENCES

Berenzweig, A. L., & Ellis, D. P. (2001). Locating singing

voice segments within music signals. In Proceedings of

the 2001 IEEE Workshop on the Applications of Signal

Processing to Audio and Acoustics (WASPAA), pp.

119–122. IEEE.

Gupta, C., Yilmaz, E., & Li, H. (2020). Automatic lyrics

alignment and transcription in polyphonic music: does

background music help? In ICASSP 2020 - 2020 IEEE

International Conference on Acoustics, Speech and

Signal Processing (ICASSP), pp. 496–500. IEEE.

He, K., Zhang, X., Ren, S., & Sun, J. (2016). Deep residual

learning for image recognition. In Proceedings of the

IEEE Conference on Computer Vision and Pattern

Recognition (CVPR), pp. 770–778. IEEE.

Hsieh, T., Cheng, K., Fan, Z., Yang, Y., & Yang, Y. (2020).

Addressing the confounds of accompaniments in singer

identification. In ICASSP 2020-2020 IEEE

International Conference on Acoustics, Speech and

Signal Processing (ICASSP), pp. 1–5. IEEE.

Hu, J., Shen, L., & Sun, G. (2018). Squeeze-and-excitation

networks. In Proceedings of the IEEE Conference on

Computer Vision and Pattern Recognition (CVPR), pp.

7132–7141. IEEE.

Huang, H. M., Chen, W. K., Liu, C. H., & You, S. D.

(2018). Singing voice detection based on convolutional

neural networks. In 2018 7

International Symposium

on Next Generation Electronics (ISNE), pp. 1–4. IEEE.

Krause, M., Müller, M., & Weiß, C. (2021). Singing voice

detection in opera recordings: a case study on

robustness and generalization. Electronics, 10(10),

1214. MDPI.

Lee, K., Choi, K., & Nam, J. (2018). Revisiting singing

voice detection: a quantitative review and the future

outlook. In Proceedings of the 19

International

Society for Music Information Retrieval Conference

(ISMIR), pp. 506–513. Elsevier.

Leglaive, S., Hennequin, R., & Badeau, R. (2015). Singing

voice detection with deep recurrent neural networks. In

IEEE International Conference on Acoustics, Speech

and Signal Processing (ICASSP), pp. 121–125. IEEE.

Lehner, B., Schlüter, J., & Widmer, G. (2018). Online,

loudness-invariant vocal detection in mixed music

signals. In IEEE/ACM Transactions on Audio, Speech,

and Language Processing, 26(8), pp. 1369 – 1380.

IEEE.

Lin, L., Kong, Q., Jiang, J., & Xia, G. (2021). A unified

model for zero-shot music source separation,

transcription and synthesis. In Proceedings of 22

International Conference on Music Information

Retrieval (ISMIR). Elsevier.

Nobutaka, O., Kenichi, M., Jonathan, L. R., Hirokazu, K.,

& Shigeki, S. (2008). Separation of a monaural audio

signal into harmonic/percussive components by

complementary diffusion on spectrogram. In 16

European Signal Processing Conference (EUSIPCO),

pp. 1–4. IEEE.

Rocamora, M., & Herrera, P. (2007). Comparing audio

descriptors for singing voice detection in music audio

files. In Proceedings of 11

Brazilian Symposium on

Computer Music, pp. 187–196.

Schlüter, J. (2016). Learning to pinpoint singing voice from

weakly labeled examples. In International Society for

Music Information Retrieval (ISMIR), pp. 44 – 50.

Elsevier.

Schlüter, J., & Grill, T. (2015). Exploring data

augmentation for improved singing voice detection

with neural networks. In International Society for

Music Information Retrieval (ISMIR), pp.121 – 126.

Elsevier.

Simonyan, K., & Zisserman, A. (2014). Very deep

convolutional networks for large-scale image

recognition. arXiv preprint arXiv:1704.02216.

Szegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S.,

Anguelov, D., Erhan, D., Vanhoucke, V., &

Rabinovich, A. (2015). Going deeper with

convolutions. In Proceedings of the IEEE Conference

on Computer Vision and Pattern Recognition (CVPR),

pp. 1–9. IEEE.

Voigtlaender, P., Krause, M., Osep, A., Luiten, J., Sekar, B.

B. G., Geiger, A., & Leibe, B. (2019). MOTS: Multi-

object tracking and segmentation. In Proceedings of the

IEEE/CVF Conference on Computer Vision and

Pattern Recognition (CVPR), pp. 7942–7951. IEEE.

Zeiler, M. D., & Fergus, R. (2014). Visualizing and

understanding convolutional networks. In European

Conference on Computer Vision (ECCV), pp. 818–833.

Springer.

Zhao, S., Li, Q., He, T., & Wen, J. (2022). A step-by-step

gradient penalty with similarity calculation for text

summary generation. Neural Processing Letters, 1–16.

Zhao, S., Liang, Z., Wen, J., & Chen, J. (2022). Sparsing

and smoothing for the seq2seq Models. IEEE

Transactions on Artificial Intelligence, 1–10.

Zhao, S., Zhang, T., Hu, M., Chang, W., & You, F. (2022).

AP-BERT: Enhanced pre-trained model through

average pooling. Applied Intelligence, 52(14), 15929–

15937.

Singing Voice Detection Based on a Deeper Convolutional Neural Network

341