Fuzzy Expert System of the Decision Making Support on Foreign Direct

Investment

Eugene E. Fedorov

1 a

, Liubov O. Kibalnyk

2 b

, Lesya O. Petkova

1 c

Maryna M. Leshchenko

1 d

and Vladyslav M. Pasenko

1 e

Cherkasy State Technological University, 460 Shevchenko Blvd., Cherkasy, 18006, Ukraine

The Bohdan Khmelnytsky National University of Cherkasy, 81 Shevchenko Blvd., Cherkasy, 18031, Ukraine

Keywords:

Fuzzy Expert Decision Support System, Foreign Direct Investment, Swarm Metaheuristics, Optimization

Methods, Operator.

Abstract:

The fuzzy expert decision support system for foreign direct investment was developed in the research. A

quality criterion was chosen for the proposed fuzzy expert system, which considers the created fuzzy expert

system’s speciﬁcs and allows assessing the probability of future decisions. A metaheuristic method was cre-

ated based on an adaptive gravitational search algorithm to determine the parameters of the proposed fuzzy

expert system. A numerical study was carried out; the parameters of membership functions for linguistic

input variables were determined; the parameters of the membership functions for the values of the linguistic

output variable were determined. The proposed optimization method based on swarm metaheuristics and a

fuzzy expert system make it possible to intellectualize the technology of making decisions on foreign direct

investment.

1 INTRODUCTION

The decision-making systems for foreign direct in-

vestment are very popular nowadays. The regres-

sion (Milovanovi

c and Markovi

c, 2022) and auto-

regressive (Kurecic and Kokotovic, 2017) methods

are usually used to create decision-making systems

for foreign direct investment based on machine learn-

ing. The construction of only linear models is the

disadvantage of such methods. The knowledge base

(most often in the form of production rules) and

an inference mechanism are used to create decision-

making systems for foreign direct investment based

on expert systems (

Samanovi

c et al., 2010). The dis-

advantages of such systems include the fact that they

operate only with quantitative estimates, while it is

easier for the operator to work with qualitative esti-

mates.

The fuzzy expert systems are currently used to

simplify the interaction between a human and a com-

https://orcid.org/0000-0003-3841-7373

https://orcid.org/0000-0001-7659-5627

https://orcid.org/0000-0003-4519-3726

https://orcid.org/0000-0002-0210-9582

https://orcid.org/0000-0002-7411-2625

puter system. These expert systems usually use the

Larsen, Mamdani, Tsukamoto, and Sugeno fuzzy

inference mechanisms (Ruan, 1997; Tsoukalas and

Uhrig, 1997).

The disadvantages of such systems include the

fact that the procedure for determining their param-

eters is not automated (Abe, 1997; Rotshtein et al.,

2001). The optimization methods are currently ac-

tively used to determine the parameters of fuzzy ex-

pert systems.

Modern optimization methods suffer from one or

more of the following disadvantages:

• have high computational complexity;

• fall into a local extremum with a high probability;

• do not guarantee convergence.

In this regard, there is an actual problem of opti-

mization methods’ insufﬁcient efﬁciency.

Metaheuristics (modern heuristics) are used to

speed up ﬁnding a quasi-optimal solution to optimiza-

tion problems and reduce the probability of hitting a

local extremum (Talbi, 2009; Engelbrecht, 2007; Yu

and Gen, 2010; Nakib and Talbi, 2017; Yang, 2018a;

Subbotin et al., 2016). Metaheuristics expand the pos-

sibilities of heuristics by combining heuristic methods

based on a high-level strategy (Blum and Raidl, 2016;

Fedorov, E., Kibalnyk, L., Petkova, L., Leshchenko, M. and Pasenko, V.

Fuzzy Expert System of the Decision Making Support on Foreign Direct Investment.

DOI: 10.5220/0011930700003432

In Proceedings of 10th International Conference on Monitoring, Modeling Management of Emergent Economy (M3E2 2022), pages 15-22

ISBN: 978-989-758-640-8; ISSN: 2975-9234

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

Glover and Kochenberger, 2003; Yang, 2018b; Mart

et al., 2018; Gendreau and Potvin, 2019).

Modern metaheuristics suffer from one or more of

the following disadvantages:

• insufﬁcient method accuracy (Alba et al., 2013);

• there is only an abstract description of the method

or the description of the method is focused on

solving only a speciﬁc problem (Doerner et al.,

2007);

• the procedure for determining parameter values is

not automated (Grygor et al., 2019);

• the inﬂuence of the iteration number on the so-

lution search process is not taken into account

(Bozorg-Haddad, 2017);

• there is no possibility to solve problems of condi-

tional optimization (Fedorov et al., 2019);

• there is no possibility to use non-binary potential

solutions (Radosavljevi

c, 2018);

• the method convergence is not guaranteed

(Chopard and Tomassini, 2018).

In this regard, the problem of constructing efﬁ-

cient metaheuristic optimization methods arises (Du

and Swamy, 2016; Brownlee, 2011).

One of the popular metaheuristics is the gravita-

tional search algorithm (Rashedi et al., 2009), which

belongs to swarm metaheuristics.

The task of building fuzzy expert systems that use

the method of parametric identiﬁcation for adaptation

and tuning is actual for our research.

The goal of this research is to improve the efﬁ-

ciency of decisions on foreign direct investment by

creating a fuzzy expert system trained based on meta-

heuristics.

The following tasks were set and solved:

1) to develop a fuzzy expert decision support system

for foreign direct investment;

2) to select a quality criterion for the proposed fuzzy

expert system;

3) to create a metaheuristic method based on an

adaptive gravitational search algorithm to deter-

mine the proposed fuzzy expert system parame-

ters;

4) to conduct numerical research.

2 THE FUZZY EXPERT

DECISION SUPPORT SYSTEM

FOR FOREIGN DIRECT

INVESTMENT

The foreign direct investment analysis is based on

the data of the GDP per capita volume, inﬂation rates,

goods and services exports volume, and labor force

indicators. To make decisions on foreign direct in-

vestment, a fuzzy expert system is proposed. It in-

volves the following steps:

1) linguistic variables formation;

2) fuzzy knowledge base formation;

3) Mamdani fuzzy inference mechanism formation:

• fuzziﬁcation;

• sub-conditions aggregation;

• conclusions activation;

• aggregation of conclusions;

• defuzziﬁcation.

4) identiﬁcation of parameters based on metaheuris-

tics.

2.1 Linguistic Variables Formation

The following input variables were chosen:

• the volume of gross domestic product (GDP) per

capita (per year, US dollars), x

;

• the inﬂation indicator (according to the consumer

price index, which reﬂects the annual percentage

change in the cost for the average consumer of

purchasing a goods and services basket, per year,

%), x

;

• the volume of goods and services export indicator

(total volume, per year, USD), x

;

• the labor force indicator (labor force is people

aged 15 and over who provide labor for the pro-

duction of goods and services, per year, number

of people), x

The following indicators were chosen as linguistic

input variables. They are qualitative indicators:

• the GDP volume ˜x

with values

= little,

= medium,

= much, where the

ranges are fuzzy sets

= {(x

,µ

))},

= {(x

,µ

))},

= {(x

,µ

))};

• the inﬂation indicator ˜x

with values

little,

= medium,

= much, where the

ranges are fuzzy sets

= {(x

,µ

))},

= {(x

,µ

))},

= {(x

,µ

))};

M3E2 2022 - International Conference on Monitoring, Modeling Management of Emergent Economy

• the volume of goods and services export indica-

tor ˜x

with values

= little,

= medium,

= much, where the ranges are fuzzy sets

= {(x

,µ

))},

= {(x

,µ

))},

= {(x

,µ

))};

• the labor force indicator ˜x

with values

= little,

= medium,

= much, where

the ranges are fuzzy sets

= {(x

,µ

))},

= {(x

,µ

))},

= {(x

,µ

))}.

The volume of foreign direct investment (net ﬂows

for the year, USD) was chosen as a clear output vari-

able ˜y. It is a qualitative indicator.

The volume of foreign direct investment was

chosen ˜y with its values

= little,

medium,

= much, where the ranges are fuzzy

sets

= {(y,µ

(y))},

= {(y,µ

(y))},

= {(y,µ

(y))};

2.2 Fuzzy Knowledge Base Formation

Fuzzy knowledge is represented as the following

fuzzy rules that contain a linguistic output variable

: IF ˜x

is ˜a

AND ˜x

is ˜a

2 j

AND ˜x

is ˜a

AND ˜x

is ˜a

then ˜y is

In the case of linguistic variables speciﬁc values,

fuzzy knowledge is presented in relational form in ta-

ble 1.

Table 1: Relational form of fuzzy knowledge representa-

tion.

The rule ˜x

˜x

˜y

... ... ... ... ... ...

2.3 Mamdani Fuzzy Inference

Mechanism Formation

2.3.1 Fuzziﬁcation

We will determine the truth degree of each sub-

condition of each rule, using the membership function

i j

As membership functions of sub-conditions, we

chose:

• piecewise linear Z-shaped function, i.e.

) =







1, x

≤ a

−x

−a

, a

< x

< b

0, x

≥ b

,i ∈ 1, 4

• piecewise linear Π-shaped function, i.e.

) =











0, x

≤ a

−a

, a

≤ x

≤ b

1, b

≤ x

≤ c

−x

−c

, c

≤ x

≤ d

0, x

≥ d

,i ∈ 1, 4

• piecewise linear S-shaped function, i.e.

) =







0, x

≤ c

−c

, c

< x

< d

1, x

≥ d

,i ∈ 1, 4,

where a

, b

, c

, d

- membership function param-

eters.

2.3.2 Sub-Condition Aggregation

The condition membership functions for each rule R

are determined based on the minimum value method:

i=1

i, f (n,i)

) = min

i∈1,4

i, f (n,i)

)

where f – a function that returns the value number of

the i-th linguistic input variable of the n-th rule and is

determined on the basis of table 1. For example, if the

linguistic input variable ˜x

rules R

matters

, then

f (81,1) = 3.

2.3.3 Activation of Conclusions

The membership functions of the conclusion for each

rule R

are determined based on the minimum value

method (based on the Mamdani rule):

g(n)

(y) = min



i=1

i, f (n,i)

),µ

g(n)

(y)



where g – a function that returns the value number of

the linguistic output variable of n-th rule and deter-

mined on the basis of table 1.

For example, if the linguistic output variable ˜y of

the rule R

, then g(81) = 3.

A piecewise linear triangular function was chosen

as the membership functions of the conclusions, i.e.

(y) =











0, y ≤ e

y−e

−e

, e

≤ y ≤ u

−y

−u

, u

≤ y ≤ v

0, y ≥ v

,m ∈ 1, 3,

where e

– membership function parameters.

In the case of such a membership function, the

kernel of each fuzzy set

is:

ker

= {y ∈ Y |µ

(y) = 1} = {u

Fuzzy Expert System of the Decision Making Support on Foreign Direct Investment

2.3.4 Aggregation of Conclusions

The membership functions of the ﬁnal conclusion are

deﬁned, which contains a linguistic output variable

based on the maximum value method:

(Y ) = max

n∈1,81

{µ

(n)

(y)}

2.3.5 Defuzziﬁcation

The volumes of foreign direct investment are deter-

mined basedon the centroid method:

∗

∑

y∈Y

(y)y

∑

y∈Y

(y)

,Y =



1,2,3



3 QUALITY CRITERION FOR

THE PROPOSED FUZZY

EXPERT SYSTEM

The objective function is chosen as a quality crite-

rion, representing the accuracy as probability of cor-

rect foreign direct investment

F =

∑

p=1

,[y

= d

] → max

[p = q] =



1, p = q

0, p ̸= q

(1)

where d

– test foreign direct investment,

– foreign direct investment received as a result

of fuzzy inference,

P – number of test implementations,

θ = (a

,...,a

,...,e

) – parameter vector of membership functions.

4 METAHEURISTIC METHOD

BASED ON AN ADAPTIVE

GRAVITATIONAL SEARCH

ALGORITHM FOR

DETERMINING THE

PARAMETERS OF THE

PROPOSED FUZZY EXPERT

SYSTEM

The particle velocity (not the gravitational constant)

depends on the iteration number in this method, which

provides control over the convergence rate of the

method, as well as providing a global search at the

initial iterations, and a local search at the ﬁnal itera-

tions. The parameter vector of membership functions

corresponds to the position vector of one particle x.

The quality criterion is used as the goal function (1).

1. Initialization.

1.1. Setting the gravitational constant G, the max-

imum number of iterations N, the population

size K, the length of the particle position vec-

tor M (it corresponds to the length of the pa-

rameter vector of membership functions and is

equal to 25), the minimum and maximum val-

ues for the position vector x

min

, x

max

, j ∈ 1,M,

the minimum and maximum values for the ve-

locity vector v

min

, v

max

, j ∈ 1,M .

1.2. The best position vector randomly generating

∗

= (x

∗

,...,x

∗

= x

min

+ (x

max

− x

min

)U(0,1),

where U(0,1) – a function that returns a uni-

formly distributed random number in a range

[0,1].

1.3. The initial population creation

1.3.1. Particle number k = 1, P =

1.3.2. A position vector at random x

generating

= (x

,...,x

k j

= x

min

+ (x

max

− x

min

)U(0,1).

1.3.3. Random velocity vector v

generating

= (v

,...,v

i j

= v

min

+ (v

max

− v

min

)U(0,1).

1.3.4. If (x

) /∈ P, then P = P ∪ {(x

)},

k = k + 1.

1.3.5. If k ≤ K, then go to step 1.3.2.

2. Iteration number n = 1.

3. The computation of the best and worst particle of

a population from a target function

l = arg min

F(x

),x

best

= x

l = arg max

F(x

),x

worst

= x

4. The computation of all particles masses.

5. The computation of the gravitational force acting

between all pairs of particles

5.1. m

= G

F(x

)−F(x

worst

)

F(x

best

)−F(x

worst

)

,k ∈ 1,K.

5.2. M

∑

s=1

,k ∈ 1,K.

6. The computation of the gravitational force acting

between all pairs of particles

= G

d(x

) + ε

− x

),k,l ∈ 1, K,

where d(x

) – distance between particles k and

l (e.g. Euclid distance).

M3E2 2022 - International Conference on Monitoring, Modeling Management of Emergent Economy

7. The computation of the resulting force acting on

all particles

= U(0,1), k, l ∈ 1, K

∑

l = 1

l ̸= k

,k ∈ 1,K

8. Modiﬁcation of the acceleration of all particles

,k ∈ 1,K

9. Speed modiﬁcation of all particles

= U(0,1), k ∈ 1,K

= r

+ a

,k ∈ 1,K

10. Modiﬁcation all of the particles’ position, taking

into account the iteration number

10.1. x

= x

+ v



1 −



,k ∈ 1,K

10.2. x

k j

= max{x

min

k j

},x

k j

min{x

max

k j

}, j ∈ 1,M,k ∈ 1,K

11. If n < N, then n = n +1, go to step 3

The result is x

∗

5 NUMERICAL RESEARCH

Numerical research was carried out using the Keras

submodule of the TensorFlow module. The Pandas

module was used to ﬁll in missing values through lin-

ear interpolation, as well as for tabular data I/O oper-

ations. The Scikit-fuzzy module was used to create a

fuzzy expert system.

The fuzzy expert system was researched using

the World Bank economic indicators database (https:

//databank.worldbank.org/home.aspx). The economic

indicators of 145 countries for 10 years were used.

The size of the original sample was 1450.

For the proposed adaptive gravity search algo-

rithm, the gravity constant G was 100, the maximum

number of iterations was 1000, and the population

size was 50.

The comparison results of the proposed fuzzy ex-

pert system with the operator are presented in table 2.

Table 2: Comparison results of the proposed fuzzy expert

system with an operator.

Accuracy

fuzzy expert system operator

0.98 0.8

The comparison results of the proposed fuzzy ex-

pert system with the proposed meta-heuristic adaptive

gravitational search algorithm (AGSA) and the tradi-

tional meta-heuristic adaptive gravitational search al-

gorithm (AGSA) operator are presented in table 3.

Table 3: Comparison results of the proposed fuzzy expert

system of the proposed meta-heuristic and the traditional

meta-heuristic.

Accuracy

GSA AGSA

0.93 0.98

Figure 1 shows the accuracy for the proposed

fuzzy expert system trained based on the proposed

meta-heuristic adaptive gravitational search algorithm

(AGSA) and on the proposed meta-heuristic gravita-

tional search algorithm (GSA).

Figure 1: Accuracy of the proposed fuzzy expert system

with GSA and AGSA.

The comparison results of the proposed fuzzy ex-

pert system trained on the basis of back-propagation

(BP) and the proposed meta-heuristic adaptive gravi-

tational search algorithm (AGSA) are presented in ta-

ble 4.

Figure 2: Accuracy of the proposed fuzzy expert system

with BP and AGSA.

Figure 2 shows the accuracy for the proposed

Fuzzy Expert System of the Decision Making Support on Foreign Direct Investment

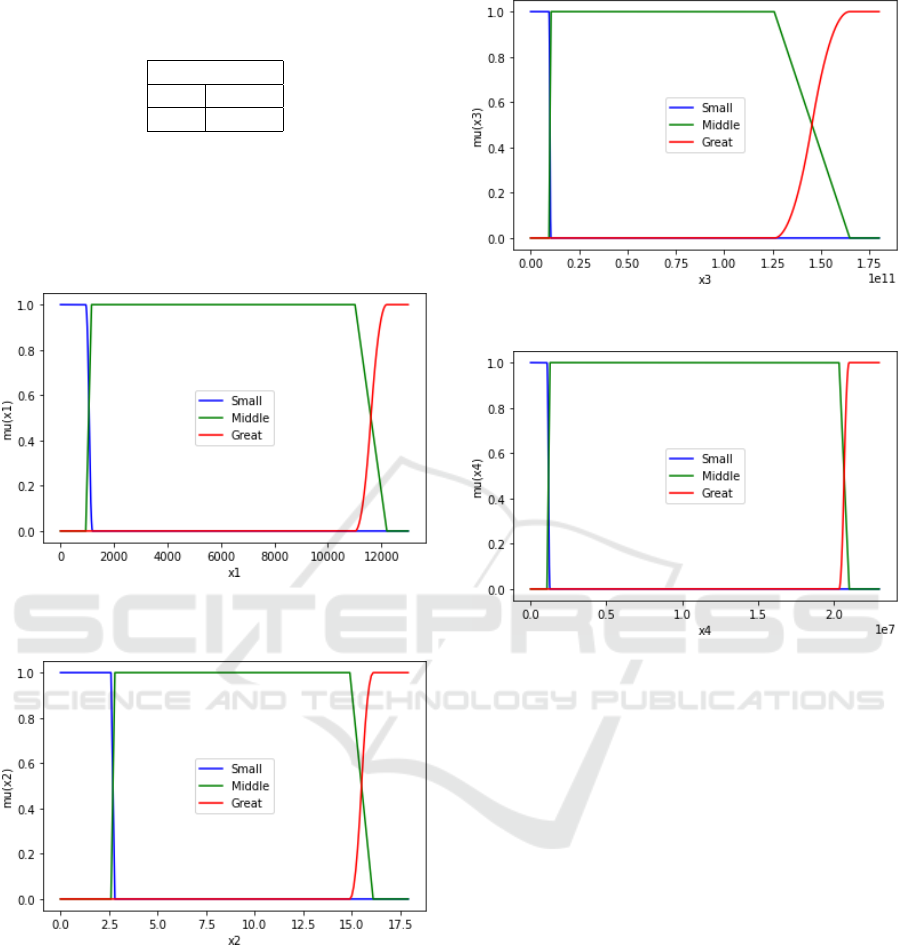
Table 4: Comparison results of the proposed fuzzy expert

system based on the back-propagation method and proposed

meta-heuristic.

Accuracy

BP AGSA

0.90 0.98

fuzzy expert system trained on the basis of back-

propagation (BP) and the proposed meta-heuristic

adaptive gravitational search algorithm (AGSA).

Figures 3-7 shows the membership functions for

the values of linguistic variables ˜x

, ˜x

and y.

Figure 3: Membership functions for linguistic variable val-

ues ˜x

Figure 4: Membership functions for linguistic variable val-

ues ˜x

6 DISCUSSION

The traditional non-automatic approach to assessing

the foreign direct investment effectiveness reduces the

accuracy of a correct assessment (table 2). The pro-

posed method eliminates this disadvantage.

The traditional method of the gravitational search

algorithm ignores the iteration number during the par-

ticle position calculating; this reduces the accuracy of

Figure 5: Membership functions for linguistic variable val-

ues ˜x

Figure 6: Membership functions for linguistic variable val-

ues ˜x

ﬁnding a solution (table 3); requires a large number of

parameters associated with the gravitational constant

calculating. The proposed method eliminates these

shortcomings.

The traditional approach to training a fuzzy expert

system based on back propagation reduces the prob-

ability of correct estimation (table 4). The proposed

method eliminates this disadvantage.

7 CONCLUSIONS

1. Relevant optimization methods and expert sys-

tems were investigated as part of the decision-

making technology for foreign direct investment.

The research results showed that the most effec-

tive is the use of fuzzy expert systems, the param-

eters of which are identiﬁed by means of meta-

heuristic methods today.

2. A fuzzy expert decision support system for for-

eign direct investment has been developed. The

proposed system simpliﬁes the interaction be-

tween the operator and the computer system

M3E2 2022 - International Conference on Monitoring, Modeling Management of Emergent Economy

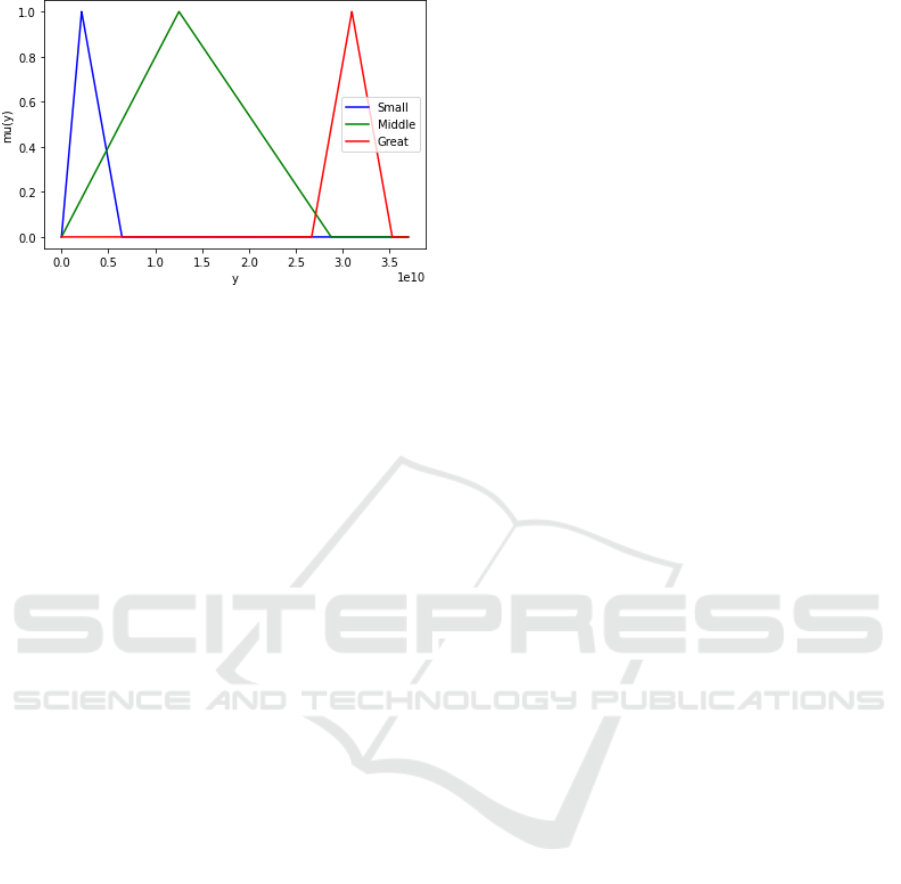
Figure 7: Membership functions for linguistic variable val-

ues ˜y.

through the use of qualitative indicators, and also

allows to identify its parameters using the pro-

posed swarm metaheuristics.

3. A quality criterion is proposed; it considers the

speciﬁcs of the created fuzzy expert system and

allows assessing of the decisions accuracy.

4. A swarm metaheuristic algorithm based on an

adaptive gravitational search algorithm has been

created; it provides control over the rate of method

convergence, as well as providing global search at

the initial iterations, and local search at the ﬁnal

iterations due to adaptive control of the particle

velocity.

5. The proposed optimization method based on

swarm metaheuristics and a fuzzy expert system

make it possible to intellectualize the technol-

ogy of making decisions on foreign direct invest-

ment. Prospects for further research involve test-

ing the proposed method and system on a wider

test database set.

REFERENCES

Abe, S. (1997). Neural Networks and Fuzzy Systems: The-

ory and Application. Kluwer Academic Publishers,

Boston. https://doi.org/10.1007/978-1-4615-6253-5.

Alba, E., Nakib, A., and Siarry, P., editors (2013). Meta-

heuristics for Dynamic Optimization, volume 433

of Studies in Computational Intelligence. Springer-

Verlag, Berlin.

Blum, C. and Raidl, G. R. (2016). Hybrid Meta-

heuristics: Powerful Tools for Optimization. Ar-

tiﬁcial Intelligence: Foundations, Theory, and Al-

gorithms. Springer, Cham. https://doi.org/10.1007/

978-3-319-30883-81.

Bozorg-Haddad, O. (2017). Meta-heuristic and Evolution-

ary Algorithms for Engineering Optimization. Wiley

& Sons, Hoboken, New Jersey.

Brownlee, J. (2011). Clever Algorithms: Nature-Inspired

Programming Recipes. Melbourne. https://github.

com/clever-algorithms/CleverAlgorithms.

Chopard, B. and Tomassini, M. (2018). An Introduction

to Metaheuristics for Optimization. Natural Comput-

ing Series. Springer, Cham. https://doi.org/10.1007/

978-3-319-93073-2.

Doerner, K. F., Gendreau, M., Greistorfer, P., Gutjahr, W.,

Hartl, R. F., and Reimann, M., editors (2007). Meta-

heuristics: Progress in Complex Systems Optimiza-

tion, volume 39 of Operations Research/Computer

Science Interfaces Series. Springer, New York. https:

//doi.org/10.1007/978-0-387-71921-4.

Du, K.-L. and Swamy, M. N. S. (2016). Search and Op-

timization by Metaheuristics: Techniques and Algo-

rithms Inspired by Nature. Springer, Cham. https:

//doi.org/10.1007/978-3-319-41192-7.

Engelbrecht, A. P. (2007). Computational Intelligence: an

introduction. Wiley & Sons, Chichester, West Sussex,

2 edition.

Fedorov, E., Lukashenko, V., Utkina, T., Lukashenko, A.,

and Rudakov, K. (2019). Method for parametric iden-

tiﬁcation of gaussian mixture model based on clonal

selection algorithm. In Luengo, D., Subbotin, S.,

Arras, P., Bodyanskiy, Y. V., Henke, K., Izonin, I.,

Levashenko, V. G., Lytvynenko, V., Parkhomenko,

A., Pester, A., Shakhovska, N., Sharpanskykh, A.,

Tabunshchyk, G., Wolff, C., Wuttke, H., and Zaitseva,

E., editors, Proceedings of the Second International

Workshop on Computer Modeling and Intelligent Sys-

tems (CMIS-2019), Zaporizhzhia, Ukraine, April 15-

19, 2019, volume 2353 of CEUR Workshop Proceed-

ings, pages 41–55. CEUR-WS.org. http://ceur-ws.

org/Vol-2353/paper4.pdf.

Gendreau, M. and Potvin, J.-Y., editors (2019). Handbook

of Metaheuristics, volume 272 of International Se-

ries in Operations Research & Management Science.

Springer-Verlag, New York. https://doi.org/10.1007/

978-3-319-91086-4.

Glover, F. and Kochenberger, G. A., editors (2003). Hand-

book of Metaheuristics, volume 57 of International

Series in Operations Research & Management Sci-

ence. Kluwer Academic Publishers, Kochenberger,

Dordrecht. https://doi.org/10.1007/b101874.

Grygor, O. O., Fedorov, E. E., Utkina, T. Y., Lukashenko,

A. G., Rudakov, K. S., Harder, D. A., and

Lukashenko, V. M. (2019). Optimization method

based on the synthesis of clonal selection and anneal-

ing simulation algorithms. Radio Electronics, Com-

puter Science, Control, (2):90–99. https://doi.org/10.

15588/1607-3274-2019-2-10.

Kurecic, P. and Kokotovic, F. (2017). The relevance of po-

litical stability on fdi: A var analysis and ardl models

for selected small, developed, and instability threat-

ened economies. Economies, 5(3):22. https://doi.org/

10.3390/economies5030022.

Mart

ı, R., Pardalos, P. M., and Resende, M. G. C., editors

(2018). Handbook of Heuristics. Springer, Cham.

https://doi.org/10.1007/978-3-319-07124-4.

Milovanovi

c, D. and Markovi

c, N. (2022). Strategic deci-

sion making and inﬂuence of economic freedoms on

Fuzzy Expert System of the Decision Making Support on Foreign Direct Investment

foreign direct investment (FDI) in Bosnia and Herze-

govina. Strategic Management, 27:44–56. https://

www.smjournal.rs/index.php/home/article/view/239.

Nakib, A. and Talbi, E.-G., editors (2017). Metaheuristics

for Medicine and Biology. Studies in Computational

Intelligence. Springer-Verlag, Berlin. https://doi.org/

10.1007/978-3-662-54428-0.

Radosavljevi

c, J. (2018). Metaheuristic Optimization in

Power Engineering. The Institution of Engineering

and Technology, New York. https://doi.org/10.1049/

PBPO131E.

Rashedi, E., Nezamabadi-pour, H., and Saryazdi, S. (2009).

Gsa: A gravitational search algorithm. Informa-

tion Sciences, 179(13):2232–2248. https://doi.org/10.

1016/j.ins.2009.03.004.

Rotshtein, A., Shtovba, S., and Mostav, I. (2001). Fuzzy

rule based innovation projects estimation. In Proceed-

ings Joint 9th IFSA World Congress and 20th NAFIPS

International Conference (Cat. No. 01TH8569), vol-

ume 1, pages 122–126 vol.1. https://doi.org/10.1109/

NAFIPS.2001.944238.

Ruan, D., editor (1997). Intelligent Hybrid Systems:

Fuzzy Logic, Neural Networks, and Genetic Algo-

rithm. Kluwer Academic Publishers. https://doi.org/

10.1007/978-1-4615-6191-0.

Subbotin, S., Oliinyk, A., Levashenko, V., and Zaitseva,

E. (2016). Diagnostic Rule Mining Based on Arti-

ﬁcial Immune System for a Case of Uneven Distri-

bution of Classes in Sample. Communications - Sci-

entiﬁc Letters of the University of Zilina, 18(3):3–11.

https://doi.org/10.26552/com.C.2016.3.3-11.

Talbi, E.-G. (2009). Metaheuristics: From Design to Imple-

mentation. Wiley & Sons, Hoboken, New Jersey.

Tsoukalas, L. H. and Uhrig, R. E. (1997). Fuzzy and Neural

Approaches in Engineering. John Wiley & Sons, Inc,

New York.

Yang, X.-S., editor (2018a). Nature-inspired Algorithms

and Applied Optimization. Studies in Computational

Intelligence. Springer, Cham. https://doi.org/10.1007/

978-3-319-67669-2.

Yang, X.-S. (2018b). Optimization Techniques and Appli-

cations with Examples. Wiley & Sons, Hoboken, New

Jersey.

Yu, X. and Gen, M. (2010). Introduction to Evolutionary

Algorithms. Decision Engineering. Springer-Verlag,

London. https://doi.org/10.1007/978-1-84996-129-5.

Samanovi

c, M.,

Cukusi

c, M., and Jadri

c, M. (2010). Rule

based approach to determining the inﬂuence of vari-

ous business regulations on the amount of foreign di-

rect investment in a country. In Proceedings of the ITI

2010, 32nd International Conference on Information

Technology Interfaces, Cavtat.

M3E2 2022 - International Conference on Monitoring, Modeling Management of Emergent Economy