Recurrence Measures of Complexity in Energy Market Dynamics

Andrii O. Bielinskyi

1,5 a

, Vladimir N. Soloviev

1,4 b

, Viktoria V. Solovieva

5 c

Serhiy O. Semerikov

1,2,3 d

and Michael Radin

6 e

Kryvyi Rih State Pedagogical University, 54 Gagarin Ave., Kryvyi Rih, 50086, Ukraine

Kryvyi Rih National University, 11 Vitalii Matusevych Str., Kryvyi Rih, 50027, Ukraine

Institute for Digitalisation of Education of the National Academy of Educational Sciences of Ukraine,

9 M. Berlynskoho Str., Kyiv, 04060, Ukraine

Kyiv National Economic University Named After Vadym Hetman, 54/1 Peremogy Ave., Kyiv, 03680, Ukraine

State University of Economics and Technology, 16 Medychna Str., Kryvyi Rih, 50005, Ukraine

Rochester Institute of Technology, 1 Lomb Memorial Dr, Rochester, NY 14623, U.S.A.

Keywords:

Crude Oil, Natural Gas, Recurrence Plot, Recurrence Quantiﬁcation Analysis, Crash, Indicator-Precursor.

Abstract:

The instability of the price dynamics of the energy market from a theoretical point of view indicates the

inadequacy of the dominant paradigm of the quantitative description of pricing processes, and from a practical

point of view, it leads to abnormal shocks and crashes. Through the recurrence quantiﬁcation analysis, we

analyze and construct indicators of intermittent events in energy indices, where periods of regular behavior

are replaced by periods of chaotic behavior, which could explain the emergence of crisis events. For further

analysis, we have chosen daily data of Henry Hub natural gas spot prices, WTI spot prices, and Europe Brent

spot prices. Our empirical results present that all of the presented recurrence measures respond in a particular

way during crashes and can be effectively implemented for risk management strategies.

1 INTRODUCTION

Global economic and ﬁnancial systems rely on crude

oil to maintain stability, making it a strategic resource

for national economic development (Zhang and Wu,

2019; Dong et al., 2018). The importance of exam-

ining various factors that may affect crude oil prices

is therefore critical to investors, government agen-

cies, and other stakeholders. Many factors contribute

to crude oil price ﬂuctuations, including fundamen-

tal factors (such as supply and demand of crude oil)

(Wu and Zhang, 2014) and non-fundamental factors

(such as speculations and investor sentiment) (Ji et al.,

2019). Speciﬁcally, the global economic environ-

ment, political security between oil-producing coun-

tries and their neighbors, and economic policy uncer-

tainty prove to have a signiﬁcant impact on crude oil

prices.

https://orcid.org/0000-0002-2821-2895

https://orcid.org/0000-0002-4945-202X

https://orcid.org/0000-0002-8090-9569

https://orcid.org/0000-0003-0789-0272

https://orcid.org/0000-0001-9951-7955

Regarding the strategic role of crude oil in eco-

nomic progress, the market volatility of crude oil

prices has had a substantial negative effect on the

economy, speciﬁcally in those countries that are de-

pendent on imports of crude oil. The impact of many

drivers on crude oil price volatility has thus been in-

vestigated in a variety of publications, and crude oil

market mechanism has become a controversial topic

in academia (Coleman, 2012; Sari et al., 2011; D

ees

et al., 2007). While this was going on, some studies

underlined the substantial risks associated with crude

oil price changes, as well as their complexity and

stochastic nature (Zhang and Wang, 2015; Shahzad

et al., 2022; Yin and Wang, 2022; Zhang et al., 2023).

Oil prices are generally referred to as benchmark

prices by both WTI and Brent contracts. Hedge funds

and traders typically select one or the other contract.

Consequently, there is considerable interest in the

WTI-Brent pricing structure, including the shapes of

the futures curves, the absolute price differences be-

tween the two benchmarks, and the degree of integra-

tion between the two markets. Hedge funds and ﬁnan-

cial institutions heavily trade these markets (directly

and indirectly). As a result, the prices of jet fuel, heat-

122

Bielinskyi, A., Soloviev, V., Solovieva, V., Semerikov, S. and Radin, M.

Recurrence Measures of Complexity in Energy Market Dynamics.

DOI: 10.5220/0011931800003432

In Proceedings of 10th International Conference on Monitoring, Modeling Management of Emergent Economy (M3E2 2022), pages 122-133

ISBN: 978-989-758-640-8; ISSN: 2975-9234

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

ing oil, diesel, and gasoline are highly inﬂuenced by

these markets. The price spread between WTI and

Brent is also used as the basis for a number of deriva-

tive ﬁnancial products, such as swaps and options.

The microeconomic theory states that the supply

and demand condition determines the fundamental

value of crude oil price assets. The ﬁnancialization of

crude oil in the past decade, however, has increased

the role of speculation in crude oil prices, making the

process of determining crude oil prices more difﬁcult

(Kilian, 2009; Flood and Hodrick, 1990).

The natural gas industry has achieved strong

growth in recent years because of the large demand

market, sufﬁcient low-cost supply, and active global

natural gas trade. The forecasting of natural gas prices

is one of the most crucial topics in ﬁnance since

this resource is important for trading, electric power

production planning, and regulatory decision-making.

Nowadays, Henry Hub in the U.S., NBP in the U.K.,

and LNG in Japan represent major international trad-

ing centers of natural gas. These three centers have

become an important reference point for determining

the international level of natural gas prices. Among

them, Henry Hub has the highest market liquidity, the

largest inﬂuence, and the best reﬂection of the market

supply and demand. On the other hand, in addition to

the basic factors of supply and demand, the price of

natural gas is driven by multiple factors such as ex-

treme weather, wars, and geopolitics (Li et al., 2021).

Considering the highly nonlinear and non-

stationary characteristics of crude oil and natural gas

markets under the inﬂuence of complex factors, it is of

great research signiﬁcance to improve the accuracy of

early identiﬁcation of crisis phenomena in those mar-

kets. In this paper, we present indicators (indicators-

precursors) based on recurrence analysis.

2 METHODOLOGY OF

RECURRENCE ANALYSIS

In 1890 Poincar

e introduced Poincar

e recurrence the-

orem (Poincar

e, 2017), which states that certain sys-

tems return to their arbitrarily close, or exactly the

same initial states after a sufﬁciently long but ﬁnite

time. Such property in the case of deterministic be-

havior of the system allows us to make conclusions

regarding its future development.

2.1 Time Delay Method

The state of the system can be described by the set

of variables. Its observational state can be expressed

through a d-dimensional vector or matrix, where each

of its components refers to a single variable that rep-

resents a property of the system. After a while, the

variables change, resulting in different system states.

Usually, not all relevant variables can be captured

from our observations. Often, only a single variable

may be observed. Thakens’ theorem (Takens, 1981)

that was mentioned in previous sections ensures that

it‘s possible to reconstruct the topological structure of

the trajectory formed by the state vectors, as the data

collected for this single variable contains information

about the dynamics of the whole system.

For an approximate reconstruction of the origi-

nal dynamics of the observed system, we project the

time series onto a Reconstructed Phase Space (Eck-

mann and Ruelle, 1985; Kantz and Schreiber, 2003;

Ott et al., 1994) with the commonly used time delay

method (Kantz and Schreiber, 2003) which relied on

the embedding dimension and time delay.

The embedding dimension is being the dimension-

ality of the reconstructed system (corresponds to the

number of relevant variables that may differ from one

system to another. The time delay parameter speciﬁes

the temporal components of the vector components.

2.2 Recurrence Plot

Recurrence plot (RP) have been introduced to study

dynamics and recurrence states of complex systems.

When we create RP, at ﬁrst, from recorded time se-

ries we reconstruct phase-space trajectory. Then, ac-

cording to Eckmann et al. (Eckmann et al., 1987), we

consider a trajectory

⃗

X(i) on the reconstructed trajec-

tory. The recurrence plot is an array of dots in a N ×N

matrix, where dot is placed at (i, j) whenever

⃗

X( j) is

sufﬁciently close to

⃗

X(i), and both axes are time axes

which mathematically can be expressed as

i j

= Θ(ε−



⃗

X(i) −

⃗

X( j)



for i, j = 1, ...,N,

(1)

where ∥ ∥ is a norm (representing the spatial distance

between the states at times i and j); ε is a predeﬁned

recurrence threshold, and Θ (·) is the Heaviside func-

tion. As a result, the matrix captures a total of N

binary similarity values.

Typically, L

-norm is applied to determine the

pairwise similarity between two vectors. According

to Webber and Zbilut (Webber and Zbilut, 2005), the

-norm (Taxicab metric), the L

-norm (Euclidean

metric), and the L

∞

-norm (Chebyshev metric) can

serve as candidates for measuring distance between

trajectories in phase space.

Also, as it can be seen from equation (1), the sim-

ilarity between vectors is determined by a threshold

Recurrence Measures of Complexity in Energy Market Dynamics

123

ε. The choice of ε > 0 ensures that all vectors that

lie within this radius are similar to each other, and

that dissimilarity up to a certain error is permitted

(Poincar

e, 2017).

The ﬁxed radius for recurrent states is the com-

monly used condition, which leads to equally sized

ε-neighborhoods. The shape in which neighborhoods

lie is determined by the distance metric. Applying the

ﬁxed threshold with the distance metric, we deﬁne re-

currence matrices that are symmetric along the middle

diagonal. The self-similarity of the multi-dimensional

vectors reﬂects in the middle diagonal, which is com-

monly referred to as the line of identity (LOI). In

contrast, it is not guaranteed that a recurrence ma-

trix is symmetric if the condition of the ﬁxed number

of nearest neighbors is applied. For speciﬁc purposes

(e.g., quantiﬁcation of recurrences), it can be useful to

exclude the LOI from the RP, as the trivial recurrence

of a state with itself might not be of interest (Charles

et al., 2015).

2.2.1 Recurrence Plots and their Structures

The main purpose of RP is the visualization of tra-

jectories and hidden patterns of the systems (Marwan

et al., 2007; Charles et al., 2015).

The dots within RP, representing the time evolu-

tion of the trajectories, exhibit characteristic large-

scale and small-scale patterns. Large-scale patterns

of RP can be classiﬁed as

• homogeneous – autonomous and stationary sys-

tems, which consist of many recurrence points

that are homogeneously distributed (relaxation

times are short);

• periodic – long, uninterrupted, and diagonally

oriented structures that represent which indicate

periodic behavior. These lines are usually dis-

tributed regularly;

• drift – systems with patterns paling or darkening

from the LOI to the outer corners of RP;

• disrupted – systems with drastic changes as well

as extreme events in the system dynamics.

The small-scale clusters can represent a combina-

tion of isolated dots (abrupt events). Similar evolu-

tion at different periods in time or in reverse temporal

order will present diagonal lines (deterministic struc-

tures) as well as vertical/horizontal lines to inscribe

laminar states (intermittency) or systems that paused

at singularities. For the quantitative description of the

system, such small-scale clusters serve the base of the

recurrence quantiﬁcation analysis (RQA).

2.3 Recurrence Quantiﬁcation Analysis

The graphic representation of the system suits per-

fectly for a qualitative description. However, the

main disadvantage of graphical representation is that

it forces users to subjectively intuit and interpret pat-

terns and structures presented within the recurrence

plot. Also, with the increasing size of RP, they can be

hardly depicted on graphical display as a whole. As

a result, we need to work with separated parts of the

original plot. Analysis in such a way may create new

defects, which should distort objectivity of the ob-

served patterns and lead to incorrect interpretations.

To overcome such limitation and spread an objective

assessment among observers, in the early 1990s by

Webber and Zbilut (Webber and Zbilut, 1994; Zbilut

and Webber, 1992) were introduced deﬁnitions and

procedures to quantify RP’s complexity, and later, it

has been extended by Marwan et al. (Marwan et al.,

2002).

The ﬁrst known measure of the RQA is recurrence

rate, which measures the probability that the studied

process will recur (RR):

RR =

∑

i, j=1

i, j

. (2)

Another measure is based on frequency distribu-

tion of line structures in the RP. First, we consider the

histogram of the length of the diagonal structures in

the RP

P(l) =

∑

i, j=1

(1 − R

i−1, j−1

)

× (1 − R

i+l, j+l

)

l−1

∏

k=0

i+k, j+k

(3)

The percentage of recurrence points that form di-

agonal segments of minimal length l

min

parallel to the

main diagonal is the measure of determinism (DET ):

DET =

∑

l=l

min

lP(l)

∑

l=1

lP(l). (4)

Systems that are characterized by long diagonal

lines are presented to be periodic. From chaotic

signals, we would expect short diagonal lines, and

stochastic processes would not present any diagonal

lines. Performing the RQA, typically, we rely on the

lines with minimal length, which excludes the shorter

lines, which may be spurious for characterizing deter-

ministic processes. In our case, l

min

= 2 is considered.

In case when l

min

= 1, DET and RR are identical.

Considering diagonal line segments, we can em-

phasize the longest one – L

max

. This indicator mea-

sures the maximum time that two trajectories remain

M3E2 2022 - International Conference on Monitoring, Modeling Management of Emergent Economy

124

close to each other and can be interpreted as the max-

imum prediction time:

max

= max(

{

|i = 1, .. .,N

}

), (5)

where N

∑

l⩾l

min

P(l) is the total number of diago-

nal lines.

Divergence (DIV ) is the inverse of L

max

charac-

terizes the exponential divergence of the phase space

trajectory (Goldberger et al., 2000; Kirchner et al.,

2014):

DIV = 1

max

. (6)

For longer diagonal lines system is more deter-

ministic and, therefore, the measure of divergence is

also lower. The smaller L

max

, the more divergent are

trajectories and more chaotic the studied system. Ac-

cording to Eckmann et al. (Eckmann et al., 1987),

DIV can be used to estimate the largest positive Lya-

punov exponent.

Another measure which is related to the diago-

nal line segments is the average diagonal line length

mean

∑

l=l

min

lP(l)

∑

l=l

min

P(l) (7)

It can be interpreted as the mean prediction hori-

zon of the system, and it measures average time that

two trajectories remain close to each other.

Using the classic Shannon entropy, we can mea-

sure the hidden complexity of recurrence structures

in the RP. In accordance with this study, the entropy

of diagonal line histogram (DLEn) is of the greatest

interest. It can be deﬁned as:

DLEn = −

∑

l=l

min

p(l) ln p(l) (8)

and

p(l) = P(l)

∑

l=l

min

P(l), (9)

where p(l) captures the probability that a diagonal

line has exactly length l, and DLEn reﬂects the com-

plexity of deterministic structure in the system. The

more uniform is the frequency distribution of diago-

nal lines, the higher the value of DLEn. If there is

predominant deterministic behavior with a particular

period l, then DLEn becomes lower.

As it was mentioned, the RP structure consists

of vertical (horizontal lines). For them Marwan and

Webber (Marwan and Webber, 2015) proposed addi-

tional recurrence measures. The ﬁrst of them is the

laminarity (LAM) Analogously to the equation (4),

which measures the percentage of diagonal lines with

minimal length l

min

in the RP, we can calculate the

fraction of recurrence points forming vertical struc-

tures of minimal length v

min

LAM =

∑

v=v

min

vP(v)

∑

v=1

vP(v) (10)

with

P(v) =

∑

i, j=1

(1 − R

i, j−1

)

× (1 − R

i, j+v

)

v−1

∏

k=0

i, j+k

(11)

as the histogram of lengths of vertical lines.

Since it measures the overall amount of vertical

lines, it characterizes the percentage of laminar states

within the system. If LAM increases, then there are

more vertical or diagonal structures than isolated re-

current points.

Similarly to L

max

, we can deﬁne the measure

which will indicate the maximum time that a system

holds an unchangeable pattern – the maximal vertical

lines length (V

max

= max(

{

|i = 1, .. .,N

}

), (12)

where N

∑

v⩾v

min

P(v) is the total number of verti-

cal lines.

Vertical line divergence (V DIV ) is the analogous

to (6), which can be related to the rate of divergence

from laminar state:

V DIV = 1

max

. (13)

Consequently, we can deﬁne the average time that

two trajectories remain at a speciﬁc state – trapping

time (T T ):

T T =

∑

v=v

min

vP(v)

∑

v=v

min

P(v). (14)

For high T T values we would expect the system to

consist of more laminar states, whereas low T T val-

ues would indicate abrupt changes in the system’s dy-

namics.

The variability of laminar states with different du-

ration time can be measured in the same way as for

diagonal lines – using Shannon entropy. The com-

plexity of vertical lines can be measures according to

the following equation:

V LEn = −

∑

v=v

min

p(v)ln p(v) (15)

with

p(v) = P(v)

∑

v=v

min

P(v) (16)

Recurrence Measures of Complexity in Energy Market Dynamics

125

indicating the probability of a vertical line to have

length v ⩾ v

min

In the same manner, we can quantify the variation

(complexity) of abrupt changes during the studied pe-

riods in the energy markets. Regarding equation (7),

we can quantify the average time of divergence when

two trajectories in the phase-space remain out of re-

currence threshold ε. This measure can be called as

average white vertical line length (WV L

mean

WV L

mean

∑

w=w

min

wP(w)

∑

w=w

min

P(w), (17)

where P(w) is the frequency of white vertical lines in

the RP. This measure can be interpreted as the mean

horizon of unpredictability of the system.

This kind of complexity is associated with the

white vertical lines in the RP and can be quantiﬁed

in the following way:

WV LEn = −

∑

w=w

min

p(w)ln p(w) (18)

with

p(w) = P(w)

∑

w=w

min

P(w) (19)

indicating the probability of a white vertical line to

have length w ⩾ w

min

The further measure is based on the ration be-

tween DET and RR, and known as ratio (DET /RR):

DET /RR = N

∑

l=l

min

P(l)

∑

l=1

lP(l)

(20)

In the same manner, we can deﬁne another mea-

sure which is based on the ratio between LAM and

DET :

LAM/DET =

∑

v=v

min

vP(v) ·

∑

l=1

lP(l)

∑

v=1

vP(v) ·

∑

l=l

min

lP(l).

(21)

This measures can be used to uncover hidden tran-

sitions in the dynamics of the system (Webber and

Zbilut, 1994).

3 RESULTS AND ANALYSIS

Regarding previous studies, we present additional

analysis on co-movement between 3 energy-related

indices and construct indicators or indicators-

precursors based on the using recurrence analysis.

The presented work uses daily data of Henry Hub

natural gas spot prices (US$/MMBTU) ranged from

7 February 1997 to 18 October 2022; Cushing, OK

WTI spot prices FOB (US$/BBL) ranged from 20

May 1987 to 17 October 2022; Europe Brent spot

prices FOB (US$/BBL) ranged from 20 May 1987 to

17 October 2022 (U.S. Energy Information Adminis-

tration, 1997, 1986).

In ﬁgure 1 are presented:

• the dynamics of the initial time series;

• standardized returns, where returns can be calcu-

lated as G(t) = [x(t + ∆t) − x(t)]/x(t) and their

standardized version as g(t) = [G(t) − ⟨G⟩]/σ;

• probability density function of the standardized

returns.

(a)

(b)

(c)

Figure 1: Initial time series (a), standardized returns (b),

and pdf of standardized returns of WTI spot prices (WTI),

Europe Brent spot prices (Brent), and Henry Hub natural

gas spot prices (Henry Hub).

M3E2 2022 - International Conference on Monitoring, Modeling Management of Emergent Economy

126

We can see that most periods in energy markets

are deﬁned by events that exceed ±3σ. Both WTI and

Brent returns are characterized by much more exten-

sive crashes. Previous studies pointed out that such

events are located in fat-tails of the probability dis-

tribution. Such crashes are the main source of high

complexity and non-linearity in the studied systems.

Most of our results are based on the sliding win-

dow approach. The idea here is to take a sub-window

of a predeﬁned length w. For that sub-window, we

perform recurrence quantiﬁcation analysis, get neces-

sary indicators that are appended to the array. Then,

the window is shifted by a predeﬁned time step h, and

the procedure is repeated until the time series is com-

pletely exhausted.

We have performed RQA under sliding window

procedure for standardized returns and standardized

initial time series (Soloviev et al., 2020; Bielinskyi

and Soloviev, 2018; Bielinskyi et al., 2022, 2021c,b,

2020). We have found that standardized initial time

series better expresses internal complexity and recur-

rent properties of the energy market indices.

RQA was performed for the following parameters:

• embedding dimension d

= 1;

• time delay τ = 1;

• recurrence threshold ε = 0.3;

• L

-norm as a candidate for measuring distance be-

tween trajectories in phase space;

• minimum diagonal line length l

min=2

;

• minimum vertical line length v

min

= 2;

• minimum white vertical line length w

min

= 2;

• sliding window length w = 500 days;

• sliding window time step h = 1 day.

Worth to mention that the experiments were per-

formed for sliding window lengths of 250 days and

500 days. We have chosen the second option since it

represents a more reliable and smoother dynamics of

all the presented indicators. All described measures

result into highly volatile variation with the sliding

window of 250 days that difﬁcult to interpret.

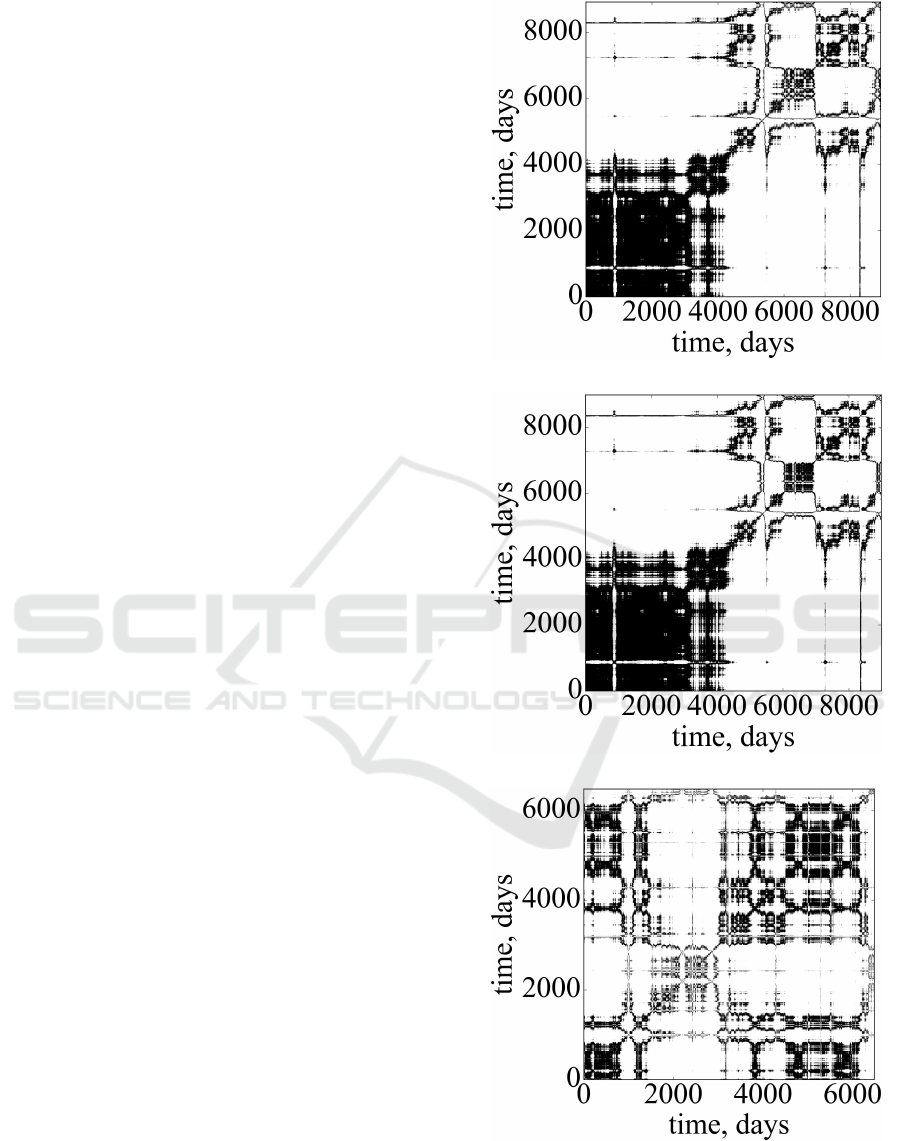
In ﬁgure 2 are presented RPs for the studied series.

Recurrence plots in ﬁgure 2 represent that the

studied energy markets are highly inhomogeneous.

As it was expected, nonlinear structure of WTI and

Brent is presented to be very similar, comparing to

Henry Hub. Recurrence structure of all indices varies

across time. They do not follow a certain pattern, pre-

sented to be non-periodic, and there are differences

in the patterns that concern the frequency of their ap-

pearance, shape, and size. It should be noticed that

for the oil markets ﬁrst 4000 days are presented to be

(a)

(b)

(c)

Figure 2: Recurrence plots calculated for WTI (a), Brent

(b), and Henry Hub (c) standardized time series.

Recurrence Measures of Complexity in Energy Market Dynamics

127

highly recurrent, while the remaining days seem to be

more volatile, which is indicated by high proportion

of white regions. The recurrence structure of Henry

Hub index is presented to be more uniformly dis-

tributed. The variations of recurrence patterns should

be more noticeable during crashes. Recurrence quan-

titative indicators should give a more accurate repre-

sentation of the complex, chaotic structure of the stud-

ied markets.

Figure 3 represents recurrence measures of deter-

minism (DET ) and laminarity (LAM).

(a)

(b)

(c)

Figure 3: Recurrence measures of determinism (DET ) and

laminarity (LAM) calculated for WTI (a), Europe Brent (b),

and Henry Hub (c) indices.

In ﬁgure 3 we see that DET and LAM increase

during crisis events of all markets. We may conclude

that those critical states are characterized by high de-

gree of laminarity and determinism. Crashes are pre-

sented to be highly complex and deterministic. Their

degree of predictability becomes higher, and corre-

sponding recurrence measures seem to be indicators

or even indicators-precursors of such changes.

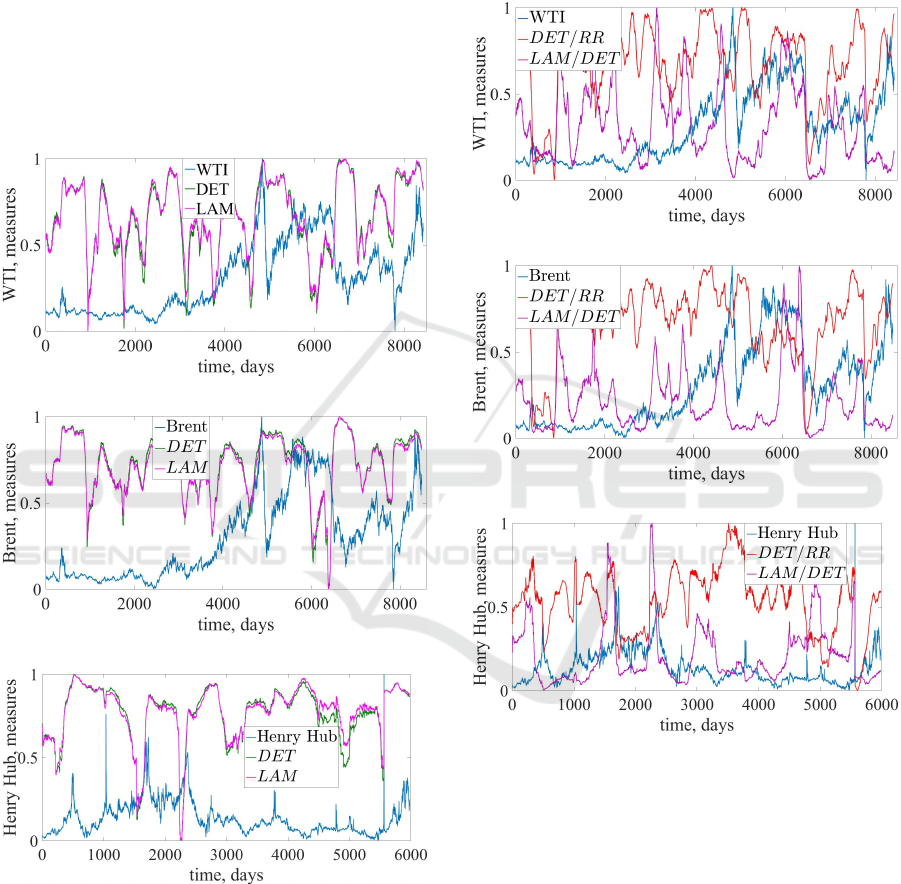
Figure 4 represents recurrence measures of ratios

DET /RR and LAM/DET .

(a)

(b)

(c)

Figure 4: Recurrence measures (DET /RR) and

(LAM/DET ) calculated for WTI (a), Europe Brent

(b), and Henry Hub (c) indices.

From ﬁgure 4 we can see that both measures de-

crease during crisis events of energy indices. For ratio

DET /RR we may say that the overall percentage of

recurrence points in RP becomes higher than the per-

centage of only diagonal structures in RP. For ratio

LAM/DET we see precisely the same behavior dur-

ing crashes, i.e., it starts to decline during crisis or

even in advance. Thus, it can be seen that the over-

all determinism of the system during crashes is much

higher than the degree of laminarity.

Figure 5 shows recurrence measures of diagonal

M3E2 2022 - International Conference on Monitoring, Modeling Management of Emergent Economy

128

(DIV ) and vertical line (V DIV ) divergences.

(a)

(b)

(c)

Figure 5: Recurrence measures of diagonal line divergence

(DIV ) and vertical line divergence (V DIV ) calculated for

WTI (a), Europe Brent (b), and Henry Hub (c) indices.

Figure 5 demonstrates that the divergence of deter-

ministic and laminar structure of energy-related mar-

kets becomes lower during critical states. Since both

measures are inverse quantities to maximum diagonal

and vertical line length (L

max

and V

max

), such behav-

ior has to be obvious. Previous measures have made

it clear to us that the crisis phenomena of energy in-

dices are characterized by a high degree of determin-

ism and laminarity. In this case, the lengths of diag-

onal and vertical lines should also increase, which in-

dicate an increase in the horizon of predictability and

immutability.

Figure 6 represents recurrence measures of recur-

rence rate (RR), average diagonal line length (L

mean

and trapping time (T T ).

(a)

(b)

(c)

Figure 6: Recurrence measures of recurrence rate (RR), av-

erage diagonal line length (L

mean

), and trapping time (T T )

calculated for WTI (a), Europe Brent (b), and Henry Hub

In ﬁgure 6 we see that recurrence rate increases

during crisis phenomena. This means that the total

number of trajectories in the phase space that are close

enough to each other becomes larger on the eve of a

crisis or at the moment of its onset. Thus, the proba-

bility of recurrence state increases during crash. Re-

garding previous measures, RR and L

mean

, we see that

the average degree of predictability during crisis in-

creases. The same can be seen for trapping time: aver-

age degree of changeability increases during crashes.

Based on this indicator, we may conclude that the sys-

tem is ‘trapped’ in a state of crisis.

Figure 7 presents recurrence measures of aver-

age white vertical line length (WV L

mean

), and diago-

nal, vertical and white vertical line entropies (DLEn,

V LEn, and WV LEn).

From ﬁgure 7 we can see that all the presented

Recurrence Measures of Complexity in Energy Market Dynamics

129

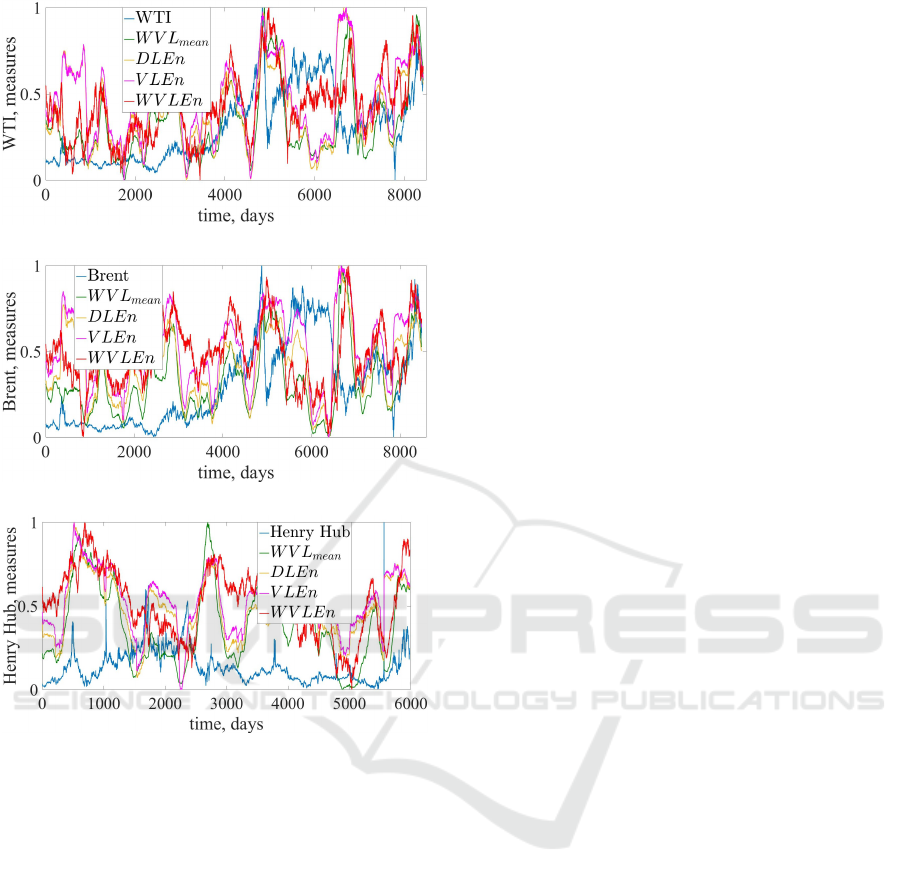
(a)

(b)

(c)

Figure 7: Recurrence measures of average white vertical

line length (WV L

mean

), diagonal line entropy (DLEn), ver-

tical line entropy (V LEn), and white vertical line entropy

(WV LEn) calculated for WTI (a), Europe Brent (b), and

Henry Hub (c) indices.

quantitative measures of recurrence begin to increase

during crises, indicating a special state of the market

at these points in time. The average white vertical

line length shows that crisis events are characterized

not only by the determinism of the dynamics of mar-

ket movement, but also by the dissimilarity of these

events to many previous ones, since the length of the

white vertical lines is becoming an increasing trend.

It can also be said that the market represents a much

more deterministic structure than a laminar one. Also,

the degree of volatility of these events can knock the

market dynamics out of the limits of the epsilon value.

The diagonal line entropy also shows an increas-

ing trend. Since the Shannon entropy is maximal with

a uniform distribution, it can be concluded that the

collapse events of energy indices are characterized by

different horizons of predictability. That is, in the pre-

crisis dynamics there is no black diagonal line of the

same length, which is the dominant one. During a cri-

sis, horizons of determinism appear, which gain even

more weight if compared with the rest.

The vertical line entropy increases similarly to

DLEn. We may assume that similarly to diagonal

lines laminar states have different horizons of invari-

ability during crash events, and these horizons of in-

variability have greater tendency to uniform distribu-

tion.

The white vertical line entropy increases similarly

to other entropies. This dynamics is consistent with

the WV L

mean

measure.

4 CONCLUSIONS

In this paper, we have studied highly nonlinear and

nonstationary dynamics of oil and gas markets from

the perspective of the recurrence analysis. Taking

into account daily data of Henry Hub natural gas spot

prices from 7 February 1997 to 18 October 2022, WTI

spot prices from 20 May 1987 to 17 October 2022,

and Europe Brent spot prices for the same period as

WTI, we have drown some conclusions from the em-

pirical results.

Firstly, recurrence plots presented that the stud-

ied markets demonstrate highly inhomogeneous. As

it was expected, nonlinear structure of WTI and Brent

is presented to be very similar, comparing to Henry

Hub. Recurrence structure of all indices varies across

time. They do not follow a certain pattern, and there

are differences in frequency, shape, and size of black-

and white-dot patterns that appear across time.

From quantitative measures of complexity, we

have drawn the following conclusions:

1. Crash events of energy-related indices are charac-

terized by high degree of laminarity and determin-

ism. Crashes are presented to be highly complex

and deterministic.

2. The overall percentage of recurrence points in RP

becomes higher than the percentage of only diag-

onal structures in RP. At the same time, the per-

centage of diagonal lines in RP during crises is

much higher than the percentage of vertical lines.

Thus, the overall degree of determinism is larger

than laminarity.

3. The divergence of deterministic and laminar

structure of WTI, Brent, and Henry Hub becomes

lower during critical states that indicate higher de-

gree of repeatability in the dynamics of the stud-

ied systems. Also, it gives understanding that

M3E2 2022 - International Conference on Monitoring, Modeling Management of Emergent Economy

130

the phase-space trajectories become close to each

other during critical phenomena of ﬁnancial sys-

tems.

4. Such measures as recurrence rate, mean diagonal

line length, and trapping time also increase dur-

ing crisis phenomena. This means that the total

number of trajectories in the phase space that are

close enough to each other becomes larger before

or during crash. Therefore, the probability of re-

currence state increases, and the average degree of

predictability becomes higher. A larger portion of

vertical lines indicates that the system is ‘trapped’

in a state of crisis for a particular period of time.

5. Entropy-based measures and, particularly, white

vertical line measures show that energy-related in-

dices represent complex nonlinear patterns that

combine not only horizons of determinism and

laminarity, but also some dissimilarity patterns re-

ﬂected into white lines.

The applied approach to WTI, Brent, and Henry

Hub indices approve that the energy market is an

open, highly complex, chaotic, and nonlinear sys-

tem that depends on different technical and funda-

mental factors. Although RPs and RQA give promis-

ing results for crisis prediction and the construction

of early-warning indicators, it needs further develop-

ment to give applicable trading strategies relying on

recurrence indicators and further development of au-

tonomous trading bots.

Also, since the proposed recurrence measures are

only indicators (indicators-precursors) that give the

possibility to monitor crisis phenomena at a particular

moment of the market’s existence, forecasting of such

events requires integration of the proposed indicators

with the particular forecasting models (Yin and Wang,

2022; Fang et al., 2023; Li et al., 2021; Zhang et al.,

2023; Zou et al., 2023; Guliyev and Mustafayev,

2022; Kiv et al., 2021). It seems a promising direction

at the junction of artiﬁcial intelligence and fuzzy logic

methods (Bielinskyi et al., 2021a; Bondarenko, 2021;

Kmytiuk and Majore, 2021; Kobets and Novak, 2021;

Kucherova et al., 2021; Lukianenko and Strelchenko,

2021; Miroshnychenko et al., 2021).

At the same time, we intend to investigate cross-

recurrences between energy indices and different

technical and fundamental indicators using such ap-

proaches as cross- and joint-recurrence quantiﬁcation

analysis (Ashe and Egan, 2023; He and Huang, 2020;

Romano et al., 2004).

ACKNOWLEDGMENTS

This work was supported by the Ministry of

Education and Science of Ukraine (project No.

0122U001694).

REFERENCES

Ashe, S. and Egan, P. (2023). Examining ﬁnancial and

business cycle interaction using cross recurrence plot

analysis. Finance Research Letters, 51:103461. https:

//doi.org/10.1016/j.frl.2022.103461.

Bielinskyi, A., Semerikov, S., Serdyuk, O., Solovieva,

V., Soloviev, V. N., and Pichl, L. (2020). Econo-

physics of sustainability indices. In Kiv, A., edi-

tor, Proceedings of the Selected Papers of the Spe-

cial Edition of International Conference on Monitor-

ing, Modeling & Management of Emergent Economy

(M3E2-MLPEED 2020), Odessa, Ukraine, July 13-

18, 2020, vol. 2713 of CEUR Workshop Proceedings,

pages 372–392. CEUR-WS.org. https://ceur-ws.org/

Vol-2713/paper41.pdf.

Bielinskyi, A., Soloviev, V., Semerikov, S., and Solovieva,

V. (2021a). Identifying stock market crashes by fuzzy

measures of complexity. Neiro-Nechitki Tekhnolohii

Modelyuvannya v Ekonomitsi, 2021(10):3–45. https:

//doi.org/10.33111/nfmte.2021.003.

Bielinskyi, A. O., Hushko, S. V., Matviychuk, A. V.,

Serdyuk, O. A., Semerikov, S. O., and Soloviev, V. N.

(2021b). Irreversibility of ﬁnancial time series: a case

of crisis. In Kiv, A. E., Soloviev, V. N., and Se-

merikov, S. O., editors, Proceedings of the Selected

and Revised Papers of 9th International Conference

on Monitoring, Modeling & Management of Emergent

Economy (M3E2-MLPEED 2021), Odessa, Ukraine,

May 26-28, 2021, volume 3048 of CEUR Workshop

Proceedings, pages 134–150. CEUR-WS.org. https:

//ceur-ws.org/Vol-3048/paper04.pdf.

Bielinskyi, A. O., Matviychuk, A. V., Serdyuk, O. A.,

Semerikov, S. O., Solovieva, V. V., and Soloviev,

V. N. (2022). Correlational and non-extensive na-

ture of carbon dioxide pricing market. In Ignatenko,

O., Kharchenko, V., Kobets, V., Kravtsov, H., Tara-

sich, Y., Ermolayev, V., Esteban, D., Yakovyna, V.,

and Spivakovsky, A., editors, ICTERI 2021 Work-

shops, volume 1635 CCIS of Communications in

Computer and Information Science, pages 183–199,

Cham. Springer International Publishing. https://doi.

org/10.1007/978-3-031-14841-5 12.

Bielinskyi, A. O., Serdyuk, O. A., Semerikov, S. O., and

Soloviev, V. N. (2021c). Econophysics of cryptocur-

rency crashes: a systematic review. In Kiv, A. E.,

Soloviev, V. N., and Semerikov, S. O., editors, Pro-

ceedings of the Selected and Revised Papers of 9th

International Conference on Monitoring, Modeling &

Management of Emergent Economy (M3E2-MLPEED

2021), Odessa, Ukraine, May 26-28, 2021, volume

3048 of CEUR Workshop Proceedings, pages 31–

Recurrence Measures of Complexity in Energy Market Dynamics

131

133. CEUR-WS.org. https://ceur-ws.org/Vol-3048/

paper03.pdf.

Bielinskyi, A. O. and Soloviev, V. N. (2018). Complex

network precursors of crashes and critical events in

the cryptocurrency market. CEUR Workshop Pro-

ceedings, 2292:37 – 45. https://ceur-ws.org/Vol-2292/

paper02.pdf.

Bondarenko, M. (2021). Modeling relation between at-

the-money local volatility and realized volatility of

stocks. Neiro-Nechitki Tekhnolohii Modelyuvannya

v Ekonomitsi, 2021(10):46–66. https://doi.org/10.

33111/nfmte.2021.046.

Charles, L., Webber, J., Cornel, I., and Norbert, M., edi-

tors (2015). Recurrence Plots and Their Quantiﬁca-

tions: Expanding Horizons, vol.180 of Springer Pro-

ceedings in Physics. Springer. https://doi.org/10.1007/

978-3-319-29922-8.

Coleman, L. (2012). Explaining crude oil prices using

fundamental measures. Energy Policy, 40:318–324.

https://doi.org/10.1016/j.enpol.2011.10.012.

Dong, Y., Zhang, M., and Zhou, R. (2018). Classiﬁcation

of network game trafﬁc using machine learning. In

Yuan, H., Geng, J., Liu, C., Bian, F., and Surapunt,

T., editors, Geo-Spatial Knowledge and Intelligence,

pages 134–145, Singapore. Springer Singapore. https:

//doi.org/10.1007/978-981-13-0893-2 15.

ees, S., Karadeloglou, P., Kaufmann, R. K., and S

anchez,

M. (2007). Modelling the world oil market: Assess-

ment of a quarterly econometric model. Energy Pol-

icy, 35(1):178–191. https://doi.org/10.1016/j.enpol.

2005.10.017.

Eckmann, J.-P., Kamphorst, S. O., and Ruelle, D. (1987).

Recurrence plots of dynamical systems. Europhysics

Letters (EPL), 4(9):973–977. https://dx.doi.org/10.

1209/0295-5075/4/9/004.

Eckmann, J.-P. and Ruelle, D. (1985). Ergodic theory of

chaos and strange attractors. Rev. Mod. Phys., 57:617–

656. https://doi.org/10.1103/RevModPhys.57.617.

Fang, T., Zheng, C., and Wang, D. (2023). Forecasting the

crude oil prices with an emd-isbm-fnn model. En-

ergy, 263:125407. https://doi.org/10.1016/j.energy.

2022.125407.

Flood, R. P. and Hodrick, R. J. (1990). On testing for spec-

ulative bubbles. Journal of Economic Perspectives,

4(2):85–101. https://www.aeaweb.org/articles?id=10.

1257/jep.4.2.85.

Goldberger, A. L., Amaral, L. A. N., Glass, L., Haus-

dorff, J. M., Ivanov, P. C., Mark, R. G., Mietus,

J. E., Moody, G. B., Peng, C.-K., and Stanley, H. E.

(2000). Physiobank, physiotoolkit, and physionet:

components of a new research resource for complex

physiologic signals. Circulation, 101(23):e215–e220.

https://doi.org/10.1161/01.cir.101.23.e215.

Guliyev, H. and Mustafayev, E. (2022). Predicting the

changes in the wti crude oil price dynamics using ma-

chine learning models. Resources Policy, 77:102664.

https://doi.org/10.1016/j.resourpol.2022.102664.

He, Q. and Huang, J. (2020). A method for analyz-

ing correlation between multiscale and multivari-

ate systems—multiscale multidimensional cross re-

currence quantiﬁcation (mmdcrqa). Chaos, Solitons

& Fractals, 139:110066. https://doi.org/10.1016/j.

chaos.2020.110066.

Ji, Q., Bouri, E., Roubaud, D., and Kristoufek, L. (2019).

Information interdependence among energy, cryp-

tocurrency and major commodity markets. Energy

Economics, 81:1042–1055. https://doi.org/10.1016/j.

eneco.2019.06.005.

Kantz, H. and Schreiber, T. (2003). Nonlinear Time Se-

ries Analysis. Cambridge University Press, 2 edition.

https://doi.org/10.1017/CBO9780511755798.

Kilian, L. (2009). Not all oil price shocks are alike: Dis-

entangling demand and supply shocks in the crude

oil market. American Economic Review, 99(3):1053–

69. https://www.aeaweb.org/articles?id=10.1257/aer.

99.3.1053.

Kirchner, M., Schubert, P., Liebherr, M., and Haas, C. T.

(2014). Detrended ﬂuctuation analysis and adap-

tive fractal analysis of stride time data in parkinson’s

disease: Stitching together short gait trials. PLOS

ONE, 9(1):1–6. https://doi.org/10.1371/journal.pone.

0085787.

Kiv, A. E., Soloviev, V. N., Semerikov, S. O., Danylchuk,

H. B., Kibalnyk, L. O., Matviychuk, A. V., and

Striuk, A. M. (2021). Machine learning for pre-

diction of emergent economy dynamics III. In Kiv,

A. E., Soloviev, V. N., and Semerikov, S. O., edi-

tors, Proceedings of the Selected and Revised Papers

of 9th International Conference on Monitoring, Mod-

eling & Management of Emergent Economy (M3E2-

MLPEED 2021), Odessa, Ukraine, May 26-28, 2021,

volume 3048 of CEUR Workshop Proceedings, pages

i–xxxi. CEUR-WS.org. https://ceur-ws.org/Vol-3048/

paper00.pdf.

Kmytiuk, T. and Majore, G. (2021). Time series forecasting

of agricultural product prices using Elman and Jordan

recurrent neural networks. Neiro-Nechitki Tekhnolohii

Modelyuvannya v Ekonomitsi, 2021(10):67–85. https:

//doi.org/10.33111/nfmte.2021.067.

Kobets, V. and Novak, O. (2021). EU countries clustering

for the state of food security using machine learning

techniques. Neiro-Nechitki Tekhnolohii Modelyuvan-

nya v Ekonomitsi, 2021(10):86–118. https://doi.org/

10.33111/nfmte.2021.086.

Kucherova, H., Honcharenko, Y., Ocheretin, D., and Bil-

ska, O. (2021). Fuzzy logic model of usability of

websites of higher education institutions in the con-

text of digitalization of educational services. Neiro-

Nechitki Tekhnolohii Modelyuvannya v Ekonomitsi,

2021(10):119–135. https://doi.org/10.33111/nfmte.

2021.119.

Li, J., Wu, Q., Tian, Y., and Fan, L. (2021). Monthly henry

hub natural gas spot prices forecasting using varia-

tional mode decomposition and deep belief network.

Energy, 227:120478. https://doi.org/10.1016/j.energy.

2021.120478.

Lukianenko, D. and Strelchenko, I. (2021). Neuromodel-

ing of features of crisis contagion on ﬁnancial mar-

kets between countries with different levels of eco-

nomic development. Neiro-Nechitki Tekhnolohii Mod-

M3E2 2022 - International Conference on Monitoring, Modeling Management of Emergent Economy

132

elyuvannya v Ekonomitsi, 2021(10):136–163. https:

//doi.org/10.33111/nfmte.2021.136.

Marwan, N., Carmen Romano, M., Thiel, M., and Kurths, J.

(2007). Recurrence plots for the analysis of complex

systems. Physics Reports, 438(5):237–329. https://

doi.org/10.1016/j.physrep.2006.11.001.

Marwan, N. and Webber, C. L. (2015). Mathematical

and computational foundations of recurrence quan-

tiﬁcations. In Webber, C. L. and Marwan, N., ed-

itors, Recurrence Quantiﬁcation Analysis: Theory

and Best Practices, pages 3–43. Springer Interna-

tional Publishing, Cham. https://doi.org/10.1007/

978-3-319-07155-8 1.

Marwan, N., Wessel, N., Meyerfeldt, U., Schirdewan, A.,

and Kurths, J. (2002). Recurrence-plot-based mea-

sures of complexity and their application to heart-

rate-variability data. Phys. Rev. E, 66:026702. https:

//doi.org/10.1103/physreve.66.026702.

Miroshnychenko, I., Kravchenko, T., and Drobyna, Y.

(2021). Forecasting electricity generation from re-

newable sources in developing countries (on the ex-

ample of Ukraine). Neiro-Nechitki Tekhnolohii Mod-

elyuvannya v Ekonomitsi, 2021(10):164–198. https:

//doi.org/10.33111/nfmte.2021.164.

Ott, E., Sauer, T., and Yorke, J. (1994). Coping with Chaos.

Wiley Series in Nonlinear Science. Wiley.

Poincar

e, H. (2017). The Three-Body Problem and the

Equations of Dynamics: Poincar

e’s Foundational

Work on Dynamical Systems Theory. Astrophysics

and Space Science Library. Springer, Cham, 1 edition.

https://doi.org/10.1007/978-3-319-52899-1.

Romano, M. C., Thiel, M., Kurths, J., and von Bloh,

W. (2004). Multivariate recurrence plots. Physics

Letters A, 330(3):214–223. https://doi.org/10.1016/j.

physleta.2004.07.066.

Sari, R., Soytas, U., and Hacihasanoglu, E. (2011). Do

global risk perceptions inﬂuence world oil prices? En-

ergy Economics, 33(3):515–524. https://doi.org/10.

1016/j.eneco.2010.12.006.

Shahzad, U., Jena, S. K., Tiwari, A. K., Do

gan, B., and

Magazzino, C. (2022). Time-frequency analysis be-

tween bloomberg commodity index (bcom) and wti

crude oil prices. Resources Policy, 78:102823. https:

//doi.org/10.1016/j.resourpol.2022.102823.

Soloviev, V. N., Bielinskyi, A. O., and Kharadzjan, N. A.

(2020). Coverage of the coronavirus pandemic

through entropy measures. CEUR Workshop Pro-

ceedings, 2832:24 – 42. https://ceur-ws.org/Vol-2832/

paper02.pdf.

Takens, F. (1981). Detecting strange attractors in turbu-

lence. In Rand, D. and Young, L.-S., editors, Dynam-

ical Systems and Turbulence, Warwick 1980, pages

366–381, Berlin, Heidelberg. Springer Berlin Heidel-

berg. https://doi.org/10.1007/BFb0091924.

U.S. Energy Information Administration (1986). Spot

prices for crude oil and petroleum products. https:

//www.eia.gov/dnav/pet/pet pri spt s1 d.htm.

U.S. Energy Information Administration (1997). Natural

gas spot and futures prices (nymex). https://www.eia.

gov/dnav/ng/NG PRI FUT S1 W.htm.

Webber, C. and Zbilut, J. (2005). Recurrence quantiﬁcation

analysis of nonlinear dynamical systems. In Riley,

M. A. and Orden, G. C. V., editors, Tutorials in Con-

temporary Nonlinear Methods for the Behavioral Sci-

ences, chapter 2. National Science Foundation (NSF).

Webber, C. L. and Zbilut, J. P. (1994). Dynamical assess-

ment of physiological systems and states using re-

currence plot strategies. Journal of Applied Physi-

ology, 76(2):965–973. https://doi.org/10.1152/jappl.

1994.76.2.965.

Wu, G. and Zhang, Y.-J. (2014). Does china factor mat-

ter? an econometric analysis of international crude oil

prices. Energy Policy, 72:78–86. https://doi.org/10.

1016/j.enpol.2014.04.026.

Yin, T. and Wang, Y. (2022). Predicting the price of wti

crude oil futures using artiﬁcial intelligence model

with chaos. Fuel, 316:122523. https://doi.org/10.

1016/j.fuel.2021.122523.

Zbilut, J. P. and Webber, C. L. (1992). Embeddings and

delays as derived from quantiﬁcation of recurrence

plots. Physics Letters A, 171(3):199–203. https:

//doi.org/10.1016/0375-9601(92)90426-M.

Zhang, Y., He, M., Wen, D., and Wang, Y. (2023). Fore-

casting crude oil price returns: Can nonlinearity help?

Energy, 262:125589. https://doi.org/10.1016/j.energy.

2022.125589.

Zhang, Y.-J. and Wang, J. (2015). Exploring the wti crude

oil price bubble process using the markov regime

switching model. Physica A: Statistical Mechanics

and its Applications, 421:377–387. https://doi.org/10.

1016/j.physa.2014.11.051.

Zhang, Y.-J. and Wu, Y.-B. (2019). The time-varying

spillover effect between wti crude oil futures returns

and hedge funds. International Review of Economics

& Finance, 61:156–169. https://doi.org/10.1016/j.

iref.2019.02.006.

Zou, Y., Yu, L., and He, K. (2023). Forecasting crude oil

risk: A multiscale bidirectional generative adversarial

network based approach. Expert Systems with Appli-

cations, 212:118743. https://doi.org/10.1016/j.eswa.

2022.118743.

Recurrence Measures of Complexity in Energy Market Dynamics

133