Nonlinear Analysis of the Dynamics of Sales of Electric Automobiles in

the Chinese Market

Serhii Kurkula

1 a

, Nataliia Maksyshko

1 b

, Dmytro Ocheretin

1 c

and Serhii Cheverda

1 d

Zaporizhzhia National University, 66 Zhukovskogo Str., Zaporizhzhia, 69600, Ukraine

Keywords:

Electric Car Market, Dynamics of Sales Volumes, Time Series, Normalized Hurst Range Method, Phase

Analysis, Method of Recurrence Plots.

Abstract:

The article is devoted to the research of the dynamics of sales of electric automobiles in the Chinese market

using non-linear analysis tools. The relevance of the work is due, on the one hand, to the sharp development

of the electric vehicle segment in the global automobile market, in which China’s market share was 45% of

sales in 2020. On the other hand, the use of different approaches to forecasting the sales of electric vehicles

leads to unsatisfactory results. The article analyzes the nature of the properties of the dynamics of sales of

electric automobiles in the Chinese market using non-linear analysis tools. The initial data for the analysis

is the time series of monthly sales volumes from January 2016 to June 2022 of the leading manufacturers of

electric vehicles. For the research, three methods of nonlinear dynamics were used: the Hurst normalized

range method, phase analysis, and the recurrence plots method. The calculations were carried out in the R

software environment. As a result of applying the Hurst normalized range method, the fractal nature of time

series, the property of trend stability, and the presence of long-term memory were revealed. The use of phase

analysis made it possible to reveal cyclicity in dynamics, to evaluate the characteristics of attractors (quasi-

cycles) and their features for each agent on the market. The construction of recurrence plots, their topological

and quantitative analysis conﬁrmed the deterministic nature of the dynamics. The results of the research can

be used to select relevant forecasting methods and their parameters.

1 INTRODUCTION

The policy of developed countries regarding the trans-

formation of the fuel and energy market indicates

that transport (one of the main consumers of energy)

has begun to move rapidly towards reducing the con-

sumption of fossil fuels. The most important indica-

tor of change in this process has been an increase in

the production of electric vehicles, which is increas-

ing amid high expectations of pent-up demand.

The main reasons that favor the increasing popu-

larity of electric vehicles in the world can be divided

into three groups. The ﬁrst group includes legislative

factors: sales are stimulated in different countries by

various methods. The most popular of them: subsi-

dies or discounts when buying the automobile free

parking spaces (as opposed to paid spaces for cars

with internal combustion engines), free charging of

https://orcid.org/0000-0003-0717-0291

https://orcid.org/0000-0002-0473-7195

https://orcid.org/0000-0001-6705-6381

https://orcid.org/0000-0003-2161-037X

cars in specially designated places. The second group

of factors is concern for the environment: govern-

ments encourage citizens to buy automobiles that do

not produce carbon dioxide during operation, and so-

cially responsible citizens tend to buy such automo-

biles. The third group of factors includes energy se-

curity: the price of oil and gasoline depends on the

global market. The number of countries that produce

and export them is small; a large number of countries

may suffer as a result of unpredictable phenomena in

the oil market or supply disruptions. In contrast, elec-

tricity generation is more diversiﬁed in terms of its

generation capacity.

Competition in the ﬁeld of electric transport gives

rise to new technologies, enterprises, business mod-

els, and, ﬁnally, new markets. Today, at the stage of

formation of the global market for electric vehicles,

the total volume of investments in the production of

electric vehicles and the creation of an infrastructure

for it is rapidly increasing all over the world. The se-

quence of decisions that will be made during this pe-

riod is laid the foundation for the future architecture

Kurkula, S., Maksyshko, N., Ocheretin, D. and Cheverda, S.

Nonlinear Analysis of the Dynamics of Sales of Electric Automobiles in the Chinese Market.

DOI: 10.5220/0011932500003432

In Proceedings of 10th International Conference on Monitoring, Modeling Management of Emergent Economy (M3E2 2022), pages 185-195

ISBN: 978-989-758-640-8; ISSN: 2975-9234

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

185

of the global market: from educational and produc-

tion standards, the organization of urban infrastruc-

ture to new business models and market regulation

conditions.

The automotive market is an object that is de-

veloping quite actively, and the importance of the

transport business for the global economy and the

economies of individual countries is constantly grow-

ing. According to Bloomberg rating agency estimates

by 2040 (in less than 20 years) electric automobile

sales will account for 2/3 of the global automotive

market (McKerracher and Wagner, 2021). Therefore,

the study of the nature of the dynamics of the electric

vehicle market is of signiﬁcant scientiﬁc and practical

interest.

The global market for electric vehicles is devel-

oping, so it is necessary to determine the models for

its development. Based on the statistical analysis of

the electric vehicle market, it can be revealed that

China is today the main player in electric vehicle

sales and market penetration. In particular, in 2013,

China achieved phenomenal growth in vehicle sales

speciﬁcally in the segment of battery electric vehicles

(BEV) and hybrid vehicles (PHEV). For six consecu-

tive years from 2012 to 2017, the annual growth rate

of the market volume is at least 45 per cent (Jin and

He, 2019). And in 2020, according to the Interna-

tional Energy Agency (Paoli et al., 2022), the Chinese

market accounted for almost 45 per cent of global

sales. Thus, the study of the development dynamics

of the electric vehicle market in China is necessary

as a basis for further research in the markets of other

countries.

2 RELATED WORKS

Zhang et al. (Zhang et al., 2017) presents Singular

Spectral Analysis (SSA) as a one-dimensional time

series model and Vector Autoregressive Model (VAR)

as a multivariate model that displays the sales volume

of automobiles with electric and hybrid engines in

China. Empirical calculation results show that SSA

satisfactorily indicates the market trend. The VAR

model, which contains exogenous parameters related

to the market, according to the authors, can signiﬁ-

cantly improve the accuracy of the results when used

to build forecasts.

The price of charging the automobile is important

for owners during its operation. Zhang et al. (Zhang

et al., 2018) proposes a pricing model for public-

private partnership projects of automobile charging

infrastructure in China, which is based on the use of

the system dynamics (SD) method. In paper (Dhakal

and Min, 2021), based on predictive data on the num-

ber of automobiles, a simulation of the spread of elec-

tric vehicles is presented using the example of France

and Germany.

Articles (Zhu and Du, 2018; Ensslen et al., 2019)

are devoted to predicting the dynamics of the distri-

bution of electric vehicles within the European Union.

For this, logistic models are used, in particular, the lo-

gistic and Bass diffusion model (Zhu and Du, 2018),

which is used in (Ensslen et al., 2019) to predict the

number of cars used in Beijing.

An overview of the methods that are used to pre-

dict the penetration of electric vehicles into the pas-

senger vehicle market is presented in (Jochem et al.,

2018). Two groups of models are distinguished:

econometric models with disaggregated data (such

as discrete choice) and simulation models based on

agents. Some methods have been found to have a

stronger methodological basis, while others require

complex datasets or can be more ﬂexibly combined

with other methods. Despite the absence of a domi-

nant method, Jochem et al. (Jochem et al., 2018) jus-

tify the advantage of hybrid approaches and managed

data that take into account micro and macro aspects,

which allows obtaining more accurate results.

In (Rietmann et al., 2020), using a logistic growth

model, a long-term forecast of stocks of electric ve-

hicles in 26 countries on ﬁve continents is provided.

The ﬁndings show that in 2032, 30 per cent of the

global vehicle ﬂeet will be electric vehicles. However,

the results obtained by the authors also demonstrate

signiﬁcant differences between countries, which may

be due to differences in government support.

Electric vehicle sales are inﬂuenced by many fac-

tors (especially in China) and there are not many sales

forecasting models available. In particular, Wan et al.

(Wan et al., 2021) used decomposition and integration

procedures based on the TEI@I methodology. So, in

the forecasting model, principal component regres-

sion analysis (PCR) was used to work with a linear

relationship. Then a BP neural network and a sup-

port vector machine (SVM) were used to work with

non-linear dependence. In the last step, all models

were integrated together. The Granger causality test

and the degree of gray correlation are used to quan-

tify the factors that affect EV sales through consumer

network data analysis. On the example of two auto-

mobile models, it was found that the PCR-BP models

and the PCR-SVM models have better predictive per-

formance than one model. According to the authors,

this approach is more suitable for making decisions

about forecasting markets for similar products.

Dingab and Li (Dingab and Li, 2021) proposes to

use the modiﬁed gray model as a promising tool for

M3E2 2022 - International Conference on Monitoring, Modeling Management of Emergent Economy

186

predicting sales of electric vehicles.

The use of different approaches to forecasting the

sales of electric vehicles indicates that the quality of

the results is not satisfactory. A common feature of

almost all almost all forecasting methods that are pre-

sented in the review is that they provide for the sub-

ordination of volume dynamics to a linear paradigm.

However, today it is a recognized fact that the dy-

namics of most markets does not obey the law of nor-

mal distribution, and therefore their modeling by tra-

ditional methods leads to signiﬁcantly unsatisfactory

results. The linear paradigm has been replaced by

a nonlinear paradigm (Peters, 1994), which is based

on the recognition of the fractal nature of the market

and is actively developed for analysis and modeling,

including in (Perepelitsa and Maksyshko, 2012) and

(Maksyshko et al., 2020). This statement is based on

such features of time series (TS) of indicators charac-

terizing ﬁnancial markets: the lack of independence

of levels, the presence of long-term memory, and oth-

ers (Derbentsev et al., 2019; Kmytiuk and Majore,

2021). The use of statistical methods for their re-

search and further forecasting (as the ultimate goal

of the analysis) turns out to be inadequate. Therefore,

there is a need to use new, different from statistical,

methods of analysis.

The purpose of this research is to diagnose the na-

ture and properties of the dynamics of sales of elec-

tric vehicles in the Chinese market using non-linear

analysis tools for further use in choosing a relevant

forecasting method.

3 MATERIALS

The object of analysis of this research is the sales vol-

umes of cars, which are contained in the reports of

the China Association of Automobile Manufacturers

(CAAM, 2022) and published by the online publica-

tion “Chinese Cars” (Chi, 2022).

An analysis of the structure of the electric vehicle

market in China revealed that in the period from Jan-

uary 2016 to June 2022, 37.5 per cent of the electric

vehicle market belongs to ﬁve automakers, namely:

BYD, Mercedes-Benz, Roewe, Geely, Chery. Most

of these companies are representatives of the Chinese

automotive industry, which is due, in particular, to

state support for manufacturers of this type of trans-

port (Qian et al., 2019). Let’s characterize these com-

panies in more detail.

BYD is the only automobile manufacturer that has

mastered batteries, electric motors, and vehicle con-

trol technologies. BYD was founded in 1995 as a pio-

neer in the battery technology industry. Its stated goal

is to change the world by creating a complete zero-

emission ecosystem that runs on clean energy and re-

duces dependence on oil. BYD’s innovative products

are leaders in many sectors, including battery electric

vehicles, buses, medium and heavy duty trucks and

forklifts. In 2003, the company entered the automo-

tive business, and in 2005, the ﬁrst BYD brand au-

tomobile went on sale (BYD North America, 2022).

The company holds 16 per cent of the electric vehicle

market in China.

Mercedes-Benz is a world-famous automaker that

in recent years has been investing more resources in

its advanced research and design capabilities in China

as the new center of gravity for the auto industry (Shi-

rouzu, 2021). The company holds 9 per cent of the

electric vehicle market in China.

Roewe is owned by the Shanghai Automotive In-

dustry Corporation (SAIC) and is one of the few Chi-

nese luxury brands that actually manufacture mod-

ernized copies of older Rover models (Roewe, 2022).

The company holds 6 per cent of the electric vehicle

market in China.

Geely Auto Group is a leading automobile man-

ufacturer that was founded in 1997 as a subsidiary

of Zhejiang Geely Holding Group. For the past ﬁve

years, the company has maintained its position as the

best-selling Chinese brand (Geely, 2022). The com-

pany holds 4 per cent of the electric vehicle market in

China.

Chery was founded in 1997 under the patronage

of state-owned companies and holdings, as well as

smaller investors. In 2006, Ukraine was one of the

ﬁrst countries to introduce the assembly of automo-

biles of this brand outside China. In 2012, in pursuit

of a globalization strategy, Chery and Jaguar Land

Rover Motors jointly invested in the establishment of

Chery Jaguar Land Rover Motors Co., Ltd., which

is China’s ﬁrst Sino-British automobile joint venture

(Chery, 2022). The company holds 3 per cent of the

electric vehicle market in China.

Thus, we will analyze the nature of the dynamics

of the behavior of agents of the electric car market

in China on the basis of time series (TS) of monthly

sales volumes of automobile companies (manufactur-

ers) BYD, Chery, Geely, Mercedes-Benz and Roewe.

These automakers were selected based on the fact that

they are among the top 9 most popular electric mobile

brands in terms of sales for the period from January

2016 to June 2022 (Chi, 2022) and have sufﬁcient

data for analysis for this period. When analyzing the

dynamics, we will identify the sales volumes of elec-

tric vehicles with the volume of demand for them.

Nonlinear Analysis of the Dynamics of Sales of Electric Automobiles in the Chinese Market

187

4 METHODOLOGY

To identify the nonlinear (chaotic) behavior of eco-

nomic data, various methods of time series analysis

are used (Faggini, 2014). In particular, tests for deter-

ministic chaos have been developed for this purpose,

which allow one to study the main features of chaotic

phenomena: nonlinearity, a fractal attractor, and sen-

sitivity to initial conditions.

In this research, to diagnose the nature and proper-

ties of the dynamics of sales of electric vehicles in the

Chinese market, we will use three tools for analyzing

nonlinear dynamics, namely: traditional R/S-analysis

– the Hurst normalized range method, phase analysis

and recurrence analysis.

For the purpose of a general assessment of the

fractal properties of time series, we use the Hurst nor-

malized range algorithm for analysis (Peters, 1994).

It is known that if the system gives the Hurst statistics

for a sufﬁciently long period, then this indicates the

result of interrelated events. As is known, a measure

of the mutual connection of events is the correlation

coefﬁcient. The inﬂuence of the present on the future

can be represented by the following correlation:

C = 2

2H−1

− 1, (1)

where C – measure of correlation,

H – Hurst exponent.

The range of the Hurst exponent (H) is the interval

[0; 1]. The indicator value allows classifying all time

series into three groups:

1) H = 0,5;

2) 0 ≤ H < 0,5;

3) 0,5 < H ≤ 1.

The value H = 0,5 indicates a random time series:

the events are random and not correlated (C = 0 ac-

cording to (1)). The present does not affect the future.

If H ∈ (0,5; 1], then the considered time series is

persistent or trend-resistant and is characterized by

the effect of long-term memory. Events are the more

correlated, the closer the value is to 1 (correspond-

ingly, C also approaches 1 or 100 per cent correlation

according to (1)).

The value H ∈ [0; 0,5) corresponds to antipersis-

tent or ergodic time series. In a loose deﬁnition, an-

tipersistence means reverting to the mean or, in other

terminology, reversing (alternating positive and nega-

tive increments) more often than in a random process.

Thus, the Hurst exponent (H) is decisive in diagnos-

ing the nature of the development of a system or pro-

cess.

To check the validity of the results on the presence

of long-term memory based on the value of the Hurst

exponent (H), we will use a test for random mixing of

the levels of the time series.

Phase analysis is one of the effective methods for

obtaining information about the nature of the dynam-

ics of the system under consideration (Perepelitsa and

Maksyshko, 2012). To the time series (X = (x(t), t =

1, n)) that characterizes the dynamics of demand in

the market of electric vehicles, we will apply such

a presentation method, which can be used to return

from the observed state of the system to its previous

state. This “return” is implemented by the method of

time delays and is produced by constructing a phase

trajectory (phase portrait) of dimension ρ:

(X) =



(x(t), x(t + 1), ..., x(t + ρ − 1)), t = 1, n



(2)

which is a set of points called “ρ-history”. For any

time series, the list of all its M-histories determines

the corresponding set of points in the pseudo-phase

(or lag) space. In this case, when using the terms

“phase portrait” or “phase trajectory” it means that

the neighboring points of the set (2) are connected by

segments of a straight or curved line for clarity.

Thus, the graphic representation of the system on

the phase plane (or in the phase space), along the co-

ordinate axes of which the values of the variables of

the system (TS levels) are plotted, is called the phase

portrait of the system. The behavior of phase points in

time, which is described by the phase trajectory and

the set of such phase trajectories for any initial con-

ditions form a phase portrait. A phase portrait is a

mathematical method for representing the behavior of

a system and a geometric representation of individual

movements, and also displays the state of equilibrium,

periodic and chaotic movement of a phase point, the

logic of the system’s behavior and its dependence on

external and internal inﬂuences.

Objective information about the nature of the be-

havior of a dynamic process can be obtained by ob-

serving the time series X, based on the Takens theo-

rem (Takens, 1981): if the system generating the time

series is m-dimensional and inequality ρ ≥ 2m + 1 is

satisﬁed, then in the general case, phase trajectories

reﬂect the dynamics of the system under study. There

is a dipheomorphism between the phase trajectories

and the true data generated by the system. This result

allows one to draw conclusions about the behavior of

the system based on observational data, and, more-

over, to obtain information to predict this behavior.

Analysis of the phase portrait makes it possible to

determine the type and characteristic features of the

dynamics of a particular system. To deepen such an

analysis, Eckmann et al. (Eckmann et al., 1987) pro-

posed in 1987 a new diagnostic tool, the recurrence

plot.

M3E2 2022 - International Conference on Monitoring, Modeling Management of Emergent Economy

188

The recurrence plot is a projection of the ρ-

dimensional pseudo-phase space onto the surface. Let

point x

-correspond to the point of the phase trajec-

tory (2), which describes a dynamical system in m-

dimensional space at times t = i, for i = 1, ..., n. Then

the recurrence plot is an array of points, where non-

zero elements with coordinates (i, j) correspond to the

case when the distance between x

and x

is less then

γ:

i, j

= θ



γ −



− x





, x

∈ R

, i, j = 1, ..., n,

(3)

where γ – size of the point x



− x



– distance between points,

θ(·) – Heaviside function.

For the practical reconstruction of the attractor for

a given time series, it is necessary to determine the

values of the parameters: ρ – the embedding dimen-

sion of the time series, d – the time lag of the time

series (Rotshtein and Katelnikov, 2014).

To determine the time lag of the time series, the

function (S) – the adjusted mutual information func-

tion (AMI) was used for the time series under re-

search, which takes into account non-linear correla-

tions (Hegger and Kantz, 1999):

S = −

∑

i j

(Φ

(X)) · ln

i j

(Φ

(X))

, (4)

where p

i j

(Φ

(X)) – joint probability that an obser-

vation falls into the i-th interval and the observation

time d later falls into the j-th;

– the probability to ﬁnd a time series value in

the i-th interval;

– the probability to ﬁnd a time series value in

the j-th interval.

To calculate the optimal time lag of the time se-

ries (d), we will use the tseriesChaos library of the R

environment.

To determine the embedding dimension of the

time series, the false nearest neighbor method given

in (Kennel et al., 1992) was used. This method is

based on the assumption that at the next iterations the

neighboring points of the phase trajectory remain suf-

ﬁciently close. But if the nearest points move away

from one another, then they are called false nearest

neighbors. The task of the method is to choose such a

dimension of the time series (ρ), in which the propor-

tion of points that have false neighbors is minimized.

Based on the calculated parameters of the embed-

ding dimension and time lag, recurrence diagrams

of time series are built. The analysis of the statisti-

cal characteristics of the recurrence diagram makes

it possible to determine the measures of complexity

of the structure of the recurrence diagrams (Wallot,

2017):

• percent recurrence (%REC),

• percent determinism (%DET),

• average (ADL) and maximum (MDL) diagonal

lines lengths of the recurrence diagram.

The construction and determination of the statis-

tical characteristics of recurrence diagrams will be

implemented in the R environment using the tseri-

esChaos and nonlinearTseries libraries.

Based on the analysis of the statistical character-

istics of the recurrence diagram, it is possible to de-

termine the presence of homogeneous processes with

independent random values; processes with slowly

changing parameters; periodic and oscillating pro-

cesses that correspond to nonlinear systems. Thus, the

analysis of the recurrence surface makes it possible to

evaluate the characteristics of a non-linear object on

relatively short time series, which makes it possible

to make prompt decisions regarding the control of the

object.

5 RESULTS

The analysis of the behavior of Chinese electric auto-

mobiles market agents was carried out on the basis of

monthly sales data from January 2016 to June 2022

of ﬁve automobile companies (BYD, Chery, Geely,

Mercedes-Benz, Roewe) (ﬁgure 1).

Time series of sales of electric vehicles in the Chi-

nese market denoted by X

= (x(t), t = 1, n), k = 1, 5

where n is the length of the time series, k is the index

assigned to the corresponding manufacturer (in or-

der of priority): BYD, Chery, Geely, Mercedes-Benz,

Roewe.

Table 1 shows the results of the Hurst exponent

calculations (H) for these time series and the value of

the Hurst exponent (H

mixing

) obtained after applying

the mixing test.

Table 1: The value of the Hurst exponent for the series of

dynamics of sales volumes of electric automobiles of man-

ufacturing companies for the period from January 2016 to

June 2022.

Manufacturer (TS) H H

mixing

BYD (X

) 0,84655 0,56659

Chery (X

) 0,82696 0,58156

Geely (X

) 0,81668 0,57214

Mercedes-Benz (X

) 0,86762 0,54563

Roewe (X

) 0,87330 0,59666

According to table 1, we can conclude that all time

series of sales volumes (demand for electric automo-

biles) of all manufacturers have signs of persistence,

Nonlinear Analysis of the Dynamics of Sales of Electric Automobiles in the Chinese Market

189

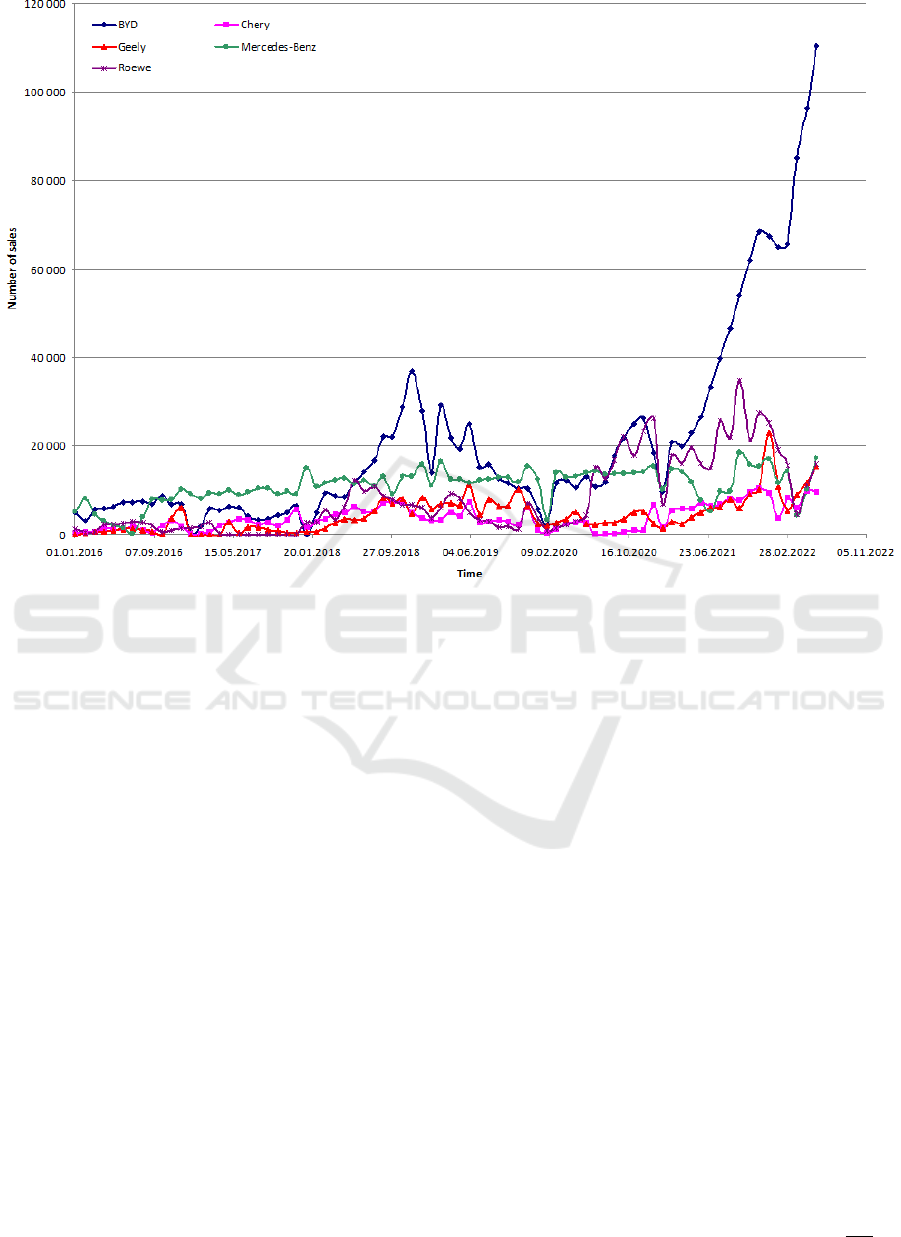
Figure 1: Number of sales of electric vehicles in the Chinese market from January 2016 to June 2022.

that is, they have a long-term memory. This is evi-

denced by the following:

a) the value of the Hurst exponents for all time se-

ries are in the interval H ∈ [0, 817; 0,873], which

corresponds to the area of black noise;

b) the results of the mixing test

mixing

∈ [0, 546; 0, 597]) conﬁrm the signif-

icance of the time series structure: its violations

lead to the complete destruction of the trace of

long-term memory.

The presence of signiﬁcant Hurst statistics for the

time series of sales of electric vehicles is explained by

the following reasoning.

The change in the volume of demand for electric

vehicles is based on an increase in the overall demand

for vehicles, the perception of buyers of a certain ex-

pediency to follow the trend in energy security (in-

creased charging stations), legislative incentives and

social responsibility (concern for the environment).

The demand for electric vehicles is partly determined

by fundamental information such as the state of the

energy market, public discussion of environmental is-

sues, current economic circumstances, expectations,

and so on. This information is often useful in mak-

ing decisions when purchasing a type of vehicle. Of

great importance in this belongs to the marketing ac-

tivities of manufacturing companies, the volume and

quality of their offers on the market. Another impor-

tant component of demand volumes is the extent to

which buyers are able to pay for a new and usually

more expensive product (an electric car). This “sen-

sory component” is also analyzed, and as a result, a

certain range of demand volume is formed around the

existing one. This combination of information and

thoughts results in displacement of volumes. If buy-

ers see that the trend is in line with their positive ex-

pectations for a particular electric vehicle, they start

buying like others. Yesterday’s activity has an im-

pact on today – the market remains mindful of yes-

terday’s trend. The bias will change when demand

reaches the upper limit of some actual value. At this

point, the offset will change. The interesting thing is

that the “range” of demand does not remain constant,

but changes. New information regarding a particular

electric vehicle (innovations and shortcomings) or the

market as a whole can change this range and cause a

sharp increase in sales volumes of the manufacturer

(in particular, the introduction of breakthrough inno-

vations) or a negative turn in the market situation, or

for an individual seller (in particular, in case of deﬁ-

ciencies, and so on).

Let’s proceed to the consideration of the results

of the phase analysis of time series X

, k = 1, 5 of

M3E2 2022 - International Conference on Monitoring, Modeling Management of Emergent Economy

190

sales of electric vehicles in the Chinese market. Fig-

ure 2 shows phase portraits in a two-dimensional

pseudo-phase (lag) space Φ

) =

{

(x(t), x(t + 1))

}

k = 1, 5.

A more detailed analysis of phase portraits makes

it possible to identify the following individual fea-

tures.

In the dynamics of sales of the automobile com-

pany BYD (Figure 2a)), at the beginning of the ob-

servation period for the ﬁrst 5 years (from January

2016 to February 2021), almost stable quasi-cycles

of length 7 were observed, which indicates the pres-

ence of long-term memory in them (conﬁrmed by the

value H ≈ 0,85). However, since February 2021, the

dynamics has changed dramatically in the direction

of increasing sales volumes and almost no cyclicity

when moving along the bisector of the coordinate an-

gle. This indicates an increase in the memory depth

of the time series.

The dynamics of sales of automobile companies

Chery and Gelly (Figure 2b), c)) are characterized

by shorter quasi-cycles (length 4 or 5), and there is

an increase in the amplitude of these quasi-cycles

in the ﬁnal interval of the time series (from Febru-

ary 2021 to June 2022), but no signiﬁcant movement

along the bisector of the coordinate angle is observed.

The dynamics is characterized by less trend resis-

tance, which is conﬁrmed by the values H ≈ 0,83)

and H ≈ 0,82) for the respective manufacturers.

The dynamics of sales of automobile companies

Mercedes-Benz and Roewe (Figure 2d), e)) is char-

acterized by the presence of the longest quasi-cycles

(length 9), their slow movement along the bisector of

the coordinate angle (increase in volumes) and an in-

crease in amplitude. This is evidence that the dynam-

ics of sales volumes of these manufacturers is charac-

terized by the greatest trend resistance (conﬁrmed by

the value of the Hurst exponent H ≈ 0,87) for both

companies).

Thus, the analysis of phase portraits Φ

) in a

two-dimensional pseudo-phase (lag) space makes it

possible to identify the characteristic features of the

dynamics of sales volumes of each agent in the Chi-

nese electric car market.

At the ﬁrst stage, using the tseriesChaos library

of the R environment, the values of the embedding

dimension (ρ) and the time lag (d) of the considered

time series were calculated (table 2).

At the second stage, using the tseriesChaos and

nonlinearTseries libraries in the R environment, re-

currence plots were constructed (ﬁgure 3a)-f)) and

their statistical characteristics were determined (ta-

ble 3).

The topology of the recurrence plots for electric

Table 2: The value of the embedding dimension (ρ) and

time lag (d) for the series of dynamics of sales volumes

of electric automobiles of manufacturing companies for the

period from January 2016 to June 2022.

Manufacturer (TS)

The embedding

dimension (ρ)

The time

lag (d)

BYD (X

) 5 9

Chery (X

) 4 3

Geely (X

) 4 3

Mercedes-Benz (X

) 4 1

Roewe (X

) 6 2

Table 3: Statistical characteristics of recurrence plots of

electric automobiles sales in China from January 2016 to

June 2022.

Manufacturer (TS) %REC %DET ADL MDL

BYD (X

) 2,381 100 0 42

Chery (X

) 1,429 100 0 70

Geely (X

) 1,429 100 0 70

Mercedes-Benz (X

) 1,333 100 0 75

Roewe (X

) 1,471 100 0 68

automobiles sales in China shows abrupt changes in

the dynamics of the system that generates the time se-

ries and causes white areas or bands to appear. On

the recurrence plots, there is a gradual change in the

parameters of the behavior of the agents of the auto-

mobile market, and there is also a drift of the attrac-

tor (white lower and upper corners of the diagram,

crosses). The absence of short diagonal stripes on the

recurrence plots indicates the absence of a stochas-

tic process and the non-return of the trajectory to the

same region of the phase space in different time peri-

ods.

The determinism of the behavior of companies in

the automobile market is conﬁrmed by the calculated

statistical characteristics of recurrence plots, which

are shown in table 3.

The value of the %REC indicator for all time se-

ries falls within the interval from 1% to 5%, which

indicates the regular behavior of the time series.

The measure of determinism (%DET) of the re-

currence plot characterizes the level of system pre-

dictability. Diagonal structures show the time during

which a segment of the trajectory comes very close to

another segment of the trajectory. For all ﬁve recur-

rence plots, the level of predictability is 100%. Note

that this measure does not determine the real deter-

minism of the process.

The average diagonal lines lengths (ADL) char-

acterizes the average time during which two sections

of the trajectory pass close to each other, and can be

considered as the average predictability time of the

system. An interesting fact is that, according to the

Nonlinear Analysis of the Dynamics of Sales of Electric Automobiles in the Chinese Market

191

(a)

(b)

(c)

(d)

(e)

Figure 2: Phase portraits in a two-dimensional pseudo-phase space Φ

) =

{

(x(t), x(t + 1))

}

, k = 1, 5 for time series

, k = 1, 5 from January 2016 to June 2022: a) BYD, b) Chery, c) Gelly, d) Mercedes-Benz, e) Roewe.

calculation results, the smallest average predictability

time of time series is 0.

The maximum diagonal lines lengths (MDL) char-

acterizes the length of the trend. The shortest trend is

in the BYD time series (42 points), and the longest is

in Mercedes-Benz (75 points).

6 CONCLUSION

The research analyzes the nature and properties of the

dynamics of sales of electric automobiles in the Chi-

nese market using non-linear analysis tools.

The initial data for the analysis is the time series

M3E2 2022 - International Conference on Monitoring, Modeling Management of Emergent Economy

192

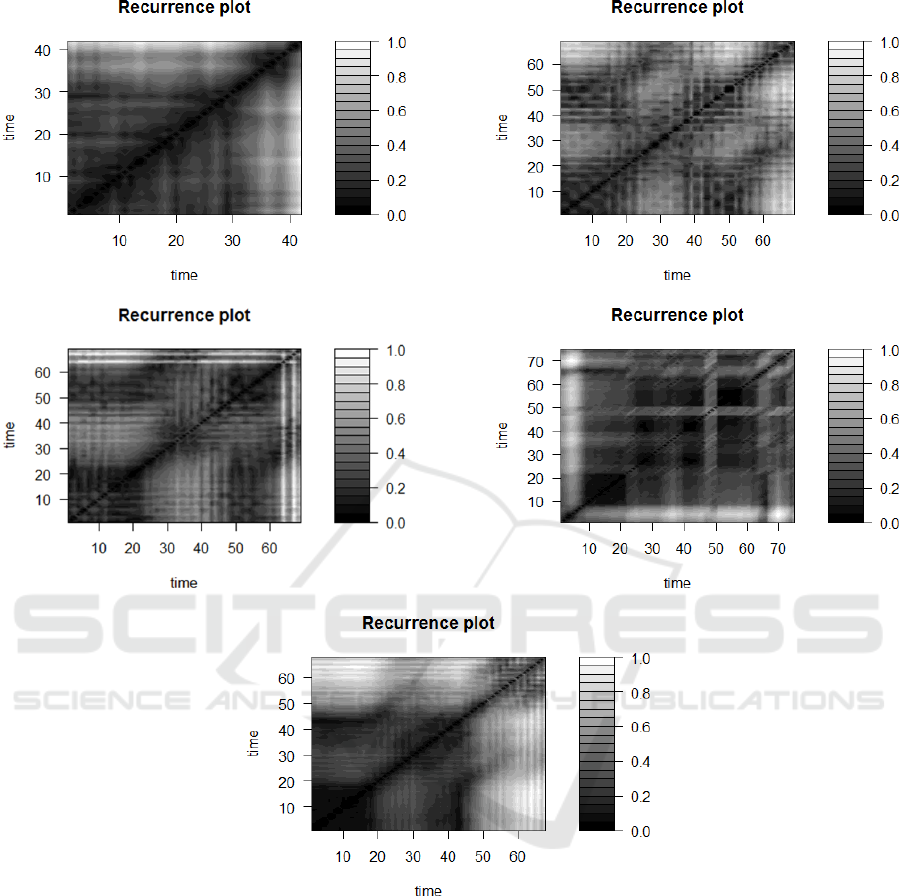
(a) (b)

(c)

(d)

(e)

Figure 3: Recurrence plots of electric automobiles sales in China from January 2016 to June 2022: a) BYD, b) Chery, c)

Gelly, d) Mercedes-Benz, e) Roewe.

of monthly sales volumes from January 2016 to June

2022 of ﬁve automobile companies: BYD, Chery,

Geely, Mercedes-Benz and Roewe.

For the research, three methods of nonlinear dy-

namics were used, namely: traditional R/S-analysis –

the method of normalized Hurst range, phase analysis

and the method of recurrence plots.

As a result of applying the Hurst normalized range

method, the property of trend stability of time series

was revealed, which indicates the presence of long-

term memory in them. Therefore, we can conclude

that the time series of sales of electric automobiles in

the Chinese market have a non-linear (fractal) nature.

It follows that the use of forecasting methods based on

the classical approach is not adequate and may lead to

an unsatisfactory forecasting result. When choosing

a method for predicting sales of electric automobiles

and their parameters, it is necessary to take into ac-

count the presence of long-term memory and, prefer-

ably, its characteristics.

However, fractal analysis, which is based on the

use of the Hurst normalized range method, allows

Nonlinear Analysis of the Dynamics of Sales of Electric Automobiles in the Chinese Market

193

only qualitative conclusions to be drawn regarding the

properties of the electric vehicle market as a whole, as

well as the properties of the trend stability of each of

the time series that were considered. The quantitative

characteristics obtained by this method are averaged

over the entire series. Therefore, to obtain differen-

tiated characteristics of the identiﬁed memory, it is

promising to research these time series using fractal

analysis methods, which are based on the sequential

R/S analysis algorithm (Perepelitsa and Maksyshko,

2012).

The use of phase analysis in a two-dimensional

phase spase made it possible to identify the pres-

ence or absence of cyclicity in dynamics at some time

intervals, to evaluate the characteristics of attractors

(quasi-cycles) and their features for each agent in the

Chinese electric automobiles market. The results ob-

tained are the basis for further research in the direc-

tion of a more detailed research of the identiﬁed fea-

tures in the dynamics due to decomposition the phase

portrait into quasicycles, determining their character-

istics, analyzing the dynamics of the overall dimen-

sions of quasicycles and their centers of attraction.

The construction of recurrence plots in ρ-

dimensional phase spase and their topological anal-

ysis made it possible to conﬁrm the presence of at-

tractor drift for all agents in the Chinese electric auto-

mobiles market. A gradual change in the parameters

of the behavior of agents was also revealed.

Quantitative analysis of recurrence plots based

on the calculation of measures of complexity of

their structure (in particular, the percent recurrence

(%REC) and the percent determinism (%DET) also

made it possible to conﬁrm the fractal (deterministic)

nature of the nature of the dynamics of sales of elec-

tric vehicles in the Chinese market. It should be noted

that at the moment the input data of the research are

characterized by a short time series. This, obviously,

affects both the possibilities, and the features, and the

results of using the applied methods. However, their

application – each separately and in combination –

provides an opportunity to gain new knowledge about

the characteristics of the dynamics in a new market

that is rapidly developing and has prospects in the

global economy – the market for electric vehicles.

The results of the research can be used to select

relevant forecasting methods and their parameters.

REFERENCES

(2022). Car Sales in China. https://www.chinamobil.ru/eng/

sales/sales.

BYD North America (2022). Bus: BYD Motors - BYD

USA. https://en.byd.com/bus/bus-byd-motors.

CAAM (2022). China Association of Automobile Manu-

facturers (CAAM). http://en.caam.org.cn/.

Chery (2022). Introduction. https://www.

cheryinternational.com/pc/aboutchery/introduction/.

Derbentsev, V., Velykoivanenko, H., and Datsenko, N.

(2019). Machine learning approach for fore-

casting cryptocurrencies time series. Neiro-

Nechitki Tekhnolohii Modelyuvannya v Ekonomitsi,

2019(8):65–93.

Dhakal, T. and Min, K.-S. (2021). Macro Study of

Global Electric Vehicle Expansion. Foresight and STI

Governance, 15(1):67–73. https://doi.org/10.17323/

2500-2597.2021.1.67.73.

Dingab, S. and Li, R. (2021). Forecasting the sales and

stock of electric vehicles using a novel self-adaptive

optimized grey model. Engineering Applications of

Artiﬁcial Intelligence, 100:104148. https://doi.org/10.

1016/j.engappai.2020.104148.

Eckmann, J.-P., Kamphorst, S. O., and Ruelle, D. (1987).

Recurrence Plots of Dynamical Systems. Euro-

physics Letters, 4(9):973–977. https://doi.org/10.

1209/0295-5075/4/9/004.

Ensslen, A., Will, C., and Jochem, P. (2019). Simulating

Electric Vehicle Diffusion and Charging Activities in

France and Germany. World Electr. Veh. J., 10(4):73.

https://doi.org/10.3390/wevj10040073.

Faggini, M. (2014). Chaotic time series analysis in

economics: Balance and perspectives. Chaos:

An Interdisciplinary Journal of Nonlinear Science,

24(4):042101. https://doi.org/10.1063/1.4903797.

Geely (2022). Overview : Geely Global. http://global.geely.

com/overview.

Hegger, R. and Kantz, H. (1999). Practical implementation

of nonlinear time series methods: The TISEAN pack-

age. Chaos: An Interdisciplinary Journal of Nonlin-

ear Science, 9(2):413–435. https://doi.org/10.1063/1.

166424.

Jin, L. and He, H. (2019). Comparison of the electric car

market in China and the United States. Working paper

2019-10, International Council on Clean Transporta-

tion. https://theicct.org/wp-content/uploads/2021/06/

ICCT

US-China EV-mkt-comp 20190523.pdf.

Jochem, P., J., J., Vilchez, G., Ensslen, A., Sch

auble, J.,

and Fichtner, W. (2018). Methods for forecasting the

market penetration of electric drivetrains in the pas-

senger car market. Transport Reviews, 38(3):322–348.

https://doi.org/10.1080/01441647.2017.1326538.

Kennel, M. B., Brown, R., and Abarbanel, H. D. I.

(1992). Determining embedding dimension for phase-

space reconstruction using a geometrical construction.

Phys. Rev. A, 45(6):3403. https://doi.org/10.1103/

PhysRevA.45.3403.

Kmytiuk, T. and Majore, G. (2021). Time series forecasting

of agricultural product prices using Elman and Jordan

recurrent neural networks. Neiro-Nechitki Tekhnolohii

Modelyuvannya v Ekonomitsi, 2021(10):67–85.

Maksyshko, N., Vasylieva, O., Kozin, I., and Perepelitsa,

V. (2020). Comparative analysis of the attractive-

M3E2 2022 - International Conference on Monitoring, Modeling Management of Emergent Economy

194

ness of investment instruments based on the analysis

of market dynamics. In Kiv, A., editor, Proceedings

of the Selected Papers of the Special Edition of In-

ternational Conference on Monitoring, Modeling &

Management of Emergent Economy (M3E2-MLPEED

2020), Odessa, Ukraine, July 13-18, 2020, volume

2713 of CEUR Workshop Proceedings, pages 219–

238. CEUR-WS.org. http://ceur-ws.org/Vol-2713/

paper18.pdf.

McKerracher, C. and Wagner, S. (2021). At Least Two-

Thirds of Global Car Sales Will Be Electric by 2040.

https://cutt.ly/vVTyg5R.

Paoli, L., Dasgupta, A., and McBain, S. (2022). Electric ve-

hicles. Tracking report, International Energy Agency.

https://www.iea.org/reports/electric-vehicles.

Perepelitsa, V. and Maksyshko, N. (2012). Analiz i

prognozirovanie evolyuczii ekonomicheskikh sistem:

problemy strukturirovaniya dannykh v usloviyakh

neopredelennosti i predprognoznogo analiza [Analy-

sis and forecasting of the economic systems evolution:

problems of data structuring in conditions of uncer-

tainty and pre-forecast analysis]. Lambert Academic

Publishing.

Peters, E. E. (1994). Fractal Market Analysis: Applying

Chaos Theory to Investment and Analysis. John Wiley

& Sons, Inc.

Qian, L., Grisol

ıa, J. M., and Soopramanien, D. (2019). The

impact of service and government-policy attributes on

consumer preferences for electric vehicles in China.

Transportation Research Part A: Policy and Practice,

122:70–84. https://doi.org/10.1016/j.tra.2019.02.008.

Rietmann, N., H

ugler, B., and Lieven, T. (2020). Forecast-

ing the trajectory of electric vehicle sales and the con-

sequences for worldwide CO2 emissions. Journal of

Cleaner Production, 261:121038. https://doi.org/10.

1016/j.jclepro.2020.121038.

Roewe (2022). Roewe Brand - SAIC Roewe ofﬁcial web-

site. https://www.roewe.com.cn/about-us.

Rotshtein, A. P. and Katelnikov, D. I. (2014). Fuzzy-chaotic

time series prediction. Optoelectronic information-

power technologies, 27(1):42–55. https://oeipt.vntu.

edu.ua/index.php/oeipt/article/view/332.

Shirouzu, N. (2021). Home from home: Mercedes-

Benz doubles down on China. https://tinyurl.com/

mvkksnn6.

Takens, F. (1981). Detecting strange attractors in turbu-

lence. Dynamical systems and turbulence, 898:366–

382. https://doi.org/10.1007/BFb0091924.

Wallot, S. (2017). Recurrence Quantiﬁcation Analysis of

Processes and Products of Discourse: A Tutorial in

R. Discourse Processes, 54(5-6):382–405. https://doi.

org/10.1080/0163853X.2017.1297921.

Wan, J. P., Xie, L. Q., and Hu, X. F. (2021). Study on the

electric vehicle sales forecast with TEI@I methodol-

ogy. International Journal of Knowledge Engineer-

ing and Data Mining, 7(1-2):1–38. https://doi.org/10.

1504/IJKEDM.2021.119836.

Zhang, L., Zhao, Z., Xin, H., Chai, J., and Wang, G. (2018).

Charge pricing model for electric vehicle charging

infrastructure public-private partnership projects in

China: A system dynamics analysis. Journal of

Cleaner Production, 199:321–333. https://doi.org/10.

1016/j.jclepro.2018.07.169.

Zhang, Y., Zhong, M., Geng, N., and Jiang, Y. (2017).

Forecasting electric vehicles sales with univariate and

multivariate time series models: The case of China.

PLOS ONE, 12(5):e0176729. https://doi.org/10.1371/

journal.pone.0176729.

Zhu, Z. and Du, H. (2018). Forecasting the Number of

Electric Vehicles: A Case of Beijing. IOP Con-

ference Series: Earth and Environmental Science,

170(4):042037. https://doi.org/10.1088/1755-1315/

170/4/042037.

Nonlinear Analysis of the Dynamics of Sales of Electric Automobiles in the Chinese Market

195